Study of the Bearing Capacity of Stiffened Tall Offshore Wind Turbine Towers during the Erection Phase
Abstract
:1. Introduction
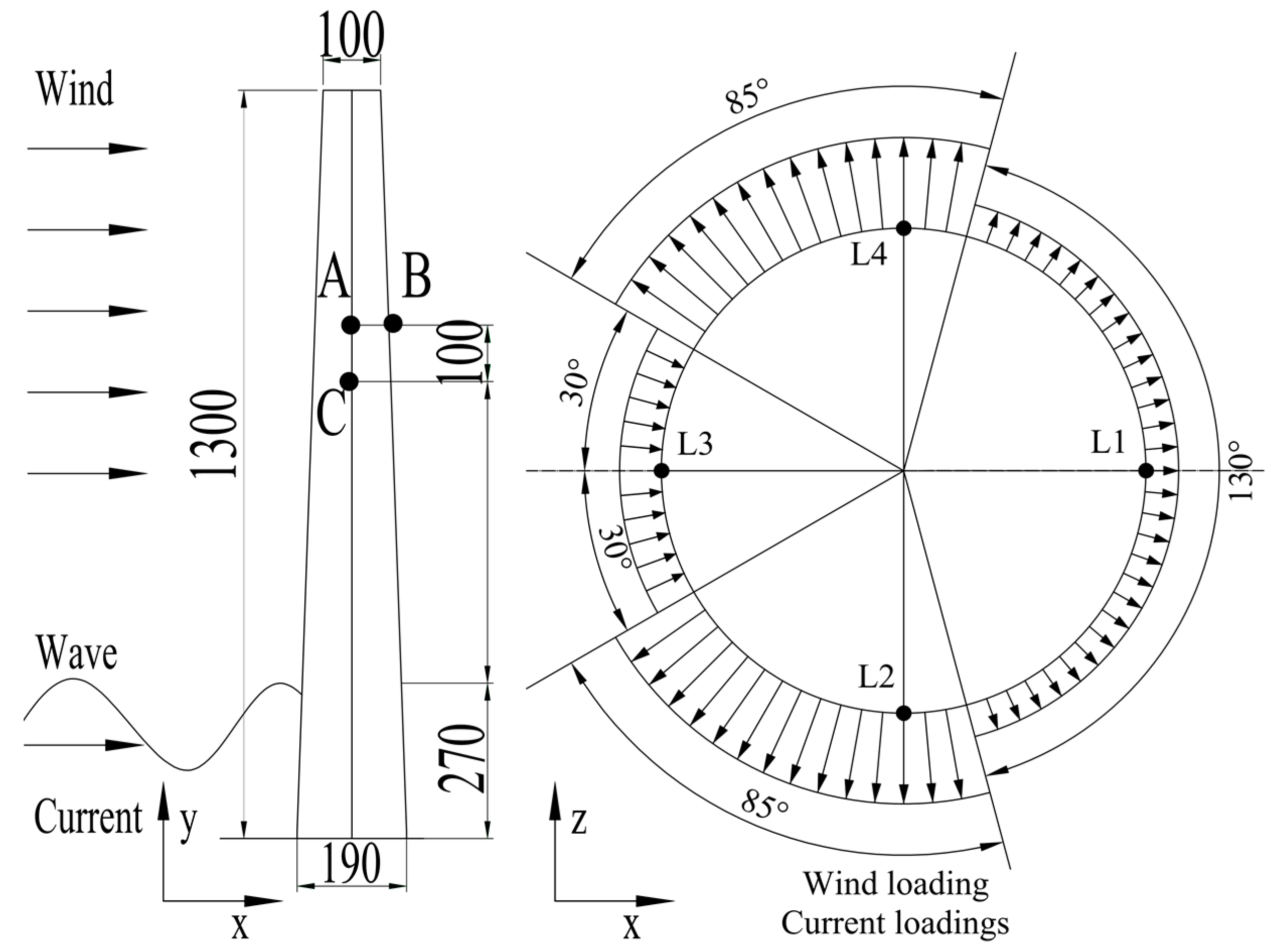
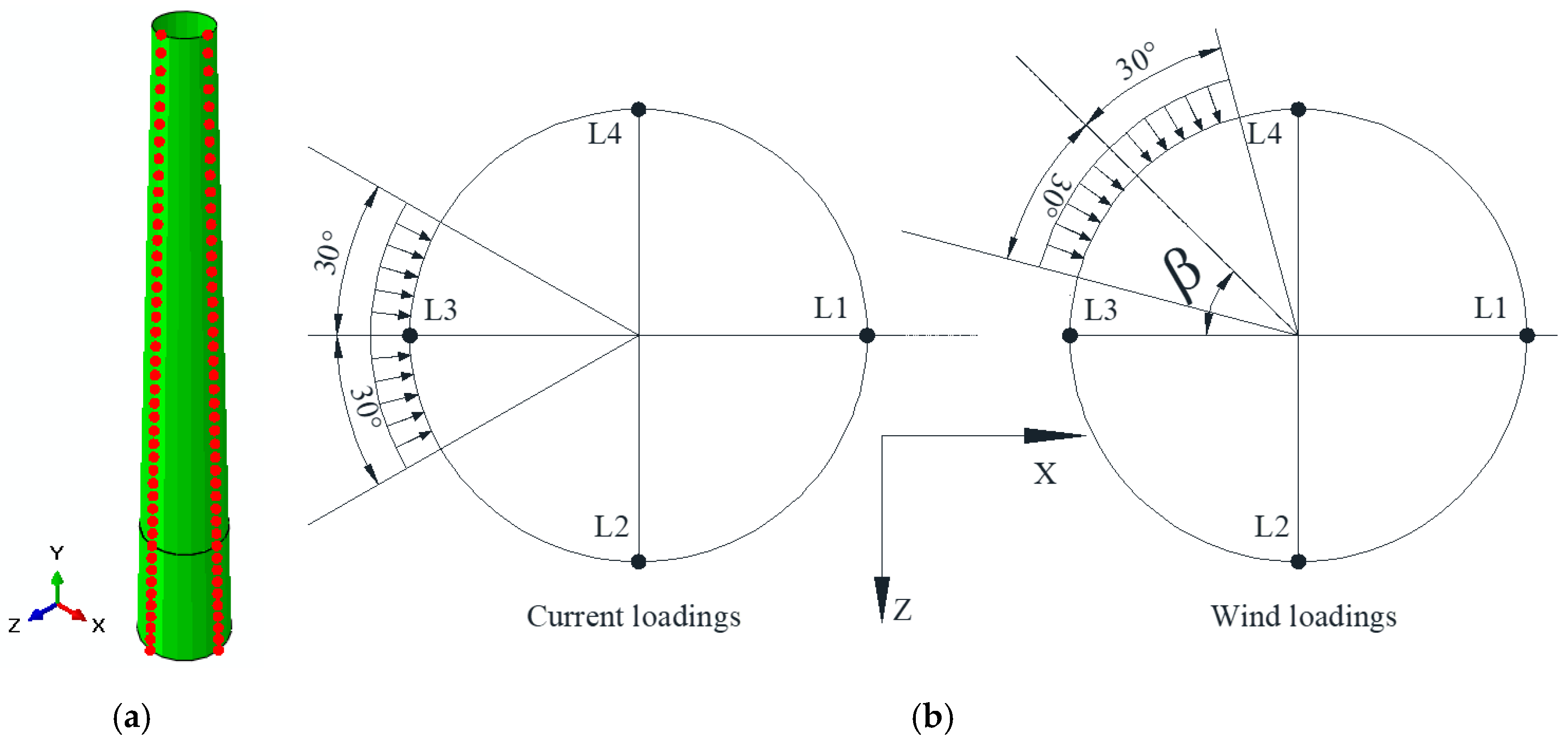
2. A Numerical Study
2.1. Validation of the Numerical Model
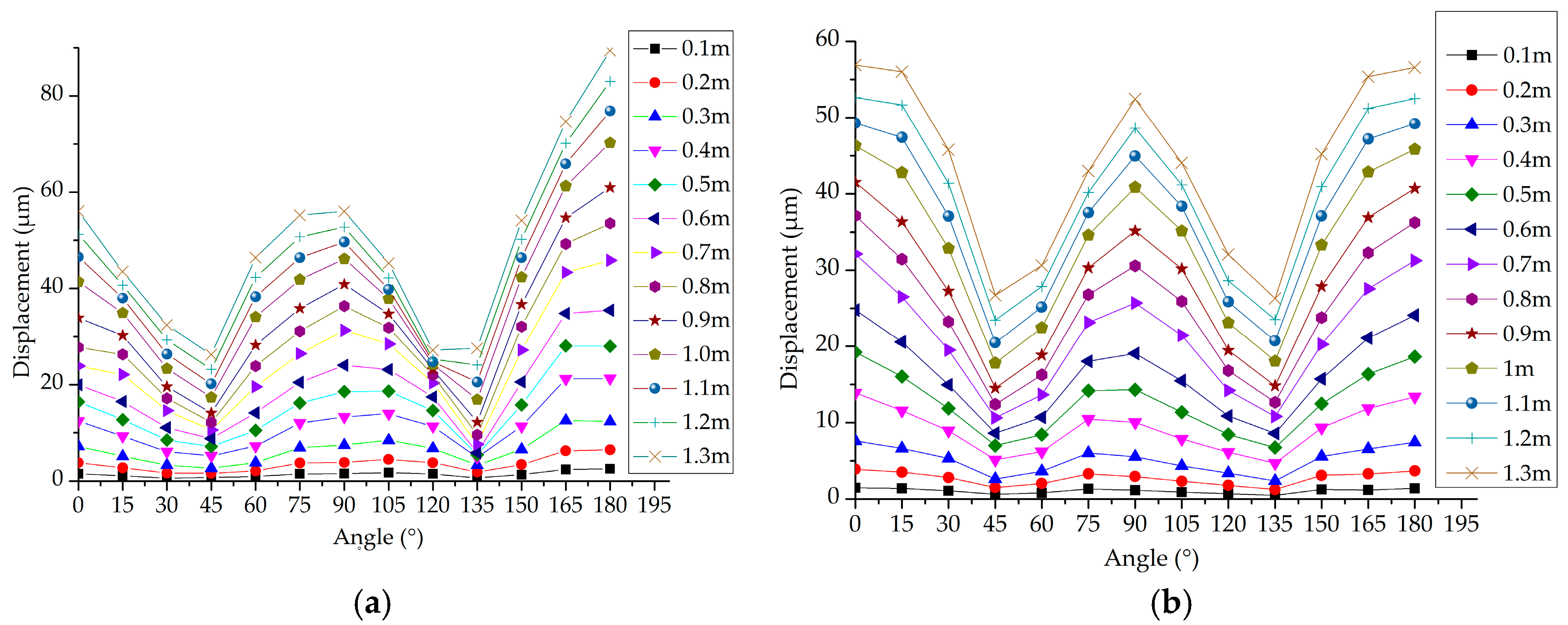
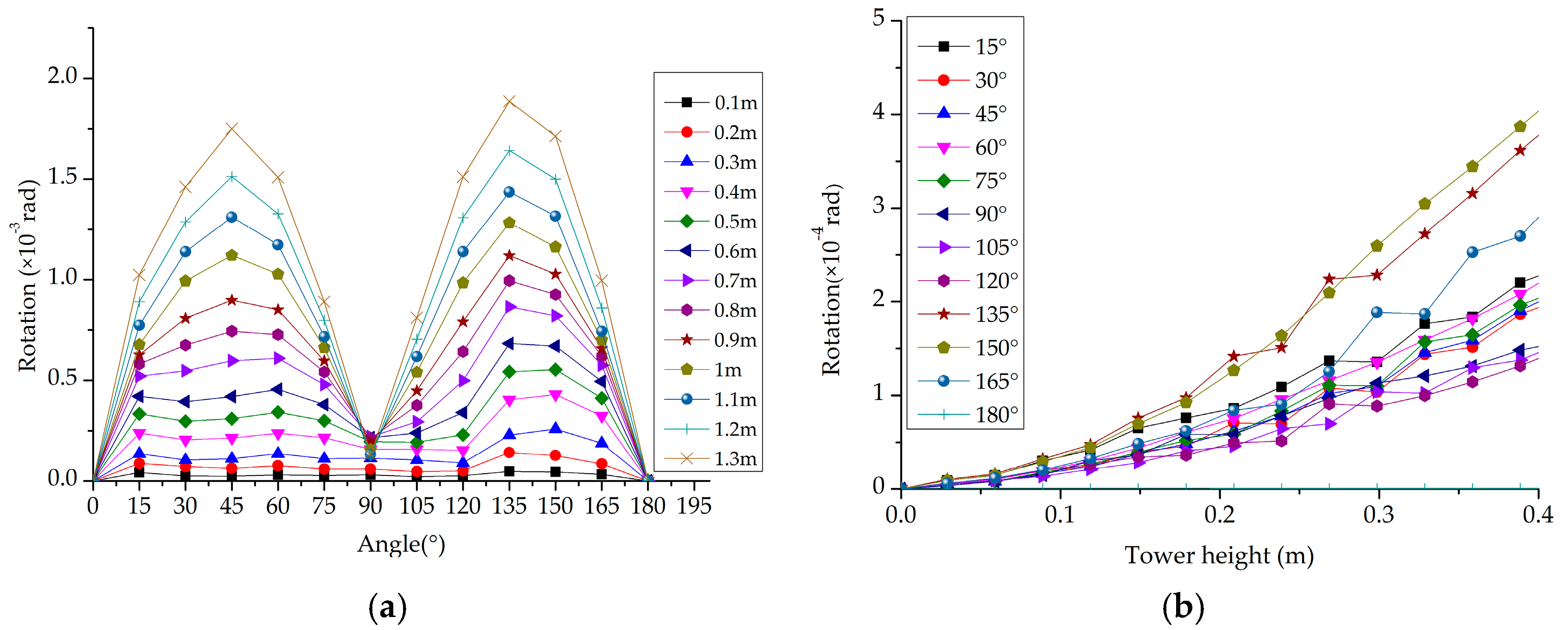
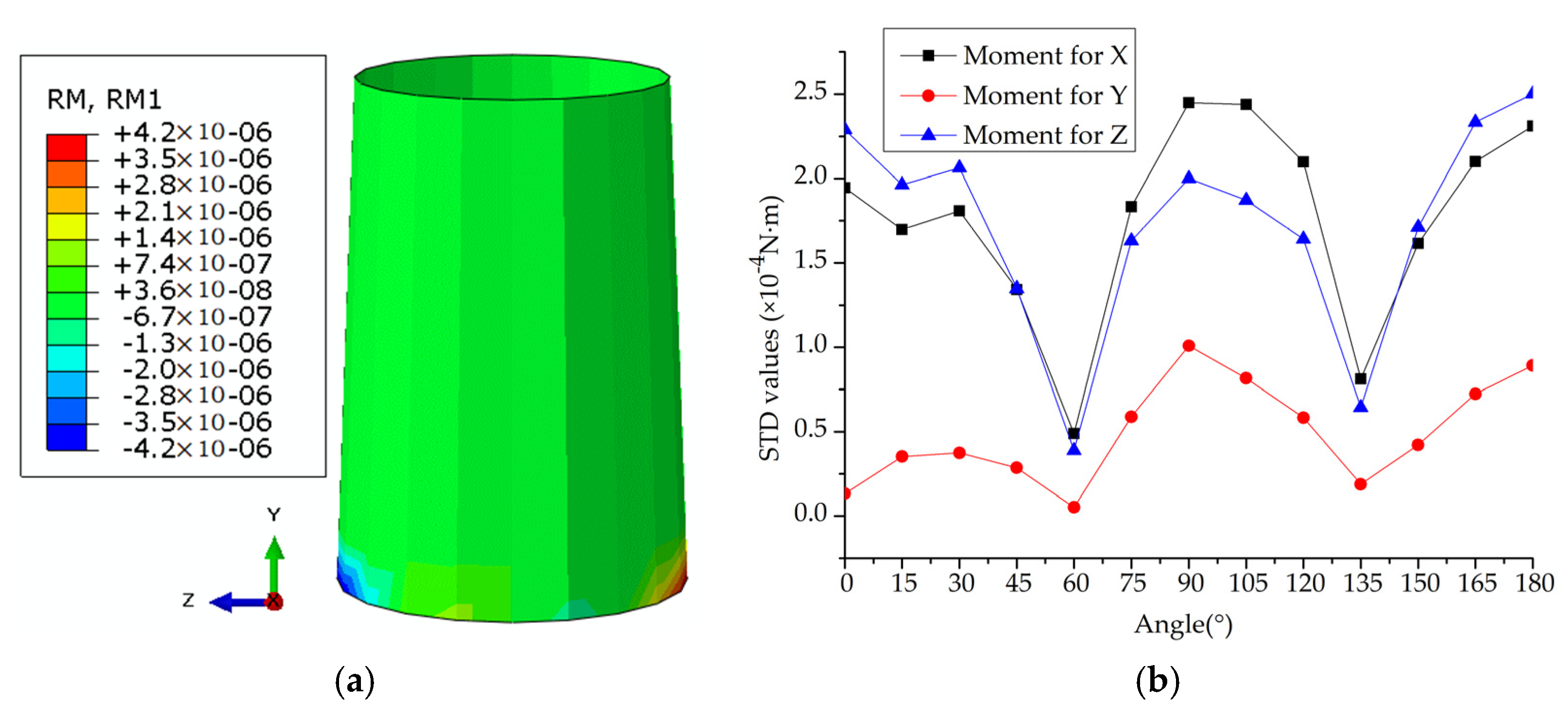
2.2. Effect of Direction Angles between Wind and Current
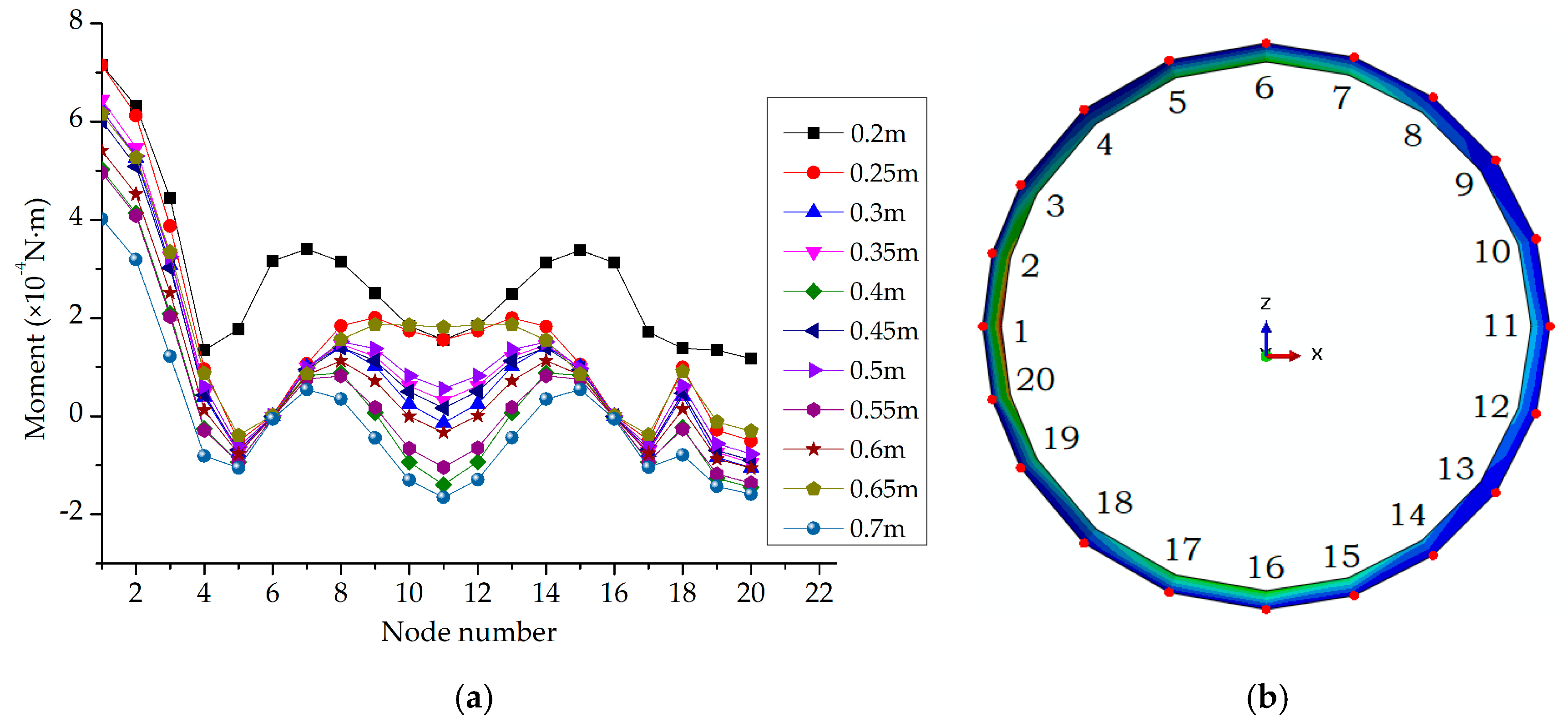
2.3. Effect of Water Depth
3. Bearing Capacity of the Offshore Tower with Stiffeners
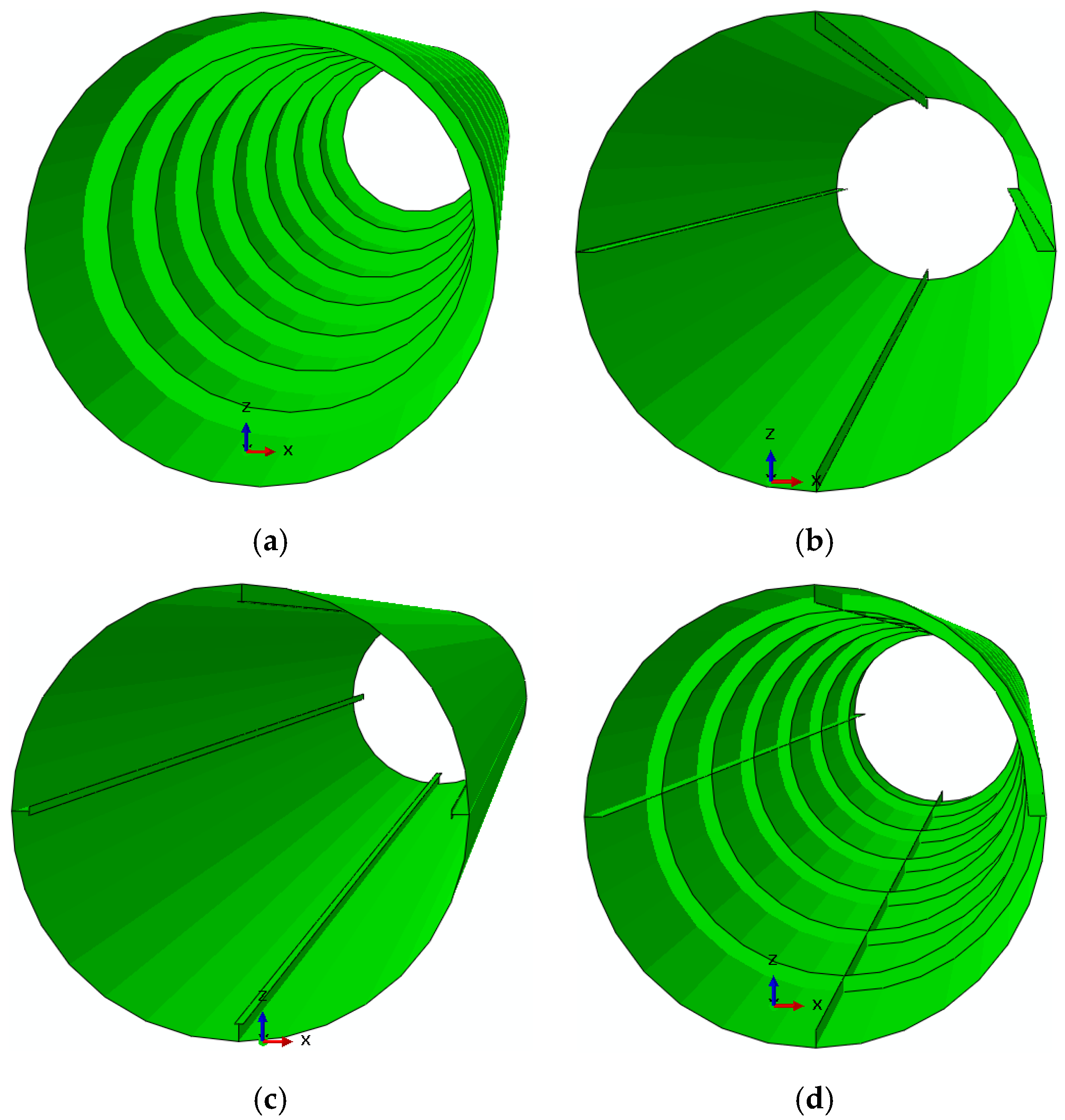
3.1. Tower Models
3.2. Stiffeners Mass
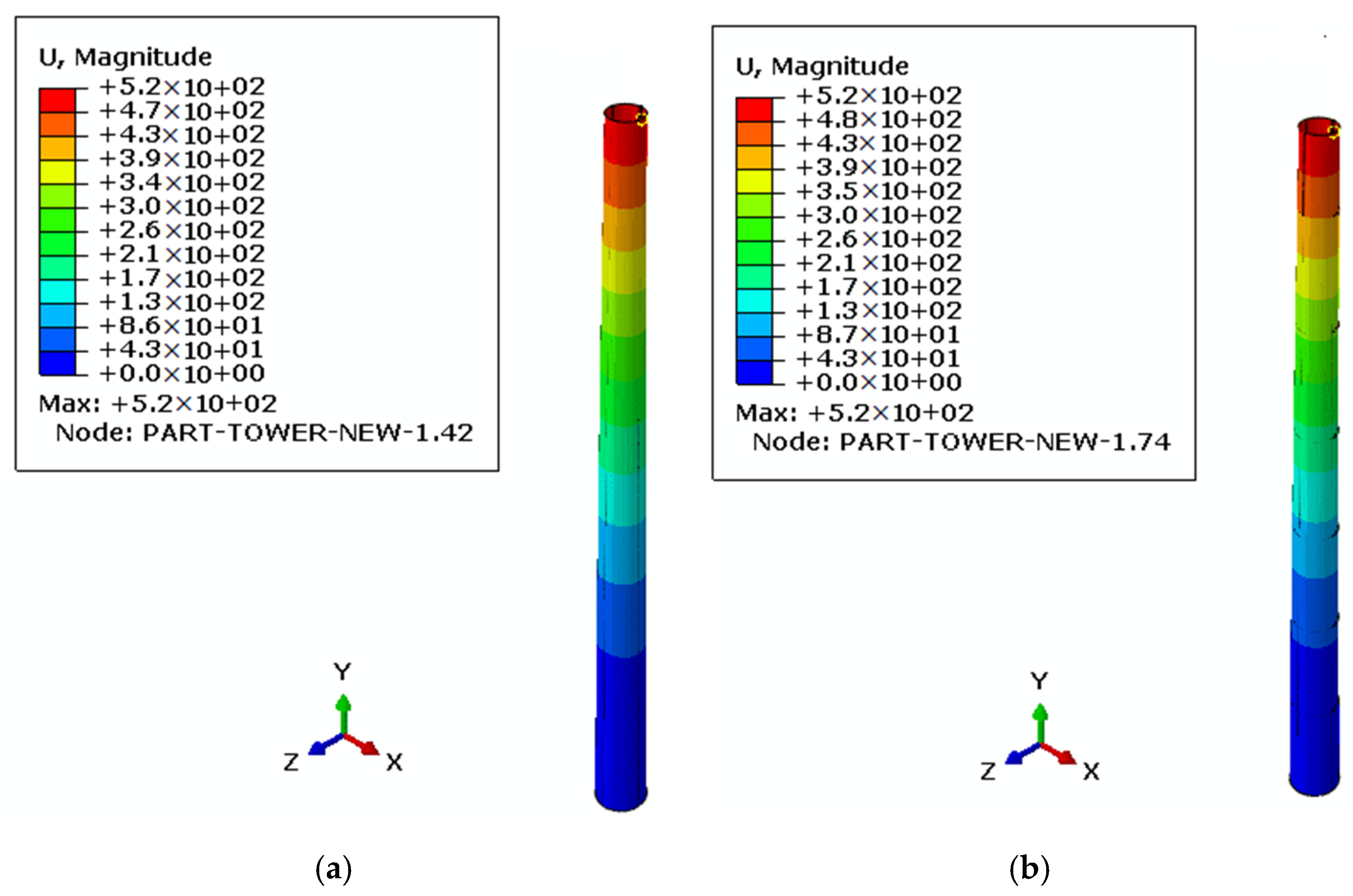
3.3. Buckling Analysis of the Tower
3.3.1. On the Effect of Gravity
3.3.2. On the Effect of the Horizontal Actions
3.3.3. On the Effect of the Eccentricity
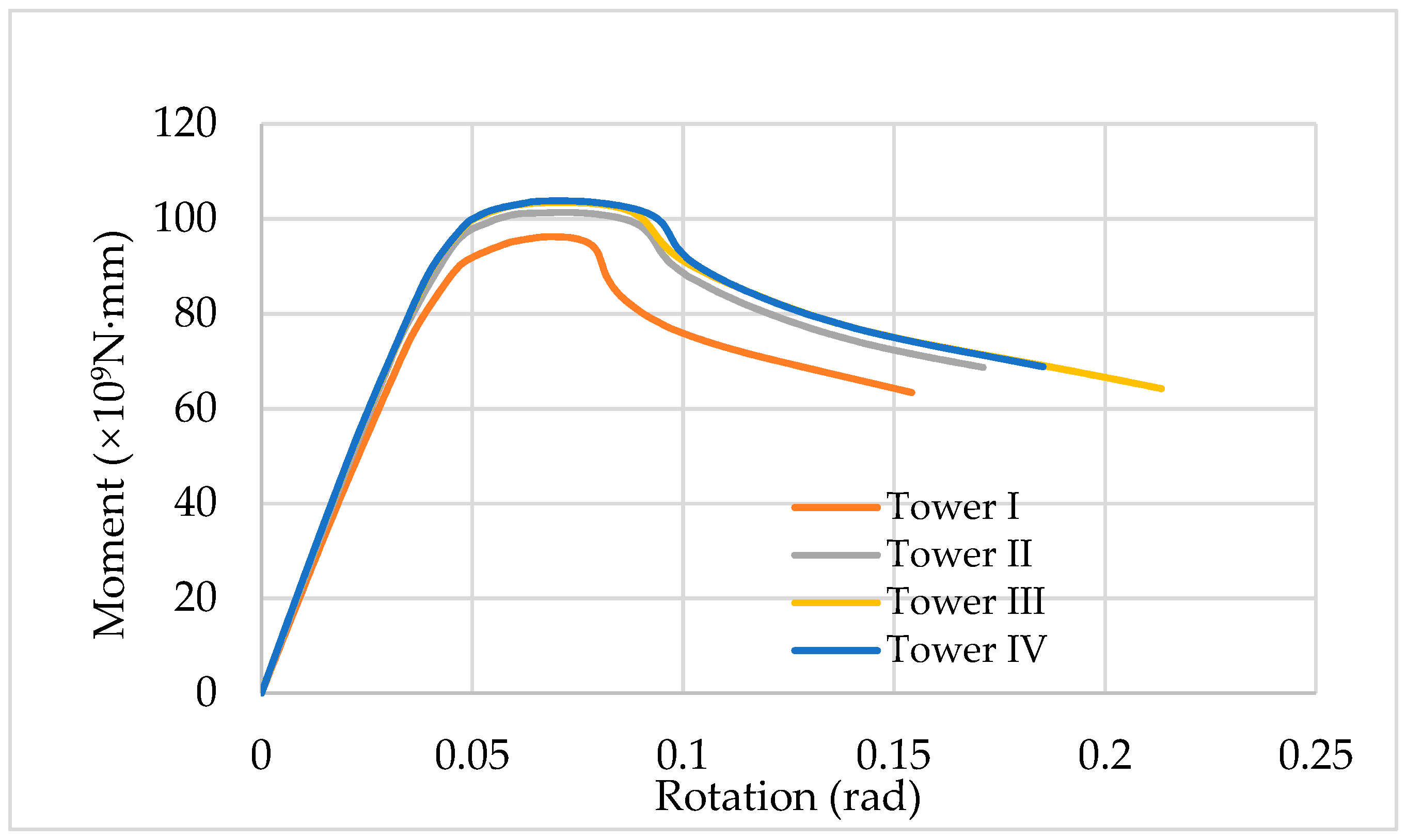
3.4. Strength Analysis of Towers I, II, III, IV
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arapogianni, A.; Moccia, J. Wind in Our Sails: The Coming of Europe’s Offshore Wind Energy Industry; European Wind Energy Association: Brussels, Belgium, 2011. [Google Scholar]
- Wang, L.; Ishihara, T. A study of the effects of foundation uplift on the seismic loading of wind turbine tower and shallow foundation using a new dynamic Winkler model. Eng. Struct. 2020, 219, 110745. [Google Scholar] [CrossRef]
- Ko, Y.-Y. A simplified structural model for monopile-supported offshore wind turbines with tapered towers. Renew. Energy 2020, 156, 777–790. [Google Scholar] [CrossRef]
- Li, M.; Kefal, A.; Oterkus, E.; Oterkus, S. Structural health monitoring of an offshore wind turbine tower using iFEM methodology. Ocean Eng. 2020, 204, 107291. [Google Scholar] [CrossRef]
- Sadowski, A.J.; Camara, A.; Málaga-Chuquitaype, C.; Dai, K. Seismic analysis of a tall metal wind turbine support tower with realistic geometric imperfections. Earthq. Eng. Struct. Dyn. 2017, 46, 201–219. [Google Scholar] [CrossRef] [Green Version]
- Jin, Q.; Li, V.C. Structural and durability assessment of ECC/concrete dual-layer system for tall wind turbine towers. Eng. Struct. 2019, 196, 109338. [Google Scholar] [CrossRef]
- Fu, B.; Zhao, J.; Li, B.; Yao, J.; Teifouet, A.R.M.; Sun, L.; Wang, Z. Fatigue reliability analysis of wind turbine tower under random wind load. Struct. Saf. 2020, 87, 101982. [Google Scholar] [CrossRef]
- Huo, T.; Tong, L. An approach to wind-induced fatigue analysis of wind turbine tubular towers. J. Constr. Steel Res. 2020, 166, 105917. [Google Scholar] [CrossRef]
- Qiu, B.; Lu, Y.; Sun, L.; Qu, X.; Xue, Y.; Tong, F. Research on the damage prediction method of offshore wind turbine tower structure based on improved neural network. Measurement 2020, 151, 107141. [Google Scholar] [CrossRef]
- Abraham, A.; Dasari, T.; Hong, J. Effect of turbine nacelle and tower on the near wake of a utility-scale wind turbine. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103981. [Google Scholar] [CrossRef] [Green Version]
- Stavridou, N.; Efthymiou, E.; Gerasimidis, S.; Baniotopoulos, C.C. Investigation of stiffening scheme effectiveness towards buckling stability enhancement in tubular steel wind turbine towers. Steel Compos. Struct. 2015, 19, 1115–1144. [Google Scholar] [CrossRef]
- Gkantou, M.; Rebelo, C.; Baniotopoulos, C. Life Cycle Assessment of Tall Onshore Hybrid Steel Wind Turbine Towers. Energies 2020, 13, 3950. [Google Scholar] [CrossRef]
- Yadav, K.K.; Gerasimidis, S. Imperfection insensitive thin cylindrical shells for next generation wind turbine towers. J. Constr. Steel Res. 2020, 172, 106228. [Google Scholar] [CrossRef]
- Koulatsou, K.G.; Kazakis, G.; Gantes, C.J.; Lagaros, N.D. Resonance Investigation and its Effects on Weight Optimization of Tubular Steel Wind Turbine Towers, The 1st International Conference on Optimization-Driven Architectural Design (OPTARCH 2019). Procedia Manuf. 2020, 44, 4–11. [Google Scholar] [CrossRef]
- O’Leary, K.; Pakrashi, V.; Kelliher, D. Optimization of composite material tower for offshore wind turbine structures. Renew. Energy 2019, 140, 928–942. [Google Scholar] [CrossRef]
- Dimopoulos, C.A.; Gantes, C.J. Comparison of stiffening types of the cutout in tubular wind turbine towers. J. Constr. Steel Res. 2013, 83, 62–74. [Google Scholar] [CrossRef]
- Jay, A.; Myers, A.T.; Mirzaie, F.; Mahmoud, A.; Torabian, S.; Smith, E.; Schafer, B.W. Large scale bending tests of slender, tapered, spirally welded steel tubes. J. Struct. Eng. 2016, 142, 04016136. [Google Scholar] [CrossRef]
- Alonso-Martinez, M.; Felipe, J.M.A.; Alvarez-Rabanal, P.; Díaz, J.J.C. Wind turbine tower collapse due to flange failure: FEM and DOE analyses. Eng. Fail. Anal. 2019, 104, 932–949. [Google Scholar] [CrossRef]
- Patil, A.; Jung, S.; Kwon, O.-S. Structural performance of a parked wind turbine tower subjected to strong ground motions. Eng. Struct. 2016, 120, 92–102. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H.; Xin, Y.; Li, J.; Li, C. Fragility analyses of offshore wind turbines subjected to aerodynamic and sea wave loadings. Renew. Energy 2020, 160, 1269–1282. [Google Scholar] [CrossRef]
- Zhang, X.-L.; Liu, J.-X.; Han, Y.; Du, X.-L. A framework for evaluating the bearing capacity of offshore wind power foundation under complex loadings. Appl. Ocean Res. 2018, 80, 66–78. [Google Scholar] [CrossRef]
- ABAQUS/Standard and ABAQUS/Explicit-Version 6.8-1; Abaqus Theory Manual; Dassault System: Vélizy-Villacoublay, France, 2008; Available online: https://www.doc88.com/p-439722564721.html (accessed on 26 September 2020).
- Hu, Y.; Yang, J.; Baniotopoulos, C.; Wang, X.; Deng, X. Dynamic analysis of offshore steel wind turbine towers subjected to wind, wave and current loading during construction. Ocean Eng. 2020, 216, 108084. [Google Scholar] [CrossRef]
- ENV 1991-01-04: Actions on Structures; CEN: Brussels, Belgium, 1991.
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Newman, J.N. Marine Hydrodynamics; The MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Hu, Y.; Baniotopoulos, C.C.; Yang, J. Effect of internal stiffening rings on the structural response of steel wind turbine towers. Eng. Struct. 2014, 81, 148–161. [Google Scholar] [CrossRef]
- Hu, Y.; Baniotopoulos, C.C.; Yang, J. Repowering Steel Tubular Wind Turbine Towers Enhancing them by Internal Stiffening Rings. Energies 2020, 13, 1538. [Google Scholar] [CrossRef] [Green Version]















| Material | Density | Elasticity Module | Poisson’s Ratio | Yield Stress | Plastic Strain |
|---|---|---|---|---|---|
| Steel | 7.85 g/cm3 | 205 GPa | 0.3 | 345 GPa | 0 |
| 428 GPa | 0.1 |
| Maximum von Mises Stress (MPa) | Maximum Deformation (mm) | |
|---|---|---|
| Tower I | 127.2 | 558.8 |
| Tower II | 118.5 | 516.5 |
| Tower III | 117.4 | 520.9 |
| Tower IV | 119.4 | 527 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Yang, J.; Baniotopoulos, C. Study of the Bearing Capacity of Stiffened Tall Offshore Wind Turbine Towers during the Erection Phase. Energies 2020, 13, 5102. https://doi.org/10.3390/en13195102
Hu Y, Yang J, Baniotopoulos C. Study of the Bearing Capacity of Stiffened Tall Offshore Wind Turbine Towers during the Erection Phase. Energies. 2020; 13(19):5102. https://doi.org/10.3390/en13195102
Chicago/Turabian StyleHu, Yu, Jian Yang, and Charalampos Baniotopoulos. 2020. "Study of the Bearing Capacity of Stiffened Tall Offshore Wind Turbine Towers during the Erection Phase" Energies 13, no. 19: 5102. https://doi.org/10.3390/en13195102
APA StyleHu, Y., Yang, J., & Baniotopoulos, C. (2020). Study of the Bearing Capacity of Stiffened Tall Offshore Wind Turbine Towers during the Erection Phase. Energies, 13(19), 5102. https://doi.org/10.3390/en13195102







