Modelling of a Three-Body Hinge-Barge Wave Energy Device Using System Identification Techniques
Abstract
1. Introduction
- White-box models. Based only on physical considerations, i.e., hydrodynamic modelling.
- Black-box models. Based only on SIT.
- Grey-box models. Combination of hydrodynamic modelling and SIT.
2. System Identification Applied to Wave Energy Converters
- “A parametric structure is chosen for the model,”
- “a suitable input signal, is synthesized and input to the experimental system,”
- “the input signal, and resulting output signal, are recorded,”
- “an identification algorithm is used to determine the optimal parameter vector, which minimizes some error metric between the actual measured output and that produced by the identified parametric model .”
2.1. Time-Domain Data
2.2. Frequency-Domain Data
2.3. Wave Energy Data Sources
- Linear potential theory,
- nonlinear boundary-element methods (BEMs),
- smooth particle hydrodynamics (SPH), and
- computational fluid dynamics (CFD).
- “Significant cost and the need for a physical prototype” [13].
- Generally, prototypes are not full scale, which introduces scaling effects in the experiments [13].
- “Measurement errors are present” [8].
- For free surface elevation to body motion models, there may be limitations on the range of excitation signals available [13].
- “Tank wall reflections may further limit the range and duration of viable tests” [13].
- The only way to constraint different modes of motion is with mechanical restraints, which can add friction and alter the device dynamics [13].
- “All NWTs are implemented by utilizing mathematical models, which necessarily are an approximation of the real system under study” [8].
- “Furthermore, the approximated equations utilized are resolved with numerical techniques, which introduce additional numerical errors. As a result, a NWT simulation does not completely correspond to the time-evolution of the real system” [8].
- “LPT-based NWTs assume small amplitude oscillations. This is a major limitation of this modelling approach, since WECS are designed to operate over a wide range of sea conditions where large amplitude motions will result from energetic waves or sustained wave/WEC resonance. At this expanded amplitude range, the linearising assumptions are invalid, as nonlinear effects become relevant” [13].
- “CFD-based simulations take excessively long time to perform the numerical computation of the response. Typical computation times can be up to 1000 times the simulation time” [13].
2.4. WEC Models
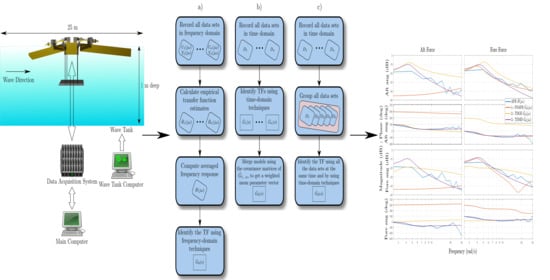
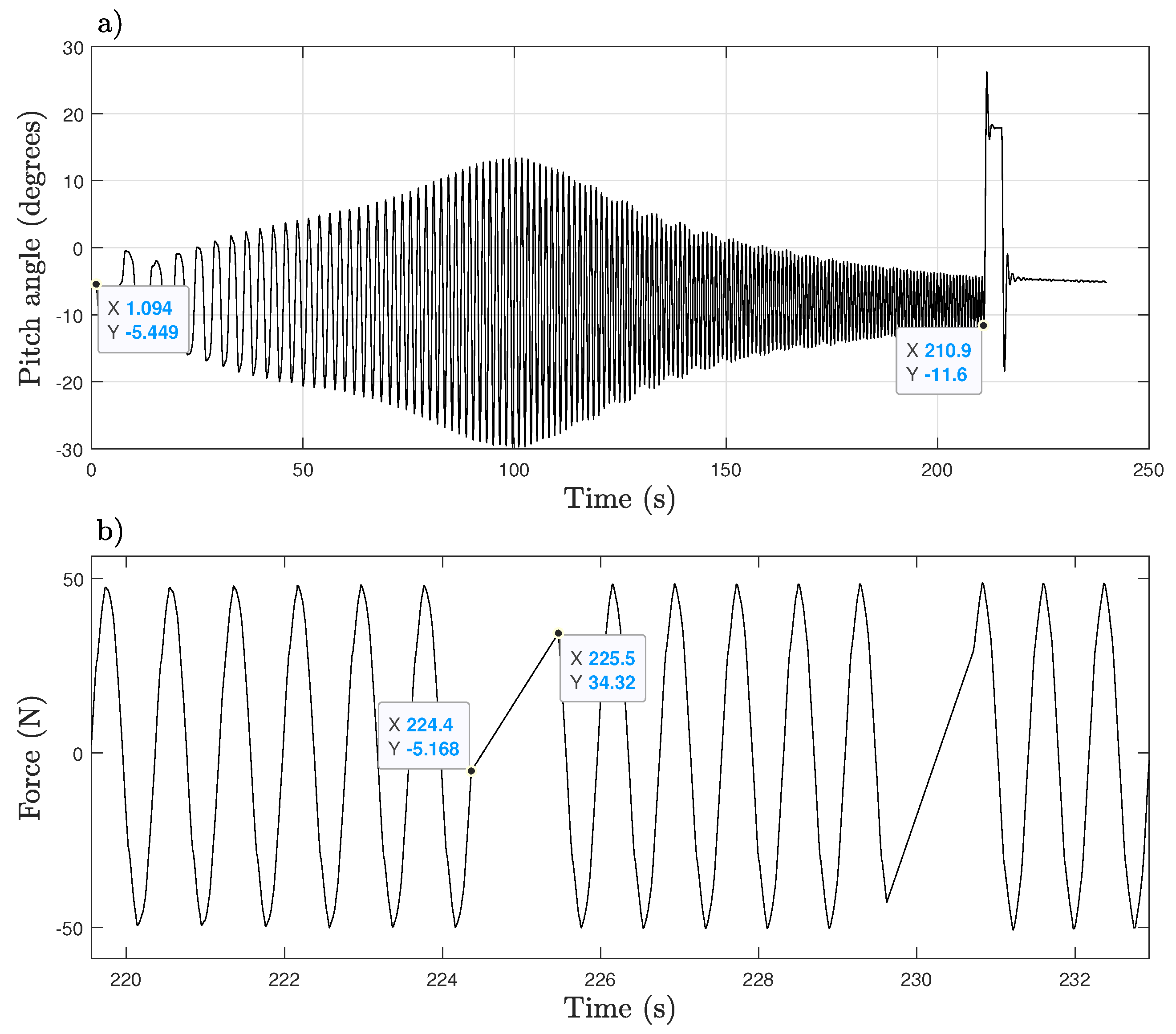
3. Case Study
4. Results
- “Good coverage of the frequencies where the system has a significant non-zero frequency response,”
- “good coverage of the full input and output signal ranges (if the system is nonlinear),” and
- “economic use of the test time.”
4.1. Data Preprocessing
4.2. Linear Model Estimation
- Model identified using frequency-domain SIT and averaged frequency response (FDAFR). See Figure 8a.
- Compute the averaged frequency response of all of the ETFEs.
Note that this is the same methodology as employed in [19]. - Model identified using time-domain SIT and a global estimate (TDGE). See Figure 8b.
- Estimate (identify) the continuous transfer function for each dataset in using time-domain SIT.
- Compute a global estimate using the covariance matrices of each estimated transfer function to get a weighted mean parameter vector.
- Model identified using time-domain SIT and merged data (TDMD). See Figure 8c.
- Merge the data for all the recorded input and output signals.
- Estimate the continuous transfer function with these merged data, using the time-domain SIT described in Section 2.1. When estimating the transfer function in this way, the prediction error vector is formed over the entire collection of experiments, assigning equal weight to observations in each experiment, i.e., the identification is done using all the input and output signals of the five experiments () at the same time.
4.3. Model Validation
5. Conclusions and Future Research Directions
Author Contributions
Funding
Conflicts of Interest
References
- Ringwood, J.; Bacelli, G.; Fusco, F. Energy-Maximizing Control of Wave-Energy Converters: The Development of Control System Technology to Optimize Their Operation. IEEE Control Syst. Mag. 2014, 34, 30–55. [Google Scholar]
- Ringwood, J. Wave energy control: Status and perspectives 2020. In Proceedings of the IFAC World Congress 2020, Berlin, Germany, 11–17 July 2020. [Google Scholar]
- Ljung, L. Perspectives on system identification. Annu. Rev. Control 2010, 34, 1–12. [Google Scholar] [CrossRef]
- Cummins, W. The impulse response function and ship motions. Schiffstechnik 1962, 47, 101–109. [Google Scholar]
- O’Cathain, M.; Leira, B.J.; Ringwood, J. Modelling of Multibody Marine Systems with Application to Wave-Energy Devices. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007. [Google Scholar]
- Paparella, F.; Bacelli, G.; Paulmeno, A.; Mouring, S.E.; Ringwood, J.V. Multibody Modelling of Wave Energy Converters Using Pseudo-Spectral Methods With Application to a Three-Body Hinge-Barge Device. IEEE Trans. Sustain. Energy 2016, 7, 966–974. [Google Scholar] [CrossRef]
- Paparella, F.; Ringwood, J.V. Optimal Control of a Three-Body Hinge-Barge Wave Energy Device Using Pseudospectral Methods. IEEE Trans. Sustain. Energy 2017, 8, 200–207. [Google Scholar] [CrossRef]
- Giorgi, S.; Davidson, J.; Jakobsen, M.; Kramer, M.; Ringwood, J.V. Identification of dynamic models for a wave energy converter from experimental data. Ocean Eng. 2019, 183, 426–436. [Google Scholar] [CrossRef]
- Bacelli, G.; Coe, R.; Patterson, D.; Wilson, D. System Identification of a Heaving Point Absorber: Design of Experiment and Device Modeling. Energies 2017, 10, 472. [Google Scholar] [CrossRef]
- Cho, H.; Bacelli, G.; Coe, R. Linear and Nonlinear System Identification of a Wave Energy Converter. In Proceedings of the 6th Marine Energy Technology Symposium, Washington, DC, USA, 30 April–2 May 2018. [Google Scholar]
- Sun, L.; Zang, J.; Stansby, P.; Carpintero Moreno, E.; Taylor, P.H.; Eatock Taylor, R. Linear diffraction analysis of the three-float multi-mode wave energy converter M4 for power capture and structural analysis in irregular waves with experimental validation. J. Ocean Eng. Mar. Energy 2017, 3, 51–68. [Google Scholar] [CrossRef]
- Jaramillo-Lopez, F.; Flannery, B.; Murphy, J.; Ringwood, J.V. Black-box Modelling of a Three-Body Hinge-Barge Wave Energy Device via Forces Responses. In Proceedings of the 4th International Conference on Renewable Energies Offshore, Lisbon, Portugal, 12–15 October 2020. [Google Scholar]
- Davidson, J.; Giorgi, S.; Ringwood, J.V. Identification of Wave Energy Device Models From Numerical Wave Tank Data—Part 1: Numerical Wave Tank Identification Tests. IEEE Trans. Sustain. Energy 2016, 7, 1012–1019. [Google Scholar] [CrossRef]
- Ljung, L. Identification for control: Simple process models. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; pp. 4652–4657. [Google Scholar]
- Ljung, L. Experiments with Identification of Continuous Time Models. In Proceedings of the 15th IFAC Symposium on System Identification, Saint-Malo, France, 6–8 July 2009; pp. 1175–1180. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Ljung, L. System Identification Toolbox for Use with MATLAB: Reference (R2019b); The MathWorks, Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Ozdemir, A.A.; Gumussoy, S. Transfer Function Estimation in System Identification Toolbox via Vector Fitting. IFAC-PapersOnLine 2017, 50, 6232–6237. [Google Scholar] [CrossRef]
- Garcia-Violini, D.; Pena-Sanchez, Y.; Faedo, N.; Windt, C.; Ringwood, J. LTI energy-maximising control for the Wave Star wave energy converter: Identification, design, and implementation. In Proceedings of the IFAC World Congress 2020, Berlin, Germany, 11–17 July 2020. [Google Scholar]
- LIR-NOTF. LIR National Ocean Test Facility, Cork, Ireland. 2020. Available online: http://www.lir-notf.com/wavebasins/ (accessed on 23 June 2020).
- Davidson, J.; Costello, R. Efficient Nonlinear Hydrodynamic Models for Wave Energy Converter Design— A Scoping Study. J. Mar. Sci. Eng. 2020, 8, 35. [Google Scholar] [CrossRef]
- Davidson, J.; Giorgi, S.; Ringwood, J.V. Linear parametric hydrodynamic models for ocean wave energy converters identified from numerical wave tank experiments. Ocean Eng. 2015, 103, 31–39. [Google Scholar] [CrossRef]
- Mocean Energy. Mocean Energy News. 2020. Available online: https://www.mocean.energy/wave-energy-news/ (accessed on 10 April 2020).
- Stansby, P.; Carpintero Moreno, E.; Stallard, T.; Maggi, A. Three-float broad-band resonant line absorber with surge for wave energy conversion. Renew. Energy 2015, 78, 132–140. [Google Scholar] [CrossRef]
- Seapower. Seapower. 2020. Available online: http://www.seapower.ie/ (accessed on 10 April 2020).
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Philos. Trans. R. Soc. A 2012, 370, 365–380. [Google Scholar] [CrossRef] [PubMed]
- de Almeida, A.; Moura, P. Desalination with wind and wave power. In Solar Desalination for the 21st Century; NATO Security through Science Series; Springer: Dordrecht, The Nertherlands, 2007; pp. 305–325. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Y.; Zheng, S. Numerical study on the performance of a wave energy converter with three hinged bodies. Renew. Energy 2016, 99, 1276–1286. [Google Scholar] [CrossRef]
- Offshore Energy. WECCA Completes Scaled Wave Energy Device. 2016. Available online: https://www.offshore-energy.biz/wecca-completes-scaled-wave-energy-device-prize/ (accessed on 10 April 2020).
- Soderstrom, T.; Stoica, P. System Identification; Prentice-Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]









| Input-Output | AFR / | ||||
|---|---|---|---|---|---|
| Data | 37 N | 53 N | 85 N | 102 N | 134 N |
| FDAFR strategy | |||||
| TDGE strategy | |||||
| TDMD strategy |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaramillo-Lopez, F.; Flannery, B.; Murphy, J.; Ringwood, J.V. Modelling of a Three-Body Hinge-Barge Wave Energy Device Using System Identification Techniques. Energies 2020, 13, 5129. https://doi.org/10.3390/en13195129
Jaramillo-Lopez F, Flannery B, Murphy J, Ringwood JV. Modelling of a Three-Body Hinge-Barge Wave Energy Device Using System Identification Techniques. Energies. 2020; 13(19):5129. https://doi.org/10.3390/en13195129
Chicago/Turabian StyleJaramillo-Lopez, Fernando, Brian Flannery, Jimmy Murphy, and John V. Ringwood. 2020. "Modelling of a Three-Body Hinge-Barge Wave Energy Device Using System Identification Techniques" Energies 13, no. 19: 5129. https://doi.org/10.3390/en13195129
APA StyleJaramillo-Lopez, F., Flannery, B., Murphy, J., & Ringwood, J. V. (2020). Modelling of a Three-Body Hinge-Barge Wave Energy Device Using System Identification Techniques. Energies, 13(19), 5129. https://doi.org/10.3390/en13195129