The Modelling and Experimental Validation of a Cryogenic Packed Bed Regenerator for Liquid Air Energy Storage Applications
Abstract
1. Introduction
1.1. Background and Motivation
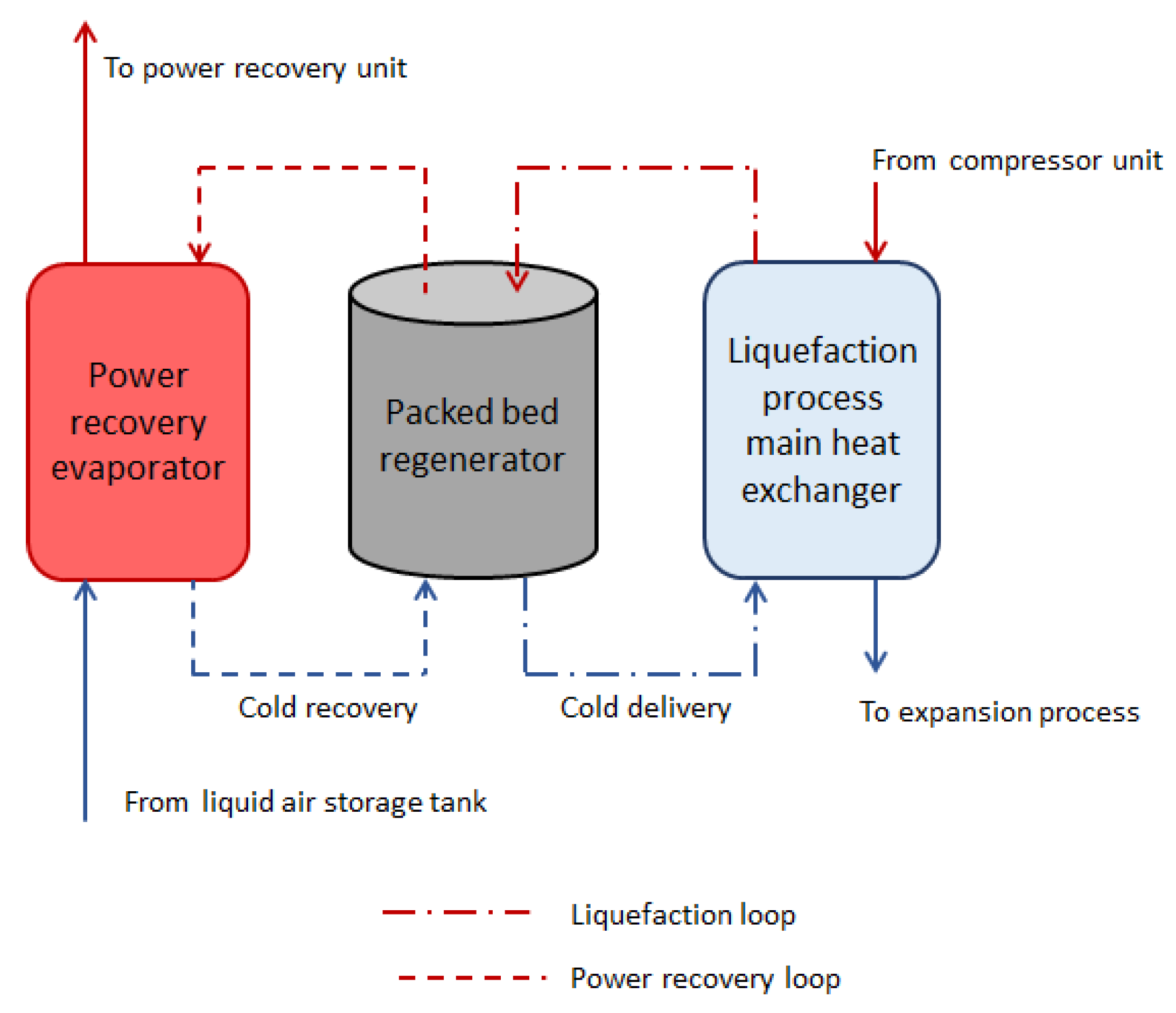
1.2. Choice of High-Grade Storage Concept
1.3. Modelling of Packed Bed Regenerators
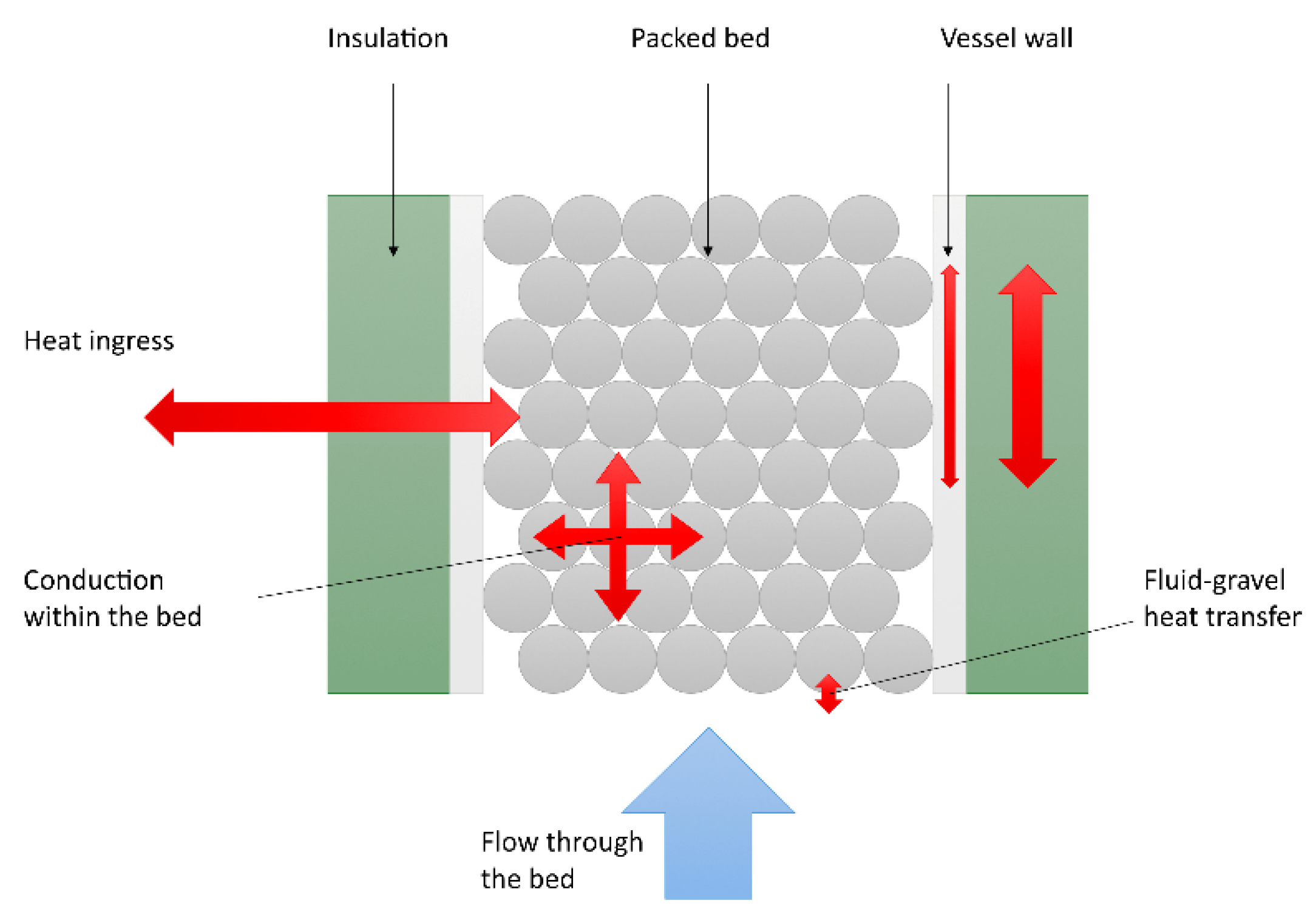
2. Theoretical Model of a Packed Bed Regenerator
- Particles can be treated as round and uniform with a characteristic diameter for the purpose of calculating the solid-to-gas phase heat transfer coefficient.
- There is no temperature gradient across the particle, i.e., the Biot number is near zero.
- Flow only travels in the axial direction with no recirculation and with a uniform velocity across the diameter of the PBR (plug flow).
- Heat transferred by conduction through the solid phase in the axis of the PBR is negligible.
- Heat is lost to the environment through the walls of the PBR, but the resulting temperature gradient at right angles to the flow, is negligible (i.e., the store is well insulated).
- The gas-to-particle heat transfer coefficient can be approximated using an empirical relationship between the Nusselt and Reynolds number, with temperature-dependent fluid properties. The length term is based on the particle diameter and the velocity term on the superficial velocity (velocity for an empty packed bed).
- The heat capacity (Cp) of the particles varies only with temperature.
- The thermal conductivity of the particles (k) can be approximated to a constant value with no variation with temperature.
- The thermal conductivity through the packed bed can be approximated to the volume-averaged value of the solid and liquid phases.
- Fluid properties vary with both temperature and pressure.
- The void fraction is constant in axial and radial directions.Radiative heat transfer is negligible due to the low temperature.
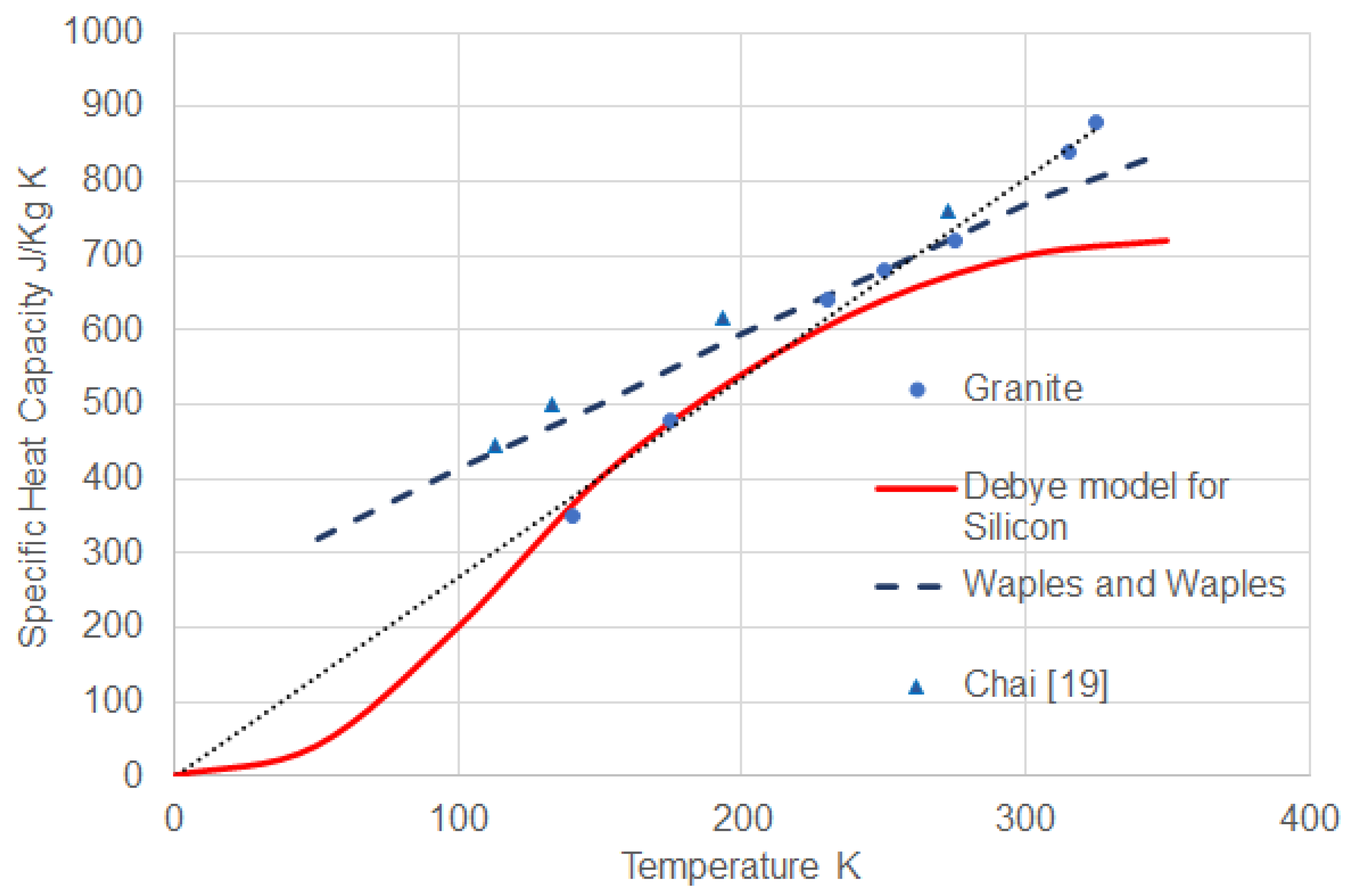
3. Determination of Physical Properties
4. Experimental Study of a Lab-Scale PBR
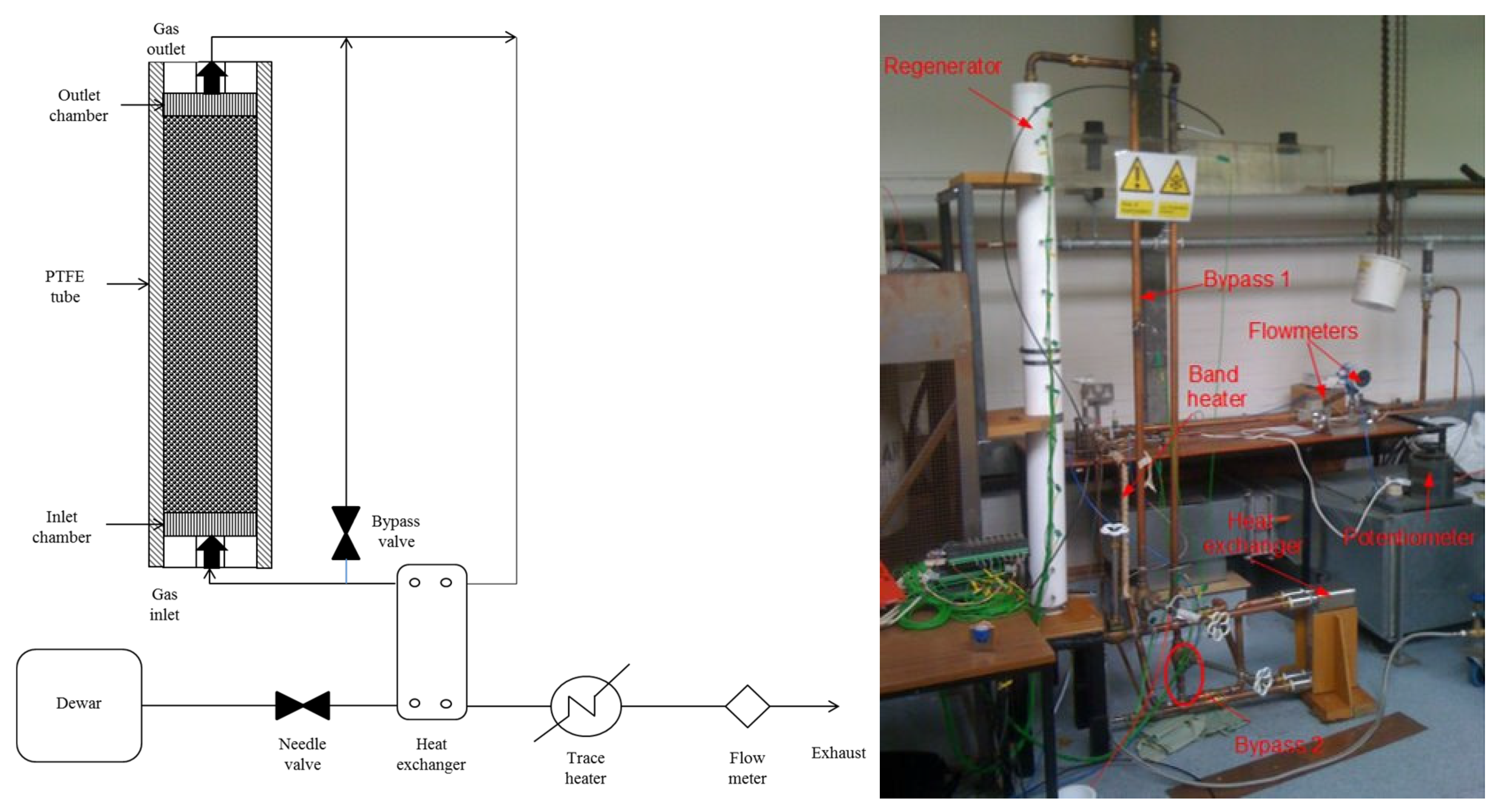
4.1. Description of the Test Rig
4.2. Determination of Void Fraction
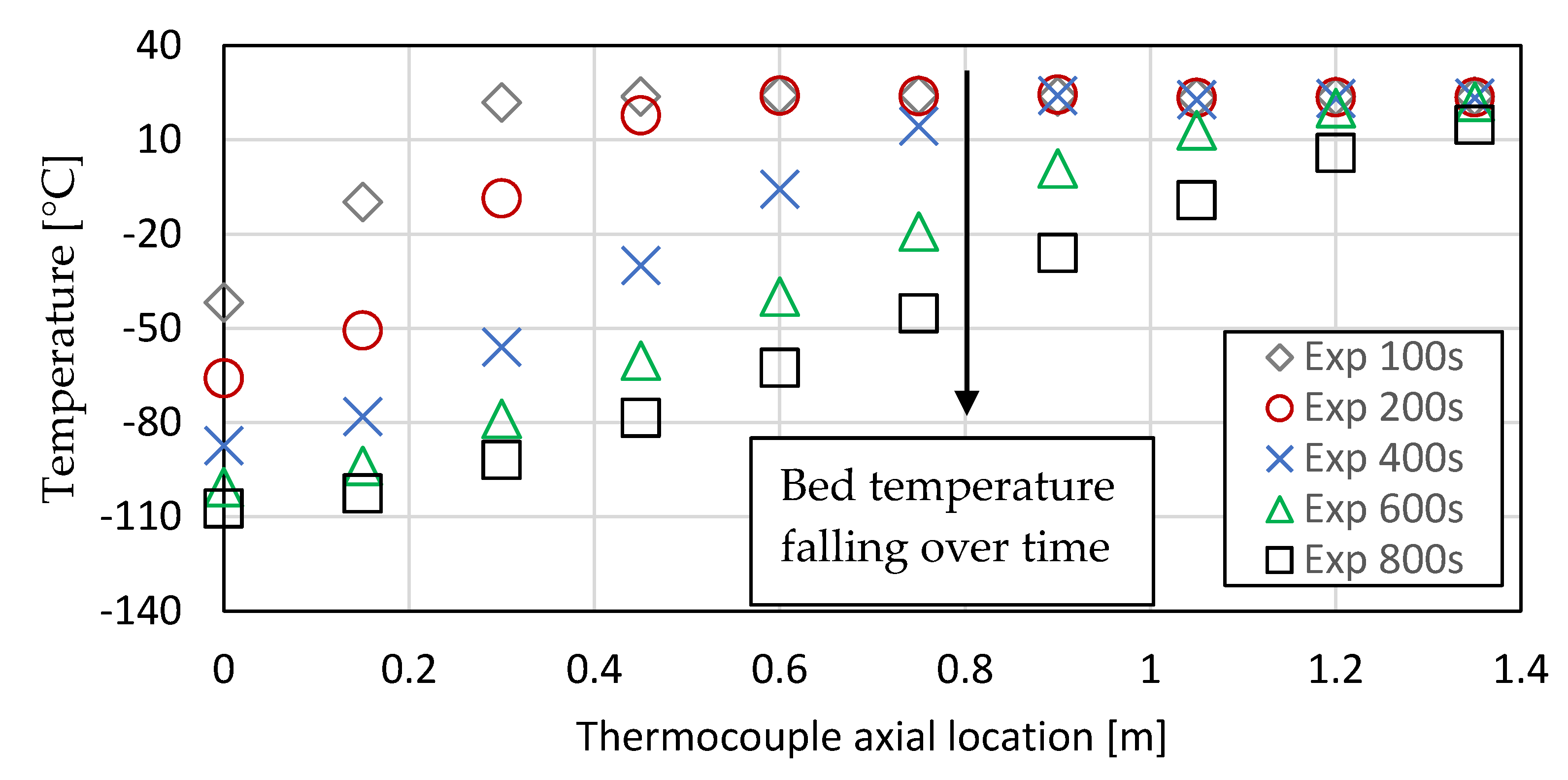
5. Experimental Results
6. Modelling
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Aw,i | Packed bed inner wall area |
| Aw,o | Packed bed outer wall area |
| a | Specific surface area of packed particles |
| Ds | Diameter of particle |
| kw | Packed bed wall thermal conductivity |
| ke | Packed bed effective thermal conductivity |
| Nul | Laminar Nusselt number |
| Nut | Turbulent Nusselt number |
| hw | Packed bed internal wall heat transfer coefficient |
| h | Heat transfer coefficient between fluid and packed bed particles |
| P | Pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| Tf | Temperature of fluid |
| Ts | Temperature of solid particle |
| Tw | Temperature of packed bed wall |
| T∞ | Ambient temperature |
| t | Time |
| u | Interstitial packed bed fluid velocity |
| u0 | Superficial packed bed fluid velocity |
| h∞ | Heat transfer coefficient from outer wall to ambient |
| x | Axial distance along the PBR |
| ρf | Fluid density |
| ρs | Packed bed particle density |
| ρw | Packed bed wall density |
| Cp,f | Fluid specific heat capacity |
| Cp,s | Solid particle specific heat capacity |
| Cp,w | Packed bed wall specific heat |
| µ | Fluid viscosity |
| ε | Void fraction |
References
- Strbac, G.; Aundedi, M.; Pudjianto, D.; Djapic, P.; Teng, F.; Sturt, A.; Dejvises, J.; Sansom, R.; Yufit, V.; Brandon, N. Strategic assessment of the role and value of energy storage systems in the UK low carbon energy future. In Report for the Carbon Trust; Imperial College: London, UK, 2012; Available online: http://www.carbontrust.com/media/129310/energy-storage-systems-role-value-strategic-assessment.pdf (accessed on 20 February 2014).
- IEA (2019) World Energy Outlook; Paris. Available online: https://www.iea.org/reports/world-energy-outlook-2019 (accessed on 2 October 2020).
- Legrand, M.; Rodríguez-Antón, L.M.; Martinez-Arevalo, C.; Gutiérrez-Martín, F. Integration of liquid air energy storage into the Spanish power grid. Energy 2019, 187, 115965. [Google Scholar] [CrossRef]
- May, G.J.; Davidson, A.; Monahov, B. Lead batteries for utility energy storage: A review. J. Energy Storage 2018, 15, 145–157. [Google Scholar] [CrossRef]
- Morgan, R.; Nelmes, S.; Gibson, E.; Brett, G. An analysis of a large-scale liquid air energy storage system. Proc. Inst. Civil Eng. 2015, 168, 135–144. [Google Scholar] [CrossRef]
- Morgan, R.; Nelmes, S.; Gibson, E.; Brett, G. Liquid air energy storage—Analysis and first results from a pilot scale demonstration plant. Appl. Energy 2015, 137, 845–853. [Google Scholar] [CrossRef]
- Peng, X.; She, X.; Cong, L.; Zhang, T.; Li, C.; Li, Y.; Wang, L.; Tong, L.; Ding, Y. Thermodynamic study on the effect of cold and heat recovery on performance of liquid air energy storage. Appl. Energy 2018, 221, 86–99. [Google Scholar] [CrossRef]
- Pike Wilson, E.; Morgan, R.; Cundy, A. Cryogenic thermal energy storage systems. In Proceedings of the ASME-ATI-UIT 2015 Conference on Thermal Energy Systems: Production, Storage, Utilization and the Environment, Naples, FL, USA, 7–20 May 2015. [Google Scholar]
- Hüttermann, L.; Span, R. Influence of the heat capacity of the storage material on the efficiency of thermal regenerators in liquid air energy storage systems. Energy 2019, 174, 236–245. [Google Scholar] [CrossRef]
- Kuipers, J.A.M. Computational Fluid Dynamics Applied to Chemical Reaction Engineering; Springer: Berlin, Germany, 1999. [Google Scholar]
- Cascetta, M.; Cau, G.; Puddu, P.; Serra, F. Numerical Investigation of a Packed Bed Thermal Energy Storage System with Different Heat Transfer Fluids. Energy Procedia 2014, 45, 598–607. [Google Scholar] [CrossRef]
- Xu, C.; Li, X.; Wang, Z.; He, Y.; Bai, F. Effects of solid particle properties on the thermal performance of a packed-bed molten-salt thermocline thermal storage system. Appl. Therm. Eng. 2013, 57, 69–80. [Google Scholar] [CrossRef]
- van Antwerpen, W.; du Toit, C.G.; Rousseau, P.G. A review of correlations to model the packing structure and effective thermal conductivity in packed beds of mono-sized spherical particles. Nucl. Eng. Des. 2010, 240, 1803–1818. [Google Scholar] [CrossRef]
- Achenbach, E. Heat and flow characteristics of packed beds. Exp. Therm. Fluid Sci. 1995, 10, 17–27. [Google Scholar] [CrossRef]
- Klein, P.; Roos, T.H.; Sheer, T.J. Experimental Investigation into a Packed Bed Thermal Storage Solution for Solar Gas Turbine Systems. Energy Procedia 2014, 49, 840–849. [Google Scholar] [CrossRef]
- Zanganeh, G.; Pedretti, A.; Haselbacher, A.; Steinfeld, A. Design of packed bed thermal energy storage systems for high-temperature industrial process heat. Appl. Energy 2015, 137, 812–822. [Google Scholar] [CrossRef]
- Chai, L.; Liu, J.; Wang, L.; Yue, L.; Yang, L.; Sheng, Y.; Chen, H.; Tan, C. Cryogenic energy storage characteristics of a packed bed at different pressures. Appl. Therm. Eng. 2014, 63, 439–446. [Google Scholar] [CrossRef]
- Oró, E.; Chiu, J.N.; Martin, V.; Cabeza, L.F. Comparative study of different numerical models of packed bed thermal energy storage systems. Appl. Therm. Eng. 2013, 50, 384–392. [Google Scholar] [CrossRef]
- Wilmott, J. Dynamics of Regenerative Heat Transfer; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- White, A.J. Loss analysis of thermal reservoirs for electrical energy storage schemes. Appl. Energy 2011, 88, 4150–4159. [Google Scholar] [CrossRef]
- Vortmeyer, D. Packed bed thermal dispersion models and consistent sets of coefficients. Chem. Eng. Process. Process Intensif. 1989, 26, 263–268. [Google Scholar] [CrossRef]
- Mawire, A.; McPherson, M.; Heetkamp, R.V.D.; Mlatho, S. Simulated performance of storage materials for pebble bed thermal energy storage (TES) systems. Appl. Energy 2009, 86, 1246–1252. [Google Scholar] [CrossRef]
- Hänchen, M.; Brückner, S.; Steinfeld, A. High-temperature thermal storage using a packed bed of rocks—Heat transfer analysis and experimental validation. Appl. Therm. Eng. 2011, 31, 1798–1806. [Google Scholar] [CrossRef]
- McTigue, J.D.; Markides, C.N.; White, A.J. Performance response of packed-bed thermal storage to cycle duration perturbations. J. Energy Storage 2018, 19, 379–392. [Google Scholar] [CrossRef]
- White, A.; McTigue, J.; Markides, C. Wave propagation and thermodynamic losses in packed-bed thermal reservoirs for energy storage. Appl. Energy 2014, 130, 648–657. [Google Scholar] [CrossRef]
- Ergun, S.; Orning, A.A. Fluid flow through randomly packed columns and fluidized beds. Ind. Eng. Chem. 1949, 41, 1179–1184. [Google Scholar] [CrossRef]
- Allen, K.G.; Von Backström, T.W.; Kröger, D.G. Packed Rock Bed Thermal Storage in Power Plants: Design Considerations. Energy Procedia 2014, 49, 666–675. [Google Scholar] [CrossRef]
- Consolmagno, G.J.; Schaefer, M.W.; Schaefer, B.E.; Britt, D.T.; Macke, R.J.; Nolan, M.C.; Howell, E.S. The measurement of meteorite heat capacity at low temperatures using liquid nitrogen vaporization. Planet. Space Sci. 2013, 87, 146–156. [Google Scholar] [CrossRef]
- Waples, D.W.; Waples, J.S. A Review and Evaluation of Specific Heat Capacities of Rocks, Minerals, and Subsurface Fluids. Part 1: Minerals and Nonporous Rocks. Nat. Resour. Res. 2004, 13, 97–122. [Google Scholar] [CrossRef]
- Debye, P. Zur Theorie der spezifischen Wärmen. Ann. Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef]
- Pike-Wilson, E.; Gardhouse, T.; Morgan, R.; Heikal, M. Measurement and simulation of low temperature packed bed regenerators. In Proceedings of the 4th UK Heat Transfer Conference, Edinburgh, UK, 7–8 September 2015. [Google Scholar]
- Gopal, J.M.; Tretola, G.; Morgan, R.; de Sercey, G.; Atkins, A.; Vogiatzaki, K. Understanding Sub and Supercritical Cryogenic Fluid Dynamics in Conditions Relevant to Novel Ultra Low Emission Engines. Energies 2020, 13, 3038. [Google Scholar] [CrossRef]
- Rao, G.S.; Sharma, K.; Chary, S.; Bakar, R.; Rahman, M.; Kadirgama, K.; Noor, M. Experimental study on heat transfer coefficient and friction factor of a Al203 nanofluid in a packed bed column. J. Mech. Eng. Sci. 2011, 1, 1–15. [Google Scholar] [CrossRef]
- Opitz, F.; Treffinger, P. Packed bed thermal energy storage model. Generalized approach and experimental validation. Appl. Therm. Eng. 2014, 73. [Google Scholar] [CrossRef]
- Martin, H. Low Peclet number particle-to-fluid heat and mass transfer in packed beds. Chem. Eng. Sci. 1978, 33. [Google Scholar] [CrossRef]
- Geissbühler, L.; Kolman, M.; Zanganeh, G.; Haselbacher, A.; Steinfeld, A. Analysis of industrial-scale high-temperature combined sensible/latent thermal energy storage. Appl. Therm. Eng. 2016, 101. [Google Scholar] [CrossRef]




| Gravel Sample | Cp (J/kg K) | |
|---|---|---|
| Test 1 | Test 2 | |
| 1 | 518 | 504 |
| 2 | 498 | 492 |
| 3 | 479 | 512 |
| 4 | 515 | 516 |
| Gravel | Void Fraction |
|---|---|
| Quartzite 10 mm | 0.44 |
| Quartzite 20 mm | 0.45 |
| Flint 20 mm (for reference) | 0.49 |
| Test | Gravel Diameter [mm] | Void Fraction | Particle Diameter (mm) | Mass Flow Coefficient | Reynolds Number | Pressure (barg) | Flow Rate (g/s) |
|---|---|---|---|---|---|---|---|
| 1 | 20 | 0.325 | 17 | 0.63 | 4706 | 1.29 | 7 |
| 2 | 20 | 0.350 | 20 | 0.65 | 6105 | 1.37 | 7.6 |
| 3 | 20 | 0.325 | 20 | 0.63 | 5251 | 1.35 | 6.7 |
| 4 | 20 | 0.350 | 20 | 0.63 | 7991 | 1.55 | 9.6 |
| 5 | 20 | 0.350 | 20 | 0.65 | 8179 | 1.58 | 9.2 |
| 6 | 20 | 0.350 | 20 | 0.65 | 8356 | 1.64 | 9.2 |
| 7 | 10 | 0.470 | 14 | 0.58 | 3315 | 1.65 | 8.2 |
| 8 | 10 | 0.400 | 14 | 0.58 | 2387 | 1.31 | 6 |
| 9 | 10 | 0.460 | 14 | 0.56 | 3417 | 1.63 | 8.5 |
| 10 | 10 | 0.450 | 14 | 0.56 | 3452 | 1.74 | 8.5 |
| 11 | 10 | 0.443 | 14 | 0.56 | 4776 | 1.89 | 10.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morgan, R.; Rota, C.; Pike-Wilson, E.; Gardhouse, T.; Quinn, C. The Modelling and Experimental Validation of a Cryogenic Packed Bed Regenerator for Liquid Air Energy Storage Applications. Energies 2020, 13, 5155. https://doi.org/10.3390/en13195155
Morgan R, Rota C, Pike-Wilson E, Gardhouse T, Quinn C. The Modelling and Experimental Validation of a Cryogenic Packed Bed Regenerator for Liquid Air Energy Storage Applications. Energies. 2020; 13(19):5155. https://doi.org/10.3390/en13195155
Chicago/Turabian StyleMorgan, Robert, Christian Rota, Emily Pike-Wilson, Tim Gardhouse, and Cian Quinn. 2020. "The Modelling and Experimental Validation of a Cryogenic Packed Bed Regenerator for Liquid Air Energy Storage Applications" Energies 13, no. 19: 5155. https://doi.org/10.3390/en13195155
APA StyleMorgan, R., Rota, C., Pike-Wilson, E., Gardhouse, T., & Quinn, C. (2020). The Modelling and Experimental Validation of a Cryogenic Packed Bed Regenerator for Liquid Air Energy Storage Applications. Energies, 13(19), 5155. https://doi.org/10.3390/en13195155





