Effects of Nozzle Exit Position on Condenser Outlet Split Ejector-Based R600a Household Refrigeration Cycle
Abstract
:1. Introduction
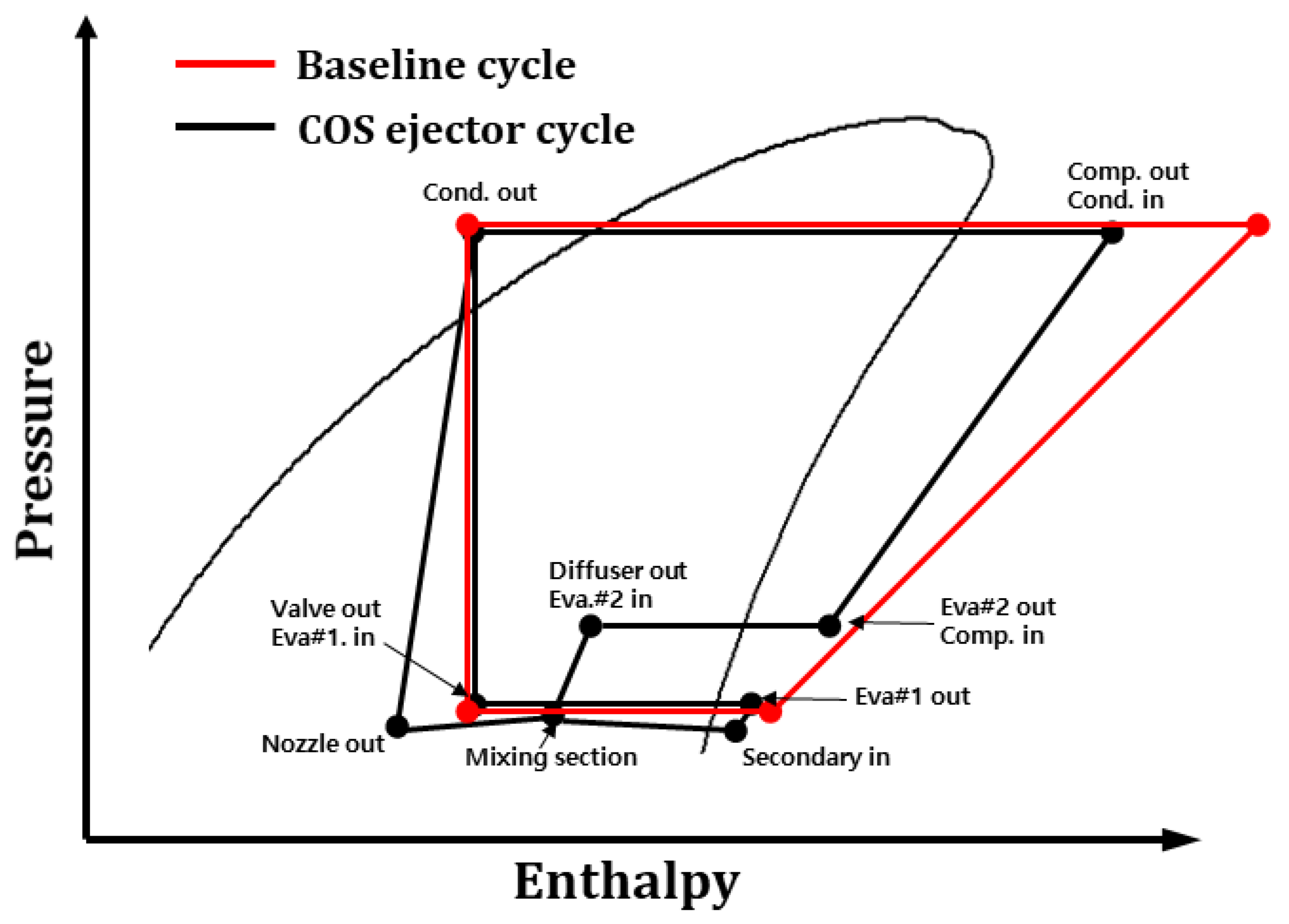
2. Experimental Setup and Test Procedure
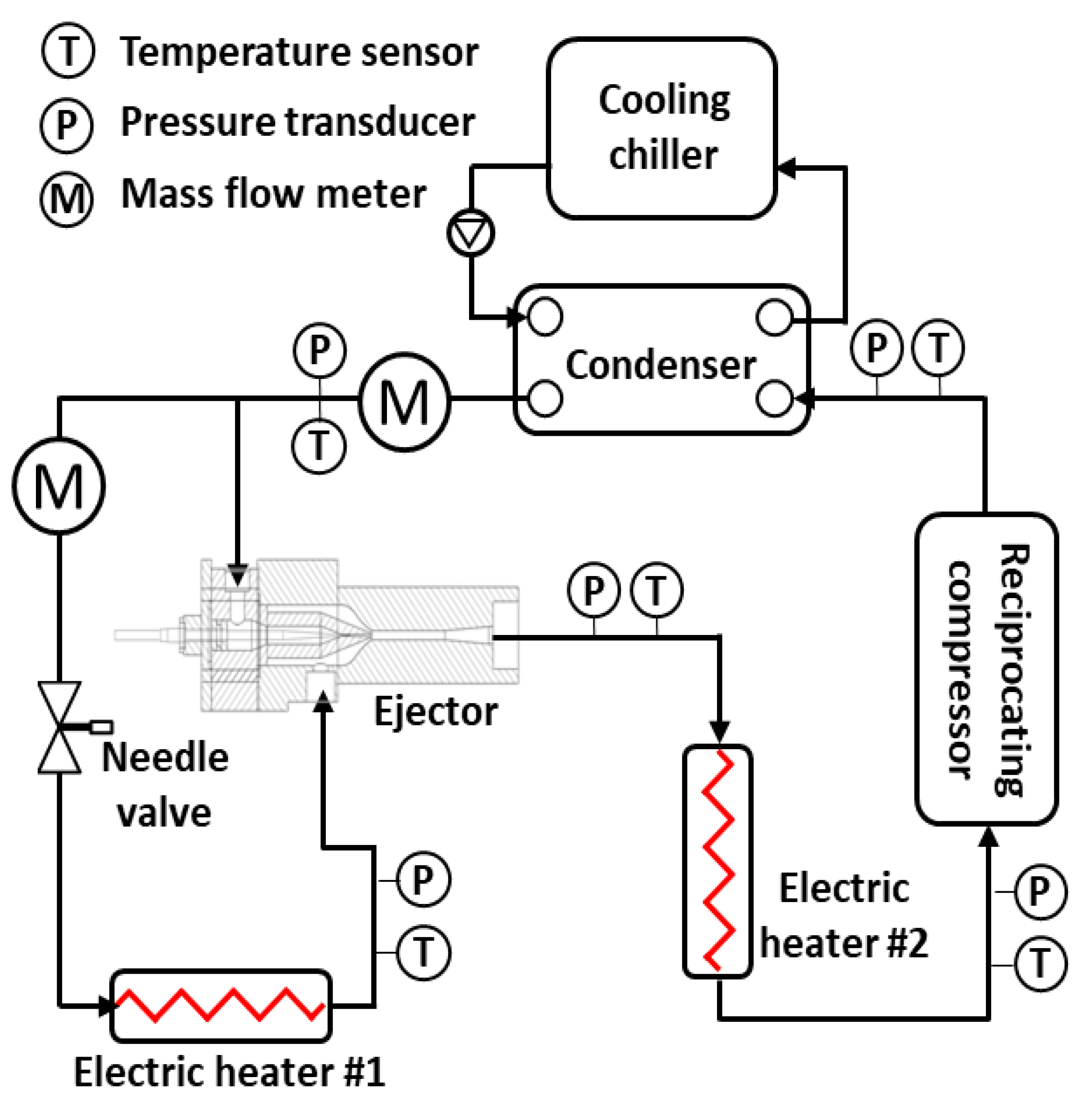
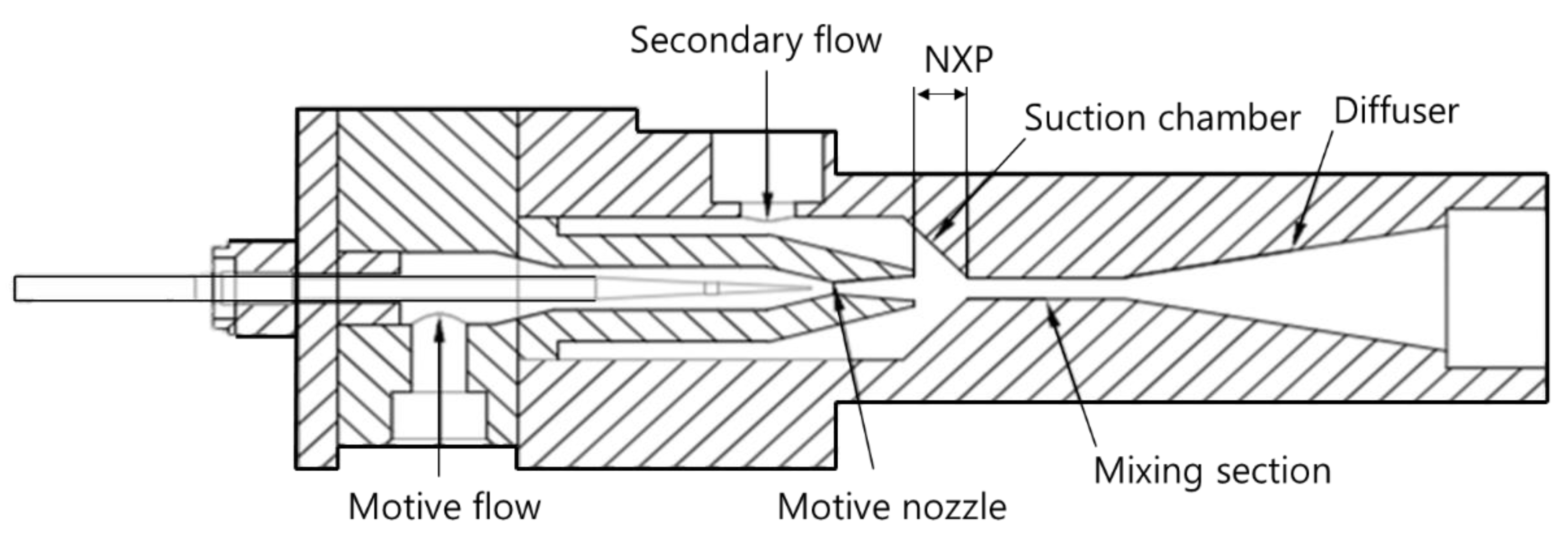
2.1. Experimental Setup
2.2. Test Procedure and Data Reduction
3. Results and Discussion
3.1. Effects of Compressor Speed on the COS Ejector Cycle
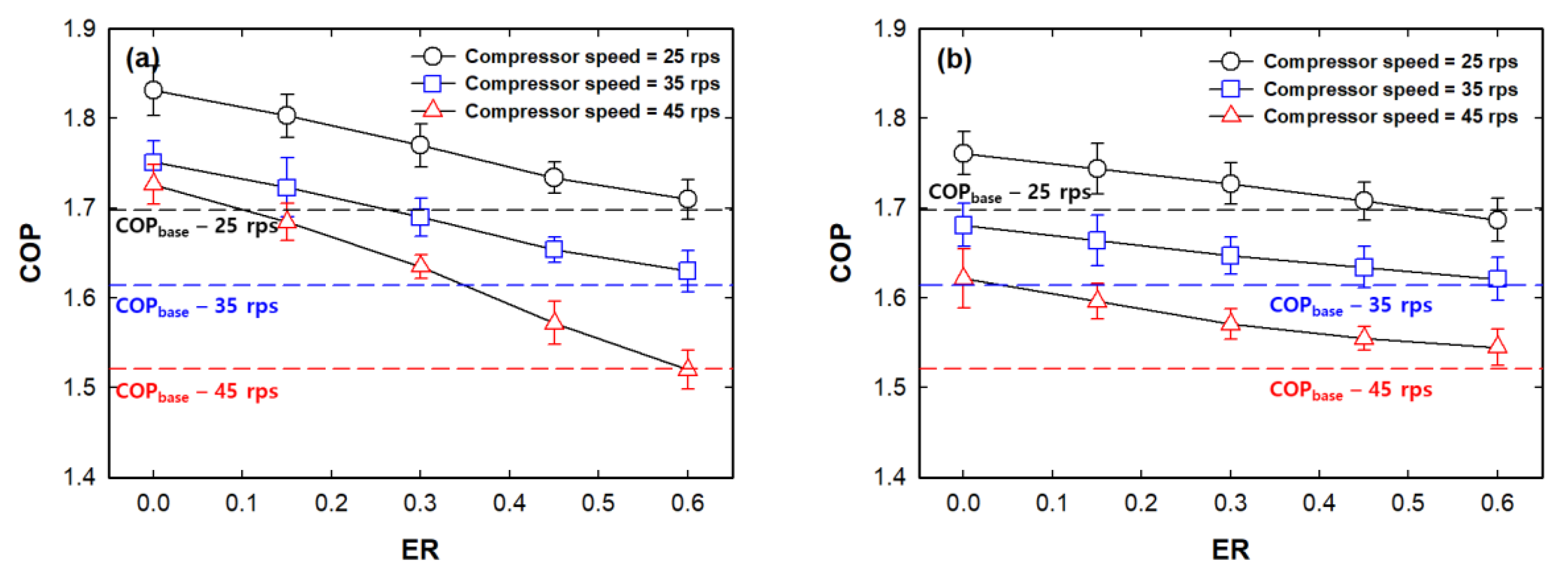
3.2. Effects of ER on the COS Ejector Cycle
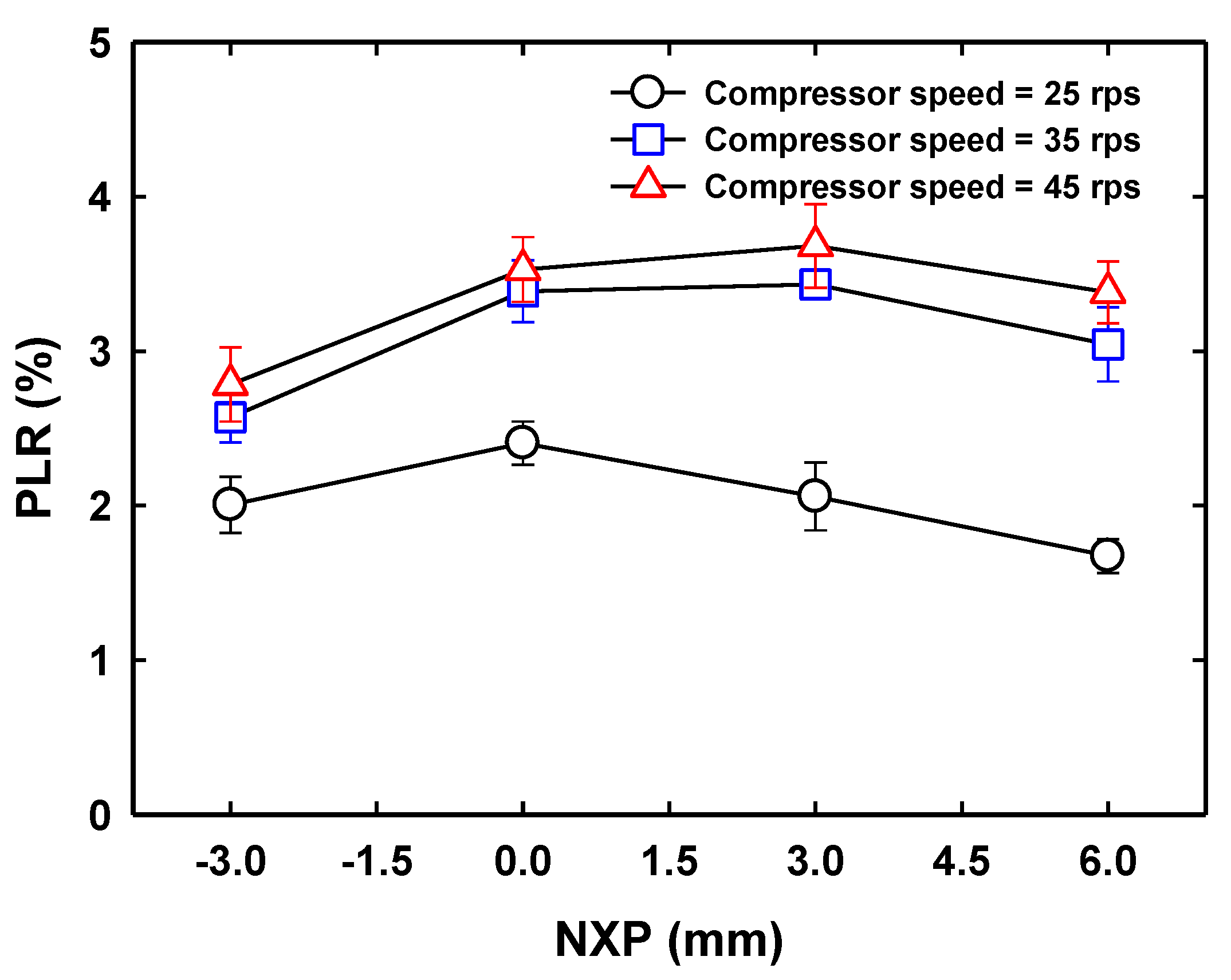
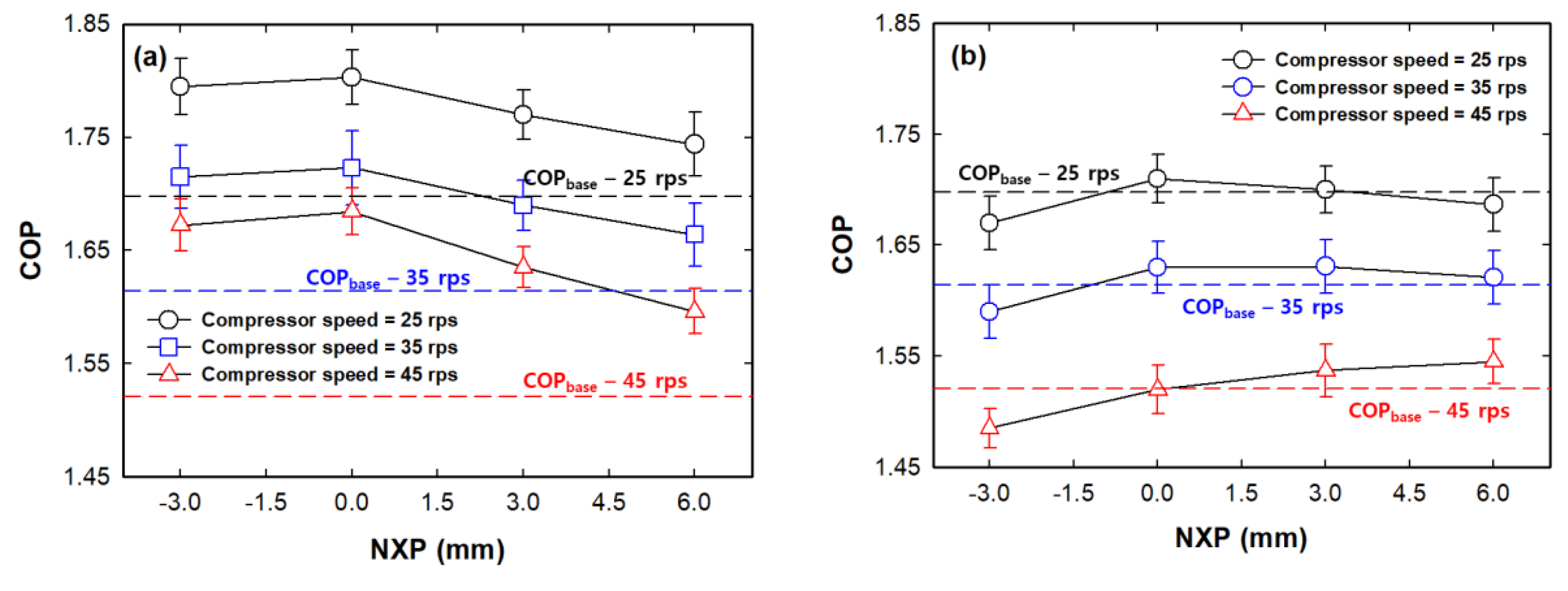
3.3. Effects of NXP on the COS Ejector Cycle
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| COP | coefficient of performance. |
| COS | condenser outlet split |
| ER | entrainment ratio |
| PLR | pressure lifting ratio |
| NXP | nozzle exit position |
Nomenclature
| comp | compressor |
| cond | condenser |
| h | specific enthalpy (kJ Kg−1) |
| mass flow rate (kg h−1) | |
| P | pressure (kPa) |
| cooling capacity (W) | |
| compressor work (W) | |
| Subscripts | |
| eva | evaporator |
| high | high-temperature evaporator |
| in | inlet |
| low | low-temperature evaporator |
| mot | motive |
| out | outlet |
| s | secondary |
References
- Cheng, W.L.; Yuan, X.D. Numerical analysis of a novel household refrigerator with shape-stabilized PCM (phase change material) heat storage condensers. Energy 2013, 59, 265–276. [Google Scholar] [CrossRef]
- Yang, M.; Jung, C.; Kang, Y. Development of high efficiency cycles for domestic refrigerator-freezer application. Energy 2015, 93, 2258–2266. [Google Scholar] [CrossRef]
- Jeon, Y.; Lee, S.; Kim, W.; Jung, J.; Kim, Y. Numerical study on the optimal design of injection-hole geometries of a twin rotary compressor in a liquid injection heat pump. Appl. Them. Eng. 2017, 25, 1178–1188. [Google Scholar] [CrossRef]
- Sun, Z.C.; Ma, X.; Ma, L.X.; Li, W.; Kukulka, D. Flow boiling heat transfer characteristics in horizontal, three-dimensional enhanced tubes. Energies 2019, 12, 927. [Google Scholar] [CrossRef] [Green Version]
- Jeon, Y.; Kim, D.; Jung, J.; Jang, D.S.; Kim, Y. Comparative performance evaluation of conventional and condenser outlet split ejector-based domestic refrigerator-freezers using R600a. Energy 2018, 161, 1085–1095. [Google Scholar] [CrossRef]
- Jeon, Y.; Kim, S.; Kim, D.; Chung, H.J.; Kim, Y. Performance characteristics of an R600a household refrigeration cycle with a modified two-phase ejector for various ejector geometries and operating conditions. Appl. Energy 2017, 205, 1059–1067. [Google Scholar] [CrossRef]
- Aridhi, E.; Albouchi, A.; Mami, A. Observability and controllability study of a household refrigerator exposed to an outdoor cold airflow using bond graph approach. Int. J. Air-Cond. Refrig. 2017, 25, 175001. [Google Scholar] [CrossRef]
- Nguyen, M.P. Overall optimization and exergy analysis of an air conditioning using a series-series conunterflow arrangement of water chillers. Int. J. Air-Cond. Refrig. 2019, 27, 1950034. [Google Scholar]
- Shabgard, H.; Bergman, T.; Sharifi, N.; Faghri, A. High temperature latent heat thermal energy storage using heat pipes. Int. J. Heat Mass Transf. 2010, 53, 2979–2988. [Google Scholar] [CrossRef]
- Esarte, J.; Blanco, J.; Bernardini, A.; San-José, J. Optimizing the design of a two-phase cooling system loop heat pipe: Wick manufacturing with the 3D selective laser melting printing technique and prototype testing. Appl. Them. Eng. 2017, 111, 407–419. [Google Scholar] [CrossRef]
- Gay, N. Refrigerating System. U.S. Patent Application Publication US183 1931. [Google Scholar]
- Elbel, S.; Hrnjak, P. Flash gas bypass for improving the performance of transcritical R744 systems that use microchannel evaporators. Int. J. Refrig. 2004, 27, 724–735. [Google Scholar] [CrossRef]
- Chen, W.; Shi, C.; Zhang, S.; Chen, H.; Chong, D.; Yan, J. Theoretical analysis of ejector refrigeration system performance under overall modes. Appl. Energy 2017, 185, 2074–2084. [Google Scholar] [CrossRef]
- Macia, L.; Castilla, R.; Gamez-montero, P.J.; Camacho, S.; Codina, E. Numerical simulation of a supersonic ejector for vacuum generation with explicit and implicit solver in open foam. Energies 2019, 12, 3553. [Google Scholar] [CrossRef] [Green Version]
- Shovon, M.; Kumar, R.; Kim, T.; Kim, H. Study on the conceptual design of a solar ejector refrigeration system. Int. J. Air-Cond. Refrig. 2020, 28, 2030001. [Google Scholar] [CrossRef]
- He, Y.; Deng, J.; Li, Y.; Ma, L. A numerical contrast on the adjustable and fixed trancritical CO2 ejector using exergy flux distribution analysis. Energy Convers. Manag. 2019, 196, 729–738. [Google Scholar] [CrossRef]
- Bodys, J.; Smolka, J.; Banasiak, K.; Palacz, M.; Haida, M.; Nowak, A.J. Performance improvement of the R744 two-phase ejector with an implemented suction nozzle bypass. Int. J. Refrig. 2018, 90, 216–228. [Google Scholar] [CrossRef] [Green Version]
- Jeon, Y.; Jung, J.; Kim, D.; Kim, S.; Kim, Y. Effects of ejector geometries on performance of ejector-expansion R410A air conditioner considering cooling seasonal performance factor. Appl. Energy 2017, 205, 761–768. [Google Scholar] [CrossRef]
- Lawrence, N.; Elbel, S. Experimental investigation of a two-phase ejector cycle suitable for use with low-pressure refrigerants R134a and R1234yf. Int. J. Refrig. 2014, 38, 310–322. [Google Scholar] [CrossRef]
- Oshitani, H.; Yamanaka, Y.; Takeuchi, H.; Kusano, K.; Ikegami, M.; Takano, Y.; Ishizaka, N.; Sugiura, T. Vapor Compression Cycle Having Ejector. U.S. Patent Application Publication US 2005/0268644 A1.
- Lawrence, N.; Elbel, S. Theoretical and practical comparison of two-phase ejector refrigeration cycles including first and second law analysis. Int. J. Refrig. 2013, 36, 1220–1232. [Google Scholar] [CrossRef]
- Kim, S.; Jeon, Y.; Chung, H.J.; Kim, Y. Performance optimization of an R410A air-conditioner with a dual evaporator ejector cycle based on cooling seasonal performance factor. Appl. Energy 2018, 131, 988–997. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Kus, W.; Fic, A.; Bulinski, Z.; Nowak, A.; Banasiak, K.; Hafner, A. CFD-based shape optimization of a CO2 two-phase ejector mixing section. Appl. Them. Eng. 2016, 95, 62–69. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Wang, X.; Zhao, H. Design and numerical investigation of an adaptive nozzle exit position ejector in multi-effect distillation desalination system. Energy 2017, 140, 673–681. [Google Scholar] [CrossRef]
- Wu, H.; Liu, Z.; Han, B.; Li, Y. Numerical investigation of the influences of mixing chamber geometries on steam ejector performance. Desalination 2014, 353, 15–20. [Google Scholar] [CrossRef]
- Yan, J.; Li, S.; Liu, Z. Numerical investigation on optimization of ejector primary nozzle geometries with fixed/varied nozzle exit position. Appl. Them. Eng. 2020, 175, 115426. [Google Scholar] [CrossRef]
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results; NIST Technical Note 1297; NIST: Gaithersburg, MD, USA, 1994. [Google Scholar]


| Component | Variable | Values |
|---|---|---|
| Compressor | Type | Reciprocating |
| Cylinder volume | 1.531 × 10−5 m3 | |
| Working fluid | R600a | |
| Condenser | Type | Coaxial double pipe |
| Length | 2.07 m | |
| Diameter | 1.27 × 10−2 m | |
| Rated capacity | 500 W | |
| Evaporator | Type | Cartridge (insert) |
| Rated capacity | 300 W | |
| Needle valve | Orifice diameter | 1.19 × 10−3 m |
| Ejector | Nozzle throat diameter | 8.5 × 10−4 m |
| Nozzle outlet diameter | 9.7 × 10−4 m | |
| NXP | −3–6 mm | |
| Mixing section diameter | 3.0 mm | |
| Mixing section length | 36 mm | |
| Diffuser angle | 5° |
| Operating Condition | Range | Interval |
|---|---|---|
| Compressor speed (rps) | 25–45 | 10 |
| ER | 0–0.6 | 0.15 |
| NXP (mm) | −3–6 | 3 |
| Condensing pressure (kPa) | 500 | — |
| Evaporating pressure (kPa) | 70 | — |
| Subcooling (°C) | 3 | — |
| Superheat (°C) | 5 | — |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, Y.; Kim, H.; Ahn, J.H.; Kim, S. Effects of Nozzle Exit Position on Condenser Outlet Split Ejector-Based R600a Household Refrigeration Cycle. Energies 2020, 13, 5160. https://doi.org/10.3390/en13195160
Jeon Y, Kim H, Ahn JH, Kim S. Effects of Nozzle Exit Position on Condenser Outlet Split Ejector-Based R600a Household Refrigeration Cycle. Energies. 2020; 13(19):5160. https://doi.org/10.3390/en13195160
Chicago/Turabian StyleJeon, Yongseok, Hoon Kim, Jae Hwan Ahn, and Sanghoon Kim. 2020. "Effects of Nozzle Exit Position on Condenser Outlet Split Ejector-Based R600a Household Refrigeration Cycle" Energies 13, no. 19: 5160. https://doi.org/10.3390/en13195160
APA StyleJeon, Y., Kim, H., Ahn, J. H., & Kim, S. (2020). Effects of Nozzle Exit Position on Condenser Outlet Split Ejector-Based R600a Household Refrigeration Cycle. Energies, 13(19), 5160. https://doi.org/10.3390/en13195160






