Optimization of a Stirling Engine by Variable-Step Simplified Conjugate-Gradient Method and Neural Network Training Algorithm

Abstract

The present study develops a novel optimization method for designing a Stirling engine by combining a variable-step simplified conjugate gradient method (VSCGM) and a neural network training algorithm. As compared with existing gradient-based methods, like the conjugate gradient method (CGM) and simplified conjugate gradient method (SCGM), the VSCGM method is a further modified version presented in this study which allows the convergence speed to be greatly accelerated while the form of the objective function can still be defined flexibly. Through the automatic adjustment of the variable step size, the optimal design is reached more efficiently and accurately. Therefore, the VSCGM appears to be a potential and alternative tool in a variety of engineering applications. In this study, optimization of a low-temperature-differential gamma-type Stirling engine was attempted as a test case. The optimizer was trained by the neural network algorithm based on the training data provided from three-dimensional computational fluid dynamic (CFD) computation. The optimal design of the influential parameters of the Stirling engine is yielded efficiently. Results show that the indicated work and thermal efficiency are increased with the present approach by 102.93% and 5.24%, respectively. Robustness of the VSCGM is tested by giving different sets of initial guesses.

1. Introduction

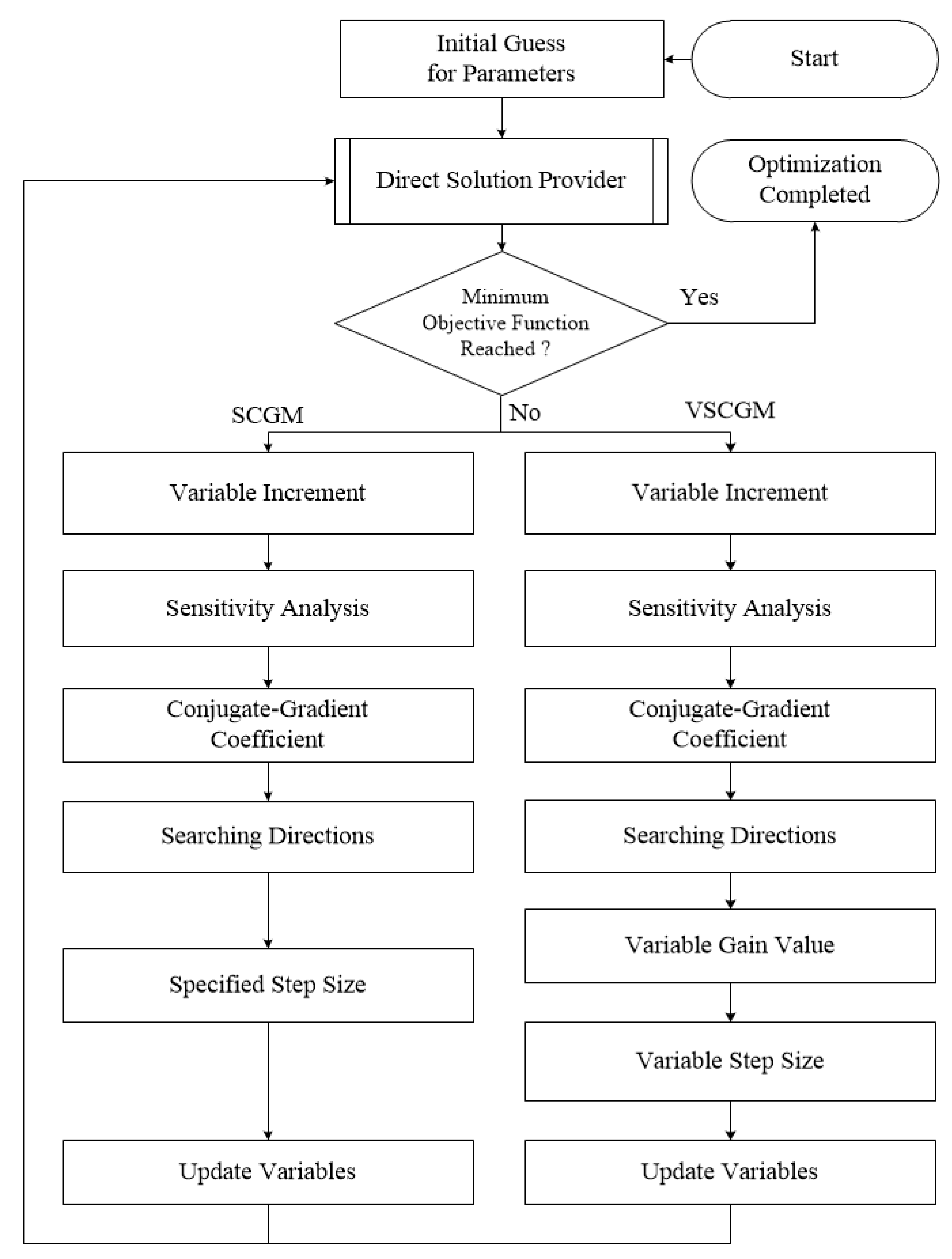
The traditional conjugate gradient method is mainly based on the steepest-descent method or Newton method [1]. The steepest-descent method can reach the immediate neighboring area of the optimal point; however, the searching ability is reduced as the distance between the iterative and the optimal points is small [2]. The Newton method is also referred to as a gradient-based optimization method [3]. Compared to the steepest-descent method, the convergence speed of the Newton method is even faster. Unfortunately, if the position of the original point is too far away from the optimal point, the iteration of the Newton method may fail to achieve convergence. The traditional conjugate gradient method (CGM) combines the above two methods and thus takes advantage of them. However, the feasibility of this method is still limited because the form of the objective function should be cast into a sum of squared difference [4], and hence, it is not suitable for multi-goal optimization.

Cheng and Chang [5] proposed a simplified conjugate gradient method (SCGM). The SCGM method is referred to as a local optimization scheme that is suitable for the search for optimal parameters within a bounded range. With this method, the step sizes corresponding to the designed parameters are fixed during iteration, and the sensitivity of the objective function to the perturbations of the designed parameters are evaluated directly using direct numerical differentiation. In this manner, the objective function can be defined flexibly and not limited to a sum of squared difference form. Besides, the SCGM method features a simplification in the mathematical formulation, and hence, it has been widely applied in the optimization of various engineering devices, such as fuel cells [6], thermoelectric coolers [7], micro reformers [8], and so on. However, one major disadvantage of this method is that the SCGM method may slow down the convergence because the step size is fixed.

For further improving the SCGM method, in this study an efficient method, which is named variable-step simplified conjugate gradient method (VSCGM), is proposed. This method is a further modified version of the SCGM method. In the VSCGM method, the step size of the iteration can be varied and adjusted automatically, and the adjustment is dependent on the gain function and ratio of search directions. The VSCGM allows the convergence speed to be greatly accelerated while the form of the objective function can still be defined flexibly.

In this study, a direct solution provider is built based on the deep learning neural network algorithm, which learns to map inputs to outputs given a training dataset of examples. The training process involves finding a set of weights in the network that are accurate enough at solving the specific problems. The first step towards the artificial neuron was taken by McCulloch and Pitts in 1943 inspired by neurobiology [9,10]. Rosenblatt [11] used a probabilistic model for information storage and organization simulating the perception and learning ability of the brain. Lately, DARPA employed a layered method to explore this new terrain and the development of DARPA on the neural network model was described in [12]. Rumelhart, McClelland, and PDP Research Group [13] assumed the mind includes a great number of elementary units connected in a neural network. Recently, there have been many neural models proposed by related researchers. Rumelhart, Hinton, and Williams [14,15] presented a backpropagation model that can efficiently calculate the gradient of the loss function with respect to the weights of the network. It is feasible to use gradient methods for training multi-layer networks and updating weights to minimize loss. Munakata [16] introduced the fundamentals of the backpropagation model and stated that a neural network is composed of artificial neurons and interconnections. Such a network can be viewed as a graph, neurons as nodes, and interconnections as edges. A general review of the backpropagation model is given by Goodfellow, Bengio, and Courville [17]. In machine learning, especially deep learning, the backpropagation model is an algorithm widely used in the training of feedforward neural networks with supervised learning. Among the known methods with the backpropagation model, the Levenberg–Marquardt method [18] appears to be the fastest method for training moderate-sized feedforward neural networks. Thus, in the present study, the neural network algorithm is developed based on this method [19].

On the other hand, the Stirling engine is referred to as an external combustion engine, which may be operated at a low-temperature difference between high and low thermal reservoirs, and compatible with a variety of heat sources like solar energy, geothermal energy, and industrial waste. Besides, the engine features low noise, high efficiency, and safe operation; therefore, the Stirling engine can serve as an alternative power machine to improve global warming and reduce the usage of fossil energy. In terms of the mechanical structure, Stirling engines are divided into three configurations: alpha-, beta-, and gamma-types [20]. Among them, the gamma-type Stirling engines are the most popular configuration to exploit low-temperature thermal energy. Recently, Cheng, Le, and Huang [21] developed a computational fluid dynamics (CFD) module of a low-temperature-differential gamma-type Stirling engine that might be used for recycling the waste heat at 423 to 700 K. They used the CFD module to investigate the effects of the geometrical and operating parameters on the indicated power output and thermal efficiency of the engine; however, in their parametric analysis, when the effects of a parameter were investigated to find the optimal value of the parameter, all other parameters were fixed at prescribed values; therefore, the optimization is referred to as one-parameter optimization. To improve the performance of a real engine, the one-parameter optimization is not practical, and the optimizer should be capable of dealing with multi-parameter optimization.

As a test case for testing the present approach, optimization of the low-temperature-differential gamma-type Stirling engine was attempted. The dataset for training the neural network was prepared based on the CFD computational results using a similar module of Cheng, Le, and Huang [21]. Given input geometrical parameters, the trained neuron network then served as the direct solution provider and outputs numerical information of the indicated power output and the thermal efficiency of the engine.

On the other hand, an objective function is defined in terms of the indicated power output and the thermal efficiency of the engine and is calculated by the direct solution provider. Meanwhile, with the help of the neural network algorithm, the VSCGM method was employed to iteratively adjust multiple parameters until the objective function is minimized and the optimum group of the parameters is obtained.

2. Optimization Methods

2.1. CGM Method

With the traditional conjugate gradient method (CGM), the objective function (J) to minimize is typically defined as the sum of squares of the differences

$$J={\displaystyle \sum _{i=1}^{\mathrm{I}}{(v_i-\overline{v_i})}^2}$$

(1)

where v_i and $\overline{v_i}$ are the iterative and the compared quantities, respectively, and I is the number of input data. The gradient of the objective function for the designed parameters, {X_j | j = 1, 2,.., k} where k is the number of designed parameters, is then expressed in terms of the sensitivity coefficients $\partial v_i/\partial X$ as

$$\frac{\partial J}{\partial X_j}={\displaystyle \sum _{i=0}^{I}2(v_i-\overline{v_i})}\frac{\partial v_i}{\partial X_j} j=1, 2, \dots , k$$

(2)

The conjugate gradient coefficient (γ_j) is expressed as the ratio of gradients of objective functions of two consecutive iteration steps:

$${\gamma }_j^n={[{(\frac{\partial J}{\partial X_j})}^n/{(\frac{\partial J}{\partial X_j})}^{n-1}]}^2 j=1, 2, \dots , k$$

(3)

where n is the index of the iteration step. Next, the search direction is calculated as a linear combination of the conjugated gradient coefficient and gradients of the objective function.

$$P_j^n={(\frac{\partial J}{\partial X_j})}^n+{\gamma }_j^n{P}_j^{n-1} j=1, 2, \dots , k$$

(4)

The designed parameter is then updated as follows:

$$X_j^{n+1}=X_j^n-{\beta }_j{P}_j^n j=1, 2, \dots , k$$

(5)

In the CGM method, for different designed parameters {X_j | j = 1, 2,.., k} the corresponding step sizes {βj | j = 1, 2,.., k} are different. They are obtained by solving a set of simultaneous linear algebraic equations. Meanwhile, the sensitivity coefficient ∂v_i/∂X_j with each of the designed parameters is calculated from the solution of a partial differential equation (PDE). Thus, if there are k designed parameters, one may have k PDEs to solve for the values of the k sensitivity coefficients. These sensitivity coefficients are introduced into (2) to determine the gradient of objective function ∂J/∂X_j.

2.2. SCGM Method

In the SCGM method proposed by Cheng and Chang [5], the step sizes corresponding to the designed parameters are fixed during iteration. That is

β_j = C_j    j = 1, 2,.., k

(6)

The task of the sensitivity analysis is to evaluate the sensitivity of the objective function J for the designed parameter, which is represented with the gradient of objective function ∂J/∂X_j and is evaluated directly using direct numerical differentiation as

$$\frac{\partial J}{\partial X_j}=\frac{\Delta J}{\Delta X_j} j= 1, 2,.., k$$

(7)

The perturbations in the designed parameters ΔX_j can be specified readily by trial and error. In this study, these perturbations are ranged between 0.0001 and 0.001 depending on the complexity of the problem. In the optimization process, the values are fixed generally.

In this manner, it is not necessary to solve any equation for the sensitivity coefficients nor the step sizes, and hence, the tedious computation process is greatly simplified. Furthermore, the objective function is not limited to the form of the sum of the squared difference; however, one major disadvantage of this method is that the SCGM method may slow down the convergence because the step size is fixed. Under these circumstances, the present study developed a novel optimization method that is named variable-step simplified conjugate gradient method (VSCGM), which is described in the successive section.

2.3. VSCGM Method

The VSCGM method is a further modified version of the SCGM method, which can reduce the time to reach convergence while the form of the objective function can still be defined flexibly. Finding an optimum design can be accomplished by following almost the same problem-solving process of the SCGM method.

In the VSCGM method, the gradient of objective function ∂J/∂X_j is calculated by using the same direct numerical differentiation method as described with (7); however, since the distance between the iterative and the optimal points is gradually decreased in the iterations, the values of the step sizes and the perturbations of the designed parameters for the sensitivity analysis are varied. For this purpose, the perturbations in the designed parameters ΔX_j⁽ⁿ⁾ is determined at each iteration as

$$\Delta X_j^{\left(n\right)}=\Delta X_j^{\left(1\right)}\times \frac{{\beta }_j^{\left(1\right)}}{{\beta }_j^{(n-1)}} j= 1, 2,.., k$$

(8)

where ΔG_j⁽¹⁾ and β_j⁽¹⁾ are the initial values of the perturbations and the step sizes, respectively, in the first iteration. It is noted that as the iterative point approaches the optimal point, the step sizes β_j⁽¹⁾ should be reduced to its minimum such that the iteration may not jump over the optimal point. Thus, the step sizes are expressed with

$$\{\begin{array}{l}{\beta }_j^{(n)}={\beta }_j^{(n-1)}\times {(R_{j,\min })}^{G_{j,\min }} ,R_j^{(n)}\le R_{j,\min }\\ {\beta }_j^{(n)}={\beta }_j^{(n-1)}\times {(R_j^{(n)})}^{G_j^{(n)}},R_{j,\min }<R_j^{(n)}<R_{j,Max}\\ {\beta }_j^{(n)}={\beta }_j^{(n-1)}\times {(R_{j,Max})}^{G_{j,Max}},R_{j,Max}\le R_j^{(n)}\end{array} j= 1, 2,.., k$$

(9)

where

$$G_j^{(n)}=(\frac{R_j^{(n)}-R_{j,\min }}{R_{j,Max}-R_{j,\min }})\times (G_{j,\min }-G_{j,Max})+G_{j,Max} j= 1, 2,.., k$$

(10)

and

$$R_j^{(n)}=\frac{P_j^{(n)}}{P_j^{(n-1)}} j=1, 2,.., k$$

(11)

The variable step size is automatically adjusted with (9) to (11) in terms of the gain function (G_j⁽ⁿ⁾) and the ratio of search directions (R_j⁽ⁿ⁾). The gain function is calculated by using a linear interpolation between two extreme values, G_j,min and G_j,Max. The two extreme values need to be appropriately specified by the user. In this study, the minimum and maximum gain function values are assigned to be 1.0 and 3.0, respectively. Through the gain function, the influence of the ratio of search directions is introduced to the adjustment of the step sizes. Note that the step sizes can be enlarged or reduced depending on the magnitudes of the gain function and the ratio of search directions. In this way, when the iterative point is still far away from the optimal point, the step sizes can be increased to facilitate the search. On contrary, the step sizes will be decreased when the iterative point gets into the immediate neighboring area of the optimal point; however, to avoid a steep rise or steep drop in the step sizes, it is necessary to prescribe the upper and the lower bounds of the ratio of search directions (R_j,Max, R_j,min) properly.

Through the automatic adjustment of the variable step size, the optimal design is reached more efficiently and accurately. Figure 1 shows the comparison in the solution process between VSCGM and SCGM with computation flow charts, and the difference between the two methods can be seen.

3. Neural Network Algorithm

3.1. CFD Module Generating Dataset of Training

Here, the three-dimensional CFD computation is done by using a numerical module similar to that of Cheng, Le, and Huang [21]. The physical model with geometrical parameters of the engine is shown in Figure 2. The space of the engine includes three chambers, namely an expansion chamber, compression chamber, and regenerator. The expansion chamber at the bottom contacts with the high-temperature energy sources, whereas the compression chamber at the top is cooled by a heat sink. The regenerator between the two chambers helps recycle the exhaust heat from the hot working fluid. The two moving parts, the piston and displacer, are connected to a flywheel.

The mathematical model in the CFD analysis is described briefly as follows:

Mass equation:

$$\frac{\partial \rho }{\partial t}+\frac{\partial \rho u}{\partial x}+\frac{\partial \rho v}{\partial y}+\frac{\partial \rho \mathrm{w}}{\partial z}=0$$

(12)

where ρ is the fluid density, and u, v and w are the velocity components in the x-, y-, and z-directions.

Momentum equations:

x-direction

$$\begin{array}{l}\frac{\partial \left(\rho u\right)}{\partial t}+\frac{\partial \left(\rho u^2+p\right)}{\partial x}+\frac{\partial \left(\rho uv\right)}{\partial y}+\frac{\partial \left(\rho uw\right)}{\partial z}=\\ \frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}+\frac{\partial \left(-\overline{\rho {u^{\prime }}^2}\right)}{\partial x}+\frac{\partial \left(-\overline{\rho v^{\prime }{u}^{\prime }}\right)}{\partial y}+\frac{\partial \left(-\overline{\rho w^{\prime }{u}^{\prime }}\right)}{\partial z}\end{array}$$

(13)

y-direction

$$\begin{array}{l}\frac{\partial \left(\rho v\right)}{\partial t}+\frac{\partial \left(\rho vu\right)}{\partial x}+\frac{\partial \left(\rho v^2+p\right)}{\partial y}+\frac{\partial \left(\rho vw\right)}{\partial z}=\\ \frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}+\frac{\partial \left(-\overline{\rho u^{\prime }{v}^{\prime }}\right)}{\partial x}+\frac{\partial \left(-\overline{\rho {v^{\prime }}^2}\right)}{\partial y}+\frac{\partial \left(-\overline{\rho w^{\prime }{v}^{\prime }}\right)}{\partial z}\end{array}$$

(14)

z-direction

$$\begin{array}{l}\frac{\partial \left(\rho w\right)}{\partial t}+\frac{\partial \left(\rho wu\right)}{\partial x}+\frac{\partial \left(\rho wv\right)}{\partial y}+\frac{\partial \left(\rho w^2+p\right)}{\partial z}=\\ \frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial y}+\frac{\partial {\tau }_{zz}}{\partial z}+\frac{\partial \left(-\overline{\rho u^{\prime }{w}^{\prime }}\right)}{\partial x}+\frac{\partial \left(-\overline{\rho v^{\prime }{w}^{\prime }}\right)}{\partial y}+\frac{\partial \left(-\overline{\rho { w^{\prime }}^2}\right)}{\partial z}\end{array}$$

(15)

Energy conservation equation:

$$\begin{array}{l}\frac{\partial (\rho e)}{\partial t}+\frac{\partial (\rho ue)}{\partial x}+\frac{\partial (\rho ve)}{\partial y}+\frac{\partial (\rho we)}{\partial z}=\\ \frac{DP}{Dt}+\frac{\partial }{\partial x}\left[\left(\lambda +\frac{c_p{\mu }_t}{{\mathit{Pr}}_t}\right)\frac{\partial T}{\partial x}\right]+\frac{\partial }{\partial y}\left[\left(\lambda +\frac{c_p{\mu }_t}{{\mathit{Pr}}_t}\right)\frac{\partial T}{\partial y}\right]\\ +\frac{\partial }{\partial z}\left[\left(\lambda +\frac{c_p{\mu }_t}{{\mathit{Pr}}_t}\right)\frac{\partial T}{\partial z}\right]\end{array}$$

(16)

where c_p is the specific heat of working fluid, Pr_t is turbulence Prandtl number, and μ_t is the eddy viscosity.

The realizable k-ε model is selected for the numerical model because it simulates accurately a wide range of boundary layer flow with a pressure gradient. The realizable k-ε model includes the following two well-known transport equations:

Turbulent kinetic energy equation (k-equation):

$$\frac{\partial }{\partial t}(pk)+\frac{\partial }{\partial x_j}(\rho k{u}_j)=\frac{\partial }{\partial }\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k+G_b-\rho \epsilon -Y_M+S_k$$

(17)

where G_k and G_b denote the generation of turbulence kinetic energy due to the mean velocity gradients and buoyancy, respectively.

Viscous dissipation of turbulent kinetic energy equation (ε-equation):

$$\frac{\partial }{\partial t}\left(\rho \epsilon \right)+\frac{\partial }{\partial x_j}\left(\rho \epsilon u_j\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+\rho C_{1}S\epsilon -\rho C_2\frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}+ C_{1\epsilon }\frac{\epsilon }{k}{C}_{3\epsilon }{G}_b+S_{\epsilon }$$

(18)

where $C_1=\max \left[0.43,\frac{\chi }{\chi +5}\right]$, $C_{1\epsilon }=1.44$, $C_2=1.9$, ${\sigma }_k=1.0$, ${\sigma }_{\epsilon }=1.2$, $\chi =S\frac{k}{\epsilon }$, and $S=\sqrt{2S_{ij}{S}_{ij}}$.

Detailed information regarding the coefficients with the above mathematical model, boundary conditions, fluid properties of the CFD module is available in [21]. The framework of the CFD module is briefly described in

Table 1. Computational fluid dynamics (CFD) simulation framework.

Turbulence model	Realizable k-ε model
Porous medium model	Darcy–Forchheimer law
Pressure-velocity coupling	PISO
Spatial discretization	Second-order upwind scheme
Equation of state	Soave–Redlich–Kwong real-gas model
Number of elements	1,141,047

. Major geometric and operating parameters of a baseline engine considered in the computation are provided in

Table 2. Parameters with the baseline case.

Parameter	Value
Phase angle θph (deg.)	90
Piston diameter Dp (m)	0.17
Porosity ϕ	0.9
Rotation speed ω (rpm)	100
Displacer stroke sd (m)	0.04
Piston stroke sp (m)	0.08
Charged pressure Pch (bar)	5
Equilibrium position of piston xp (m)	0.196
Heating Temperature TH (K)	423
Cooling Temperature TL (K)	300
Working fluid	Helium
Indicated Power (W)	161.616
Thermal Efficiency (%)	16.532

. The baseline engine is used as the test case to demonstrate the performance of the present approach.

The present Stirling engine is referred to as a low-temperature-differential engine that can be applied in waste heat recovery. The engine is driven between an ambient temperature of 300 K and a heating temperature of 423 K. Both the two temperatures are constant during optimization. In a particular application, the heating temperature may reach 700 K. The heating conditions with all the test cases are already given in detail in

Table 3. CFD computation results.

Case	ω [rpm]	Pch [bar]	θph [deg]	Dp [m]	xp [m]	sd [m]	TH [K]	ϕ	W [Watt]	ε [%]
1	100	1	90	0.17	0.196	0.04	423	0.9	33.495	10.417
2	100	2	90	0.17	0.196	0.04	423	0.9	67.966	12.820
3	100	3	90	0.17	0.196	0.04	423	0.9	102.501	15.191
4	100	5	90	0.17	0.196	0.04	423	0.9	161.616	16.532
5	100	7	90	0.17	0.196	0.04	423	0.9	217.457	17.277
6	100	9	90	0.17	0.196	0.04	423	0.9	271.267	17.794
7	100	5	70	0.17	0.196	0.04	423	0.9	142.664	15.556
8	100	5	80	0.17	0.196	0.04	423	0.9	154.294	16.211
9	100	5	95	0.17	0.196	0.04	423	0.9	162.973	16.638
10	100	5	97.5	0.17	0.196	0.04	423	0.9	163.776	16.686
11	100	5	100	0.17	0.196	0.04	423	0.9	164.183	16.722
12	100	5	102.5	0.17	0.196	0.04	423	0.9	165.674	16.985
13	100	5	105	0.17	0.196	0.04	423	0.9	168.071	17.375
14	100	5	107.5	0.17	0.196	0.04	423	0.9	164.156	17.109
15	100	5	110	0.17	0.196	0.04	423	0.9	160.242	16.838
16	100	5	90	0.17	0.196	0.04	470	0.9	228.422	19.921
17	100	5	90	0.17	0.196	0.04	500	0.9	264.706	21.262
18	100	5	90	0.17	0.196	0.04	550	0.9	313.565	22.930
19	100	5	90	0.17	0.196	0.04	600	0.9	346.658	23.281
20	100	5	90	0.17	0.196	0.04	700	0.9	432.119	23.655
21	100	5	90	0.17	0.196	0.04	423	0.7	158.124	12.567
22	100	5	90	0.17	0.196	0.04	423	0.8	160.069	13.629
23	100	5	90	0.17	0.196	0.04	423	0.9	161.615	16.532
24	100	5	90	0.17	0.196	0.04	423	0.915	164.067	17.488
25	100	5	90	0.17	0.196	0.04	423	0.93	166.815	18.518
26	100	5	90	0.17	0.196	0.04	423	0.95	164.633	18.900
27	100	5	90	0.17	0.196	0.04	423	0.97	162.767	20.276
28	100	5	90	0.17	0.196	0.04	423	0.99	158.087	22.235
29	30	5	90	0.17	0.196	0.04	423	0.9	22.368	11.913
30	60	5	90	0.17	0.196	0.04	423	0.9	87.817	17.659
31	80	5	90	0.17	0.196	0.04	423	0.9	132.797	17.840
32	90	5	90	0.17	0.196	0.04	423	0.9	147.652	17.103
33	120	5	90	0.17	0.196	0.04	423	0.9	181.683	15.138
34	150	5	90	0.17	0.196	0.04	423	0.9	205.998	13.885
35	200	5	90	0.17	0.196	0.04	423	0.9	243.438	12.613
36	250	5	90	0.17	0.196	0.04	423	0.9	277.842	11.761
37	300	5	90	0.17	0.196	0.04	423	0.9	303.382	10.941
38	350	5	90	0.17	0.196	0.04	423	0.9	324.460	10.237
39	400	5	90	0.17	0.196	0.04	423	0.9	336.335	9.448
40	450	5	90	0.17	0.196	0.04	423	0.9	347.323	8.795
41	500	5	90	0.17	0.196	0.04	423	0.9	352.782	8.146
42	550	5	90	0.17	0.196	0.04	423	0.9	357.819	7.630
43	600	5	90	0.17	0.196	0.04	423	0.9	359.252	7.087
44	700	5	90	0.17	0.196	0.04	423	0.9	347.057	5.987
45	100	5	90	0.17	0.196	0.025	423	0.9	108.004	16.073
46	100	5	90	0.17	0.196	0.03	423	0.9	128.198	16.551
47	100	5	90	0.17	0.196	0.035	423	0.9	147.035	17.107
48	100	5	90	0.17	0.201	0.04	423	0.9	159.561	16.638
49	100	5	90	0.17	0.205	0.04	423	0.9	158.210	16.559
50	100	5	90	0.17	0.211	0.04	423	0.9	156.170	16.377
51	100	5	90	0.17	0.216	0.04	423	0.9	154.047	16.192
52	100	5	90	0.15	0.196	0.04	423	0.9	131.950	15.565
53	100	5	90	0.16	0.196	0.04	423	0.9	146.496	16.008
54	100	5	90	0.18	0.196	0.04	423	0.9	177.939	16.812
55	100	5	90	0.19	0.196	0.04	423	0.9	192.662	16.685

and more information is available in [21].

In the computation, the power output and the thermal efficiency of the engine are treated as performance indices. Stirling engines are characterized by the pressure–volume diagrams for the expansion and the compression chambers. By integrating the function of gas pressure with its volume in a cycle for each of the two chambers, it is possible to write an expression of the indicated power output produced by the engine, in Watt, as

$$W=\frac{\omega }{60}\left({\displaystyle \underset{cycle}{\int }{P}_{c}d{V}_c}+{\displaystyle \underset{cycle}{\int }{P}_{e}d{V}_e}\right)$$

(19)

where the symbol $\underset{cycle}{\overset{}{\int }}$ represents the cyclic integration. Thermal efficiency (ε) is calculated by

ε = W/Q

(20)

where W is indicated power output and Q is the cyclic average rate of heat transfer input.

The effects of rotation speed (ω), charged pressure (P_ch), phase angle (θ_ph), displacer stroke (s_d), piston diameter (D_p), the equilibrium position of the piston (x_p), heating temperature (T_H), and porosity (ϕ) on the power output and the thermal efficiency are evaluated. The numerical data for 55 cases are listed in Table 3. The dataset is used for training the neural network.

3.2. Neural Network

In this study, the Levenberg–Marquardt method [18] is used to update weight and bias values. The method can approach second-order training speed without having to compute the Hessian matrix [22,23]. As shown in Figure 3, in general, the neural network is defined by several neurons connected to each other. These neurons are stacked in three fully connected layers, namely, input, hidden, and output layers. That is, each neuron from one layer is connected to each neuron from the other layers. It means that the output from one neuron is used as an input to other neurons. Deep learning neural network models learn to map inputs to outputs given a training dataset from Table 3.

The training of the neural network is based on the concept of supervised learning [24]. The basic structure of a linear neuron includes weight (W), bias (b), and transfer function [f(x)] [25]. When the input value (p) passes through a network that contains weights and bias values, the weights and bias values within the network are adjusted based on the difference between targets (t) and outputs (a). The formula of a linear neuron could be written as

$$a=f(Wp+b)$$

(21)

The network structure is illustrated in Figure 4. The first layer is the input layer, which has eight neurons; the second one is the hidden layer in which there are twenty-five neurons; the third one is the output layer in which there are two neurons. Each of the hidden and the output layers contains a weighting matrix, a bias matrix, and a conversion function. The eight parameters in the input layer are the prescribed values of rotation speed, charged pressure, phase angle, piston diameter, the equilibrium position of the piston, displacer stroke, heating temperature, and porosity. On the other hand, the two variables in the output layer are indicated power output (W_id) and thermal efficiency (ε). The input values (p), weights (W), biases (b), and output values (a) are expressed in matrix form as

$$p={\left[\begin{array}{c}\omega \\ P_{ch}\\ {\theta }_{ph}\\ d_p\\ x_p\\ s_d\\ T_H\\ \varphi \end{array}\right]}_{8\times 1}, W_1={\left[\begin{array}{ccc}{W}_{1_{1,1}}& \cdots & W_{1_{1,8}}\\ W_{1_{2,1}}& \cdots & W_{1_{2,8}}\\ ⋮& \ddots & ⋮\\ W_{1_{25,1}}& \cdots & W_{1_{25,8}}\end{array}\right]}_{25\times 8}, b_1={\left[\begin{array}{c}{b}_{1_{1,1}}\\ b_{1_{2,1}}\\ ⋮\\ b_{1_{25,1}}\end{array}\right]}_{25\times 1}, x_1={\left[\begin{array}{c}{x}_{1_{11}}\\ x_{1_{2,1}}\\ ⋮\\ x_{1_{25,1}}\end{array}\right]}_{25\times 1},$$

(22a)

$$W_2=\left[\begin{array}{c}\begin{array}{ccc}{W}_{2_{1,1}}& \dots & W_{2_{1,25}}\end{array}\\ \begin{array}{ccc}{W}_{2_{2,1}}& \dots & W_{2_{2,25}}\end{array}\end{array}\right], b_2={\left[\begin{array}{c}{b}_{2_{1,1}}\\ b_{2_{2,1}}\end{array}\right]}_{2\times 1}, a={\left[\begin{array}{c}{W}_{id}\\ \epsilon \end{array}\right]}_{2\times 1}$$

(22b)

The conversion functions used in the network are

$$\{\begin{array}{c}{f}_1(W_{1}p+b_1) = \frac{e^{W_{1}p+b_1}-e^{-W_{1}p-b_1}}{e^{W_{1}p+b_1}+e^{-W_{1}p-b_1}}\\ f_2(W_2{x}_1+b_2) = W_2{x}_1+b_2\end{array}$$

(23)

To increase the amount of data used for training, a triangulation-based interpolation method was applied to generate more data based on the 55-set original data. The final training data were expanded to 3168 sets of samples in total. The data point distributions are plotted in Figure 5. Figure 5a,b displays the data of indicated power output and thermal efficiency, respectively, versus charged pressure and rotation speed.

After training, the mean squared error (MSE) and regression value (R) are examined. The numerical data of the mean squared error and regression value of training are provided in

Table 4. Mean squared error and regression value of training.

	Samples	MSE	R
Training (70%)	2218	157.68	0.9935
Validation (15%)	475	29.38	0.9988
Testing (15%)	475	54.95	0.9977

. The magnitude of MSE is an average squared difference between outputs and targets. In this table, and the values of MSE in the processes of training, validation, and testing are 157.68, 29.39, and 54.95, respectively. Besides, the R-value is the correlation between outputs and targets which is used to characterize relationships among variables. R = 1.0 means a very close relationship, and R = 0 a random relationship. In this study, the values of R in the processes are all close to 1. It means that the training is acceptable with such low errors. The error histogram and regression distribution are provided in Figure 6 and Figure 7, respectively. The bar chart plotted in Figure 6 uses three different color bars to represent the errors in the three training processes individually. It is found again that the three bars are all close to the central line which is marked in orange. It is also observed in Figure 7 that the regression data points closely agree with the fitting lines. This means that the relationship between outputs and targets are indeed rather close.

It is noticed that the CFD simulation software package itself can be used as the direct solution provider; however, the present study employs the neural network algorithm, instead of the CFD simulation software package, to serve as the direct solution provider. One major reason is that the CFD simulation software package consumes too much computation time and resources. For a typical simulation using the CFD software package on a personal computer with an Intel Core i7-7700 processor, it needs approximately 60 h to finish 10 cycles for one iteration. In a typical optimization process, the computation may exceed 2000 iterations, and hence, the time consumed in the optimization process may be longer than 120,000 h. The present study adopts a dataset involving only 55-set original data. The data are expanded to 3168-set training data by the triangulation-based interpolation method. Hence, the computation time can be reduced significantly.

4. Results and Discussion

The trained neuron network serves as the direct solution provider which provides numerical information of the thermal efficiency and the indicated power output of the engine for the VSCGM method. Then, the objective function is determined, and the designed parameters are updated by the VSCGM method. With the updated designed parameters, the neural network provides the indicated power output and the thermal efficiency for the VSCGM method again. The iteration continues until the objective function reaches a minimum value. The VSCGM method can be applied for a multi-goal and multi-parameter optimization. The objective function of optimization is calculated in terms of the indicated power output and the thermal efficiency as

$$J=\frac{1}{M\times W_{id}+N\times \epsilon }$$

(24)

On the right-hand side of the above equation, the denominator of the fraction includes two terms. The first term represents the magnitude of indicated power output, and the second term represents the magnitude of thermal efficiency. M and N are two positive weighting coefficients that are specified by the users depending on individual applications. In the present optimization, the values of M and N are assigned to be 1.0 and 8.8, respectively.

It is important to mention that among the eight parameters, some parameters have a monotonic relationship with the performance of the engine. For example, as the value of charged pressure or heating temperature increases, so does the value of the indicated power output or thermal efficiency. Those parameters are called monotonically related parameters. The parameters can then be categorized into two groups: monotonically and non-monotonically related variables. Here in this study, the optimization task is focused on the group of non-monotonically related parameters. Thus, five non-monotonically related parameters are selected to be the designed parameters, including rotation speed, phase angle, piston diameter, displacer stroke, and porosity. Note that the designed parameters are changed around the values given in Table 2 for the baseline case.

Table 5. Parameters with five-parameter optimization.

Parameter	Initial Design	Lower and Upper Bounds	Optimal Design
Rotation speed ω (rpm)	100	30~700	218.399
Phase angle θph (deg.)	90	70~110	94.885
Piston diameter Dp (m)	0.17	0.15~0.19	0.19
Displacer stroke sd (m)	0.04	0.025~0.04	0.04
Porosity ϕ	0.9	0.7~0.99	0.99
Indicated power output (W)	161.616	-	327.980
Thermal efficiency (%)	16.532	-	17.399
Minimum objective function			0.002078

conveys the initial values and the bounded ranges of the five designed parameters. The results of the indicated power output, thermal efficiency, and minimum objective function before and after the optimization are also provided in this table. A comparison between the initial and optimal designs shows that the indicated power output can be increased from 161.616 to 327.980 W, and the thermal efficiency from 16.532% to 17.399%. In the end, the objective function reaches a minimum value of 0.002078. The indicated power output and the thermal efficiency are elevated with this approach by 102.93% and 5.24%, respectively. The optimization can improve the performance of the engine remarkably. Meanwhile, the values of the designed parameters of the optimal design are determined within the bounded ranges efficiently. These values make up an important part of what influences designers when they make their design decisions.

The increase in the performance via optimization is mainly dependent on the collected dataset (Table 3), the fixed parameters (Table 2), and the lower and the upper bounds of the designed parameters (Table 5). The dataset shown in Table 3 illustrates a wider range for the indicated power while a narrower range for the thermal efficiency. Therefore, it is expected that increase of the indicated power output will be greater than that of thermal efficiency.

It is necessary to compare relative performance in the convergence speed between the VSCGM and SCGM methods. Both VSCGM and SCGM methods start from the baseline case and use the same trained neural network. Figure 8 shows the variations in the objective function, indicated power output, and thermal efficiency with the five-parameter optimization process.

There is a rapid initial change in all three quantities with VSCGM than with SCGM. The quantities then change less rapidly, and more linearly. Eventually, the objective function approaches a minimum value. It is seen that the number of iterations needed is approximately 2700 with the SCGM method, whereas with the VSCGM it is only 1700. The rapid initial change is caused by the automatic adjustment of the step size. In general, the larger step size is produced by Equation (9) in the very initial stage such that the process can be quickly facilitated to the area adjacent to the optimal point. Then, the step size is reduced to a smaller value such that the iteration can approach the optimal point smoothly. As a result, the VSCGM method can accelerate convergence significantly.

Meanwhile, note that the approach is general; therefore, it shall include but not be limited to the optimization of the low-temperature-differential gamma-type Stirling engine. The dataset can also be prepared by experiments, not just limited to numerical computation.

It is also necessary to know whether the optimization approach can lead to a unique optimal point for different initial guesses. To test the uniqueness of the optimal design, in addition to the baseline case (Initial guess 1), three additional initial guess sets (Initial guess 2 to 4) are taken into account: Figure 9 depicts the optimization processes starting from these four initial guesses in the coordinates (D_p, θ_ph, ϕ). It is found that even though the four initial points are separate in the coordinates, the four optimization processes still approach the same optimal point. This implies that the optimization method is robust, and the obtained optimal design is independent of the initial point for this case. It is noted that the present approach is not limited to the present group of designed parameters. When necessary, more designed parameters may be readily applied.

In this study, the VSCGM method is originally presented in this paper which is a novel optimization method that can be coupled with a neural network training algorithm for optimization. It has been proven that the approach is efficient and robust. It is not limited to Stirling engine optimization. It can be readily applied to optimize other energy devices.

5. Conclusions

The present study develops a variable-step simplified conjugate gradient method (VSCGM) and incorporates this method with a neural network training algorithm to optimize a low-temperature-differential gamma-type Stirling engine. The VSCGM method is a further modified version of the existing SCGM method which introduces the concept of variable step size into the optimization process. A comparison between the VSCGM and the SCGM methods shows that the number of iterations needed is approximately 2700 with the SCGM method, whereas only 1700 with the VSCGM. The VSCGM method can accelerate convergence significantly. On the other hand, the neural network training algorithm is based on the Levenberg–Marquardt method with supervised learning. The three-dimensional CFD simulation results are used as the dataset for training the neural network.

A comparison between the initial and optimal designs shows that using this approach, the indicated power output can be elevated from 161.616 to 327.980 W, and the thermal efficiency from 16.532% to 17.399%.

Meanwhile, four different initial points are adapted to test the robustness of the approach. It is found that the approach is robust, and the obtained optimal combination of the designed parameters is independent of the initial guess for this case.