A Review about the Modeling and Simulation of Electro-Quasistatic Fields in HVDC Cable Systems
Abstract
:1. Introduction
2. High-Voltage Direct Current (HVDC) Cable Insulation Materials and the Non-Linear Electric Conductivity
3. Space Charges, Surface Charges and Charge Packets
4. Numerical Simulation of Charge Transport and the Electric Field in Direct Current (DC) Cable Insulations
4.1. Equations to Simulate the Time-Varying Charge and Electric Field Distribution
4.2. Discretisation and Numerical Calculation Scheme
5. Simulation of the Electric Field and the Space Charge Density within a Cable Insulation
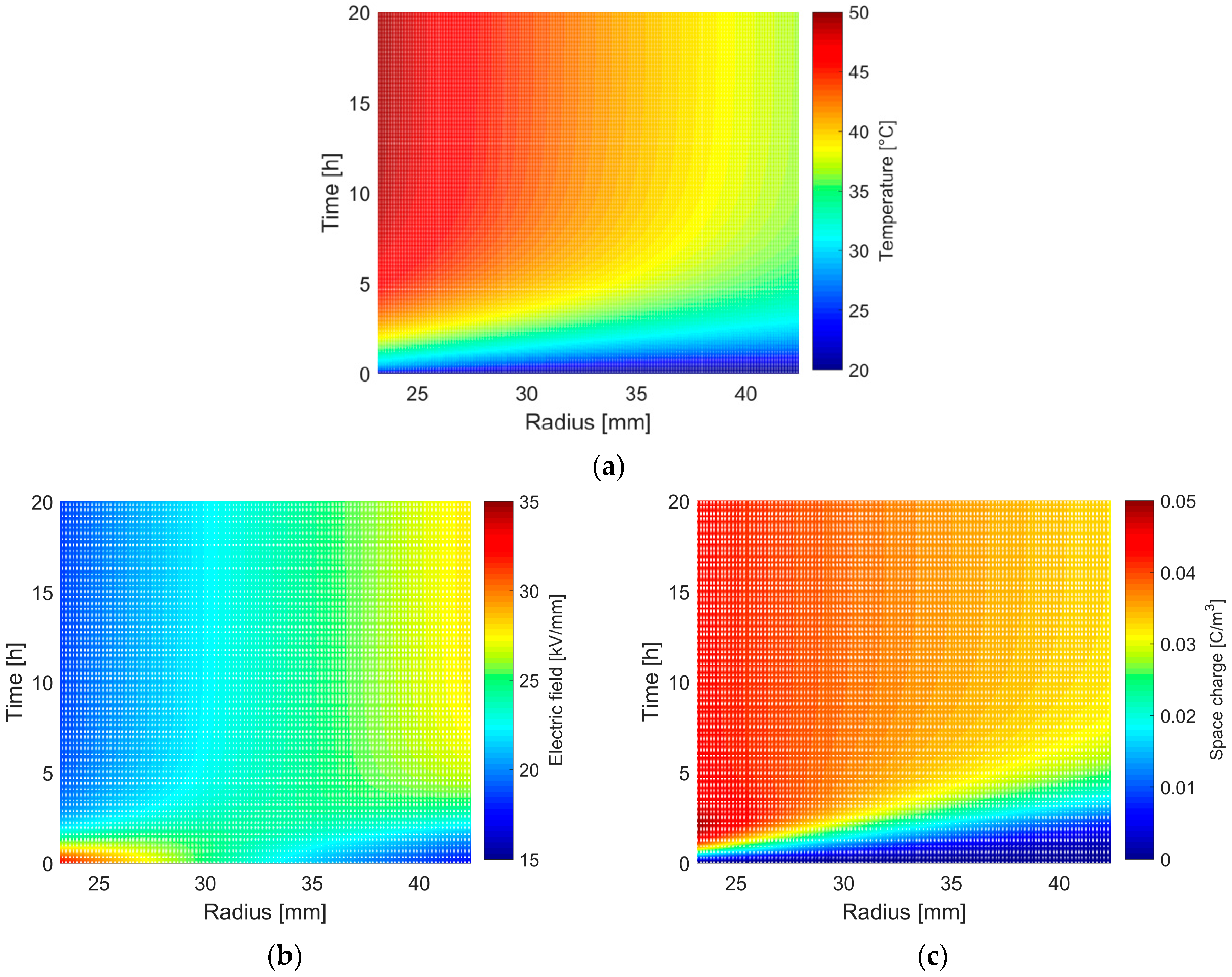
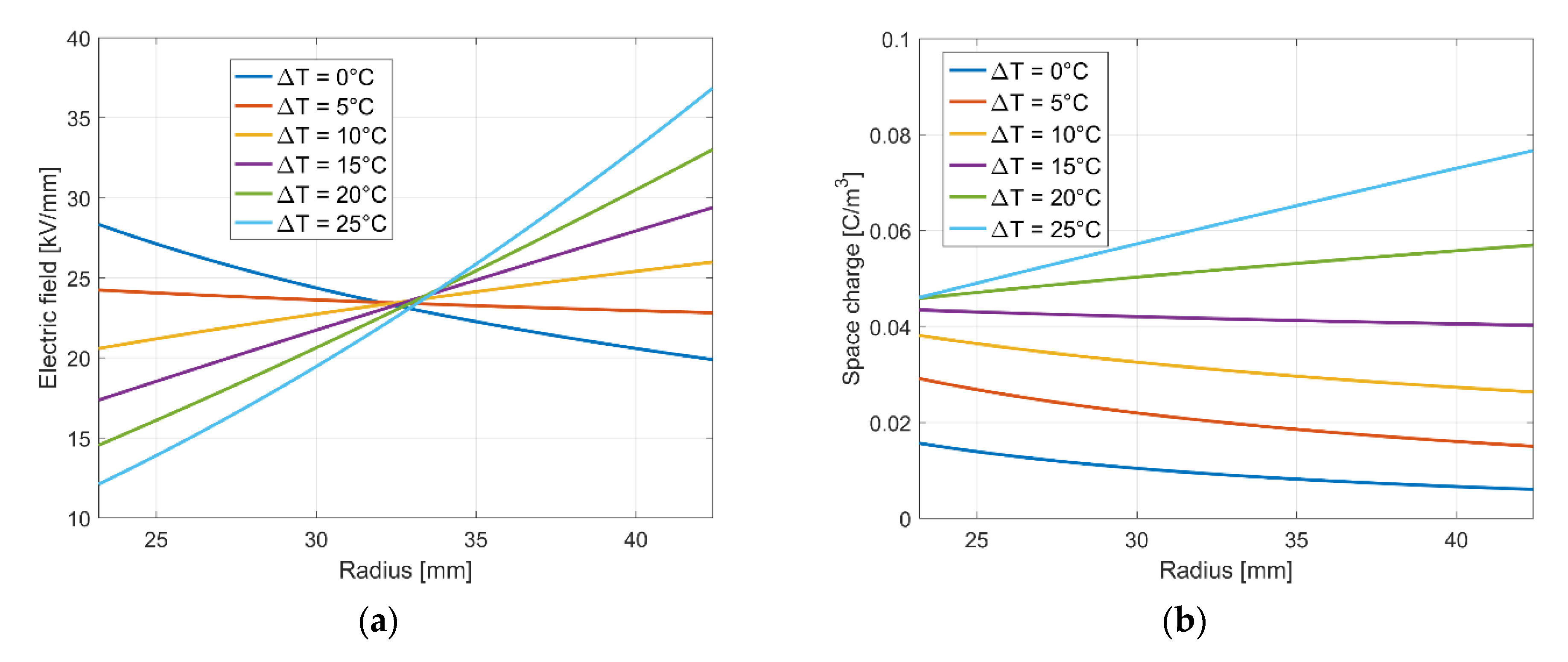
5.1. Transient and Stationary Electric Field under Various Thermal Stresses
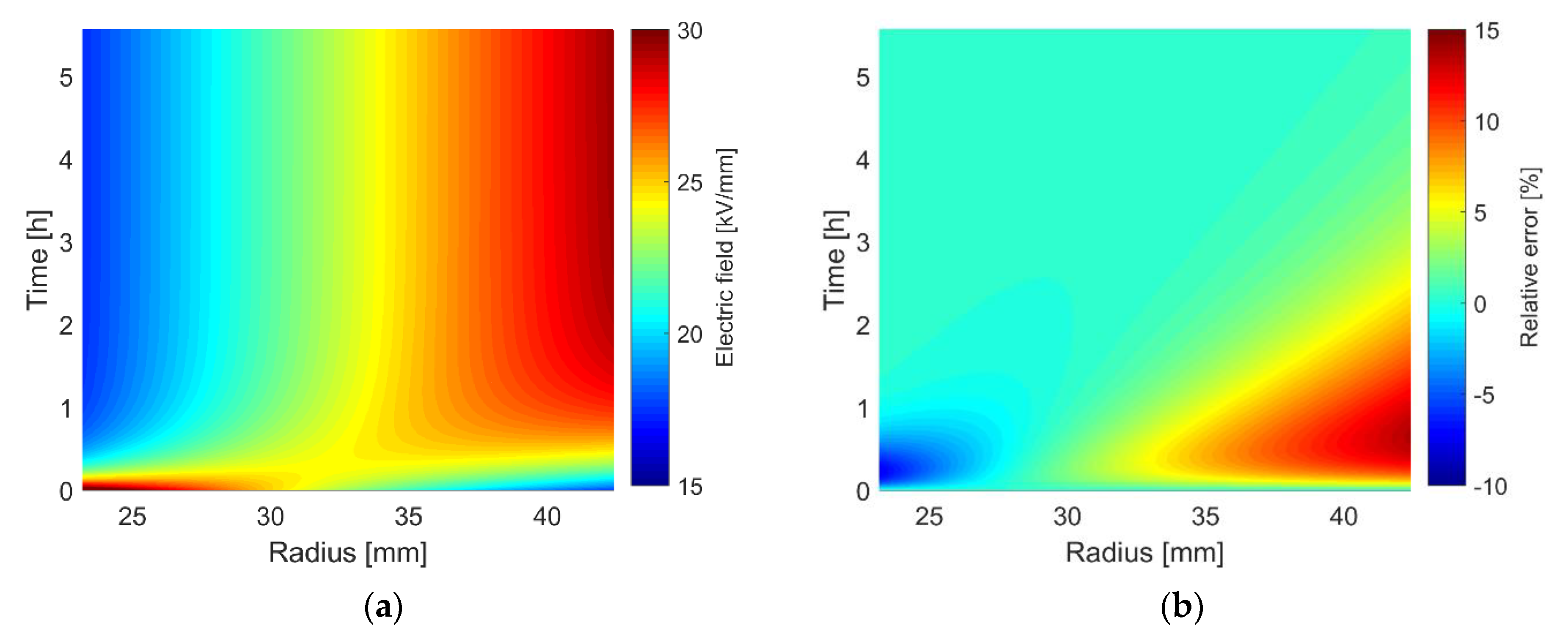
5.2. Fast Calculation of the Steady State Charge Distribution
5.3. Electric Fields in Power Cables, Considering the Environment
6. Simulation of Space Charge Effects at Interfaces and Surfaces and of Moving Charge Packets
6.1. The Stationary Field Distribution, Considering Charges in the Vicinity of Electrodes and Dual-Dielectric Interfaces
6.1.1. Modeling of Charges Close to Electrodes
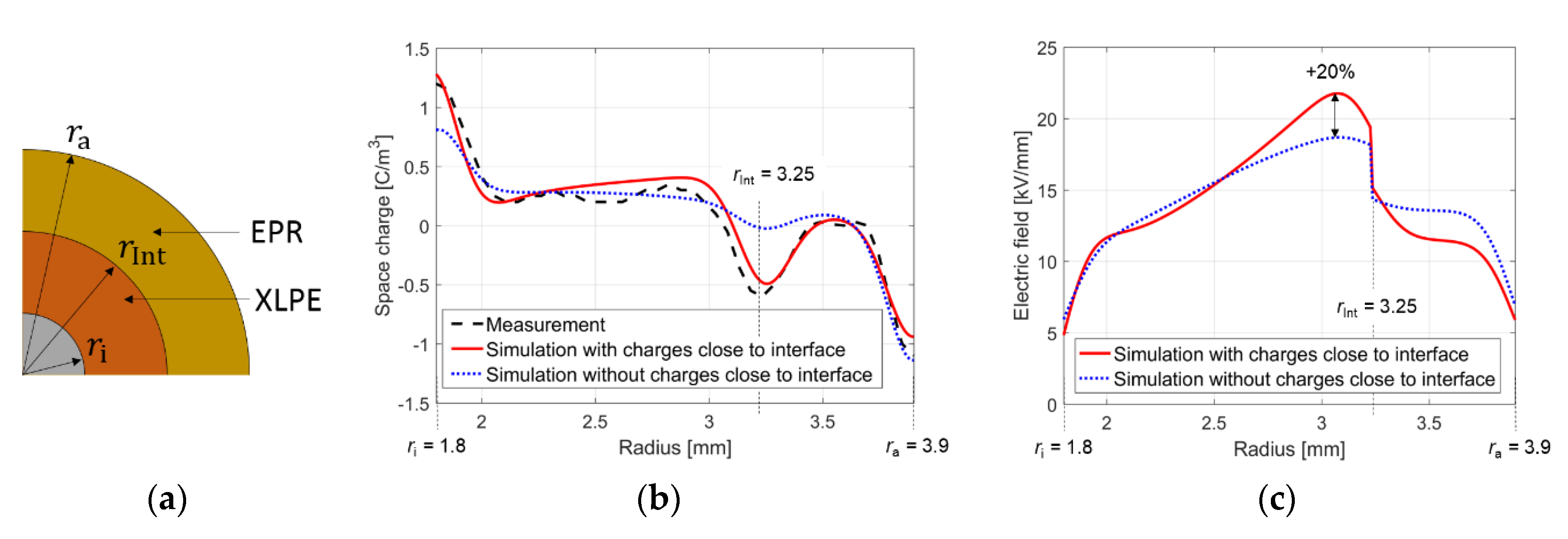
6.1.2. Modeling of Charges Close to Interfaces of Different Dielectrics
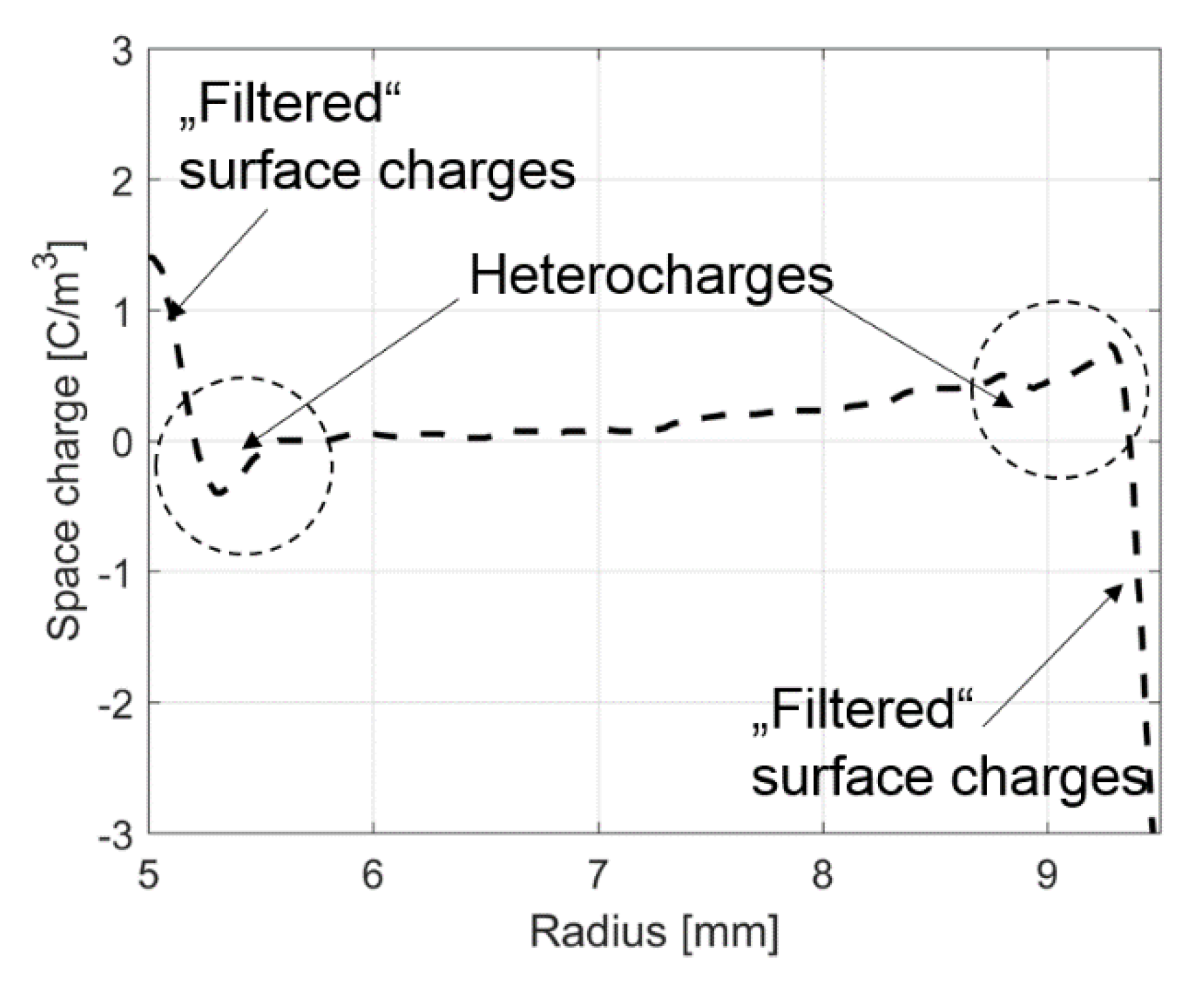
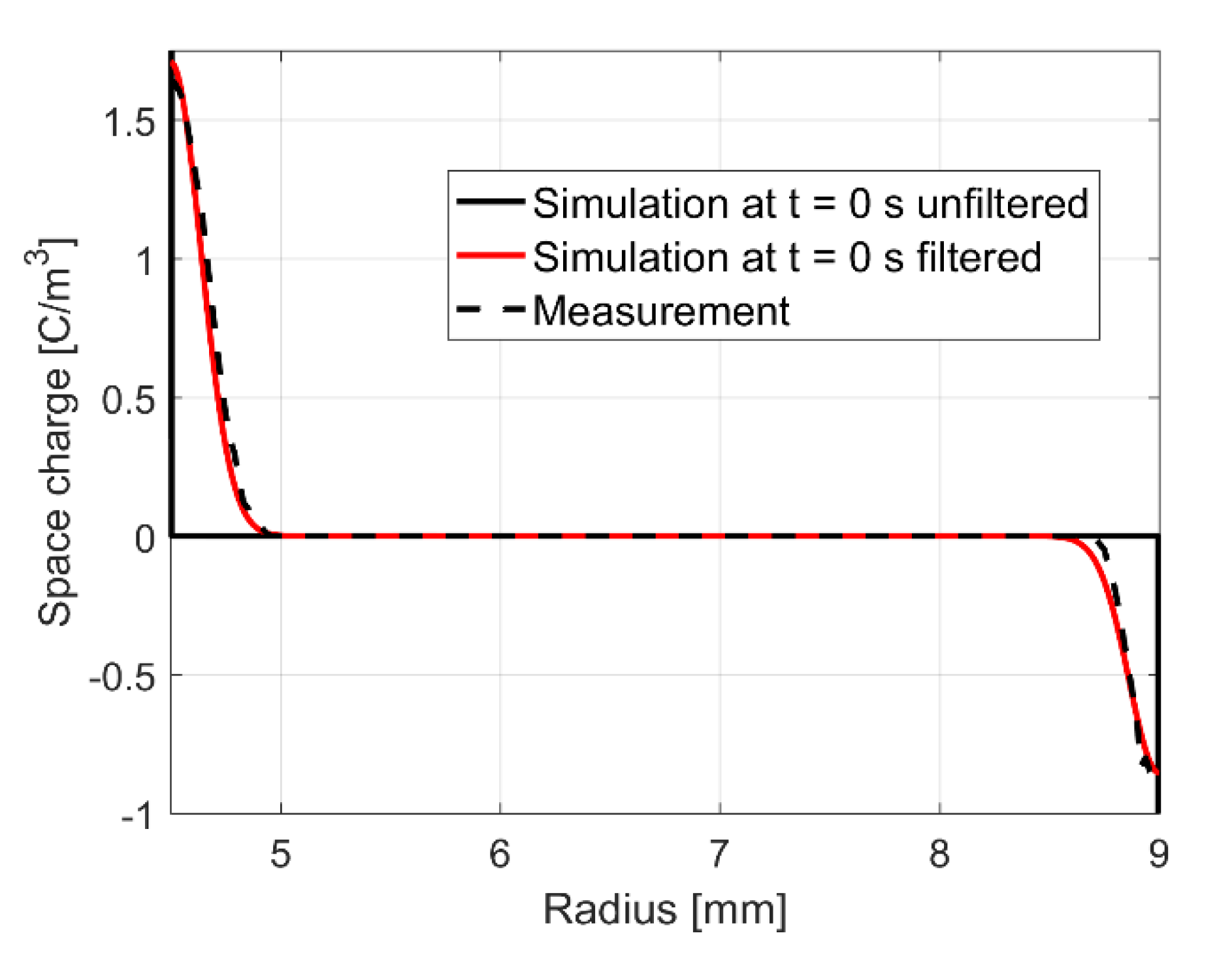
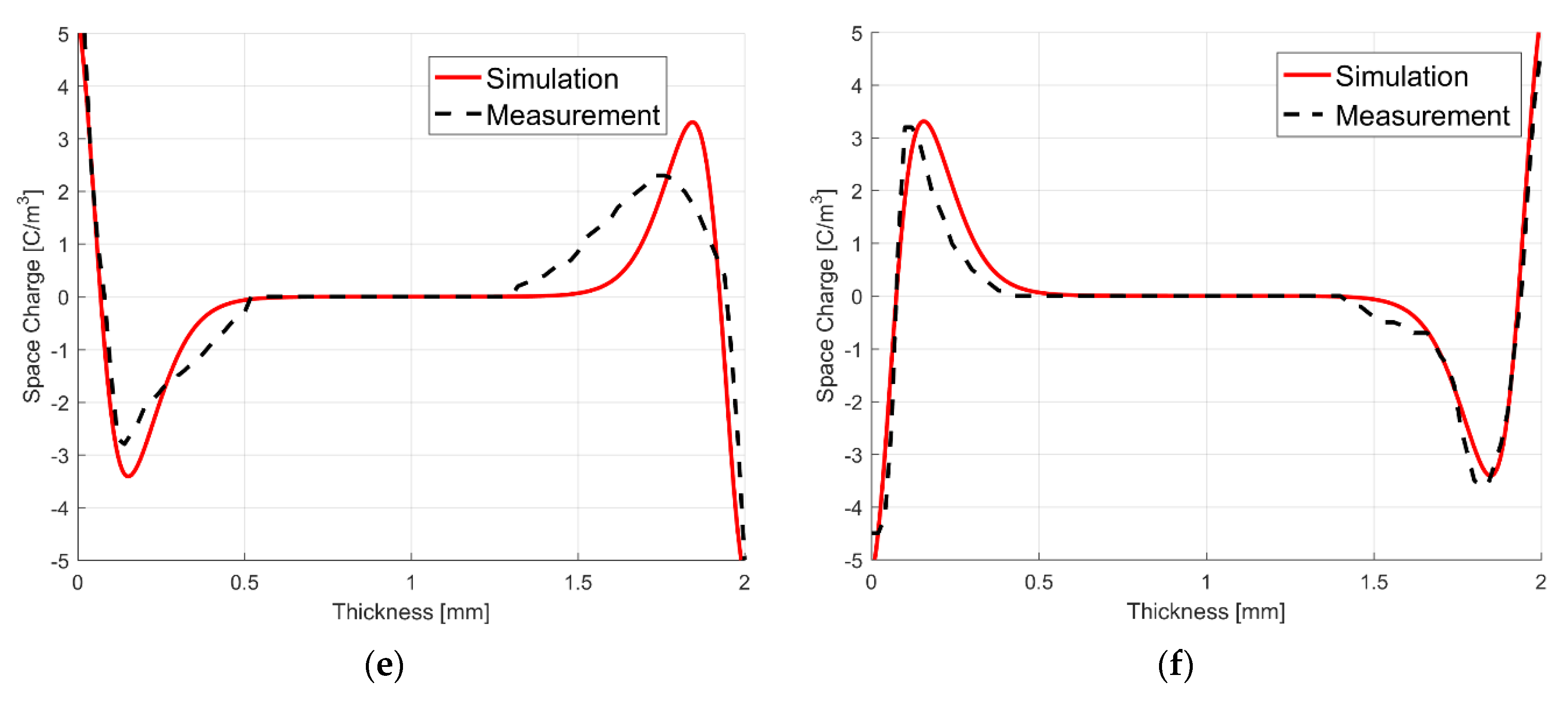
6.2. Empirical Conductivity Equation for the Simulation of Heterocharges in Polymeric Cable Insulations
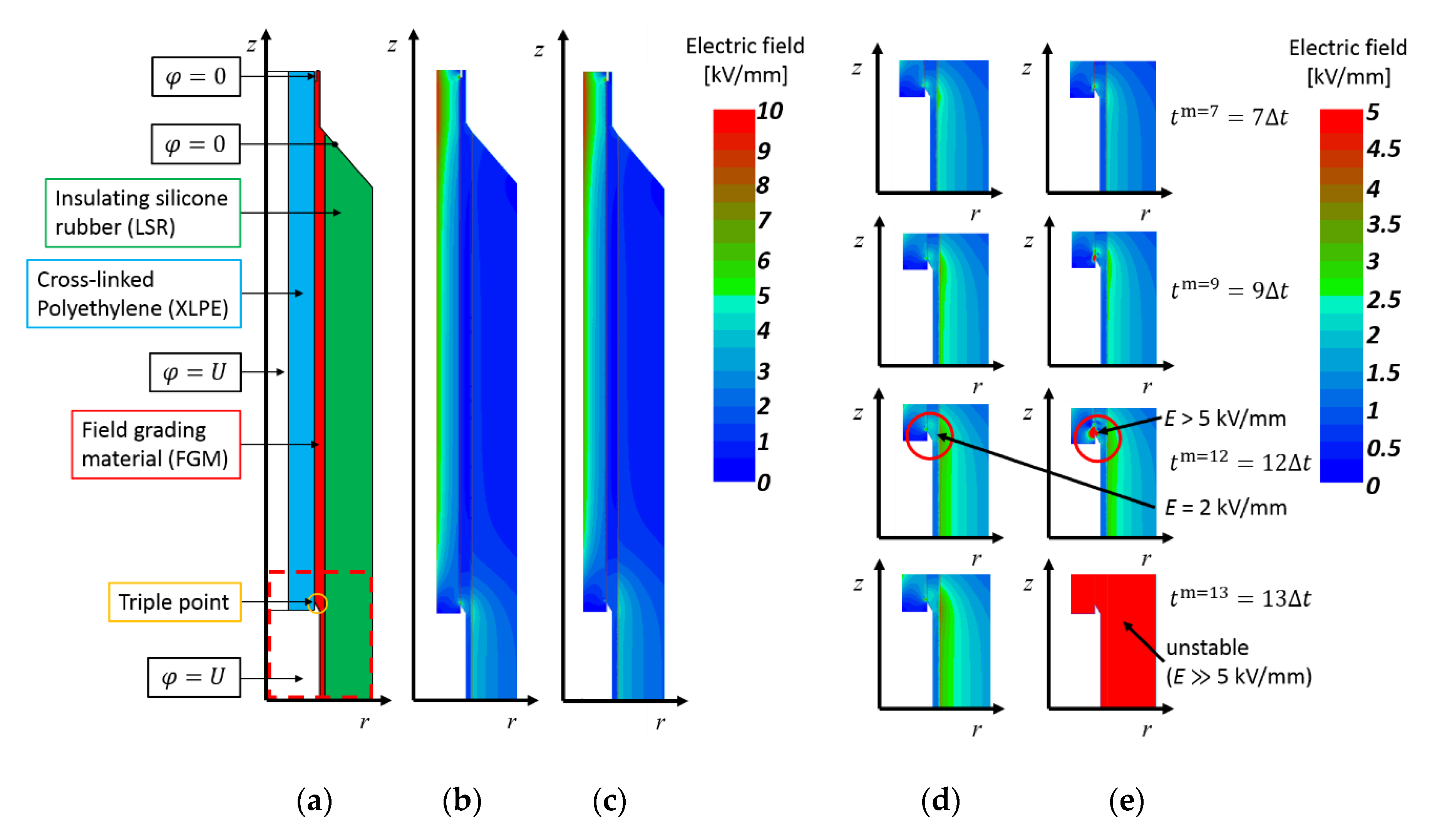
6.3. Transient Simulation of Charge Packets within a Cross-Linked Polyethylene (XLPE) Cable Insulation
- the formation of space charge regions,
- moving regions,
- a shape that is approximately maintained during motion,
- a periodic process (repetitive injection).
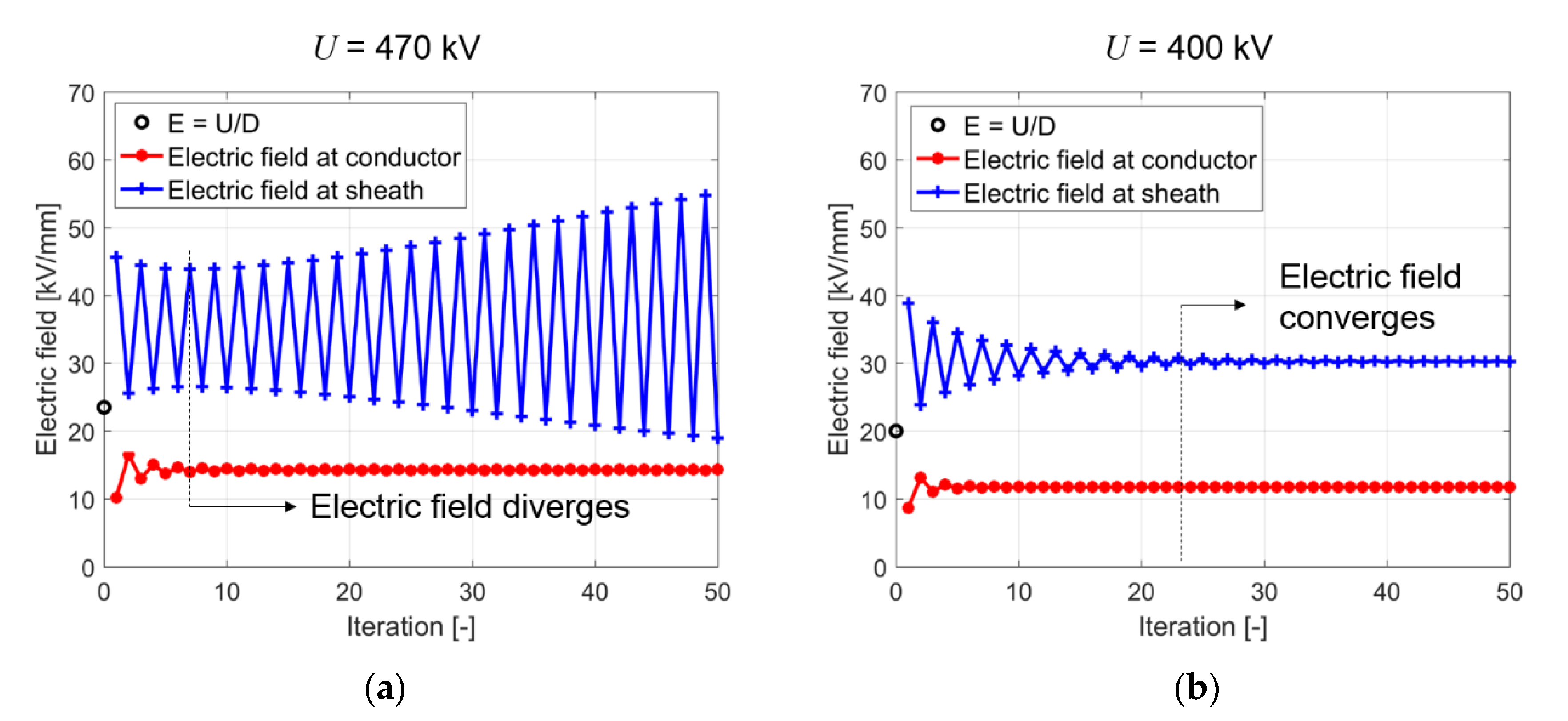
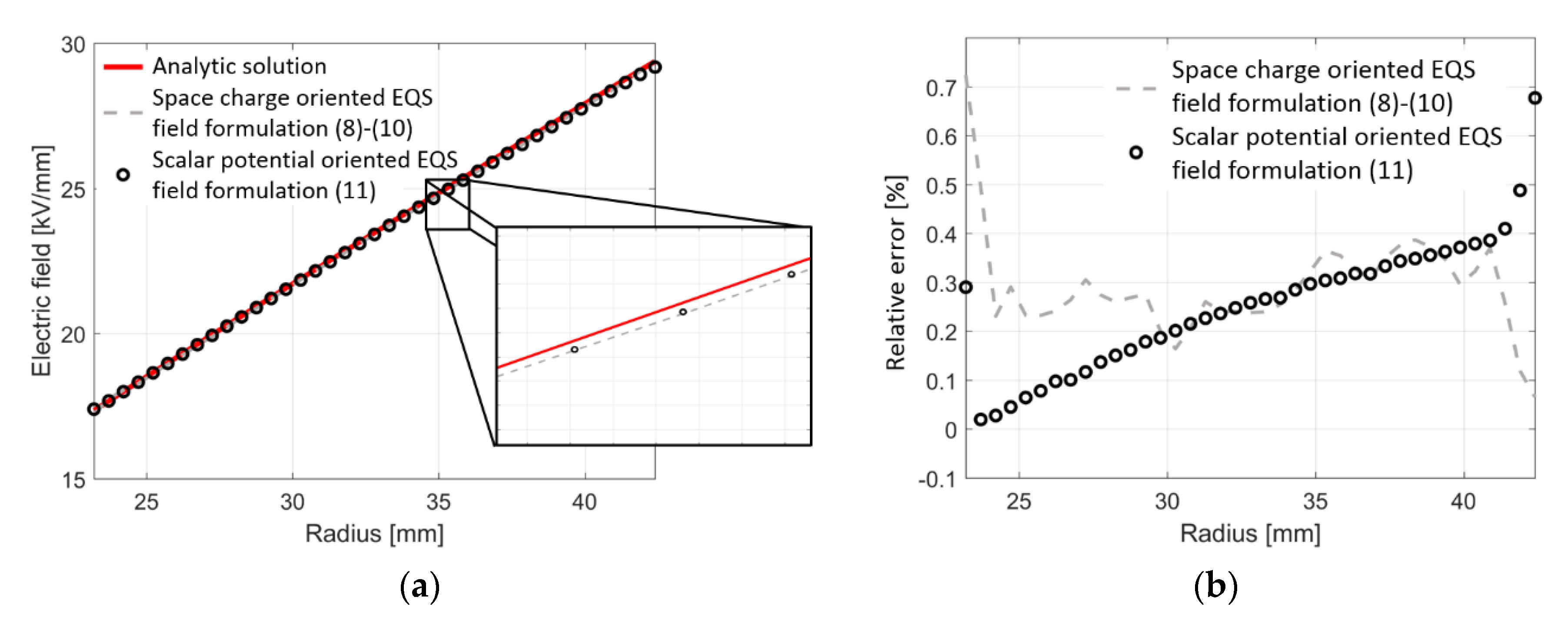
7. Accuracy of the Electric Field Computation within Cables and Cable Joints
8. The Electric Field of Ground Electrodes, Considering the Effect of Electro-Osmosis
9. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Capital letters | |
| Bh | Trapping coefficient for positive charges [1/s] |
| Be | Trapping coefficient for negative charges [1/s] |
| D | Thickness of a planar insulation [m] |
| Dh | Detrapping coefficient for positive charges [1/s] |
| De | Detrapping coefficient for positive charges [1/s] |
| Electric field [V/m] | |
| E0(r) | Electric field within a cable insulation at t = 0 [V/m] |
| E1 | Constant for the electric conductivity of FGM in (51) [V/m] |
| E2 | Constant for the electric conductivity of FGM in (51) [V/m] |
| EA,1 | Activation energy in (3) [eV] |
| EA,2 | Activation energy in (4) [eV] |
| EA,3 | Activation energy in (5) [eV] |
| Ee | Energy of charge carriers within the band diagram [eV] |
| ERef | Reference electric field in (7) [V/m] |
| ETrap | Trap depth [eV] |
| G | Discrete gradient matrix |
| GT | Discrete divergence matrix |
| I | Current [A] |
| Current density [A/m2] | |
| K1 | Conductivity constant in (3) [A/m2] |
| K2 | Conductivity constant in (4) [A/m2] |
| K3 | Conductivity constant in (5) [S/m] |
| Kcon | Conductivity variations in the vicinity of the conductor in (47) |
| Ksh | Conductivity variations in the vicinity of the sheath in (47) |
| Mc | Discrete matrix of the specific heat capacity |
| Mδ | Discrete density matrix |
| Mε | Discrete permittivity matrix |
| Mκ | Discrete electric conductivity matrix |
| Mλ | Discrete thermal conductivity matrix |
| N1 | Constant for the electric conductivity of FGM in (51) |
| N2 | Constant for the electric conductivity of FGM in (51) |
| PV | Losses per length within the conductor [W/m] |
| S0,1,2,3 | The recombination coefficients for different charge types [m3/(As∙s)] |
| T | Temperature [°C] |
| Ta | Sheath temperature [°C] |
| Ti | Conductor temperature [°C] |
| T∞ | Environment temperature [°C] |
| U | Voltage [V] |
| W | Mean band gab energy [eV] |
| Small letters | |
| aθ | Constant for the electro-osmotic hydraulic conductivity of soil in (56) |
| bθ | Constant for the electric conductivity of soil in (54) |
| b | Boundary conditions for the electric problem |
| bT | Boundary conditions for the thermal problem |
| cp | Specific heat capacity [W∙s/(kg∙K)] |
| hP = 6.626∙10−34 | Plank constant [J∙s] |
| j | Vector of current densities |
| k | Electro-osmotic hydraulic conductivity [m2/(Vs)] |
| k0,θ | Constant for the electro-osmotic hydraulic conductivity of soil in (56) |
| kB = 1.38∙10−23 | Boltzmann constant [J/K] |
| m | Discrete time index |
| m0 | Constant for the electric conductivity of FGM in (51) [m/V] |
| mFGM | Constant for the electric conductivity of FGM in (51) [m/V] |
| ncon | Conductivity increasing/decreasing factor at the conductor in (39) |
| ncon,ε | Conductivity increasing/decreasing factor at the conductor in (49) |
| ncon,κ | Conductivity increasing/decreasing factor at the conductor in (50) |
| nEPR | Conductivity increasing/decreasing factor in (45) |
| ne,t | Density of negative trapped charges [As/m3] |
| nh,t | Density of positive trapped charges [As/m3] |
| ne,μ | Density of negative mobile charges [As/m3] |
| nh,μ | Density of positive mobile charges [As/m3] |
| ne,t,0 | Trap density for negative charges [As/m3] |
| nh,t,0 | Trap density for positive charges [As/m3] |
| nsh | Conductivity increasing/decreasing factor at the sheath in (39) |
| nsh,ε | Conductivity increasing/decreasing factor at the sheath in (49) |
| nsh,κ | Conductivity increasing/decreasing factor at the sheath in (50) |
| nXLPE | Conductivity increasing/decreasing factor in (45) |
| q | Vector of electric dual cell charges |
| qT | Vector of heat sources |
| Heat flux [W/m2] | |
| Water flow due to electro-osmosis [m/s] | |
| r | Radius [m] |
| ra | Sheath radius [m] |
| ri | Conductor radius [m] |
| rInt | Interface radius of two different dielectrics [m] |
| rout | Radius of the outer sheath [m] |
| rx | Distance between the position of the highest gradient of Kcon (Ksh) and the conductor (sheath) [m] |
| s1 | Source term for negative mobile charges [A/m3] |
| s2 | Source term for positive mobile charges [A/m3] |
| s3 | Source term for negative trapped charges [A/m3] |
| s4 | Source term for positive trapped charges [A/m3] |
| t | Time [s] |
| tEND | Predefined end time [s] |
| tTrap | Time, charges remain in traps [s] |
| 1/tTrap,0 | Escape frequency [1/s] |
| uT | Vector of nodal temperatures |
| v | Constant for electric field dependency in (7) [-] |
| vκ | Velocity of the Gauss pulse (charge packet pulse) [m/s] |
| x | Coordinate for the planar insulation [m] |
| Greek capital letters | |
| ∆ | Region of additional spatial variations at the conductor and the sheath [m] |
| ∆h | Spatial discretization [m] |
| Δt | Discrete time step [s] |
| ΔtCFL | Time step, determined by the Courant-Friedrich-Levy (CFL) criterion [s] |
| Φ | Vector of nodal scalar potentials |
| Greek small letters | |
| α | Constant for temperature dependency in (6) [°C−1] |
| αout | Heat transmission coefficient [W/(K∙m2)] |
| αθ | Constant for the thermal conductivity of soil in (57) |
| β | Constant for electric field dependency in (6) [m/V] |
| βθ | Constant for the thermal conductivity of soil in (57) [(K∙m)/W] |
| 𝛾1 | Constant for electric field dependency in (3) [K∙m/V] |
| 𝛾2 | Constant for electric field dependency in (4) [m/V] |
| 𝛾3 | Constant for electric field dependency in (5) [m/V] |
| γθ | Constant for the thermal conductivity of soil in (57) [(K∙m)/W] |
| δ | Density [kg/m3] |
| δInt | Interface charges between two dielectrics [C/m2] |
| δ+ | Positive surface charges at the conductor [C/m2] |
| δ− | Negative surface charges at the sheath [C/m2] |
| 𝜀0 = 8.854∙10−12 | Dielectric constant [As/(Vm)] |
| 𝜀r | Relative permittivity |
| εr,Bulk | Constant bulk permittivity in (49) |
| ζcon | Constant that defines the gradient at the conductor in (39) [m] |
| ζcon,ε | Constant that defines the gradient at the conductor in (49) [m] |
| ζcon,κ | Constant that defines the gradient at the conductor in (50) [m] |
| ζEPR | Constant that defines the gradient in (45) [m] |
| ζsh | Constant that defines the gradient at the sheath in (39) [m] |
| ζsh,ε | Constant that defines the gradient at the sheath in (49) [m] |
| ζsh,ε | Constant that defines the gradient at the sheath in (50) [m] |
| ζXLPE | Constant that defines the gradient in (45) [m] |
| η 1 | Stop threshold for time integration |
| θ | Humidity (volumetric water content) [m3/m3] |
| κ | Electric conductivity [S/m] |
| κ0 | Conductivity constant in (6) [S/m] |
| κ0,FGM | Constant for the electric conductivity of FGM in (51) [S/m] |
| κ0,θ | Constant for the electric conductivity of soil in (54) [S/m] |
| κs | Constant for the electric conductivity of soil in (54) [S/m] |
| 𝜆 | Thermal conductivity [W/(Km)] |
| μ | Mobility of charge carriers [m2/(Vs)] |
| ρ | Space charge density [C/m3] |
| ρE | Space charge density that corresponds to the electric field dependency [C/m3] |
| ρT | Space charge density that corresponds to the temperature dependency [C/m3] |
| τ | Time constant [s] |
| φ | Electric potential [V] |
| χcon | Constant to define the gradient of (47) in the vicinity of the conductor [m] |
| χsh | Constant to define the gradient of (47) in the vicinity of the sheath [m] |
| ω | Under-relaxation parameter |
References
- Ghorbani, H.; Jeroense, M.J.P.; Olsson, C.O.; Saltzer, M. HVDC Cable Systems–Highlighting Extruded Technology. IEEE Trans. Power Deliv. 2014, 29, 414–421. [Google Scholar] [CrossRef]
- Küchler, A. High Voltage Engineering–Fundamentals, Technology, Applications, 5th ed.; Springer: Vieweg, Germany, 2018; pp. 503–513, 583–591. [Google Scholar] [CrossRef]
- Mazzanti, G.; Marzinotto, M. Extruded Cables for High Voltage Direct Current Transmission–Advances in Research and Development; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 11–40, 48–75, 88–98, 239–243. ISBN 978-1-118-09666-6. [Google Scholar]
- Ye, H.; Fechner, T.; Lei, X.; Luo, Y.; Zhou, M.; Han, Z.; Wang, H.; Zhuang, Q.; Xu, R.; Li, D. Review on HVDC cable terminations. IET High Volt. 2018, 3, 79–89. [Google Scholar] [CrossRef]
- Chen, G.; Hao, M.; Xu, Z.; Vaughan, A.; Cao, J.; Wang, H. Review of High Voltage Direct Current Cables. CSEE J. Power Energy Syst. 2015, 1, 9–21. [Google Scholar] [CrossRef]
- Teyssèdre, G.; Laurent, C. Advances in High-Field Insulating Polymeric Materials over the Past 50 Years. IEEE Electr. Insul. Mag. 2013, 29, 26–36. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, S.; Hu, J.; He, J. Polymeric Insulation Materials for HVDC Cables: Development, Challenges and Future Perspective. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1308–1318. [Google Scholar] [CrossRef]
- Hanley, T.L.; Burford, R.P.; Fleming, R.J.; Barber, K.W. A general review of polymeric insulation for use in HVDC cables. IEEE Electr. Insul. Mag. 2003, 19, 14–24. [Google Scholar] [CrossRef]
- NKT, 640 kV XLPE HVDC Cable System, NKT Brochures. Available online: https://www.nkt-no.com/fileadmin/user_upload/nkt_com/Catalogs_brochures/640kV_XLPE_LR.pdf (accessed on 30 June 2020).
- Jeroense, M.J.P.; Kreuger, F.H. Electrical Conduction in HVDC Mass-impregnated Paper Cable. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 718–723. [Google Scholar] [CrossRef]
- Jeroense, M.J.P.; Morshuis, P.H.F. Electric fields in HVDC paper insulated cables. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 225–236. [Google Scholar] [CrossRef]
- Fabiani, D.; Montanari, G.C.; Laurent, C.; Teyssèdre, G.; Morshuis, P.H.F.; Bodega, R.; Dissado, L.A. Polymeric HVDC Cable Design and Space Charge Accumulation. Part 3: Effect of Temperature Gradient. IEEE Electr. Insul. Mag. 2008, 24, 5–14. [Google Scholar] [CrossRef]
- Jörgens, C.; Kasolis, F.; Clemens, M. Numerical Simulations of Temperature Stability Limits in High Voltage Direct Current Cable Insulations. IEEE Trans. Mag. 2019, 55. [Google Scholar] [CrossRef]
- Bodega, R. Space Charge Accumulation in Polymeric High Voltage DC Cable Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006; pp. 27–30, 48, 75–88, 105–110. [Google Scholar]
- Jörgens, C.; Clemens, M. Thermal breakdown in high voltage direct current cable insulations due to space charges. Int. J. Comput. Math. Electr. Electron. Eng. (COMPEL) 2018, 37, 1689–1697. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Breakdown voltage in high voltage direct current cable insulations considering space charges. In Proceedings of the 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Lodz, Poland, 14–16 September 2017. [Google Scholar] [CrossRef]
- Dissado, L.A.; Fothergill, J.C. Electrical Degradation and Breakdown in Polymers; Peregrinus: London, UK, 1992; pp. 3–23, 27–48, 207–241. ISBN 0-86341-196-7. [Google Scholar]
- Jeroense, M.J.P. HVDC, the next generation of transmission: Highlights with focus on extruded cable systems. IEEE Trans. Electr. Electron. Eng. 2010, 5, 400–404. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Jiang, P.; Tanaka, T. Material progress toward recyclable insulation of power cables. Part 1: Polyethylene-based thermoplastic materials: Dedicated to the 80th birthday of Professor Toshikatsu Tanaka. IEEE Electr. Insul. Mag. 2019, 35, 7–19. [Google Scholar] [CrossRef]
- Teyssèdre, G.; Laurent, C. Charge Transport Modeling in Insulating Polymers: From Molecular to Macroscopic Scale. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 857–875. [Google Scholar] [CrossRef]
- Rengel, R. Messung des Raumladungsverhaltens in Polyethylen beim Einsatz als Isolierstoff in Hochspannungskabeln. Ph.D. Thesis, Eidgenössische Technische Hochschule, Zurich, The Switzerland, 1996; pp. 5–31. [Google Scholar]
- Jeroense, M. Charges and Discharges in HVDC Cables–in particular in mass-impregnated HVDC Cables. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1997; pp. 32–37, 115–132. [Google Scholar]
- Wintle, H.J. Charge Motion and Trapping in Insulators–Surface and Bulk Effects. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 1–10. [Google Scholar] [CrossRef]
- Montanari, G.C.; Morshuis, P.H.F. Space charge Phenomenology in Polymeric Insulating Materials. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 754–767. [Google Scholar] [CrossRef]
- McAllister, I.W.; Crichton, G.C.; Pedersen, A. Space Charge Fields in DC Cables. In Proceedings of the IEEE International Symposium on Electrical Insulation, Montreal, QC, Canada, 16–19 June 1996; pp. 661–665. [Google Scholar] [CrossRef] [Green Version]
- McAllister, I.W.; Crichton, G.C.; Pedersen, A. Charge Accumulation in DC Cables: A Macroscopic Approach. In Proceedings of the IEEE International Symposium on Electrical Insulation, Pittsburgh, PA USA, 5–8 June 1994; pp. 212–216. [Google Scholar] [CrossRef] [Green Version]
- Lewis, T.J. Polyethylene under Electrical Stress. IEEE Trans. Dielectr. Electr. Insul. 2002, 9, 717–729. [Google Scholar] [CrossRef]
- Steven, J.Y.; Vu, T.T.N.; Teyssedre, G.; Sinisuka, N.I. Conductivity Measurements and Space Charge Inference in Polymeric-insulated HVDC Model Cables. In Proceedings of the International Conference on High Voltage Engineering and Application (ICHVE), Poznan, Poland, 8–11 September 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Boggs, S.A.; Damon, D.H.; Hjerrild, J.; Holboll, J.T.; Henriksen, M. Effect of Insulation Properties on the Field Grading of Solid Dielectric DC Cable. IEEE Trans. Power Deliv. 2001, 16, 456–461. [Google Scholar] [CrossRef]
- Eoll, C.K. Theory of Stress Distribution in Insulation of High-Voltage DC Cables: Part I. IEEE Trans. Dielectr. Electr. Insul. 1975, EI-10, 27–35. [Google Scholar] [CrossRef]
- Riechert, U.; Vogelsang, R.; Kindersberger, J. Temperature Effect on DC Breakdown of Polyethylene Cables. In Proceedings of the 12th International Symposium on High Voltage Engineering, ISH 2001, Bangalore, India, 20–24 August 2001; pp. 537–540. [Google Scholar]
- Mauseth, F.; Haugdal, H. Electric Field Simulations of High Voltage DC Extruded Cable Systems. IEEE Electr. Insul. Mag. 2017, 33, 16–21. [Google Scholar] [CrossRef] [Green Version]
- Boggs, S.A. Semi-empirical High-field Conduction Model for Polyethylene and Implications thereof. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 97–106. [Google Scholar] [CrossRef]
- Qin, S.; Boggs, S.A. Design Considerations for High Voltage DC Components. IEEE Electr. Insul. Mag. 2012, 28, 36–44. [Google Scholar] [CrossRef]
- Lewis, T.J. Electrical Effects at Interfaces and Surfaces. IEEE Trans. Electr. Insul. 1986, EI-21, 289–295. [Google Scholar] [CrossRef]
- Fleming, R.J.; Henriksen, M.; Holboll, J.T. The Influence of Electrodes and Conditioning on Space Charge Accumulation in XLPE. IEEE Trans. Electr. Insul. 2000, 7, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Lewis, T.J. The Role of Electrodes and Breakdown Phenomena in Solid Dielectrics. IEEE Trans. Electr. Insul. 1984, EI-19, 210–216. [Google Scholar] [CrossRef]
- Maeno, Y.; Hirai, N.; Ohki, Y.; Tanaka, T.; Okashita, M.; Maeno, T. Effects of Crosslinking Byproducts on Space Charge Formation in Crosslinked Polyethylene. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 90–97. [Google Scholar] [CrossRef]
- Vissouvanadin, B.; LeRoy, S.; Teyssèdre, G.; Laurent, C.; Denizet, I.; Mammeri, M.; Poisson, B. Impact of Concentration Gradient of Polarizable Species on the Electric Field Distribution in Polymeric Insulating Material for HVDC Cable. IEEE Trans. Dielectr. Electr. Insul. 2011, 9, 833–839. [Google Scholar] [CrossRef]
- Lv, Z.; Cao, J.; Wang, X.; Wang, H.; Wu, K.; Dissado, L.A. Mechanism of Space Charge Formation in Cross Linked Polyethylene (XLPE) under Temperature Gradient. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3186–3196. [Google Scholar] [CrossRef]
- Fleming, R.J. Space Charge in Polymers, Particularly Polyethylene. Braz. J. Phys. 1999, 29, 280–294. [Google Scholar] [CrossRef] [Green Version]
- Fabiani, D.; Montanari, G.C.; Dissado, L.A.; Laurent, C.; Teyssèdre, G. Fast and Slow Charge Packets in Polymeric Materials under DC Stress. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 241–250. [Google Scholar] [CrossRef] [Green Version]
- Dissado, L.A. The origin and nature of ‘charge packets’: A short review. In Proceedings of the 10th International Conference on Solid Dielectrics, Potsdam, Germany, 4–9 July 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Dissado, L.A.; Montanari, G.C.; Fabiani, D. Fast soliton-like charge pulses in insulating polymers. J. Appl. Phys. 2011, 109, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lv, Z.; Rowland, S.M.; Wu, K. Simulation of fast charge packets transport in polymers. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena, Fort Worth, TX, USA, 22–25 October 2017; pp. 98–101. [Google Scholar] [CrossRef]
- Fabiani, D.; Montanari, G.C.; Laurent, C.; Teyssèdre, G.; Morshuis, P.H.F.; Bodega, R.; Dissado, L.A.; Campus, A.; Nilsson, U.H. Polymeric HVDC Cable Design and Space Charge Accumulation. Part 1: Insulation/Semicon Interface. IEEE Electr. Insul. Mag. 2007, 23, 11–19. [Google Scholar] [CrossRef]
- LeRoy, S.; Segur, P.; Teyssèdre, G.; Laurent, C. Description of bipolar charge transport in polyethylene using a fluid model with constant mobility: Model predictions. J. Phys. D: Appl. Phys. 2003, 37, 298–305. [Google Scholar] [CrossRef]
- Steinmetz, T.; Helias, M.; Wimmer, G.; Fichte, L.O.; Clemens, M. Electro-Quasistatic Field Simulations Based on a Discrete Electromagnetism Formulation. IEEE Trans. Mag. 2006, 42, 755–758. [Google Scholar] [CrossRef]
- Clemens, M.; Wilke, M.; Benderskaya, G.; DeGersem, H.; Koch, W.; Weiland, T. Transient Electro-Quasistatic Adaptive Simulation Schemes. IEEE Trans. Mag. 2004, 40, 1294–1297. [Google Scholar] [CrossRef]
- Lupo, G.; Petrarca, C.; Egiziano, L.; Tucci, V.; Vitelli, M. Numerical Evaluation of the Field in Cable Terminations Equipped with nonlinear Grading Materials. In Proceedings of the Annual Report Conference on Eletrical Insulation and Dielectric Phenomena (CEIDP), Atlanta, GA, USA, 25–28 October 1998; pp. 585–588. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Electric Field and Temperature Simulations of High Voltage Direct Current Cables considering the Earth Environment. Energies 2020. full paper submitted. [Google Scholar]
- LeRoy, S.; Teyssèdre, G.; Laurent, C. Numerical Methods in the Simulation of Charge Transport in Solid Dielectrics. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 239–246. [Google Scholar] [CrossRef]
- Boufayed, F.; Teyssèdre, G.; Laurent, C.; Le Roy, S.; Dissado, L.A.; Ségur, P.; Montanari, G.C. Models of bipolar charge transport in polyethylene. J. Appl. Phys. 2006, 100, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Baudoin, F.; Le Roy, S.; Teyssèdre, G.; Laurent, C. Bipolar charge transport model with trapping and recombination: An analysis of the current versus applied electric field characteristic in steady state conditions. J. Phys. D: Appl. Phys. 2008, 41, 1–10. [Google Scholar] [CrossRef]
- LeRoy, S.; Teyssèdre, G.; Laurent, C. Modelling Space Charge in a Cable Geometry. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2361–2367. [Google Scholar] [CrossRef]
- Bambery, K.R.; Fleming, R.J.; Holboll, J.T. Space charge profiles in low density polyethylene samples containing a permittivity/conductivtiy gradient. J. Phys. D: Appl. Phys. 2001, 34, 3071–3077. [Google Scholar] [CrossRef]
- Dutiné, J.; Richter, C.F.; Jörgens, C.; Schöps, S.; Clemens, M. Explicit Time Integration Techniques for Electro-and Magneto-Quasistatic Field Simulations. In Proceedings of the International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 1482–1485. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Simulation of the Electric Field in High Voltage Direct Current Cables considering the Environment. In Proceedings of the 10th International Conference on Computational Electromagnetics (CEM 2019), Edinburgh, UK, 19–20 June 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Comparison of Two Electro-Quasistatic Field Formulations for the Computation of Electric Field and Space Charges in HVDC Cable Systems. In Proceedings of the 22nd International Conference on the Computation of Electromagnetic Fields (COMPUMAG), Paris, France, 15–19 July 2019. [Google Scholar] [CrossRef]
- Richter, C.; Schoeps, S.; Dutine, J.; Schreiber, R.; Clemens, M. Transient simulation of nonlinear electro-quasi-static field problems accelerated by multiple GPUs. IEEE Trans. Mag. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Richter, C.; Schoeps, S.; Clemens, M. GPU accelerated explicit time-integration methods for electroquasi-static fields. IEEE Trans. Mag. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Lau, H. Aufbau der Raumladung in einem betriebswarmen Gleichspannungskabel. Archiv für Elektrotechnik 1970, 53, 265–275. [Google Scholar] [CrossRef]
- Coelho, C.; Aladenize, B.; Mirebeau, P. On the intrinsic space charge in a dc power cable. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Millbrae, CA, USA, 20–23 October 1996; pp. 278–282. [Google Scholar] [CrossRef]
- Coelho, C. Charges in non-homogeneous dielectrics. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Minneapolis, MN, USA, 20–23 October 1997; pp. 1–10. [Google Scholar] [CrossRef]
- Qi, X.; Boggs, S. Thermal and Mechanical Properties of EPR and XLPE Cable Compounds. IEEE Electr. Insul. Mag. 2006, 22, 19–24. [Google Scholar] [CrossRef]
- Frobin, S.J.; Niedik, C.F.; Freye, C.; Jenau, F.; Häring, D.; Schröder, G. A Generic Approach for HVDC Cable Accessories Modelling. In Proceedings of the IEEE 2nd International Conference on Dielectrics (ICD), Budapest, Hungary, 1–5 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Spitzner, M.H.; Stephan, P.; Span, R.; Hübner, C.; Kempa, P.B. VDI Wärmeatlas, 11th ed.; Springer: Berlin, Germany, 2013; pp. 19–22, 196–198, 648, 686–687. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Formulierung einer thermischen Durchschlagbedingung für Kabel der Hochspanungsgleichstromübertragung. In Proceedings of the 1. VDE Fachtagung für polymere Isolierstoffe und ihre Grenzflächen, Zittau, Germany, 17–18 May 2018; pp. 17–22, ISBN 978-3-00-059755-8. [Google Scholar]
- Christen, T. Characterization and Robustness of HVDC Insulation. In Proceedings of the 13th International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; pp. 238–241. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Electric Field Model at Interfaces and Surfaces in High Voltage Cable Systems. Int. J. Comput. Math. Electr. Electron. Eng. (COMPEL) 2020. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Fast calculation of steady-state charge distribution in high voltage power cables. Int. J. Numer. Model. El. 2020. [Google Scholar] [CrossRef]
- Wu, J.; Lan, L.; Li, Z.; Yin, Y. Simulation of Space Charge Behavior in LDPE with a Modified of Bipolar Charge Transport Model. In Proceedings of the IEEE International Symposium on Electrical Insulating Materials, Niigata, Japan, 1–5 June 2014; pp. 65–68. [Google Scholar] [CrossRef]
- Bodega, R.; Morshuis, P.H.F.; Straathof, E.J.D.; Nilsson, U.H.; Perego, G. Characterization of XLPE MV-size DC Cables by Means of Space Charge Measurements. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Kansas City, MO, USA, 15–18 October 2006; pp. 11–14. [Google Scholar] [CrossRef]
- Bauer, C.A.; Nease, R.J. A study of the Superposition of Heat Fields and the Kennelly Formula as Applied to Underground Cable Systems. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1957, 76, 1330–1333. [Google Scholar] [CrossRef]
- Holyk, C.; Anders, G.J. Power Cable Rating Calculations—A Historical Perspective. IEEE Ind. Appl. Mag. 2015, 21, 6–64. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Abdel-hadi, O.N. Temperature Distributions around Buried Cables. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 1158–1166. [Google Scholar] [CrossRef]
- Heinhold, L.; Stubbe, R. Kabel und Leitungen für Starkstrom, 5th ed.; Publics MCD Verlag: Erlangen, Germany, 1999; pp. 271–295, 306–318. ISBN 3-89578-088-X. [Google Scholar]
- Peschke, E.; Olshausen, R.v. Kabelanlagen für Hoch-Und Höchstspannung; Publics MCD Verlag: Erlangen, Germany, 1998; pp. 72–77. ISBN 3-89578-057-X. [Google Scholar]
- Ebert, S.; Sill, F.; Diederichs, J. Extruded XLPE DC Underground-Cable Technology and Experiences up to 525 kV–A Key Building Block for the German “Energiewende”; VDE-Hochspannungstechnik: Berlin, Germany, 2016; pp. 8–13. ISBN 978-3-8007-4310-0. [Google Scholar]
- High Voltage Cable Systems–Cables and Accessories up to 550 kV, nkt Datasheet. Available online: https://www.cablejoints.co.uk/upload/NKT_Cables_Extra_High_Voltage_132kV_220kV_400kV_500kV___Brochure.pdf (accessed on 3 June 2020).
- Hjerrild, J.; Holboll, J.; Henriksen, M.; Boggs, S. Effect of Semicon-Dielectric Interface on Conductivity and Electric Field Distribution. IEEE Trans. Electr. Insul. 2002, 9, 596–603. [Google Scholar] [CrossRef] [Green Version]
- Boggs, S.A. A Rational Consideration of Space Charge. IEEE Electr. Insul. Mag. 2004, 20, 22–27. [Google Scholar] [CrossRef]
- Bahrman, M.P.; Johnson, B.K. The ABC of HVDC Transmission Technologies–An overview of High Voltage Direct Current Systems and Applications. IEEE Power Energy Mag. 2007, 5, 32–44. [Google Scholar] [CrossRef]
- Delpino, S.; Fabiani, D.; Montanari, G.C.; Laurent, C.; Teyssèdre, G.; Morshuis, P.H.F.; Bodega, R.; Dissado, L.A. Polymeric HVDC Cable Design and Space Charge Accumulation. Part 2: Insulation Interfaces. IEEE Electr. Insul. Mag. 2008, 24, 14–24. [Google Scholar] [CrossRef]
- Rogti, F.; Mekhaldi, A.; Laurent, C. Space Charge Behavior at Physical Interfaces in Cross-linked Polyethylene under DC Field. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1478–1485. [Google Scholar] [CrossRef]
- Kreuger, F.H. Industrial High DC Voltage; Delft University Press: Delft, The Netherlands, 1995; pp. 8–15. ISBN 90-407-1110-0. [Google Scholar]
- Bodega, R.; Perego, G.; Morshuis, P.H.F.; Nilsson, U.H.; Smit, J.J. Space Charge and Electric Field Characteristics of Polymeric-type MV-size DC Cable Joint Models. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Nashville, TN, USA, 16–19 October 2005; pp. 507–510. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Empirical Conductivity Equation for the Simulation of Space Charges in Polymeric HVDC Cable Insulations. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athene, Greece, 10–13 September 2018. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Empirical Conductivity Equation for the Simulation of the Stationary Space Charge Distribution in Polymeric HVDC Cable Insulations. Energies 2019, 12, 3018. [Google Scholar] [CrossRef] [Green Version]
- Jörgens, C.; Clemens, M. Modeling the Field in Polymeric Insulation Including Nonlinear Effects due to Temperature and Space Charge Distributions. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Fort Worth, TX, USA, 22–25 October 2017; pp. 10–13. [Google Scholar] [CrossRef]
- Wang, X.; Yoshimura, N.; Murata, K.; Tanaka, Y.; Takada, T. Space-charge characteristics in polyethylene. J. Phys. D: Appl. Phys. 1998, 84, 1546–1550. [Google Scholar] [CrossRef]
- Takeda, T.; Hozumi, N.; Suzuki, H.; Okamoto, T. Factors of Hetero Space Charge Generation in XLPE under dc Electric Field of 20 kV/mm. Electr. Eng. Jpn. 1999, 129, 13–21. [Google Scholar] [CrossRef]
- Mizutani, T. Space Charge Measurement Techniques and Space Charge in Polyethylene. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 923–933. [Google Scholar] [CrossRef]
- Imburgia, A.; Miceli, R.; Sanseverino, E.R.; Romano, P.; Viola, F. Review of Space Charge Measurement Systems: Acoustic, Thermal and Optical Methods. IEEE Trans. Dielectr. Electr. Insul. 2015, 23, 3126–3142. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Conductivity-based model for the simulation of homocharges and heterocharges in XLPE high-voltage direct current cable insulation. IET Sci. Meas. Technol. 2019, 13, 975–983. [Google Scholar] [CrossRef]
- LeRoy, S.; Boufayed, F.; Baudoin, F.; Teyssèdre, G.; Laurent, C. A User-friendly Tool for Simulating the Time-Dependent Field Distribution in PE Insulation on the Basis of a Physical Approach. In Proceedings of the 7th International Conference on Power Insulated Cables (JICABLE’07), Paris, France, 24–28 June 2007; Available online: http://www.jicable.org/2007/Actes/Session_C71/JIC07_C711.pdf (accessed on 30 June 2020).
- Fu, M.; Dissado, L.A.; Chen, G.; Fothergill, J.C. Space Charge Formation and its Modified Electric Field under Applied Voltage Reversal and Temperature Gradient in XLPE Cable. IEEE Trans. Electr. Insul. 2008, 15, 851–860. [Google Scholar] [CrossRef] [Green Version]
- Kumara, J.R.S.S.; Serdyuk, Y.V.; Gubanski, S.M. Surface Potential Decay on LDPE and LDPE/Al2O3 Nano-Composites: Measurements and Modeling. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3466–3475. [Google Scholar] [CrossRef]
- Boudou, L.; Guastavino, J. Influence of temperature on low-density polyethylene films through conduction measurement. J. Phys. D Appl. Phys. 2002, 35, 1555–1561. [Google Scholar] [CrossRef]
- Bambery, K.R.; Fleming, R.J. Space Charge Accumulation in Two Power Cables Grades of XLPE. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 103–109. [Google Scholar] [CrossRef]
- Lim, F.N.; Fleming, R.J.; Naybour, R.D. Space Charge Accumulation in Power Cable XLPE Insulation. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 273–281. [Google Scholar] [CrossRef]
- Karlsson, M.; Xu, X.; Gaska, K.; Hillborg, H.; Gubanski, S.M.; Gedde, U.W. DC Conductivity Measurements of LDPE: Influence of Specimen Preparation Method and Polymer Morphology. In Proceedings of the 25th Nordic Insulation Symposium, Issue No. 25, Västerås, Sweden, 19–21 June 2017. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Gaska, K.; Karlsson, M.; Hillborg, H.; Gedde, U.W. Precision electric characterization of LDPE specimens made by different manufacturing processes. In Proceedings of the IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athene, Greece, 10–13 September 2018. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Sancho, I.; Fontán, L. 2D and 3D Finite Elements Analysis to Identify the Influence of Cylindrical Voids in Power Cables. IEEE AFRICON 2009. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Sancho, I.; Fontán, L.; Malumbres, J. Influence of Voids withion Electric Fields in HVDC Power Cables. In Proceedings of the 8th International Conference on Insulated Power Cables, Paris, France, 19–23 June 2011. [Google Scholar]
- He, M.; Chen, G.; Lewin, P.L. Field distortion by a single cavity in HVDC XLPE cable under steady state. IET High Volt. 2016, 1, 107–114. [Google Scholar] [CrossRef]
- Secklehner, M.; Hering, M.; Hinrichsen, V. Characterization of Fillers for HVDC Field Grading Materials; CIGRÉ Colloquium: Winnipeg, MB, Canada, 2017; pp. 1–8. [Google Scholar]
- Späck-Leigsnering, Y.; Gjonaj, E.; De Gersem, H.; Weiland, T.; Gießel, M.; Hinrichsen, V. Investigation of Thermal Stability for a Station Class Surge Arrester. IEEE J. Multiscale Multiphysics Comput. Tech. 2016, 1, 120–128. [Google Scholar] [CrossRef]
- Hussain, R.; Hinrichsen, V. Simulation of Thermal Behavior of a 320 kV HVDC Cable Joint with Nonlinear Resistive Field Grading under Impulse Voltage Stress; CIGRÉ Colloquium: Winnipeg, MB, Canada, 2017; pp. 1–8. [Google Scholar]
- Cigré working group B4.61. General Guidelines for HVDC Electrode Design, Technical Brochure; Cigré: Paris, France, 2017; ISBN 978-2-85873-378-1. [Google Scholar]
- Schmidt, G.; Fiegl, B.; Kolbeck, S. HVDC transmission and the environment. Power Eng. J. 1996, 10, 204–210. [Google Scholar] [CrossRef]
- Kimbark, E.W. Direct Current Transmission, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1971; pp. 391–483. ISBN 0-471-47580-7. [Google Scholar]
- Gray, D.H.; Mitchell, J.K. Fundamental aspects of electro-osmosis in soil. J. Soil Mech. Found. Div. 1967, 93, 209–236. [Google Scholar]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; pp. 251–320. ISBN 978-0-471-46302-7. [Google Scholar]
- Segall, B.A.; Bruell, C.J. Electroosmotic Contaminant-Removal Processes. J. Environ. Eng. 1992, 118, 84–100. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Noborio, K.; McInnes, K.J.; Heilman, J.L. Field measurements of soil electrical conductivity and water content by time-domain reflectometry. Comput. Electron. Agric. 1994, 11, 131–142. [Google Scholar] [CrossRef]
- Scott, J.H. Electrical and Magnetic Properties of Rock and Soil, U.S. Geological Survey Technical Letter, Special Project-16, May 26, 1966; Electromagnetic Pulse Theoretical Notes, Note 18, AFWL EMP 2-1, April 1971. Available online: https://pubs.usgs.gov/of/1983/0915/report.pdf (accessed on 24 September 2020). [CrossRef] [Green Version]
- Mcbratney, A.B.; Whelan, B.M.; Minasny, B. Comparing temperature correction models for soil electric conductivity measurements. Precis. Agric. 2011. [Google Scholar] [CrossRef]
- Longmire, C.L.; Smith, K.S. A Universal Impedance for Soil, Topical Report for Period 1 July–30 September 1975. 1975, pp. 3–23, Accession Number: ADA025759. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a025759.pdf (accessed on 24 September 2020).
- Delfino, F.; Procopio, R.; Rossi, M.; Rachidi, F. Influence of frequency-dependent soil electrical parameters on the evaluation of lightning electromagnetic fields in air and underground. J. Geophys. Res. 2009, 114, D11113. [Google Scholar] [CrossRef]
- Bai, W.; Kong, L.; Guo, A. Effects of physical properties on electrical conductivity of compacted lateritic soil. J. Rock Mech. Geotech. Eng. 2013, 5, 406–411. [Google Scholar] [CrossRef] [Green Version]
- Brevik, E.C.; Fenton, T.E.; Lazari, A. Soil electrical conductivity as a function of soil water content and implications for soil mapping. Precis. Agric. 2006, 7, 393–404. [Google Scholar] [CrossRef]
- Samouëlian, A.; Cousin, I.; Tabbagh, A.; Bruand, A.; Richard, G. Electrical resistivity survey in soil science: A review. Soil Tillage Res. Elsevier 2005, 83, 173–193. [Google Scholar] [CrossRef] [Green Version]
- Hansbo, S. Soil Improvements by means of Electro-Osmosis. In Proceedings of the International Conference on Case Histories in Geotechnical Engineering, Arlington, VA, USA, 11–16 August 2008; Available online: http://scholarsmine.mst.edu/icchge/6icchge/session07/41 (accessed on 30 June 2020).
- Nikolaev, I.V.; Leong, W.H.; Rosen, M.A. Experimental Investigation of Soil Thermal Conductivity over a Wide Temperature Range. Int. J. Thermophys. 2013, 34, 1110–1129. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Modeling the Electro-Quasistatic Field of Ground Electrodes under the Influence of Electro-Osmosis. In Proceedings of the IEEE International Conference on Dielectrics (ICD), Valencia, Spain, 6–31 July 2020. full paper accepted. [Google Scholar]
- Zagorscak, R.; Sedighi, M.; Thomas, H.R. Effects of Thermo-Osmosis on Hydraulic Behavior of Saturated Clays. Int. J. Geomech. 2017, 17, 04016068-1. [Google Scholar] [CrossRef]
- Villas, J.E.T.; Portela, C.M. Soil Heating Around the Ground Electrode of an HVDC System by Interaction of Electrical, Thermal, and Electroosmotic Phenomena. IEEE Trans. Power Deliv. 2003, 18, 874–881. [Google Scholar] [CrossRef]






| Constant | Value | Constant | Value | Constant | Value |
|---|---|---|---|---|---|
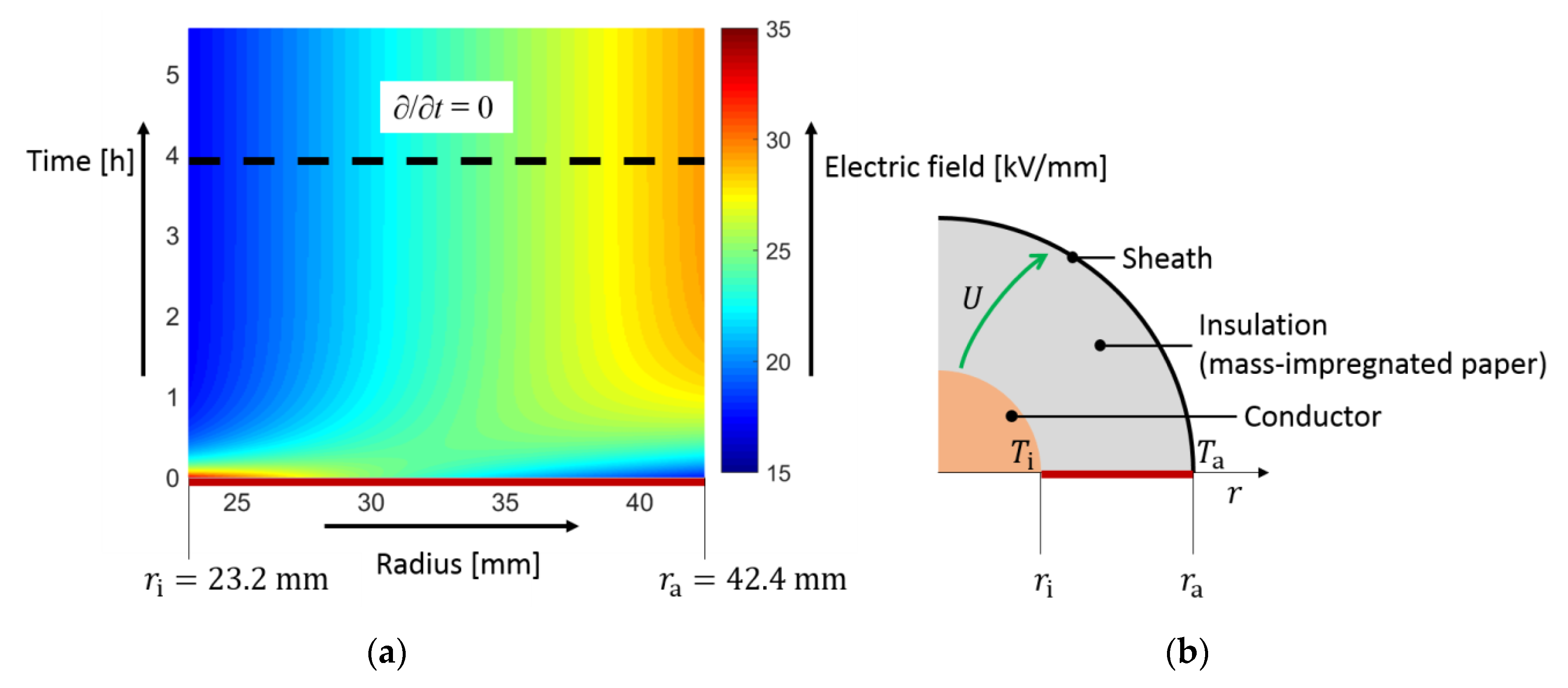
| U | 450 kV | κ0 | 1 × 10−16 S/m | T∞ | 20 °C |
| I | 1500 A | α | 0.1 °C−1 | λ | 0.167 W/(K∙m) |
| ri | 23.2 mm | β (for (6)) | 0.03 mm/kV | δ∙cp | 2.5 × 106 J/(m3 K) |
| ra | 42.4 mm | v (for (7)) | 0.7031 | αout | 5 W/(K∙m2) |
| εr | 3.5 | ERef (for (7)) | 8.622 kV/mm | - | - |
| Ref. | χ | rx | Insulation Thickness | Width of Charge Region Δ |
|---|---|---|---|---|
| [72], U = 15 kV | 8 μm | 40 μm | 300 μm | 0.267∙D |
| [73], U = 90 kV | 0.12 mm | 0.60 mm | 4.5 mm | 0.22∙(ra − ri) |
| [91], XLPE, planar, +U | 0.052 mm | 0.25 mm | 2 mm | 0.26∙D |
| [91], XLPE, planar, −U | 0.052 mm | 0.25 mm | 2 mm | 0.26∙D |
| [91], XLPE, cylindrical, +U | 0.0875 mm | 0.44 mm | 3.5 mm | 0.28∙(ra − ri) |
| [91], XLPE, cylindrical, −U | 0.0875 mm | 0.44 mm | 3.5 mm | 0.28∙(ra − ri) |
| [91], LDPE, planar, +U | 0.052 mm | 0.25 mm | 2 mm | 0.26∙D |
| [91], LDPE, planar, −U | 0.052 mm | 0.25 mm | 2 mm | 0.26∙D |
| [93], U = 40 kV | 0.052 mm | 0.25 mm | 2 mm | 0.26∙D |
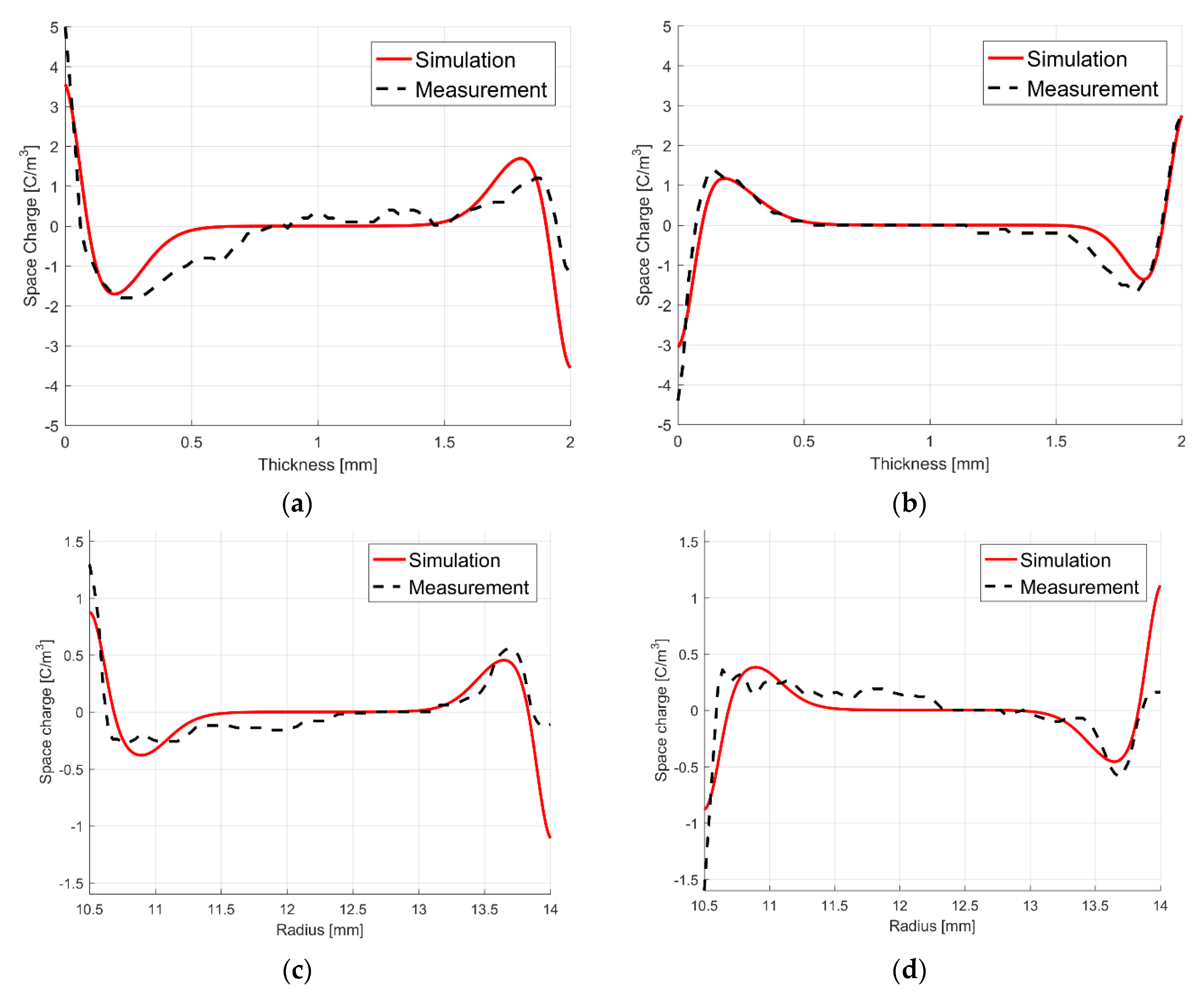
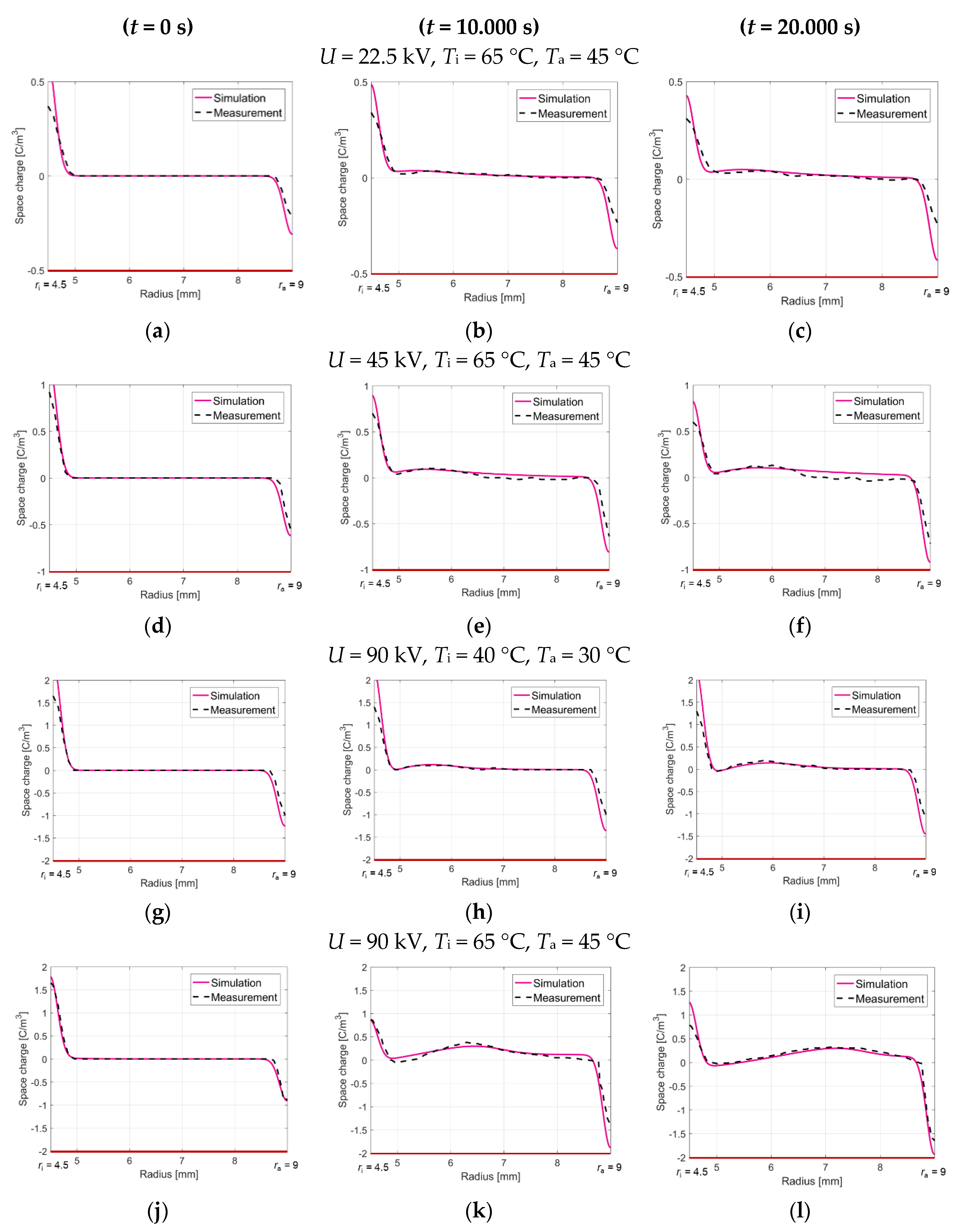
| (a) | (b) | (c) | (d) |
|---|---|---|---|
| U = 22.5 kV | U = 45 kV | U = 90 kV | U = 90 kV |
| Ti = 65 °C | Ti = 65 °C | Ti = 40 °C | Ti = 65 °C |
| Ta = 45 °C | Ta = 45 °C | Ta = 30 °C | Ta = 45 °C |
| ncon,ε = 1.5 | ncon,ε = 1.5 | ncon,ε = 1.5 | ncon,ε = 1.1 |
| nsh,ε = 1.0 | nsh,ε = 1.0 | nsh,ε = 1.0 | nsh,ε = 1.0 |
| ζcon,ε = 4.5 × 10−4 m | ζcon,ε = 4.5 × 10−4 m | ζcon,ε = 4.5 × 10−4 m | ζcon,ε = 4.5 × 10−4 m |
| vκ = 3 × 10−8 m/s | vκ = 3∙10−8 m/s | vκ = 5 × 10−8 m/s | vκ = 7.5 × 10−8 m/s |
| ncon,κ = 1.2 | ncon,κ = 1.5 | ncon,κ = 4.5 | ncon,κ = 13 |
| nsh,κ = 1.0 | nsh,κ = 1.0 | nsh,κ = 1.0 | nsh,κ = 1.0 |
| ζcon,κ = 9 × 10−7 m | ζcon,κ = 9 × 10−7 m | ζcon,κ = 9 × 10−7 m | ζcon,κ = 9 × 10−7 m |
| t = 0 s | t = 10.000 s | t = 20.000 s | |
|---|---|---|---|
| (a) | |||
| Equations (49) and (50) | 5.3% | 6.1% | 10.2% |
| [14] | 5.3% | 6.8% | 8.6% |
| (b) | |||
| Equations (49) and (50) | 5.5% | 15.0% | 22.1% |
| [14] | 5.5% | 12.3% | 17.0% |
| (c) | |||
| Equations (49) and (50) | 5.4% | 6.0% | 6.3% |
| [14] | 5.4% | 9.2% | 14.7% |
| (d) | |||
| Equations (49) and (50) | 1.3% | 5.8% | 12.5% |
| [14] | 1.2% | 32.9% | 34.6% |
| Model | Description of Charge Dynamics | Limitations |
|---|---|---|
| Equations (3)–(7) | Charge accumulation due to a temperature gradient. | Computation of an average charge density of one sign only. No effects at interfaces and surfaces. |
| Equations (39) or (45) and (40) | Charge distribution within the insulation and at interfaces and surfaces. | Limited to the stationary case and the additional constants are difficult to determine |
| Equation (47) | Description of the stationary bulk and heterocharge distribution in polymeric insulations. | Limited to the stationary case and heterocharges only. |
| Equations (49) and (50) | Simulation of transient processes, homo and heterocharges at interfaces and charges within the bulk. | Many additional constants are used that change over time and are determined by space charge measurements. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jörgens, C.; Clemens, M. A Review about the Modeling and Simulation of Electro-Quasistatic Fields in HVDC Cable Systems. Energies 2020, 13, 5189. https://doi.org/10.3390/en13195189
Jörgens C, Clemens M. A Review about the Modeling and Simulation of Electro-Quasistatic Fields in HVDC Cable Systems. Energies. 2020; 13(19):5189. https://doi.org/10.3390/en13195189
Chicago/Turabian StyleJörgens, Christoph, and Markus Clemens. 2020. "A Review about the Modeling and Simulation of Electro-Quasistatic Fields in HVDC Cable Systems" Energies 13, no. 19: 5189. https://doi.org/10.3390/en13195189
APA StyleJörgens, C., & Clemens, M. (2020). A Review about the Modeling and Simulation of Electro-Quasistatic Fields in HVDC Cable Systems. Energies, 13(19), 5189. https://doi.org/10.3390/en13195189