Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions
Abstract
:1. Introduction
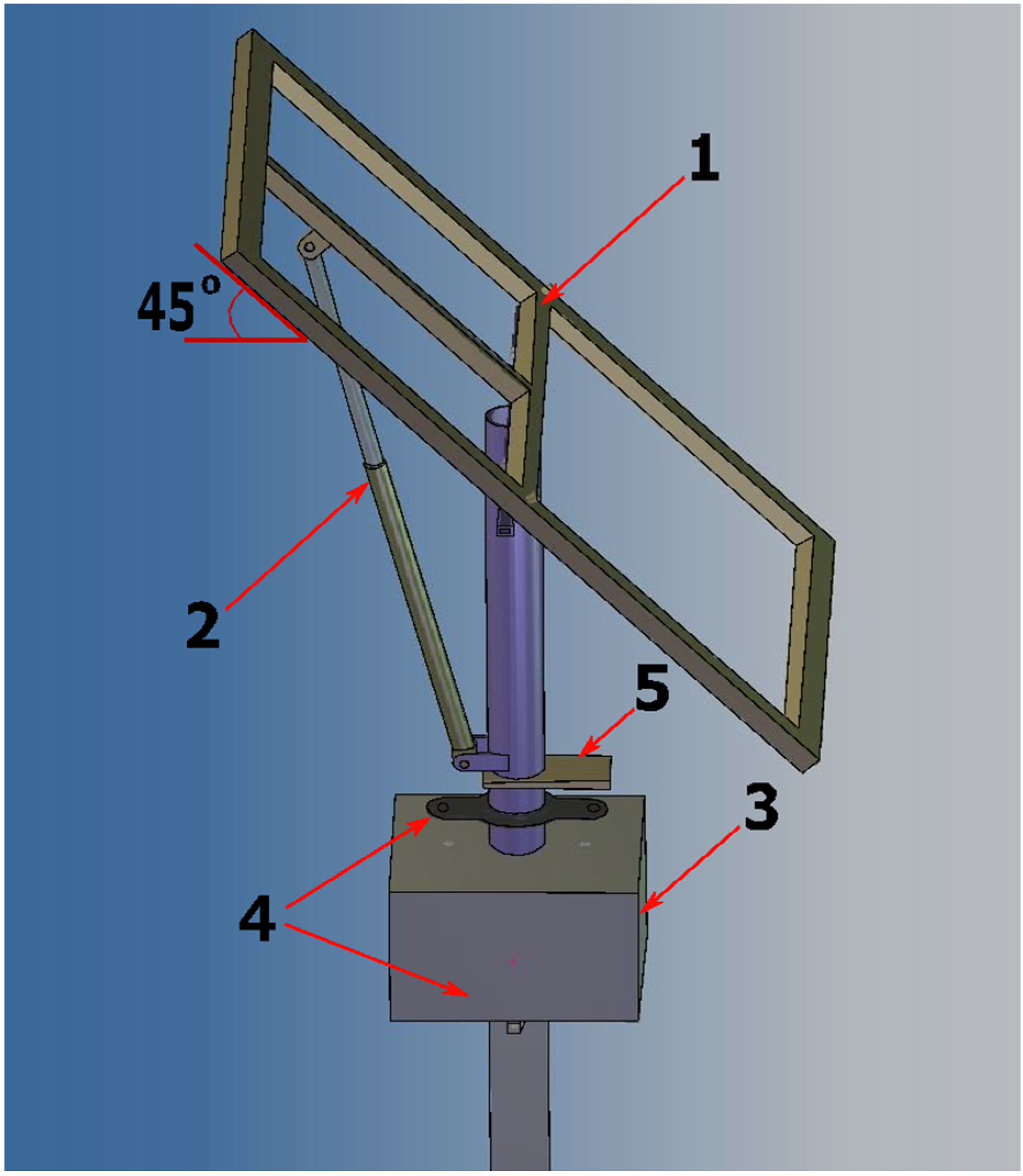
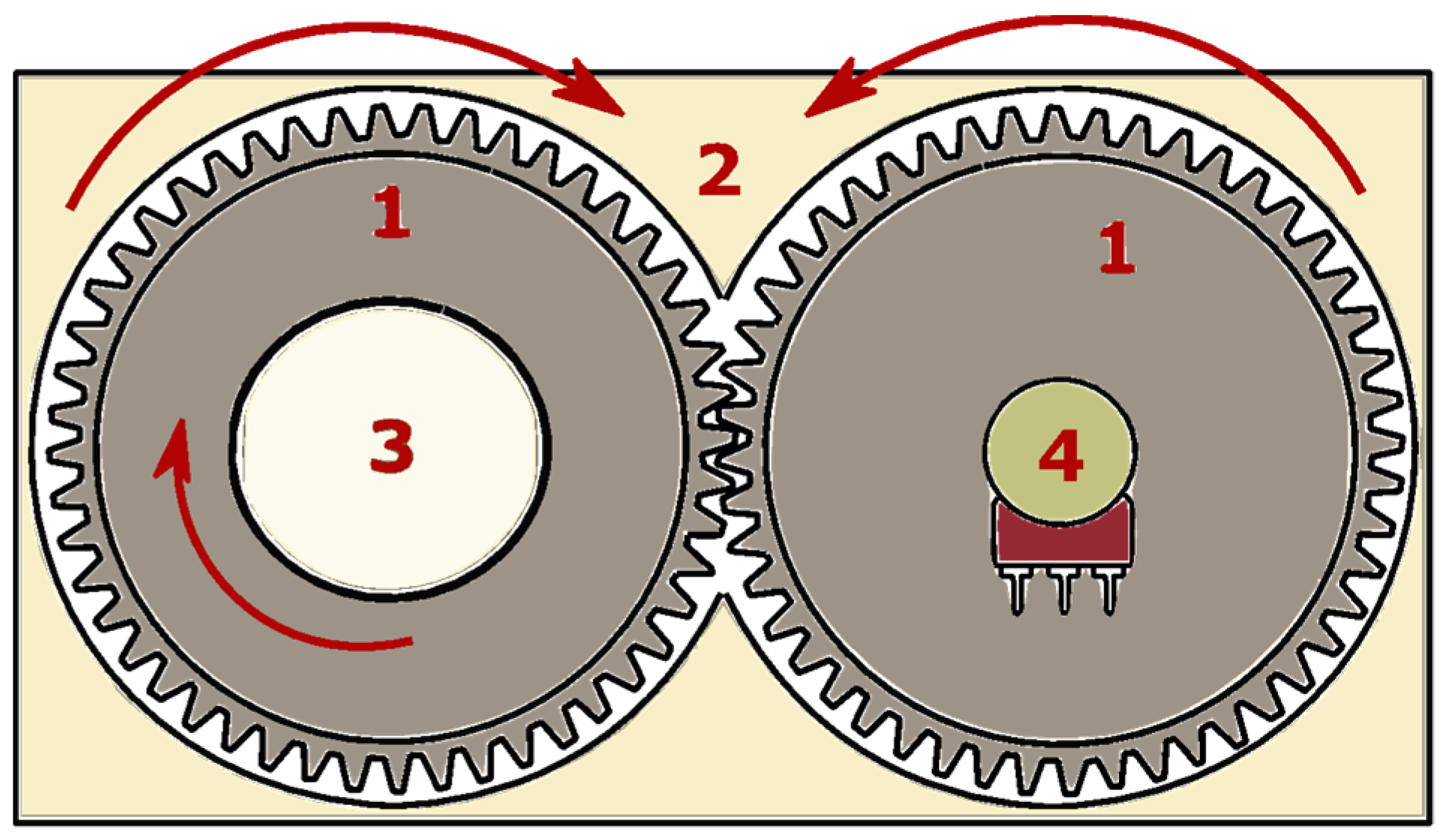
2. The Structure and Design Features of the Developed Single-Axis Solar Tracking Systems
3. Block Diagram of Electronic Control Units for Solar Trackers
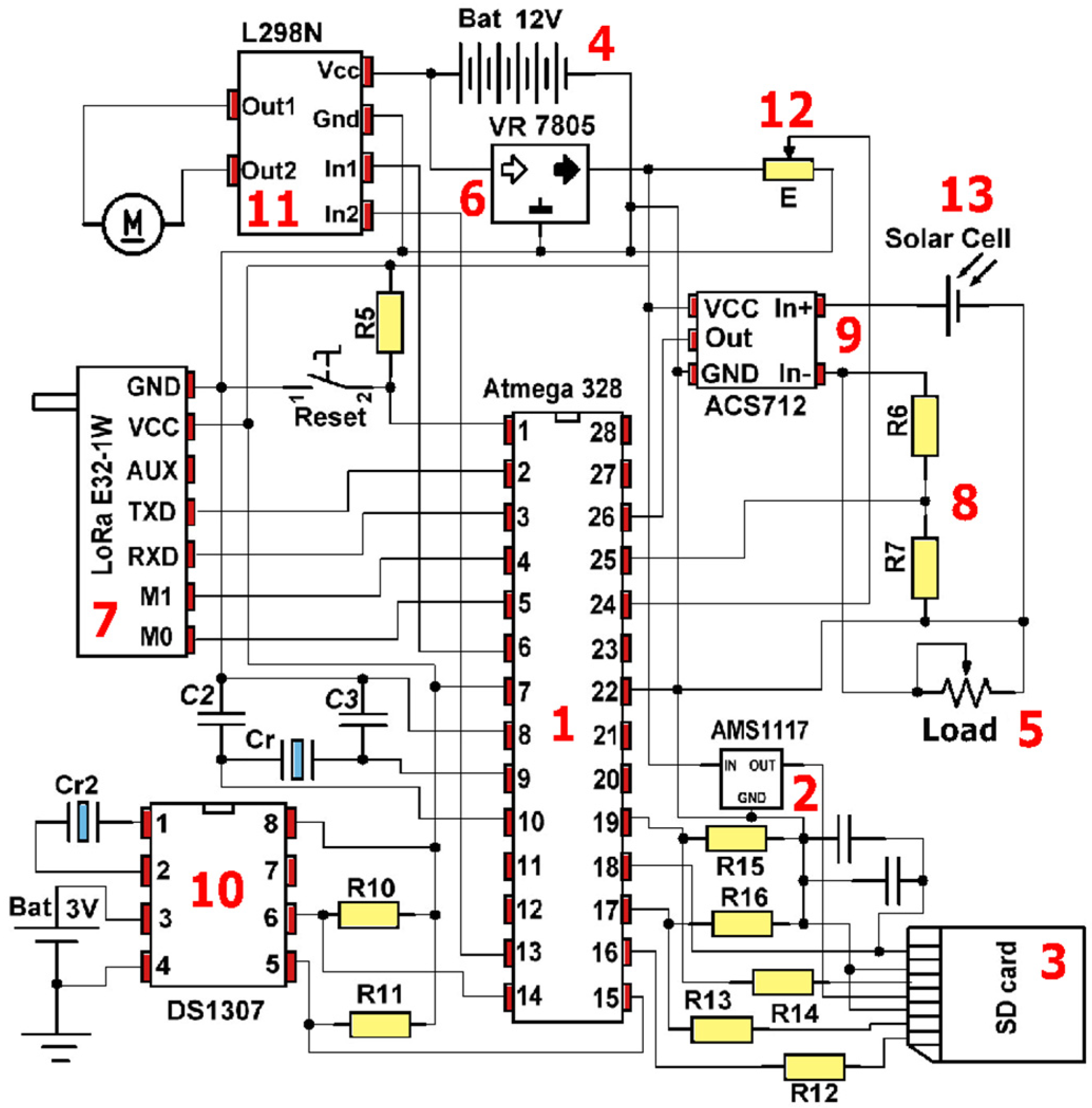
3.1. Solar Tracking System Based on Astronomical Calculations of the Sun’s Position
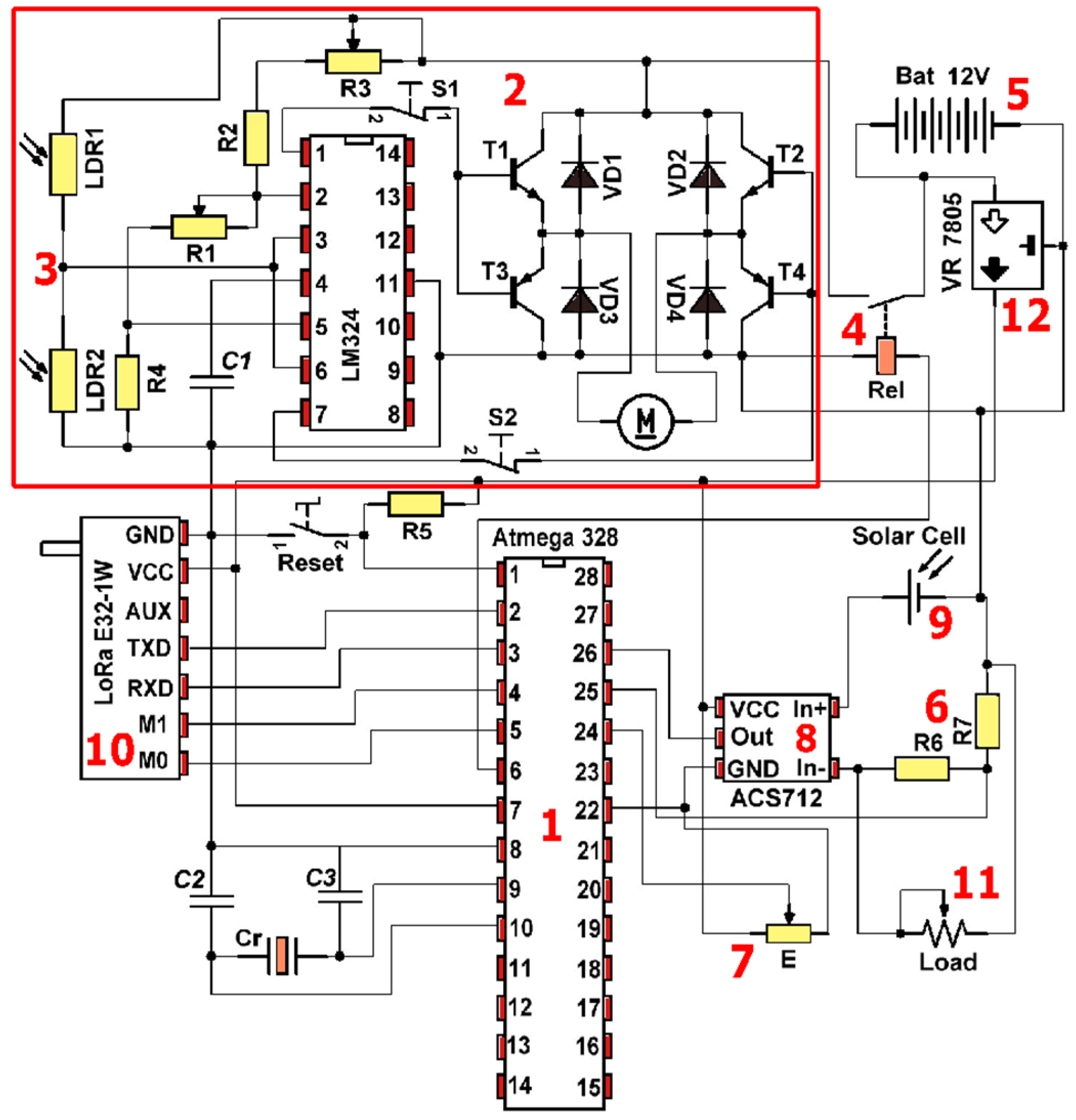
3.2. Solar Tracking System Based on Photosensitive Sensors
4. Algorithms for Single-Axis Solar Tracking Systems
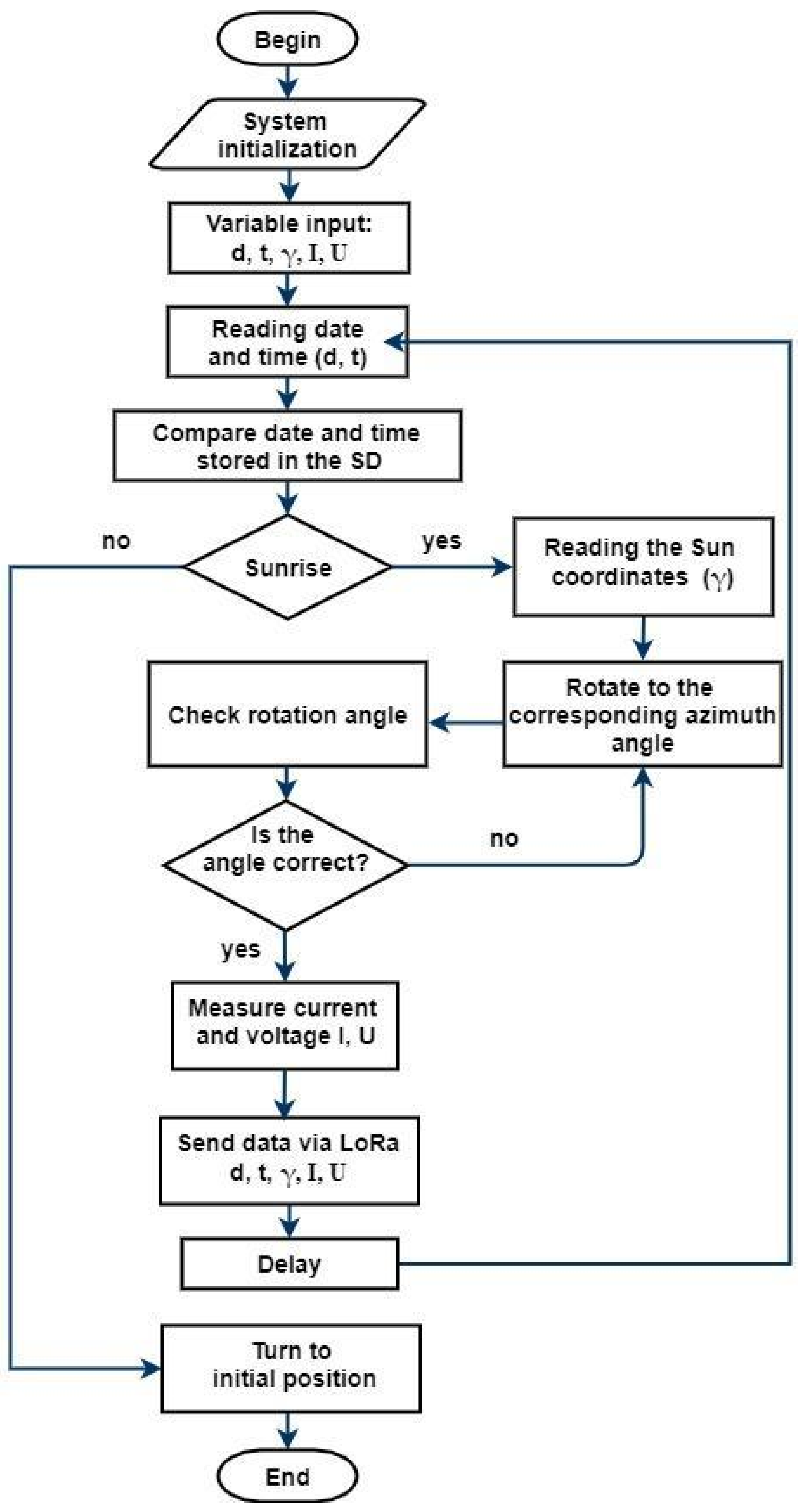
4.1. Algorithm for a Single-Axis Solar Tracker Based on an Astronomical Date
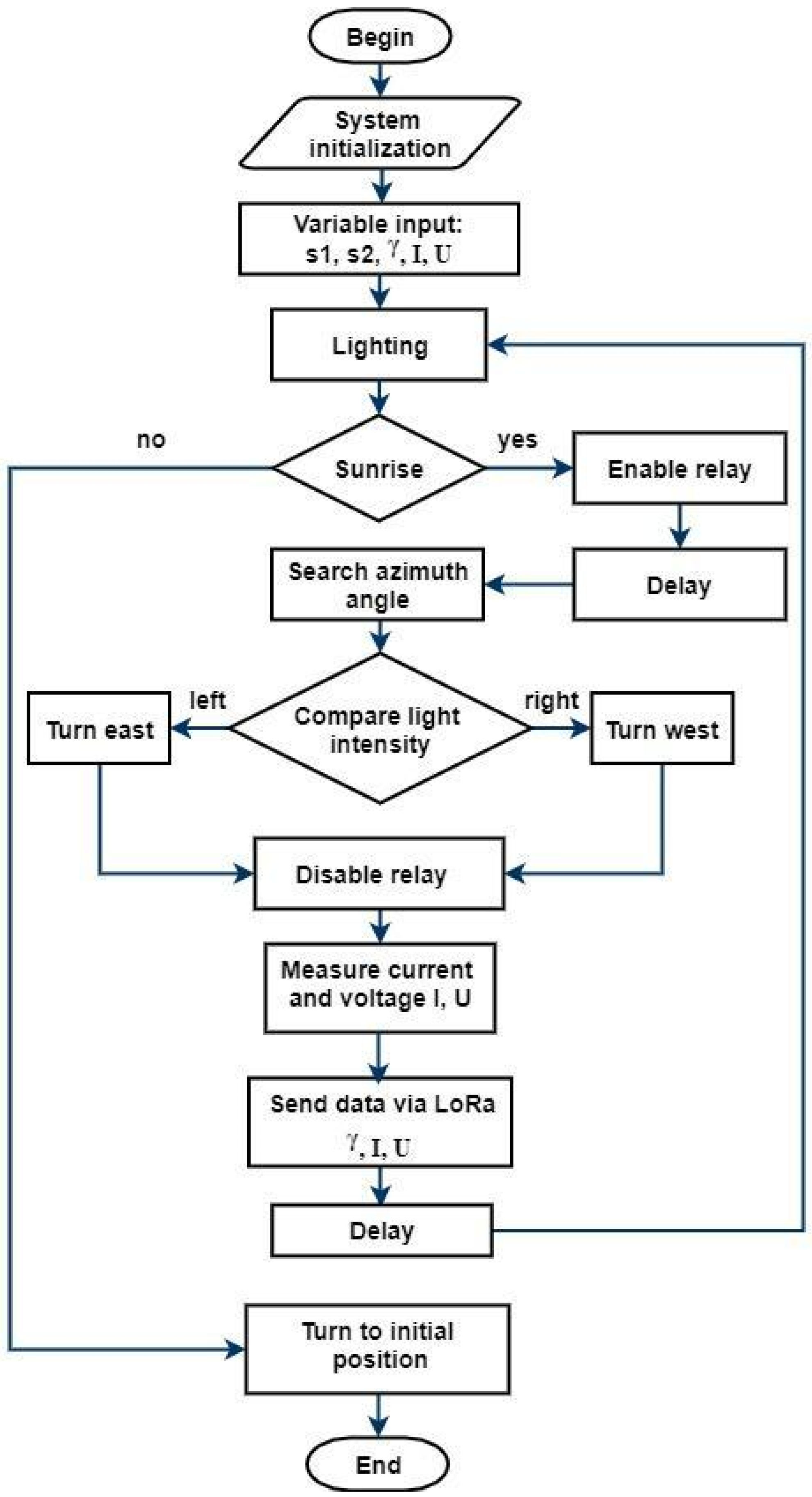
4.2. Algorithm for a Single-Axis Solar Tracker Based on Photosensors
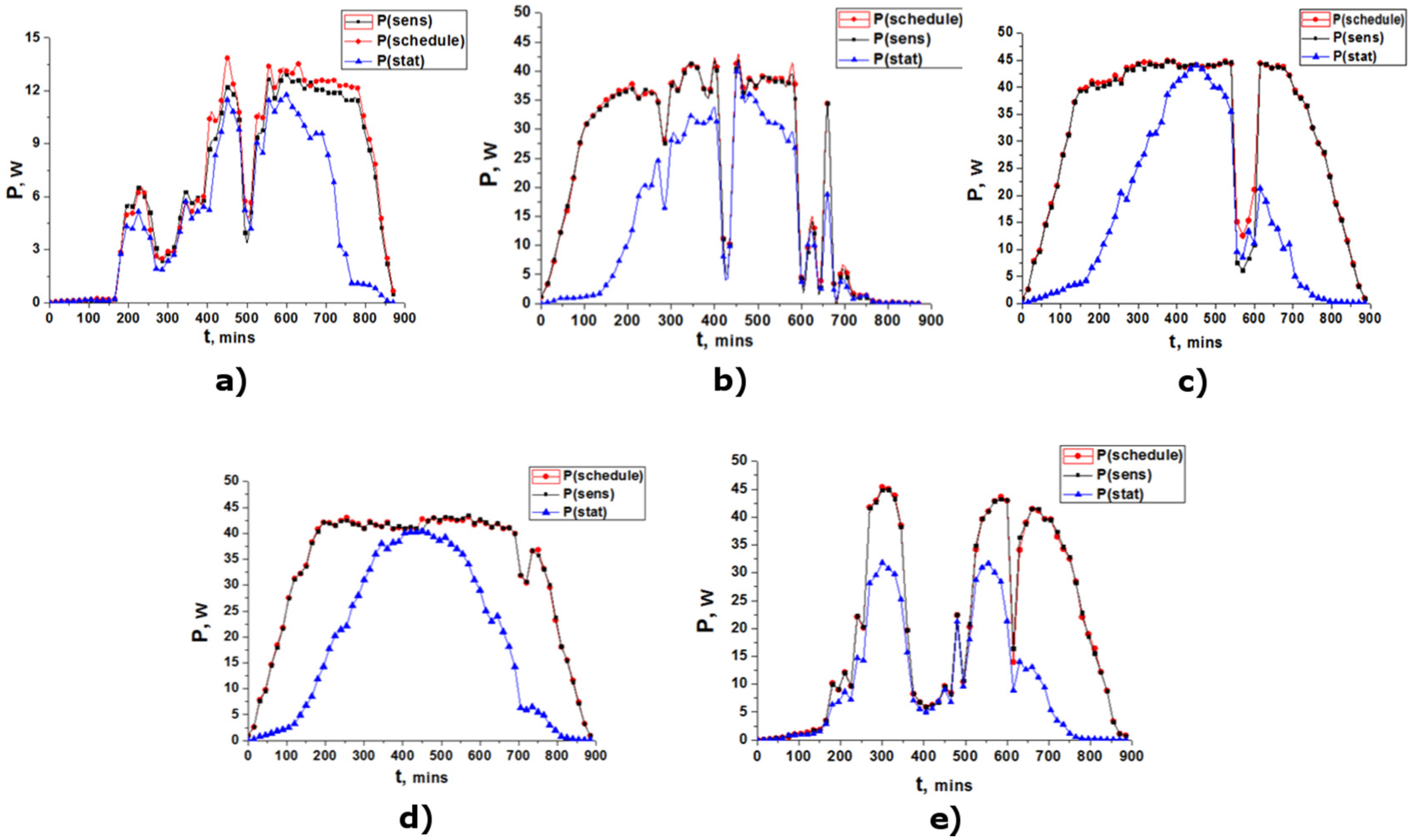
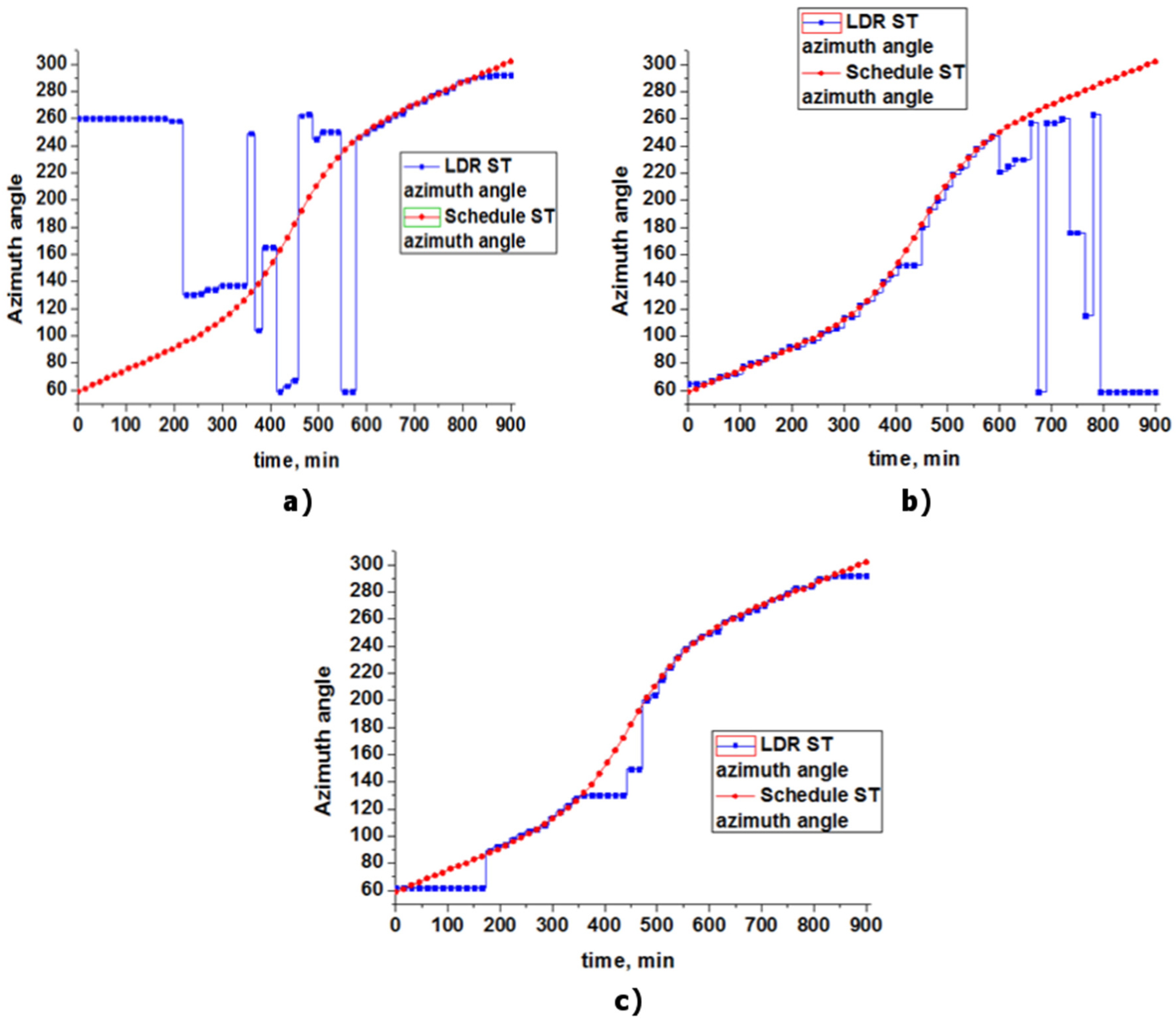
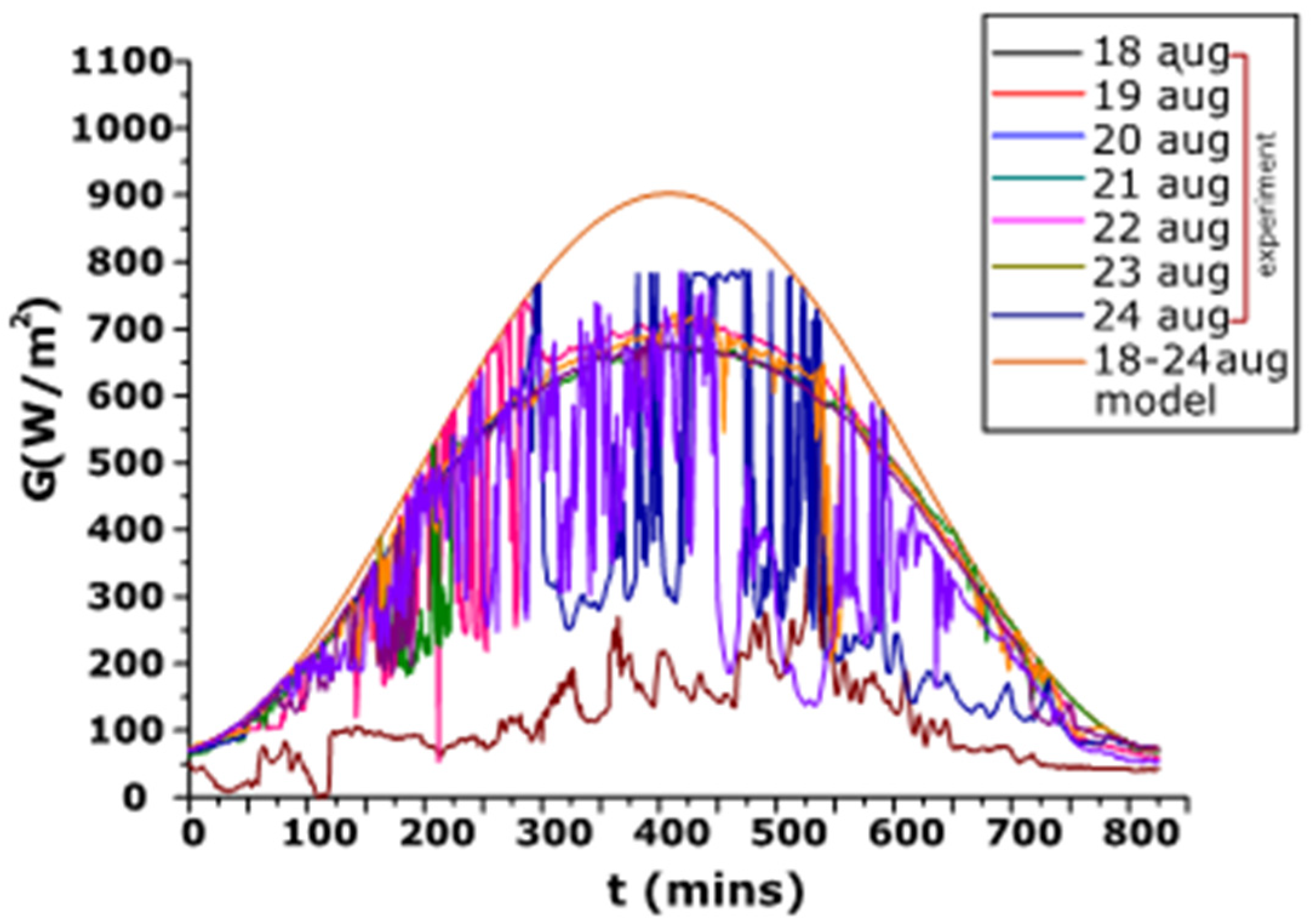
5. Experimental Results and Discussion
6. The Calculation of the Efficiency
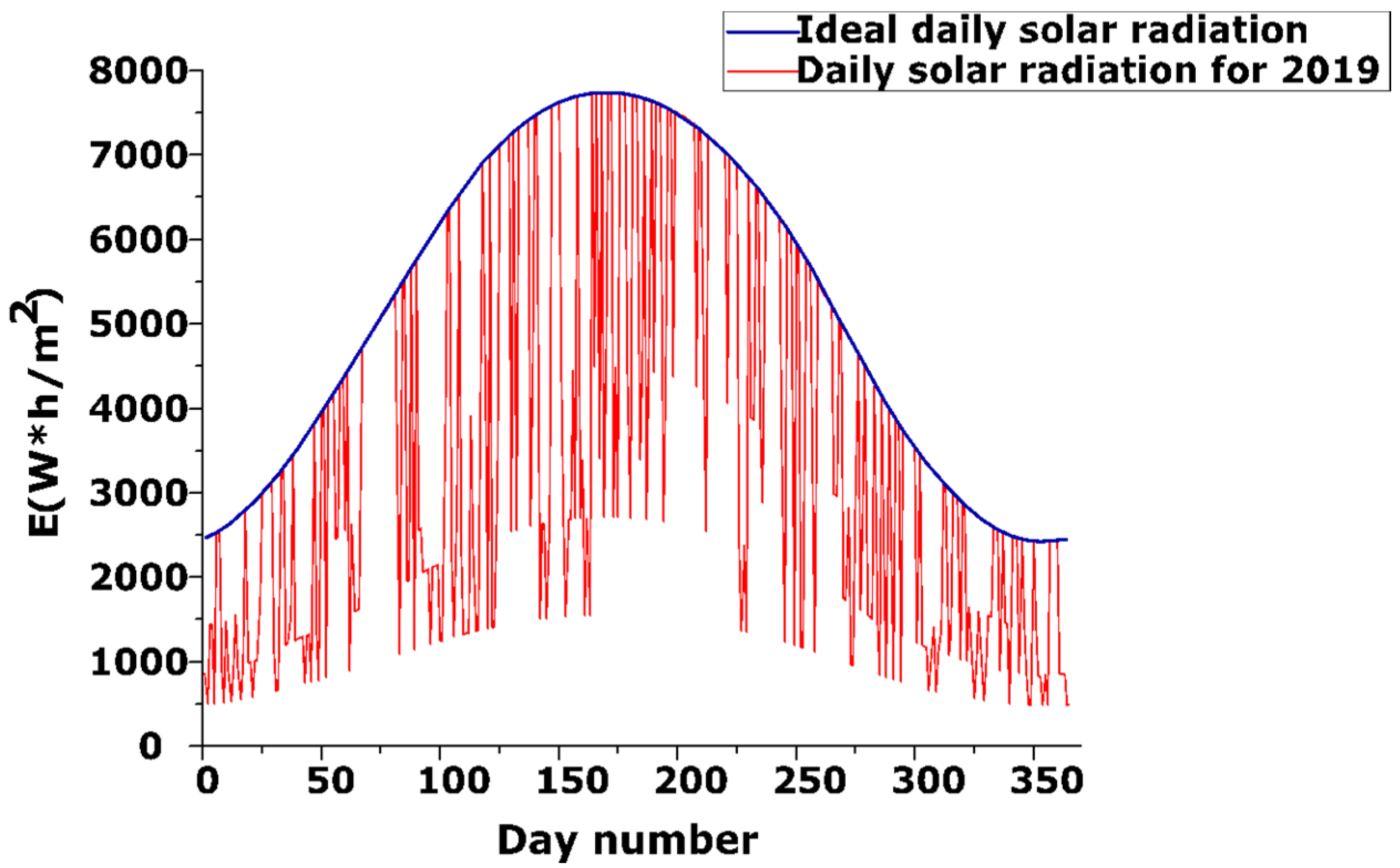
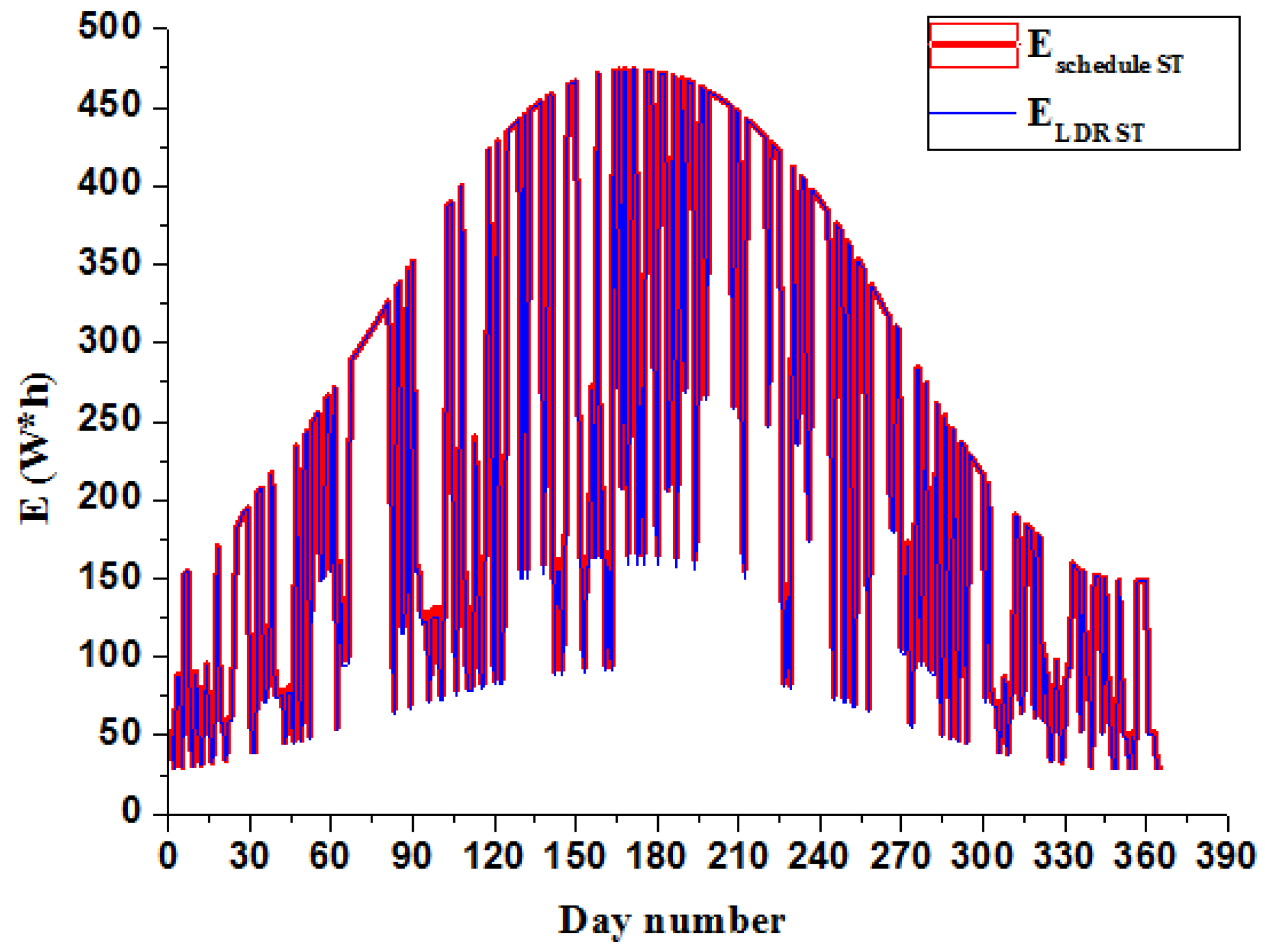
7. Modeling the Performance of the Tracker Taking into Account the Weather Conditions during the Year
- In rainy weather conditions, the solar radiation level is 0.2 of the calculated Gmodel value on a corresponding day;
- In cloudy weather, the solar radiation level is 0.45 of the calculated Gmodel value on a corresponding day;
- On days with variable cloud cover, the solar radiation flux reaches 0.66 of the calculated Gmodel on a corresponding day.
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mwasilu, F.; Justo, J.J.; Kim, E.-K.; Do, T.D.; Jung, J.-W. Electric vehicles and smart grid interaction: A review on vehicle to grid and renewable energy sources integration. Renew. Sustain. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Rodrigues, S.; Torabikalaki, R.; Faria, F.; Cafôfo, N.; Chen, X.; Ivaki, A.R.; Mata-Lima, H.; Morgado-Dias, F. Economic feasibility analysis of small scale PV systems in different countries. Sol. Energy 2016, 131, 81–95. [Google Scholar] [CrossRef]
- Saymbetov, A.K.; Nurgaliyev, M.K.; Nalibayev, Y.D.; Kuttybay, N.B.; Svanbayev, Y.A.; Dosymbetova, G.B.; Tulkibaiuly, Y.; Meiirkhanov, A.K.; Kopzhan, Z.K.; Gaziz, K.A. Intelligent Energy Efficient Wireless Communacation System for Street Lighting. In Proceedings of the International Conference on Computing and Network Communications (CoCoNet), Astana, Kazakhstan, 15–17 August 2018. [Google Scholar]
- Tukymbekov, D.; Saymbetov, A.; Nurgaliyev, M.; Kuttybay, N.; Nalibayev, Y.; Dosymbetova, G. Intelligent energy efficient street lighting system with predictive energy consumption. In Proceedings of the International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019. [Google Scholar]
- Singh, R.; Kumar, S.; Gehlot, A.; Pachauri, R. An imperative role of sun trackers in photovoltaic technology: A review. Renew. Sustain. Energy Rev. 2018, 82, 3263–3278. [Google Scholar] [CrossRef]
- Kuttybay, N.; Mekhilef, S.; Saymbetov, A.; Nurgaliyev, M.; Meiirkhanov, A.; Dosymbetova, G.; Kopzhan, Z. An Automated Intelligent Solar Tracking Control System with Adaptive Algorithm for Different Weather Conditions. In Proceedings of the 2019 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Selangor, 29 June 2019. [Google Scholar]
- Mousazadeh, H.; Keyhani, A.; Javadi, A.; Mobli, H.; Abrinia, K.; Sharifi, A. A review of principle and sun-tracking methods for maximizing solar systems output. Renew. Sustain. Energy Rev. 2009, 13, 1800–1818. [Google Scholar] [CrossRef]
- Saymbetov, A.K.; Nurgaliyev, M.K.; Tulkibaiuly, Y.; Toshmurodov, Y.K.; Nalibayev, Y.D.; Dosymbetova, G.B.; Kuttybay, N.B.; Gylymzhanova, M.M.; Svanbayev, Y.A. Method for Increasing the Efficiency of a Biaxial Solar Tracker with Exact Solar Orientation. Appl. Sol. Energy 2018, 54, 126–130. [Google Scholar] [CrossRef]
- Senpinar, A.; Cebeci, M. Evaluation of power output for fixed and two-axis tracking PVarrays. Appl. Energy 2012, 92, 677–685. [Google Scholar] [CrossRef]
- Huang, B.; Sun, F. Feasibility study of one axis three positions tracking solar PV with low concentration ratio reflector. Energy Convers. Manag. 2007, 48, 1273–1280. [Google Scholar] [CrossRef]
- Nsengiyumva, W.; Chen, S.G.; Hu, L.; Chen, X. Recent advancements and challenges in Solar Tracking Systems (STS): A review. Renew. Sustain. Energy Rev. 2018, 81, 250–279. [Google Scholar] [CrossRef]
- Gil, F.G.; Martin, M.D.S.; Vara, J.P.; Calvo, J.R.; Perlovsky, L.; Dionysiou, D.D.; Mastorakis, N.E. A review of solar tracker patents in Spain. In Proceedings of the 3rd WSEAS International Conference on Energy Planning, Energy Saving, Environmental Education, EPESE ’09, 3rd WSEAS International Conference on Renewable Energy Sources, RES ’09, 3rd WSEAS International Conference on Waste Management, WWAI ’09, Canary Islands, Spain, 1–3 July 2009; pp. 292–297. [Google Scholar]
- Helwa, N.H.; Bahgat, A.B.G.; El Shafee, A.M.R.; El Shenawy, E.T. Computation of the Solar Energy Captured by Different Solar Tracking Systems. Energy Sources 2000, 22, 35–44. [Google Scholar] [CrossRef]
- Helwa, N.H.; Bahgat, A.B.G.; El Shafee, A.M.R.; El Shenawy, E.T. Maximum Collectable Solar Energy by Different Solar Tracking Systems. Energy Sources 2000, 22, 23–34. [Google Scholar] [CrossRef]
- Gordon, J.; Wenger, H.J. Central-station solar photovoltaic systems: Field layout, tracker, and array geometry sensitivity studies. Sol. Energy 1991, 46, 211–217. [Google Scholar] [CrossRef]
- Gay, C.F.; Yerkes, J.W.; Wilson, J.H. Performance advantages of two-axis tracking for large flat-plate photovoltaic energy systems. In Proceedings of the Photovoltaic Specialists Conference, Record (A84-22957 09-44), San Diego, CA, USA, 27–30 September 1982; Volume 16, pp. 1368–1371. [Google Scholar]
- Koussa, M.; Cheknane, A.; Hadji, S.; Haddadi, M.; Noureddine, S. Measured and modelled improvement in solar energy yield from flat plate photovoltaic systems utilizing different tracking systems and under a range of environmental conditions. Appl. Energy 2011, 88, 1756–1771. [Google Scholar] [CrossRef]
- Alexandru, C.; Tatu, N.I. Optimal design of the solar tracker used for a photovoltaic string. J. Renew. Sustain. Energy 2013, 5, 23133. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Tang, R. Optical performance of inclined south-north single-axis tracked solar panels. Energy 2010, 35, 2511–2516. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Tang, R. Optical performance of vertical single-axis tracked solar panels. Renew. Energy 2011, 36, 64–68. [Google Scholar] [CrossRef]
- Fahad, H.M.; Islam, A.; Islam, M.; Hasan, F.; Brishty, W.F.; Rahman, M. Comparative Analysis of Dual and Single Axis Solar Tracking System Considering Cloud Cover. In Proceedings of the International Conference on Energy and Power Engineering (ICEPE), Dhaka, Bangladesh, 14–16 March 2019. [Google Scholar]
- Al-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in solar photovoltaic tracking systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Huang, B.; Ding, W.; Huang, Y. Long-term field test of solar PV power generation using one-axis 3-position sun tracker. Sol. Energy 2011, 85, 1935–1944. [Google Scholar] [CrossRef]
- Kacira, M.; Simsek, M.; Babur, Y.; Demirkol, S. Determining optimum tilt angles and orientations of photovoltaic panels in Sanliurfa, Turkey. Renew. Energy 2004, 29, 1265–1275. [Google Scholar] [CrossRef]
- Huang, B.-J.; Huang, Y.-C.; Chen, G.-Y.; Hsu, P.-C.; Li, K. Improving Solar PV System Efficiency Using One-Axis 3-Position Sun Tracking. Energy Procedia 2013, 33, 280–287. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.P. Performance study on the east–west oriented single-axis tracked panel. Energy 2009, 34, 1530–1538. [Google Scholar] [CrossRef]
- Al-Mohamad, A. Efficiency improvements of photo-voltaic panels using a Sun-tracking system. Appl. Energy 2004, 79, 345–354. [Google Scholar] [CrossRef]
- Lorenzo, E.; Pérez, M.; Ezpeleta, A.; Acedo, J. Design of tracking photovoltaic systems with a single vertical axis. Prog. Photovolt. Res. Appl. 2002, 10, 533–543. [Google Scholar] [CrossRef]
- Obara, S.; Matsumura, K.; Aizawa, S.; Kobayashi, H.; Hamada, Y.; Suda, T. Development of a solar tracking system of a nonelectric power source by using a metal hydride actuator. Sol. Energy 2017, 158, 1016–1025. [Google Scholar] [CrossRef]
- Lazaroiu, G.C.; Longo, M.; Roscia, M.; Pagano, M. Comparative analysis of fixed and sun tracking low power PV systems considering energy consumption. Energy Convers. Manag. 2015, 92, 143–148. [Google Scholar] [CrossRef]
- Sefa, I.; Demirtaş, M.; Çolak, I. Application of one-axis sun tracking system. Energy Convers. Manag. 2009, 50, 2709–2718. [Google Scholar] [CrossRef]
- Chin, C.S.; Babu, A.; McBride, W. Design, modeling and testing of a standalone single axis active solar tracker using MATLAB/Simulink. Renew. Energy 2011, 36, 3075–3090. [Google Scholar] [CrossRef]
- Hoffmann, F.M.; Molz, R.F.; Kothe, J.V.; Nara, E.O.B.; Tedesco, L.P.C. Monthly profile analysis based on a two-axis solar tracker proposal for photovoltaic panels. Renew. Energy 2018, 115, 750–759. [Google Scholar] [CrossRef]
- Yilmaz, S.; Ozcalik, H.R.; Dogmus, O.; Dincer, F.; Akgol, O.; Karaaslan, M. Design of two axes sun tracking controller with analytically solar radiation calculations. Renew. Sustain. Energy Rev. 2015, 43, 997–1005. [Google Scholar] [CrossRef]
- Barsoum, N. Fabrication of Dual-Axis Solar Tracking Controller Project. Intell. Control. Autom. 2011, 2, 57–68. [Google Scholar] [CrossRef] [Green Version]
- El Kadmiri, Z.; El Kadmiri, O.; Masmoudi, L.; Bargach, M.N. A Novel Solar Tracker Based on Omnidirectional Computer Vision. J. Sol. Energy 2015, 2015, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Tudorache, T.; Kreindler, L. Design of a solar tracker system for PV power plants. Acta Polytech. Hung. 2010, 7, 23–39. [Google Scholar]
- Pattanasethanon, S. The Solar Tracking System by Using Digital Solar Position Sensor. Am. J. Eng. Appl. Sci. 2010, 3, 678–682. [Google Scholar] [CrossRef] [Green Version]
- Algarin, R.; Arturo, C.; Castro, A.J.O.; Casas, J.N. Dual-axis solar tracker for using in photovoltaic systems. Int. J. Renew. Energy 2017, 7, 137–145. [Google Scholar]
- Sungur, C. Multi-axes sun-tracking system with PLC control for photovoltaic panels in Turkey. Renew. Energy 2009, 34, 1119–1125. [Google Scholar] [CrossRef]
- Roth, P.; Georgiev, A.; Boudinov, H. Cheap two axis sun following device. Energy Convers. Manag. 2005, 46, 1179–1192. [Google Scholar] [CrossRef]
- Kamala, J.; Joseph, A. Solar tracking for maximum and economic energy harvesting. Int. J. Eng. Technol. 2014, 5, 5030–5037. [Google Scholar]
- Ranganathan, R.; Mikhael, W.; Kutkut, N.; Batarseh, I. Adaptive sun tracking algorithm for incident energy maximization and efficiency improvement of PV panels. Renew. Energy 2011, 36, 2623–2626. [Google Scholar] [CrossRef]
- Nayak, S.R. Solar Tracking Application. IOSR J. Eng. 2012, 2, 1278–1281. [Google Scholar] [CrossRef]
- Sidek, M.; Azis, N.; Hasan, W.; Ab Kadir, M.; Shafie, S.; Radzi, M. Automated positioning dual-axis solar tracking system with precision elevation and azimuth angle control. Energy 2017, 124, 160–170. [Google Scholar] [CrossRef]
- Gregor, R.; Takase, Y.; Rodas, J.; Carreras, L.; Gregor, D.; López, A. Biaxial Solar Tracking System Based on the MPPT Approach Integrating ICTs for Photovoltaic Applications. Int. J. Photoenergy 2015, 2015, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Fathabadi, H. Novel high efficient offline sensorless dual-axis solar tracker for using in photovoltaic systems and solar concentrators. Renew. Energy 2016, 95, 485–494. [Google Scholar] [CrossRef]
- Tharamuttam, J.K.; Ng, A.K. Design and Development of an Automatic Solar Tracker. Energy Procedia 2017, 143, 629–634. [Google Scholar] [CrossRef]
- Ho, M.-C.; Lai, A.-C.; Chong, K.-K.; Tan, M.-H.; Lim, B.H.; King, Y.J.; Lee, J.-V. Design and Construction of Prototype Mobile Sun-Tracking System for Concentrator Photovoltaic System. Energy Procedia 2017, 142, 736–742. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, J.; Harding, B.J.; Makela, J.J.; Domínguez-García, A.D. Spoofing GPS Receiver Clock Offset of Phasor Measurement Units. IEEE Trans. Power Syst. 2013, 28, 3253–3262. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Gong, S.; Dimitrovski, A.; Li, H. Time Synchronization Attack in Smart Grid: Impact and Analysis. IEEE Trans. Smart Grid 2013, 4, 87–98. [Google Scholar] [CrossRef]
- Skvortzov, V.Y.; Lee, H.-K.; Bang, S.; Lee, Y. Application of Electronic Compass for Mobile Robot in an Indoor Environment. In Proceedings of the 2001 IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Cho, S.Y.; Park, C.G. Tilt compensation algorithm for 2-axis magnetic compass. Electron. Lett. 2003, 39, 1589. [Google Scholar] [CrossRef]
- Ojeda, L.; Borenstein, J. Experimental results with the KVH C-100 fluxgate compass in mobile robots. In Proceedings of the IASTED International Conference on Robotics and Applications, Honolulu, HI, USA, 14–16 August 2000. [Google Scholar]
- Kwon, W.; Roh, K.-S.; Sung, H.-K. Particle filter-based heading estimation using magnetic compasses for mobile robot navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–18 May 2006. [Google Scholar]
- Lee, K.; Kim, Y.; Yun, J.; Lee, J. Magnetic-interference-free dual-electric compass. Sens. Actuators A Phys. 2005, 120, 441–450. [Google Scholar] [CrossRef]
- Nurgaliyev, M.; Saymbetov, A.; Yashchyshyn, Y.; Kuttybay, N.; Tukymbekov, D. Prediction of energy consumption for LoRa based wireless sensors network. Wirel. Netw. 2020, 26, 3507–3520. [Google Scholar] [CrossRef]
- Ioniţă, M.A.; Alexandru, C. Dynamic optimization of the tracking system for a pseudo-azimuthal photovoltaic platform. J. Renew. Sustain. Energy 2012, 4, 053117. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, G.; Zhu, Z.; Li, W.; Cai, Z. Numerical study on the properties of an active sun tracker for solar streetlight. Mechatronics 2013, 23, 1215–1222. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, J.; Yang, X. Design and performance analysis of a solar tracking system with a novel single-axis tracking structure to maximize energy collection. Appl. Energy 2020, 264, 114647. [Google Scholar] [CrossRef]
- World-weather.ru. Available online: https://world-weather.ru/pogoda/kazakhstan/almaty/ (accessed on 6 September 2020).



| Parameters | Fixed | Developed LDR Solar Tracker | Developed Schedule Solar Tracker |
|---|---|---|---|
| Installation | Easy | Moderate | Moderate |
| Mechanism | No mechanism | Simple | Simple |
| Cost | Cheap | Moderate | Moderate |
| Design | Simple | Moderate | Moderate |
| Maintenance | Less | Moderate | Moderate |
| Efficiency at sunny weather | Reference efficiency | 57.4% > Fixed system | 57.4% > Fixed system |
| Efficiency at cloudy/rainy weather | Reference efficiency | >32.2% Fixed system | >37.7% than Fixed system >4.2% than LDR ST |
| Date | Esc, W·h | ELDR, W·h | Efix, W·h |
|---|---|---|---|
| 1 July 2020 | 372 | 357 | 270 |
| 2 July 2020 | 1220 | 1206 | 785 |
| 3 July 2020 | 1757 | 1748 | 1098 |
| 8 July 2020 | 1775 | 1776 | 1111 |
| 9 July 2020 | 1158 | 1145 | 725 |
| Σ | 6282 | 6232 | 3989 |
| U, V | I, A; | P, W | t to Rotate to 1°, s | E to Rotate to 1°, J/° |
|---|---|---|---|---|
| 12.3 | 0.33 | 4.059 | 0.203 | 0.823 |
| Date | 1 July | 2 July | 3 July | 8 July | 9 July |
|---|---|---|---|---|---|
| 245 | 244 | 244 | 243 | 242 | |
| tr, s | 49.735 | 49.532 | 49.532 | 49.329 | 49.126 |
| Pr, W | 4.0542 | 4.0542 | 4.0542 | 4.0542 | 4.0542 |
| E, J | 201.635 | 200.812 | 200.812 | 199.989 | 199.166 |
| Weather | Number of Days | Eschedule, kW·h | ELDR, kW·h |
|---|---|---|---|
| Rainy/cloudy | 142 | 194.8 | 186.6 |
| Partly cloudy weather | 59 | 175.13 | 173.12 |
| Clear | 164 | 905.86 | 905.86 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuttybay, N.; Saymbetov, A.; Mekhilef, S.; Nurgaliyev, M.; Tukymbekov, D.; Dosymbetova, G.; Meiirkhanov, A.; Svanbayev, Y. Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions. Energies 2020, 13, 5226. https://doi.org/10.3390/en13195226
Kuttybay N, Saymbetov A, Mekhilef S, Nurgaliyev M, Tukymbekov D, Dosymbetova G, Meiirkhanov A, Svanbayev Y. Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions. Energies. 2020; 13(19):5226. https://doi.org/10.3390/en13195226
Chicago/Turabian StyleKuttybay, Nurzhigit, Ahmet Saymbetov, Saad Mekhilef, Madiyar Nurgaliyev, Didar Tukymbekov, Gulbakhar Dosymbetova, Aibolat Meiirkhanov, and Yeldos Svanbayev. 2020. "Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions" Energies 13, no. 19: 5226. https://doi.org/10.3390/en13195226
APA StyleKuttybay, N., Saymbetov, A., Mekhilef, S., Nurgaliyev, M., Tukymbekov, D., Dosymbetova, G., Meiirkhanov, A., & Svanbayev, Y. (2020). Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions. Energies, 13(19), 5226. https://doi.org/10.3390/en13195226






