Operation Analysis of a SAG Mill under Different Conditions Based on DEM and Breakage Energy Method
Abstract
:1. Introduction
2. Simulation Principle Characteristics
2.1. Discrete Element Method
2.2. Hertz–Mindlin with Bonding
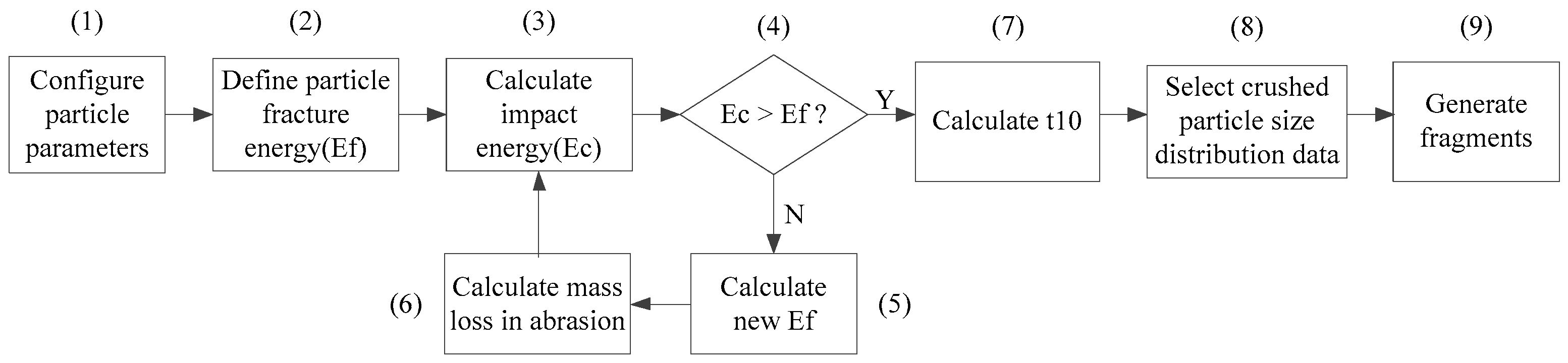
2.3. Breakage Model
3. SAG Model and Simulation Scheme
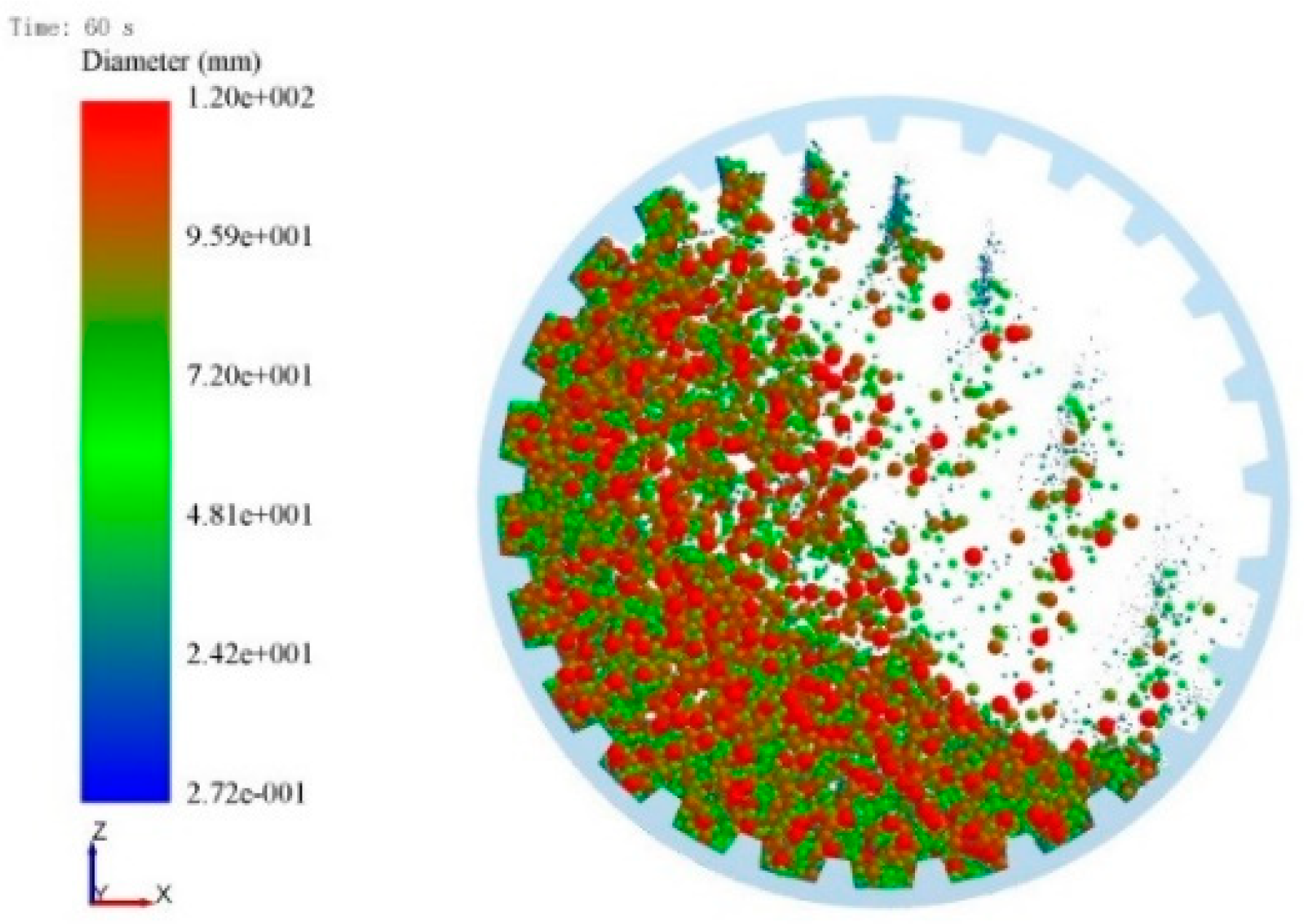
3.1. SAG Mill Model
3.2. Parameter Settings
3.3. Simulation Scheme Design
4. Simulation Results Analysis
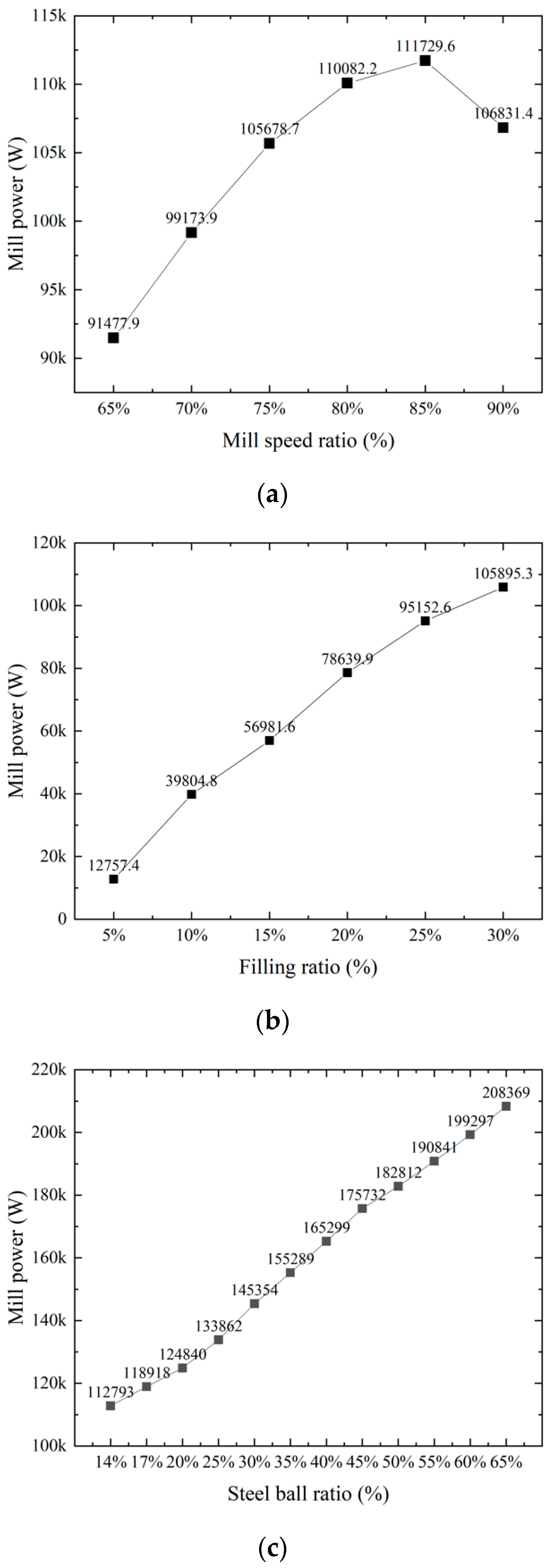
4.1. Single Parameter Case Analysis
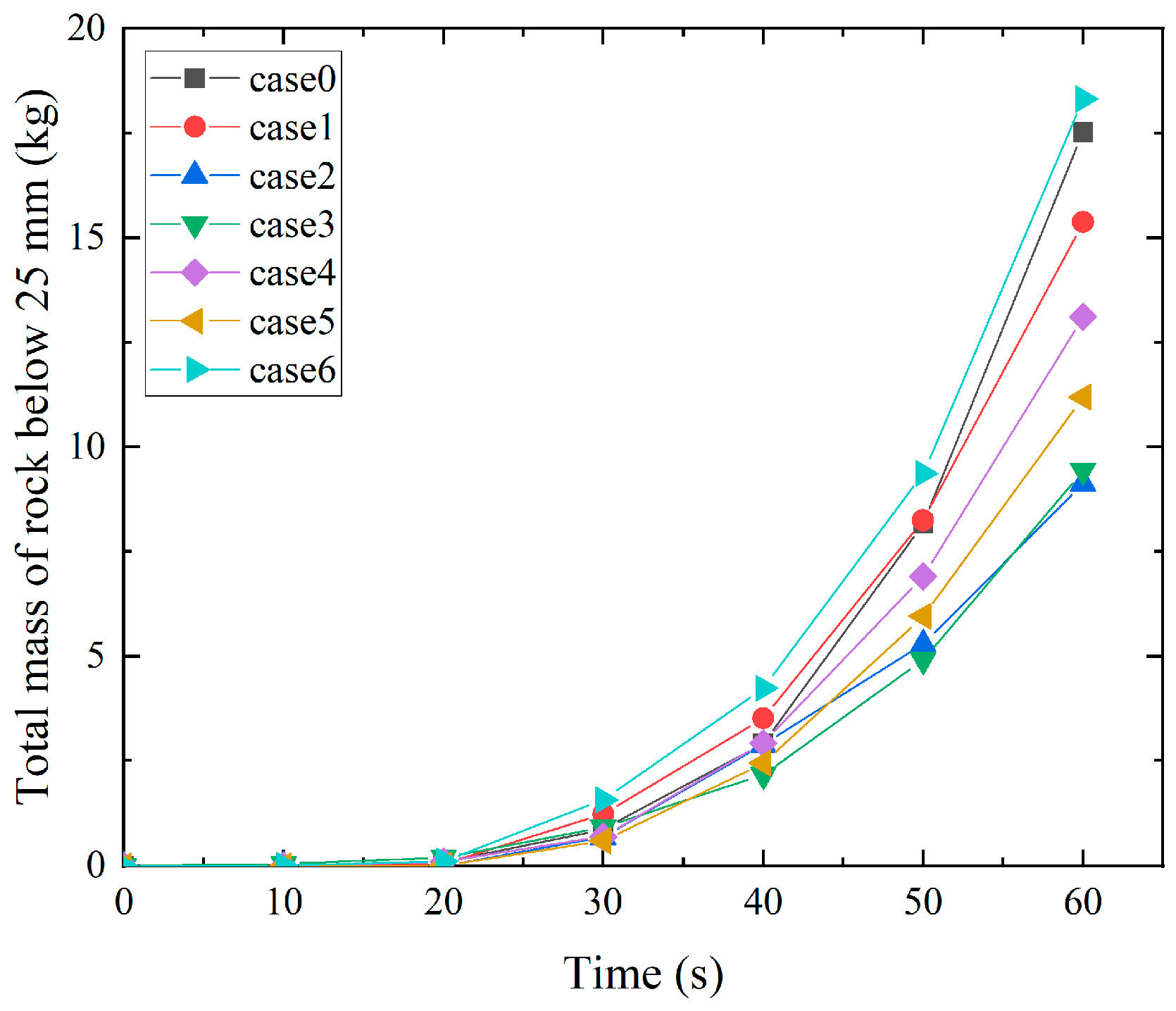
4.2. Mixed Parameter Case Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, G.R.; Fu, H.S. Discussion on design characteristics of copper slag beneficiation technology in Shuikoushan, Hunan Province. Non Ferr. Met. Eng. 2016, 6, 73–77. [Google Scholar]
- Ji, J.G.; Pan, J.J.; Wang, C.H.; Zhou, H. Tendency, causes and expectation of large-scale homemade mine-used mills. Min. Process. Equip. 2015, 43, 1–5. [Google Scholar]
- Shi, G.M.; Li, X.S.; Yin, Q.H.; Wu, C.B.; Ni, S.N. Wear and grinding of SAG pebble in the laboratory scale mills. Nonferrous Met. Eng. 2017, 7, 64–69. [Google Scholar]
- Liu, Y.; Yu, Z.S.; Yang, J.C.; Wassgren, C.; Curtis, J.S.; Guo, Y. Discrete Element Method Investigation of Binary Granular Flows with Different Particle Shapes. Energies 2020, 13, 1841. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; He, F. Modeling on the Effect of Coal Loads on Kinetic Energy of Balls for Ball Mills. Energies 2015, 8, 6859–6880. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.X. Research on Optimization of Working Parameters of SAG Mill. Master’s Thesis, Central South University, Changsha, China, 2013. [Google Scholar]
- Li, H.J.; Evertsson, M.; Lindqvist, M.; Hulthén, E.; Asbjörnsson, G. Dynamic modeling and simulation of a SAG mill-pebble crusher circuit by controlling crusher operational parameters. Miner. Eng. 2018, 127, 98–104. [Google Scholar] [CrossRef]
- Cleary, P.W. Effect of rock shape representation in DEM on flow and energy utilisation in a pilot SAG mill. Comput. Part. Mech. 2019, 6, 461–477. [Google Scholar] [CrossRef]
- Cleary, P.W.; Owen, P. Effect of particle shape on structure of the charge and nature of energy utilisation in a SAG mill. Miner. Eng. 2019, 132, 48–68. [Google Scholar] [CrossRef]
- Cleary, P.W.; Owen, P. Effect of operating condition changes on the collisional environment in a SAG mill. Miner. Eng. 2019, 132, 297–315. [Google Scholar] [CrossRef]
- Pourghahramani, P. Effects of ore characteristics on product shape properties and breakage mechanisms in industrial SAG mills. Miner. Eng. 2012, 32, 30–37. [Google Scholar] [CrossRef]
- Tavares, L.M.; Carvalho, R.M. Modeling breakage rates of coarse particles in ball mills. Miner. Eng. 2009, 22, 650–659. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.P.; Li, J. Theory and Method of Multi Objective Decision Making; Tsinghua University Press: Beijing, China, 2005. [Google Scholar]
- Zhao, J.; Cui, Q.L.; Lin, Y.; Wang, W. Multi-objective hierarchical genetic fuzzy modeling for soft-sensor of overflow particle size in grinding process. Control Decis. 2015, 30, 2187–2192. [Google Scholar]
- Owen, D.R.J.; Feng, Y.T. Parallelised finite/discrete element simulation of multi-fracturing solids and discrete systems. Eng. Comput. 2001, 18, 557–576. [Google Scholar] [CrossRef]
- Han, K.; Owen, D.R.J.; Peric, D. Combined finite/discrete element and explicit/implicit simulations of peen forming process. Eng. Comput. 2002, 19, 92–118. [Google Scholar] [CrossRef]
- Wang, G.Q.; Hao, W.J.; Wang, J.X. Discrete Element Method and Its Application in EDEM; Northwestern Polytechnical University Press: Xi’an, China, 2010. [Google Scholar]
- Cundall, P.A. A computer model for simulating progressive large scale movements in blocky rock systems. Proc. Int. Symp. Fract. 1971, 1(ii-b), 11–18. [Google Scholar]
- Tavares, L.M. Analysis of particle fracture by repeated stressing as damage accumulation. Powder Technol. 2009, 190, 327–339. [Google Scholar] [CrossRef]
- Wang, B.Q. Study on Crushing Mechanism and Impact Dynamic Characteristics of Large-Scale Sieving Crusher. Ph.D. Thesis, China Coal Research Institute, Beijing, China, 2019. [Google Scholar]
- Cavalcanti, P.P.; De Carvalho, R.M.; Das Chagas, A.S.; Da Silveira, M.W.; Tavares, L.M. Surface breakage of fired iron ore pellets by impact. Powder Technol. 2019, 342, 735–743. [Google Scholar] [CrossRef]
- Barrios, G.K.P.; Pérez-Prim, J.; Tavares, L.M. DEM Simulation of Bed Particle Compression Using the Particle Replacement Model. In Proceedings of the 2nd International Conference on Energy, Sustainability and Climate Change, Crete, Greece, 21–27 June 2015. [Google Scholar]
- Tavares, L.M.; das Neves, P.B. Microstructure of quarry rocks and relationships to particle breakage and crushing. Int. J. Miner. Process. 2008, 87, 28–41. [Google Scholar] [CrossRef]
- Saeidi, F.; Tavares, L.M.; Yahyaei, M.; Powell, M. Phenomenological model of single particle breakage as a multi-stage process. Miner. Eng. 2016, 98, 90–100. [Google Scholar] [CrossRef]
- Tavares, L.M.; King, R.P. Modeling of particle fracture by repeated impacts using continuum damage mechanics. Powder Technol. 2002, 123, 138–146. [Google Scholar] [CrossRef]
- Carvalho, R.M.; Tavares, L.M. Predicting the effect of operating and design variables on breakage rates using the mechanistic ball mill model. Miner. Eng. 2013, 43–44, 91–101. [Google Scholar] [CrossRef]
- Napier Munn, T.J.; Morrell, S.; Morrison, R.D.; Kojovic, T. Mineral comminution circuits: Their operation and optimisation. J. Exp. Nanosci. 1999, 10, 1–8. [Google Scholar]





| Symbol | Description | Value | Symbol | Description | Value |
|---|---|---|---|---|---|
| Impact breakage parameter used in the calculation of the t10 | 0.051 | Impact breakage parameter used in the calculation of the t10 | 60.4 | ||
| Maximum particle size fracture energy (J/kg) | 44.9 | Median particle size (mm) | 4.3 | ||
| Fitting parameters of fracture energy | 1.28 | Minimum particle size for breakage (mm) | 10−2 | ||
| Standard deviation of the fracture energy | 0.46 | Minimum collision energy (J) | 10−4 | ||
| Damage constant | 3.0 |
| Type of Acation | Coefficient of Restitution | Static Friction Coefficient | Rolling Friction Coefficient |
|---|---|---|---|
| Rock–Rock Collisions | 0.3 | 0.65 | 0.05 |
| Rock–Steel Collisions | 0.5 | 0.4 | 0.05 |
| Rock–Mill Collisions | 0.5 | 0.4 | 0.1 |
| Steel–Steel Collisions | 0.75 | 0.35 | 0.1 |
| Steel—Mill Collisions | 0.75 | 0.5 | 0.2 |
| Material | Density (kg/m3) | Shear Modulus (Pa) | Poisson’s Ratio |
|---|---|---|---|
| Steel ball | 7800 | 7 × 1010 | 0.3 |
| Rock | 2600 | 1 × 107 | 0.3 |
| Lining board | 7200 | 6.8 × 1010 | 0.3 |
| Case | Other Parameter Settings | Research Parameter |
|---|---|---|
| 1 | 30% of mill volume, 10% steel ball ratio | Mill speed ratio |
| 2 | 75% critical speed of mill, 10% steel ball ratio | Fill level ratio |
| 3 | 75% critical speed of mill, 30% of mill volume | Steel ball ratio |
| Case | Mill Speed Ratio (%) | Fill Level Ratio (%) | Steel Ball Ratio (%) |
|---|---|---|---|
| 0 | 80% | 15% | 10% |
| 1 | 75% | 15% | 10% |
| 2 | 85% | 15% | 10% |
| 3 | 80% | 10% | 10% |
| 4 | 80% | 20% | 10% |
| 5 | 80% | 15% | 6% |
| 6 | 80% | 15% | 14% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Q.; Zhong, C.; Liu, D.; Fu, Q.; Wang, X.; Shen, Z. Operation Analysis of a SAG Mill under Different Conditions Based on DEM and Breakage Energy Method. Energies 2020, 13, 5247. https://doi.org/10.3390/en13205247
Xie Q, Zhong C, Liu D, Fu Q, Wang X, Shen Z. Operation Analysis of a SAG Mill under Different Conditions Based on DEM and Breakage Energy Method. Energies. 2020; 13(20):5247. https://doi.org/10.3390/en13205247
Chicago/Turabian StyleXie, Qiyue, Caifengyao Zhong, Daifei Liu, Qiang Fu, Xiaoli Wang, and Zhongli Shen. 2020. "Operation Analysis of a SAG Mill under Different Conditions Based on DEM and Breakage Energy Method" Energies 13, no. 20: 5247. https://doi.org/10.3390/en13205247






