Numerical Study of CO2 Geological Storage in Saline Aquifers without the Risk of Leakage
Abstract
:1. Introduction
2. Methodology
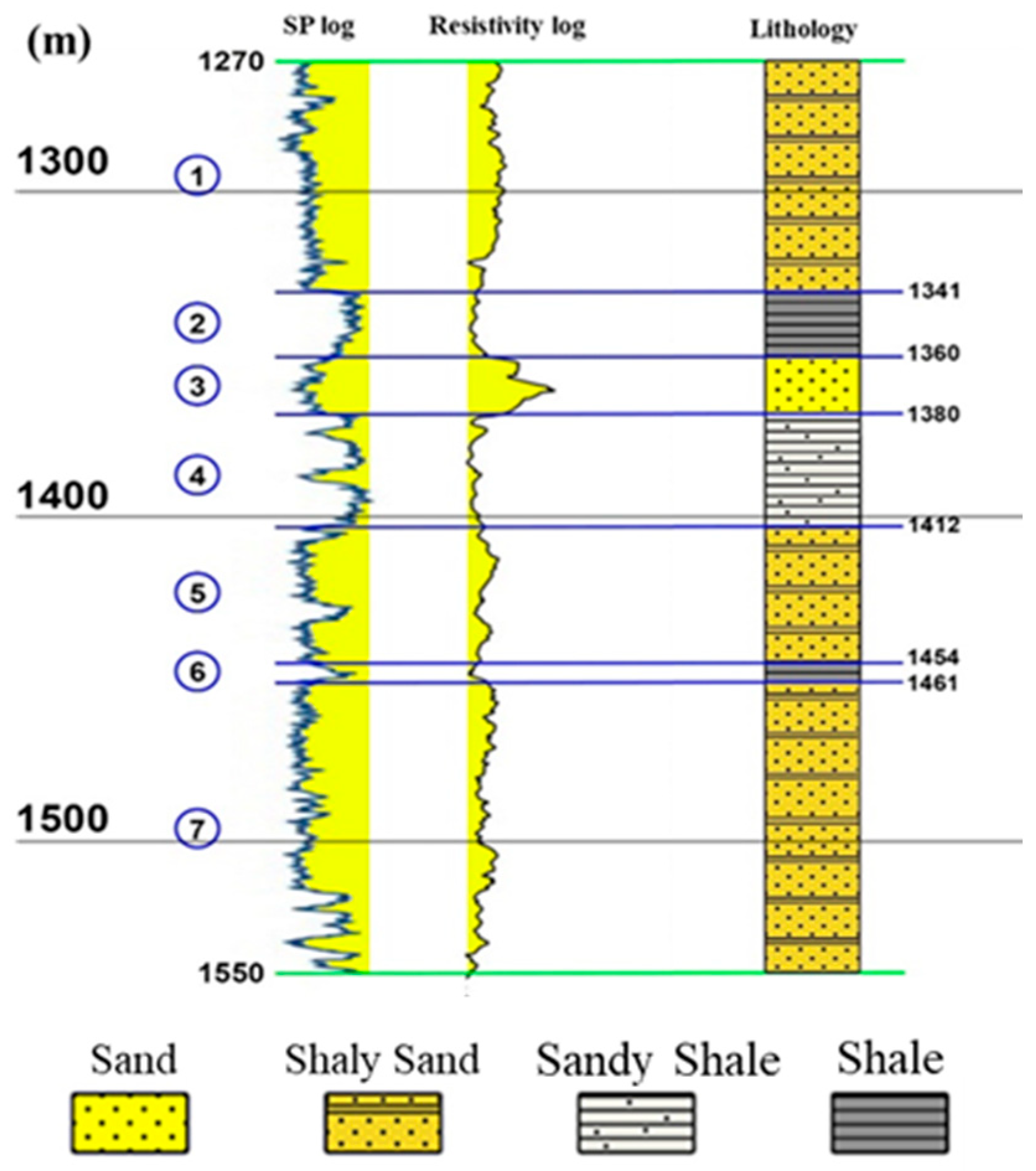
3. Geological Description
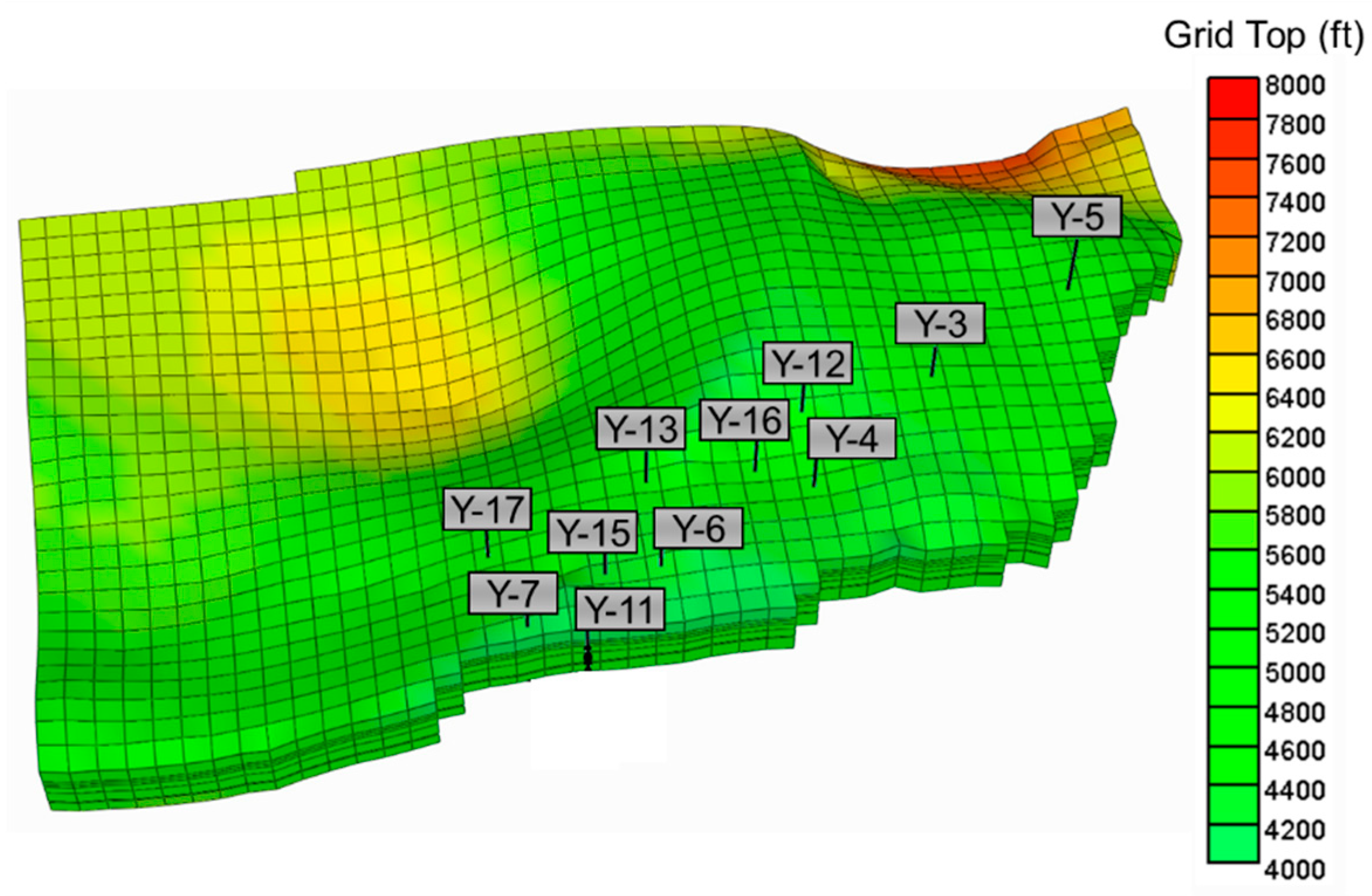
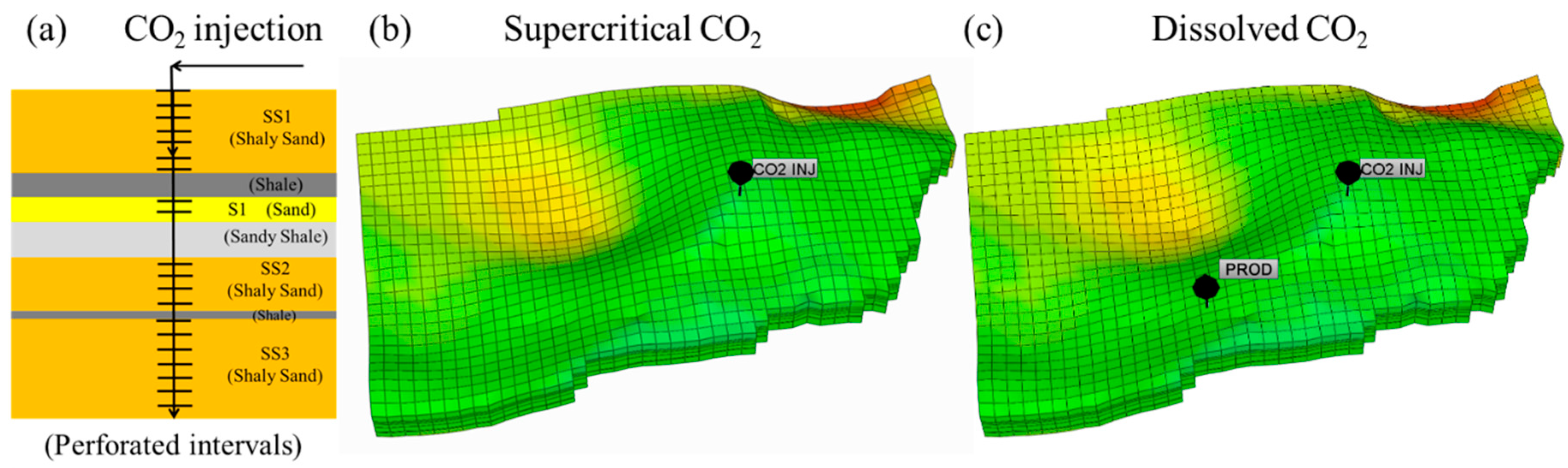
4. Simulation Model Design
5. Results and Discussion
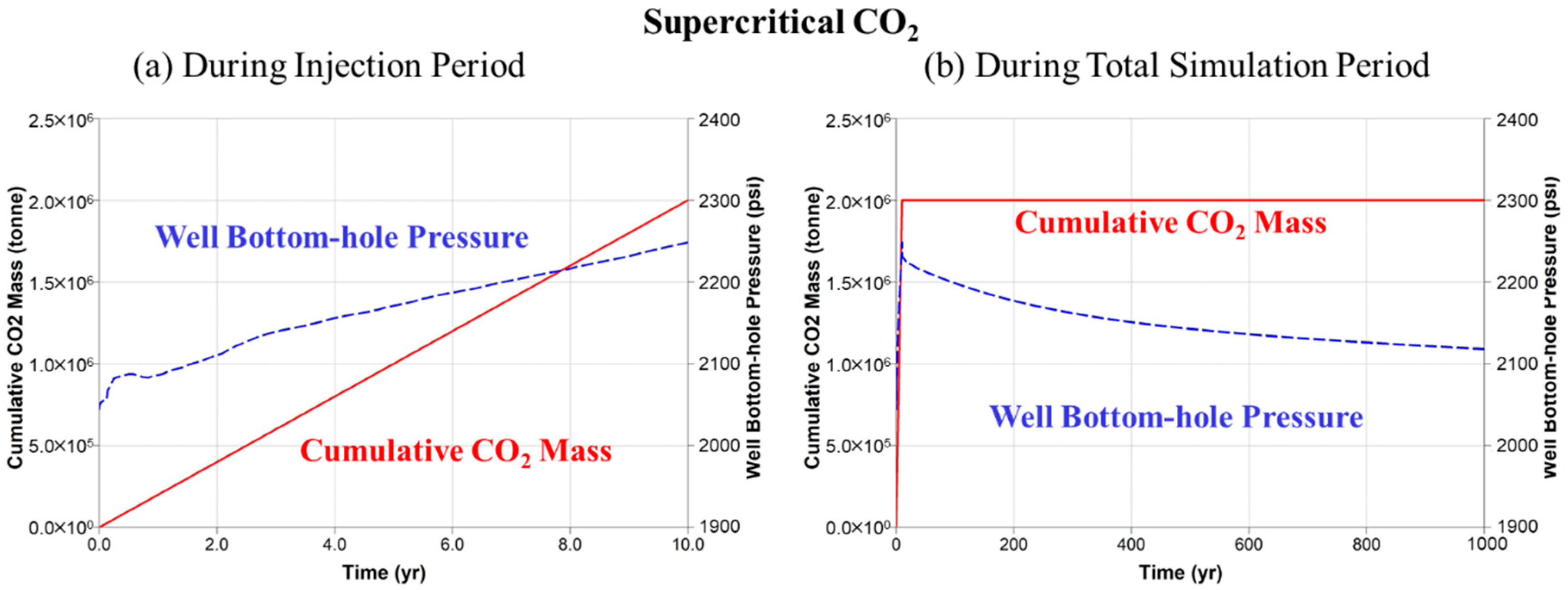
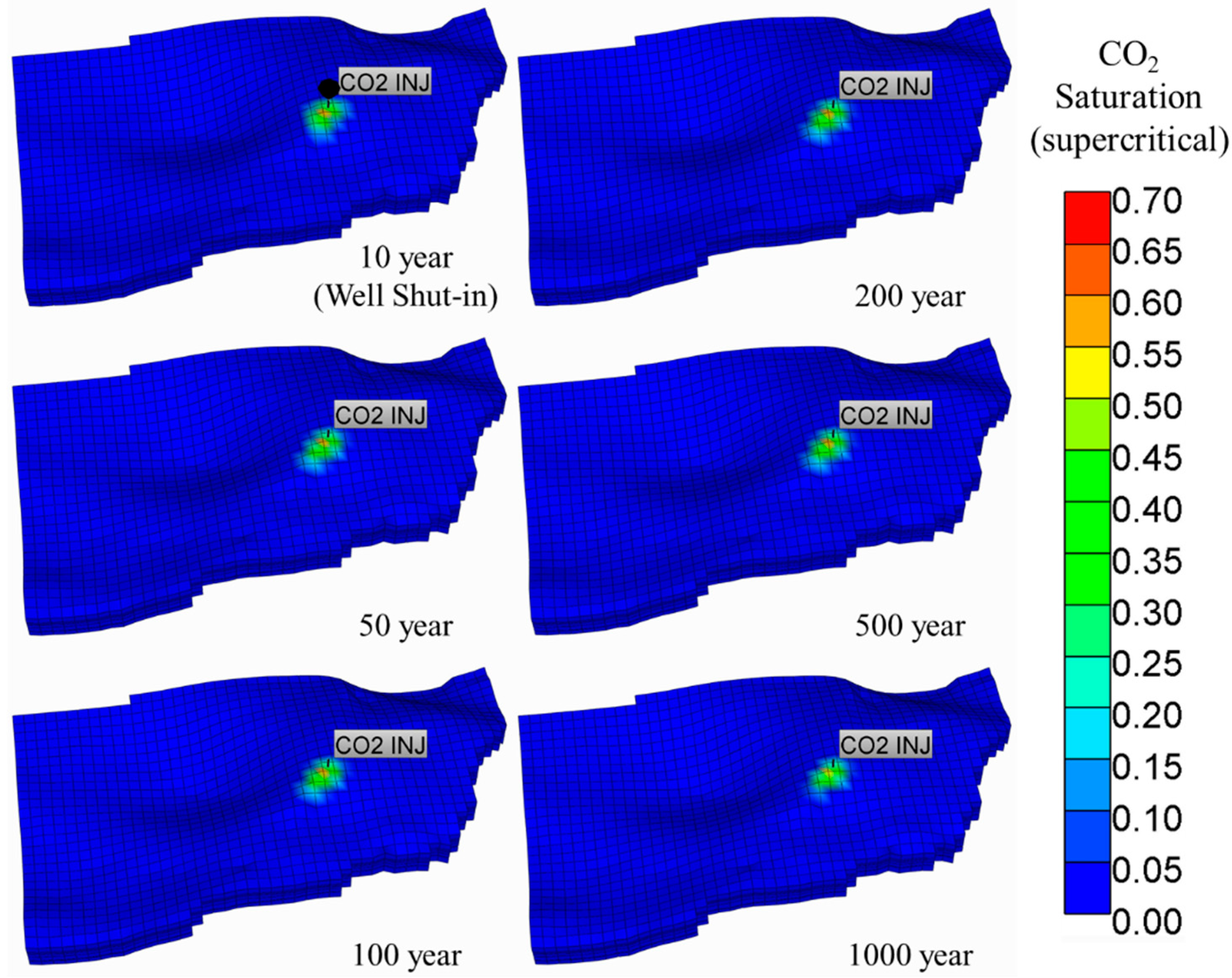
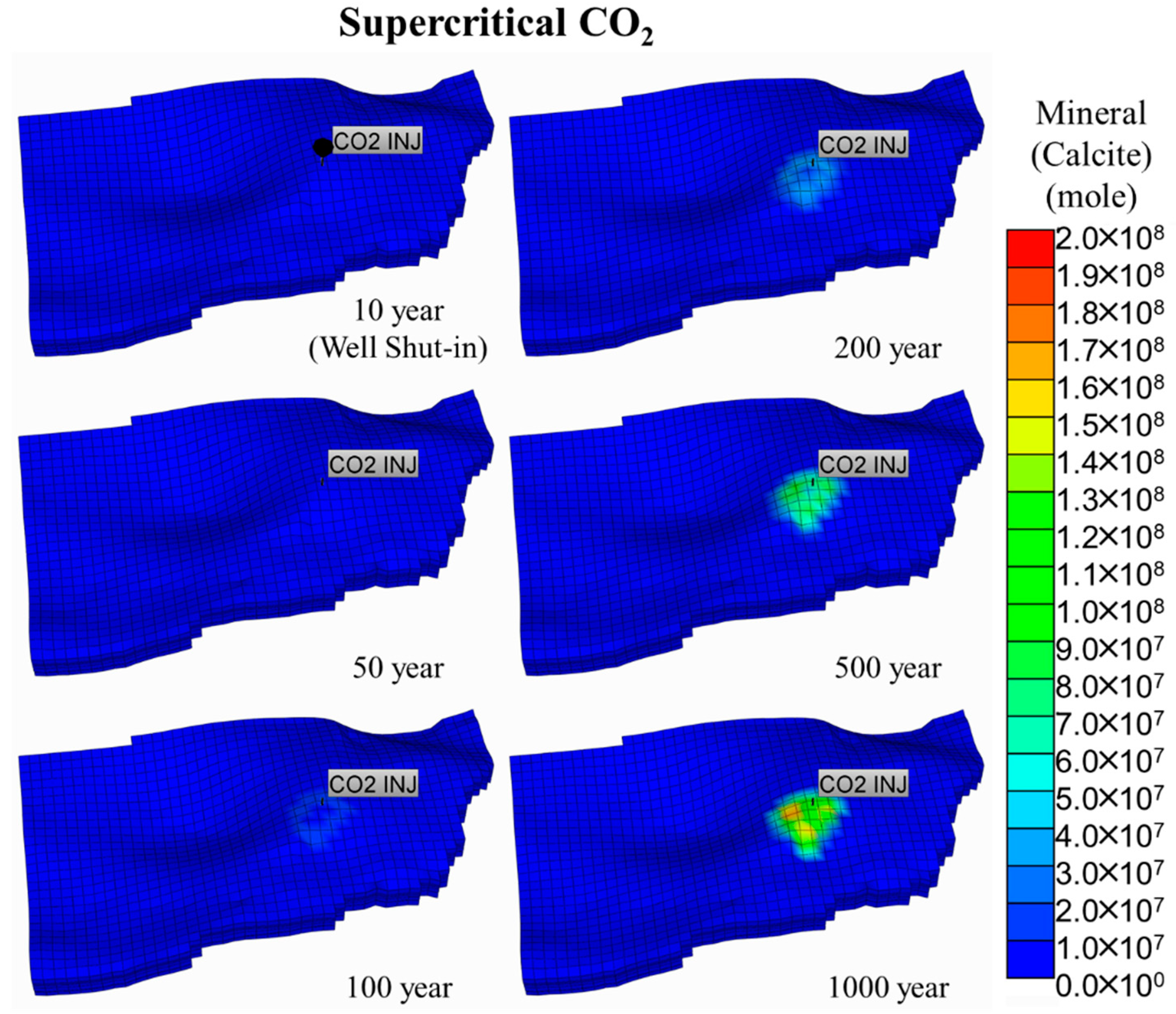
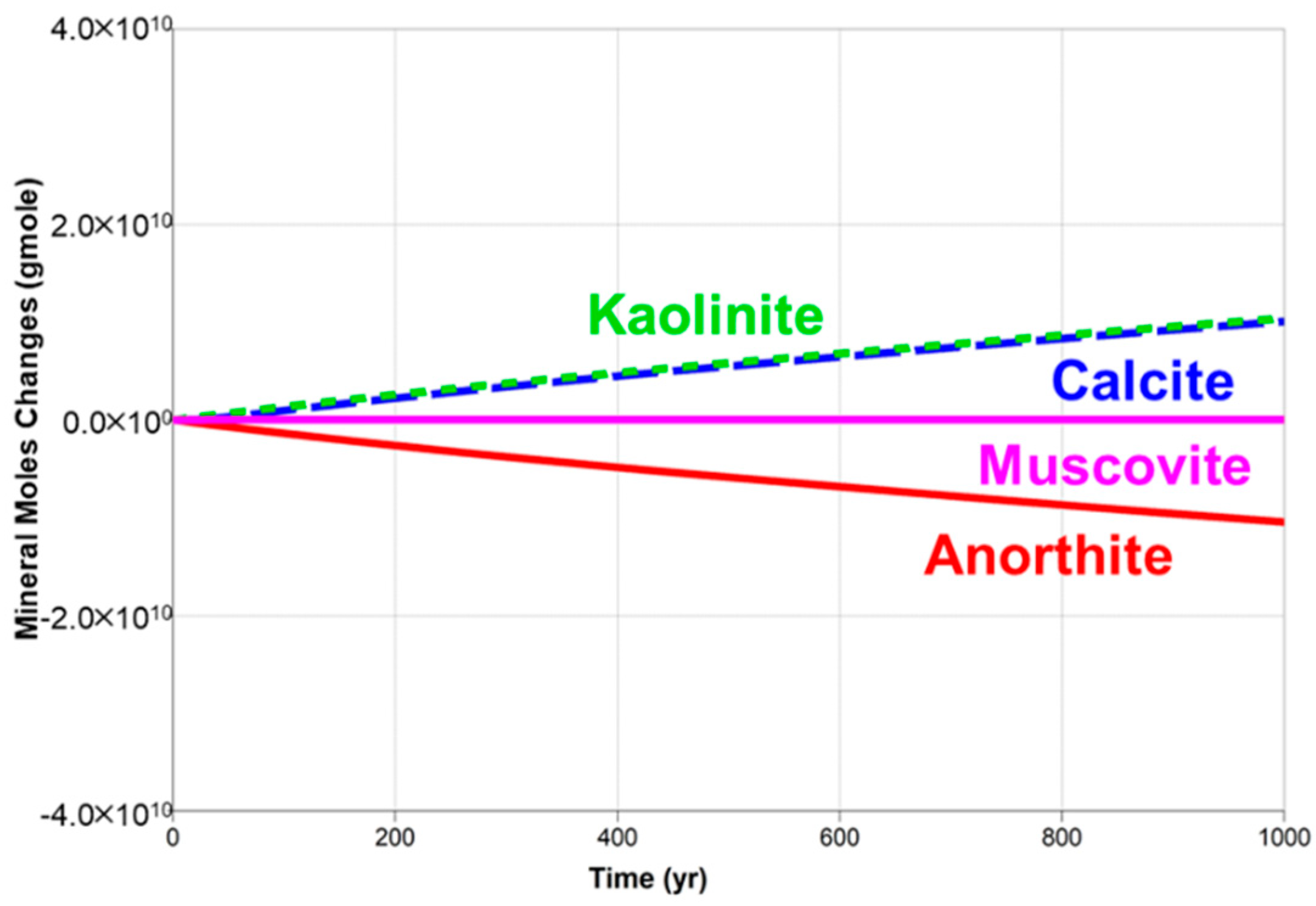
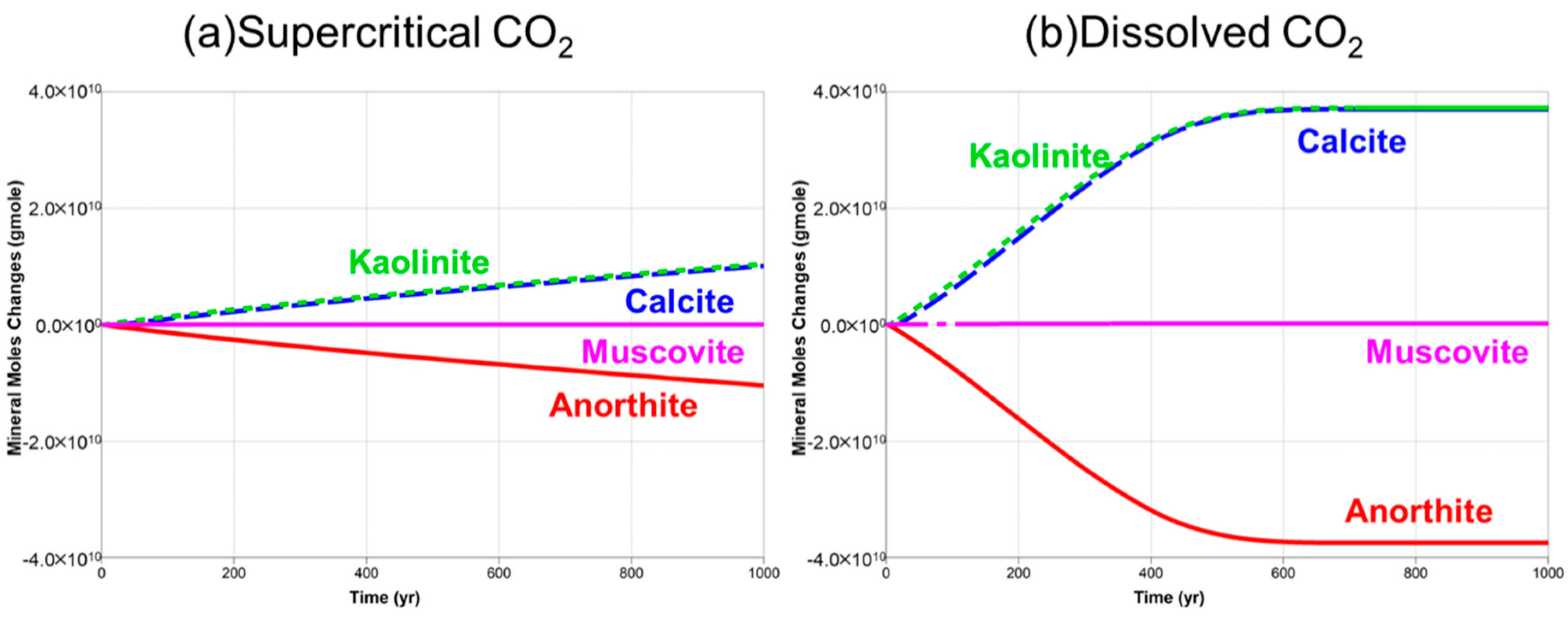
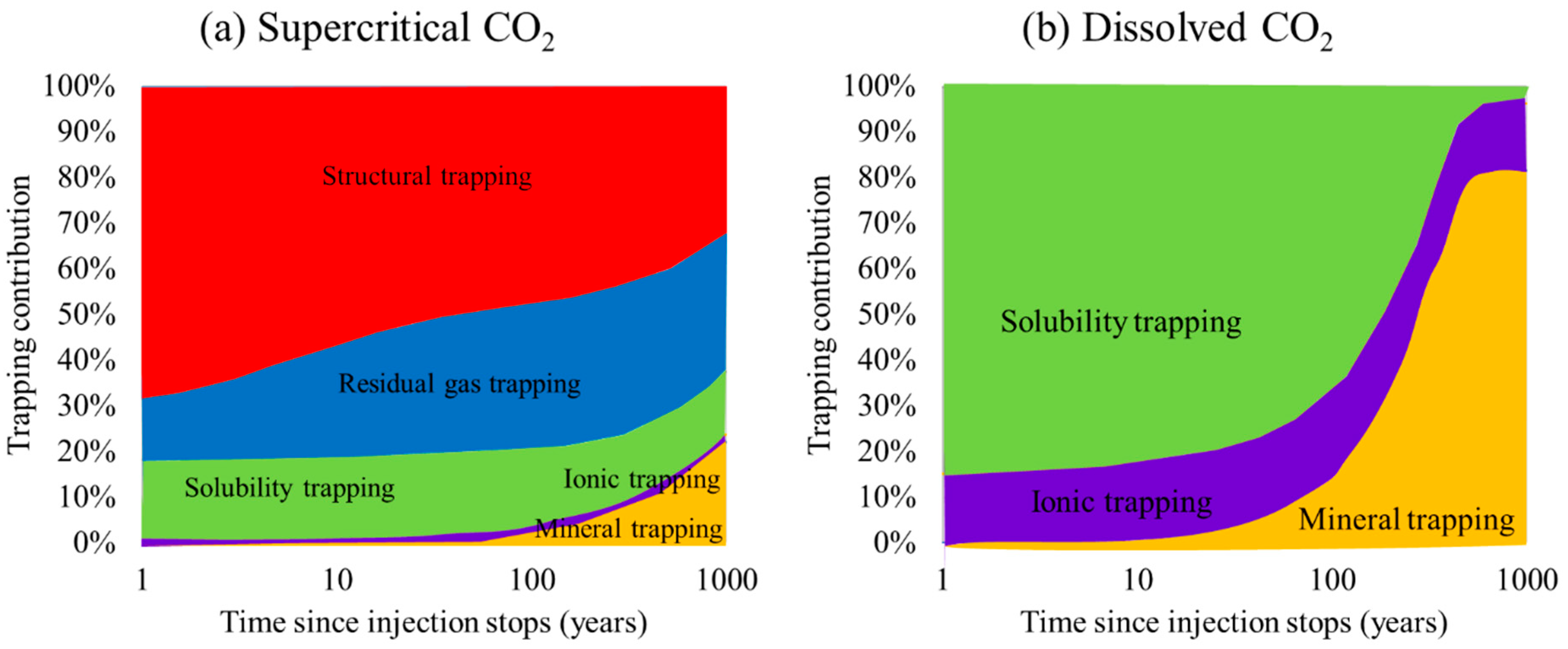
5.1. Supercritical CO2 Scenario
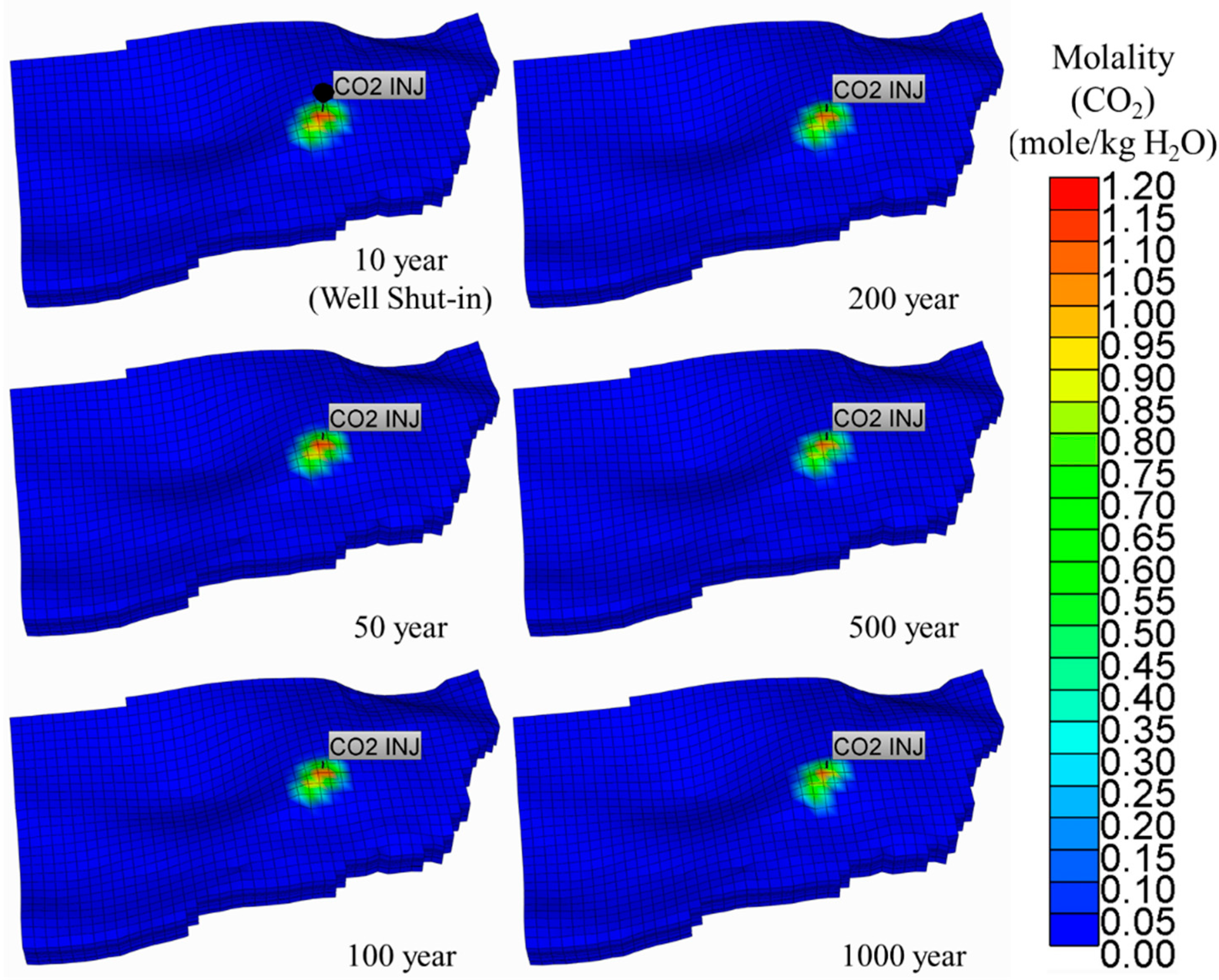
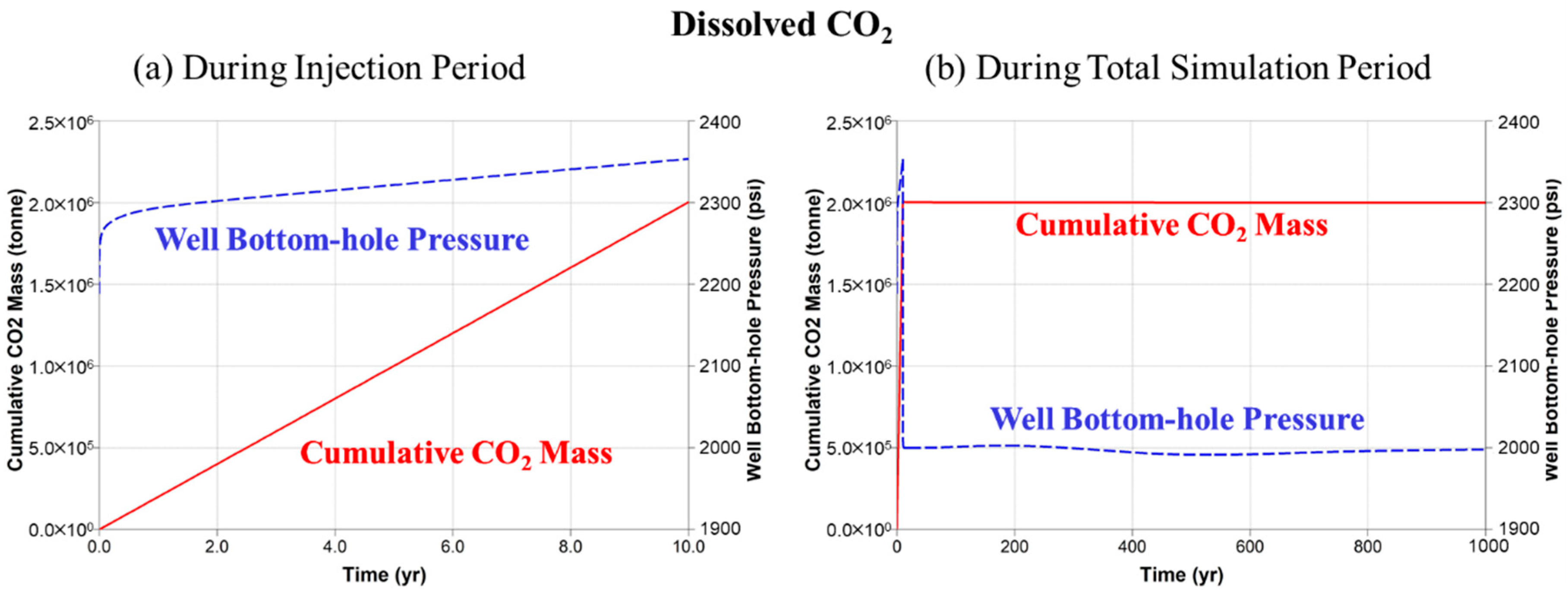
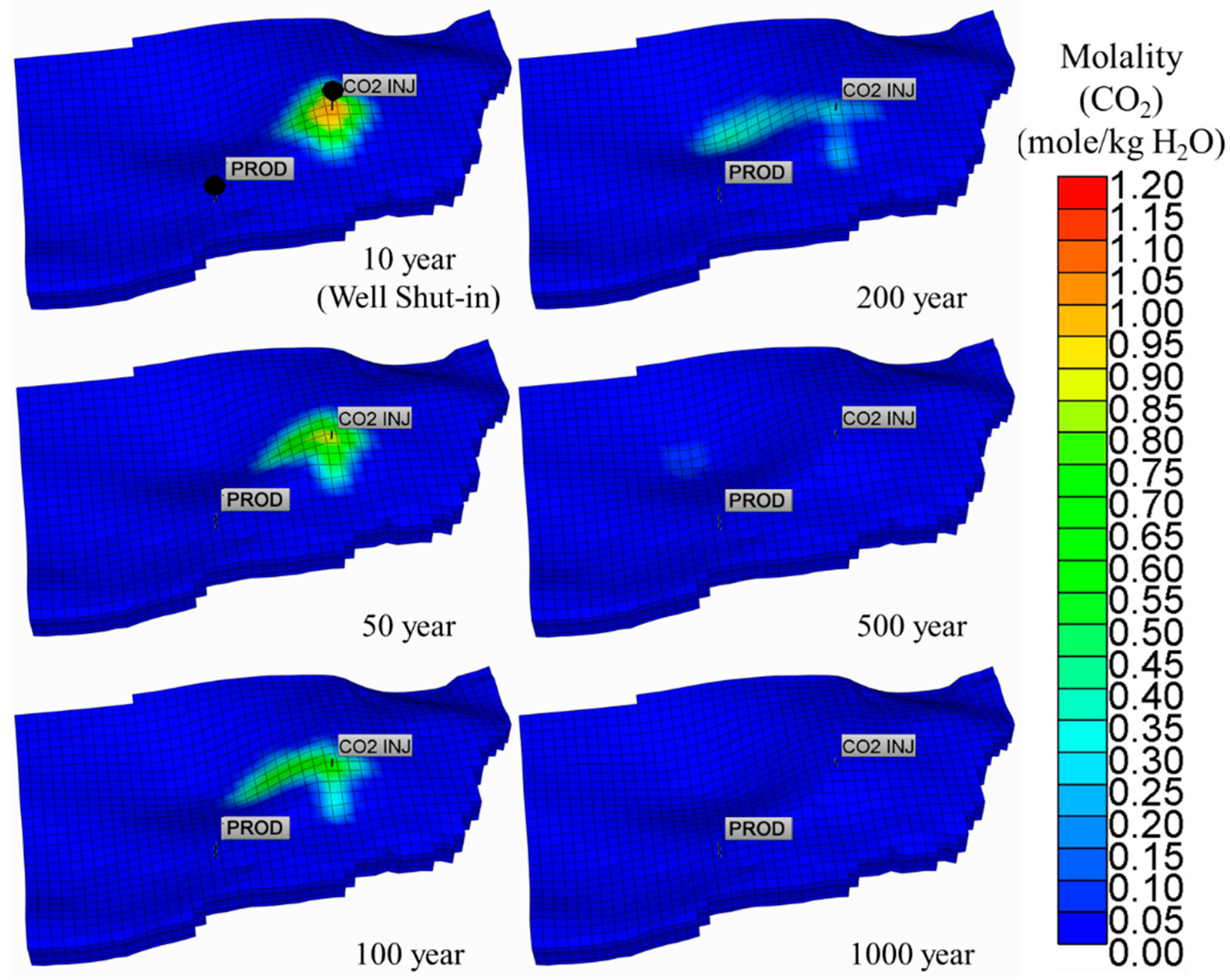
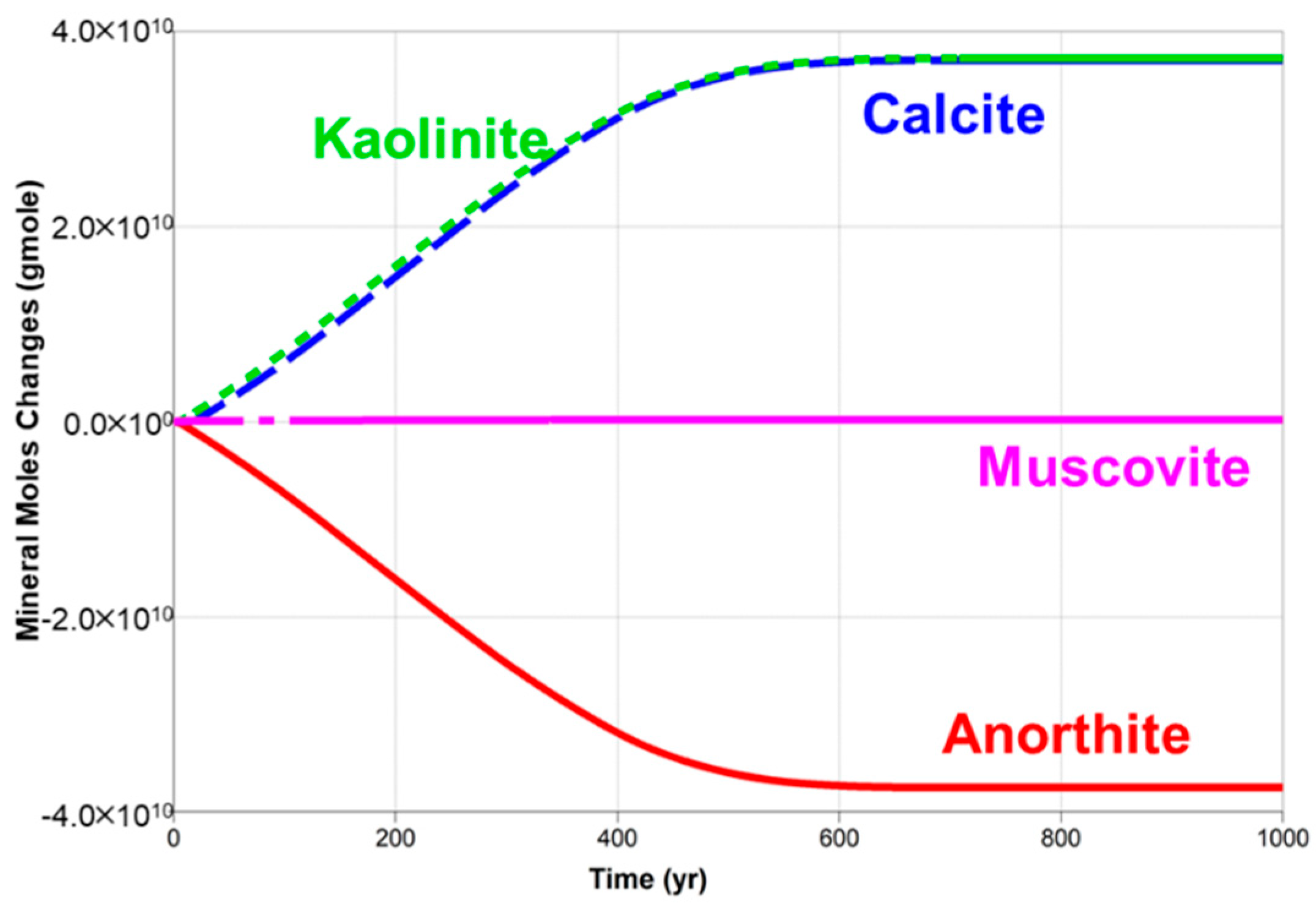
5.2. Dissolved CO2 Scenario
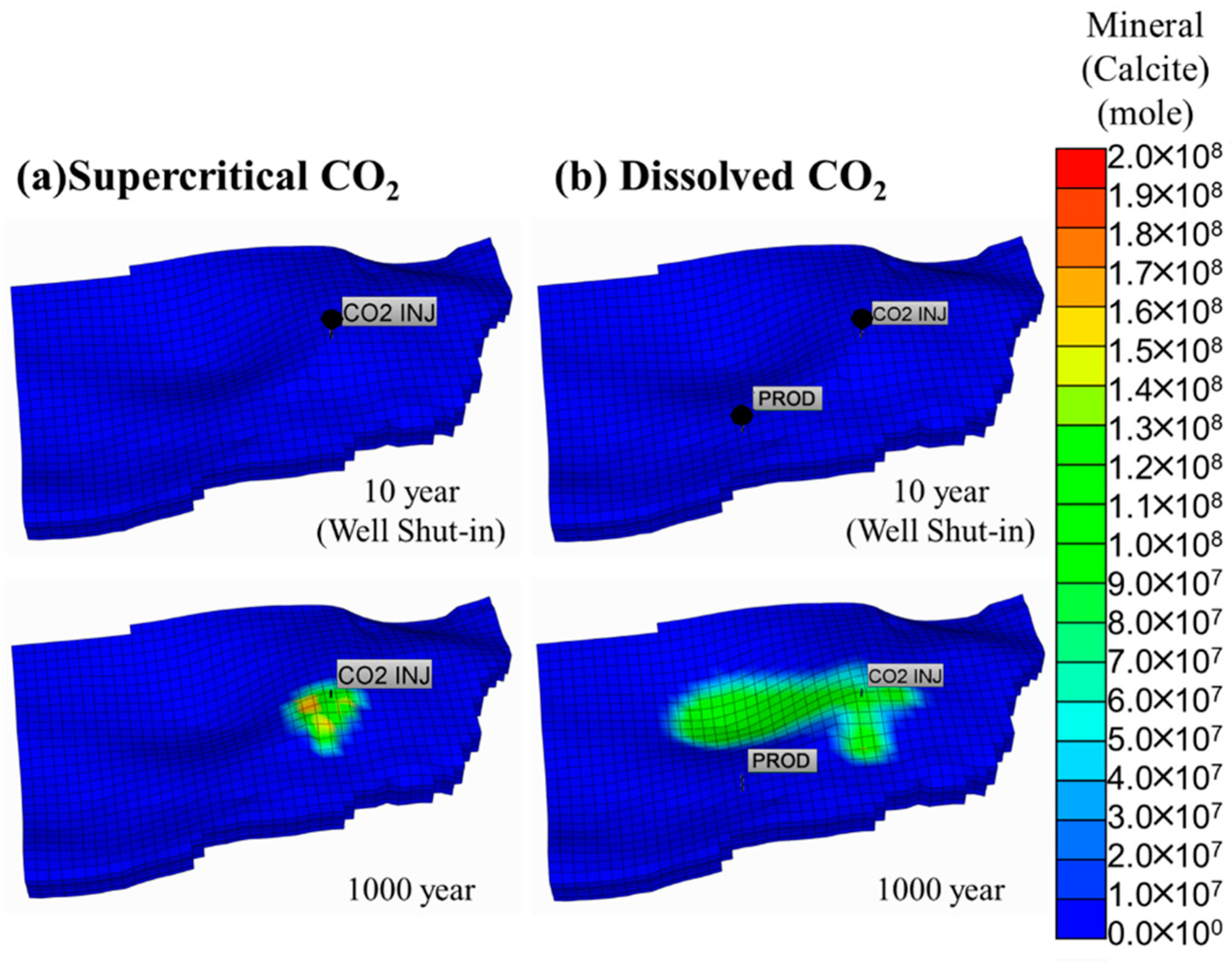
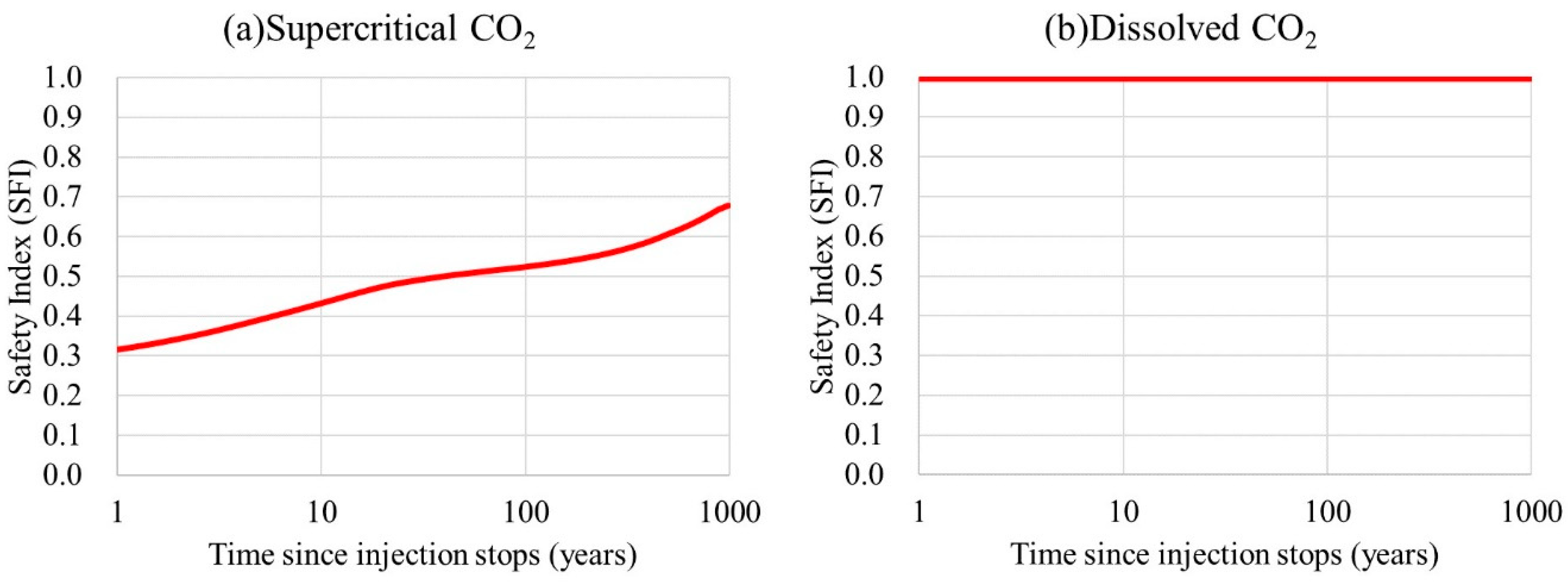
5.3. Comparison of the Supercritical CO2 and Dissolved CO2 Scenarios
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bachu, S. Legal and regulatory challenges in the implementation of CO2 geological storage: An Alberta and Canadian perspective. Int. J. Greenh. Gas Control 2008, 2, 259–273. [Google Scholar] [CrossRef]
- Yanagi, K.; Nakamura, A. Towards a low/zero carbon society for the Asia-Pacific Region: Policy and legal development for carbon capture and storage (CCS) in Japan. In Sustainability and Law; Springer: Cham, Switzerland, 2020; pp. 585–605. [Google Scholar]
- Bachu, S.; Gunter, W.; Perkins, E. Aquifer disposal of CO2: Hydrodynamic and mineral trapping. Energy Convers. Manag. 1994, 35, 269–279. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H.; Green, C.P.; Ennis-King, J. Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments. Int. J. Greenh. Gas Control 2015, 40, 238–266. [Google Scholar] [CrossRef]
- IPCC. IPCC Special Report on Carbon Dioxide Capture and Storage. In Prepared by Working Group III of the Intergovernmental Panel on Climate Change; Metz, B., Davidson, H., de Coninck, C., Loos, M., Meyer, L.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005; p. 442. [Google Scholar]
- Burton, M.; Bryant, S.L. Surface dissolution: Minimizing groundwater impact and leakage risk simultaneously. Energy Procedia 2009, 1, 3707–3714. [Google Scholar] [CrossRef] [Green Version]
- Pool, M.; Carrera, J.; Vilarrasa, V.; Silva, O.; Ayora, C. Dynamics and design of systems for geological storage of dissolved CO2. Adv. Water Resour. 2013, 62, 533–542. [Google Scholar] [CrossRef]
- Ganjdanesh, R.; Bryant, S.; Orbach, R.; Pope, G.; Sepehrnoori, K. Coupled carbon dioxide sequestration and energy production from geopressured/geothermal aquifers. SPE J. 2014, 19, 239–248. [Google Scholar] [CrossRef]
- Matter, J.; Takahashi, T.; Goldberg, D. Experimental evaluation of in situ CO2-water-rock reactions during CO2 injection in basaltic rocks: Implications for geological CO2 sequestration. Geochem. Geophys. Geosystems 2007, 8. [Google Scholar] [CrossRef]
- Matter, J.; Stute, M.; Snæbjörnsdottir, S.; Oelkers, E.; Gislason, S.; Aradottir, E.; Gunnlaugsson, E. Rapid carbon mineralization for permanent disposal of anthropogenic carbon dioxide emissions. Science 2016, 352, 1312–1314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Snæbjörnsdóttir, S.Ó.; Oelkers, E.H.; Mesfin, K.; Aradóttir, E.S.; Dideriksen, K.; Gunnarsson, I.; Gunnlaugsson, E.; Matter, J.M.; Stute, M.; Gislason, S.R. The chemistry and saturation states of subsurface fluids during the in situ mineralisation of CO2 and H2S at the CarbFix site in SW-Iceland. Int. J. Greenh. Gas Control 2017, 58, 87–102. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, B.Z.; Nghiem, L.; Shen, C.H.; Lin, Z.S. Effects of complex sandstone–shale sequences of a storage formation on the risk of CO2 leakage: Case study from Taiwan. Int. J. Greenh. Gas Control 2013, 17, 376–387. [Google Scholar] [CrossRef]
- Kumar, A.; Noh, M.H.; Ozah, R.C.; Pope, G.A.; Bryant, S.L.; Sepehrnoori, K.; Lake, L.W. Reservoir simulation of CO 2 storage in aquifers. SPE J. 2005, 10, 336–348. [Google Scholar] [CrossRef]
- Nghiem, L.; Sammon, P.; Grabenstetter, J.; Ohkuma, H. Modeling CO2 storage in aquifers with a fully-coupled geochemical EOS compositional simulator. In SPE/DOE Symposium on Improved Oil Recovery; Society of Petroleum Engineers: Tulsa, Oklahoma, 17–21 April 2004. [Google Scholar]
- Land, C.S. Calculation of imbibition relative permeability for two-and three-phase flow from rock properties. Soc. Pet. Eng. J. 1968, 8, 149–156. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Bethke, C. Geochemical Reaction Modeling: Concepts and Applications; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Nghiem, L.; Shrivastava, V.; Kohse, B.; Hassam, M.; Yang, C. Simulation and optimization of trapping processes for CO2 storage in saline aquifers. J. Can. Pet. Technol. 2010, 49, 15–22. [Google Scholar] [CrossRef]
- Li, Y.K.; Nghiem, L.X. Phase equilibria of oil, gas and water/brine mixtures from a cubic equation of state and Henry’s law. Can. J. Chem. Eng. 1986, 64, 486–496. [Google Scholar] [CrossRef]
- GAMS. Solmineq.88 Geochemical Aqueous Equilibrium Models; Geochemical Applications & Modelling Software Ltd.: Edmonton, AB, Canada, 2011. [Google Scholar]
- GAMS. GAMSPath Geochemical Reaction Path Models; Geochemical Applications & Modelling Software Ltd.: Edmonton, AB, Canada, 2011. [Google Scholar]
- Thibeau, S.; Nghiem, L.X.; Ohkuma, H. A modelling study of the role of selected minerals in enhancing CO2 mineralization during CO2 aquifer storage. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: Anaheim, CA, USA, 11–14 November 2007. [Google Scholar]
- Lin, Q.-H. In-Situ Stress and Fault Reactivation Potential in Response to Fluid Injection in Yunghoshan Structure. Master’s Thesis, National Central University, Taoyuan, Taiwan, 2014. [Google Scholar]



| Parameter | Unit | Value | |
|---|---|---|---|
| Porosity | Sand | frac. | 0.25 |
| Shaly Sand | frac. | 0.23 | |
| Sandy Shale | frac. | 0.05 | |
| Shale | frac. | 0.025 | |
| Permeability | Sand | mD | 530 |
| Shaly Sand | mD | 200 | |
| Sandy Shale | mD | 0.001 | |
| Shale | mD | 0.0001 | |
| Formation Pressure @ 5400 ft | psi | 2445 | |
| Formation Temperature @ 5400 ft | °F | 162 | |
| Intra-Aqueous Chemical Reactions | Keq at 33 °C |
|---|---|
| Al(OH)2+ + 2H+ Al3+ + 2H2O | 4.75 |
| CO2(aq) + H2O H+ + HCO3- | −6.35 |
| CO32- + H+ HCO3- | 10.31 |
| KOH + H+ K+ + H2O | 15.43 |
| OH- + H+ H2O | 13.74 |
| Geochemical Mineral Reactions | k0β at T0 |
| Anorthite + 8H+ 4H2O + Ca2+ + 2Al3+ + 2SiO2(aq) | 25.72 at 33 °C |
| Calcite + H+ Ca2+ + HCO3- | 1.6 at 33 °C |
| Kaolinite + 6H+ 5H2O + 2Al3+ + 2SiO2(aq) | 6.77 at 33 °C |
| Muscovite + 6H+ 6H2O + K+ + 3Al3+ + 3SiO2(aq) | 12 at 25 °C |
| Primary Species | Molality (mole/kg) | Mineral | Volume Percentage (%) |
|---|---|---|---|
| H+ | 8.90 × 10−9 | Anorthite | 13.15% |
| Ca2+ | 8.75 × 10−5 | Kaolinite | 3.77% |
| K+ | 6.68 × 10−5 | Calcite | 0% |
| Al3+ | 7.24 × 10−11 | Muscovite | 6.43% |
| SiO2 | 2.35 × 10−8 | Quartz | 73.65% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-H.; Shen, C.-H.; Wu, C.-Y.; Hsieh, B.-Z. Numerical Study of CO2 Geological Storage in Saline Aquifers without the Risk of Leakage. Energies 2020, 13, 5259. https://doi.org/10.3390/en13205259
Li Y-H, Shen C-H, Wu C-Y, Hsieh B-Z. Numerical Study of CO2 Geological Storage in Saline Aquifers without the Risk of Leakage. Energies. 2020; 13(20):5259. https://doi.org/10.3390/en13205259
Chicago/Turabian StyleLi, Yuan-Heng, Chien-Hao Shen, Cheng-Yueh Wu, and Bieng-Zih Hsieh. 2020. "Numerical Study of CO2 Geological Storage in Saline Aquifers without the Risk of Leakage" Energies 13, no. 20: 5259. https://doi.org/10.3390/en13205259
APA StyleLi, Y.-H., Shen, C.-H., Wu, C.-Y., & Hsieh, B.-Z. (2020). Numerical Study of CO2 Geological Storage in Saline Aquifers without the Risk of Leakage. Energies, 13(20), 5259. https://doi.org/10.3390/en13205259






