Carrier Transmission Mechanism-Based Analysis of Front Surface Field Effects on Simplified Industrially Feasible Interdigitated Back Contact Solar Cells
Abstract
:1. Introduction
2. Materials and Methods
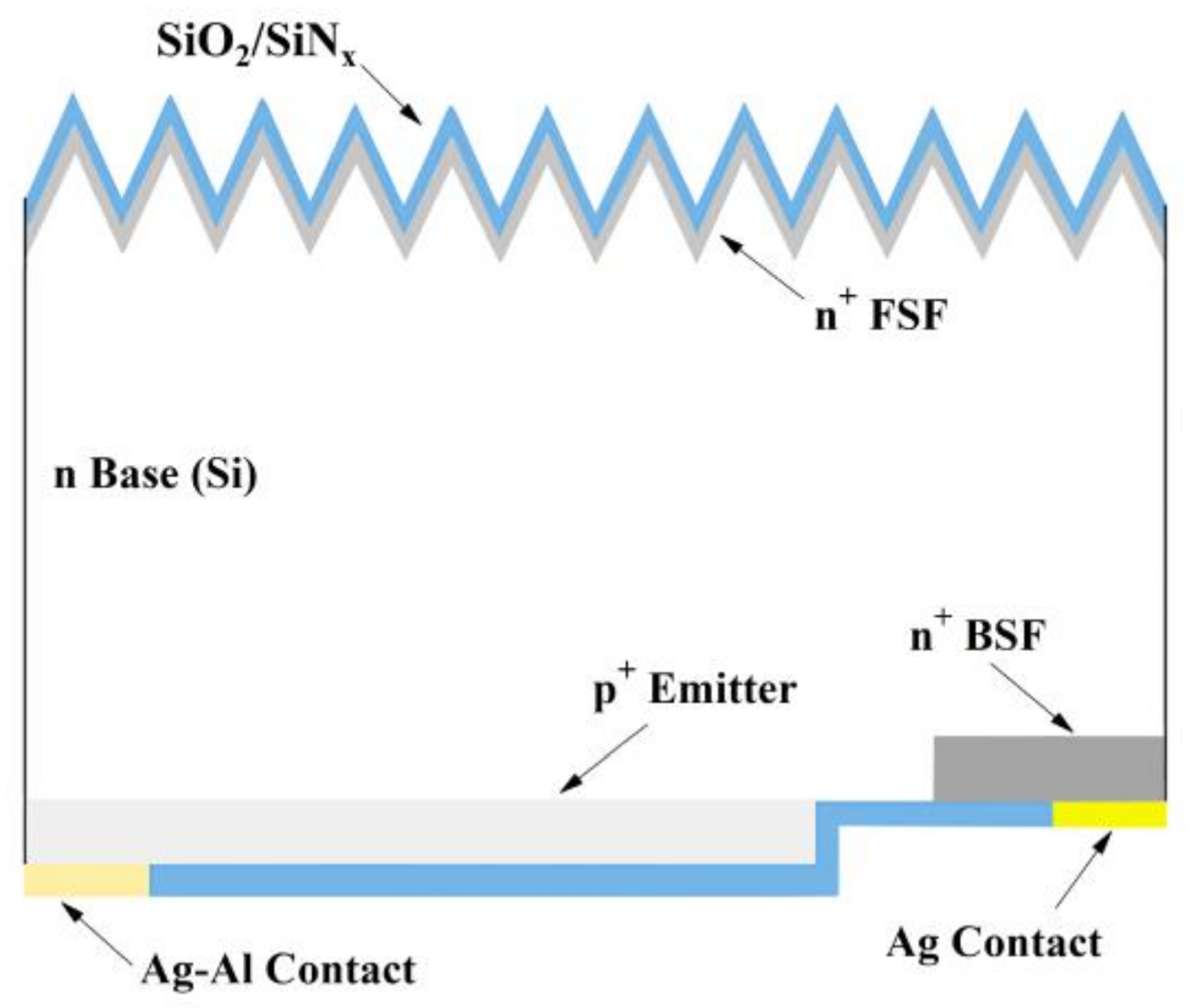
2.1. Simulation Methods
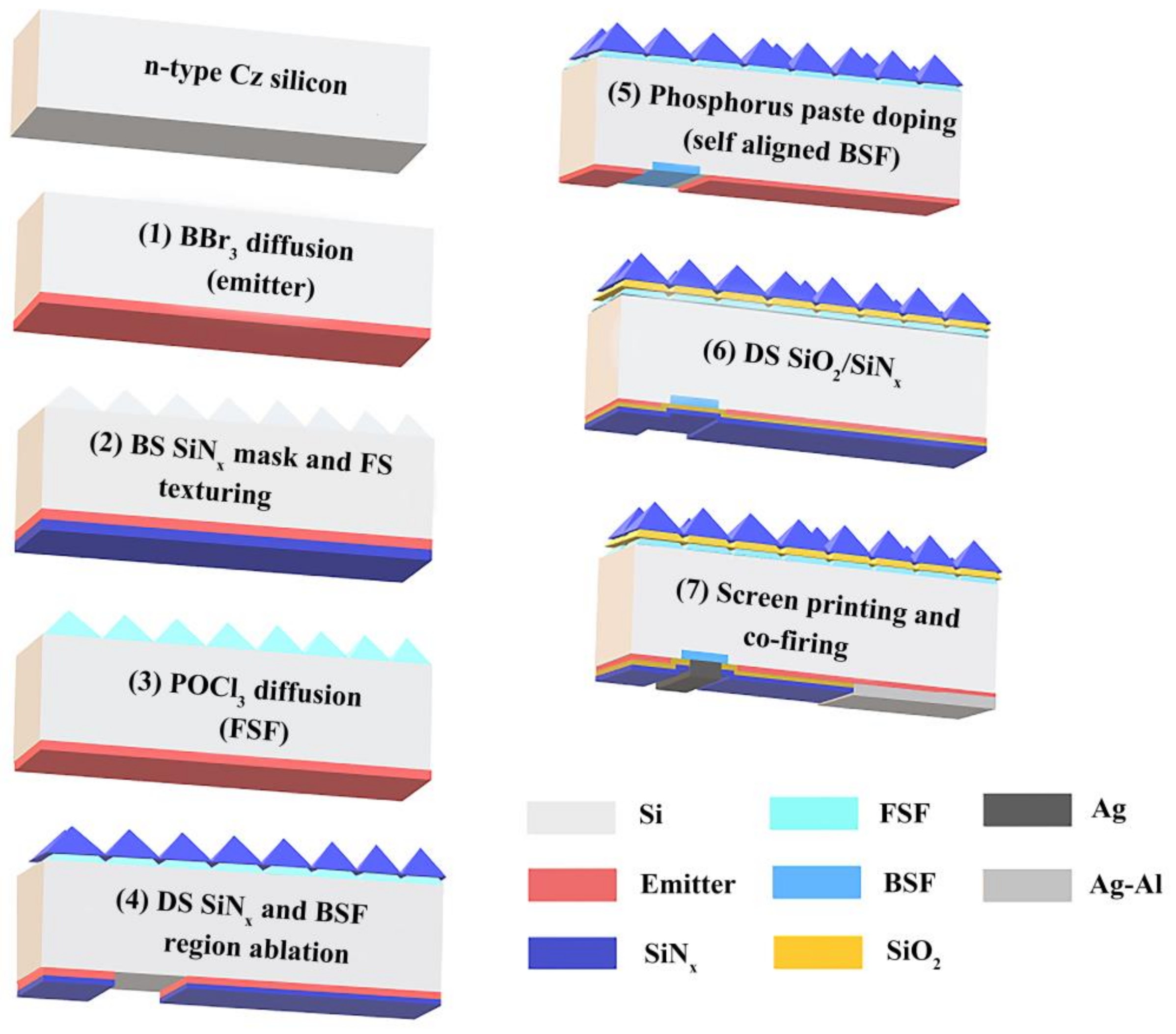
2.2. Experimental Methods
3. Results and Discussion
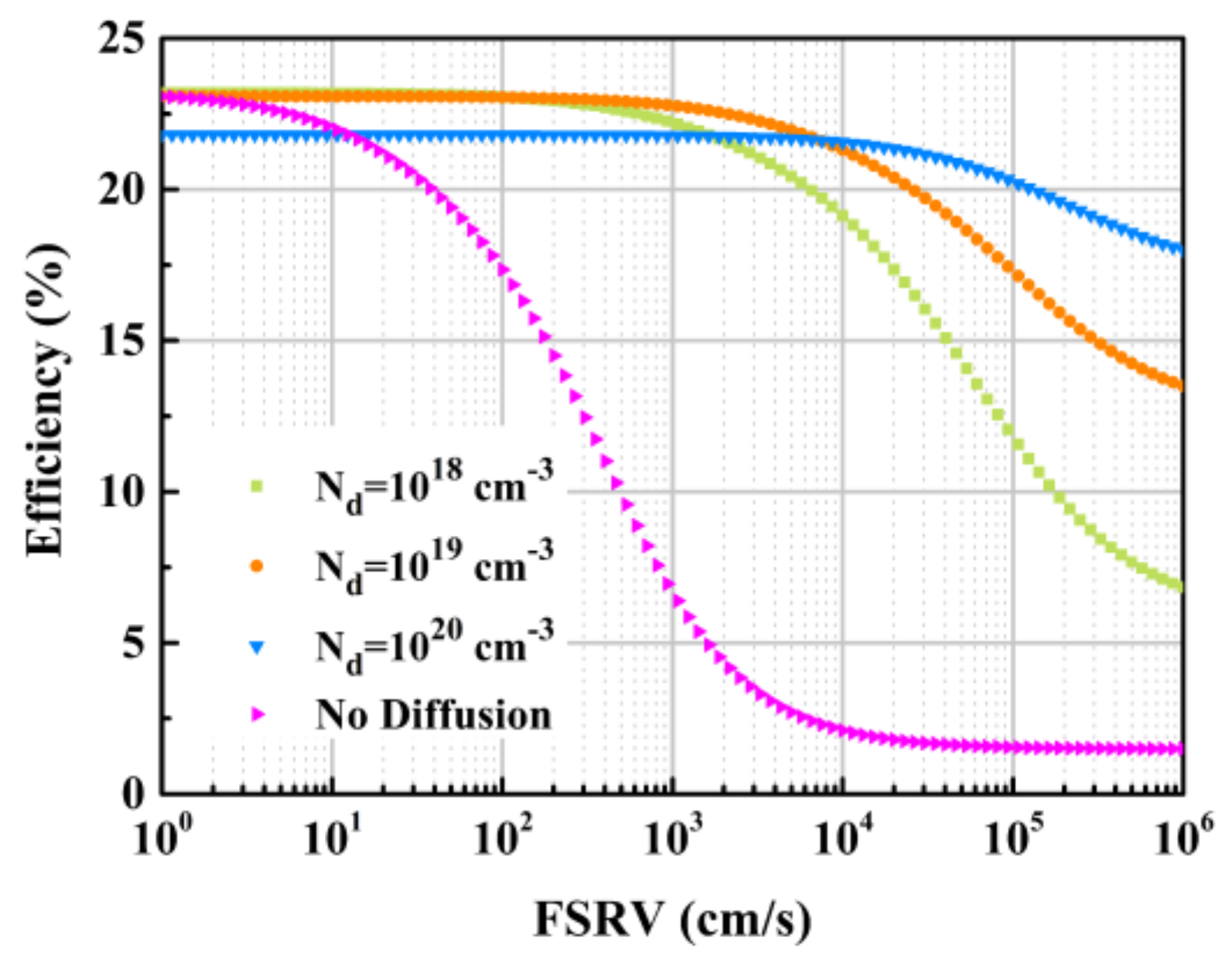
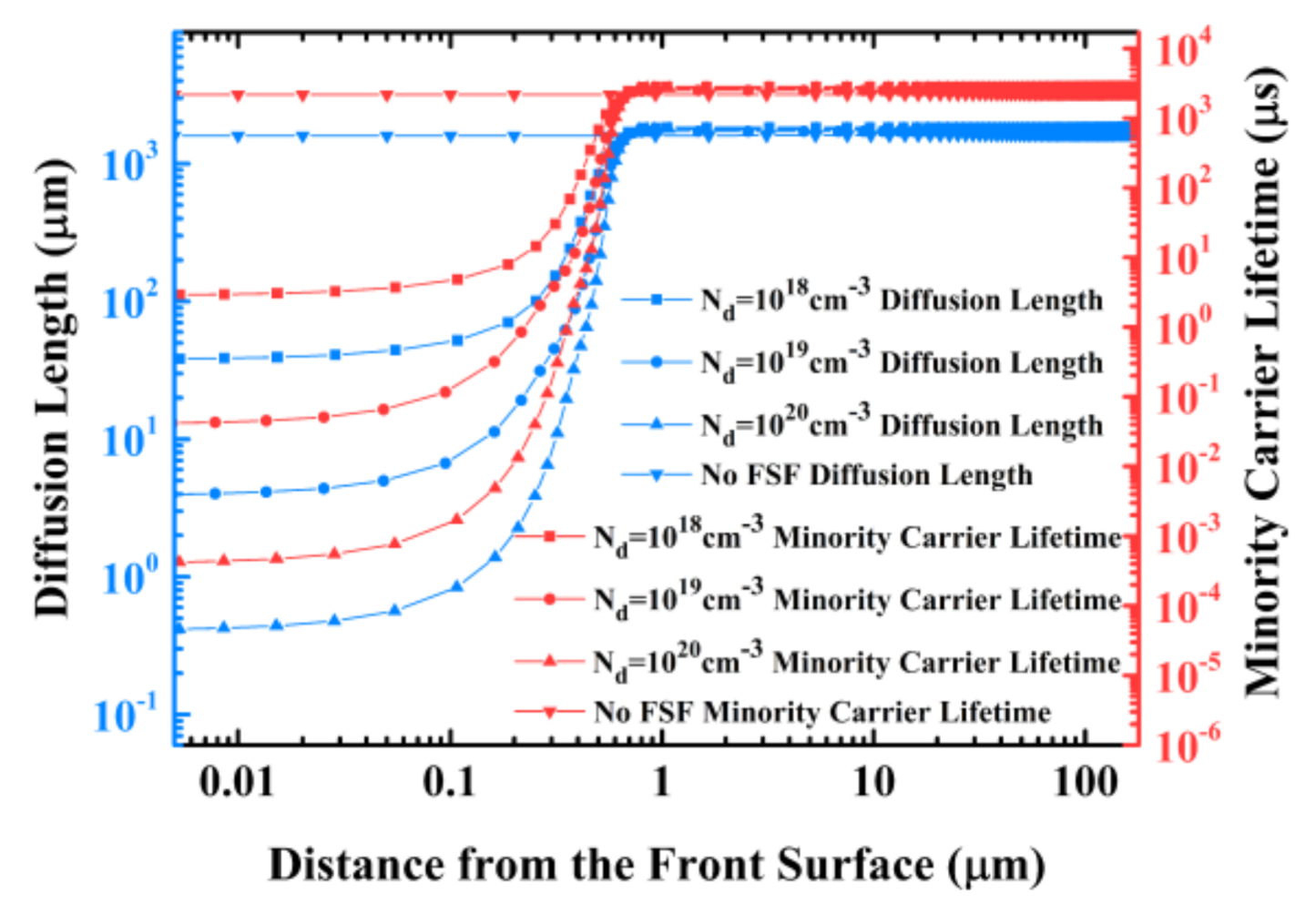
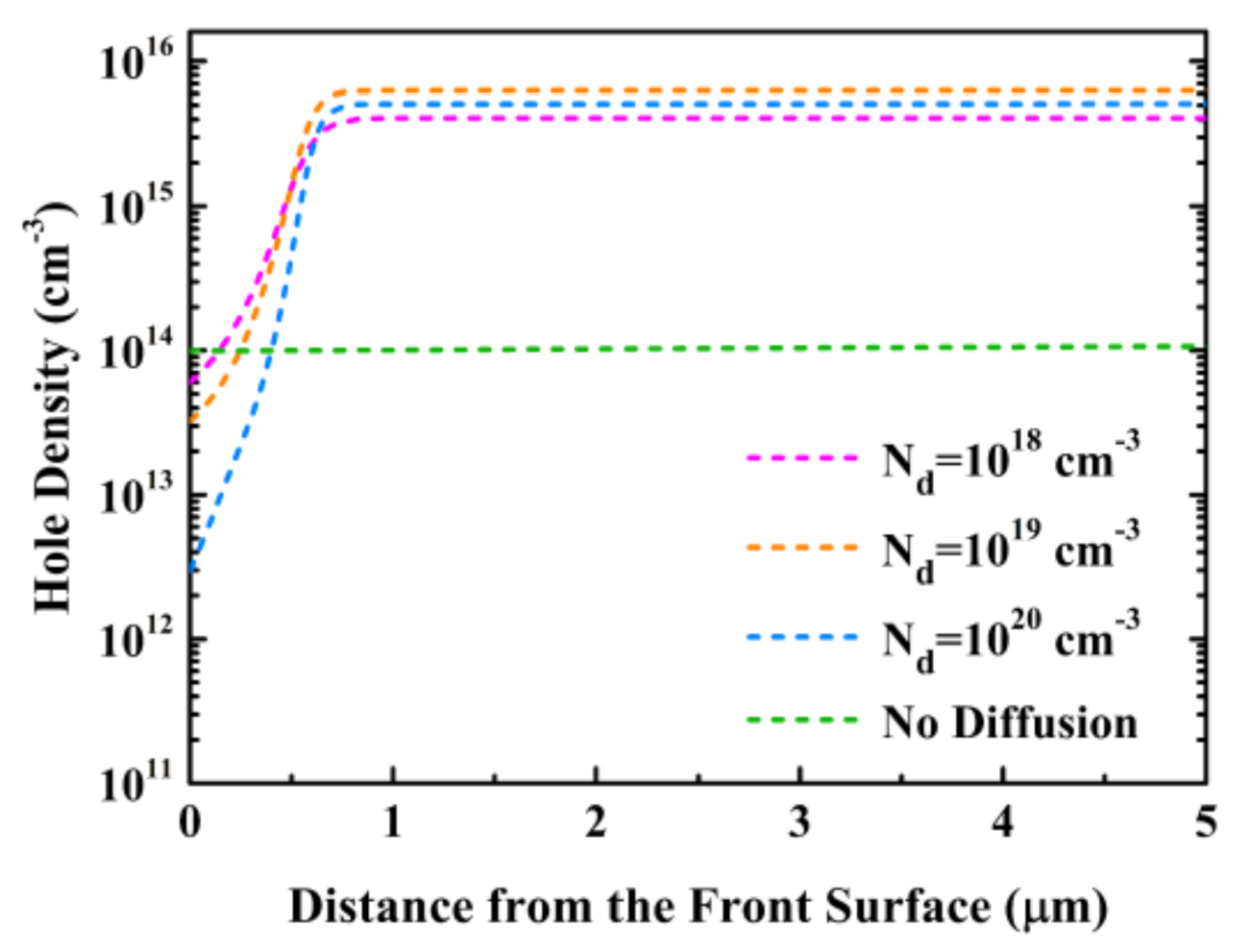
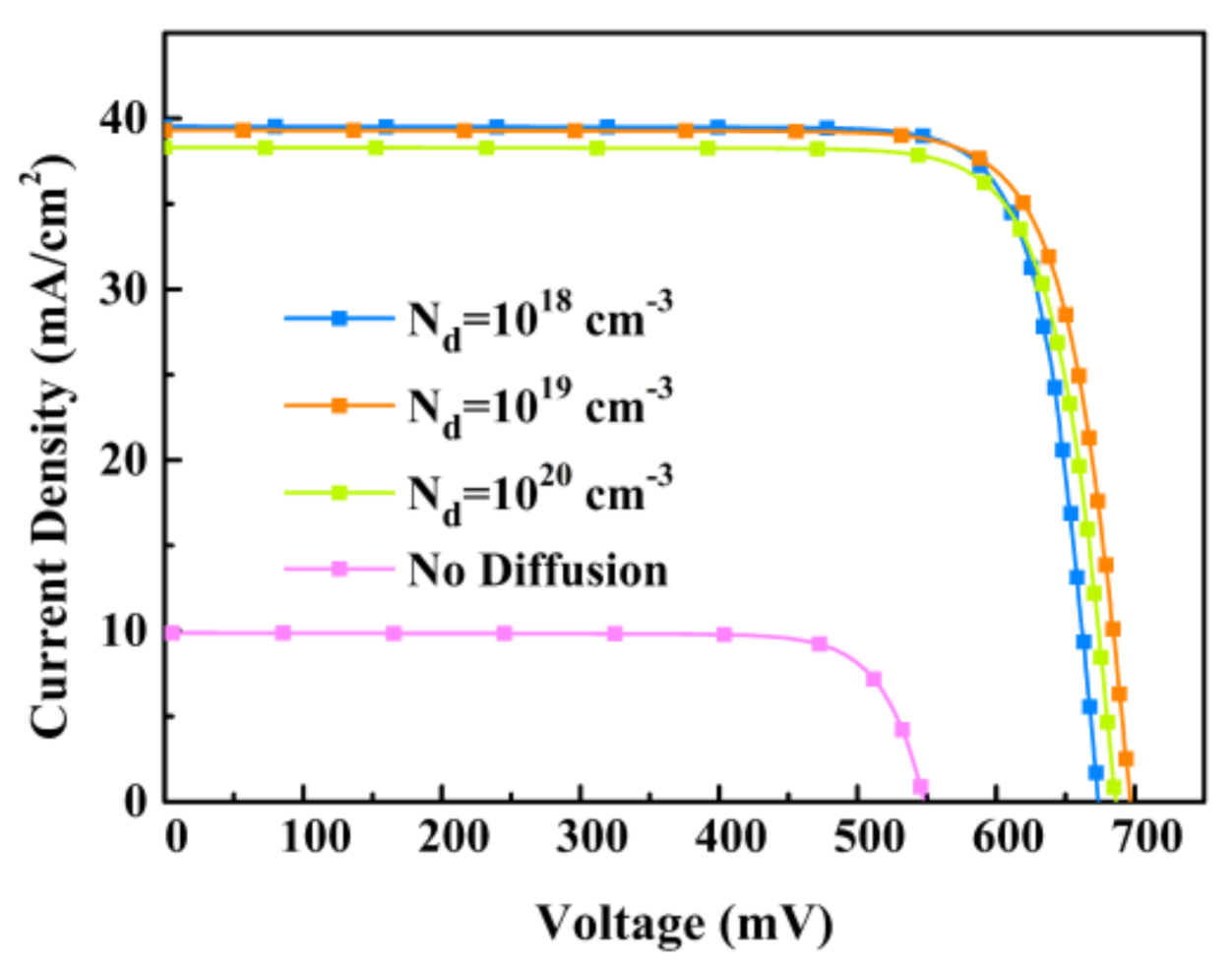
3.1. Simulation Results and Analysis
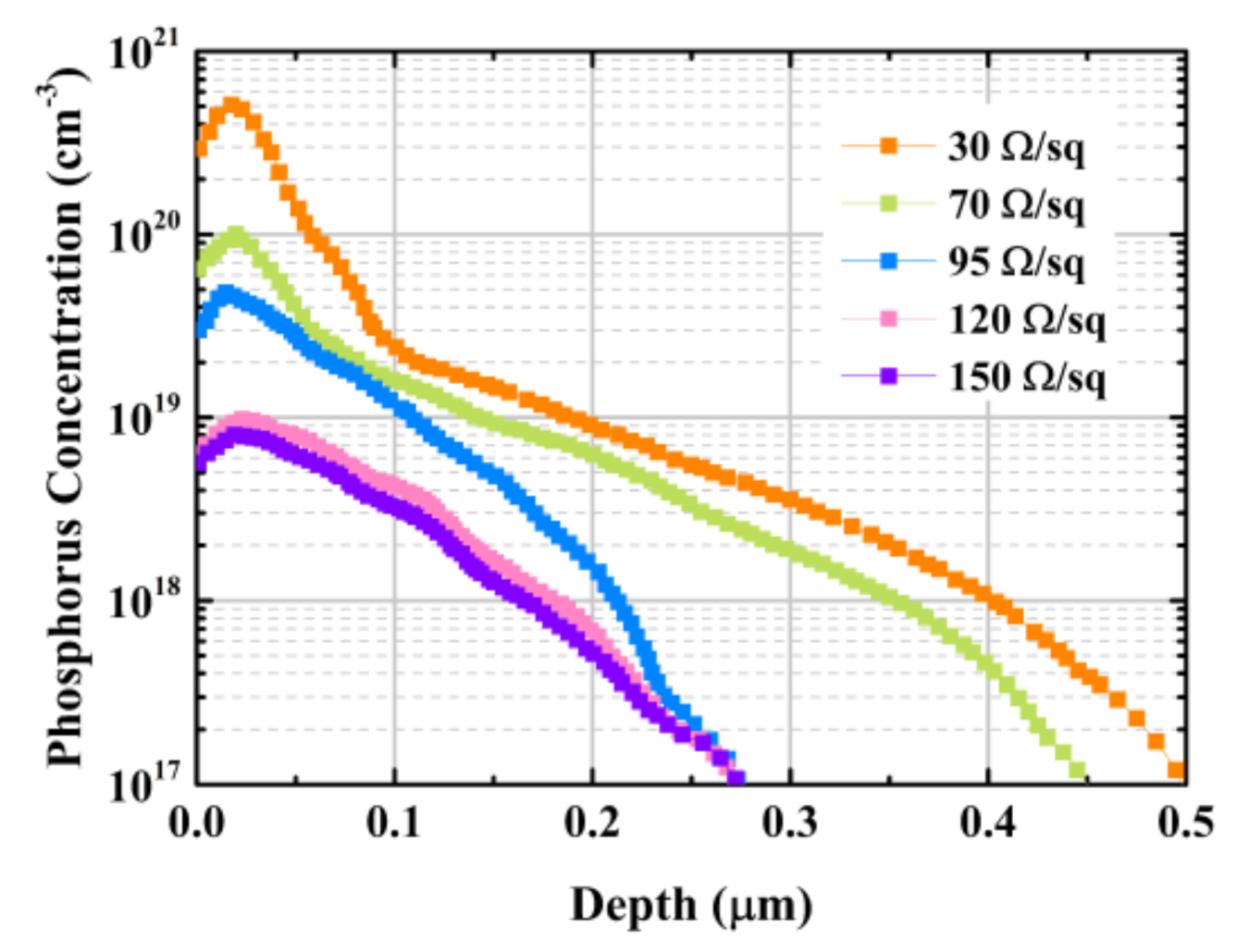
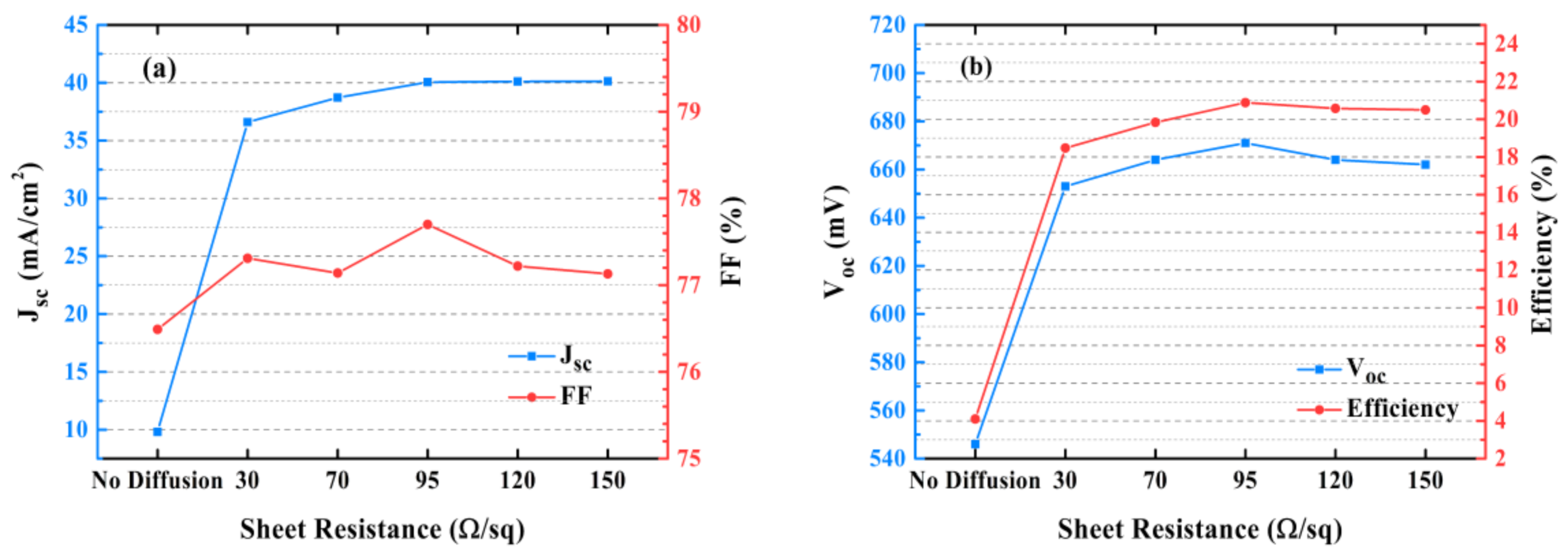
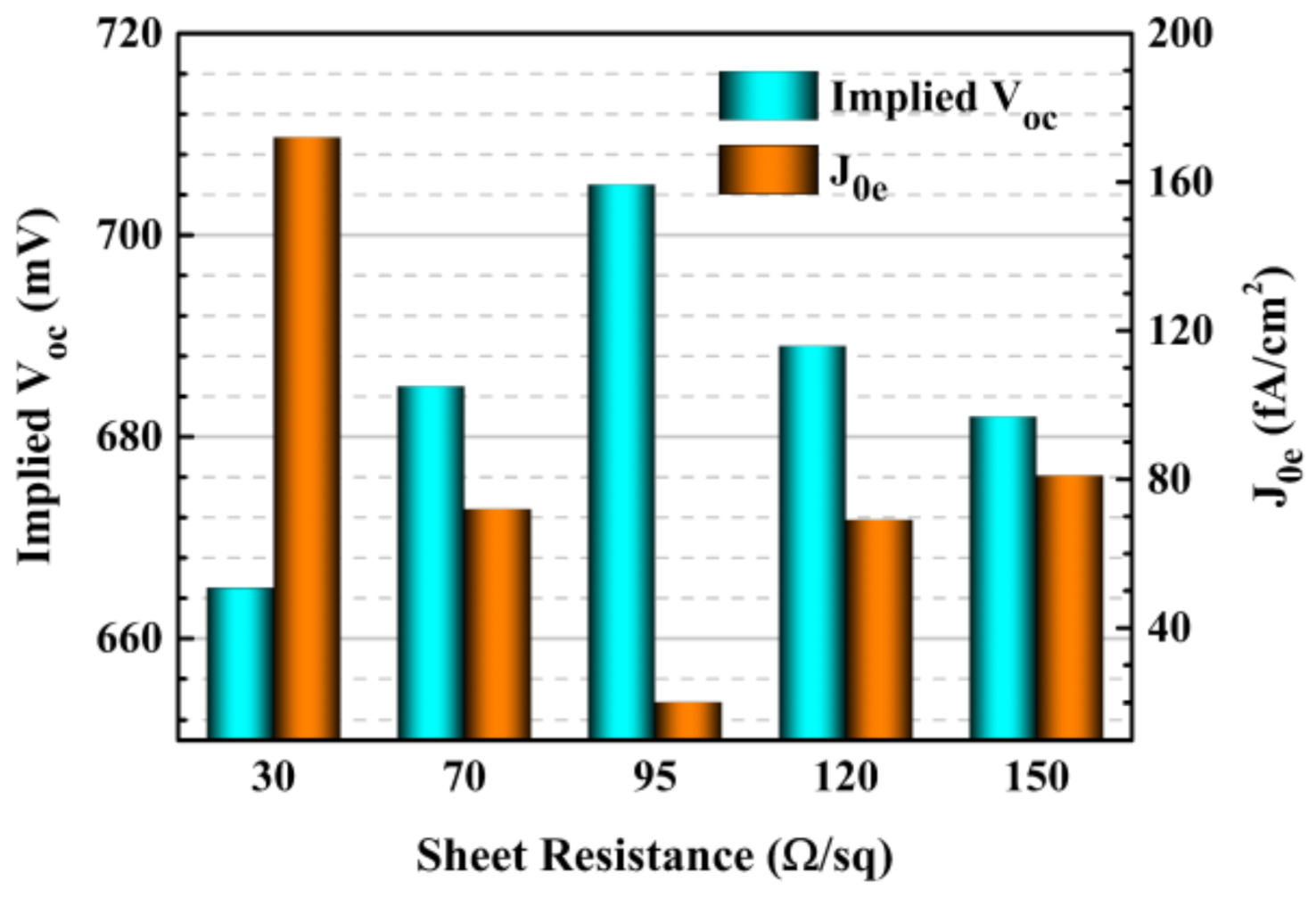
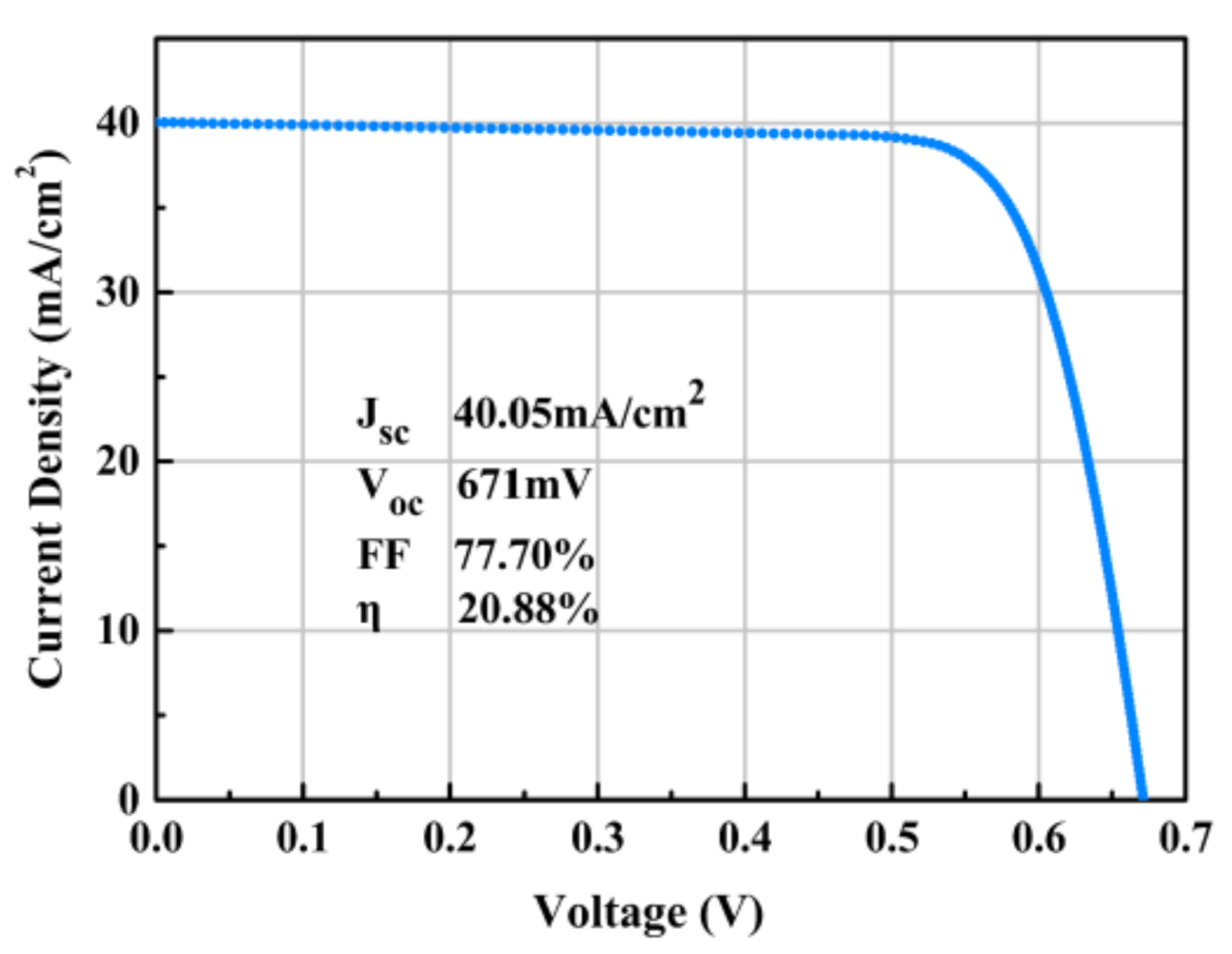
3.2. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Müller, R.; Reichel, C.; Yang, X.; Richter, A.; Benick, J.; Hermle, M. Impact of the homogeneous junction breakdown in IBC solar cells on the passivation quality of Al2O3 and SiO2: Degradation and regeneration behavior. Energy Procedia 2017, 124, 365–370. [Google Scholar] [CrossRef] [Green Version]
- Tachibana, T.; Mochizuki, T.; Shirasawa, K.; Takato, H. An investigation of internal quantum efficiency of bifacial interdigitated back contact (IBC) crystalline silicon solar cell. IEEE J. Photovolt. 2019, 9, 1526–1531. [Google Scholar] [CrossRef]
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Ho-Baillie, A.W.Y. Solar cell efficiency tables (Version 55). Prog. Photovolt. Res. Appl. 2020, 28, 3–15. [Google Scholar] [CrossRef]
- Guillevin, N.; Cesar, I.; Burgers, A.R.; Venema, P.; Wang, Z.; Zhai, J.Y.; Liu, D. Pilot line results of n-type IBC cell process in mass production environment. In Proceedings of the European Photovoltaic Solar Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–29 September 2017; pp. 205–211. [Google Scholar]
- Liu, J.; Yao, Y.; Xiao, S.; Gu, X. Review of status developments of high-efficiency crystalline silicon solar cells. J. Phys. D Appl. Phys. 2018, 51, 123001. [Google Scholar] [CrossRef]
- Ingenito, A.; Isabella, O.; Zeman, M. Simplified process for high efficiency, self-aligned IBC c-Si solar cells combining ion implantation and epitaxial growth: Design and fabrication. Sol. Energy Mater. Sol. Cells 2016, 157, 354–365. [Google Scholar] [CrossRef]
- Franklin, E.; Fong, K.; Mclntosh, K.; Fell, A.; Blakers, A.; Kho, T.; Walter, D.; Wang, D.; Zin, N.; Stocks, M.; et al. Design, fabrication and characterisation of a 24.4% efficient interdigitated back contact solar cell. Prog. Photovolt. Res. Appl. 2016, 24, 411–427. [Google Scholar] [CrossRef]
- Li, Q.; Tao, K.; Sun, Y.; Jia, R.; Wang, S.; Jin, Z.; Liu, X. Two dimensional simulation studies on amorphous silicon stack as front surface field for interdigitated back contact solar cells. Vacuum 2016, 125, 56–64. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Y.; Marmon, J.K.; Zhang, X.; Feng, Z.; Verlinden, P.J.; Shen, H. Independent Al2O3/SiNx:H and SiO2/SiNx:H passivation of p+ and n+ silicon surfaces for high-performance interdigitated back contact solar cells. IEEE J. Photovolt. 2017, 7, 51–57. [Google Scholar] [CrossRef]
- Hollemann, C.; Haase, F.; Schäfer, S.; Krügener, J.; Brendel, R.; Peibst, R. 26.1%—Efficient POLO—IBC cells: Quantification of electrical and optical loss mechanisms. Prog. Photovolt. Res. Appl. 2019, 27, 950–958. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Kawasaki, H.; Yoshida, W.; Irie, T.; Konishi, K.; Nakano, K.; Uto, T.; Adachi, D.; Kanematsu, M.; Uzu, H.; et al. Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%. Nat. Energy 2017, 2, 17032. [Google Scholar] [CrossRef]
- Procel, P.; Yang, G.; Isabella, O.; Zeman, M. Theoretical evaluation of contact stack for high efficiency IBC-SHJ solar cells. Sol. Energy Mater. Sol. Cells 2018, 186, 66–77. [Google Scholar] [CrossRef]
- Lin, H.; Ding, D.; Wang, Z.; Zhang, L.; Wu, F.; Yu, J.; Gao, P.; Ye, J.; Shen, W. Realization of interdigitated back contact silicon solar cells by using dopant-free heterocontacts for both polarities. Nano Energy 2018, 50, 777–784. [Google Scholar] [CrossRef]
- Hashmi, G.; Akand, A.R.; Hoq, M.; Rahman, H. Study of the enhancement of the efficiency of the monocrystalline silicon solar cell by optimizing effective parameters using PC1D simulation. Silicon 2018, 10, 1653–1660. [Google Scholar] [CrossRef]
- Clugston, D.A.; Basore, P.A. PC1D version 5: 32-bit solar cell modeling on personal computers. In Proceedings of the 26th IEEE Photovoltaic Specialists Conference, Anaheim, CA, USA, 29 September–3 October 1997; pp. 207–210. [Google Scholar]
- Cho, E.; Ok, Y.; Dahal, L.D.; Das, A.; Upadhyaya, V.; Rohatgi, A. Comparison of POCl3 diffusion and phosphorus ion-implantation induced gettering in crystalline Si solar cells. Sol. Energy Mater. Sol. Cells 2016, 157, 245–249. [Google Scholar] [CrossRef] [Green Version]
- Uprety, P.; Subedi, I.; Junda, M.M.; Collins, R.W.; Podraza, N.J. Photogenerated carrier transport properties in silicon photovoltaics. Sci. Rep. 2019, 9, 19015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Onno, A.; Chen, C.; Koswatta, P.; Boccard, M.; Holman, Z.C. Passivation, conductivity, and selectivity in solar cell contacts: Concepts and simulations based on a unified partial-resistances framework. J. Appl. Phys. 2019, 126, 183103. [Google Scholar] [CrossRef]
- Haug, H.; Olaisen, B.R.; Nordseth, Ø.; Marstein, E.S. A graphical user interface for multivariable analysis of silicon solar cells using scripted PC1D simulations. Energy Procedia 2013, 38, 72–79. [Google Scholar] [CrossRef] [Green Version]
- Singha, B.; Solanki, C.S. Optimization of boron spin on dopant (BSoD) diffusion for emitter formation in n-type c-Si solar cells. Mater. Today Proc. 2018, 5, 23466–23471. [Google Scholar] [CrossRef]
- Geerligs, L.J.; Macdonald, D. Base doping and recombination activity of impurities in crystalline silicon solar cells. Prog. Photovolt. Res. Appl. 2004, 12, 309–316. [Google Scholar] [CrossRef]
- Haug, H.; Greulich, J. PC1Dmod 6.2—Improved simulation of c-Si devices with updates on device physics and user interface. Energy Procedia 2016, 92, 60–68. [Google Scholar] [CrossRef]
- Basore, P.A.; Clugston, D.A. PC1D version 4 for windows: From analysis to design. In Proceedings of the 25th IEEE Photovoltaic Specialists Conference, Washington, DC, USA, 13–17 May 1996; pp. 377–381. [Google Scholar]
- Cai, X.; Zhou, X.; Liu, Z.; Jiang, F.; Yu, Q. An in-depth analysis of the silicon solar cell key parameters’ optimal magnitudes using PC1D simulations. Optik 2018, 164, 105–113. [Google Scholar] [CrossRef]
- Altermatt, P.P.; Schenk, A.; Geelhaar, F.; Heiser, G. Reassessment of the intrinsic carrier density in crystalline silicon in view of band-gap narrowing. J. Appl. Phys. 2003, 93, 1598–1604. [Google Scholar] [CrossRef]
- Altermatt, P.P.; Schumacher, J.O.; Cuevas, A.; Kerr, M.J.; Glunz, S.W.; King, R.R.; Heiser, G.; Schenk, A. Numerical modeling of highly doped Si:P emitters based on Fermi-Dirac statistics and self-consistent material parameters. J. Appl. Phys. 2002, 92, 3187–3197. [Google Scholar] [CrossRef] [Green Version]
- Zandi, S.; Saxena, P.; Razaghi, M.; Gorji, N.E. Simulation of CZTSSe thin-film solar cells in COMSOL: Three-dimensional optical, electrical, and thermal models. IEEE J. Photovolt. 2020, 10, 1503–1507. [Google Scholar] [CrossRef]
- Hermle, M.; Granek, F.; Schultz, O.; Glunz, S.W. Analyzing the effects of front-surface fields on back-junction silicon solar cells using the charge-collection probability and the reciprocity theorem. J. Appl. Phys. 2008, 103, 54507. [Google Scholar] [CrossRef]
| Parameters | Values 1 |
|---|---|
| Device area | 4 cm2 |
| Front surface texture angle | 45° |
| Front surface texture depth | 3 μm |
| External front reflectance | 5% |
| Thickness | 180 μm |
| Material | Silicon (Si) |
| Dielectric constant | 11.9 |
| Band gap | 1.124 eV |
| Intrinsic carrier density [25] | 9.65 × 109 cm−3 |
| Base dopant density | 1.15 × 1015 cm−3 |
| n+ front layer dopant density | Vary |
| n+ front layer thickness | 0.67 μm |
| Bulk recombination | 2 ms |
| Front surface recombination | Vary |
| Back surface recombination | 100 cm s−1 |
| Temperature | 25° |
| Constant intensity | 0.1 W cm−2 |
| Spectrum | AM 1.5G |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liu, A. Carrier Transmission Mechanism-Based Analysis of Front Surface Field Effects on Simplified Industrially Feasible Interdigitated Back Contact Solar Cells. Energies 2020, 13, 5303. https://doi.org/10.3390/en13205303
Li X, Liu A. Carrier Transmission Mechanism-Based Analysis of Front Surface Field Effects on Simplified Industrially Feasible Interdigitated Back Contact Solar Cells. Energies. 2020; 13(20):5303. https://doi.org/10.3390/en13205303
Chicago/Turabian StyleLi, Xiaoxuan, and Aimin Liu. 2020. "Carrier Transmission Mechanism-Based Analysis of Front Surface Field Effects on Simplified Industrially Feasible Interdigitated Back Contact Solar Cells" Energies 13, no. 20: 5303. https://doi.org/10.3390/en13205303
APA StyleLi, X., & Liu, A. (2020). Carrier Transmission Mechanism-Based Analysis of Front Surface Field Effects on Simplified Industrially Feasible Interdigitated Back Contact Solar Cells. Energies, 13(20), 5303. https://doi.org/10.3390/en13205303





