Thermal Assessment of Power Cables and Impacts on Cable Current Rating: An Overview
Abstract
:1. Introduction
2. Heat Transfer Concepts for Thermal Analysis of Power Cables
2.1. Energy Conservation and the Energy Balance Equation
- heat flow rate that enters in the power cable, and which is generated by the solar radiation for an insulated power cable installed in air, or by the neighbouring cables of a specific power cable buried in the soil;
- heat flow rate generated inside a specific power cable, by Joule, dielectric and ferromagnetic losses;
- change of heat flow rate stored inside the power cable; and,
- heat flow rate dissipated by heat transfer mechanisms (or heat losses); in the case of the underground installations, the cable system also incorporates the surrounding soil.
- (a)
- the non-infinite dimension of the soil;
- (b)
- the effect of the ambient on the soil properties;
- (c)
- the non-homogeneous soil;
- (d)
- the finite cable length;
- (e)
- the lack of cylindrical symmetry.
2.2. Non-Infinite Dimension of the Soil
2.3. The Effect of the Ambient on the Soil Properties
- (a)
- periodic variations, determined with the Fourier transform; and
- (b)
- non-periodic variations, determined with the Laplace transform.
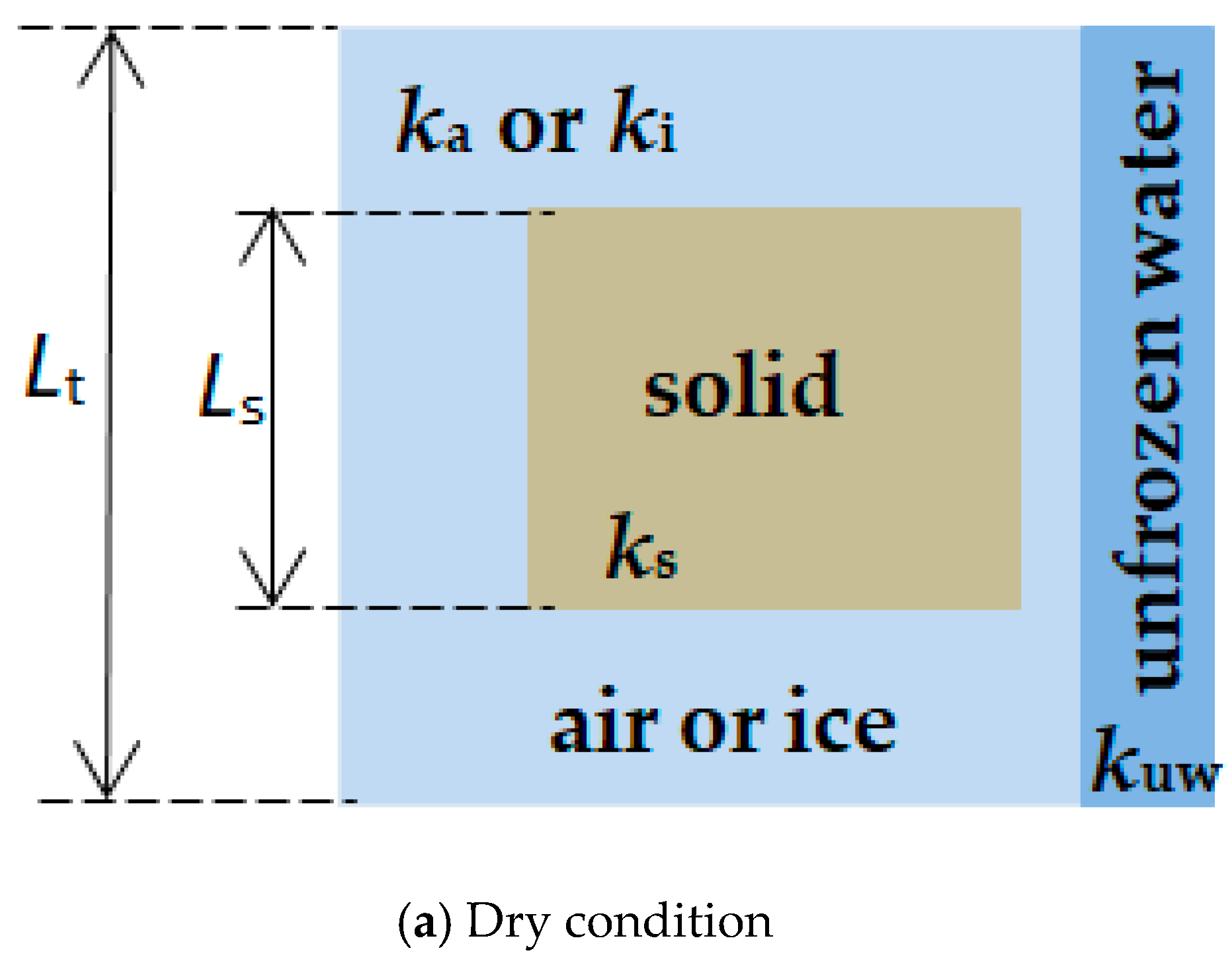
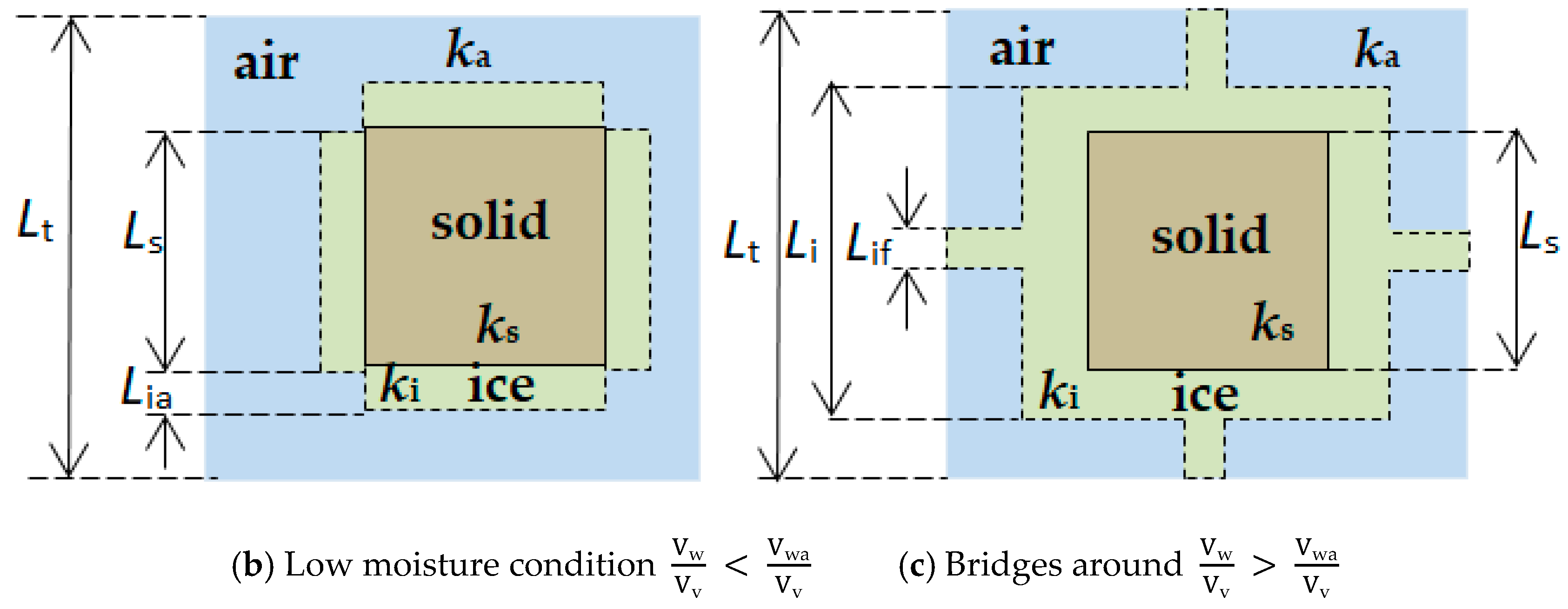
2.4. Non-Homogeneous Soil
- −
- the addition of a corrective backfill with low thermal resistivity;
- −
- the heat sources around the buried cables must be insulated;
- −
- the forced convection for the fluid around the buried cable;
- −
- an insulating fluid for the inner cooling of the cable;
- −
- installing in the hot spot zone a forced cooling system [48].
Effective Soil Thermal Conductivity
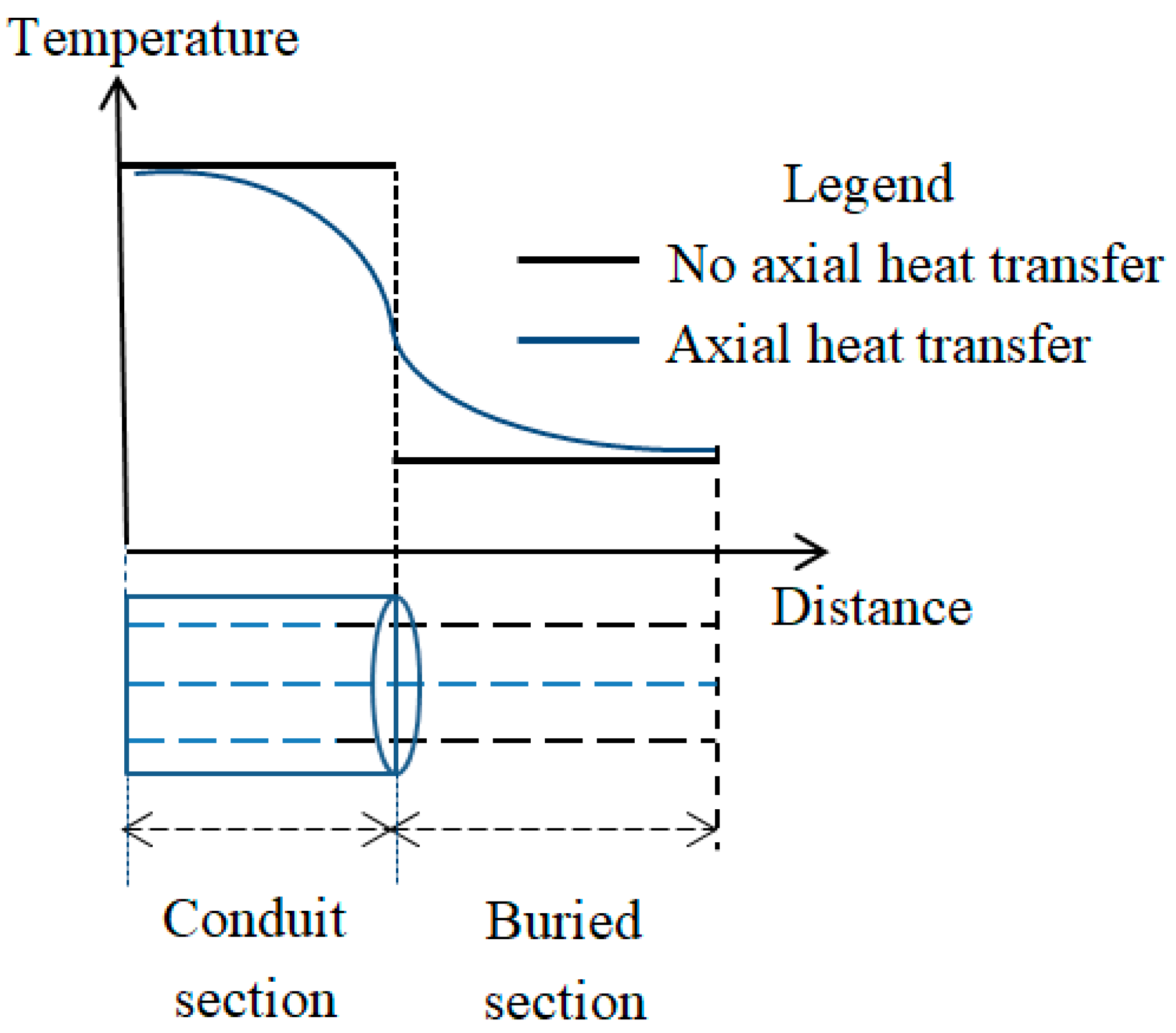
2.5. Finite Cable Length
2.6. Lack of Geometrical Symmetry
2.7. Non-Buried Cables
3. Thermal Models and Thermal Analysis Methods
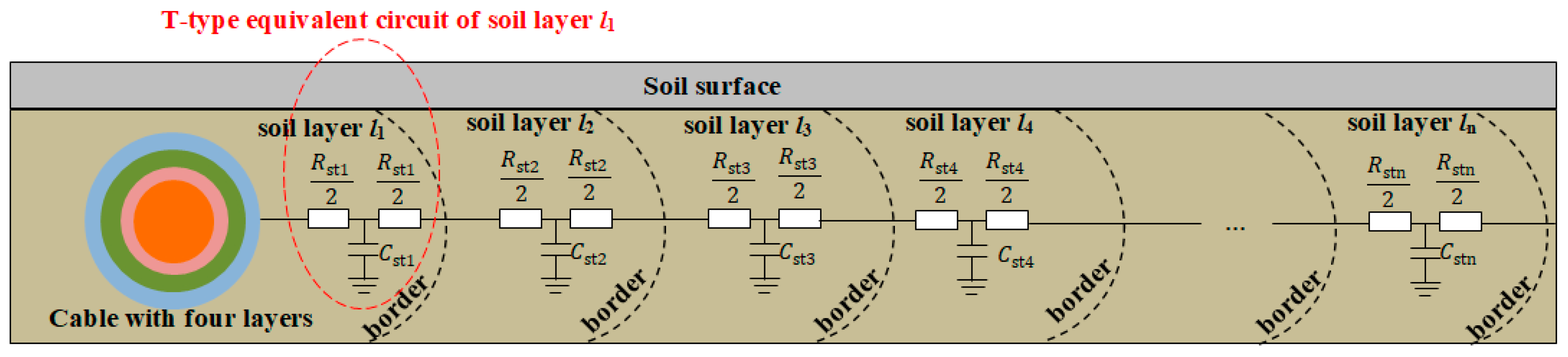
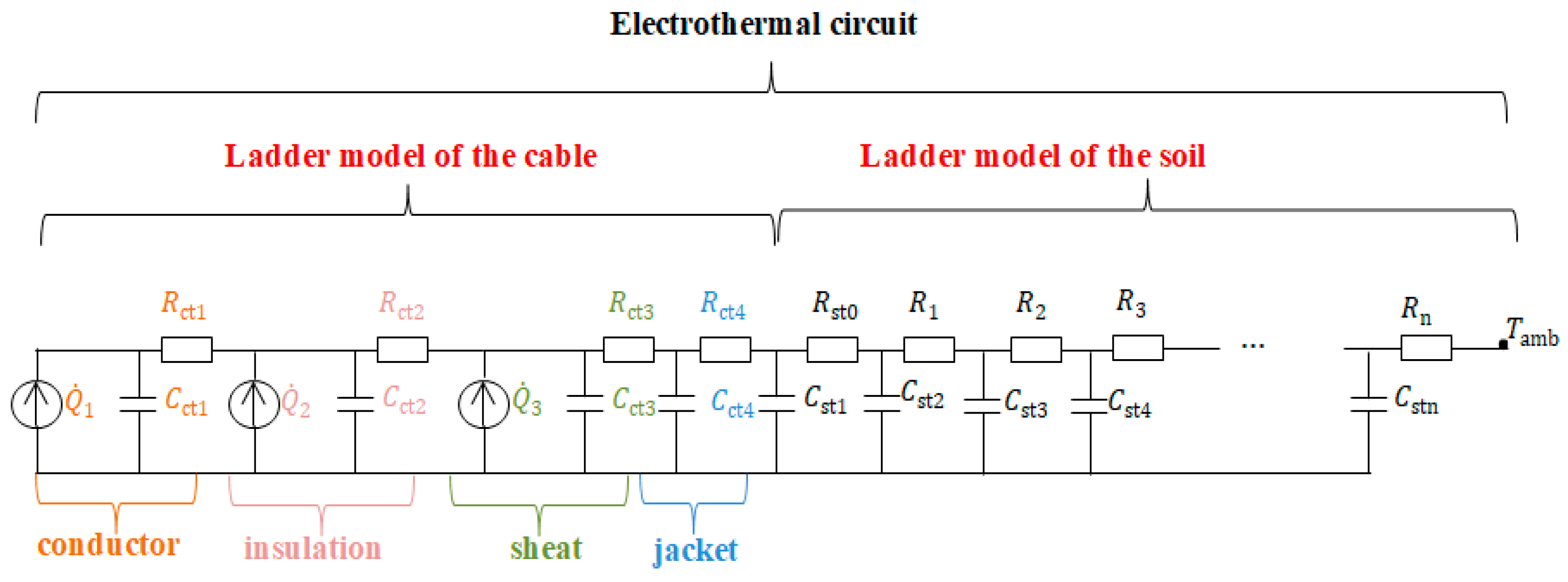
3.1. Thermal Models of Power Cables and Electrothermal Analogy
3.2. Methods for Thermal Analysis of Power Cables
3.2.1. Analytical Methods
3.2.2. Numerical Methods
4. Steady-State and Dynamic Cable Rating
4.1. Steady-State Cable Rating Calculations
- is the allowable conductor temperature rise above the ambient temperature, given by the difference between the permissible maximum conductor temperature and the ambient temperature;
- are the dielectric losses for the insulation surrounding the conductor;
- is the thermal resistance between one conductor and the sheath;
- is the thermal resistance between the sheath and the armour;
- is the thermal resistance of the external serving of the cable;
- is the thermal resistance between the cable surface and the surrounding medium;
- is the ratio of losses in the metal sheath to total losses in all conductors;
- is the ratio of losses in the armouring to total losses in all conductors;
- is the electric resistance of the conductor evaluated at the maximum allowable conductor temperature.
4.2. Dynamic Cable Rating
4.3. Effect of Harmonics on Cable Rating
4.4. Probabilistic Models and Risk Analysis for Calculation of Current Rating
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Acronyms | |
| DLR | Dynamic Line Rating |
| DTR | Dynamic Thermal Rating |
| DTS | Distributed Temperature Sensing |
| FDM | Finite Difference Method |
| FEM | Finite Element Method |
| EV | Electric Vehicles |
| IEC | International Electrotechnical Commission |
| MV | Medium Voltage |
| PVC | Polyvinyl Chloride |
| RMS | Root Mean Square |
| XLPE | Cross-Linked Polyethylene |
| Symbols | |
| dynamic matrix | |
| amplitude of the h-th harmonic | |
| thermal diffusivity | |
| input coefficient matrix | |
| constant | |
| heat capacitance matrix | |
| capacitance | |
| thermal capacity | |
| volumetric heat capacity | |
| disturbance vector | |
| specific heat capacity | |
| derating factor | |
| outside diameter of the cable | |
| damping depth of the fundamental | |
| thickness of the fictitious layer | |
| outer diameter | |
| inner diameter | |
| distance from the centre of the hottest cable and the centre of the generic cable | |
| distance from the centre of the hottest cable and the centre of the image of the generic cable | |
| exponential integral | |
| void ratio | |
| Fourier transformation | |
| Dirac function | |
| percentage of the mean temperature gradient along each phase | |
| maximum harmonic order | |
| heat transfer coefficient | |
| mean heat transfer coefficient | |
| electric current | |
| base RMS electric current | |
| permissible current rating | |
| thermal conductance | |
| thermal conductance matrix | |
| Kersten number | |
| convection matrix | |
| thermal conductivity | |
| air thermal conductivity | |
| thermal conductivity of each phase i (air, water, solid) | |
| dry thermal conductivity | |
| ice thermal conductivity | |
| thermal conductivity of each phase (solid, water, air) | |
| solid thermal conductivity | |
| saturated thermal conductivity | |
| effective thermal conductivity for parallel and horizontals isotherms | |
| effective thermal conductivity for parallel and vertical heat flux lines | |
| water thermal conductivity | |
| Laplace transform | |
| distance of the heat source from the soil surface | |
| distance of the heat sink from the fictitious layer | |
| cubic cell length | |
| solid length | |
| M | number of soil components |
| values of the time series | |
| number of cables | |
| number of finite elements | |
| load-carrying conductors | |
| Joule losses | |
| period | |
| heat flow rate | |
| change of heat flow rate | |
| conductive heat flux | |
| conductive soil heat flux | |
| volumetric heat flux (rate of heat generated per unit volume) | |
| column vector of heat flux arising from internal heat generation | |
| input vector determined by the Joule losses | |
| column vector of heat flux arising from surface convection | |
| heat flux per unit length | |
| isothermal latent heat flux | |
| thermal latent heat flux | |
| thermal resistance | |
| thermal resistance between one conductor and the sheath | |
| thermal resistance between the sheath and the armour | |
| thermal resistance of the external serving of the cable | |
| thermal resistance between the cable surface and the surrounding medium | |
| electric resistance | |
| electric resistance at the fundamental frequency | |
| conductor electric resistance at the th harmonic | |
| radius | |
| distance from the heat sink to a point N | |
| distance from the heat source to a point N | |
| heat transfer surface | |
| variable of the transformed Fourier domain | |
| absolute temperature | |
| ambient temperature | |
| relevant temperature rise | |
| temperature at the node (i,j) of the mesh | |
| Tmax | permissible maximum conductor temperature |
| mean temperature | |
| ratio between the unfrozen water volume and the total volume of the cubic cell | |
| V | volume of the cylindrical configuration |
| cubic cell volume, | |
| unfrozen water volume, | |
| dielectric losses per unit length | |
| w | dummy variable |
| horizontal coordinate | |
| vertical coordinate | |
| soil depth | |
| Greek symbols | |
| constant | |
| per unit value of the hth harmonic with respect to the base value | |
| constant | |
| constant | |
| temperature difference | |
| thickness | |
| density | |
| column vector of node temperatures | |
| volume fraction of a phase | |
| ratio of losses in the metal sheath layer to total conductor losses | |
| ratio of losses in the steel armour layer to total conductor losses | |
| volume fraction of each phase | |
| electric conductivity | |
| soil thermal resistivity | |
| porosity | |
| time | |
| phase angle of the h-th harmonic | |
| vector of state variables | |
| fundamental angular frequency | |
| Subscripts | |
| a | air |
| c | continuous phase |
| cond | conductive |
| conv | convective |
| gen | generated |
| h | harmonic |
| i | ice |
| i | phase (air, water, solid) |
| in | input |
| lat | latent |
| n | air, water, solid |
| out | output |
| p | packing |
| rad | radiative |
| s | soil |
| sat | saturated |
| stor | stored |
| each layer of soil | |
| tot | total |
| u | unfrozen |
| w | water |
References
- Montanari, G.C.; Mazzanti, G.; Simoni, L. Progress in electrothermal life modeling of electrical insulation during the last decades. IEEE Trans. Dielectr. Electr. Insul. 2002, 9, 730–745. [Google Scholar] [CrossRef]
- Mazzanti, G. The combination of electrothermal stress, load cycling and thermal transients and its effects on the life of high voltage ac cables. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 1168–1179. [Google Scholar] [CrossRef]
- Bragatto, T.; Cresta, M.; Gatta, F.M.; Geri, A.; Maccioni, M.; Paulucci, M. Underground MV power cable joints: A non-linear thermal circuit model and its experimental validation. Electr. Power Syst. Res. 2017, 149, 190–197. [Google Scholar] [CrossRef]
- Zhao, Y.; Han, Z.; Xie, Y.; Fan, X.; Nie, Y.; Wang, P.; Liu, G.; Hao, Y.; Huang, J.; Zhu, W. Correlation Between Thermal Parameters and Morphology of Cross-Linked Polyethylene. IEEE Access 2020, 8, 19726–19736. [Google Scholar] [CrossRef]
- Nielsen, T.V.M.; Jakobsen, S.; Savaghebi, M. Dynamic Rating of Three–Core XLPE Submarine Cables for Offshore Wind Farms. Appl. Sci. 2019, 9, 800. [Google Scholar] [CrossRef]
- Anders, G.J.; Napieralski, A.; Zubert, M.; Orlikowski, M. Advanced modeling techniques for dynamic feeder rating systems. IEEE Trans. Ind. Appl. 2003, 39, 619–626. [Google Scholar] [CrossRef]
- Singh, K. Cable monitoring solution—Predict with certainty. In Proceedings of the 12th IET International Conference on Developments in Power System Protection (DPSP 2014), Copenhagen, Denmark, 31 March–3 April 2014; pp. 1–3. [Google Scholar]
- Bascom, E.C., III; Clairmont, B. Considerations for advanced temperature monitoring of underground power cables. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014. [Google Scholar]
- Anders, G.J. Rating of Electric Power Cables; McGraw–Hill: New York, NY, USA, 1997. [Google Scholar]
- Anders, G. Rating of Electric Power Cables in Unfavorable Thermal Environment; IEEE Press: Piscataway, NJ, USA, 2005. [Google Scholar]
- Benato, R.; Colla, L.; Dambone Sessa, S.; Marelli, M. Review of high current rating insulated cable solutions. Electr. Power Syst. Res. 2016, 133, 36–41. [Google Scholar] [CrossRef]
- Zhou, C.; Yi, H.; Dong, X. Review of recent research towards power cable life cycle management. High Volt. 2017, 2, 179–187. [Google Scholar] [CrossRef]
- Chatzipetros, D.; Pilgrim, J.A. Review of the Accuracy of Single Core Equivalent Thermal Model for Offshore Wind Farm Cables. IEEE Trans. Power Deliv. 2018, 33, 1913–1921. [Google Scholar] [CrossRef]
- Pérez–Rúa, J.A.; Cutululis, N.A. Electrical Cable Optimization in Offshore Wind Farms–A Review. IEEE Access 2019, 7, 85796–85811. [Google Scholar] [CrossRef]
- Dong, Y.; McCartney, J.S.; Lu, N. Critical review of thermal conductivity models for unsaturated soils. Geotech. Geol. Eng. 2015, 33, 207–221. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Z. Review of soil thermal conductivity and predictive models. Int. J. Therm. Sci. 2017, 117, 172–183. [Google Scholar] [CrossRef]
- Lauria, D.; Pagano, M.; Petrarca, C. Transient Thermal Modelling of HV XLPE Power Cables: Matrix approach and experimental validation. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar]
- Kennelly, A.E. Current Carrying Capacity of Electric Cables, Submerged, Buried or Suspended in the Air. Electr. World 1893, 22, 183–201. [Google Scholar]
- Neher, J.H. The temperature rise of buried cables and pipes. Trans. Am. Inst. Elect. Eng. 1949, 68, 9–21. [Google Scholar] [CrossRef]
- Neher, J.H.; McGrath, M.H. The calculation of the temperature rise and load capability of cable systems. Trans. Am. Inst. Elect. Eng. Power App. Syst. Part III 1957, 76, 752–772. [Google Scholar] [CrossRef]
- Purushothaman, S.; de León, F.; Terracciano, M. Calculation of cable thermal rating considering non-isothermal earth surface. IET Gener. Transmiss. Distrib. 2014, 8, 1354–1361. [Google Scholar] [CrossRef]
- Kutateladze, S.S. Fundamentals of Heat Transfer; Academic: New York, NY, USA, 1963. [Google Scholar]
- De Vries, D.A.; Philip, J.R. Soil Heat Flux, Thermal Conductivity, and the Null-alignment method. Soil Sci. Soc. Am. J. 1986, 50, 12–18. [Google Scholar] [CrossRef]
- Buchan, G.D. Soil Temperature Regime, Chapter 14. In Soil and Environmental Analysis: Physical Methods, 2nd ed.; Smith, K.A., Mullins, C.E., Eds.; Marcel Dekker Inc.: New York, NY, USA, 2000; pp. 539–594. [Google Scholar]
- Philip, J.R.; de Vries, D.A. Moisture movement in porous materials under temperature gradients. Trans. Am. Geophys. Union. 1957, 38, 222–232. [Google Scholar] [CrossRef]
- Van Wijk, W.R.; Derksen, W.J. Sinusoidal temperature variation in a layered soil. In Physics of Plant Environment; van Wijk, W.R., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1963; pp. 171–209. [Google Scholar]
- Van Wijk, W.R. General temperature variations in a homogeneous soil. In Physics of Plant Environment; van Wijk, W.R., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1963; pp. 144–170. [Google Scholar]
- IEC 60287-1-3: Calculations of the Continuous Current Rating of Cables (100% Load Factor); International Electrotechnical Commission: Geneva, Switzerland, 1982.
- Gouda, O.E. Formation of the dried out zone around underground cables loaded by peak loadings. In Modeling, Simulation & Control; Asme Press: Athens, Greece, 1986; Volume 7, pp. 35–46. [Google Scholar]
- Kroener, E.; Vallati, A.; Bittelli, M. Numerical simulation of coupled heat, liquid water and water vapor in soils for heat dissipation of underground electrical power cables. Appl. Therm. Eng. 2014, 70, 510–523. [Google Scholar] [CrossRef]
- IEC 60287–1–1. In Electric Cables–Calculation of the Current Rating–Part 1–1: Current Rating Equations (100% Load Factor) and Calculation of Losses–General; International Electrotechnical Commission: Geneva, Switzerland, 2006.
- Malmedal, K.; Bates, C.; Cain, D.K. The Heat and Buried Cable Conundrum: A Method to Help Determine Underground Cable Ampacity. IEEE Ind. Appl. Mag. 2016, 22, 20–31. [Google Scholar] [CrossRef]
- Hruška, M.; Clauser, C.; De Doncker, R.W. Influence of dry ambient conditions on performance of underground medium-voltage DC cables. Appl. Therm. Eng. 2019, 149, 1419–1426. [Google Scholar] [CrossRef]
- Singh, D.N.; Devid, K. Generalized relationships for estimating soil thermal resistivity. Exp. Therm. Fluid Sci. 2000, 22, 133–143. [Google Scholar] [CrossRef]
- Gouda, O.E.; El Dein, A.Z.; Amer, G.M. Effect of the Formation of the Dry Zone around Underground Power Cables on Their Ratings. IEEE Trans. Power Deliv. 2011, 26, 972–978. [Google Scholar] [CrossRef]
- Anders, G.J.; Radhakrishna, H.S. Power cable thermal analysis with consideration of heat and moisture transfer in the soil. IEEE Trans. Power Deliv. 1988, 3, 1280–1288. [Google Scholar] [CrossRef]
- Millar, R.J.; Lehtonen, M. A robust framework for cable rating and temperature monitoring. IEEE Trans. Power Deliv. 2006, 21, 313–321. [Google Scholar] [CrossRef]
- Donazzi, F.; Occhini, E.; Seppi, A. Soil thermal and hydrological characteristics in designing underground cables. Proc. Inst. Elect. 1979, 126, 506–516. [Google Scholar] [CrossRef]
- Groeneveld, G.J.; Snijders, A.L.; Koopmans, G.; Vermeer, J. Improved method to calculate the critical conditions for drying out sandy soils around power cables. IEEE Proc. 1984, 131 Pt C, 42–53. [Google Scholar] [CrossRef]
- Freitas, D.S.; Prata, A.T.; de Lima, A.J. Thermal performance of underground power cables with constant and cyclic currents in presence of moisture migration in the surrounding soil. IEEE Trans. Power Deliv. 1996, 11, 1159–1170. [Google Scholar] [CrossRef]
- Hartley, J.G.; Black, W.Z. Transient simultaneous heat and mass transfer in moist unsaturated soils. Asme Trans. 1981, 103, 376–382. [Google Scholar] [CrossRef]
- Yenchek, M.R.; Cole, G.P. Thermal modelling of portable power cables. IEEE Trans. Ind. Appl. 1997, 33, 72–79. [Google Scholar] [CrossRef]
- Anders, G.J.; Napieralski, A.; Kulesza, Z. Calculation of the internal thermal resistance and ampacity of 3-core screened cables with fillers. IEEE Trans. Power Deliv. 1999, 14, 729–734. [Google Scholar] [CrossRef]
- Schmidt, N.P. Comparison between IEEE and CIGRE ampacity standards. IEEE Trans. Power Deliv. 1999, 14, 1555–1562. [Google Scholar] [CrossRef]
- Garrido, C.; Antonio, F.O.; Cidras, J. Theoretical model to calculate steady-state and transient ampacity and temperature in buried cables. IEEE Trans. Power Deliv. 2003, 18, 667–678. [Google Scholar] [CrossRef]
- Demoulias, C.; Labridis, D.P.; Dokopoulos, P.S.; Gouramanis, K. Ampacity of Low-Voltage Power Cables Under Nonsinusoidal Currents. IEEE Trans. Power Deliv. 2007, 22, 584–594. [Google Scholar] [CrossRef]
- de León, F.; Anders, G.J. Effects of backfilling on cable ampacity analyzed with the finite element method. IEEE Trans. Power Del. 2008, 23, 537–543. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G.J.; Cherukupalli, S. Underground cable hot spot. IEEE Trans. Power Deliv. 2020, 35, 592–599. [Google Scholar] [CrossRef]
- Tobin, B.; Zadehgol, H.; Ho, K.; Welsh, G.; Prestrud, J. A water cooling system to improve ampacity in underground urban distribution cables. In Proceedings of the 2005/2006 IEEE/PES Transmission and Distribution Conference and Exhibition, Dallas, TX, USA, 21–24 May 2006; pp. 432–437. [Google Scholar]
- Klimenta, D.; Tasi, D.; Jevti, M. The use of hydronic asphalt pavements as an alternative method of eliminating hot spots of underground power cables. Appl. Therm. Eng. 2020, 168, 114818. [Google Scholar] [CrossRef]
- He, H.; Zhao, Y.; Dyck, M.F.; Si, B.; Jin, H.; Lv, J.; Wang, J. A modified normalized model for predicting effective soil thermal conductivity. Acta Geotech. 2017, 12, 1281–1300. [Google Scholar] [CrossRef]
- Yan, H.; He, H.; Dyck, M.; Jin, H.; Li, M.; Si, B.; Lv, J. A generalized model for estimating effective soil thermal conductivity based on the Kasubuchi algorithm. Geoderma 2019, 353, 227–242. [Google Scholar] [CrossRef]
- De Vries, D.A. Thermal properties of soils. In Physics of the Plant Environment; Van Wijk, W.R., Ed.; John Wiley & Sons: New York, NY, USA, 1963; pp. 210–235. [Google Scholar]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Tarnawski, V.R.; Momose, T.; Leong, W.H. Assessing the impact of quartz content on the prediction of soil thermal conductivity. Geotechnique 2009, 59, 331–338. [Google Scholar] [CrossRef]
- Farouki, O.T. Thermal properties of soils. In Cold Regions Science and Engineering 1981; CRREL Monograph 81–1; US Army Corps of Engineers, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1981. [Google Scholar]
- Brandon, T.L.; Mitchell, J.K. Factors influencing thermal resistivity of sands. J. Geotech. Eng. 1989, 115, 1683–1698. [Google Scholar] [CrossRef]
- Smits, K.M.; Sakaki, T.; Limsuwat, A.; Illangasekare, T.H. Thermal conductivity of sands under varying moisture and porosity in drainage–wetting cycles. Vadose Zone J. 2010, 9, 172–180. [Google Scholar] [CrossRef]
- Aduda, B.O. Effective thermal conductivity of loose particulate systems. J. Mater. Sci. 1996, 31, 6441–6448. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; Leong, W.H.; Gori, F.; Buchan, G.D.; Sundberg, J. Interparticle contact heat transfer in soil systems at moderate temperatures. Int. J. Energy Res. 2002, 26, 1345–1358. [Google Scholar] [CrossRef]
- Yu, X.B.; Zhang, N.; Pradhan, A.; Puppala, A.J. Thermal conductivity of sand-kaolin clay mixtures. Environ. Geotech. 2016, 3, 190–202. [Google Scholar] [CrossRef]
- Zhang, N.; Yu, X.B.; Pradhan, A.; Puppala, A.J. Thermal conductivity of quartz sands by thermo-TDR probe and model prediction. Asce J. Mater. Civ. Eng. 2015, 27, 04015059. [Google Scholar] [CrossRef]
- Campbell, G.S.; Jungbauer, J.D.; Bidlake, W.R.; Hungerford, R.D. Predicting the effect of temperature on soil thermal conductivity. Soil Sci. 1994, 158, 307–313. [Google Scholar] [CrossRef]
- Hiraiwa, Y.; Kasubuchi, T. Temperature dependence of thermal conductivity of soil over a wide range of temperature (5–75 °C). Eur. J. Soil Sci. 2000, 51, 211–218. [Google Scholar] [CrossRef]
- Tarnawski, V.R.; Gori, F. Enhancement of the cubic cell soil thermal conductivity model. Int. J. Energy Res. 2002, 26, 143–157. [Google Scholar] [CrossRef]
- Smits, K.M.; Sakaki, T.; Howington, S.E.; Peters, J.F.; Illangasekare, T.H. Temperature dependence of thermal properties of sands across a wide range of temperatures (30–70 °C). Vadose Zone J. 2013, 12, 1–8. [Google Scholar] [CrossRef]
- Vargas, W.L.; McCarthy, J.J. Heat conduction in granular materials. AIChE J. 2001, 47, 1052–1059. [Google Scholar] [CrossRef]
- Wiener, O. Abhandl math-phys Kl Konigl. SachsischenGes 1912, 32, 509. [Google Scholar]
- Tian, Z.; Lu, Y.; Horton, R.; Ren, T. A simplified de Vries-based model to estimate thermal conductivity of unfrozen and frozen soil. Eur. J. Soil Sci. 2016, 67, 564–572. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Horton, R.; Ren, T. A new perspective on soil thermal properties. Soil Sci. Soc. Am. J. 2001, 65, 1641–1647. [Google Scholar] [CrossRef]
- Gori, F. A theoretical model for predicting the effective thermal conductivity of unsaturated frozen soils. In Proceedings of the Fourth International Conference on Permafrost; National Academy Press: Fairbanks, AL, USA; Washington, DC, USA, 1983; pp. 363–368. [Google Scholar]
- He, H.; Noborio, K.; Johansen, O.; Dyck, M.F.; Lv, J. Normalized concept for modelling effective soil thermal conductivity from dryness to saturation. Eur. J. Soil Sci. 2020, 71, 27–43. [Google Scholar] [CrossRef]
- Johansen, O. Thermal Conductivity of Soils. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, 1975. [Google Scholar]
- Liu, G.; Xu, Z.; Ma, H.; Hao, Y.; Wang, P.; Wu, W.; Xie, Y.; Guo, D. An improved analytical thermal rating method for cables installed in short-conduits. Int. J. Electr. Power Energy Syst. 2020, 123, 106223. [Google Scholar] [CrossRef]
- IEC Standard 60287-2-1-2015. In Electric Cables—Calculation of the Current Rating—Thermal Resistance-Calculation of Thermal Resistance; International Electrotechnical Commission: Geneva, Switzerland, 2015.
- Vaucheret, P.; Hartlein, R.A.; Black, W.Z. Ampacity Derating Factors for Cables Buried in Short Segments of Conduit. IEEE Trans. Power Deliv. 2005, 20, 560–565. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G. Ampacity Reduction Factors for Cables Crossing Thermally Unfavorable Regions. IEEE Trans. Power Deliv. 2001, 16, 444–448. [Google Scholar] [CrossRef]
- Maximov, S.; Venegas, V.; Guardado, J.L.; Moreno, E.L.; López, R. Analysis of underground cable ampacity considering non–uniform soil temperature distributions. Electr. Power Syst. Res. 2016, 132, 22–29. [Google Scholar] [CrossRef]
- Degefa, M.Z.; Lehtonen, M.; Millar, R.J. Comparison of Air-Gap Thermal Models for MV Power Cables Inside Unfilled Conduit. IEEE Trans. Power Deliv. 2012, 27, 1662–1669. [Google Scholar] [CrossRef]
- Benato, R.; Dambone Sessa, S. A New Multiconductor Cell Three–Dimension Matrix–Based Analysis Applied to a Three–Core Armoured Cable. IEEE Trans. Power Deliv. 2018, 33, 1636–1646. [Google Scholar] [CrossRef]
- Zhou, B.; Le, Y.; Fang, Y.; Yang, F.; Dai, T.; Sun, L.; Liu, J.; Zou, L. Temperature field simulation and ampacity optimization of 500 kV HVDC cable. J. Eng. 2019, 2019, 2448–2453. [Google Scholar]
- Hamdan, M.A.; Pilgrim, J.A.; Lewin, P.L. Effect of Sheath Plastic Deformation on Electric Field in Three Core Submarine Cables. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018; pp. 342–345. [Google Scholar]
- Huang, R.; Pilgrim, J.A.; Lewin, P.L.; Scott, D.; Morrice, D. Managing cable thermal stress through predictive ratings. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Seattle, WA, USA, 7–10 June 2015; pp. 110–113. [Google Scholar]
- Hughes, T.J.; Henstock, T.J.; Pilgrim, J.A.; Dix, J.K.; Gernon, T.M.; Thompson, C.E.L. Effect of Sediment Properties on the Thermal Performance of Submarine HV Cables. IEEE Trans. Power Deliv. 2015, 30, 2443–2450. [Google Scholar] [CrossRef]
- Callender, G.; Ellis, D.; Goddard, K.F.; Dix, J.; Pilgrim, J.; Erdmann, M. Low Computational Cost Model for Convective Heat Transfer from Submarine Cables. IEEE Trans. Power Deliv. 2020, in press. [Google Scholar] [CrossRef]
- Arias Velásquez, R.M.; Mejía Lara, J.V. New methodology for design and failure analysis of underground transmission lines. Eng. Fail. Anal. 2020, 115, 104604. [Google Scholar] [CrossRef]
- Diaz–Aguiló, M.; De León, F.; Jazebi, S.; Terracciano, M. Ladder–Type Soil Model for Dynamic Thermal Rating of Underground Power Cable. IEEE Power Energy Technol. Syst. J. 2014, 1, 21–30. [Google Scholar] [CrossRef]
- Olsen, R.S.; Holboell, J.; Gudmundsdottir, U.S. Dynamic temperature estimation and real time emergency rating of transmission cables. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Nahman, J.; Tanaskovic, M. Calculation of the loading capacity of high voltage cables laid in close proximity to heat pipelines using iterative finite-element method. Int. J. Electr. Power Energy Syst. 2018, 103, 310–316. [Google Scholar] [CrossRef]
- Naskar, A.K.; Bhattacharya, N.K.; Sarkar, D. Transient thermal analysis of underground power cables using two dimensional finite element method. Microsyst. Technol. 2018, 24, 1279–1293. [Google Scholar] [CrossRef]
- Lux, J.; Czerniuk, T.; Olschewski, M.; Hill, W. Non–concentric Ladder Soil Model for Dynamic Rating of Buried Power Cables. IEEE Trans. Power Deliv. (Early Access) 2020, in press. [Google Scholar] [CrossRef]
- Hanna, M.A.; Chikhani, A.Y.; Salama, M.M.A. Thermal analysis of power cable systems in a trench in multi-layered soil. IEEE Trans. Power Deliv. 1998, 13, 304–309. [Google Scholar] [CrossRef]
- Nahman, J.; Tanaskovic, M. Determination of the current carrying capacity of cables using the finite element method. Electr. Power Syst. Res. 2002, 61, 109–117. [Google Scholar] [CrossRef]
- Jenkins, L.; Fahmi, N.; Yang, J. Application of dynamic asset rating on the UK LV and 11 kV underground power distribution network. In Proceedings of the 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017; pp. 1–6. [Google Scholar]
- Al–Saud, M.S. Assessment of thermal performance of underground current carrying conductors. IET Gener. Transm. Distrib. 2011, 5, 630–639. [Google Scholar] [CrossRef]
- Nguyen, N.K.; Vu, P.T.; Tlusty, J. New approach of thermal field and ampacity of underground cables using adaptive hp-FEM. In Proceedings of the IEEE PES T&D, New Orleans, LA, USA, 19–22 April 2010. [Google Scholar] [CrossRef]
- Desmet, J.; Putman, D.; Vanalme, G.; Belmans, R.; Vandommelent, D. Thermal analysis of parallel underground energy cables. In Proceedings of the CIRED 2005—18th International Conference and Exhibition on Electricity Distribution, Turin, Italy, 6–9 June 2005; pp. 1–4. [Google Scholar]
- Benato, R.; Dambone Sessa, S.; Forzan, M.; Marelli, M.; Pietribiasi, D. Core laying pitch–long 3D finite element model of an AC three–core armoured submarine cable with a length of 3 meter. Electr. Power Syst. Res. 2017, 150, 137–143. [Google Scholar] [CrossRef]
- Demoulias, C.; Labridis, D.P.; Dokopoulos, P.S.; Gouramanis, K. Influence of metallic trays on the ac resistance and ampacity of low-voltage cables under non-sinusoidal currents. Electr. Power Syst. Res. 2008, 78, 883–896. [Google Scholar] [CrossRef]
- Hwang, C.C.; Chang, J.J.; Chen, H.Y. Calculation of ampacities for cables in trays using finite elements. Electr. Power Syst. Res. 2000, 54, 75–81. [Google Scholar] [CrossRef]
- Ocłoń, P.; Cisek, P.; Pilarczyk, M.; Taler, D. Numerical simulation of heat dissipation processes in underground power cable system situated in thermal backfill and buried in a multilayered soil. Energy Convers. Manag. 2015, 951, 352–370. [Google Scholar] [CrossRef]
- Multiphysics, COMSOL. Comsol Multi-Physics User Guide (Version 4.3 a); COMSOL: USA, 2012. Available online: https://cdn.comsol.com/doc/4.3/COMSOL_ReleaseNotes.pdf (accessed on 1 September 2020).
- Guide, ANSYS FLUENT User. Release 14.0; ANSYS. Inc.: USA, 2011. Available online: http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Users%20Guide.pdf (accessed on 3 September 2020).
- Korovkin, N.; Greshnyakov, G.; Dubitsky, S. Multiphysics approach to the boundary problems of power engineering and their application to the analysis of load-carrying capacity of power cable line. In Proceedings of the Electric Power Quality and Supply Reliability Conference (PQ), Rakvere, Estonia, 11–13 June 2014; pp. 341–346. [Google Scholar]
- Zhang, Y.; Chen, X.; Zhang, H.; Liu, J.; Zhang, C.; Jiao, J. Analysis on the temperature field and the ampacity of XLPE submarine HV cable based on electro-thermal-flow multiphysics coupling simulation. Polymers 2020, 12, 952. [Google Scholar] [CrossRef]
- Ren, Y.; Wu, K.; Coker, D.F.; Quirke, N. Thermal transport in model copper-polyethylene interfaces. J. Chem. Phys. 2019, 151, 174708. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Y.; Ruan, X. The critical particle size for enhancing thermal conductivity in metal nanoparticle-polymer composites. J. Appl. Phys. 2018, 123, 074302. [Google Scholar] [CrossRef]
- Dubitsky, S.; Greshnyakov, G.; Korovkin, N. Refinement of underground power cable ampacity by multiphysics FEA simulation. Int. J. Energy 2015, 9, 12–19. [Google Scholar]
- Dubitsky, S.; Greshnyakov, G.; Korovkin, N. Comparison of finite element analysis to IEC-60287 for predicting underground cable ampacity. In Proceedings of the IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar]
- Olsen, R.S.; Anders, G.J.; Holboell, J.; Gudmundsdottir, U.S. Modelling of dynamic transmission cable temperature considering soil-specific heat thermal resistivity, and precipitation. IEEE Trans. Power Del. 2013, 28, 1909–1917. [Google Scholar] [CrossRef]
- Enescu, D.; Russo, A.; Porumb, R.; Seritan, G. Dynamic Thermal Rating of Electric Cables: A Conceptual Overview. In Proceedings of the 55th International Universities Power Engineering Conference, Torino, Italy, 1–4 September 2020. in press. [Google Scholar]
- Meliopoulos, A.P.S.; Martin, M.A. Calculation of secondary cable losses and ampacity in the presence of harmonics. IEEE Trans. Power Deliv. 1992, 7, 451–459. [Google Scholar] [CrossRef]
- Hiranandani, A. Calculation of cable ampacities including the effects of harmonics. Ind. Appl. Mag. 1998, 4, 42–51. [Google Scholar] [CrossRef]
- Palmer, J.A.; Degeneff, R.C.; McKernan, T.M.; Halleran, T.M. Pipe-type cable ampacities in the presence of harmonics. IEEE Trans. Power Deliv. 1993, 8, 1689–1695. [Google Scholar] [CrossRef]
- Yong, J.; Xu, W. A Method to Estimate the Impact of Harmonic and Unbalanced Currents on the Ampacity of Concentric Neutral Cables. IEEE Trans. Power Deliv. 2016, 1, 1971–1979. [Google Scholar] [CrossRef]
- Biryulin, V.I.; Gorlov, A.N.; Kudelina, D.V. Calculation of Cable Lines Insulation Heating with the Account of High Harmonics Currents. In Proceedings of the 2018 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Moscow, Russia, 15–18 May 2018. [Google Scholar]
- Wang, H.; Zhou, W.; Qian, K.; Meng, S. Modelling of ampacity and temperature of MV cables in presence of harmonic currents due to EVs charging in electrical distribution networks. Intern. J. Electr. Power Energy Syst. 2019, 112, 127–136. [Google Scholar] [CrossRef]
- El-Kady, M.A. Optimization of Power Cable and Thermal Backfill Configurations. IEEE Power Appar. Syst. 1982, 12, 4681–4688. [Google Scholar] [CrossRef]
- Foty, M.S.; Anders, G.J.; Croall, S.C. Cable environment analysis and the probabilistic approach to cable rating. IEEE Trans. Power Deliv. 1990, 5, 1628–1633. [Google Scholar] [CrossRef]
- Zhao, H.C.; Lyall, J.S.; Nourbakhsh, G. Probabilistic cable rating based on cable thermal environment studying. In Proceedings of the PowerCon International Conference on Power System Technology (Cat. No.00EX409), Perth, Australia, 4–7 December 2000; Volume 2, pp. 1071–1076. [Google Scholar]
- Shabani, H.; Vahidi, B. A probabilistic approach for optimal power cable ampacity computation by considering uncertainty of parameters and economic constraints. Int. J. Electr. Power Energy Syst. 2019, 106, 432–443. [Google Scholar] [CrossRef]
- Zarchi, D.A.; Vahidi, B. Hong Point Estimate Method to analyze uncertainty in the underground cables temperature. Int. J. Electr. Power Energy Syst. 2020, 124, 106390. [Google Scholar] [CrossRef]

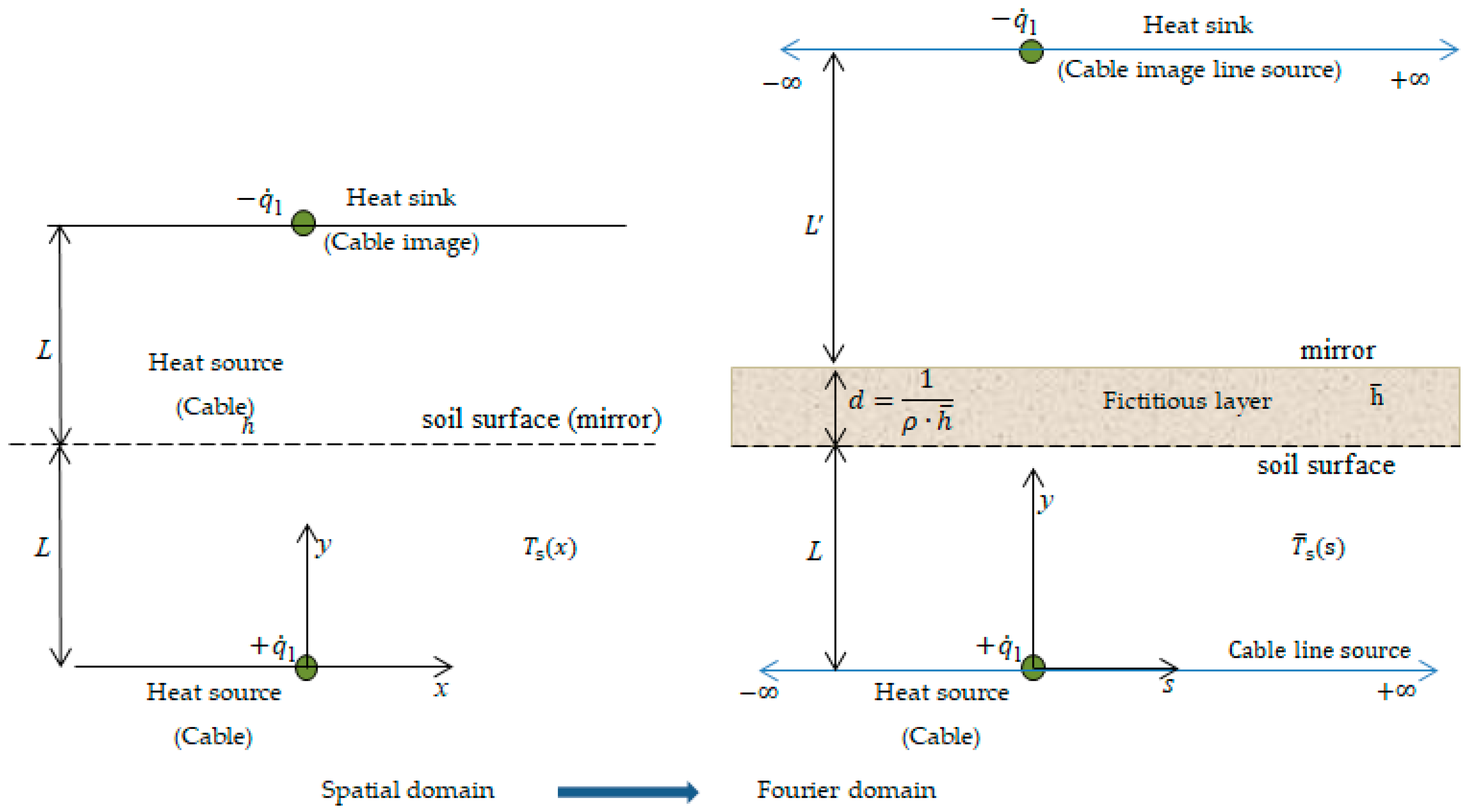
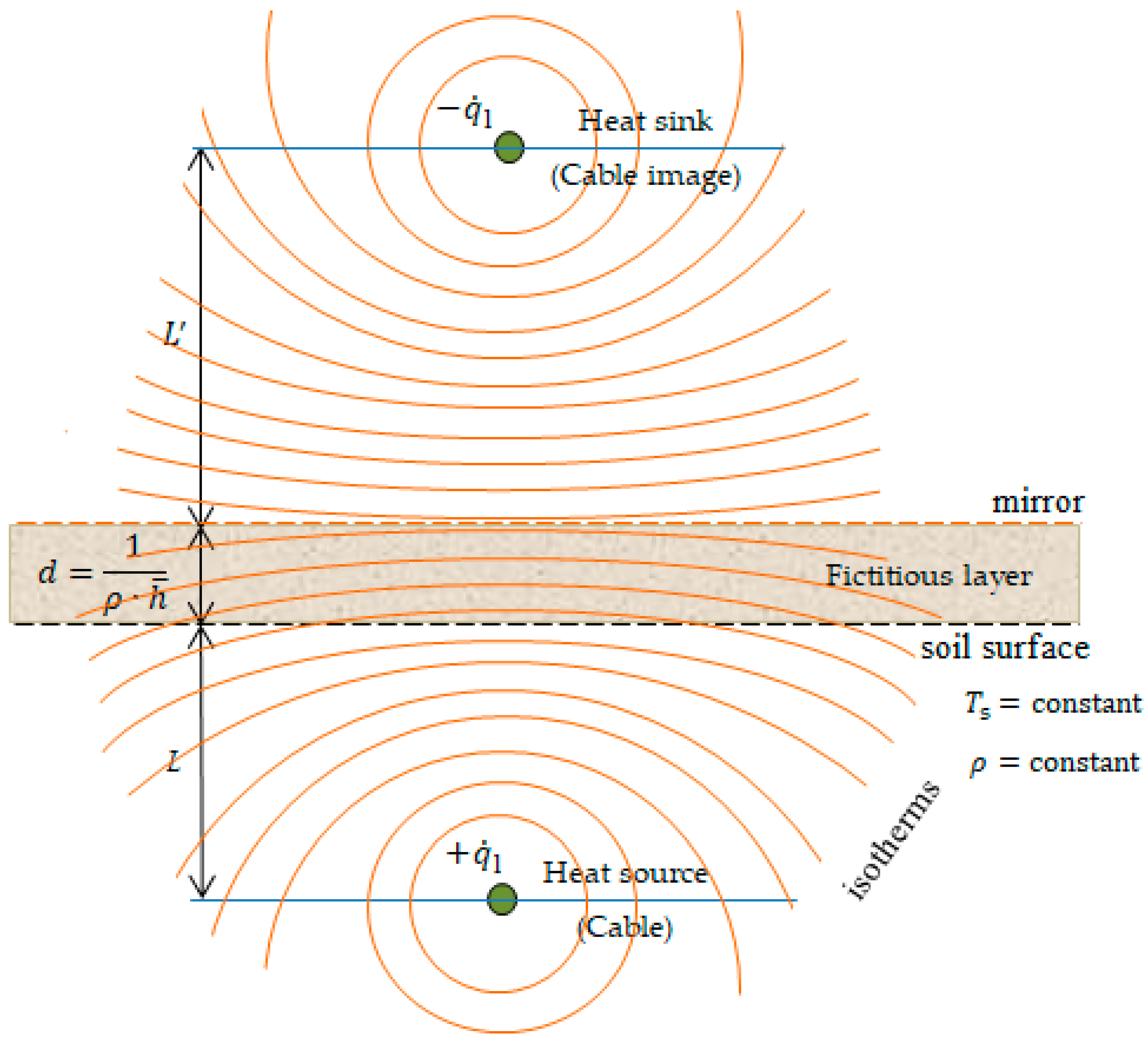
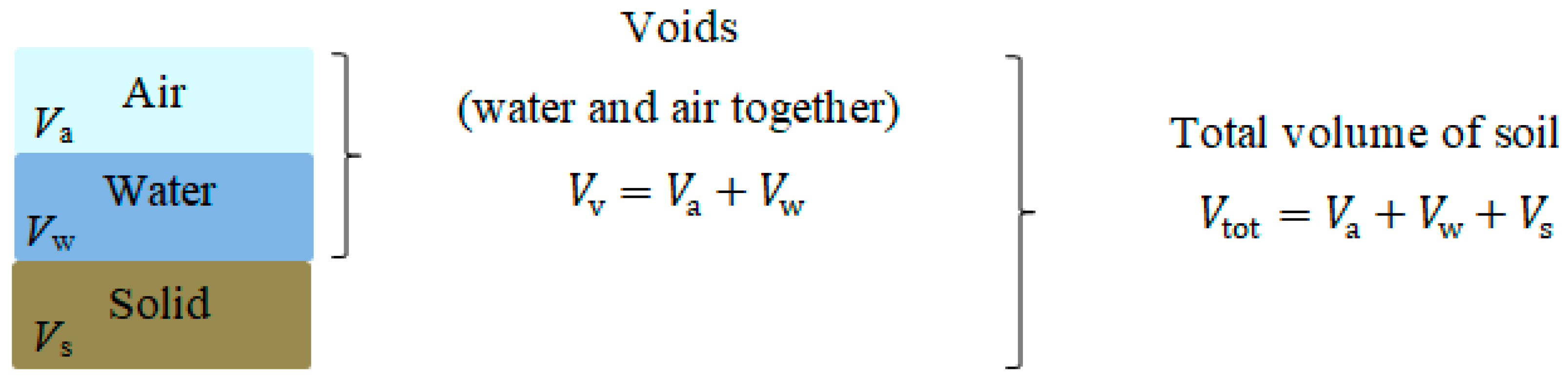
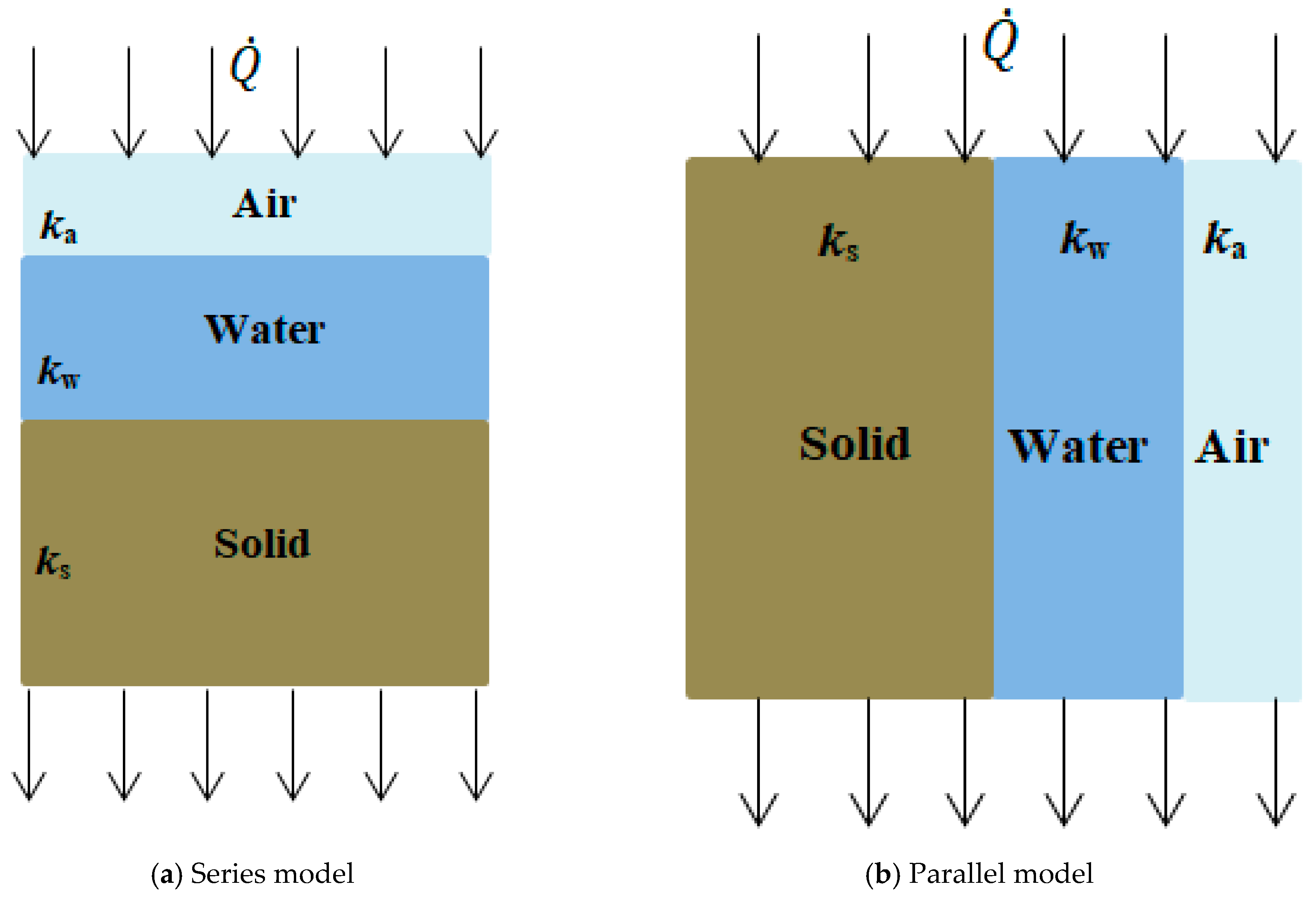
| Electrical Parameters | Symbol and Unit | Thermal Parameters | Symbol and Unit |
|---|---|---|---|
| Electric conductivity | Thermal conductivity | ||
| Electric resistance | Thermal resistance | ||
| Electric current | Heat flow rate | ||
| Capacitance | Thermal capacity | ||
| Electric potential | Absolute temperature | ||
| Ground potential | Absolute zero |
| Material | Thermal Resistivity [(m·K)/W] | Thermal Capacity (c·10−6) [J/(m3·K)] |
|---|---|---|
| Insulating materials | ||
| Paper insulation in solid-type cables | 6.0 | 2.0 |
| Paper insulation in oil-filed cables | 5.0 | 2.0 |
| PE | 3.5 | 2.0 |
| XLPE | 3.5 | 2.0 |
| Polyvinyl chloride for up to and including 3 kV cables | 5.0 | 1.7 |
| Polyvinyl chloride for greater than 3 kV cables | 6.0 | 1.7 |
| EPR for up to and including 3 kV cables | 3.5 | 2.0 |
| EPR for greater than 3 kV cables | 5.0 | 2.0 |
| Protective coverings | ||
| Compounded jute and fibrous materials | 6.0 | 2.0 |
| Rubber sandwich protection | 6.0 | 2.0 |
| Polychlroprene | 5.5 | 2.0 |
| PVC for up to and including 35 kV cables | 5.0 | 1.7 |
| PVC for greater than 35 kV cables | 6.0 | 1.7 |
| PE | 3.5 | 2.4 |
| Materials for duct installations | ||
| Concrete | 1.0 | 2.3 |
| Fiber | 4.8 | 2.0 |
| Asbestos | 2.0 | 2.0 |
| Earthenware | 1.2 | 1.8 |
| PVC | 3.5 | 2.4 |
| PE | 3.5 | 2.4 |
| Method | Computational Burden | Versatility | Geometrical Dimension | Multi-Physics Approach |
|---|---|---|---|---|
| Analytical methods | low | low | 2D/3D | no |
| Finite Difference Method (FDM) | high | medium | 2D/3D | no |
| Finite Element Method (FEM) | high | high | 2D/3D | yes |
| Thermal-electrical analogy | medium | medium | 2D | no |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enescu, D.; Colella, P.; Russo, A. Thermal Assessment of Power Cables and Impacts on Cable Current Rating: An Overview. Energies 2020, 13, 5319. https://doi.org/10.3390/en13205319
Enescu D, Colella P, Russo A. Thermal Assessment of Power Cables and Impacts on Cable Current Rating: An Overview. Energies. 2020; 13(20):5319. https://doi.org/10.3390/en13205319
Chicago/Turabian StyleEnescu, Diana, Pietro Colella, and Angela Russo. 2020. "Thermal Assessment of Power Cables and Impacts on Cable Current Rating: An Overview" Energies 13, no. 20: 5319. https://doi.org/10.3390/en13205319







