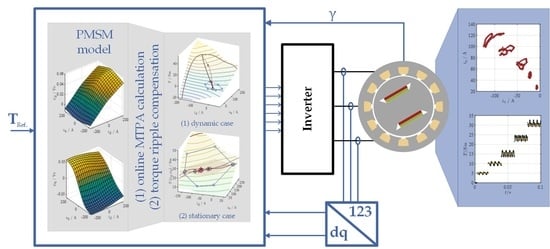
Predictive Trajectory Control with Online MTPA Calculation and Minimization of the Inner Torque Ripple for Permanent-Magnet Synchronous Machines

This paper presents an extended predictive trajectory control scheme combined with an inner torque ripple minimization considering the current-, flux-linkage-, and voltage-planes of permanent magnet synchronous machines. The extension of a fundamental machine model with flux-linkage harmonics allows the calculation of the inner torque ripple and enables its minimization. For this, the control is divided in two cases: (1) The dynamic operation or large signal behavior which uses the maximal torque gradient for the trajectory strategy during each control period for fastest dynamic operation, and (2) The stationary operation or small signal behavior, utilizing a real time capable polynomial approximation of the rotor position dependent torque hyperbolas (iso-torque curves) of permanent magnet synchronous machines for the ideal torque to current reference values. Since dynamic and steady-state operation is covered, torque to current look-up tables, such as maximum torque per ampere (MTPA)/maximum torque per volt/voltage (MTPV) look-up tables, are not required anymore. The introduced, new control approach is implemented in Matlab/Simulink based on finite element analysis and measured data. Furthermore, test-bench implementations based on measurement data are presented to show the real-time capability and precision. View Full-Text