Numerical Investigation of the Effect of Partially Propped Fracture Closure on Gas Production in Fractured Shale Reservoirs
Abstract
:1. Introduction
2. Mathematical Model Descriptions
2.1. Fluid-Governing Equations
2.2. Geomechanics-Governing Equations
2.3. Constitutive Relations
3. Numerical Schemes
3.1. Flow Equations Discretization
3.2. Geomechanics Equations Discretization
3.3. Sequential Implicit Method
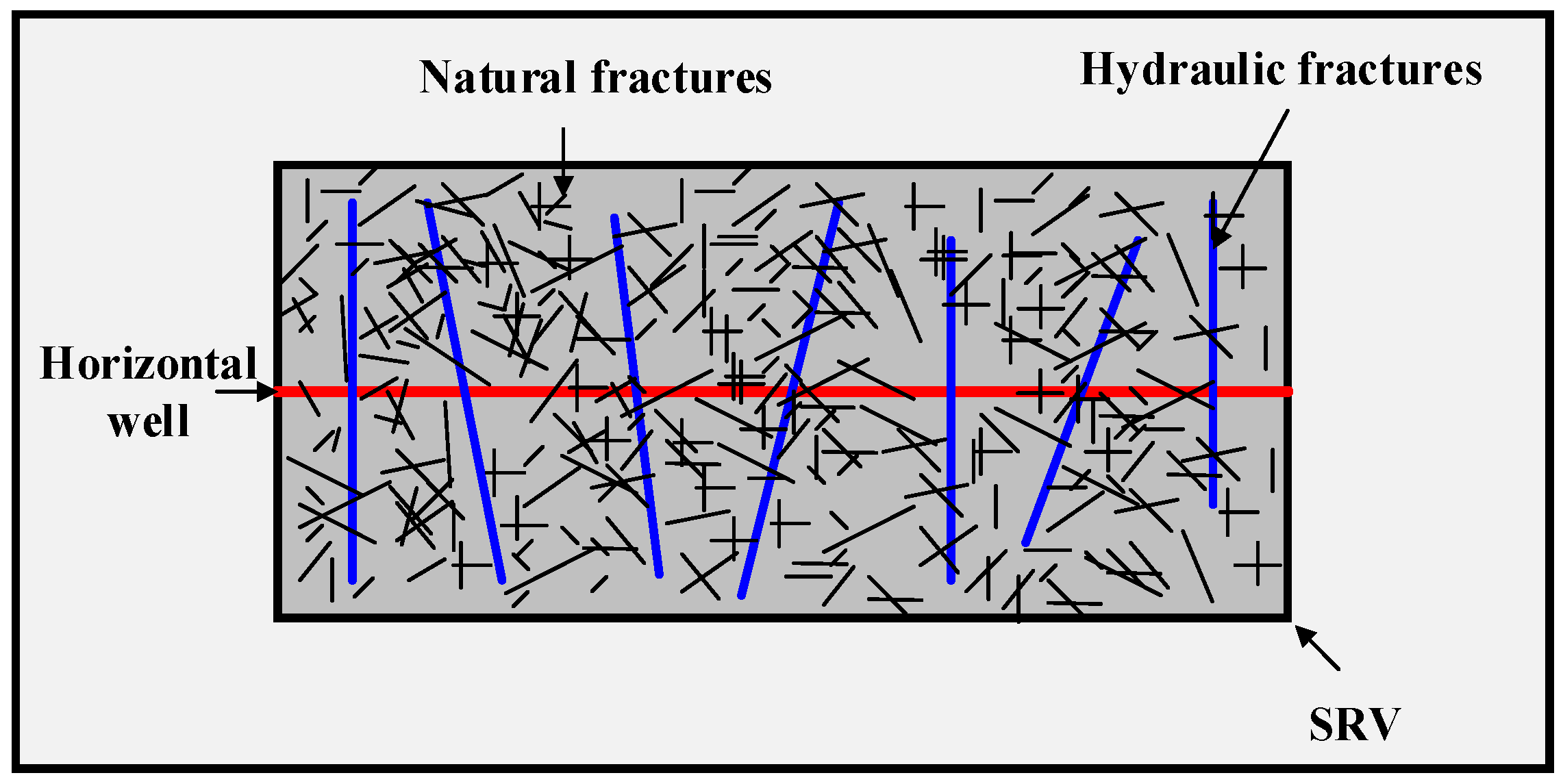
4. Numerical Examples
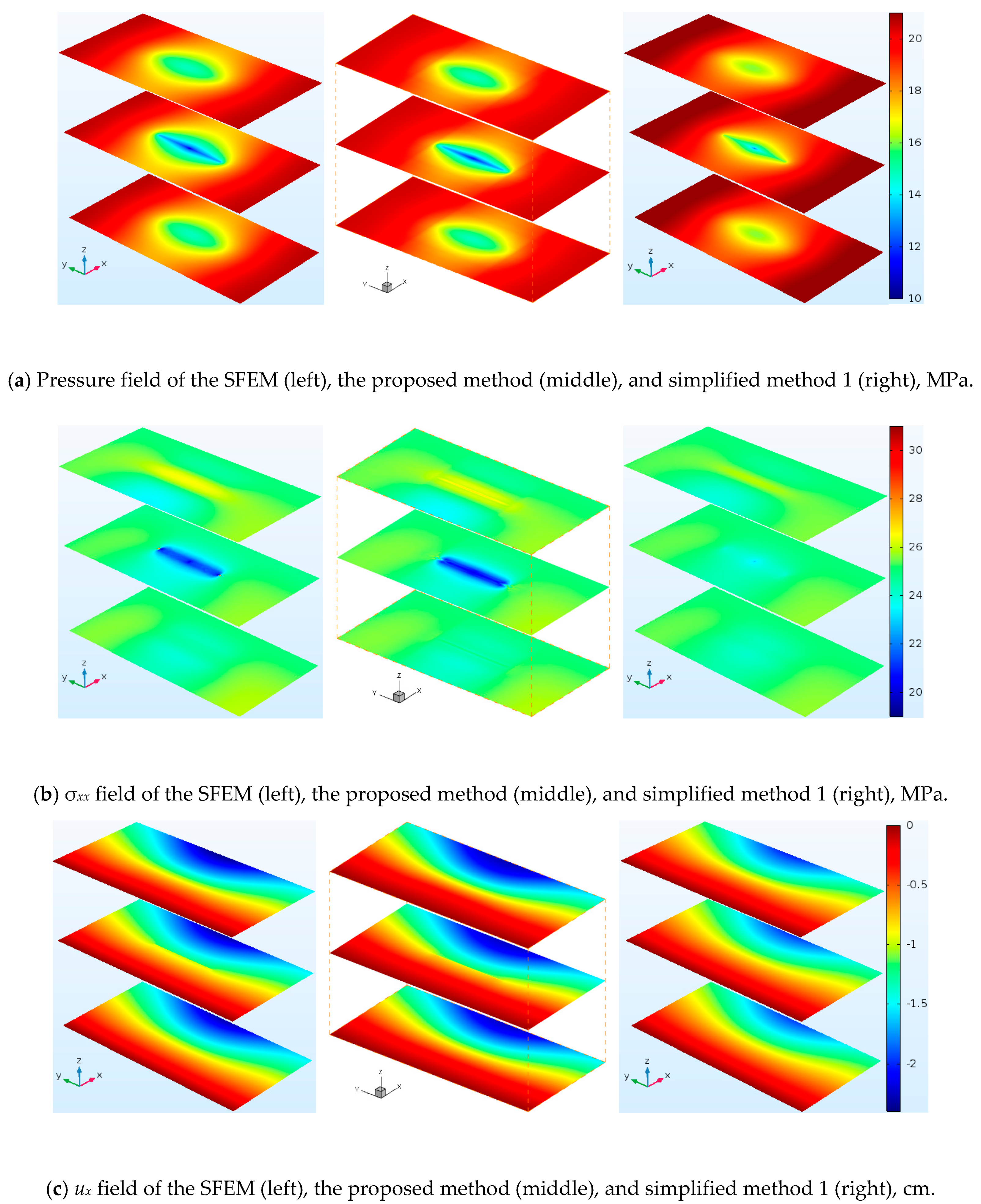
4.1. Model Verifications
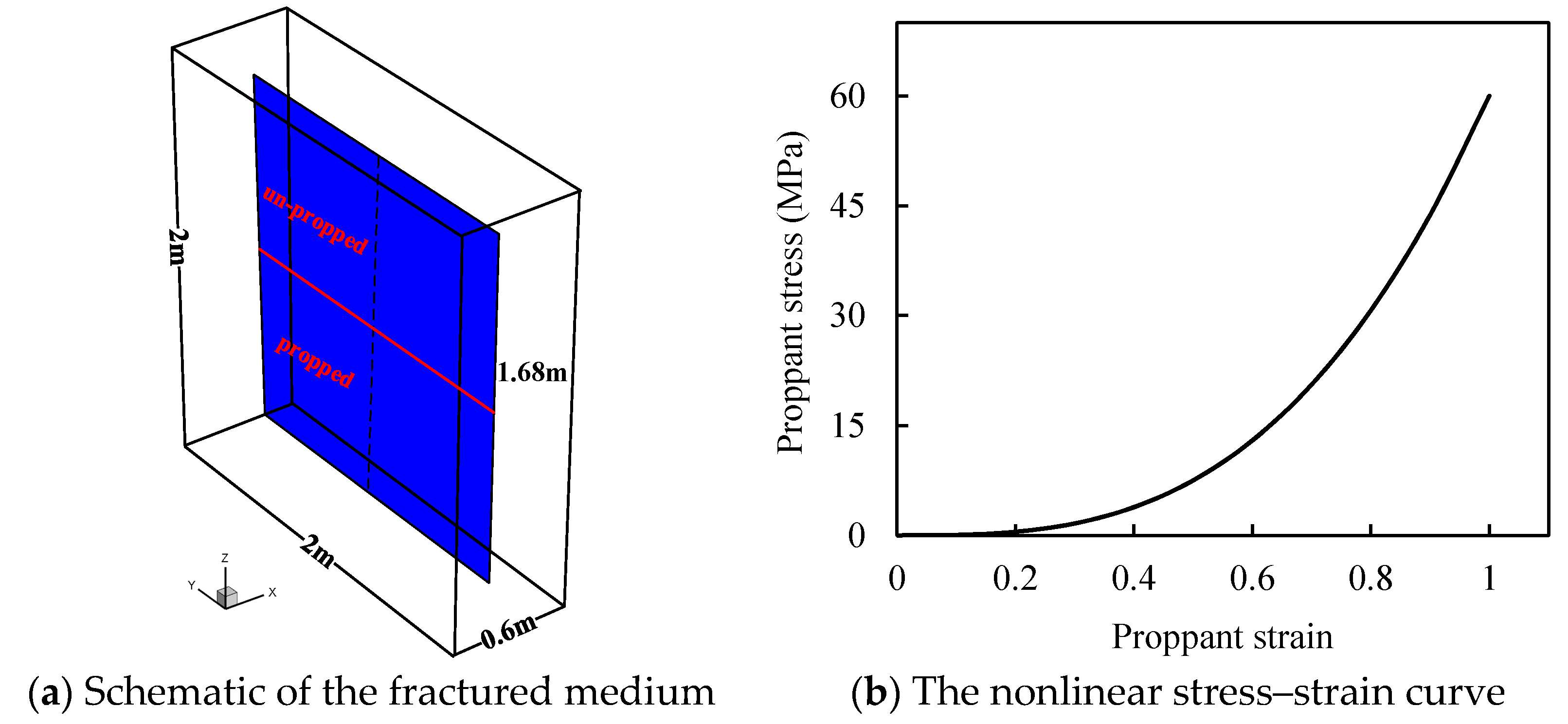
4.1.1. Partially Propped Fracture Deformation Problem
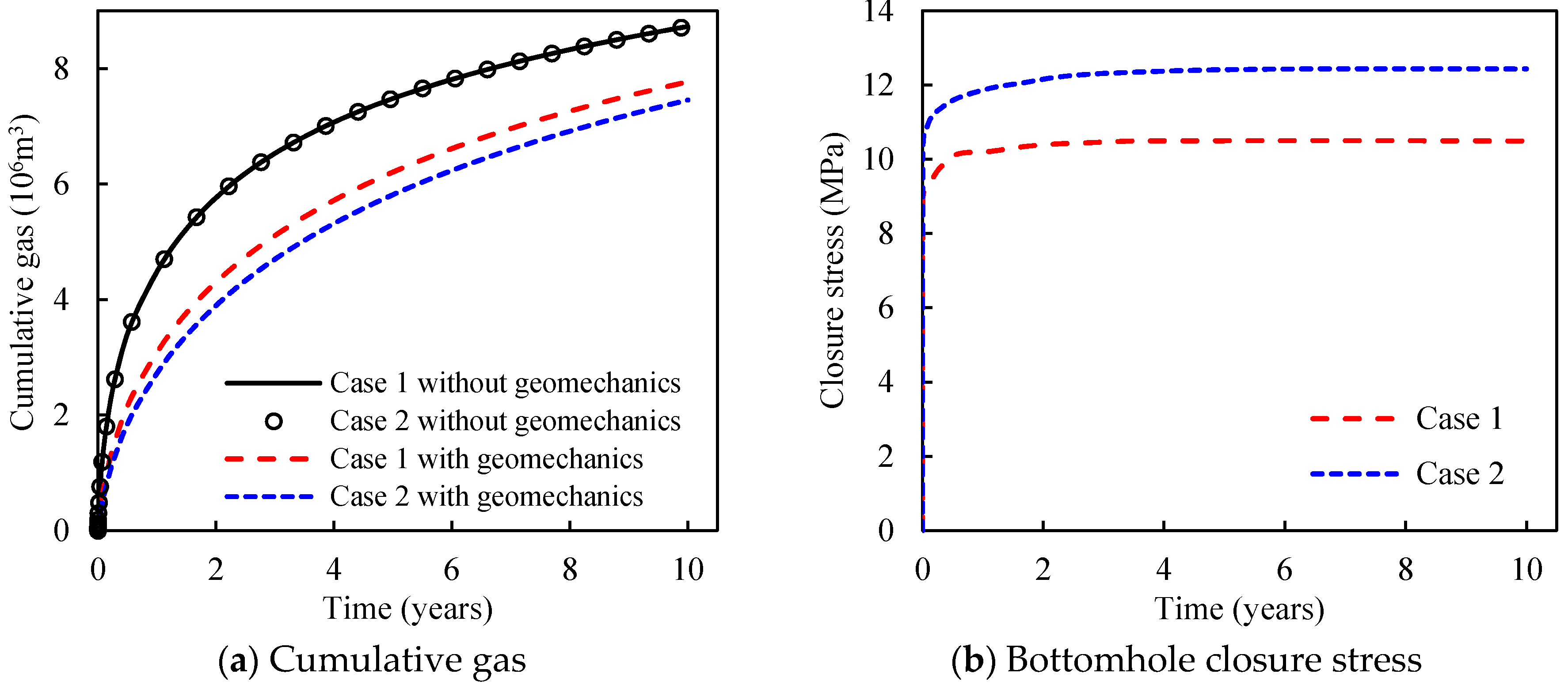
4.1.2. Gas Production and Stress Evolution in a 3D Fractured Shale Reservoir
4.2. Applications and Discussions
4.2.1. Effect of initial Aperture Distribution
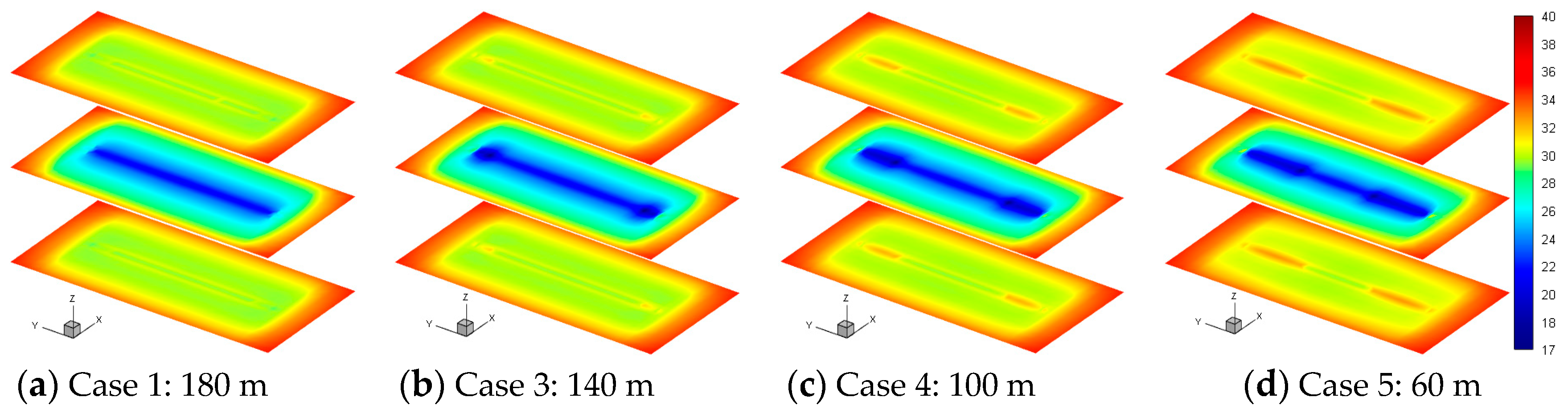
4.2.2. Effect of Propped Fracture Length
4.2.3. Effect of Propped Fracture Height
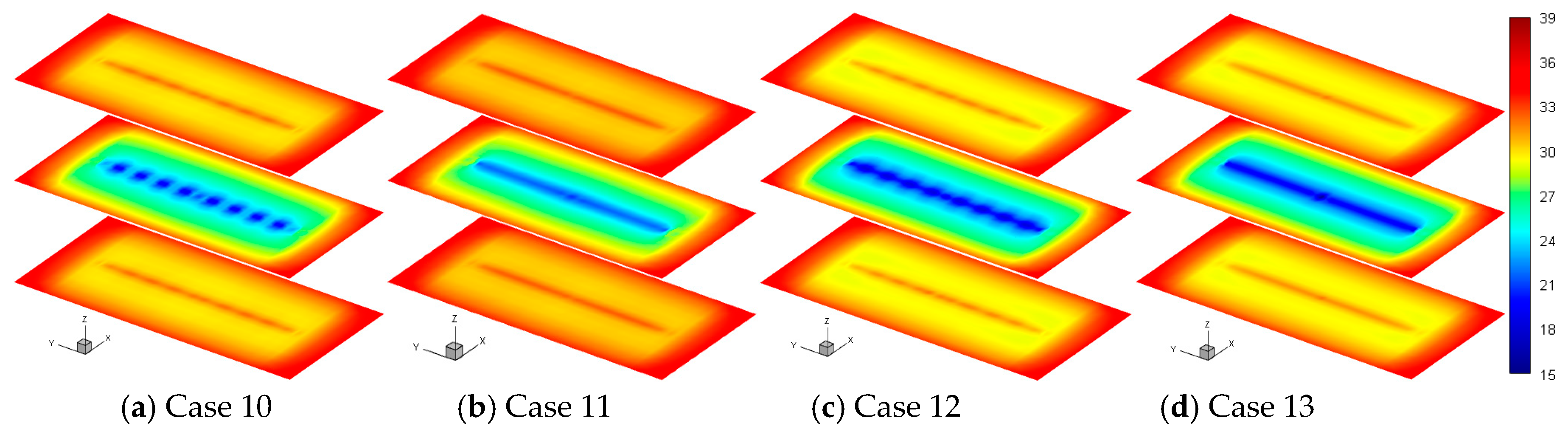
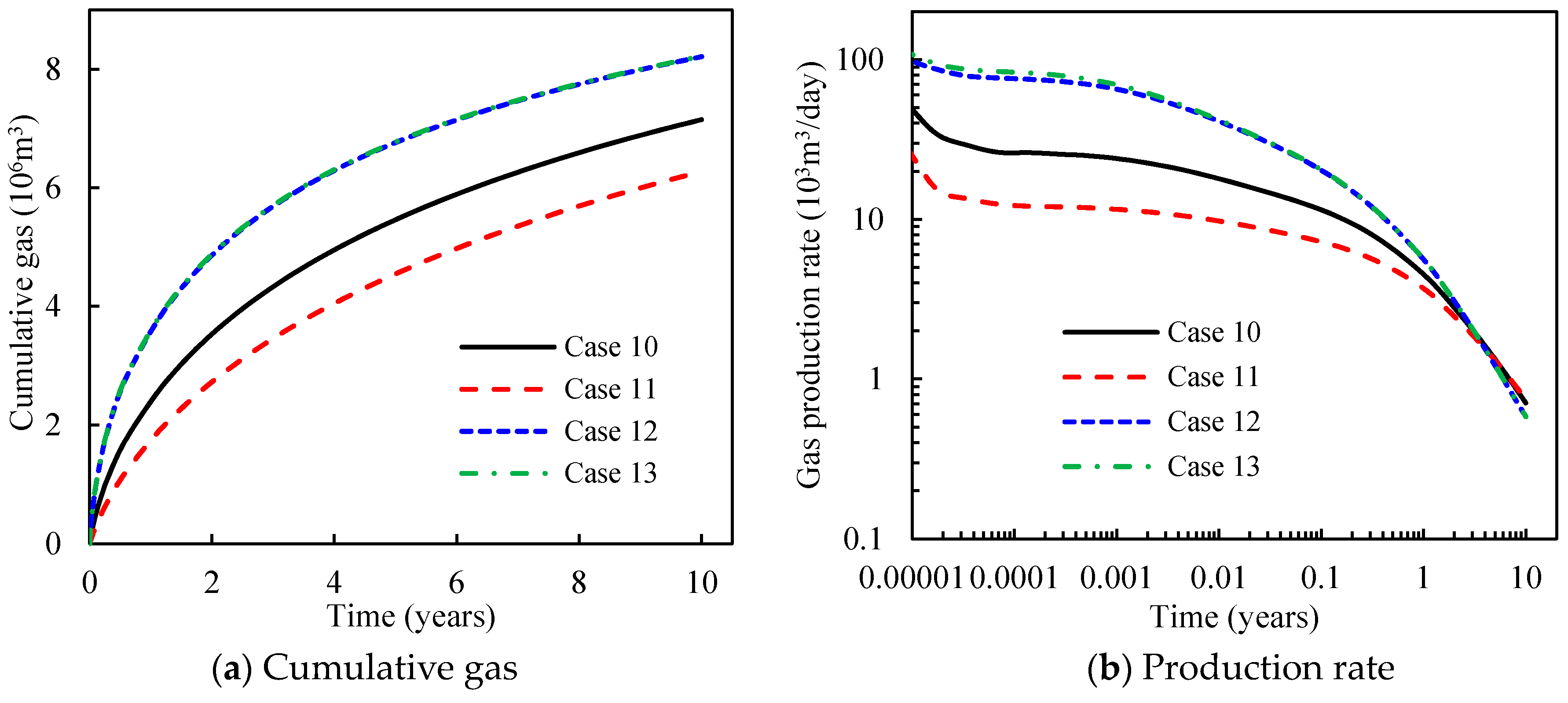
4.2.4. Effect of Proppant Distribution
5. Conclusions
- The displacement discontinuity at hydraulic fractures and the initial aperture distribution of the hydraulic fractures have significant impacts on the evolution of stress near hydraulic fractures, thus a good performance can be predicted more accurately when these effects are considered;
- Gas production is positively correlated with the propped fracture length and height, and the connectivity between the well bore and the high conductivity arch plays an important role in production;
- Proppant distribution can significantly affect well performance. A fracture with alternating propped–unpropped–propped sections is favored because the highly conductive flow channels can be generated. In this fracture, improving the connectivity between flow channels is more important than increasing the number of flow channels.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols and Variables | |
| n | unit normal vector |
| A | mass accumulation term, kg·m−3 |
| F | mass flux term, kg·m−2·s−1 |
| q | source term, kg·m−3·s−1 |
| ϕ | Lagrange porosity |
| ρg | gas density, kg·m−3 |
| m | the adsorption/desorption term of gas, kg·m−3 |
| p | gas pressure, Pa |
| M | gas molar mass, kg·kmol−1 |
| Z | gas compression factor |
| R | universal gas constant, 8.314 kJ·kmol−1·K−1 |
| T | reservoir temperature, K |
| ρr | rock bulk density, kg·m−3 |
| ρgstd | gas density at standard condition, kg·m−3 |
| VL | Langmuir’s volume, m3·kg−1 |
| PL | Langmuir’s pressure, Pa |
| k | absolute permeability, m2 |
| µ | gas viscosity, Pa·s |
| g | gravity acceleration, N·kg−1 |
| D | depth, m |
| b | Klinkenberg factor, Pa |
| c | gas compressibility, Pa−1 |
| Dk | Knudsen diffusion coefficient, 103m2·s−1 |
| v | flow rate, m·s−1 |
| σ | total stress tensor, Pa |
| ρb | bulk density, kg·m−3 |
| C | elasticity tensor of matrix, Pa |
| α | Biot coefficient of matrix |
| I | unit tensor |
| Cup | the upscaled elasticity tensor, Pa |
| Kdr | the upscaled drained bulk modulus, Pa |
| ε | strain tensor |
| u | displacement vector, m |
| pHF | the gas pressure in fracture, Pa |
| ps | the effective stress exerted on fracture faces, Pa |
| fs | the nonlinear stress–strain relationship |
| εs | normal proppant strain |
| dHF | fracture aperture, m |
| En | normal penalty parameter |
| Kf | drained bulk modulus of natural fractures, GPa |
| εv | volumetric strain |
| fk | the relationship between permeability and effective stress |
| V | element volume, m3 |
| Δt | time step, s |
| λ | gas mobility, mPa−1·s−1 |
| Tij | transmissibility between elements i and j, m3 |
| Aij | interface area, m2 |
| τ | stabilization parameter |
| M | bulk modulus, GPa |
| fint | internal force vector |
| fext | external force vector |
| K | stiffness matrix |
| Concepts | |
| EDFM | Embedded Discrete Fracture Model |
| XFEM | Extended Finite Element Method |
| PPP | Polynomial Pressure Projection |
| FVM | Finite Volume Method |
| SRV | Stimulated Reservoir Volume |
| MINC | Multiple-Interacting-Continua method |
| LBB | Ladyzhenskaya–Babuska–Brezzi condition |
| DOF | Degree Of Freedom |
| SFEM | Standard Finite Element Model |
| S-XFEM | Stabilized Extended Finite Element Method |
References
- Zhu, G.; Yao, J.; Sun, H.; Zhang, M.; Xie, M.; Sun, Z.; Lu, T. The numerical simulation of thermal recovery based on hydraulic fracture heating technology in shale gas reservoir. J. Nat. Gas Sci. Eng. 2016, 28, 305–316. [Google Scholar] [CrossRef]
- Sakmar, S.L. The global shale gas initiative: Will the United States be the role model for the development of shale gas around the world. Hous. J. Int’l. L. 2010, 33, 369. [Google Scholar]
- Yan, X.; Huang, Z.; Yao, J.; Li, Y.; Fan, D.; Sun, H.; Zhang, K. An efficient numerical hybrid model for multiphase flow in deformable fractured-shale reservoirs. SPE J. 2018, 23, 411–412,437. [Google Scholar] [CrossRef]
- Giger, F.; Reiss, L.; Jourdan, A. The reservoir engineering aspects of horizontal drilling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 16–19 September 1984; Society of Petroleum Engineers: Houston, TX, USA, 1984. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J.; Shao, J. Numerical study of hydraulic fracture propagation accounting for rock anisotropy. J. Pet. Sci. Eng. 2018, 160, 422–432. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J.; Shao, J. Study of hydraulic fracturing in an anisotropic poroelastic medium via a hybrid EDFM-XFEM approach. Comput. Geotech. 2019, 105, 51–68. [Google Scholar] [CrossRef]
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Mem. Am. Assoc. Pet. Geol. 1972, 18, 153–163. [Google Scholar] [CrossRef]
- Memon, K.R.; Mahesar, A.A.; Ali, M.; Tunio, A.H.; Mohanty, U.S.; Akhondzadeh, H.; Awan, F.U.R.; Iglauer, S.; Keshavarz, A. Influence of Cryogenic Liquid Nitrogen on Petro-Physical Characteristics of Mancos Shale: An Experimental Investigation. Energy Fuels 2020, 34, 2160–2168. [Google Scholar] [CrossRef]
- Mahesar, A.A.; Shar, A.M.; Ali, M.; Tunio, A.H.; Uqailli, M.A.; Mohanty, U.S.; Akhondzadeh, H.; Iglauer, S.; Keshavarz, A. Morphological and petro physical estimation of eocene tight carbonate formation cracking by cryogenic liquid nitrogen; a case study of Lower Indus basin, Pakistan. J. Pet. Sci. Eng. 2020, 192, 107318. [Google Scholar] [CrossRef]
- Akhondzadeh, H.; Keshavarz, A.; Al-Yaseri, A.Z.; Ali, M.; Awan, F.U.R.; Wang, X.; Yang, Y.; Iglauer, S.; Lebedev, M. Pore-scale analysis of coal cleat network evolution through liquid nitrogen treatment: A Micro-Computed Tomography investigation. Int. J. Coal Geol. 2020, 219, 103370. [Google Scholar] [CrossRef]
- Chen, Z.; Lin, M.; Wang, S.; Chen, S.; Cheng, L. Impact of un-propped fracture conductivity on produced gas huff-n-puff performance in Montney liquid rich tight reservoirs. J. Pet. Sci. Eng. 2019, 181, 106234. [Google Scholar] [CrossRef]
- Lee, T.; Park, D.; Shin, C.; Jeong, D.; Choe, J. Efficient production estimation for a hydraulic fractured well considering fracture closure and proppant placement effects. Energy Explor. Exploit. 2016, 34, 643–658. [Google Scholar] [CrossRef]
- Awan, F.U.R.; Keshavarz, A.; Akhondzadeh, H.; Al-Anssari, S.; Al-Yaseri, A.; Nosrati, A.; Ali, M.; Iglauer, S. Stable Dispersion of Coal Fines during Hydraulic Fracturing Flowback in Coal Seam Gas Reservoirs—An Experimental Study. Energy Fuels 2020, 34, 5566–5577. [Google Scholar] [CrossRef]
- Liu, Y.; Leung, J.Y.; Chalaturnyk, R. Geomechanical simulation of partially propped fracture closure and its implication for water flowback and gas production. SPE Reserv. Eval. Eng. 2018, 21, 273–290. [Google Scholar] [CrossRef]
- Zhou, L.; Shen, Z.; Wang, J.; Li, H.; Lu, Y. Numerical investigating the effect of nonuniform proppant distribution and unpropped fractures on well performance in a tight reservoir. J. Pet. Sci. Eng. 2019, 177, 634–649. [Google Scholar] [CrossRef]
- Wang, J.; Elsworth, D. Role of proppant distribution on the evolution of hydraulic fracture conductivity. J. Pet. Sci. Eng. 2018, 166, 249–262. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Yao, J.; Huang, Z. Efficient Coupled Multiphase-Flow and Geomechanics Modeling of Well Performance and Stress Evolution in Shale-Gas Reservoirs Considering Dynamic Fracture Properties. SPE J. 2020, 25. [Google Scholar] [CrossRef]
- Liu, Y.; Leung, J.Y.; Chalaturnyk, R.J.; Virues, C.J.J. New insights on mechanisms controlling fracturing-fluid distribution and their effects on well performance in shale-gas reservoirs. SPE Prod. Oper. 2019, 34, 564–585. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Warpinski, N.R.; Mayerhofer, M.; Lolon, E.P.; Vincent, M. The relationship between fracture complexity, reservoir properties, and fracture-treatment design. SPE Prod. Oper. 2010, 25, 438–452. [Google Scholar] [CrossRef]
- Cipolla, C.; Lolon, E.; Mayerhofer, M. The Effect of Proppant Distribution and Un-propped Fracture Con-ductivity on Well Performance in Unconventional Gas Reservoirs. SPE 2009, 119368. [Google Scholar]
- Sierra, L.; Sahai, R.R.; Mayerhofer, M.J. Quantification of Proppant Distribution Effect on Well Productivity and Recovery Factor of Hydraulically Fractured Unconventional Reservoirs. In Proceedings of the SPE/CSUR Unconventional Resources Conference—Canada, Calgary, AB, Canada, 30 September–2 October 2014; Society of Petroleum Engineers: Houston, TX, USA, 2014. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, T.; Du, S.; Sepehrnoori, K. Numerical study of the effect of uneven proppant distribution between multiple fractures on shale gas well performance. Fuel 2015, 142, 189–198. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Simulation of proppant distribution effect on well performance in shale gas reservoirs. In Proceedings of the SPE Unconventional Resources Conference Canada, Calgary, AB, Canada, 5–7 November 2013; Society of Petroleum Engineers: Houston, TX, USA, 2013. [Google Scholar] [CrossRef]
- Zheng, S.; Kumar, A.; Gala, D.P.; Shrivastava, K.; Sharma, M.M. Simulating Production from Complex Fracture Networks: Impact of Geomechanics and Closure of Propped/Unpropped Fractures. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019; pp. 2322–2338. [Google Scholar]
- Zheng, S.; Manchanda, R.; Sharma, M.M. Modeling Fracture Closure with Proppant Settling and Embedment during Shut-in and Production. SPE Drill. Completion 2020. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R. Development of a Novel and Computationally-Efficient Discrete-Fracture Model to Study IOR Processes in Naturally Fractured Reservoirs. In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 14–18 April 2012; Society of Petroleum Engineers: Houston, TX, USA, 2012. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Li, Y.; Fan, D. An efficient embedded discrete fracture model based on mimetic finite difference method. J. Pet. Sci. Eng. 2016, 145, 11–21. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Li, Y.; Fan, D.; Zhang, K. An efficient hydro-mechanical model for coupled multi-porosity and discrete fracture porous media. Comput. Mech. 2018, 62, 943–962. [Google Scholar] [CrossRef]
- Bochev, P.B.; Dohrmann, C.R.; Gunzburger, M.D. Stabilization of Low-order Mixed Finite Elements for the Stokes Equations. Siam J. Numer. Anal. 2004, 44, 82–101. [Google Scholar] [CrossRef]
- Liu, F.; Borja, R.I. Stabilized low-order finite elements for frictional contact with the extended finite element method. Comput. Methods Appl. Mech. Eng. 2010, 199, 2456–2471. [Google Scholar] [CrossRef]
- White, J.A.; Borja, R.I. Stabilized low-order finite elements for coupled solid-deformation/fluid-diffusion and their application to fault zone transients. Comput. Methods Appl. Mech. Eng. 2008, 197, 4353–4366. [Google Scholar] [CrossRef]
- Kim, J.; Sonnenthal, E.L.; Rutqvist, J. Formulation and sequential numerical algorithms of coupled fluid/heat flow and geomechanics for multiple porosity materials. Int. J. Numer. Methods Eng. 2012, 92, 425–456. [Google Scholar] [CrossRef]
- Kim, J.; Tchelepi, H.A.; Juanes, R. Stability and convergence of sequential methods for coupled flow and geomechanics: Fixed-stress and fixed-strain splits. Comput. Methods Appl. Mech. Eng. 2011, 200, 1591–1606. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: Glasgow, UK, 1995; p. 400. [Google Scholar]
- Zhu, G.; Chen, H.; Yao, J.; Sun, S. Efficient energy-stable schemes for the hydrodynamics coupled phase-field model. Appl. Math. Model. 2019, 70, 82–108. [Google Scholar] [CrossRef]
- Zhu, G.; Kou, J.; Yao, B.; Wu, Y.S.; Yao, J.; Sun, S. Thermodynamically consistent modelling of two-phase flows with moving contact line and soluble surfactants. J. Fluid Mech. 2019, 879, 327–359. [Google Scholar] [CrossRef]
- Zhu, G.; Kou, J.; Yao, J.; Li, A.; Sun, S. A phase-field moving contact line model with soluble surfactants. J. Comput. Phys. 2020, 405, 109170. [Google Scholar] [CrossRef]
- Wu, Y.-S.; Li, J.; Ding, D.; Wang, C.; Di, Y. A generalized framework model for the simulation of gas production in unconventional gas reservoirs. SPE J. 2014, 19, 845–857. [Google Scholar] [CrossRef]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. J. Frankl. Inst. 1917, 183, 102–105. [Google Scholar] [CrossRef]
- Song, W.; Yao, J.; Li, Y.; Sun, H.; Zhang, L.; Yang, Y.; Zhao, J.; Sui, H. Apparent gas permeability in an organic-rich shale reservoir. Fuel 2016, 181, 973–984. [Google Scholar] [CrossRef]
- Freeman, C.; Moridis, G.; Blasingame, T. A numerical study of microscale flow behavior in tight gas and shale gas reservoir systems. Transp. Porous Media 2011, 90, 253. [Google Scholar] [CrossRef]
- Zhang, Q. Hydromechanical modeling of solid deformation and fluid flow in the transversely isotropic fissured rocks. Comput. Geotech. 2020, 128, 103812. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Andrade, J. Numerical modeling of hydraulic fracture propagation, closure and reopening using XFEM with application to in-situ stress estimation. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 2033–2060. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Elsworth, D.; Qu, H.; Chen, D. Interactions of multiple processes during CBM extraction: A critical review. Int. J. Coal Geol. 2011, 87, 175–189. [Google Scholar] [CrossRef]
- Zhang, L.; Jing, W.; Yang, Y.; Yang, H.; Guo, Y.; Sun, H.; Zhao, J.; Yao, J. The investigation of permeability calculation using digital core simulation technology. Energies 2019, 12, 3273. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, Q.; Sun, W.; Wang, Z.; Zhu, X. Numerical Simulation on Non-Darcy Flow in a Single Rock Fracture Domain Inverted by Digital Images. Geofluids 2020, 2020. [Google Scholar] [CrossRef]
- Roostaei, M.; Nouri, A.; Fattahpour, V.; Chan, D. Coupled Hydraulic Fracture and Proppant Transport Simulation. Energies 2020, 13, 2822. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Wu, Y.; Haque, A.; Connell, L. Experimental study of permeability and its anisotropy for shale fracture supported with proppant. J. Nat. Gas Sci. Eng. 2017, 44, 250–264. [Google Scholar] [CrossRef]
- Kim, J.; Seo, Y.; Wang, J.; Lee, Y. History Matching and Forecast of Shale Gas Production Considering Hydraulic Fracture Closure. Energies 2019, 12, 1634. [Google Scholar] [CrossRef]
- Ghanizadeh, A.; Clarkson, C.; Deglint, H.; Vahedian, A.; Aquino, S.; Wood, J. Unpropped/propped fracture permeability and proppant embedment evaluation: A rigorous core-analysis/imaging methodology. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016; Society of Exploration Geophysicists, American Association of Petroleum: Tulsa, OK, USA, 2016; pp. 1824–1852. [Google Scholar] [CrossRef]
- Li, X.; Feng, Z.; Han, G.; Elsworth, D.; Marone, C.; Saffer, D.; Cheon, D. Permeability evolution of propped artificial fractures in Green River shale. Rock Mech. Rock Eng. 2017, 50, 1473–1485. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Feng, X.; Connell, L. Laboratory study of proppant on shale fracture permeability and compressibility. Fuel 2018, 222, 83–97. [Google Scholar] [CrossRef]
- Khoei, A.R. Extended Finite Element Method: Theory and Applications; John Wiley & Sons Inc.: West Sussex, UK, 2015; pp. 1–565. [Google Scholar]
- Multiphysics, C. Introduction to COMSOL Multiphysics; COMSOL Multiphysics: Burlington, MA, USA, 1998; Volume 9, p. 2018. [Google Scholar]
- Yan, X.; Huang, Z.; Yao, J.; Song, W.; Li, Y.; Gong, L. Theoretical analysis of fracture conductivity created by the channel fracturing technique. J. Nat. Gas Sci. Eng. 2016, 31, 320–330. [Google Scholar] [CrossRef]
- Medvedev, A.V.; Kraemer, C.C.; Pena, A.A.; Panga, M.K.R. On the mechanisms of channel fracturing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2013; Society of Petroleum Engineers: Houston, TX, USA, 2013. [Google Scholar] [CrossRef]



















| Name | Value |
|---|---|
| Initial absolute permeability of matrix, m2 | 2 × 10−20 |
| Initial absolute permeability of natural fracture, m2 | 1 × 10−17 |
| Initial absolute permeability of hydraulic fracture, m2 | 1 × 10−17 |
| Natural fracture spacing, m | 1.0 |
| Initial aperture of natural fracture and hydraulic fracture, m | 5 × 10−6, 0.01 |
| Initial porosity of matrix, natural fracture and hydraulic fracture | 0.05, 1.0, 0.5 |
| Young’s modulus of matrix, natural fracture and proppant, GPa | 40.0, 40.0, 0.04 |
| Poisson’s ratios of matrix and natural fracture | 0.2, 0.2 |
| Biot coefficient of matrix and natural fracture | 1.0, 1.0 |
| Langmuir pressure, MPa | 4.0 |
| Langmuir volume, m3/kg | 0.018 |
| Initial pressure and bottomhole pressure, MPa | 25.0, 10.0 |
| Reservoir temperature, K | 343.15 |
| Rock density, kg/m3 | 2850 |
| Well radius, m | 0.1 |
| Name | Value |
|---|---|
| Initial absolute permeability of matrix, m2 | 2 × 10−20 |
| Initial absolute permeability of natural fracture, m2 | 1 × 10−17 |
| Initial absolute permeability of hydraulic fracture, m2 | 1 × 10−11 |
| Natural fracture spacing and initial aperture of natural fracture, m | 1.0, 5 × 10−6 |
| Initial porosity of matrix, natural fracture and hydraulic fracture | 0.05, 1.0, 0.5 |
| Volume fraction of matrix sub-gridblocks | 0.15, 0.21, 0.38, 0.26 |
| Young’s modulus of matrix and natural fracture, GPa | 40.0, 0.05 |
| Poisson’s ratios of matrix and natural fracture | 0.2, 0.2 |
| Intrinsic solid grain bulk modulus, GPa | 400.0 |
| Langmuir pressure, MPa | 4.0 |
| Langmuir volume, m3/kg | 0.018 |
| Initial pressure and bottomhole pressure, MPa | 25.0, 10.0 |
| Reservoir temperature, K | 343.15 |
| Rock density, kg/m3 | 2850 |
| Well radius, m | 0.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Huang, Z.; Zhang, Q.; Fan, D.; Yao, J. Numerical Investigation of the Effect of Partially Propped Fracture Closure on Gas Production in Fractured Shale Reservoirs. Energies 2020, 13, 5339. https://doi.org/10.3390/en13205339
Yan X, Huang Z, Zhang Q, Fan D, Yao J. Numerical Investigation of the Effect of Partially Propped Fracture Closure on Gas Production in Fractured Shale Reservoirs. Energies. 2020; 13(20):5339. https://doi.org/10.3390/en13205339
Chicago/Turabian StyleYan, Xia, Zhaoqin Huang, Qi Zhang, Dongyan Fan, and Jun Yao. 2020. "Numerical Investigation of the Effect of Partially Propped Fracture Closure on Gas Production in Fractured Shale Reservoirs" Energies 13, no. 20: 5339. https://doi.org/10.3390/en13205339





