Abstract
Renewable energy sources are environmentally friendly and cost-efficient. However, the problem with these renewable resources is their heavy reliance on weather conditions. Thus, at times, these solutions are not guaranteed to meet the required demand all the time. For this, hybrid microgrids are introduced, which have a combination of both renewable energy sources and non-renewable energy resources. In this paper, a cost-efficient optimization algorithm is proposed that minimizes the use of non-renewable energy sources. It maximizes the use of renewable energy resources by meeting the demand for utility grids. Real data based on the load and demand of the utility grids in Italy is used, and a system that determines the optimal sizing of the microgrid and a daily plan is introduced to optimize the renewable resources operations. As part of the proposal, the objective function for the operation and planning of the microgrid in such a way to minimize cost is formulated. Moreover, a variant of the PSO algorithm named recurrent PSO is implemented. The recurrent PSO algorithm solves the proposed optimization objective function by minimizing the cost for the installation and working of the microgrid. Afterwards, the energy management system algorithm lays out a plan for the daily operation of the microgrid. The performance of the system is evaluated using different state-of-the-art optimization methods. The proposed work can help minimize the use of diesel generators, which not only saves financial resources but also contributes toward a green environment.
1. Introduction
This universe has been blessed with a variety of resources that generate enough power to meet the ever-growing demand for electricity. However, the generated power is sometimes of not required quality due to its stochastic nature [,]. Therefore, a single source of power is not reliable, and a shift from using a single fuel-based generation to non-single renewable energy-based sources is made. Thus, a combination of alternative sources and conventional energy sources is recommended to meet the required demand of the electricity in utility grids. Alternative sources of energy such as hydro, geothermal, biomass, wind, solar, hydrogen, and fossil fuels need to be made to work together in different combinations to meet a common demand area. This setup is often referred to as a hybrid renewable energy source (HRES) [,,].
The term HRES [,] refers to a setup that has different diesel generators operating toward meeting the required load. The demand can be fulfilled with the combination of conventional sources such as diesel generators and renewable energy sources such as photovoltaics (PV) and wind turbines (WT). Although renewable energy resources provide an environment-friendly alternative, however, the power that results from solar PV and WT is reliant on weather variations, and one cannot guarantee the required demand of the residential grids 100% of the time. To overcome this, storage batteries and backup units such as diesel generators are used to fulfill the required load that has not been achieved by renewable energy resources due to unfavourable weather conditions. Consequently, there must be the optimal placing of the components to meet the required load 100% of the time with the maximum use of renewable energy resources as opposed to non-renewable energy resources, which are not environmentally friendly and at the same time are very costly as well. There are a variety of hurdles that are outlined in different studies regarding the optimal sizing and operation of microgrids. The optimal sizing is crucial as it directly caters to the incumbent casts. In addition, it can lead to the resource over-utilization in case of estimating it wrong in the lower end and under-utilization otherwise []. However, most of these solutions proposed have a single objective in mind. For instance, an optimal sizing algorithm suggests the static cost for the setup of a microgrid but does not focus on the operating part of the microgrid. Therefore, a solution is needed to not only optimize the initial installation of the microgrid but also provide a plan for the daily operations by minimizing the use of non-renewable energy sources.
In this paper, a novel energy management system algorithm is proposed that optimally operates the microgrid. As part of the system, a new objective function is formulated that not only maximizes the use of renewable energy and minimizes the use of backup generators but also proposes an optimal energy management plan for the optimal operation of the microgrid. The study makes use of the data provided based on Italy []. The data have a daily demand load, solar radiation data, and wind speed as input features. A variant of particle swarm optimization (PSO) named as recursive particle swarm optimization (rPSO) is implemented to solve the objective function. The performance of the rPSO is evaluated with popular algorithms such as genetic algorithm, BAT, and A Mathematical Programming Language (AMPL) solvers. The rPSO leads to the cost value, which is the least among its counterparts.
The rest of the paper is structured as follows. In Section 2, we present the literature review and highlight the relevant contributions pertaining to hybrid microgrids. Section 3 covers the methodology of the system and also describes the input dataset. Section 4 illustrates the problem formulation and energy management system (EMS) algorithm in detail. Section 5 exhibits the design of the proposed system, and Section 6 outlines different interfaces of the system and the results of optimization using various algorithms. Section 7 evaluates the rPSO solver with other state-of-the-art solutions, and Section 8, finally, concludes the paper and highlights future directions of this work.
2. Related Work
In the recent past, a variety of efforts have been made to model a microgrid that meets the load demand within the available resources [,]. In modeling microgrids, different design aspects are considered. Some authors focus on the optimal battery performance [,], and some of them are more inclined toward the controlling mechanism [,,], whereas some of the recent studies also cover the energy management aspect [,]. Dursun et al. [] presented three approaches for the power management system which is comprised of wind, Proton Exchange Membrane Fuel Cell (PEMFC), and PV, where PEMFC provides backup whereas PV and wind serve as the main supply to the power management system. In the first strategy, the designed system confirms the unceasing flow of energy in the hybrid system.
A number of experiments were carried out in Matlab/Simulink to evaluate the performance in terms of battery state of charge, power limit of wind and PV, and the load demand. In the second approach, the author developed an algorithm to evaluate the battery state of charge, i.e., excess power from the power grid. If the fuel cell in the battery is exceeded with extra charge, then the fuel cell disables automatically, which results in the discharge of the battery from the primary source; otherwise, it will remain on charge until a certain defined threshold. Finally, the third approach is used for charging the fuel cell in case excessive power is generated by the main source. These approaches improve the efficiency of the battery performance with an 85% rating in the proposed system.
Wang et al. [] presented an HRES for the operational demand and optimization of renewable energy systems. The HRES comprised of renewable resources such as solar, diesel, wind, and well as storage as backup storage for preliminary optimal operation. Moreover, the HRES system provides real-time optimization integrated with prediction and responsive demand. The main objective of this study is to develop a renewable energy management strategy for demand and generation for a residential building to minimize cost and increase energy generation.
Sharafi et al. [] propose a meta-heuristic technique that measures the ideal proportions of a hybrid renewable system in a residential building. The main purpose of this study is to minimize the net per cost and CO2 emission and maximize the renewable energy ration using a multi-objective function based on particle swarm optimization in a residential building. Moreover, the proposed simulation is based on a meta-heuristic approach used for the optimal sizing of an HERS applied to zero energy buildings. Milan et al. [] proposed an optimization-based linear programming model for the optimal sizing of a zero energy building. The development aims to find the minimum cost of the renewable energy system. The presented method is based on a case study applied to a residential building located in Denmark integrated with technologies including heat pump, PV panels, and a solar collector.
Dagdougui et al. [] developed a dynamic model based on hybrid renewable energy to provide electricity and thermal comfort in residential buildings. The proposed model predictive control approach (MPC) is used to determines the optimal solution for renewable sources including WT, PV panels, biomass heating, storage batteries, solar collectors, and electrical networks. Lee et al. [] presented an approach used to determine optimal renewable energy technology, which is further used in energy supply design for buildings. The approach was defined using an RETScreen tool designed and developed by Natural Resource Canada. The experiment of the designed approach is carried out using two case studies; i.e., the first case is a unified energy system for building and solar water heating. The second case contains an electric chiller, water heating, natural gas boiler, and a heat pump. The system was considered to optimize the total net cost of renewables, co2 emission, initial cost, and net present value.
Prasad et al. [] presented a simulation-based energy system designed and developed using HOMER simulation software. The developed system consists of a standby generator, PV panels, and WT for zero energy building. The main objective of the system is to determine the optimal net cost of the energy system. Jiang et al. [] proposed a testbed approach for testing green building energy systems integrated with renewable energy sources, energy storage, and energy management. The developed architecture provides a simulation model, which is used to compute control strategies for the energy management system. The objective function is used to calculate the net per cost and CO2 emission.
For all the above-mentioned design approaches, a variety of optimization algorithms have been utilized. Some of the notable solutions include probabilistic approaches [,] to solve objective functions. Artificial neural networks (ANN) [], genetic algorithm [,], and particle swarm optimization [,] are also more commonly used in modern studies due to its generic nature toward problem solutions. Some of the sophisticated tools designed specifically for microgrids such as HOMER [,] are also utilized to provide a concrete analysis and solve the common problems in the aforementioned studies. A Mathematical Programming Language (AMPL) environment is also a famous tool to provide different solvers for optimization problems, and different studies preferred to utilize those solvers instead of using the standard optimization algorithms as they claim to have a faster response time [,].
3. Methodology for Hybrid Renewable Energy Resources Optimization in Microgrids
Renewable energy resources are scarce and should be managed with proper planning. In this section, the methodology and overall flow of the proposed work are presented. The data contain wind speed, solar radiation, and load demand. The data are preprocessed to perform operations such as interpolation for handling missing entries and normalization for removing any skewness inside records. Once the data are processed, they are given to the optimizer along with constraints to find the optimal parameters based on the objective function, which will be described in subsequent sections. The optimizer works in two phases; first, it receives the value of wind speed, solar radiation, and demand data, and it gives two intermediate optimal parameters for battery operation. The phase 1 optimal parameters alongside input parameters are given to the next phase optimizer. The second phase optimizer finds the optimal cost for the installation, maintenance, and operation of the microgrid. Finally, the EMS algorithm is run to provide the daily operational plan of the microgrid. Figure 1 illustrates the abstract diagram of the working of the proposed architecture.
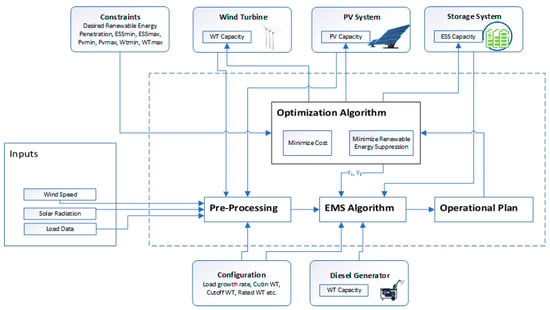
Figure 1.
Proposed methodology of optimal operation planning in microgrids.
The data that constitute the input to the system have records for multiple instances of wind speed, solar radiation, and load demand. The input data are given to the preprocessing unit, which preprocesses the data and aggregates the data of all the instances. The data have many missing entries against the parameters mentioned above. In addition, some of the columns were not in a consistent format. The preprocessor removes all such anomalies, cleans the data, and forwards it to the next block. The next important module is the optimization algorithm. The optimization algorithm takes cleaned data from the preprocessor module. It also takes system constraints and runs the algorithm to find optimal values. When the optimization algorithm finishes all the iterations and achieves the optimal results, the optimal values are given to the EMS algorithm, which gives an operation plan for the working of the microgrid.
4. Problem Formulation of Hybrid Renewable Energy Resource Optimization in Microgrids
In this section, the objective formulation of this work is discussed. The main goal of this work is to minimize the total cost and suppressed renewable energy. Hence, one of the purposes of this work is to design a multi-objective optimization problem that minimizes these two parameters and at the same time meets the load demand of a residential building in Italy. First, we define the objective function and then the EMS algorithm for the operation of the microgrid. The list of symbols and acronyms used in the subsequent section is presented at the end of the paper.
4.1. Objective Function and Constraint Modeling
The objective function formulation is described below. As described earlier, the objective of the proposed work is the optimal sizing and operation, which represents the cost and total energy suppression. Different parameters are worth considering while computing the overall cost of the system []. The total cost in most cases is the cost of microgrid operation and renewable energy suppression.
The total cost can be computed as the total cost of installation, operation, and maintenance.
The installation cost can be computed as follows.
The total operational cost can be computed as below.
The operational cost of the diesel generators can be computed as below.
The renewable energy operational cost can be computed as below.
The operational and management cost can be computed as below.
The constraint is that the renewable energy penetration must within the desired range, as shown below.
4.2. Energy Management and Optimal Operation Algorithm
To optimize the operations of the microgrid, smart energy management strategies should be adopted that consider the cost and the feasibility of the use of energy sources, among others [,]. In this work, the optimal parameters are supplied to the EMS to compute the diesel generation time, which is needed to charge the batteries. The diesel generators are operation dependent on the level of charge (SoC) in batteries. Algorithm 1 demonstrates the step by step operation of the optimal energy operation algorithm. First off, the input data are applied to the EMS algorithm. The input includes six parameters: load, Electronic Storage Systems (ESS) capacity, wind speed, solar radiation, . First, SoC is initialized to 0.5, and the diesel generator output is initialized to 760. Next, for every data item, it computes the ESS output using a load value by negating all other parameters. State of Charge (SoC) is computed by dividing the ESS output by ESS capacity and subtracting it from the existing SoC. A SoC greater than 0.9 implies that it is overcharged. In this case, the Diesel Generator (DG) output is minimum and set as 300, and a single unit increases the suppression count. Similarly, in case the SoC is between 0.8 and 0.9, in this case, the battery is sufficiently charged, and DG stays as a minimum. Alternatively, if the SoC is between y2 and 0.8, the battery is still charged, and DG remains the same. In other cases, for instance, SoC is between y1 and y2; the battery is not charged and needs 1060 kWh of diesel-generated power to charge it to a sufficient level.
An undercharged SoC less than or equal to 0.1 implies that the diesel-generated power must be increased to 2000 to make up for the necessary power. The battery is considered to be empty if the SoC < 0.1. The power generation from the DG is maximum and set as 3500. If the SoC is in an abnormal range, i.e., greater than 1 and less than 0, it is an exception, and the algorithm will return a very high amount of suppression energy, which indicates a failure; otherwise, it will compute the suppression energy and return it.
| Algorithm 1 Balance formulation between renewable and non-renewable sources |
| 1: Input Parameters: |
| 2: |
| 3: Output: |
| 4: Initialize DGoutput0 ←760 |
| 5: SoC 0 ←0.5 |
| 6: for All in Dataset do |
| 7: |
| 8: |
| 9: if SoCi > 0.9 |
| 10: |
| 11: |
| 12: |
| 13: endif |
| 14: if |
| 15: |
| 16: |
| 17: |
| 18: |
| 19: endif |
| 20: if 0.1 |
| 21: |
| 22: endif |
| 23: if |
| 24: |
| 25: endif |
| 26: endfor |
| 27: |
| 28: |
| 29: if |
| 30: |
| 31: else |
| 32: |
5. Design of Hybrid Renewable Energy Resource Optimization in Microgrids
In this section, a detailed system modeling of the proposed architecture is discussed. The following subsections cover the design of the architecture based on different UML diagrams.
5.1. Design Based on State Modeling
A state diagram represents the working state of the system and the different state transitions during the life cycle of program execution. When the system is started, it connects to the main interface. From the main interface, the state can be changed to the configuration form. From the configuration form, the user can go to either load data, in case the load data button is clicked, or an error state if other buttons are clicked. The error state always leads to the main interface. From the load data state, two operations can be performed: load data loading and weather data loading. The state can also be changed to the optimization interface, but that will lead to the error state. From the optimization interface, three states can be triggered, including RunPSO and RunGA. In PSO, a subPSO state is triggered, the results are stored, and the process ends. In GA, the subPSO state is not triggered, and only the result is stored, as shown in Figure 2.
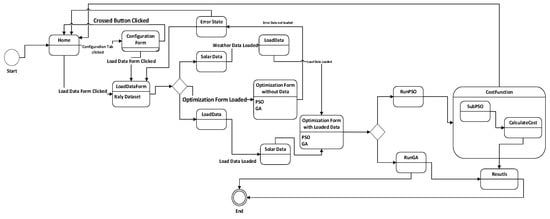
Figure 2.
State diagram of proposed system.
5.2. Design Based on Class Modeling
The class diagram of the architecture is shown in Figure 3. There are different classes, each of which is responsible for a certain functionality. There are global classes such as GlobalData, which is a bucket storing all the data and methods that can be commonly consumed by other classes. There are three optimizer classes. The rPSO algorithm has two classes, PSO and SubPSO, which overall implement the algorithm. Both PSO and SubPSO generate a particle class that represents the particle and its movement to find the solution. In either case, the results are stored in the respective result class and saved using the ResultsForm class.
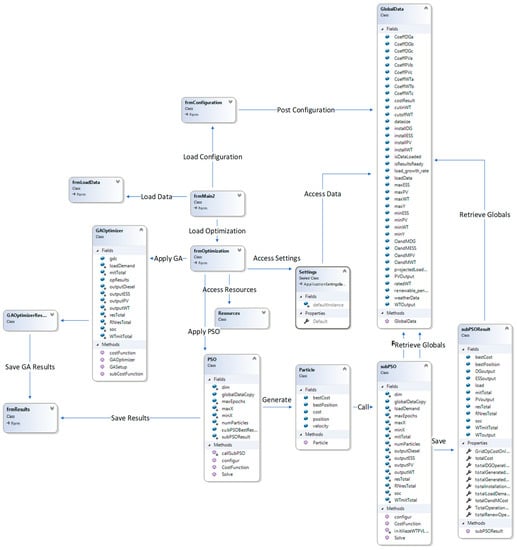
Figure 3.
Class diagram of proposed architecture.
Moreover, there are other classes such as the GAOptimizer class, which is the wrapper class for genetic algorithm implementation. The result of GAOptimizer is represented in the GAOptimizerResult class.
5.3. Design Based on Sequence Modeling
In this section, the interaction model of different components of the system is illustrated. The sequence of operations is shown in Figure 4. First off, all modules are initialized. The configuration manager loads the configuration data and receives constraints from the constraints manager. The configuration, along with constraints, is provided to the input loader. The input loader loads the data and supplies it to the pre-processor where the data are normalized, and anomalies are fixed using the interpolation. The data are supplied along with the configuration data and constraints to the optimizer. The PSO provides the particle information and the velocity to the optimizer, and the optimizer optimizes it with a PSO configuration and supplied data and constraints. The results are provided to the configuration manager and the operational plan. The operational plan devises a plan based on the EMS algorithm and gives the operational plan to the results visualizer. The visualizer visualizes the results with a graph and visual effects, which helps monitor the system.
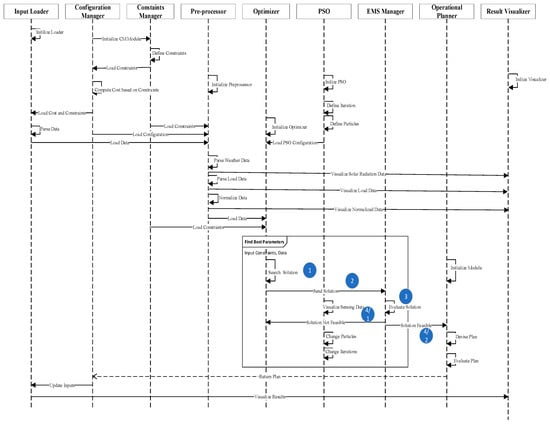
Figure 4.
Sequence of interaction in the proposed system.
6. Execution Model of Proposed System
In this section, the execution of the system is described in detail. The proposed architecture is developed in .NET framework. The core programming language is C#. Different libraries are used to provide support for rPSO, GA, and other state-of-the-art optimization algorithms. Windows forms are used for interfacing with the system, and different forms are created to take users’ data. We deploy the package on a Windows 10 operating system. Data persist in files. There is not much use of data manipulation and relations, so the use of the database is not preferred. The overview of technologies used while implementing this work is presented in Table 1.

Table 1.
Implementation stack.
The main interface that shows all the initial data in the form is shown in Figure 5. The prepopulated values are necessarily the reflection of the business requirements of the microgrid. These initial configurations can be changed if the requirements change, which makes the system very flexible. This configuration form can also act as a placeholder for optimal values. Thus, when the optimizer runs, the optimal values replace the initial values for the proper working of the microgrid. The value can be saved, and if the initial values are needed again, they can be reloaded using the load configuration click handler.
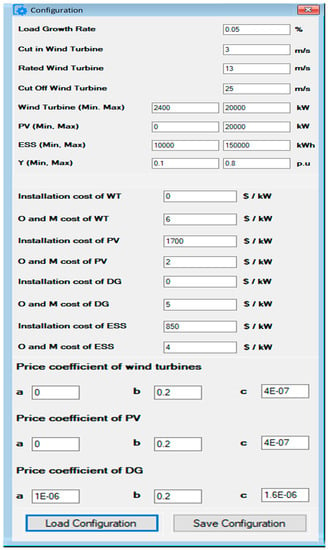
Figure 5.
Overall configuration interface.
The following interface enables users to load input data. There are three paths: load data, optimization, and results, which must be executed in sequence. If they are not executed in sequence, it will throw an exception and will make the system halt with an error, as discussed in Figure 2.
Once the data load button is clicked, the data files for weather data and load demand data are uploaded. The weather data contain data for solar radiation data and wind turbine data. The data are normalized and displayed in the form of line graphs, as shown in Figure 6, which shows graphs for load in kWh, solar radiation in Wm2, and wind speed in m/s. When the data are loaded and normalized, the optimization interface is selected where different options about selected algorithms are entered. In this work, we implemented a variant of PSO named rPSO as a core optimization algorithm. The algorithm takes parameters such as the problem dimension, the number of particles, and the number of iterations. The number of particles is selected based on the output parameters, and the dimension is the variables in the solution space. It can be seen from the interface in Figure 7 that the optimization algorithm runs on the data to produce optimal parameters such as WT, PV, ESS, y0, and y1. It also gives the time in which the optimization is completed.
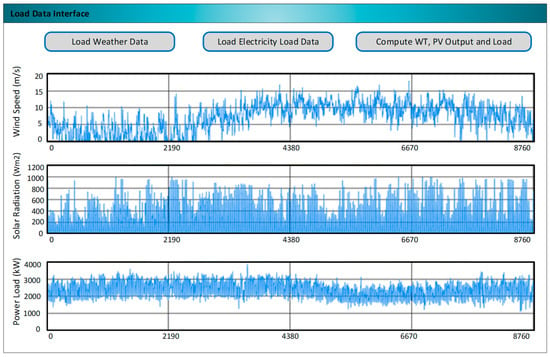
Figure 6.
Data load interface.
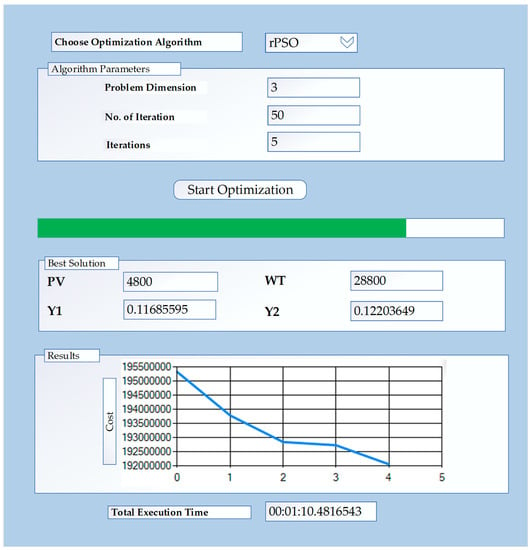
Figure 7.
Interface for optimization using recursive particle swarm optimization (rPSO).
Once the optimization algorithm runs, the EMS algorithm runs to give the operation plan based on optimal values. Figure 8 shows the optimization result interface. The results section has two distinct interfaces: Figure 8a, which is the overall summary of the optimal values, and Figure 8b, which shows the respective graphs for load, PV, and ESS, and the optimal values, which contain the installation cost, total renewable energy generated, total load demand, and other configuration values. This results interface gives an overview of the operational cost and the total installation cost. The primary motivation of the microgrid is to make the most use of renewable energy and less of diesel generators. The low operational cost is a reflection of the high use of renewable energy sources, which is the goal of hybrid microgrids.
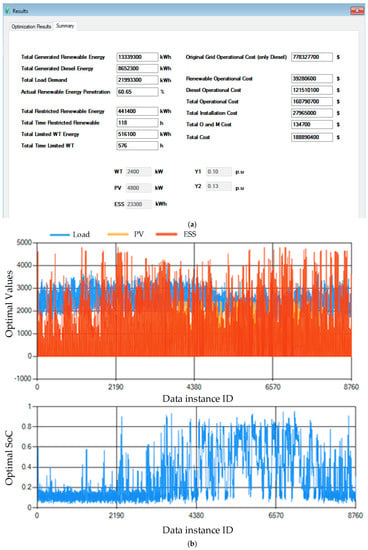
Figure 8.
Results of rPSO optimization. (a) Results summary. (b) Optimal values of design paramters.
The optimization process for each design variable based on rPSO is shown in Figure 9. It iteratively records the optimal values for each rPSO iteration and displays it in graphical form.
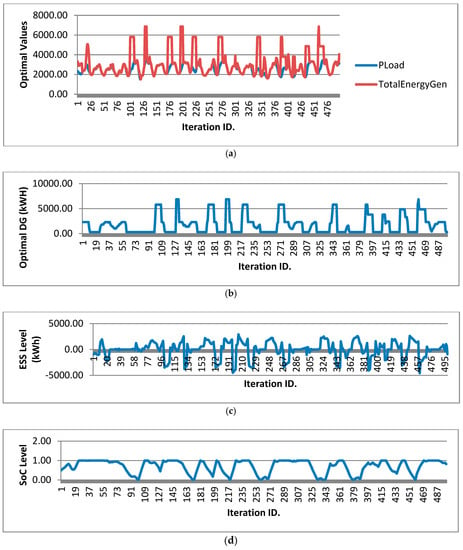
Figure 9.
Adjusted optimized values per iteration in rPSO. (a) Predicted load vs. total energy generation. (b) Optimal DG output. (c) Optimal ESS output. (d) Optimal SoC output.
7. Performance Analysis
The performance of the system is evaluated concerning cost and renewable energy penetration using different well-known algorithms. The proposed variant of PSO is evaluated with the GA, PSO algorithm, and AMPL-based Kestril and Minos solvers, and it investigated different performance metrics.
7.1. Operational Cost
The performance of the system is measured in terms of operational cost and renewable energy penetration. The cost of the system is also measured in terms of different costs such as renewable energy operational cost (CostREOpr), diesel operation cost (CostDGOpr), total load, total generated renewable energy, and total generated diesel expenses, as shown in Figure 10. The cost of the rPSO as shown in Figure 10a is lower than PSO, GA algorithms, and AMPL solvers. The maximum gain of the proposed rPSO is observed for diesel operation, which is very crucial. The low cost indicates that the diesel is operated for a lesser amount of time than its counterparts. Figure 10b shows the execution time response of different algorithms. It is evident from the figure that rPSO is the slowest in terms of execution time.
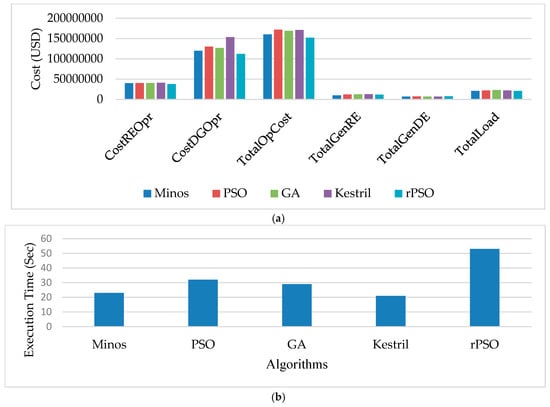
Figure 10.
Performance evaluation of operational cost based on candidate algorithms. (a) Cost analysis. (b) Execution time analysis.
Nonetheless, this execution time, shown in Figure 10b, is taken as the best among different trials based on the changes in the parameters of rPSO, such as the number of iterations and number of populations, to name a few. AMPL-based solvers are the most efficient in terms of execution time, whereas the response time of standard PSO and GA is also not much high. The fact that the deviation in execution time is not so significant while at the same time the gain in cost is significant proves that rPSO can be the preferred approach.
7.2. Renewable Energy Penetration
Renewable energy penetration represents the amount of energy-penetrated electrical grids using renewable energy sources. One of the goals of the hybrid microgrids is to fulfill the load demand of the utility grids from renewable resources, i.e., (renewable energy penetration > load). However, due to weather unpredictability, it is not possible most of the time. An intelligent microgrid is the one in which the chance of meeting load from renewable energy penetration is achieved the maximum amount of time. That being said, the goal of renewable energy penetration optimization is to use strategies to maximize energy from renewables. The objective dictates that if the load demand is low and the diesel-generated energy is low, the result of the nominator, which is energy generated from renewable sources, will be maximum. In other words, for achieving maximum renewable energy penetration, the use of a diesel generator must be minimum, and the energy generated from renewable resources must be maximum considering the projected load as the constant.
To evaluate the performance in terms of renewable energy penetration, two linear solvers, IPOPT and CPLEX, which are considered the best for the linear optimization problem, are also considered for evaluation, as shown in Figure 11. The solver whose performance is best among the others is IPOPT. CPLEX, another linear solver, is the second best, while the general-purpose PSO and GA are among the slowest. Minos also gives a better penetration value (Figure 11a). Execution time-wise, also, IPOPT is marginally leading CPLEX, while the other solvers are on the slightly lower side. Although the proposed rPSO is marginally lower than IPOPT and CPLEX, it still performs better than conventional PSO, GA, and non-linear solvers such as Kestril (Figure 11b). Therefore, rPSO is the right choice for linear and non-linear solvers and thus can be an excellent alternative to conventional PSO and GA.
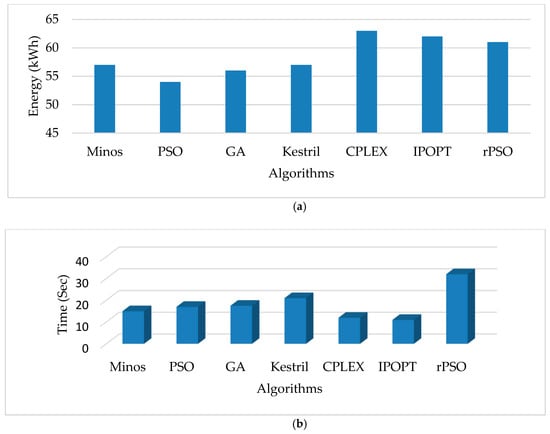
Figure 11.
Performance evaluation of renewable energy penetration of state-of-the-art algorithms. (a) Optimal renewable energy penetration in (kWh) for candidate solvers. (b) Execution time comparison with state-of-the-art algorithms.
8. Conclusions
Hybrid microgrids solve the problem of climate dependency by integrating renewable sources with traditional non-renewable sources. However, the optimal sizing and operation for the non-renewable sources have been a central focus due to environmental hazards and high operational cost. In this paper, we have proposed an objective function that minimizes the cost by maximizing the use of renewable energy resources and optimal sizing. We also proposed an energy management system algorithm to take optimal values of PV, WT, ESS, and we proposed an optimal operational plan in terms of SoC. The data under consideration were acquired from utility grids based on Italy, which include daily load demands, solar radiation, and wind speed data among the notable data. The optimization objective is solved with recursive PSO, which is a variant of the PSO algorithm that has achieved a very minimum cost by meeting the daily load of utility grids. Although other state-of-the-art methods were a bit faster, the cost they achieved was much higher, and hence, it is wise to make a compromise on time, since time is not significant in microgrids. The future direction of this work is to design the microgrid in Simscape (A Simulink library) and, after initial simulations, deploy it in a real environment.
Author Contributions
Conceptualization, S.A. and D.K.; methodology, S.A. and I.U.; software, S.A., I.U. and F.J.; validation, I.U. and D.K.; formal analysis, D.K. and I.U.; investigation, S.A. and F.J.; resources, S.A. and F.J.; data curation, I.U.; writing—original draft preparation, S.A.; writing—review and editing, S.A.; visualization, S.A., I.U. and F.J.; supervision, D.K.; project administration, D.K.; funding acquisition, D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Energy Cloud R&D Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science, ICT (2019M3F2A1073387), and this research was supported by Institute for Information & communications Technology Planning & Evaluation(IITP) grant funded by the Korea government (MSIT) (No.2018-0-01456, AutoMaTa: Autonomous Management framework based on artificial intelligent Technology for adaptive and disposable IoT). Any correspondence related to this paper should be addressed to DoHyeun Kim.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Renewable Energy Suppression | |
| Total cost, which includes all incumbent costs | |
| The initial installation cost | |
| The operational cost | |
| Maintenance cost | |
| Wind turbine capacity | |
| Per unit cost of wind turbine | |
| The total capacity of photovoltaic (solar arrays) | |
| Per unit cost of photovoltaic array | |
| The total cost of storage capacity | |
| Per unit cost of storage | |
| Diesel generator operation cost | |
| Renewable energy operation cost | |
| Total cost of all diesel generators | |
| The output cost of the ith diesel generator | |
| Manufacturing constants for diesel generators | |
| Manufacturing constants for photovoltaic | |
| Manufacturing constants for wind turbines | |
| Per unit operational and management cost of wind turbine | |
| Per unit operational and management cost of photovoltaic | |
| Per unit operational and management cost of diesel generators | |
| Per unit operational and management cost of storage systems | |
| The achieved amount of renewable energy penetration | |
| The desired renewable energy penetration | |
| Range specifier, i.e., if the desired REP is 65%, and α is 3, the REP achieved should be in the range (62%,68%) | |
| The output of first-level PSO which are used as decision variables for EMS algorithm | |
| The state ofharging level of storage systems, i.e., battery | |
| RE | Renewable energy |
| PSO | Particle swarm optimization |
| HRES | Hybrid renewable energy systems |
| PV | Photovoltaic |
| WT | Wind turbine |
| AMPL | A Mathematical Programming Language |
| rPSO | Recursive PSO |
| EMS | Energy management system |
| MPC | Model predictive control |
| ANN | Artificial neural networks |
References
- Eastin, J.; Grundmann, R.; Prakash, A. The two limits debates: Limits to Growth and climate change. Futures 2011, 43, 16–26. [Google Scholar] [CrossRef]
- Al-Saleh, Y. Renewable energy scenarios for major oil-producing nations: The case of Saudi Arabia. Futures 2009, 41, 650–662. [Google Scholar] [CrossRef]
- Bajpai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
- Deshmukh, M.; Deshmukh, S. Modeling of hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2008, 12, 235–249. [Google Scholar] [CrossRef]
- García-Vera, Y.E.; Dufo-López, R.; Bernal-Agustín, J.L. Energy management in microgrids with renewable energy sources: A literature review. Appl. Sci. 2019, 9, 3854. [Google Scholar] [CrossRef]
- Lotfi, H.; Khodaei, A. Hybrid AC/DC microgrid planning. Energy 2017, 118, 37–46. [Google Scholar] [CrossRef]
- Ramli, M.A.; Bouchekara, H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Entsoe Transparency Platform. Available online: https://transparency.entsoe.eu (accessed on 4 October 2020).
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar–wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Hongxing, Y.; Lu, L.; Zhou, W. A novel optimization sizing model for hybrid solar-wind power generation system. Sol. Energy 2007, 81, 76–84. [Google Scholar]
- Tooryan, F.; Collins, E.R.; Ahmadi, A.; Rangarajan, S.S. Distributed generators optimal sizing and placement in a microgrid using PSO. In Proceedings of the IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 614–619. [Google Scholar]
- Rastegarfar, N.; Kashanizadeh, B.; Vakilian, M.; Barband, S. Optimal placement of fast charging station in a typical microgrid in Iran. In Proceedings of the 10th International Conference on the European Energy Market (EEM), Stockholm, Sweden, 27–31 May 2013; pp. 1–7. [Google Scholar]
- Wu, J.; Guan, X. Coordinated multi-microgrids optimal control algorithm for smart distribution management system. IEEE Trans. Smart Grid 2013, 4, 2174–2181. [Google Scholar] [CrossRef]
- Kriett, P.O.; Salani, M. Optimal control of a residential microgrid. Energy 2012, 42, 321–330. [Google Scholar] [CrossRef]
- Minchala-Avila, L.I.; Garza-Castañón, L.E.; Vargas-Martínez, A.; Zhang, Y. A review of optimal control techniques applied to the energy management and control of microgrids. Procedia Comput. Sci. 2015, 52, 780–787. [Google Scholar] [CrossRef]
- Shi, W.; Xie, X.; Chu, C.-C.; Gadh, R. Distributed optimal energy management in microgrids. IEEE Trans. Smart Grid 2014, 6, 1137–1146. [Google Scholar] [CrossRef]
- García-Vera, Y.E.; Dufo-López, R.; Bernal-Agustín, J.L. Optimization of isolated hybrid microgrids with renewable energy based on different battery models and technologies. Energies 2020, 13, 581. [Google Scholar] [CrossRef]
- Dursun, E.; Kilic, O. Comparative evaluation of different power management strategies of a stand-alone PV/Wind/PEMFC hybrid power system. Int. J. Electr. Power Energy Syst. 2012, 34, 81–89. [Google Scholar] [CrossRef]
- Wang, X.; Palazoglu, A.; El-Farra, N.H. Operational optimization and demand response of hybrid renewable energy systems. Appl. Energy 2015, 143, 324–335. [Google Scholar] [CrossRef]
- Sharafi, M.; ElMekkawy, T.Y.; Bibeau, E.L. Optimal design of hybrid renewable energy systems in buildings with low to high renewable energy ratio. Renew. Energy 2015, 83, 1026–1042. [Google Scholar] [CrossRef]
- Milan, C.; Bojesen, C.; Nielsen, M.P. A cost optimization model for 100% renewable residential energy supply systems. Energy 2012, 48, 118–127. [Google Scholar] [CrossRef]
- Dagdougui, H.; Minciardi, R.; Ouammi, A.; Robba, M.; Sacile, R. Modeling and optimization of a hybrid system for the energy supply of a “Green” building. Energy Convers. Manag. 2012, 64, 351–363. [Google Scholar] [CrossRef]
- Lee, K.-H.; Lee, D.-W.; Baek, N.-C.; Kwon, H.-M.; Lee, C.-J. Preliminary determination of optimal size for renewable energy resources in buildings using RETScreen. Energy 2012, 47, 83–96. [Google Scholar] [CrossRef]
- Prasad, G.R.K.D.S.; Vijaya Kumar Reddy, K.; Saibabu, C. Integration of renewable energy sources in Zero energy buildings with economical and environmental aspects by using HOMER. Int. J. Adv. Eng. Sci. Technol. 2011, 9, 212–217. [Google Scholar]
- Jiang, Z.; Rahimi-Eichi, H. Design, modeling and simulation of a green building energy system. In Proceedings of the IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Chouder, A.; Silvestre, S.; Sadaoui, N.; Rahmani, L. Modeling and simulation of a grid connected PV system based on the evaluation of main PV module parameters. Simul. Model. Pract. Theory 2012, 20, 46–58. [Google Scholar] [CrossRef]
- Das, D.; Esmaili, R.; Xu, L.; Nichols, D. An optimal design of a grid connected hybrid wind/photovoltaic/fuel cell system for distributed energy production. In Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, Raleigh, NC, USA, 6–10 November 2005; p. 6. [Google Scholar]
- De Soto, W.; Klein, S.; Beckman, W. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Salam, Z.; Ishaque, K.; Taheri, H. An improved two-diode photovoltaic (PV) model for PV system. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India, Institute of Electrical and Electronics Engineers (IEEE), New Delhi, India, 20–23 December 2010; pp. 1–5. [Google Scholar]
- Scheffler, M.; Colombo, P. Cellular Ceramics: Structure, Manufacturing, Properties and Applications; John Wiley & Sons: Oxford, UK, 2006. [Google Scholar]
- Habib, M.; Said, S.; El-Hadidy, M.; Al-Zaharna, I. Optimization procedure of a hybrid photovoltaic wind energy system. Energy 1999, 24, 919–929. [Google Scholar] [CrossRef]
- Evans, D. Simplified method for predicting photovoltaic array output. Sol. Energy 1981, 27, 555–560. [Google Scholar] [CrossRef]
- Shahinzadeh, H.; Moazzami, M.; Fathi, S.H.; Gharehpetian, G.B. Optimal sizing and energy management of a grid-connected microgrid using HOMER software. In Proceedings of the 2016 Smart Grids Conference (SGC), Kerman, Iran, 20–21 December 2016; pp. 1–6. [Google Scholar]
- Rousis, A.O.; Tzelepis, D.; Konstantelos, I.; Booth, C.; Strbac, G. Design of a hybrid AC/DC microgrid using HOMER pro: Case study on an islanded residential application. Inventions 2018, 3, 55. [Google Scholar] [CrossRef]
- Massucco, S.; Pongiglione, P.; Saviozzi, M.; Silvestro, F.; Almaleck, P.; Serra, P. Algorithm for optimal microgrid operation and control with adaptable constraints and flexible objective function. In Proceedings of the IEEE 5th International Forum on Research and Technology for Society and Industry (RTSI), Firenze, Italy, 9 September 2019; pp. 97–102. [Google Scholar]
- Adjei, B.A.; Donkoh, E.K.; Otoo, D.; Owusu-Ansah, E.D.-G.J.; Mahama, F. Optimization of A Grid-Connected Photovoltaic System in a Densely Populated Residential Community. J. Adv. Math. Comput. Sci. 2019, 1–16. [Google Scholar] [CrossRef]
- Bahramirad, S.; Reder, W.; Khodaei, A. Reliability-constrained optimal sizing of energy storage system in a microgrid. IEEE Trans. Smart Grid 2012, 3, 2056–2062. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Smart energy management system for optimal microgrid economic operation. IET Renew. Power Gener. 2011, 5, 258–267. [Google Scholar] [CrossRef]
- Olivares, D.E.; Canizares, C.A.; Kazerani, M. A Centralized energy management system for isolated microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).