In Croatia there is only one distribution system operator divided into 21 distribution areas, which differ in size, number of metering points, network length and configuration. The data on neighboring countries distribution networks that share a similar configuration and history of occurrence can be seen in
Table 1 [
34]. The difference compared to neighboring countries DSOs is most evident in the grid losses that are significantly lower in Croatian DSO. Since all the classic ways of improving grid properties of Croatian DSO have been exhausted, FACTS devices represent the next step in distribution network development and improvement.
The purpose of the proposed algorithm is to determine the ideal busbar for FACTS implementation and the rated power of FACTS device(s). The proposed algorithm arises from the local industry growth and represents a unique example that can be applied to neighboring countries with similar power systems and similar operational challenges. The mathematical background of the proposed approach is well known [
36,
37,
38] and it has been used as a tool in the optimization process of the FACTS allocation in this paper. The Newton-Raphson method is the most widely used method for solving non-linear equations. The method is an approximation algorithm based on an initial estimate and the use of Taylor’s series expansion and can be applied on the power flow problem. The iterative method can be expressed with (2),
where
δ is system node phase angle,
V is voltage magnitude and
n is the iteration step [
37]. Further comparisons of conventional algorithms are made in References [
39,
40]. Optimization techniques mentioned in References [
41,
42] consider fewer constraints than the proposed approach. A similar optimization framework is used in Reference [
43] for battery storage systems allocation in a microgrid with significant photovoltaic generation. Algorithms in References [
21,
22,
23,
24], if applied to the network simulated in
Figure 5, would show better results in terms of reducing total network losses but an attempt to implement SVC on network buses selected by conventional algorithms would lead to legal, political and strategical challenges. The main advantage of the proposed algorithm is minimizing investment by avoiding the need to expand existing transformer station equipment or increasing transformer rated power on a selected busbar. Furthermore, avoiding physical expansion of transformer stations is crucial because building permits reduce ROI and increase total investment timeframe significantly. Due to FACTS devices high costs, all the state of the art techniques used for the FACTS allocation based on the analytical, soft-computing, hybrid approaches have the common objective function, to achieve the maximum benefit of FACTS devices implementation by determining the ideal location and the rating of the FACTS devices. Most of the state of the art techniques for FACTS allocation solve the objective function comprising the FACTS devices costs to maximal benefits of their implementation for the distribution network management resulting in voltage profile improvement as well as active power losses decrease and line loadings decrease. Beside the FACTS manufacturer power rating constraint (which includes standardized FACTS power rating values), proposed approach in this paper comprising the costs of FACTS implementation and the benefits of their implementation allocating the FACTS devices considering the constraints that cannot be found in other state of the art techniques. As mentioned before, those constraints are the transformer station construction constraint and the DSO economic willingness to investment in distribution network development constraint. Minimization of the objective function can be expressed as (3), with constraints Ω,
where
f(
ik) is the objective function,
ik is total investment for installation on node
k,
ROIk is return of investment for node
k,
ELk is equipment lifecycle,
STk is substation type for node
k,
Sm is manufacturer power rating of SVC and
SSVC is installed rated power of SVC. The starting point of the optimization is node
k0, as defined in (4), the node with highest voltage deviation.
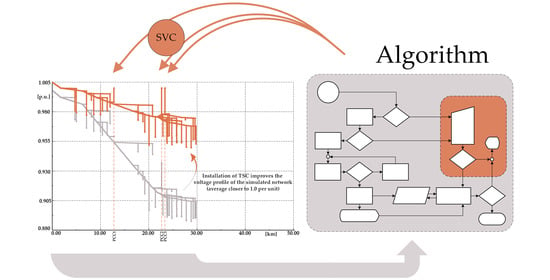
The voltage profile of the feeder is observed and the busbars with voltage lower than threshold voltage value (determined by DSO or watchdog agency rules) are taken into consideration. SVC would be installed on the busbars with the lowest voltage values if those busbars are suitable for the implementation (tower substations are not suitable). Otherwise, SVC would be installed on the next suitable busbar. SVC rated power is determined by an iterative process where rated reactive power is incrementally increased according to standardized values until acceptable voltage levels are found. SVC implementation feasibility is calculated by finding the return of investment (ROI) for the project and comparing it to the equipment lifecycle and decreased losses through optimized load flows and improved stability of supply. Initial cost depends on the type of substation and installed transformer. In Croatia’s distribution grid, installed transformers usually have power rating of 50, 100, 160, 250, 400, 630 or 1000 kVA. Transformers with power rating of 250 kVA and lower are typically installed in tower-type substations, which are not suitable for FACTS implementation. Moreover, transformers with rated power of 400 kVA face overloading for most commercially available FACTS devices. Further challenges lie in coordination with national DSO strategy, local subnet development strategy and the local government spatial plans. The objective function of the proposed algorithm is to find the optimal location for the implementation and the rating of the FACTS devices. Candidate locations for FACTS devices implementation are determined solving nonlinear system nodal equation using an iterative Newton-Raphson method comprising the mentioned constraints. FACTS devices ratings are determined iteratively too; the first FACTS device(s) rating value is the smallest standardized value; in each subsequent iteration this value increases until the predefined voltage conditions are reached. The idea of the proposed algorithm is to incorporate additional constraints to allocation techniques to improve the possibility of their practical implementation.
Beside the aspects of SVC implementation proposed with the algorithm in
Figure 4, the influence of SVC on the oscillatory stability and low voltage motor starting will be discussed. Due to distribution network specific configuration and topology without long tie lines and connected synchronous generators, the oscillatory stability analysis of distribution network is not a common research area. The modern rural distribution network could be classified as a microgrid since it has been characterized by significant integration of different RES including synchronous and asynchronous generators coupled directly or through the power inverter interface as well as controllable asynchronous motors loads in animal farm facilities. Considering these facts, the analysis of possible influence of SVC implementation on the modern rural distribution network oscillatory stability and the low-voltage motor starting seems to be reasonable.