Real-Time Energy Management of Parallel Hybrid Electric Vehicles Using Linear Quadratic Regulation
Abstract
:1. Introduction
2. Modeling for Energy Management Strategy Development
2.1. Modeling of the Studied System
2.2. Local Control of the System
2.3. Model Reduction for Energy Management Strategy
3. Proposed Real-Time Energy Management Strategy
3.1. Approach
3.1.1. Original Problem Statement
3.1.2. Problem Reformulation
3.2. Strategy Development
3.2.1. Linear Quadratic Regulation (LQR)
3.2.2. Proposed LQR-Based Strategy
3.2.3. Weighting Factor Determination
4. Comparative Evaluations by Simulation
4.1. Simulation Conditions
4.2. Results and Discussions
5. Experimental Validation of the Proposed Strategy
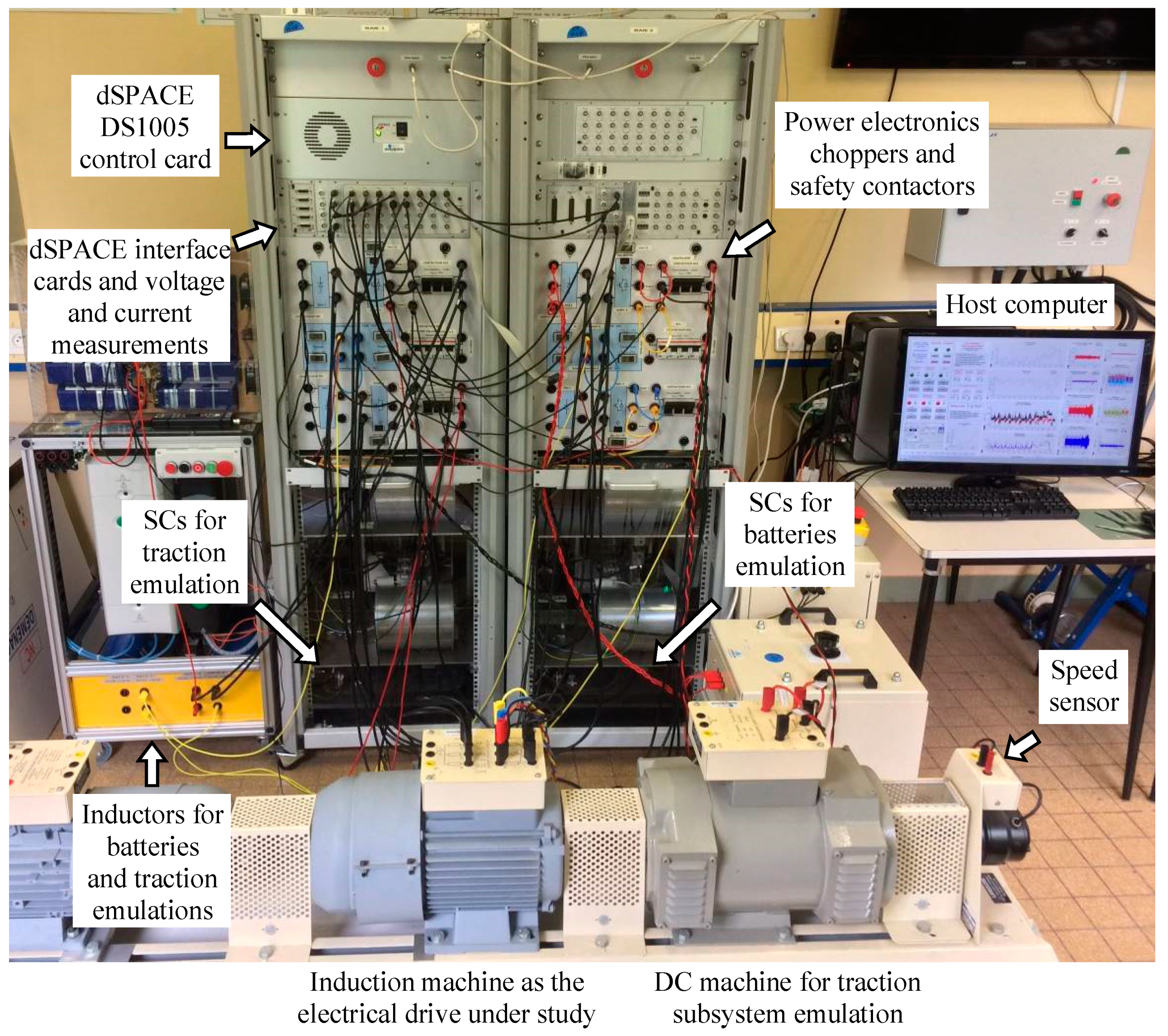
5.1. Experimental Setup
5.2. Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Bauer, N.; Mouratiadou, I.; Luderer, G.; Baumstark, L.; Brecha, R.J.; Edenhofer, O.; Kriegler, E. Global fossil energy markets and climate change mitigation—An analysis with REMIND. Clim. Change 2016, 136, 69–82. [Google Scholar] [CrossRef]
- Liu, P.; Jin, Z.; Hua, Y.; Zhang, L. Development of Test-Bed Controller for Powertrain of HEV. Energies 2020, 13, 3372. [Google Scholar] [CrossRef]
- Lee, W.; Kim, T.; Jeong, J.; Chung, J.; Kim, D.; Lee, B.; Kim, N. Control Analysis of a Real-World P2 Hybrid Electric Vehicle Based on Test Data. Energies 2020, 13, 4092. [Google Scholar] [CrossRef]
- Kim, H.; Wi, J.; Yoo, J.; Son, H.; Park, C.; Kim, H. A Study on the Fuel Economy Potential of Parallel and Power Split Type Hybrid Electric Vehicles. Energies 2018, 11, 2103. [Google Scholar] [CrossRef] [Green Version]
- Chan, C.C.; Bouscayrol, A.; Chen, K. Electric, Hybrid, and Fuel-Cell Vehicles: Architectures and Modeling. IEEE Trans. Veh. Technol. 2010, 59, 589–598. [Google Scholar] [CrossRef]
- Van Mullem, D.; Van Keulen, T.; Kessels, J.; De Jager, B.; Steinbuch, M. Implementation of an Optimal Control Energy Management Strategy in a Hybrid Truck. In Proceedings of the 6th IFAC Symposium Advances in Automotive Control, Munich, Germany, 12–14 July 2010; pp. 61–66. [Google Scholar]
- Biasini, R.; Onori, S.; Rizzoni, G. A near-optimal rule-based energy management strategy for medium duty hybrid truck. Int. J. Powertrains 2013, 2, 232–261. [Google Scholar] [CrossRef]
- Mayet, C.; Welles, J.; Bouscayrol, A.; Hofman, T.; Lemaire-Semail, B. Influence of a CVT on the fuel consumption of a parallel medium-duty electric hybrid truck. Math. Comput. Simul. 2019, 158, 120–129. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef] [Green Version]
- Uddin, K.; Moore, A.D.; Barai, A.; Marco, J. The effects of high frequency current ripple on electric vehicle battery performance. Appl. Energy 2016, 178, 142–154. [Google Scholar] [CrossRef] [Green Version]
- Erdinc, O.; Vural, B.; Uzunoglu, M. A wavelet-fuzzy logic based energy management strategy for a fuel cell/battery/ultra-capacitor hybrid vehicular power system. J. Power Sources 2009, 194, 369–380. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Hou, J.; Han, X.; Ouyang, M. Energy management strategies comparison for electric vehicles with hybrid energy storage system. Appl. Energy 2014, 134, 321–331. [Google Scholar] [CrossRef]
- Schaltz, E.; Khaligh, A.; Rasmussen, P.O. Influence of Battery/Ultracapacitor Energy-Storage Sizing on Battery Lifetime in a Fuel Cell Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2009, 58, 3882–3891. [Google Scholar] [CrossRef]
- Hredzak, B.; Agelidis, V.G.; Demetriades, G. Application of explicit model predictive control to a hybrid battery-ultracapacitor power source. J. Power Sources 2015, 277, 84–94. [Google Scholar] [CrossRef]
- Nguyen, B.-H.; German, R.; Trovao, J.P.F.; Bouscayrol, A. Real-Time Energy Management of Battery/Supercapacitor Electric Vehicles Based on an Adaptation of Pontryagin’s Minimum Principle. IEEE Trans. Veh. Technol. 2019, 68, 203–212. [Google Scholar] [CrossRef] [Green Version]
- Groot, J.; Swierczynski, M.; Stan, A.I.; Kær, S.K. On the complex ageing characteristics of high-power LiFePO4/graphite battery cells cycled with high charge and discharge currents. J. Power Sources 2015, 286, 475–487. [Google Scholar] [CrossRef]
- Savoye, F.; Venet, P.; Millet, M.; Groot, J. Impact of Periodic Current Pulses on Li-Ion Battery Performance. IEEE Trans. Ind. Electron. 2011, 59, 3481–3488. [Google Scholar] [CrossRef]
- Salmasi, F.R. Control Strategies for Hybrid Electric Vehicles: Evolution, Classification, Comparison, and Future Trends. IEEE Trans. Veh. Technol. 2007, 56, 2393–2404. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xu, J.; Gong, X.; You, C. Energy Management for a Power-Split Plug-in Hybrid Electric Vehicle Based on Dynamic Programming and Neural Networks. IEEE Trans. Veh. Technol. 2014, 63, 1567–1580. [Google Scholar] [CrossRef]
- Hou, C.; Ouyang, M.; Xu, L.; Wang, H. Approximate Pontryagin’s minimum principle applied to the energy management of plug-in hybrid electric vehicles. Appl. Energy 2014, 115, 174–189. [Google Scholar] [CrossRef]
- Moura, S.J.; Stein, J.L.; Fathy, H.K. Battery-Health Conscious Power Management in Plug-In Hybrid Electric Vehicles via Electrochemical Modeling and Stochastic Control. IEEE Trans. Control. Syst. Technol. 2012, 21, 679–694. [Google Scholar] [CrossRef]
- Bouscayrol, A.; Hautier, J.-P.; Lemaire-Semail, B. Graphic Formalisms for the Control of Multi-Physical Energetic Systems: COG and EMR. In Systemic Design Methodologies for Electrical Energy Systems; Roboam, X., Ed.; ISTE Ltd.: London, UK, 2013; pp. 89–124. [Google Scholar]
- Unger, J.; Kozek, M.; Jakubek, S. Nonlinear model predictive energy management controller with load and cycle prediction for non-road HEV. Control. Eng. Pr. 2015, 36, 120–132. [Google Scholar] [CrossRef]
- Lu, B.; Natarajan, B.; Schulz, N. Optimal control based power management in hybrid military vehicle. In Proceedings of the 2012 IEEE International Electric Vehicle Conference; Institute of Electrical and Electronics Engineers (IEEE): Greenville, SC, USA, 2012; pp. 1–7. [Google Scholar]
- Borhan, H.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V.; Di Cairano, S. MPC-Based Energy Management of a Power-Split Hybrid Electric Vehicle. IEEE Trans. Control. Syst. Technol. 2011, 20, 593–603. [Google Scholar] [CrossRef]
- Kessels, J.T.B.A.; Koot, M.W.T.; Bosch, P.V.D.; Kok, D.B. Online Energy Management for Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2008, 57, 3428–3440. [Google Scholar] [CrossRef]
- Sundstrom, O.; Guzzella, L. A generic dynamic programming Matlab function. In Proceedings of the 2009 IEEE International Conference on Control Applications; Institute of Electrical and Electronics Engineers (IEEE): St. Petersburg, Russia, 2009; pp. 1625–1630. [Google Scholar]
- Sciarretta, A.; Serrao, L.; Dewangan, P.; Tona, P.; Bergshoeff, E.; Bordons, C.; Charmpa, L.; Elbert, P.; Eriksson, L.; Hofman, T.; et al. A control benchmark on the energy management of a plug-in hybrid electric vehicle. Control. Eng. Pract. 2014, 29, 287–298. [Google Scholar] [CrossRef] [Green Version]
- Pisu, P.; Rizzoni, G. A Comparative Study of Supervisory Control Strategies for Hybrid Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2007, 15, 506–518. [Google Scholar] [CrossRef]
- Bouscayrol, A. Hardware-in-the-Loop Simulation. In The Industrial Electronics Handbook: Control and Mechatronics, 2nd ed.; Wilamowski, B.M., Irwin, J.D., Eds.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Mayet, C.; Delarue, P.; Bouscayrol, A.; Chattot, E.; Verhille, J.-N. Comparison of Different EMR-Based Models of Traction Power Substations for Energetic Studies of Subway Lines. IEEE Trans. Veh. Technol. 2016, 65, 1021–1029. [Google Scholar] [CrossRef]
- Kamal, E.; Adouane, L. Hierarchical Energy Optimization Strategy and Its Integrated Reliable Battery Fault Management for Hybrid Hydraulic-Electric Vehicle. IEEE Trans. Veh. Technol. 2018, 67, 3740–3754. [Google Scholar] [CrossRef]
- Bouscayrol, A.; Delarue, P.; Guillaud, X. Power strategies for maximum control structure of a wind energy conversion system with a synchronous machine. Renew. Energy 2005, 30, 2273–2288. [Google Scholar] [CrossRef]
- Trovao, J.P.F.; Pereirinha, P.G.; Jorge, H.M.; Antunes, C.H. A multi-level energy management system for multi-source electric vehicles—An integrated rule-based meta-heuristic approach. Appl. Energy 2013, 105, 304–318. [Google Scholar] [CrossRef]
- Delprat, S.; Lauber, J.; Guerra, T.; Rimaux, J. Control of a Parallel Hybrid Powertrain: Optimal Control. IEEE Trans. Veh. Technol. 2004, 53, 872–881. [Google Scholar] [CrossRef]
- Sundström, O.; Ambühl, D.; Guzzella, L. On Implementation of Dynamic Programming for Optimal Control Problems with Final State Constraints. Oil Gas Sci. Technol. Rev. IFP 2009, 65, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Pérez, L.V.; Bossio, G.R.; Moitre, D.; García, G.O. Optimization of power management in an hybrid electric vehicle using dynamic programming. Math. Comput. Simul. 2006, 73, 244–254. [Google Scholar] [CrossRef]
- Serrao, L.; Onori, S.; Sciarretta, A.; Guezennec, Y.; Rizzoni, G. Optimal energy management of hybrid electric vehicles including battery aging. In Proceedings of the 2011 American Control Conference; Institute of Electrical and Electronics Engineers (IEEE): San Francisco, CA, USA, 2011; pp. 2125–2130. [Google Scholar]
- Onori, S.; Tribioli, L. Adaptive Pontryagin’s Minimum Principle supervisory controller design for the plug-in hybrid GM Chevrolet Volt. Appl. Energy 2015, 147, 224–234. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal Control of Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle. IEEE Trans. Control. Syst. Technol. 2011, 19, 1279–1287. [Google Scholar] [CrossRef] [Green Version]
- Mura, R.; Utkin, V.; Onori, S. Energy Management Design in Hybrid Electric Vehicles: A Novel Optimality and Stability Framework. IEEE Trans. Control. Syst. Technol. 2015, 23, 1307–1322. [Google Scholar] [CrossRef]
- Koot, M.; Kessels, J.; Dejager, B.; Heemels, W.; VandenBosch, P.; Steinbuch, M.M. Energy Management Strategies for Vehicular Electric Power Systems. IEEE Trans. Veh. Technol. 2005, 54, 771–782. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.-C. Applied Optimal Control: Optimization, Estimation, and Control; Taylor & Francis: New York, NY, USA, 1975. [Google Scholar]
- Hofman, T.T.; Steinbuch, M.M.; Van Druten, R.; Serrarens, A. Hybrid component specification optimisation for a medium-duty hybrid electric truck. Int. J. Heavy Veh. Syst. 2008, 15, 356. [Google Scholar] [CrossRef]
- Allegre, A.-L.; Bouscayrol, A.; Verhille, J.-N.; Delarue, P.; Chattot, E.; El-Fassi, S. Reduced-Scale-Power Hardware-in-the-Loop Simulation of an Innovative Subway. IEEE Trans. Ind. Electron. 2010, 57, 1175–1185. [Google Scholar] [CrossRef]












| Parameters | Values | |
|---|---|---|
| Vehicle (Based on the Hybrid Delivery Truck Designed in [44]) | ||
| Vehicle total mass | 7514 kg | |
| Aerodynamic standard | 0.73 × 6.9 m2 | |
| Rolling coefficient | 0.008 | |
| Final drive ratio | 3.33 | |
| Wheel radius | 0.397 m | |
| Gearbox | ||
| Gearbox ratio | (7.14 4.17 2.50 1.59 1.00 0.78) | |
| Efficiency | (0.94 0.95 0.9 0.95 0.91 0.91) | |
| Belt | ||
| Belt ratio | 1 | |
| Efficiency | 0.95 | |
| ICE (Detroit Diesel Corp. Series 50 8.5 Diesel Engine) | ||
| Maximal power | 205 kW | |
| Maximal speed | 2100 rpm | |
| Idle speed | 650 rpm | |
| Maximal torque | 1100 Nm | |
| Mass density of diesel | 850 g/L | |
| Electrical Drive (PMSM) | ||
| Maximal power | 58 kW | |
| Maximal torque | 400 Nm | |
| Nominal speed | 1500 rpm | |
| Maximal speed | 4000 rpm | |
| Nominal efficiency in traction mode | 96% | |
| Nominal efficiency in regenerative mode | 90% | |
| Batteries (LiPho A123 20Ah 2010 Cells) | ||
| Battery bank capacity | 62 Ah | |
| Battery bank resistance (at 70% SoC) | 26 mΩ | |
| Battery bank OCV (at 70% SoC) | 300 V | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyễn, B.-H.; Trovão, J.P.F.; German, R.; Bouscayrol, A. Real-Time Energy Management of Parallel Hybrid Electric Vehicles Using Linear Quadratic Regulation. Energies 2020, 13, 5538. https://doi.org/10.3390/en13215538
Nguyễn B-H, Trovão JPF, German R, Bouscayrol A. Real-Time Energy Management of Parallel Hybrid Electric Vehicles Using Linear Quadratic Regulation. Energies. 2020; 13(21):5538. https://doi.org/10.3390/en13215538
Chicago/Turabian StyleNguyễn, Bảo-Huy, João Pedro F. Trovão, Ronan German, and Alain Bouscayrol. 2020. "Real-Time Energy Management of Parallel Hybrid Electric Vehicles Using Linear Quadratic Regulation" Energies 13, no. 21: 5538. https://doi.org/10.3390/en13215538
APA StyleNguyễn, B. -H., Trovão, J. P. F., German, R., & Bouscayrol, A. (2020). Real-Time Energy Management of Parallel Hybrid Electric Vehicles Using Linear Quadratic Regulation. Energies, 13(21), 5538. https://doi.org/10.3390/en13215538








