The Effect of Selected Factors on Floor Upheaval in Roadways—In Situ Testing
Abstract
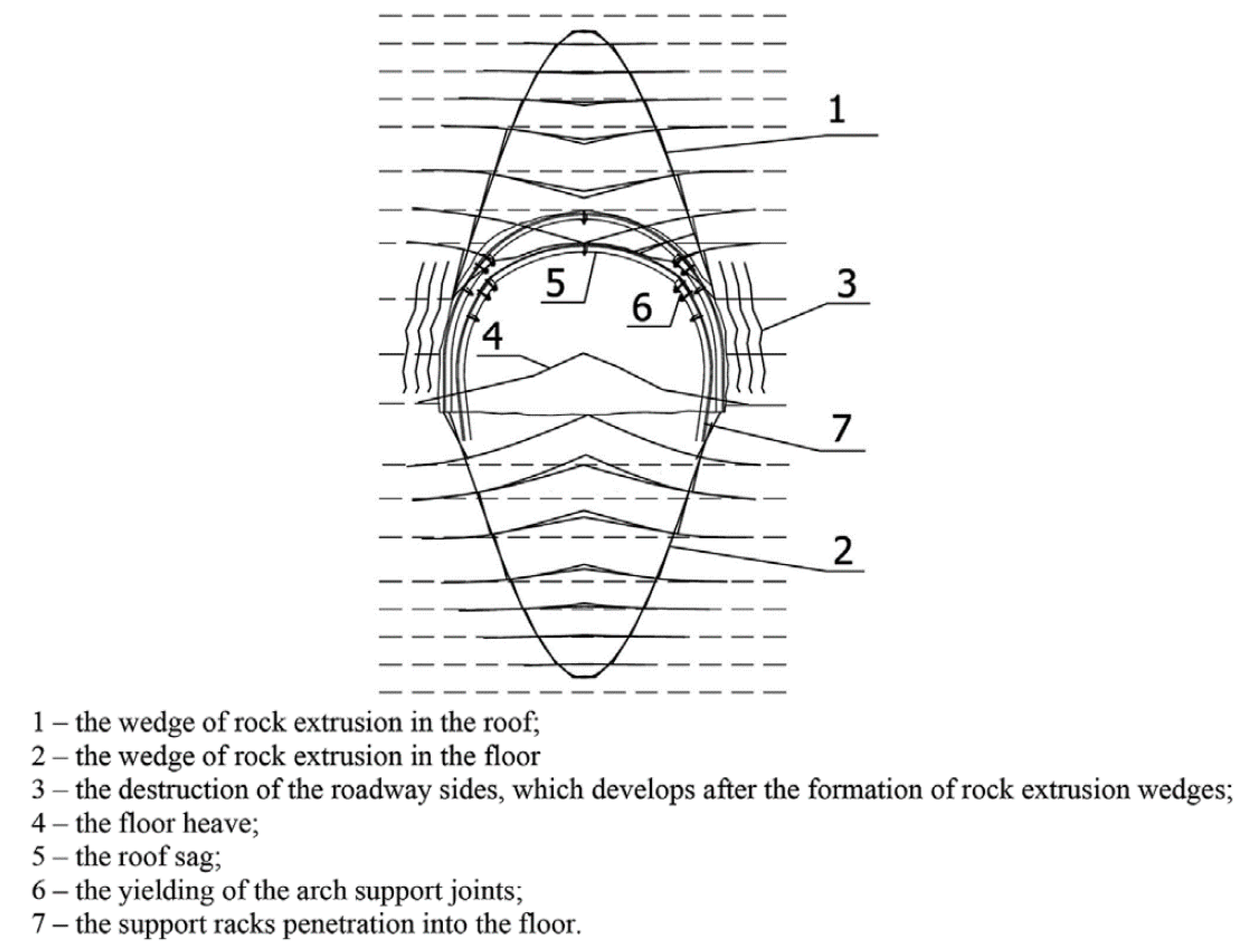
:1. The Mechanism of the Floor Upheaval in Roadways
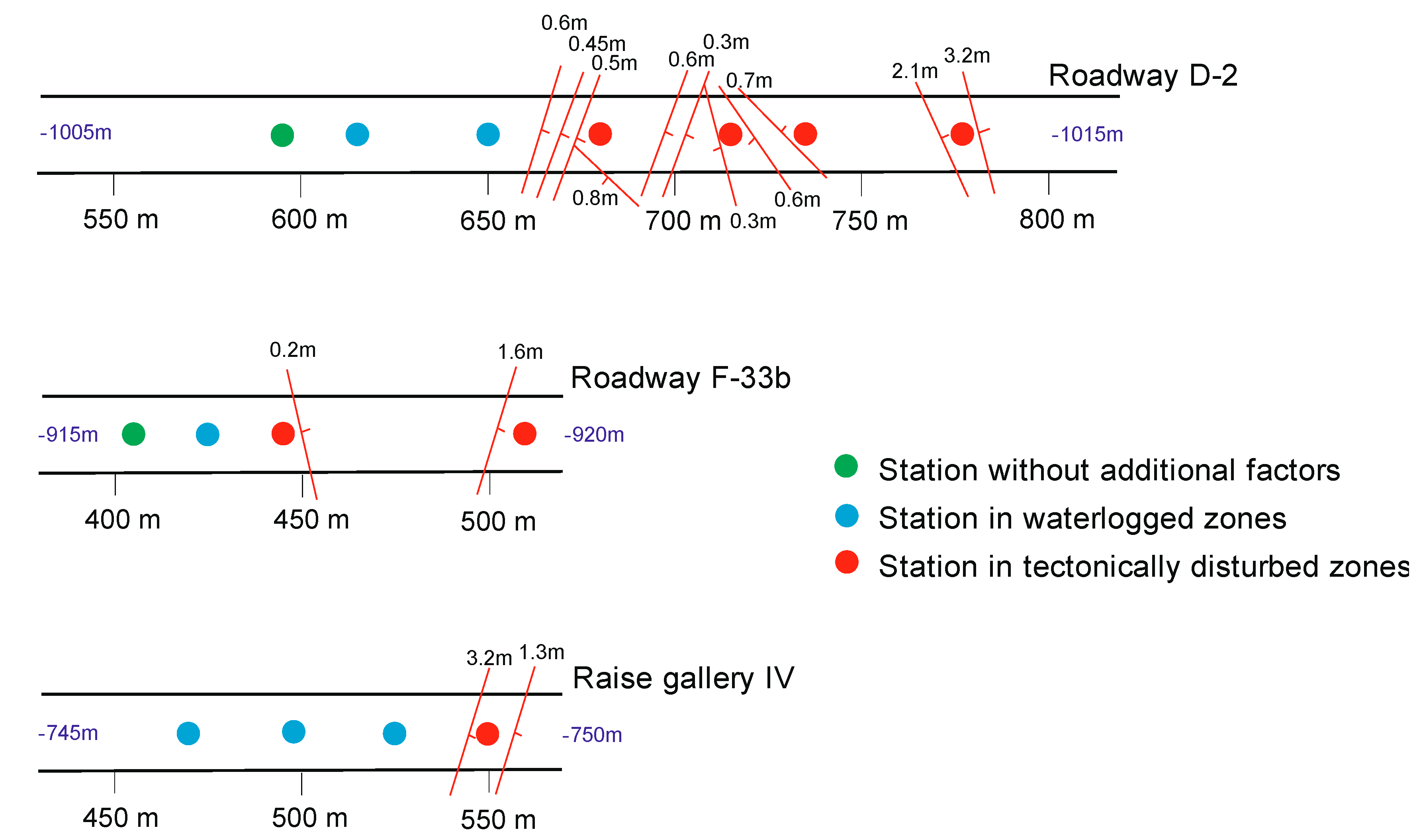
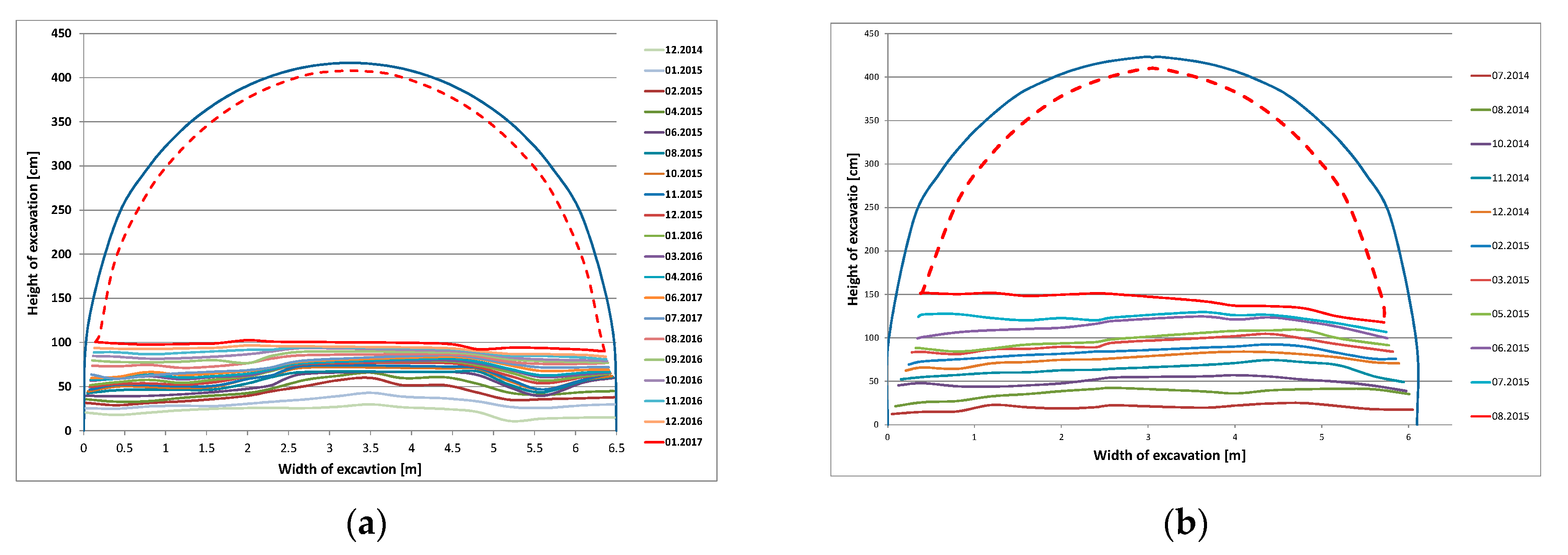
2. Location and Scope of Research
- (a)
- Roadway D-2 in the “Zofiówka” mine—average depth of 1010 m,
- (b)
- Roadway F-33b in the “Borynia” mine—average depth of 920 m,
- (c)
- Raise gallery IV in the “Piast” mine—average depth of 750 m.
- Tectonically disturbed zones (in the fault crossing the excavation),
- Waterlogged zones,
- Sections of the excavation without additional mining and geological factors influencing the deformation of the excavation.
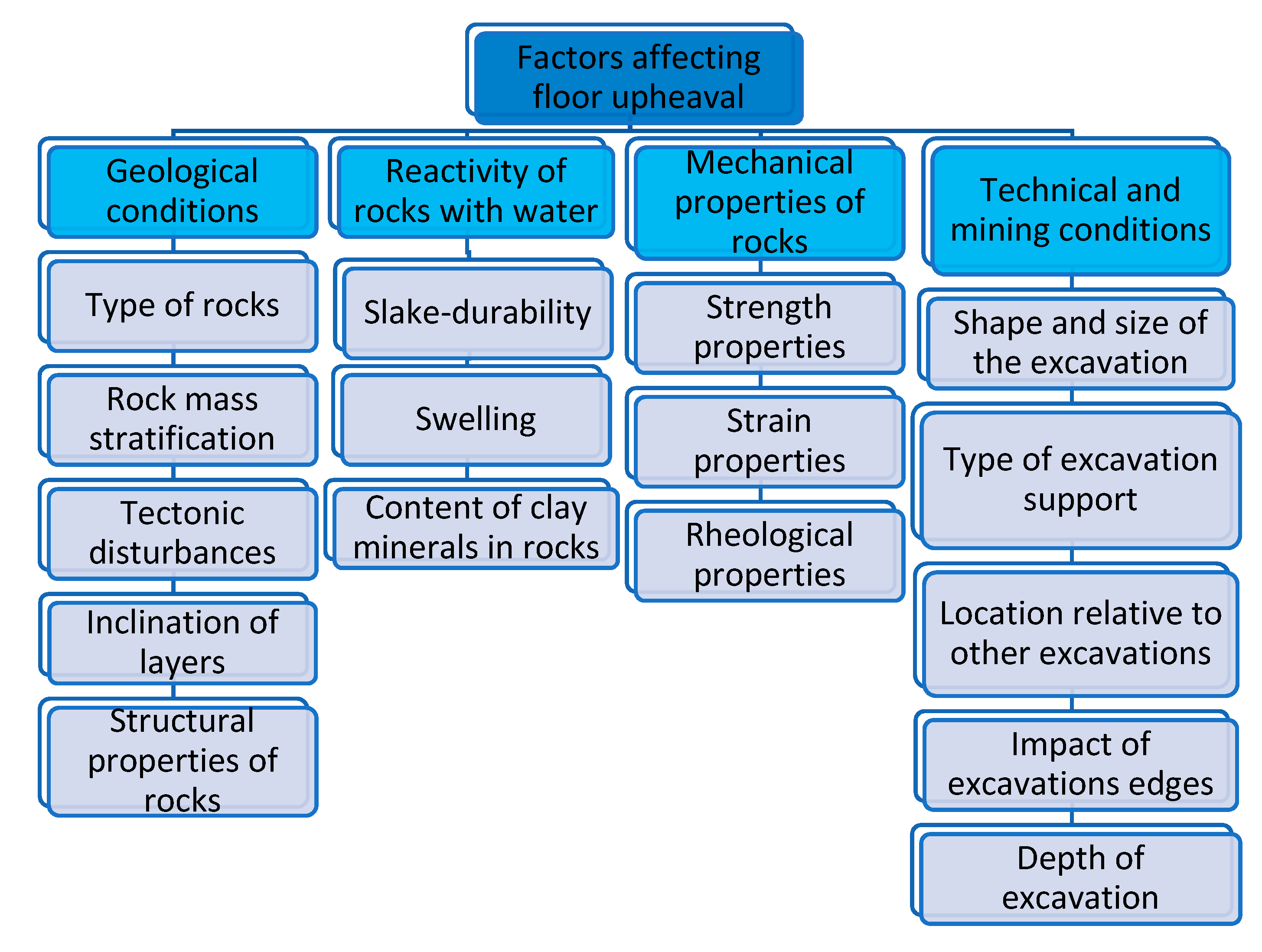
3. Analysis of Test Results
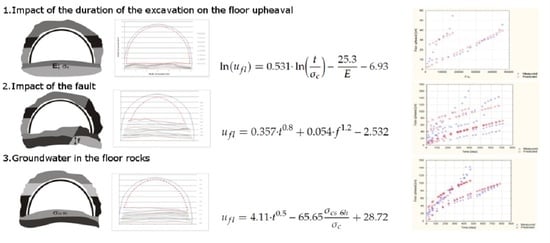
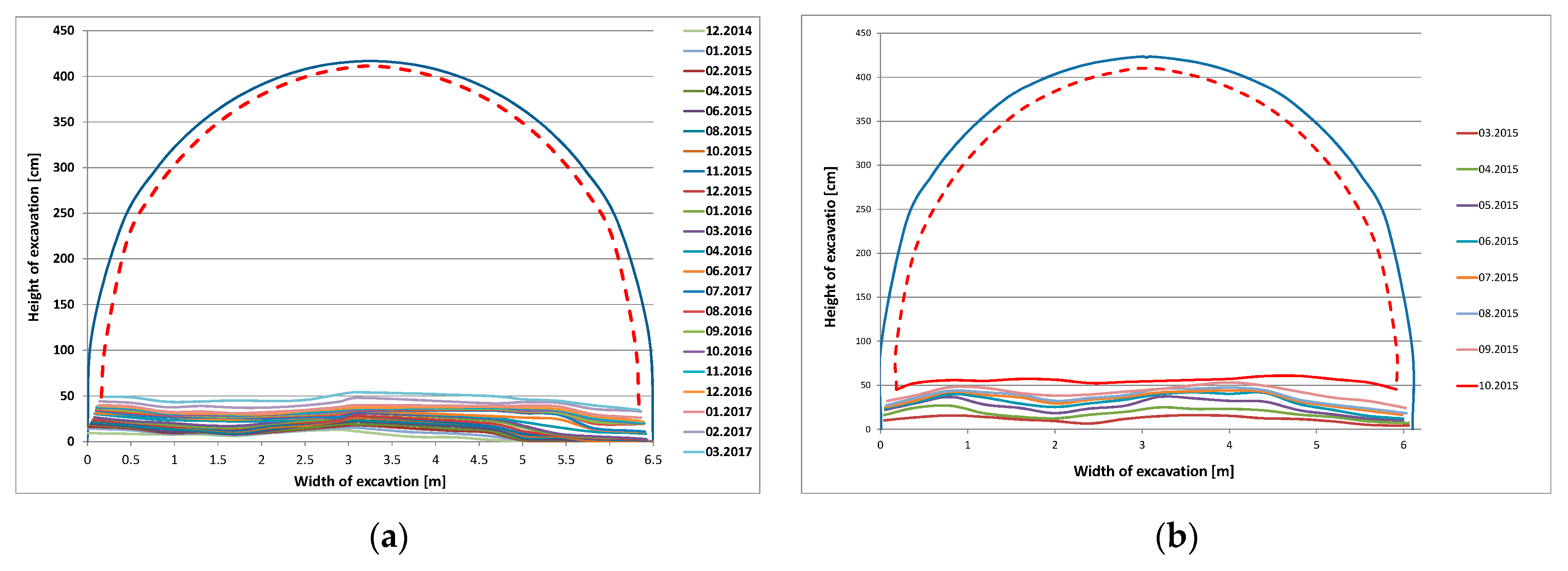
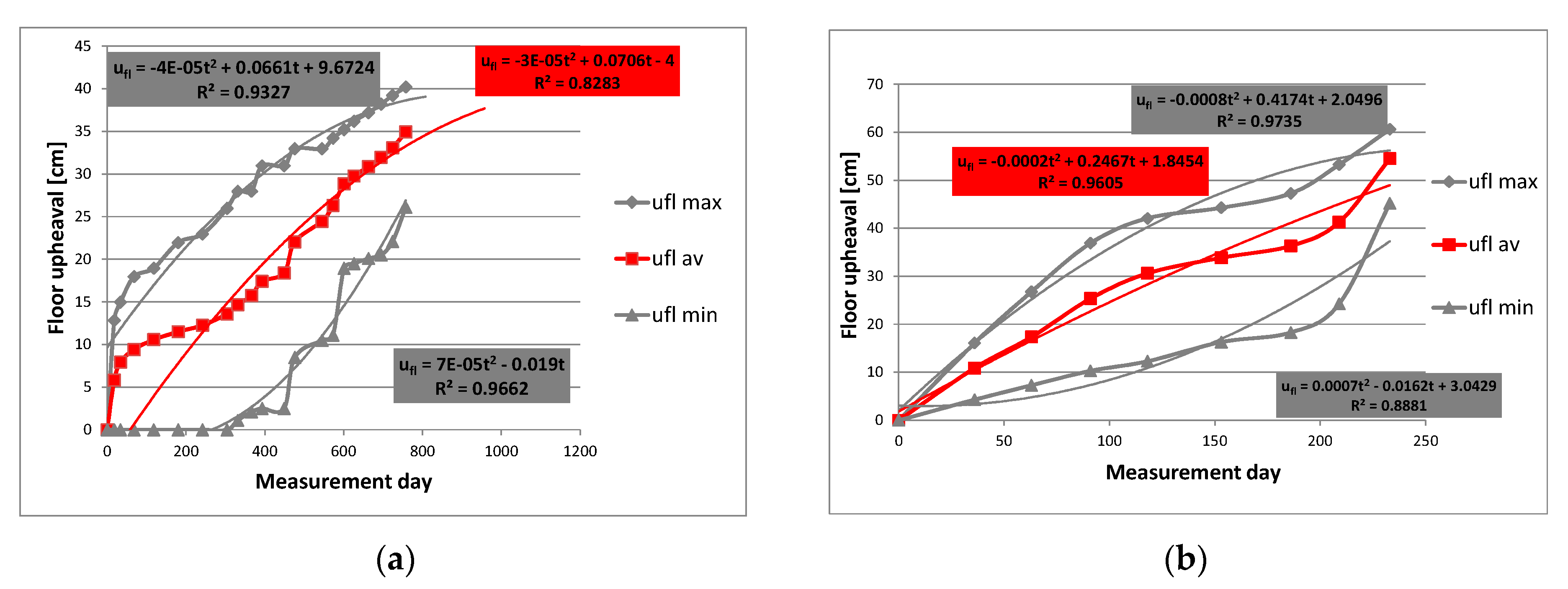
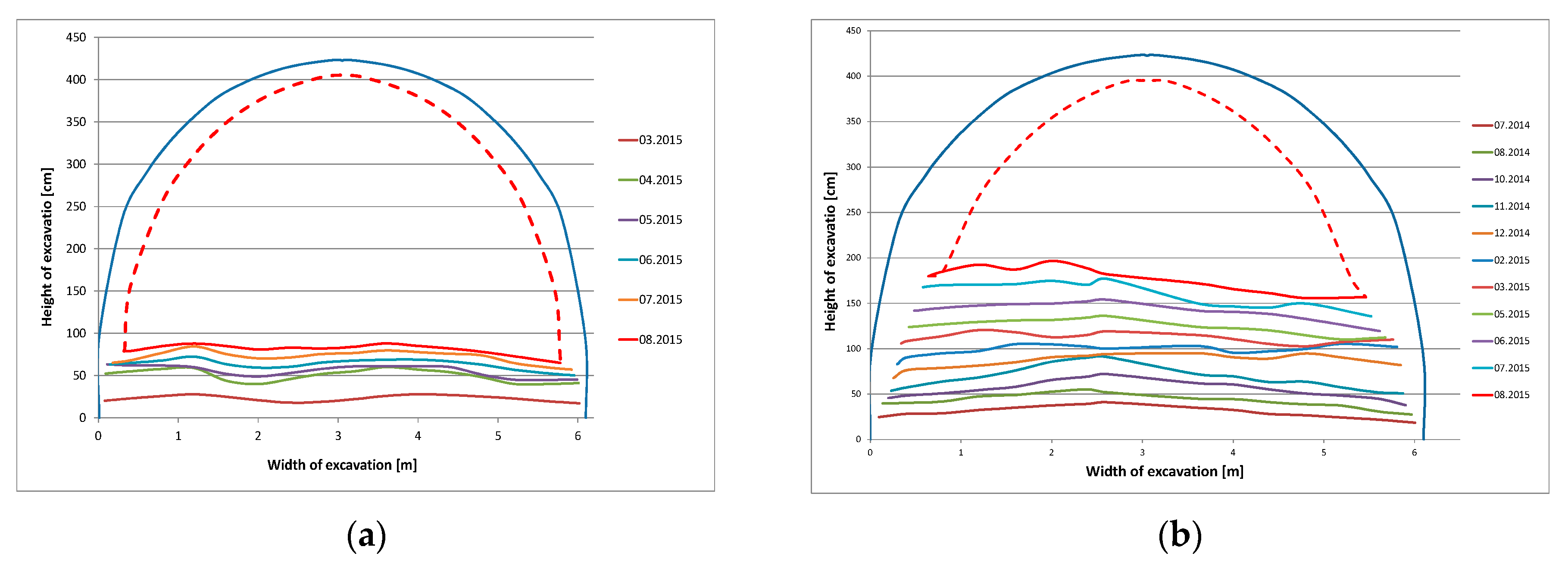
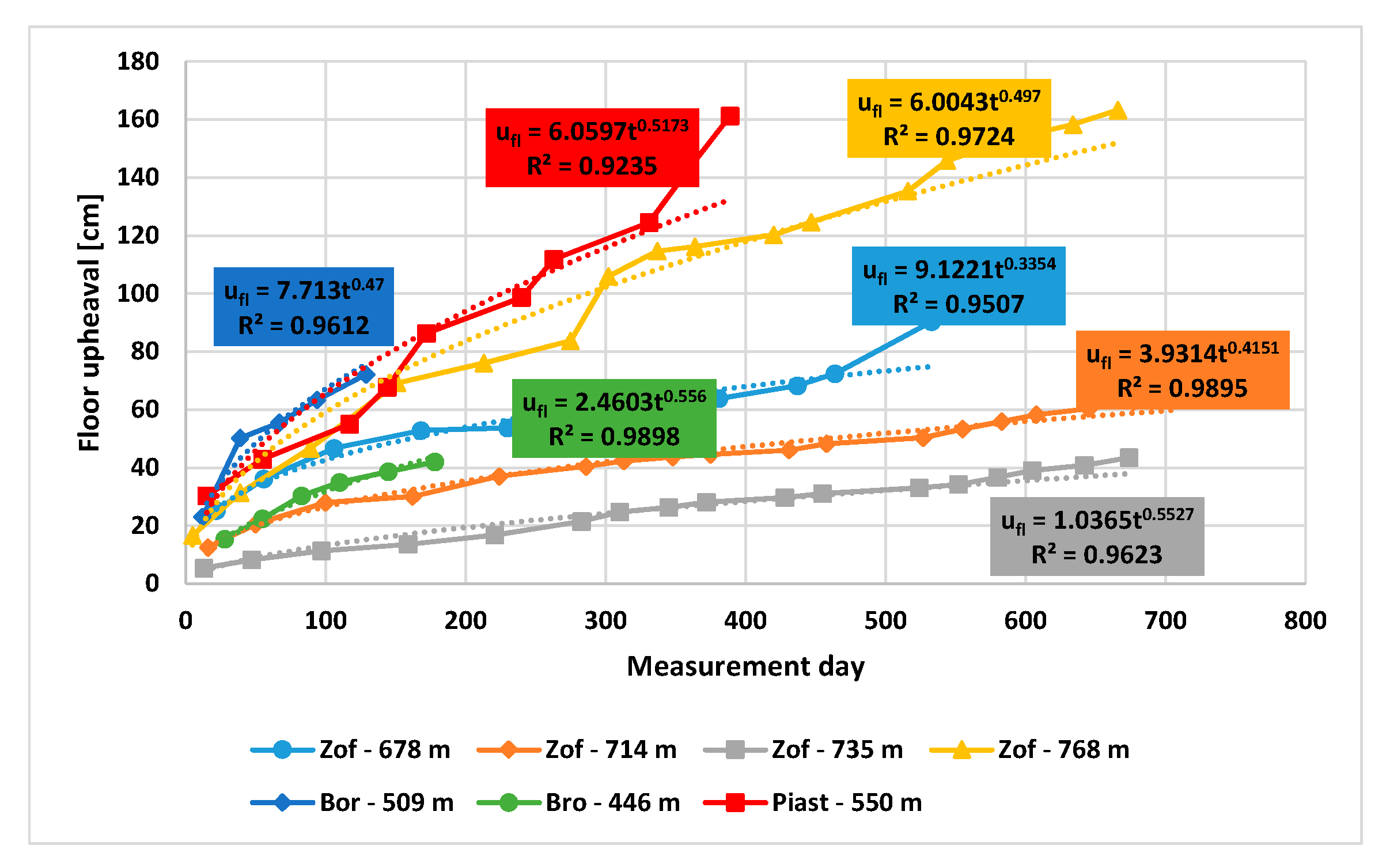
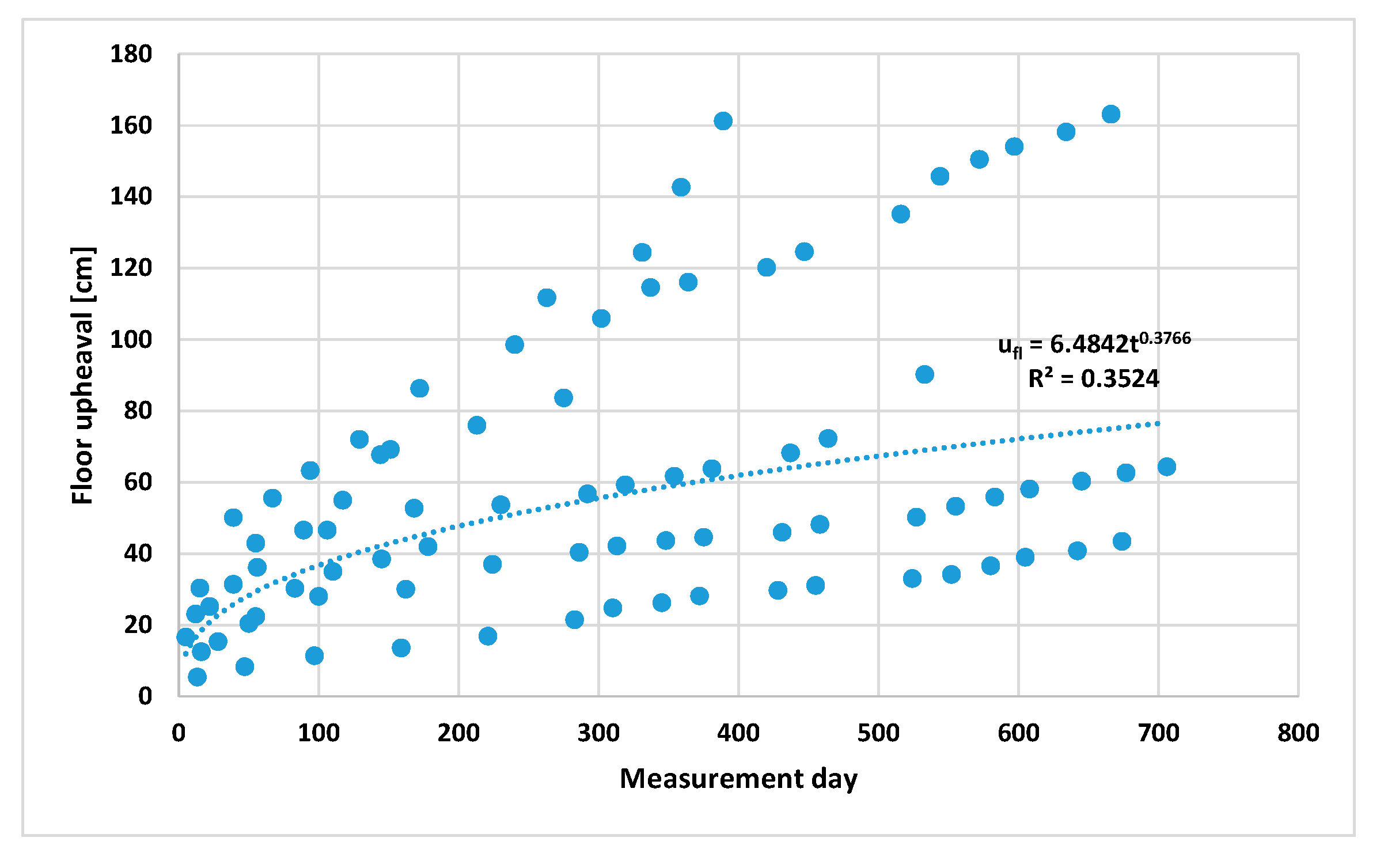
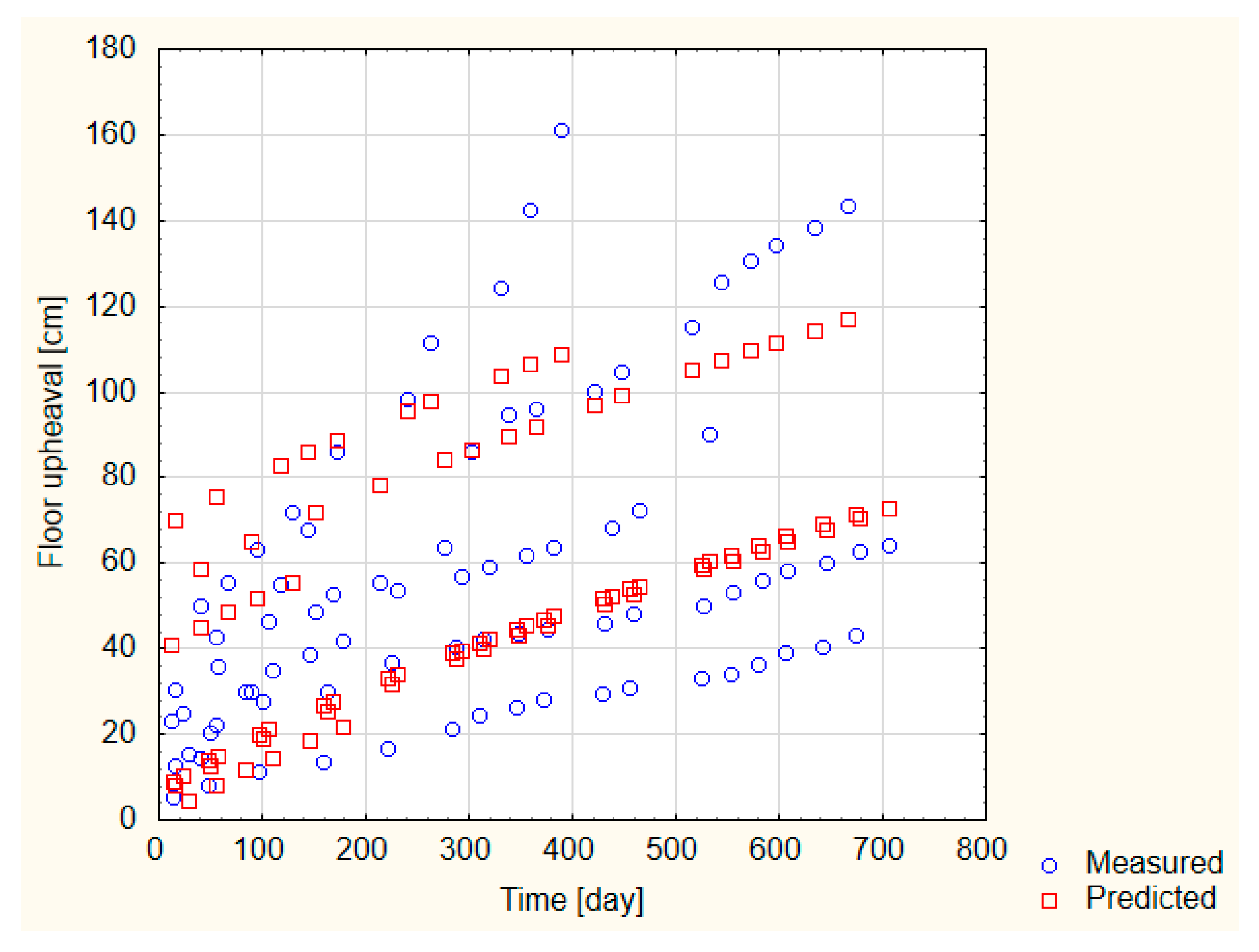
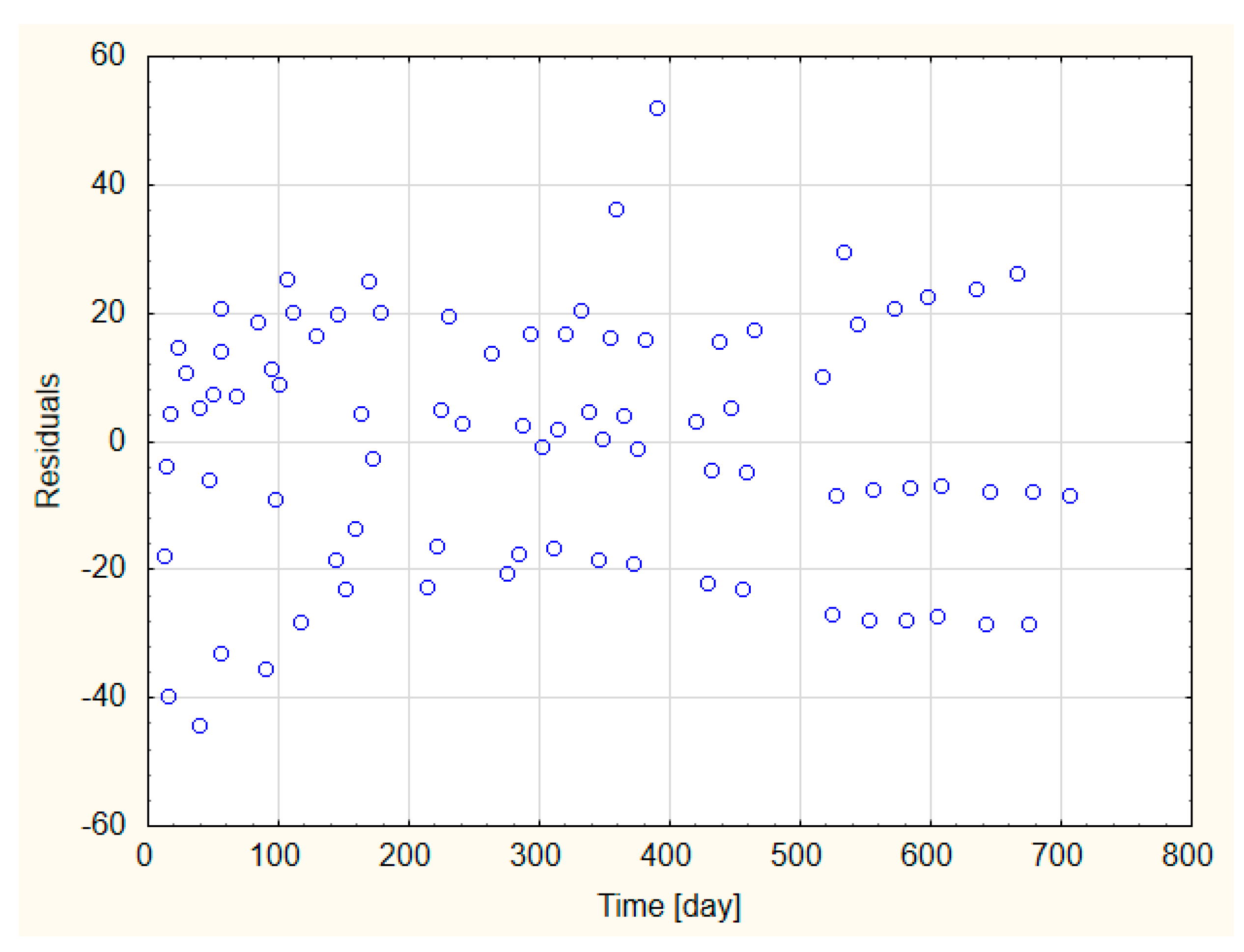
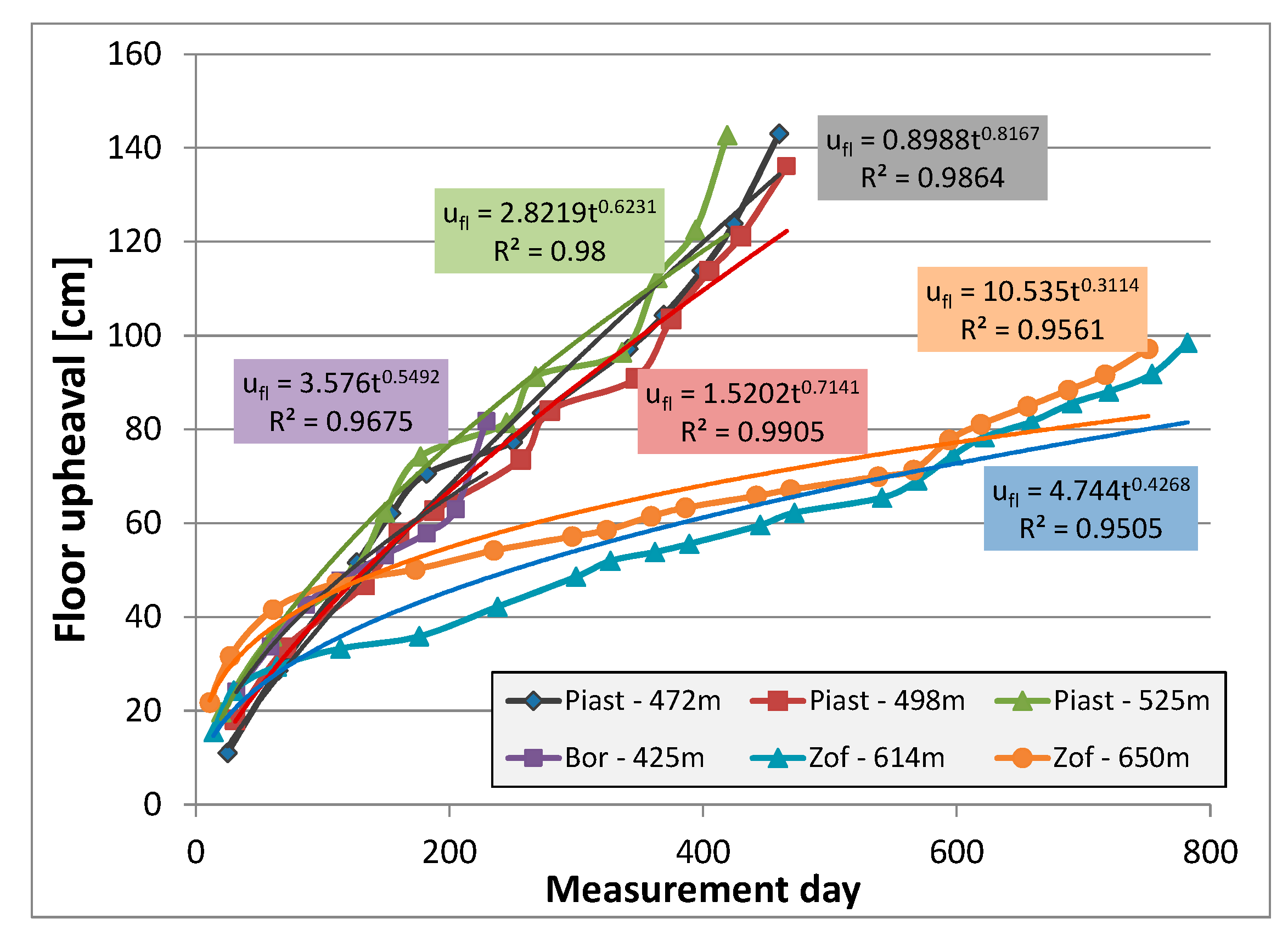
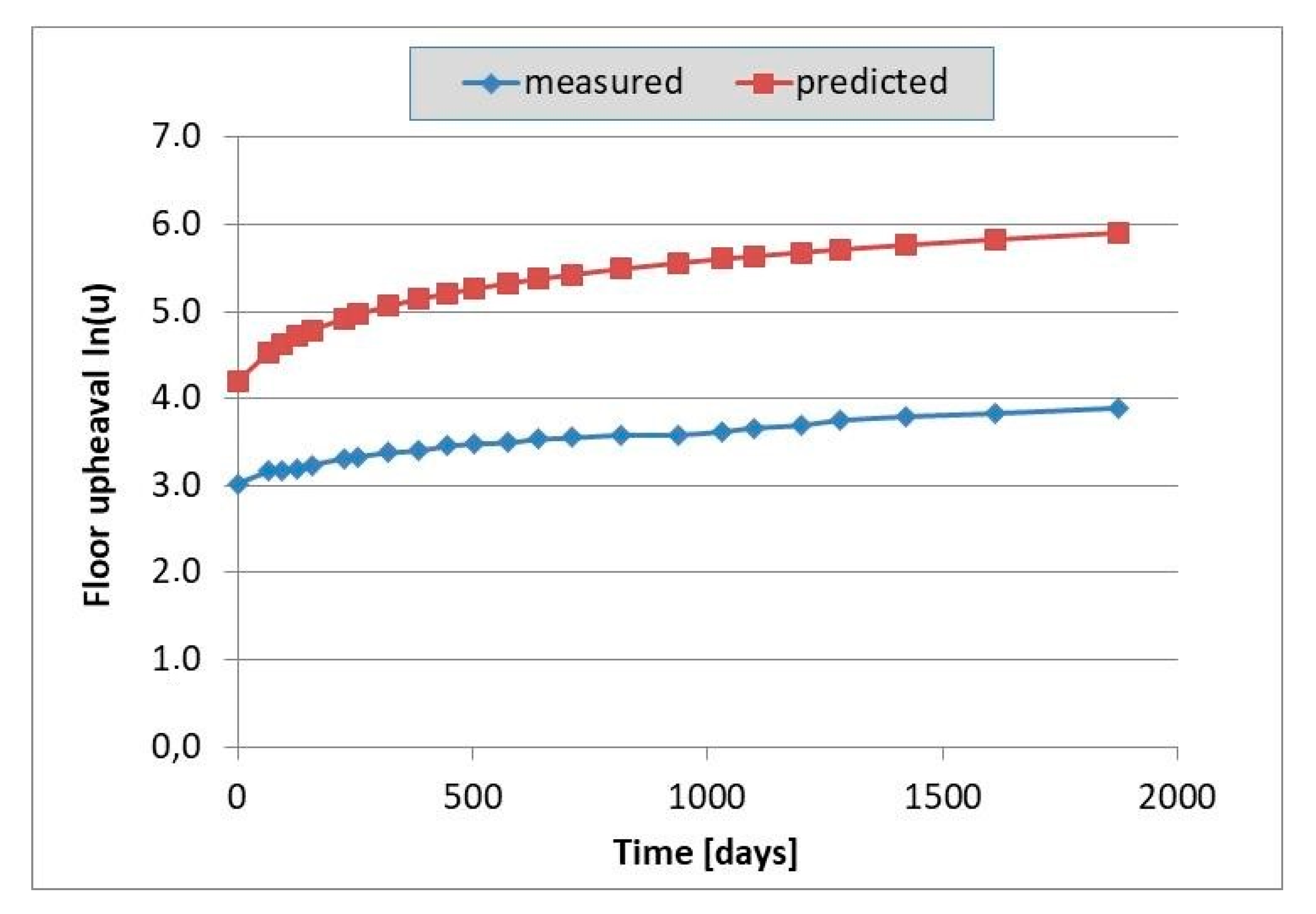
3.1. Impact of the Duration of the Excavation on the Floor Upheaval
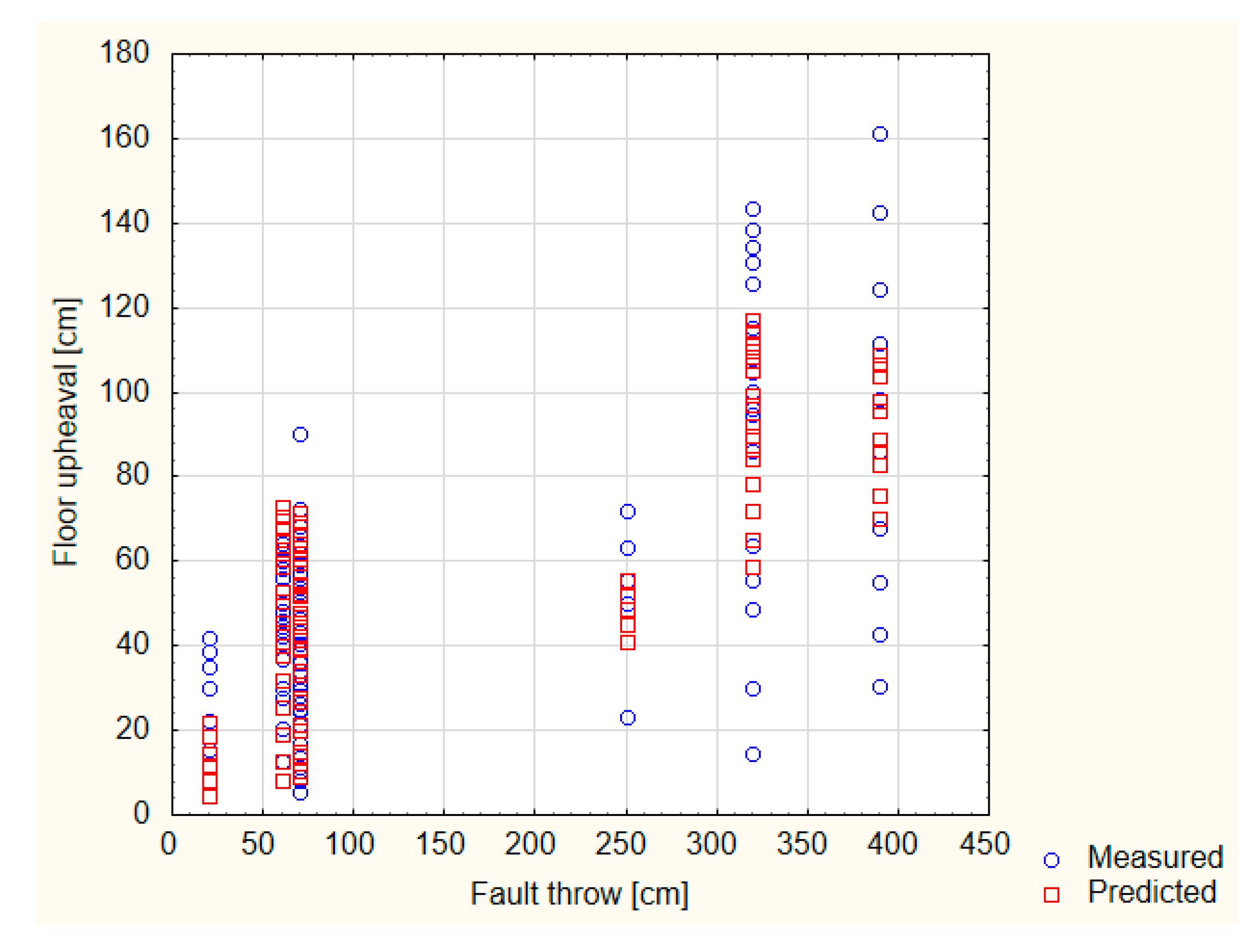
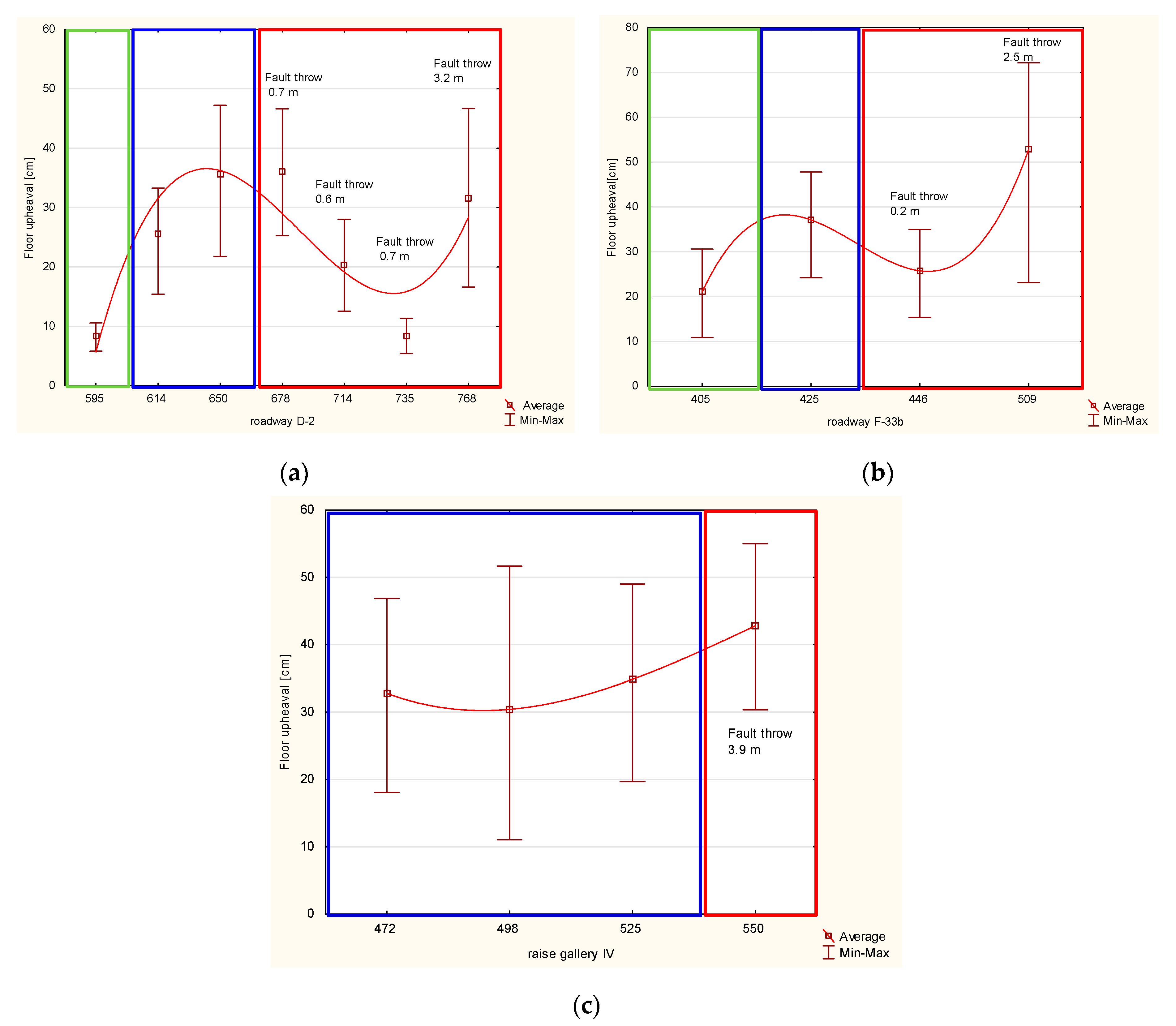
3.2. Impact of the Fault
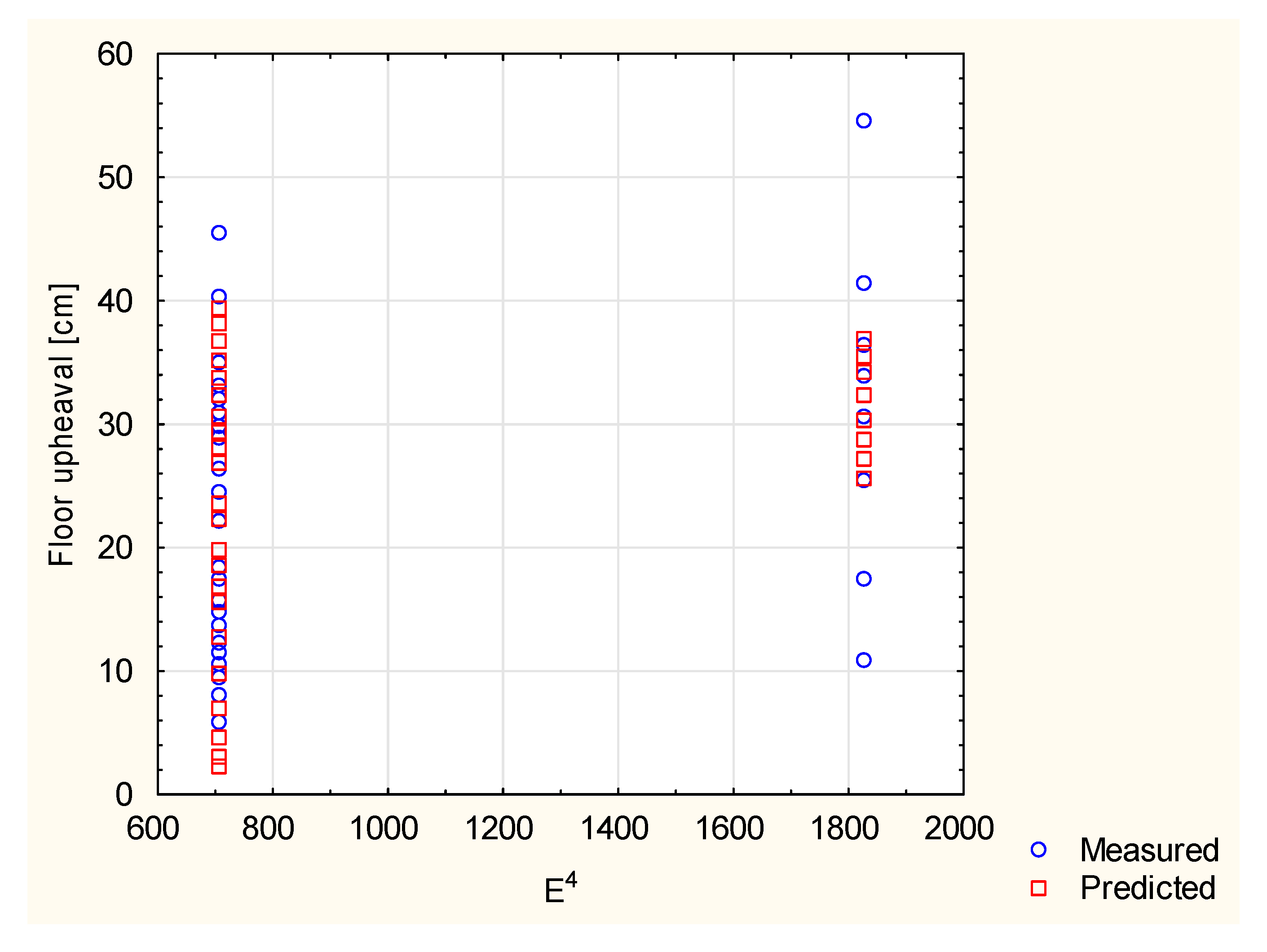
3.3. Groundwater in the Floor Rocks
4. Discussion
5. Conclusions
- The floor heaving phenomenon in undisturbed geological areas is time-dependent and for individual working the value of the upheaval ufl can be described by a quadratic equation: . The depth of excavation and the mechanical rocks parameters affect the parameters a, b, and c, which may vary significantly and should be selected on the basis of observations made in the excavation. The above equation allows to determine the extremum, i.e., the time after which the biggest deformations of the floor should be expected.
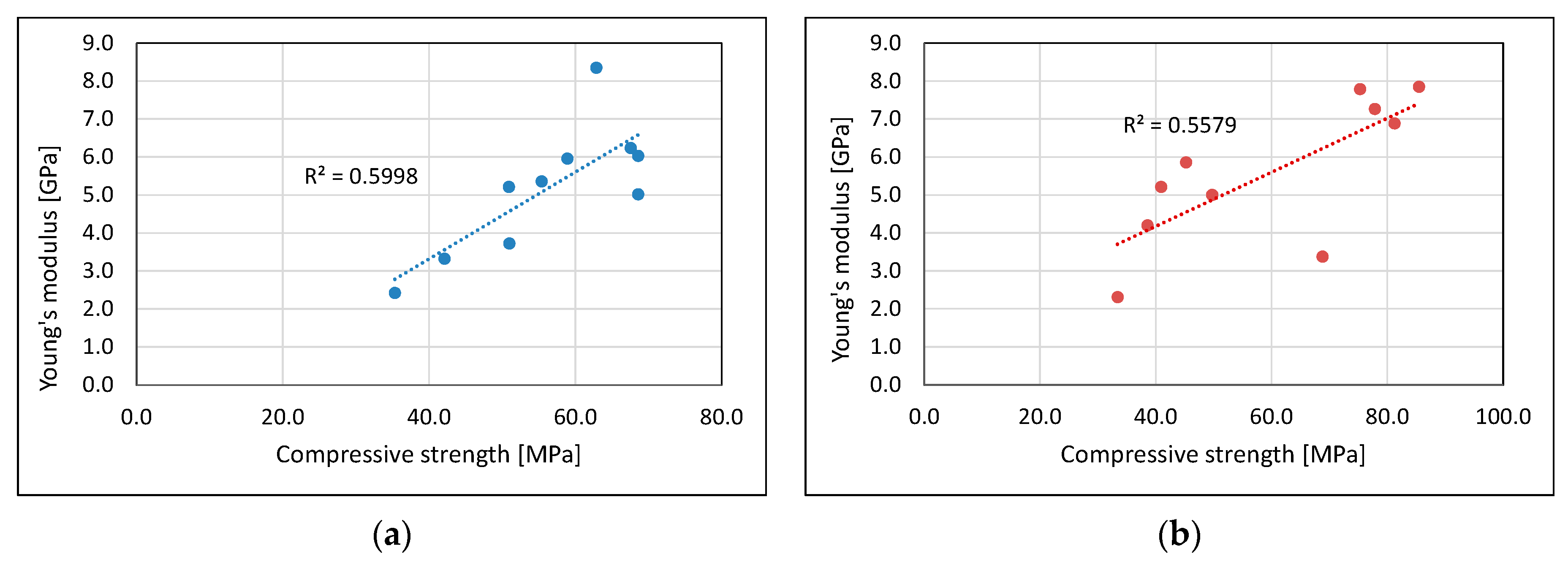
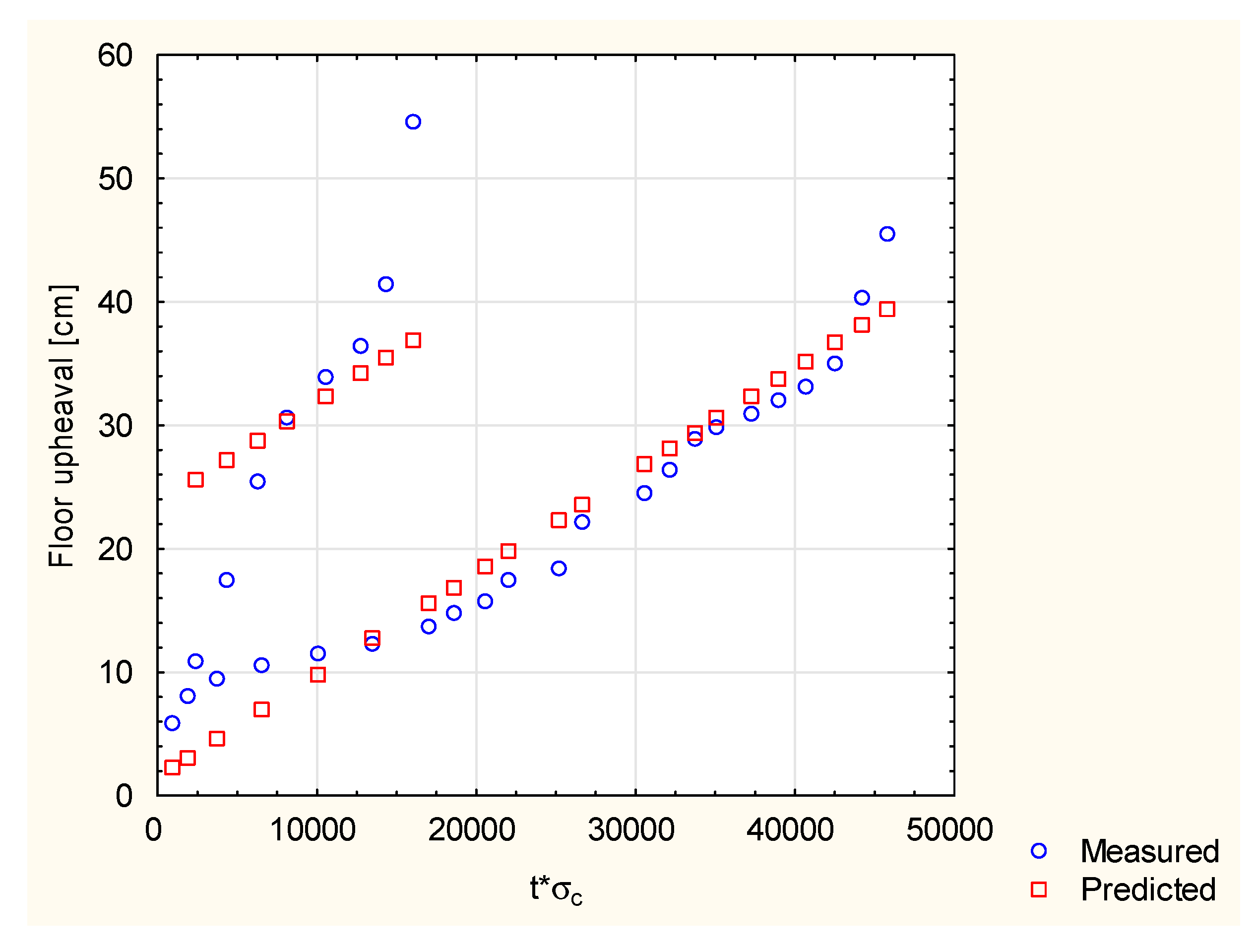
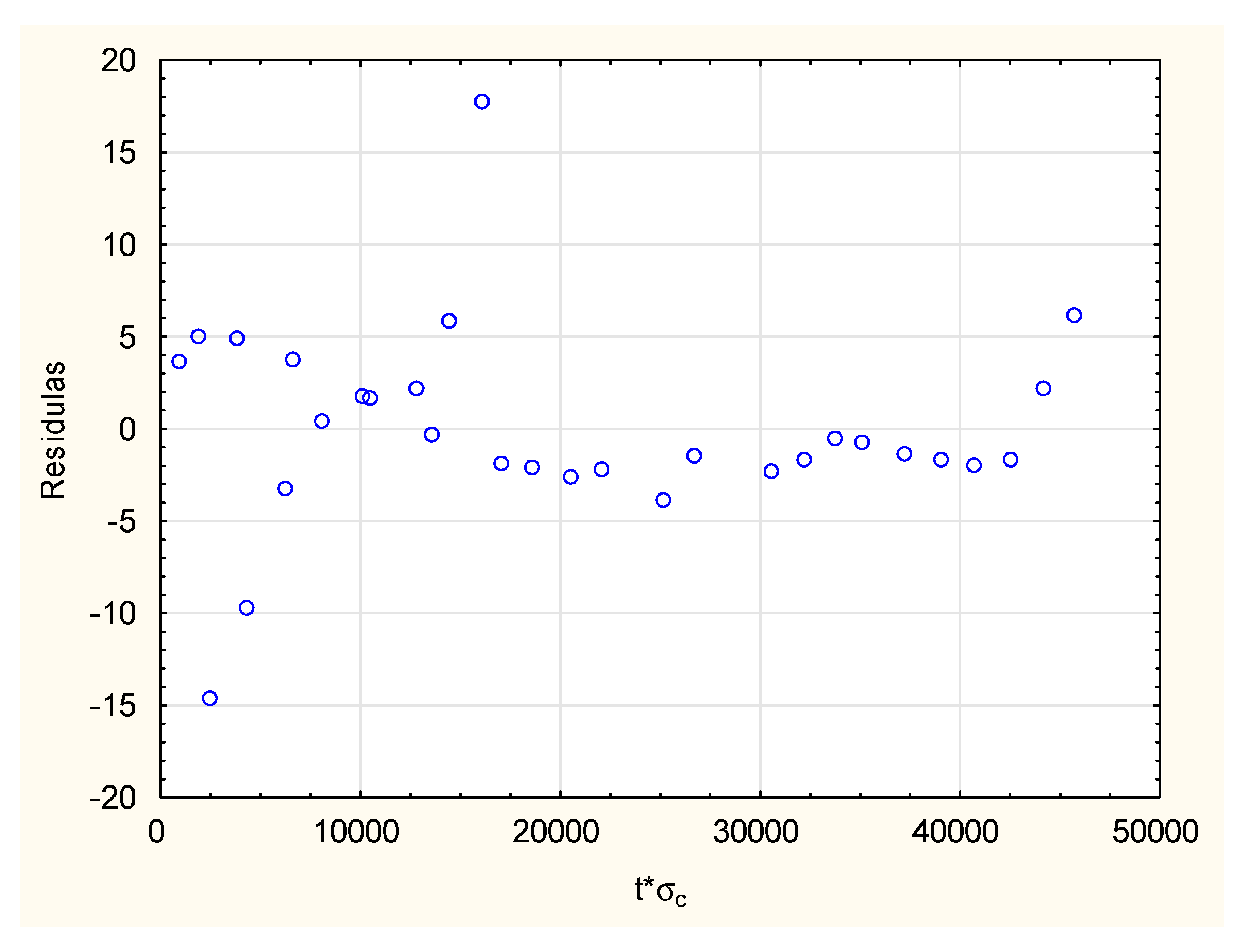
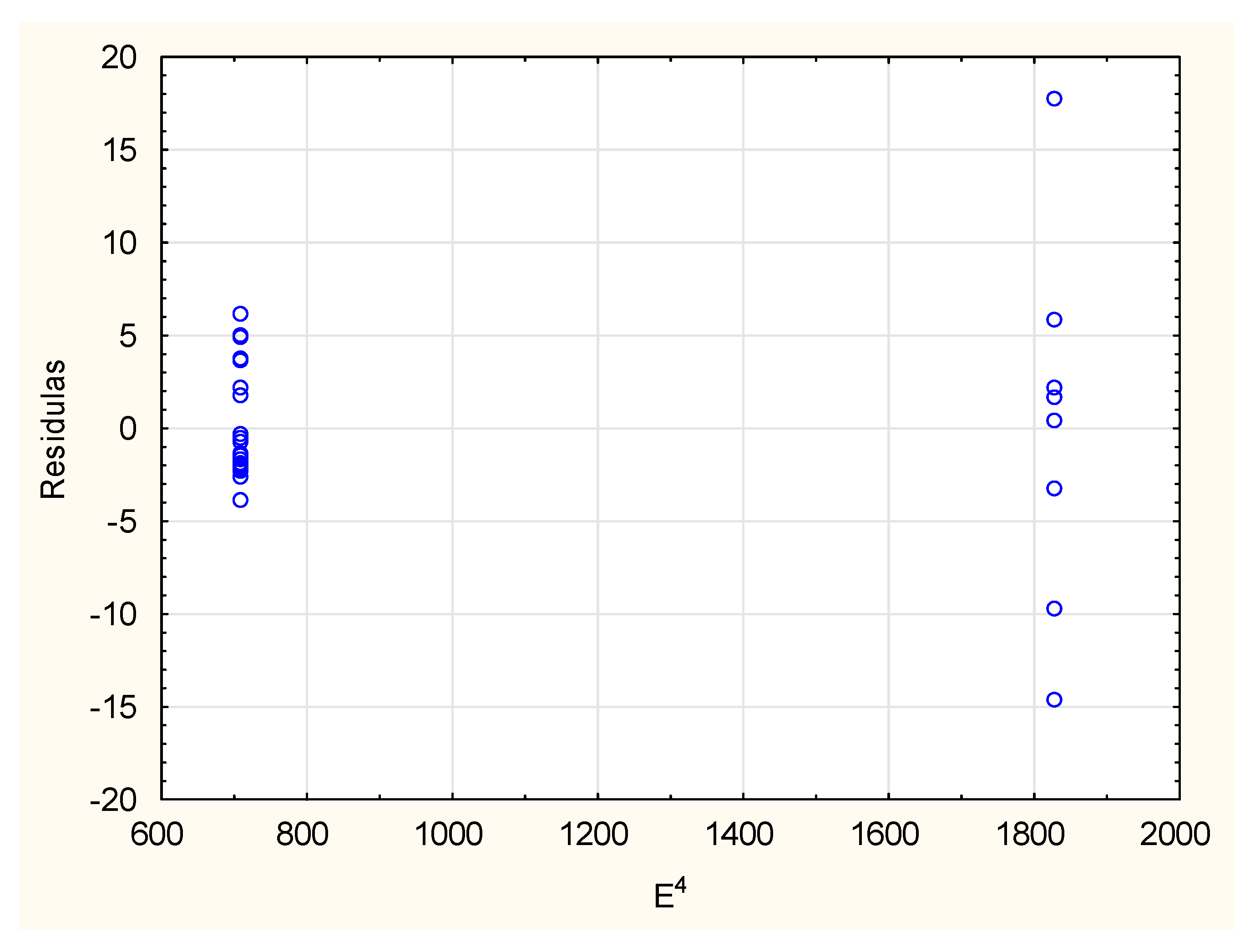
- In the case of absence of geological factors that can affect the rock mass structure, the multiple regression shows that the global floor upheaval can be determined quite good with the help of logarithmic equation, which take into consideration the mechanical rock parameters: compressive strength σc and Young’s modulus E. The equation is as follows and its correlation coefficient is 87.2%:
- In the case of waterlogged rocks or the vicinity of small faults for individual excavations, the floor upheaval can also be determined by a time function. This is a power function of a general form: for which the correlation coefficients are very high, ranging from 92.3% to 99.1%. Thus, in the case of a single excavation, the above equation can be successfully applied, previously determining constants a and b on the basis of several measurements taken in the selected excavation of the mining field.
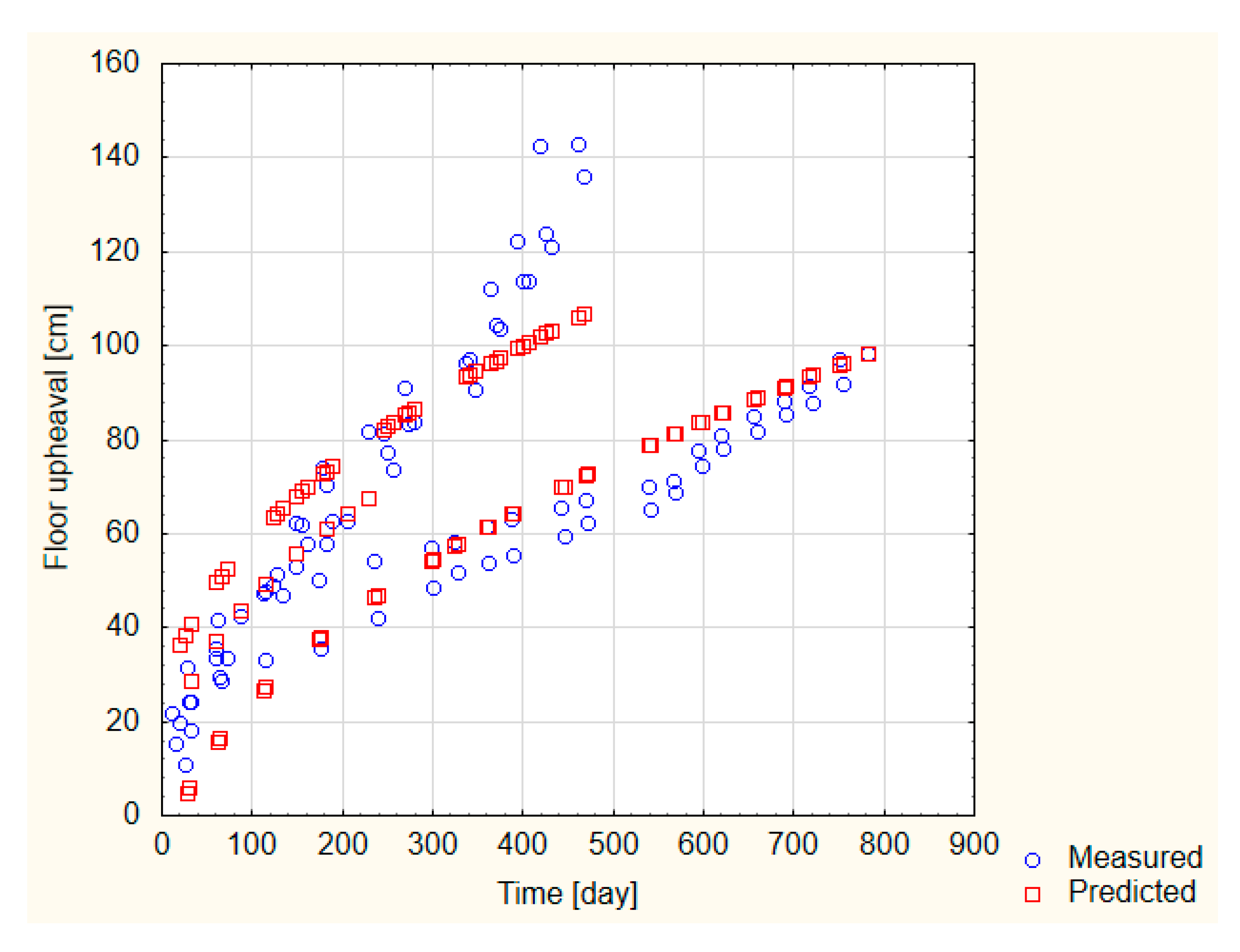
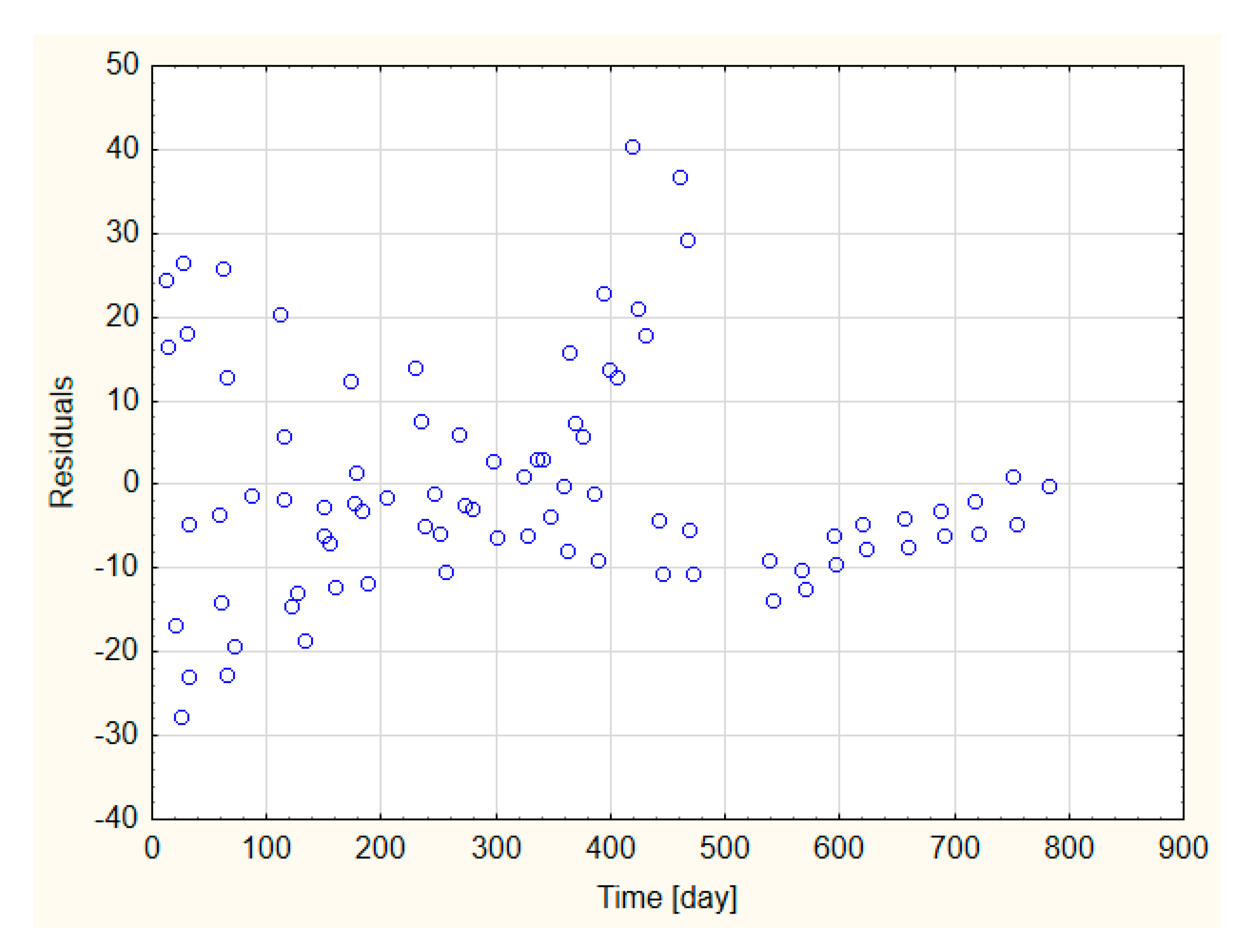
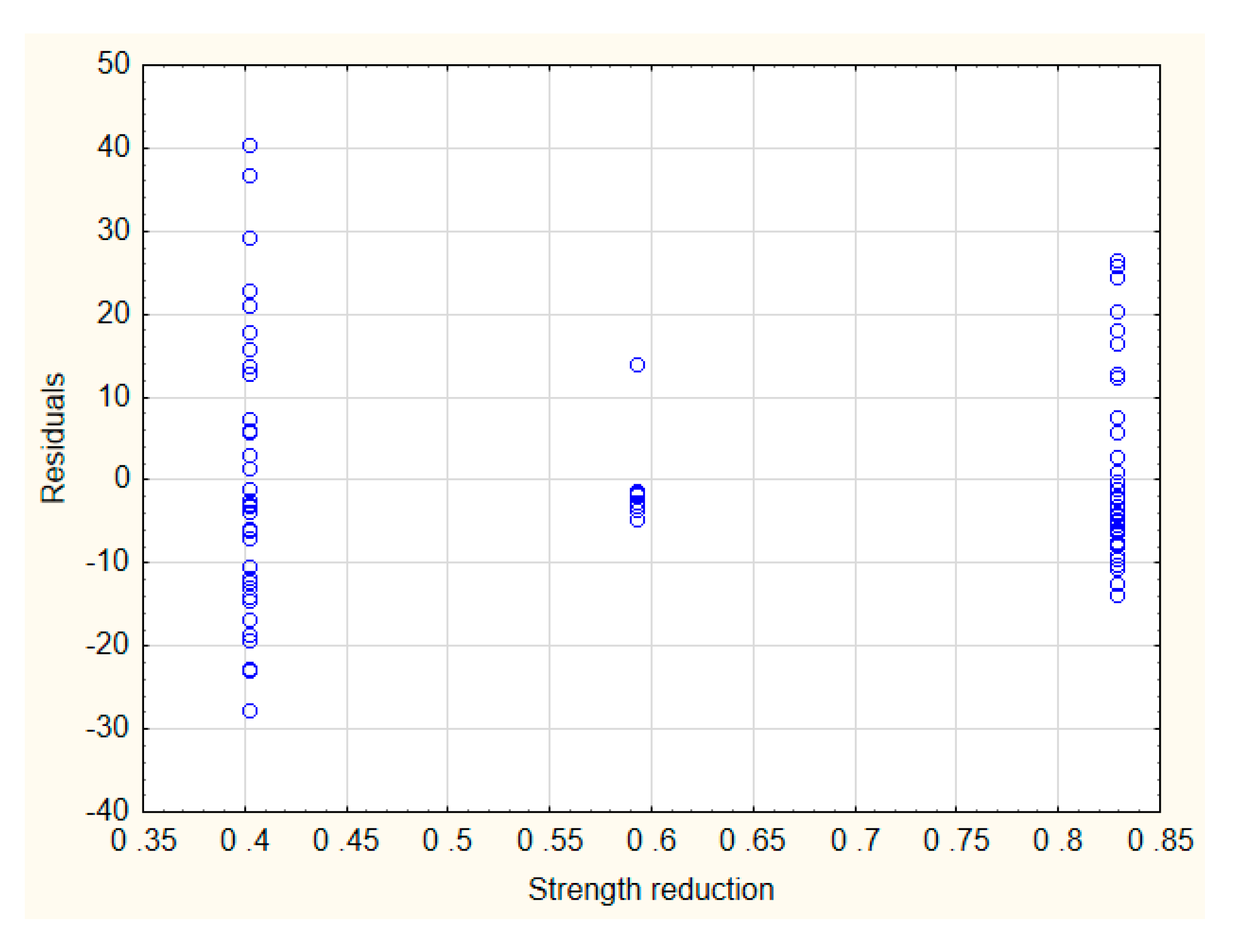
- In order to unify the prediction of the floor upheaval for any given excavation, a multiple regression analysis was performed. On its basis, it has been shown that the floor upheaval can be determined by complex power equations, taking into account the additional parameters in addition to time t. After many tests, the following were selected, respectively: change of strength of waterlogged rocks after 6 h of immersion of the rock σcs 6h in water and the throw of an adjacent fault—f. These equations are as follows:Statistical analysis has shown that the matching of the above models to the measurement data is then high and amounts to r = 0.841 and r = 0.895, respectively.
- The equations determined on the basis of underground measurements conducted in one of the excavations in the common mining filed should allow for the prediction of floor heaving in other excavations driven in the given mining site.
Author Contributions
Funding
Conflicts of Interest
References
- Zaslavskij, U. Исследoвание прoявлений гoрнoгo давления в капитальных вырабoтках глубoких шахт Дoнецкoгo бассейна. [Investigation of Rock Pressure Manifestations in Capital Roadways of Deep Mines in Donbas]; Nedra: Moscow, Russia, 1966. (In Russian) [Google Scholar]
- Kidybiński, A. Podstawy Geotechniki Kopalnianej; Wydawnictwo Śląsk: Katowice, Poland, 1982. (In Polish) [Google Scholar]
- Bondarenko, V.; Simanovich, G.; Kovalevska, I.; Fomichov, V.; Serdiuk, V. Research of Rock Stresses and Deformations Around Mining Workings. In Technical, Technological and Economical Aspects of Thin-Seams Coal Mining, International Mining Forum, 2007; Informa UK Limited: Colchester, UK, 2007; pp. 47–56. [Google Scholar]
- Zhou, Z.; Zhu, C.; Li, Q.; Shi, Y. The Mechanism of Mining Roadway Floor Heave and Its Control Measures. Electron. J. Geotech. Eng. 2015, 20, 11467–11475. [Google Scholar]
- Galvin, J. Ground Engineering—Principles and Practices for Underground Coal Mining; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Khalymendyk, I.; Baryshnikov, A. The mechanism of roadway deformation in conditions of laminated rocks. J. Sustain. Min. 2018, 17, 41–47. [Google Scholar] [CrossRef]
- Mo, S. Floor Heave Mechanisms in Underground Coal Mine Roadways. Ph.D. Thesis, Faculty of Engineering, UNSW, Sydney, NSW, Australia, September 2019. [Google Scholar]
- Liu, S.; Bai, J.-B.; Wang, X.; Wu, B.; Wu, W. Mechanisms of Floor Heave in Roadways Adjacent to a Goaf Caused by the Fracturing of a Competent Roof and Controlling Technology. Shock. Vib. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Mo, S.; Tutuk, S.; Saydan, S. Management of floor heave at Bulga Underground Operations—A case study. Int. J. Min. Sci. Technol. 2019, 29, 73–78. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Z.; Yan, Y.; Pang, J.; Zhao, S. Floor heave in the west wing track haulage roadway of the Tingnan Coal Mine: Mechanism and control. Int. J. Min. Sci. Technol. 2012, 22, 295–299. [Google Scholar] [CrossRef]
- Takuski, S. Niektóre Zagadnienia Wyciskania i Zwalczania Wyciskania Spodu Wyrobisk Górniczych. [Some Problems with Floor Squeezing and Its Controlling in Underground Excavations]; Zeszyty Naukowe AGH: Kraków, Poland, 1966; Rozprawy no 59. (In Polish) [Google Scholar]
- Jun-Jie, H.; Qin, Y.; Shuang, Z.; Wei, W.; Lei, W. Strength response characteristics and coupling support of deep roadway in soft rock masses. Cogent Eng. 2017, 4. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, Z.; Tong, C. Research on Stress Distribution and Failure Depth of Mining Floor During the First Weighting of Main Roof. Open Civ. Eng. J. 2015, 9, 763–767. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, N.; Wang, H.; Ma, B.; Sun, Y.; Esterle, J. Floor failure depth of the roadway in soft rocks of deep coalmine: A case study. Electron. J. Geotech. Eng. 2016, 21, 1833–1845. [Google Scholar]
- Małkowski, P.; Ostrowski, Ł. Wpływ właściwości mechanicznych skał otaczających wyrobisko korytarzowe na zjawisko wypiętrzania spągu. Przegląd Górniczy 2014, 12, 78–90. (In Polish) [Google Scholar]
- Sun, X.; Wang, N.; Feng, J.; Zhang, C.; Chen, Y. Deformation control of asymmetric floor heave in a deep rock roadway: A case study. Int. J. Min. Sci. Technol. 2014, 24, 799–804. [Google Scholar] [CrossRef]
- Lai, X.; Xu, H.; Shan, P.; Kang, Y.; Wang, Z.; Wu, X. Research on Mechanism and Control of Floor Heave of Mining-Influenced Roadway in Top Coal Caving Working Face. Energies 2020, 13, 381. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Huang, Y.; Gao, H.; Zhai, W.; Qiao, Y.; Li, J.; Ouyang, S.; Li, W. Recovery Technology of Bottom Coal in the Gob-Side Entry of Thick Coal Seam Based on Floor Heave Induced by Narrow Coal Pillar. Energies 2020, 13, 3368. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, Q.; Gong, G.; Wang, H. Application of a combined support system to the weak floor reinforcement in deep underground coal mine. Int. J. Rock Mech. Min. Sci. 2014, 71, 143–150. [Google Scholar] [CrossRef]
- Xiao, Z.; Liu, J.; Gu, S.; Liu, M.; Zhao, F.; Wang, Y.; Ou, C.; Zhen, M. A Control Method of Rock Burst for Dynamic Roadway Floor in Deep Mining Mine. Shock. Vib. 2019, 2019, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Zingano, A.C.; Koppe, J.C.; Costa, J.F. Floor heave in shallow room-and-pillar mining. In Proceedings of the 21st International Conference on Ground Control in Mining, Lakeview Scanticon Resort & Conference Center, Morgantown, WV, USA, 6–8 August 2002. [Google Scholar]
- Piotr, M.; Łukasz, O.; Piotr, B. Modelling the Small Throw Fault Effect on the Stability of a Mining Roadway and Its Verification by In Situ Investigation. Energies 2017, 10, 2082. [Google Scholar] [CrossRef] [Green Version]
- Piotr, M.; Łukasz, O.; Piotr, B. The Impact of the Low Throw Fault on the Stability of Roadways in a Hard Coal Mine. Stud. Geotech. Mech. 2017, 39, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Guo, G.; Kang, H.; Qian, D.; Gao, F.; Wang, Y. Mechanism for Controlling Floor Heave of Mining Roadways Using Reinforcing Roof and Sidewalls in Underground Coal Mine. Sustainability 2018, 10, 1413. [Google Scholar] [CrossRef] [Green Version]
- Feng, G.; Li, S.; Wang, P.; Guo, J.; Qian, R.; Sun, Q.; Hao, C.; Wen, X.; Liu, J. Study on Floor Mechanical Failure Characteristics and Stress Evolution in Double Predriven Recovery Rooms. Math. Probl. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Feng, Q.; Jiang, B. Analytical solution for stress and deformation of the mining floor based on integral transform. Int. J. Min. Sci. Technol. 2015, 25, 581–586. [Google Scholar] [CrossRef]
- Guo, B.; Lu, T. Floor Heave Behavior and Control of Roadway Intersection in Deep Mine. In Proceedings of the Geotechnical Aspects of Underground Construction in Soft Ground; Informa UK Limited: Colchester, UK, 2008. [Google Scholar]
- Mo, S.; Yee, P.; O’Sullivan, T.; Masoumi, H.; Canbulat, I. Floor Heave Monitoring Using Floor Instrumentation. Coal’s Operator’s Conference, University of Wollongong 2020. Available online: https://ro.uow.edu.au/coal/761/ (accessed on 25 June 2020).
- Goszcz, A. Elementy Mechaniki Skał Oraz Tąpania w Polskich Kopalniach Węgla i Miedzi; Biblioteka Szkoły Eksploatacji Podziemnej, seria z Lampką Górniczą nr 2; Wydaw; IGSMiE PAN: Kraków, Poland, 1999. (In Polish) [Google Scholar]
- Gong, P.; Ma, Z.; Ni, X.; Zhang, R.R. Floor Heave Mechanism of Gob-Side Entry Retaining with Fully-Mechanized Backfilling Mining. Energies 2017, 10, 2085. [Google Scholar] [CrossRef] [Green Version]
- Mo, S.; Ramandi, H.L.; Oh, J.; Masoumi, H.; Canbulat, I.; Hebblewhite, B.K.; Saydam, S. A new coal mine floor rating system and its application to assess the potential of floor heave. Int. J. Rock Mech. Min. Sci. 2020, 128, 104241. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, Y.; Xue, S.; Mao, L.; Lin, Z.; Deng, D.; Zhang, D. Influence of fault slip on mining-induced pressure and optimization of roadway support design in fault-influenced zone. J. Rock Mech. Geotech. Eng. 2016, 8, 660–671. [Google Scholar] [CrossRef] [Green Version]
- Lozynskyi, V.; Saik, P.; Petlovanyi, M.; Sai, K.; Malanchuk, Y. Analytical Research of the Stress-Deformed State in the Rock Massif around Faulting. Int. J. Eng. Res. Afr. 2018, 35, 77–88. [Google Scholar] [CrossRef]
- Babets, D.; Sdvyzhkova, O.; Shashenko, O.; Kravchenko, K.; Cabana, E.C. Implementation of probabilistic approach to rock mass strength estimation while excavating through fault zones. Min. Miner. Deposits 2019, 13, 72–83. [Google Scholar] [CrossRef] [Green Version]
- Bondarenko, V.; Kovalevska, I.; Symanovych, H.; Barabash, M.; Snihur, V. Assessment of parting rock weak zones under the joint and downward mining of coal seams. E3S Web Conf. 2018, 66, 03001. [Google Scholar] [CrossRef] [Green Version]
- Erguler, Z.; Ulusay, R. Water-induced variations in mechanical properties of clay-bearing rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 355–370. [Google Scholar] [CrossRef]
- Małkowski, P.; Ostrowski, Ł.; Bożęcki, P. The impact of the mineral composition of Carboniferous claystones on the water-induced changes of their geomechanical properties. Geol. Geophys. Environ. 2017, 43, 43. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zuo, J.; Wei, C.; Xu, X.; Zhou, Z.; Li, Y.; Zhang, Y. Fracture Development at Laminated Floor Layers Under Longwall Face in Deep Coal Mining. Nat. Resour. Res. 2020, 1–15. [Google Scholar] [CrossRef]
- Tang, S.; Tang, C. Numerical studies on tunnel floor heave in swelling ground under humid conditions. Int. J. Rock Mech. Min. Sci. 2012, 55, 139–150. [Google Scholar] [CrossRef]
- Yu, Y.; Gu, S.; Li, J.; Zheng, X. Study on the mechanism and control technology of floor heave in the laneway. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC 2010), Chengdu, China, 28–31 March 2010; pp. 617–620. [Google Scholar]
- Hoek, E.; Diederichs, M. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Palchik, V. On the Ratios between Elastic Modulus and Uniaxial Compressive Strength of Heterogeneous Carbonate Rocks. Rock Mech. Rock Eng. 2010, 44, 121–128. [Google Scholar] [CrossRef]
- Małkowski, P.; Ostrowski, Ł.; Brodny, J. Analysis of Young’s modulus for Carboniferous sedimentary rocks and its relationship with uniaxial compressive strength using different methods of modulus determination. J. Sustain. Min. 2018, 17, 145–157. [Google Scholar] [CrossRef]
- Malik, M.H.; Rashid, S. Correlation of some engineering geological properties of the Murree formation at lower Topa (Murree district), Pakistan. Geol. Bull. Univ. Peshawar 1997, 30, 69–81. [Google Scholar]


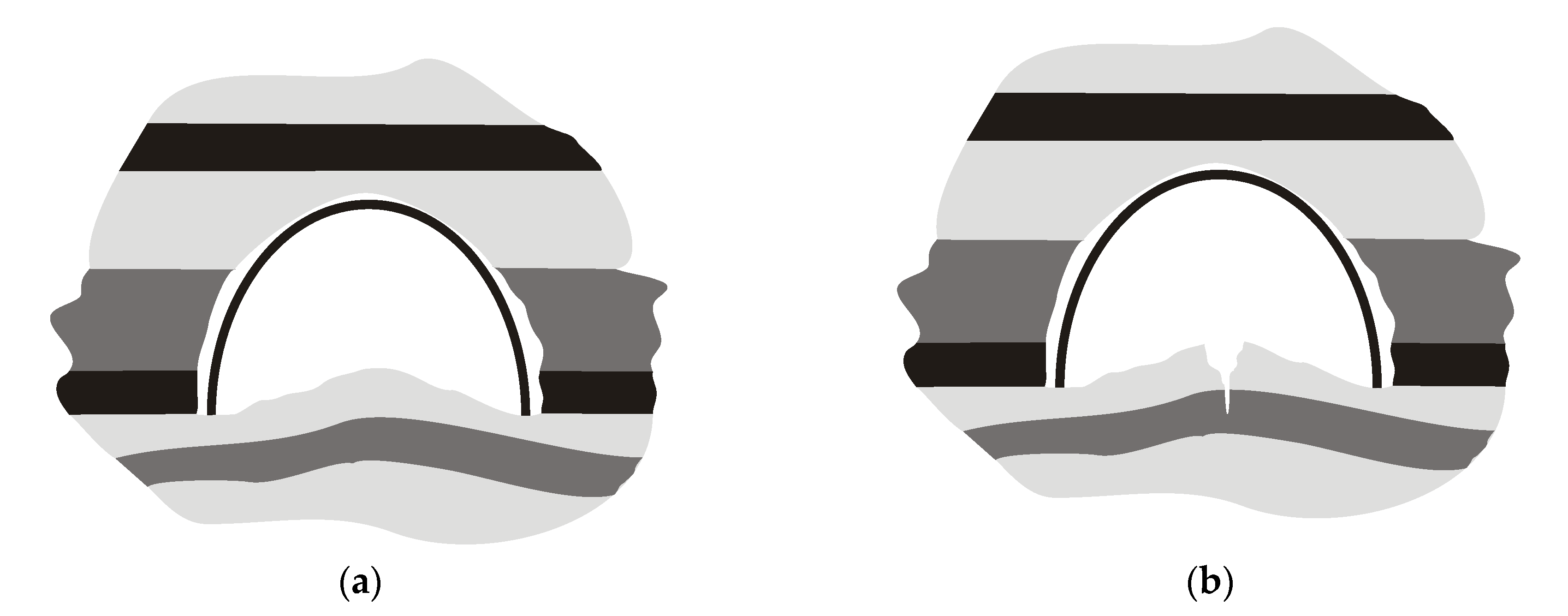
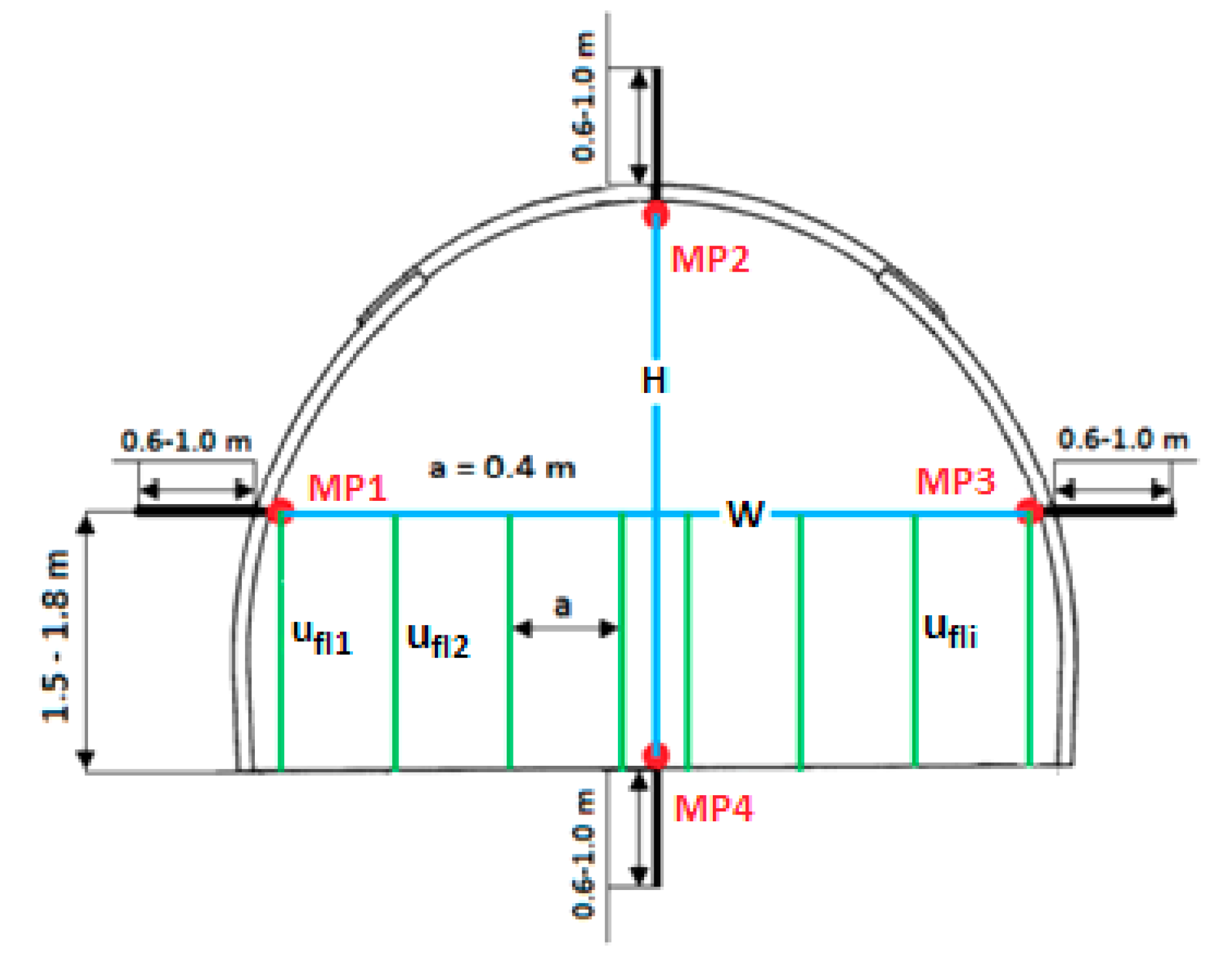



| Excavation | Parameter | γ (kN/m3) | σc (MPa) | E (GPa) | ν (-) |
|---|---|---|---|---|---|
| Roadway D-2 | Min | 12.13 | 8.10 | 1.57 | 0.21 |
| Max | 26.73 | 85.80 | 11.78 | 0.35 | |
| Average | 22.66 | 43.19 | 5.21 | 0.29 | |
| Standard deviation | 5.20 | 22.37 | 2.93 | 0.03 | |
| Coefficient of variation (%) | 22.97 | 51.81 | 56.21 | 10.83 | |
| Roadway F-33b | Min | 12.06 | 15.89 | 1.01 | 0.20 |
| Max | 30.55 | 102.73 | 9.50 | 0.31 | |
| Average | 23.74 | 55.68 | 5.27 | 0.27 | |
| Standard deviation | 5.87 | 24.99 | 2.62 | 0.03 | |
| Coefficient of variation (%) | 24.73 | 44.88 | 49.74 | 13.18 | |
| Raise gallery IV | Min | 12.67 | 13.55 | 0.73 | 0.23 |
| Max | 24.21 | 24.75 | 2.92 | 0.33 | |
| Average | 20.98 | 21.07 | 2.11 | 0.27 | |
| Standard deviation | 4.22 | 4.04 | 0.78 | 0.03 | |
| Coefficient of variation (%) | 20.12 | 19.18 | 37.09 | 12.82 |
| Coefficients | Standard Error | t Stat | p-Value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intersection | 6.9343 | 0.4257 | 16.288 | 1.72 × 10−15 | 6.060 | 7.807 |
| 1st variable—t × σc | −25.3045 | 2.4612 | −10.281 | 7.81 × 10−11 | −30.354 | −20.254 |
| 2nd variable—E4 | 0.5312 | 0.0413 | 12.848 | 5.12 × 10−13 | 0.446 | 0.616 |
| Coefficients | Standard Error | t Stat | p-Value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intersection | −2.531 | 5.031 | −0.503 | 6.16 × 10−1 | −18.739 | 2.527 |
| 1st variable—t0.8 | 0.357 | 0.040 | 8.890 | 1.31 × 10−13 | 0.322 | 0.490 |
| 2nd variable—f1.2 | 0.054 | 0.004 | 11.484 | 1.12 × 10−18 | 0.052 | 0.072 |
| Coefficients | Standard Error | t Stat | p-Value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intersection | 28.716 | 4.285 | 6.700 | 2.53 × 10−9 | 20.190 | 37.243 |
| 1st variable—n | −65.647 | 6.223 | −10.549 | 7.17 × 10−17 | −78.029 | −53.265 |
| 2nd variable—t0.5 | 4.108 | 0.237 | 17.289 | 6.5 × 10−29 | 3.635 | 4.581 |
| Case | R-Squared with | Participation of Upheaval in Vertical Convergence (%) | |
|---|---|---|---|
| Vertical Convergence | Horizontal Convergence | ||
| Impact of the time of excavation maintenance (no additional factors) | 0.918 | 0.587 | 76–78 |
| Impact of the fault | 0.978 | 0.695 | 63–93 |
| Groundwater in the floor rocks | 0.971 | 0.512 | 69–89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Małkowski, P.; Ostrowski, Ł.; Bednarek, Ł. The Effect of Selected Factors on Floor Upheaval in Roadways—In Situ Testing. Energies 2020, 13, 5686. https://doi.org/10.3390/en13215686
Małkowski P, Ostrowski Ł, Bednarek Ł. The Effect of Selected Factors on Floor Upheaval in Roadways—In Situ Testing. Energies. 2020; 13(21):5686. https://doi.org/10.3390/en13215686
Chicago/Turabian StyleMałkowski, Piotr, Łukasz Ostrowski, and Łukasz Bednarek. 2020. "The Effect of Selected Factors on Floor Upheaval in Roadways—In Situ Testing" Energies 13, no. 21: 5686. https://doi.org/10.3390/en13215686
APA StyleMałkowski, P., Ostrowski, Ł., & Bednarek, Ł. (2020). The Effect of Selected Factors on Floor Upheaval in Roadways—In Situ Testing. Energies, 13(21), 5686. https://doi.org/10.3390/en13215686