Hydrodynamics of Two-Phase Gas-Very Viscous Liquid Flow in Heat Exchange Conditions
Abstract
:1. Introduction
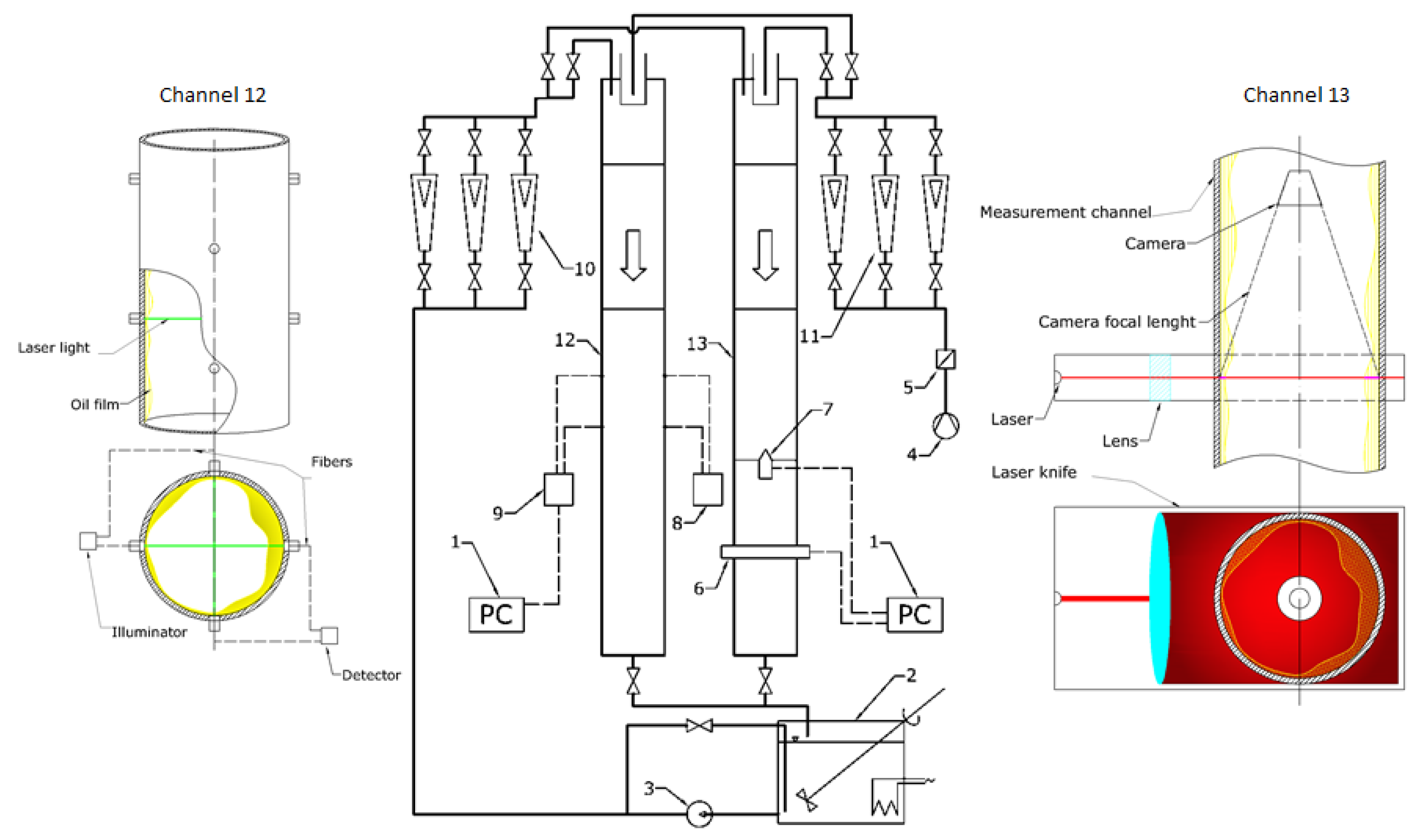
2. Materials and Methods
Experimental Setup
3. Results and Discussion
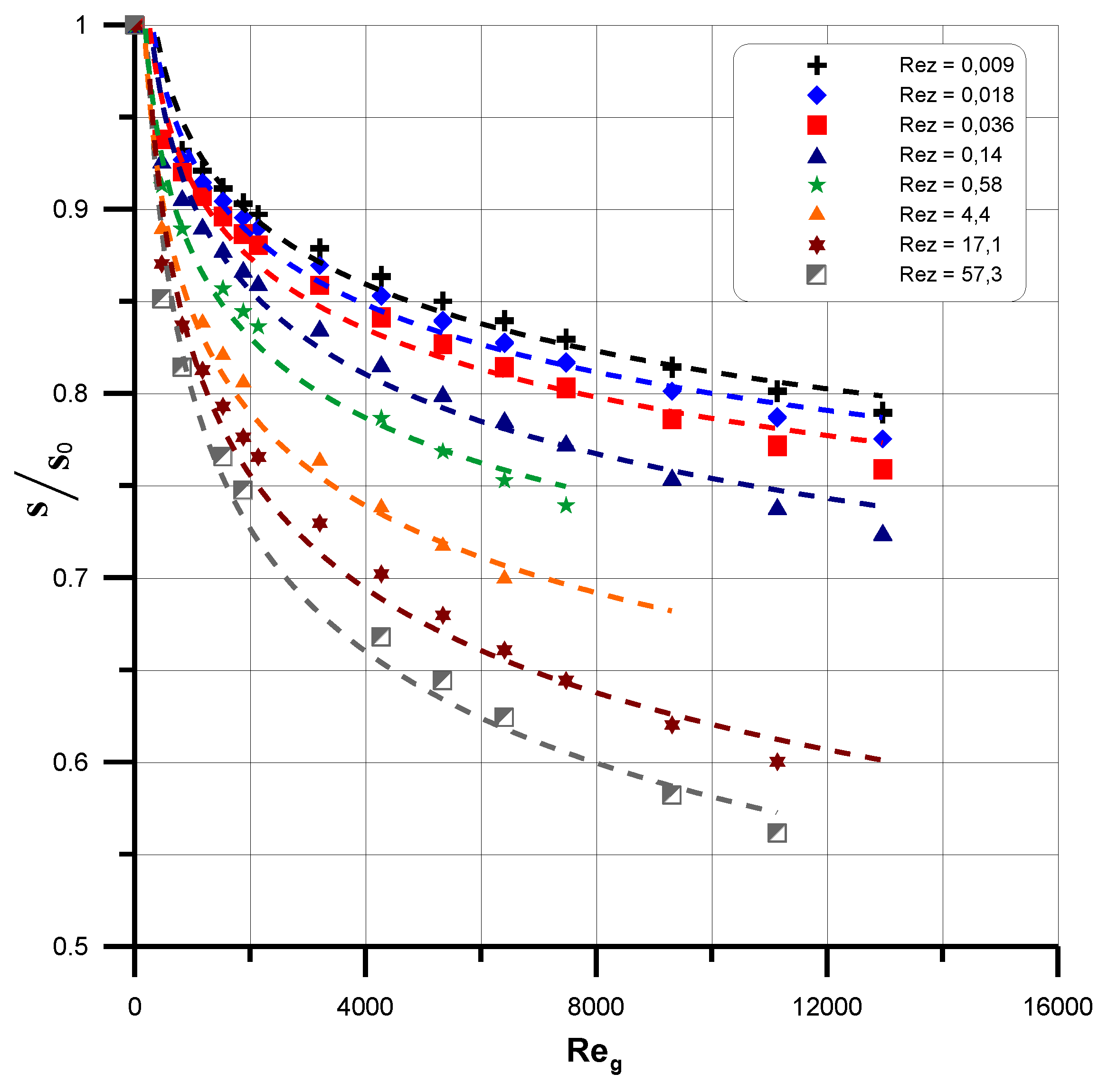
3.1. Liquid Film Thickness
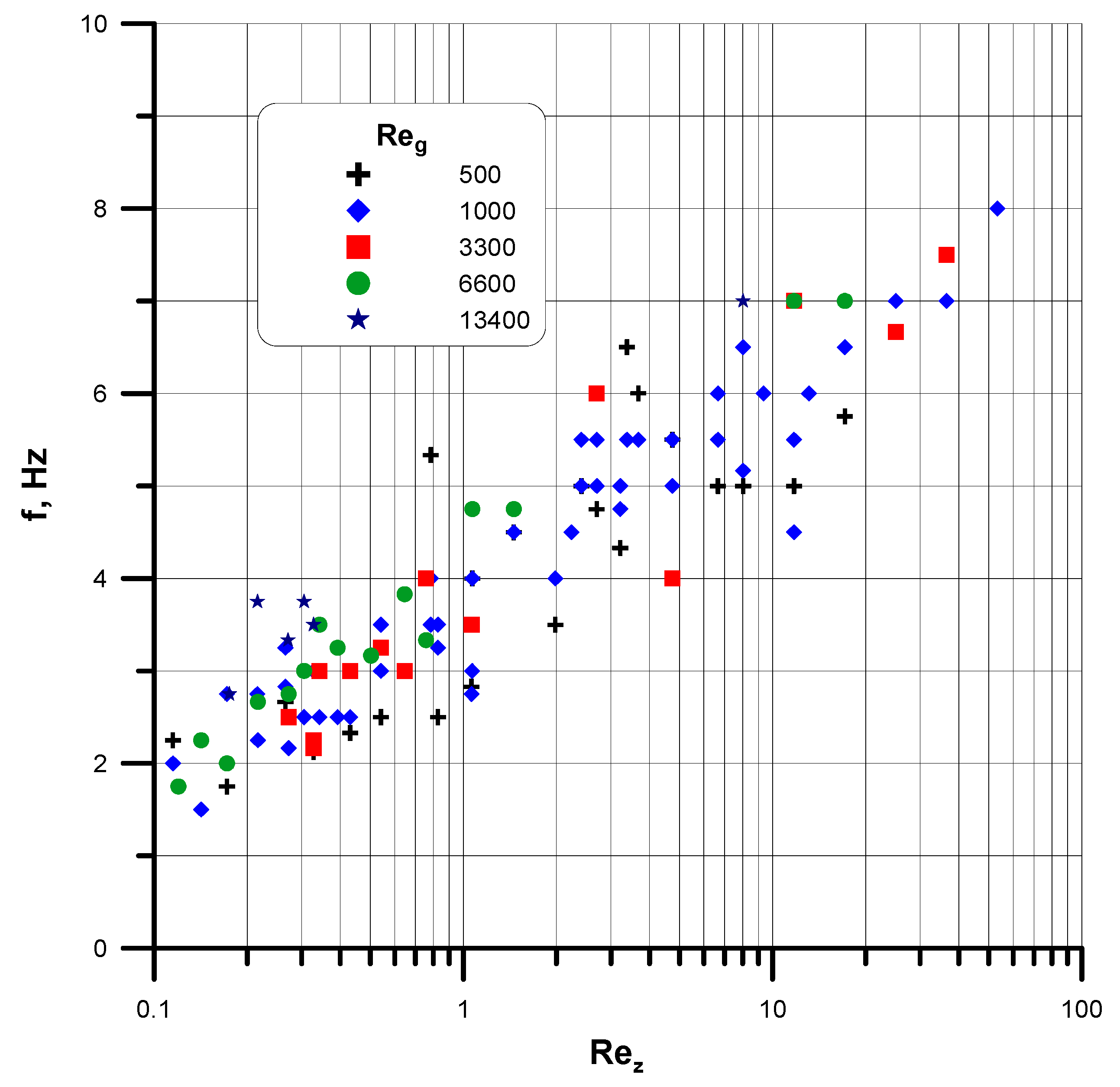
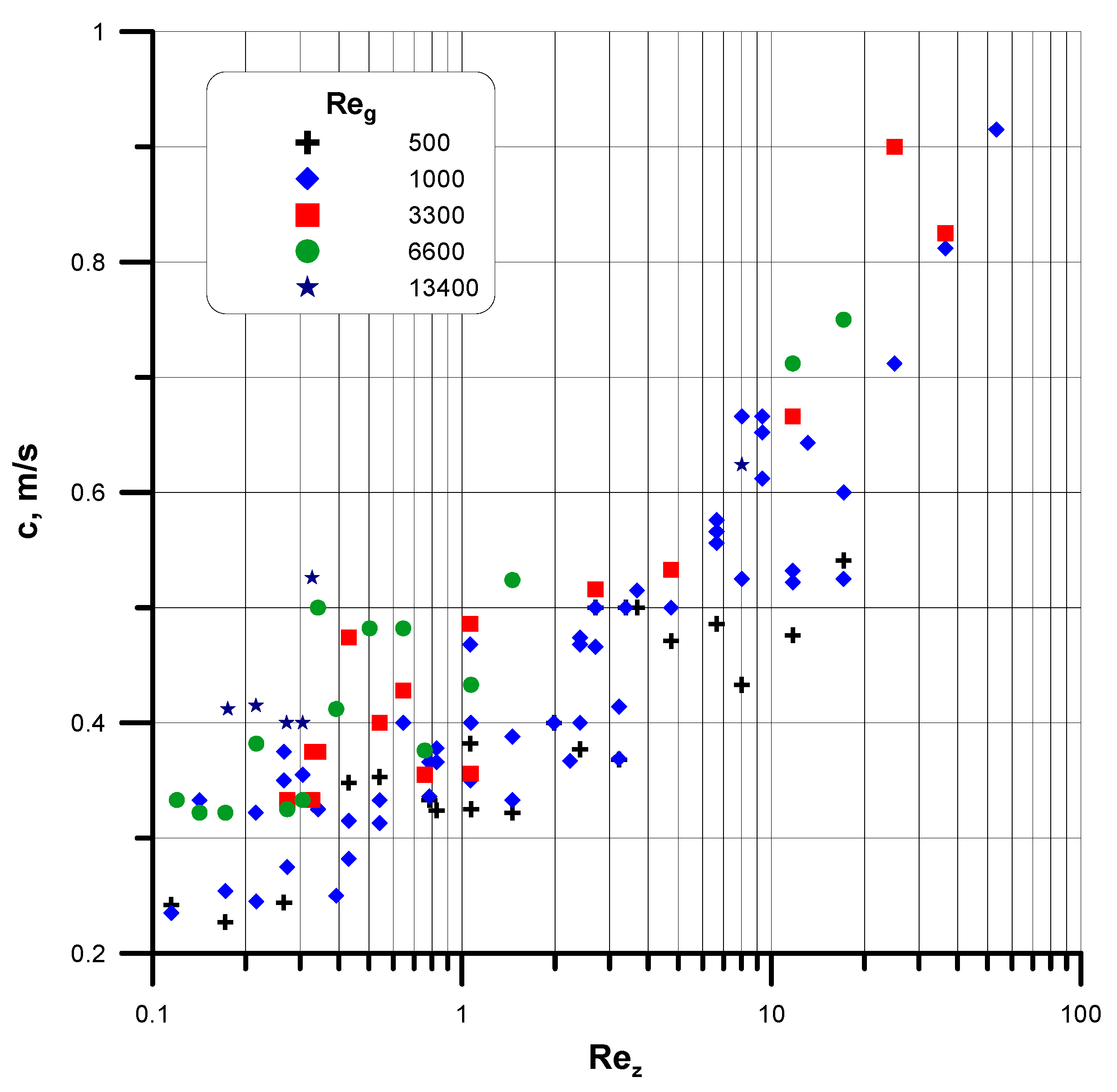
3.2. Flow Patterns
- an indication of the most likely mechanisms accompanying this flow, taking into account the range of their occurrence; and
- verification of the possible method for direct evaluation of the parameters applied in the model and the calculation methods adopted for its solution, through comparing the results of calculations with the results of the experimental tests.
- liquid film thickness, s (both locally and in terms of averaged values);
- parameters identifying the nature of wave patterns, in particular:
- ○
- amplitudes of the waves, a and their wavelength, λ,
- ○
- frequencies of the occurrence of waves, f and the velocities of their propagation, c;
- interfacial surfaces, F2F, in various conditions corresponding to the downstream flow of the liquid film.
- liquid film thickness, as the value identified both for local and averaged states;
- characteristics of waves formed on the interfacial surface, which are possible to represent by means of such liquid film parameters as: frequency and amplitude of waves on the film surface, their length and velocity of displacement along the interface; and
- mean surface of the interface between gas-viscous liquid flows, as identified for all observed forms of annular oil-air two-phase flow.
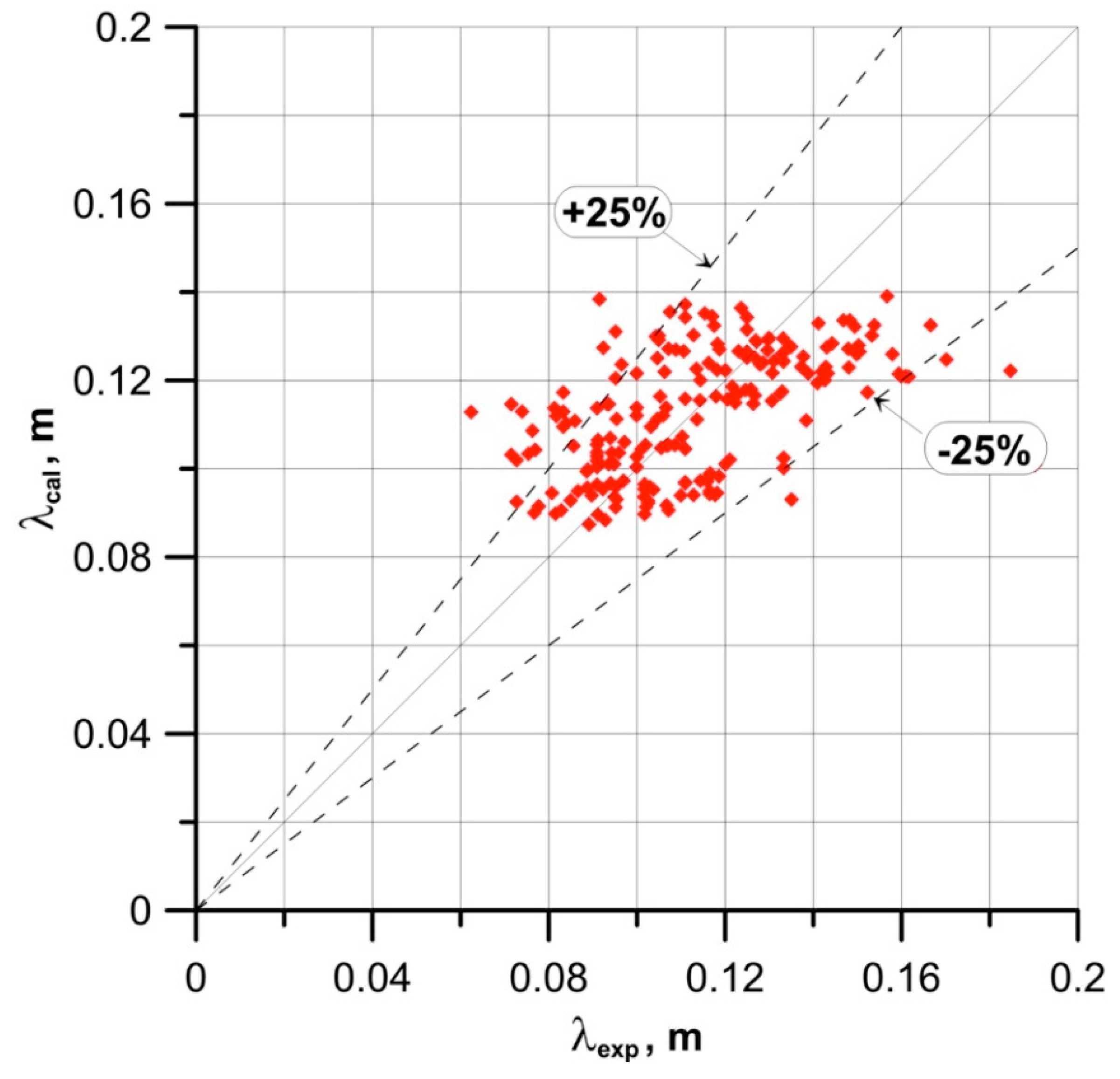
3.3. New Equations for Liquid Films
- One that is relative to the mass fraction of the gas phase (x = gg/gT) and the characteristics of the gas and liquid flow (Reg, Rel), as related to an equivalent linear dimension (ϑz):in which case, the correlation coefficient is equal to r = 0.98 and the mean standard deviation is δ = 0.18; and
- one that is relative to the Lockhart-Martinelli parameter (Xtt), as well as the gas and liquid viscosities (ηg, ηl), in the form of the equation:where ; in which case, the correlation coefficient is equal to r = 0.92 and the mean standard deviation is δ = 0.21.
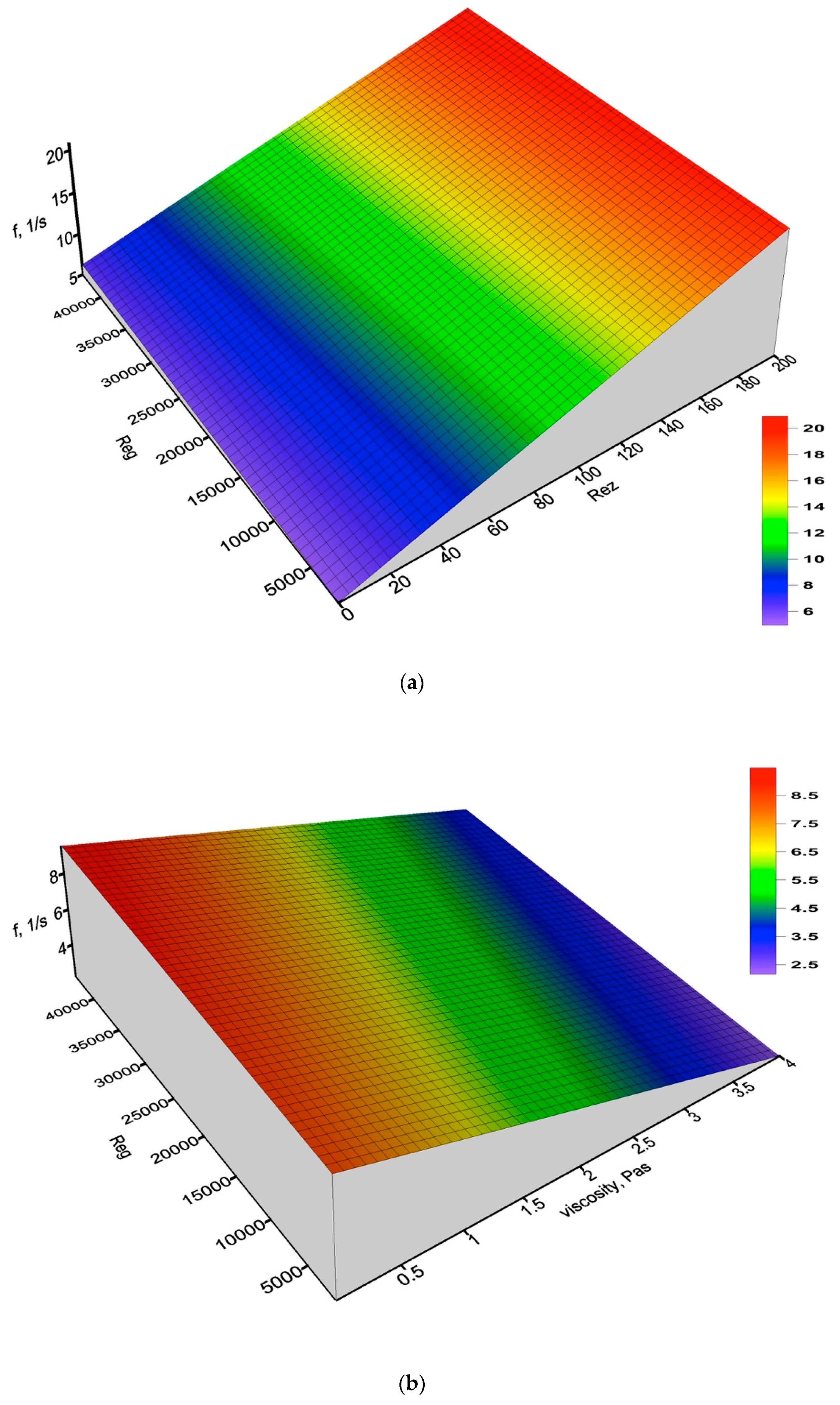
- the wave frequency, f:
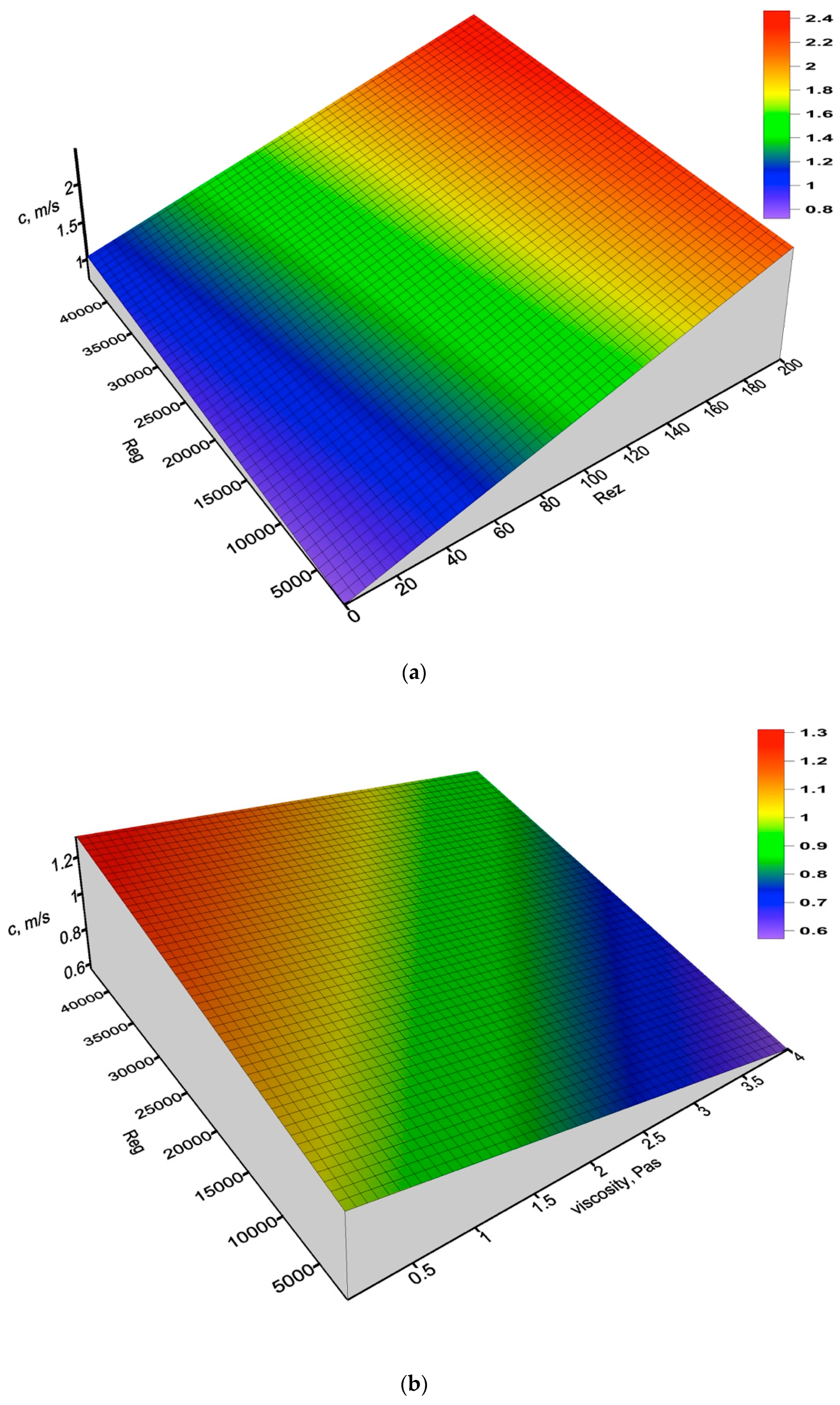
- the velocity of wave displacement, c:
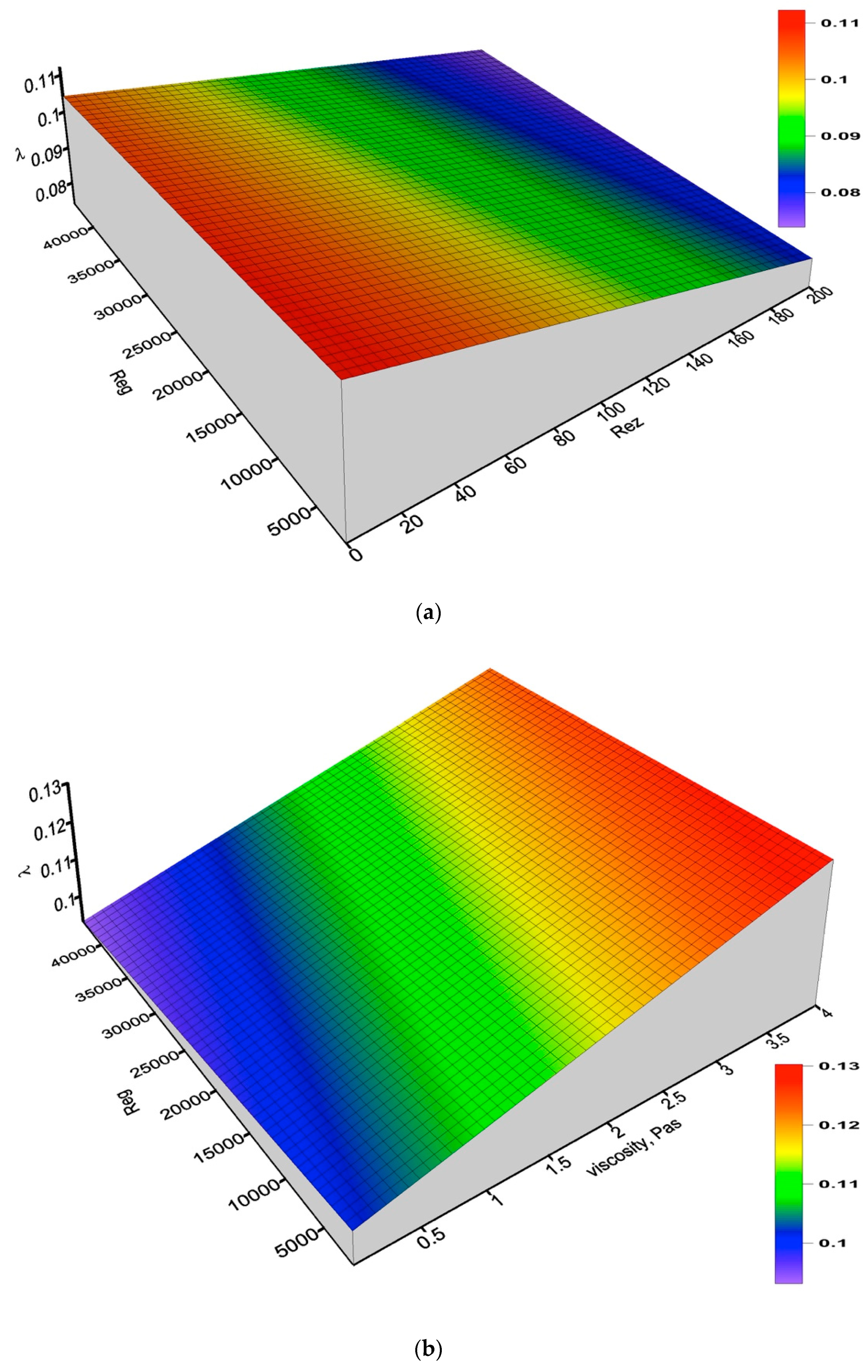
- the wavelength, λ:
- the wave amplitude, a:in which: , , and .
- mean relative error
- mean absolute error
- mean standard deviation
- for adiabatic conditions
- relative to the mass volume fraction—a case that is beneficial for conditions accompanied by heat exchange:
4. Conclusions
- The research was conducted in an unprecedented range of liquid viscosity of 0.046–3.5 Pas.
- The research demonstrated that the applied methodology for measuring the identification of liquid film parameters in a two-phase gas–liquid flow can be successfully applied to assessment of the interface between the length of pipes of a given apparatus, which plays an important role for the implementation of many operations related to the use of film apparatus in heat and mass transfer processes.
- It was found that the nature of the liquid film in two-phase air–oil flow can be very diverse. The size and nature of the resulting waves of varying amplitude and frequency depend on both the flux and viscosity of the liquid and the velocity of the gas phase.
- The designed original measuring system is also fully feasible for testing the level of interference of liquid films by determining the velocity, length and amplitude of the waves formed.
- The research resulted in the development of new dependencies that take into account the influence of selected thermal and flow parameters (including mass fraction) on the values of volumes that are specific for very viscous liquid film flows.
- The dependencies developed as a result of examining the effect of these parameters on the quantities characteristic of flowing liquid films can be fully applied for defining the operation of apparatuses with hydraulically generated liquid films.
- These dependencies improved the accuracy of calculation by 8–10%.
- The new apparatus system outlined in the paper provides the best opportunities to conduct research in the field of testing the dynamics of films of oil liquids and other dielectric liquids with a high degree of monochromatic radiation absorption.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| F | surface, m2 |
| Re | Reynolds number |
| We | Weber number |
| X | parameter of Lockhart-Martinelli |
| a | amplitude of wave, m |
| c | velocity of wave, m/s |
| d | diameter, m |
| f | frequency of wave, 1/s |
| g | mass flux, kg/(m2s) |
| ğ | gravitational acceleration, m/s2 |
| j | velocities, m/s |
| s | liquid film thickness, m |
| t | temperature, deg |
| x | mass fraction, - |
| Γ | wetting rate, kg/(ms) |
| β | volume fraction, - |
| η | viscosity, Pas |
| ϑz | equivalent linear dimension, m |
| λ | length of wave, m |
| ρ | density, kg/m3 |
| Subscripts and superscripts | |
| 0 | superficial values, |
| 2F | two-phase flow, |
| g | gas, |
| l | liquid, |
| o | gravity flow liquids, |
| p | pipe internal surface area, |
| T | total flow |
| z | equivalent values for liquids. |
References
- Hibiki, T.; Ishii, M. Interfacial area concentration in steady fully-developed bubbly flow. Int. J. Heat Mass Transf. 2001, 44, 3443–3461. [Google Scholar] [CrossRef]
- Ozar, B.; Dixit, A.; Chen, S.W.; Hibiki, T.; Ishii, M. Interfacial area concentration in gas–liquid bubbly to churn-turbulent flow regime. Int. J. Heat Fluid Flow 2012, 38, 168–179. [Google Scholar] [CrossRef]
- Shen, X.; Deng, B. Development of interfacial area concentration correlations for small and large bubbles in gas-liquid two-phase flows. Int. J. Multiph. Flow 2016, 87, 136–155. [Google Scholar] [CrossRef]
- Shen, X.; Hibiki, T. Interfacial area concentration in gas–liquid bubbly to churn flow regimes in large diameter pipes. Int. J. Heat Fluid Flow 2015, 54, 107–118. [Google Scholar] [CrossRef]
- Padilla, M.; Revellin, R.; Wallet, J.; Bonjour, J. Flow regime visualization and pressure drops of HFO-1234yf, R-134a and R-410A during downward two-phase flow in vertical return bends. Int. J. Heat Fluid Flow 2013, 40, 116–134. [Google Scholar] [CrossRef]
- Gabriel, S.; Schulenberg, T.; Albrecht, G.; Heiler, W.; Miassoedov, A.; Kaiser, F.; Wetzel, T. Optical void measurement method for stratified wavy two phase flows. Exp. Therm. Fluid Sci. 2018, 97, 341–350. [Google Scholar] [CrossRef]
- Pietrzak, M.; Witczak, S. Flow patterns and void fractions of phases during gas–liquid two-phase and gas–liquid–liquid three-phase flow in U-bends. Int. J. Heat Fluid Flow 2013, 44, 700–710. [Google Scholar] [CrossRef]
- Ebrahimi-Mamaghani, A.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N. Dynamics of two-phase flow in vertical pipes. J. Fluids Struct. 2019, 87, 150–173. [Google Scholar] [CrossRef]
- Liu, H.; Pan, L.-M.; Hibiki, T.; Zhou, W.; Ren, Q.-Y.; Li, S.-S. One-dimensional interfacial area transport for bubbly two-phase flow in vertical 5×5 rod bundle. Int. J. Heat Fluid Flow 2018, 72, 257–273. [Google Scholar] [CrossRef]
- Hamidi, M.J.; Karimi, H.; Boostani, M. Flow patterns and heat transfer of oil-water two-phase upward flow in vertical pipe. Int. J. Therm. Sci. 2018, 127, 173–180. [Google Scholar] [CrossRef]
- Smith, T.R.; Schlegel, J.P.; Hibiki, T.; Ishii, M. Two-phase flow structure in large diameter pipes. Int. J. Heat Fluid Flow 2012, 33, 156–167. [Google Scholar] [CrossRef]
- Shen, X.; Schlegel, J.P.; Hibiki, T.; Nakamura, H. Some characteristics of gas–liquid two-phase flow in vertical large-diameter channels. Nucl. Eng. Des. 2018, 333, 87–98. [Google Scholar] [CrossRef]
- Shen, X.; Sun, H.; Deng, B.; Hibiki, T.; Nakamura, H. Experimental study on interfacial area transport of two-phase bubbly flow in a vertical large-diameter square duct. Int. J. Heat Fluid Flow 2017, 67, 168–184. [Google Scholar] [CrossRef]
- Shen, X.; Hibiki, T.; Ono, T.; Sato, K.; Mishima, K. One-dimensional interfacial area transport of vertical upward bubbly flow in narrow rectangular channel. Int. J. Heat Fluid Flow 2012, 36, 72–82. [Google Scholar] [CrossRef]
- Ju, P.; Yang, X.; Schlegel, J.P.; Liu, Y.; Hibiki, T.; Ishii, M. Average liquid film thickness of annular air-water two-phase flow in 8×8 rod bundle. Int. J. Heat Fluid Flow 2018, 73, 63–73. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, J.; Li, W.Z. A two-phase, two-component model for vertical upward gas–liquid annular flow. Int. J. Heat Fluid Flow 2011, 32, 796–804. [Google Scholar] [CrossRef]
- Dang, Z.; Wang, G.; Ju, P.; Yang, X.; Bean, R.; Ishii, M.; Bajorek, S.; Bernard, M. Experimental study of interfacial characteristics of vertical upward air-water two-phase flow in 25.4 mm ID round pipe. Int. J. Heat Mass Transf. 2017, 108, 1825–1838. [Google Scholar] [CrossRef]
- Gao, Y.; Cui, Y.; Xu, B.; Sun, B.; Zhao, X.; Li, H.; Chen, L. Two phase flow heat transfer analysis at different flow patterns in the wellbore. Appl. Therm. Eng. 2017, 117, 544–552. [Google Scholar] [CrossRef]
- Jiang, C.; Bai, B.F. Flow patterns and pressure drop of downward two-phase flow in a capsule-type plate heat exchanger. Exp. Therm. Fluid Sci. 2019, 103, 347–354. [Google Scholar] [CrossRef]
- Julia, J.E.; Ozar, B.; Jeong, J.-J.; Hibiki, T.; Ishii, M. Flow regime development analysis in adiabatic upward two-phase flow in a vertical annulus. Int. J. Heat Fluid Flow 2011, 32, 164–175. [Google Scholar] [CrossRef]
- Juliá, J.E.; Hibiki, T. Flow regime transition criteria for two-phase flow in a vertical annulus. Int. J. Heat Fluid Flow 2011, 32, 993–1004. [Google Scholar] [CrossRef]
- Lee, J.; O’Neill, L.E.; Lee, S.; Mudawar, I. Experimental and computational investigation on two-phase flow and heat transfer of highly subcooled flow boiling in vertical upflow. Int. J. Heat Mass Transf. 2019, 136, 1199–1216. [Google Scholar] [CrossRef]
- Qiao, S.; Mena, D.; Kim, S. Inlet effects on vertical-downward air–water two-phase flow. Nucl. Eng. Des. 2017, 312, 375–388. [Google Scholar] [CrossRef]
- Xue, Y.; Li, H.; Hao, C.; Yao, C. Investigation on the void fraction of gas–liquid two-phase flows in vertically-downward pipes. Int. Commun. Heat Mass Transf. 2016, 77, 1–8. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Domnich, A.A. Model of a Nonuniformly Heated Viscous Flow through a Bounded Domain. Differ. Equations 2020, 56, 304–314. [Google Scholar] [CrossRef]
- Cimatti, G. The Poiseuille Flow in a Pipe with Temperature Dependent Viscosity and Prescribed Flow Rate. J. Math. Fluid Mech. 2009, 11, 415–427. [Google Scholar] [CrossRef]
- Czernek, K. Hydrodynamic Aspects of Thin-Film Apparatus Design for Very Viscous Liquids; Oficyna Wydawnicza Politechniki Opolskiej: Opole, Poland, 2013; ISBN 8364056158. [Google Scholar]
- Czernek, K.; Filipczak, G.; Witczak, S. Annular Flow Study upon Two Phase Air-Very Viscous Liquid Flow. In Proceedings of the 5th International Conference on Transport Phenomena in Multiphase Systems, HEAT, Bialystok, Poland, 20 June–3 July 2008; pp. 271–276. [Google Scholar]



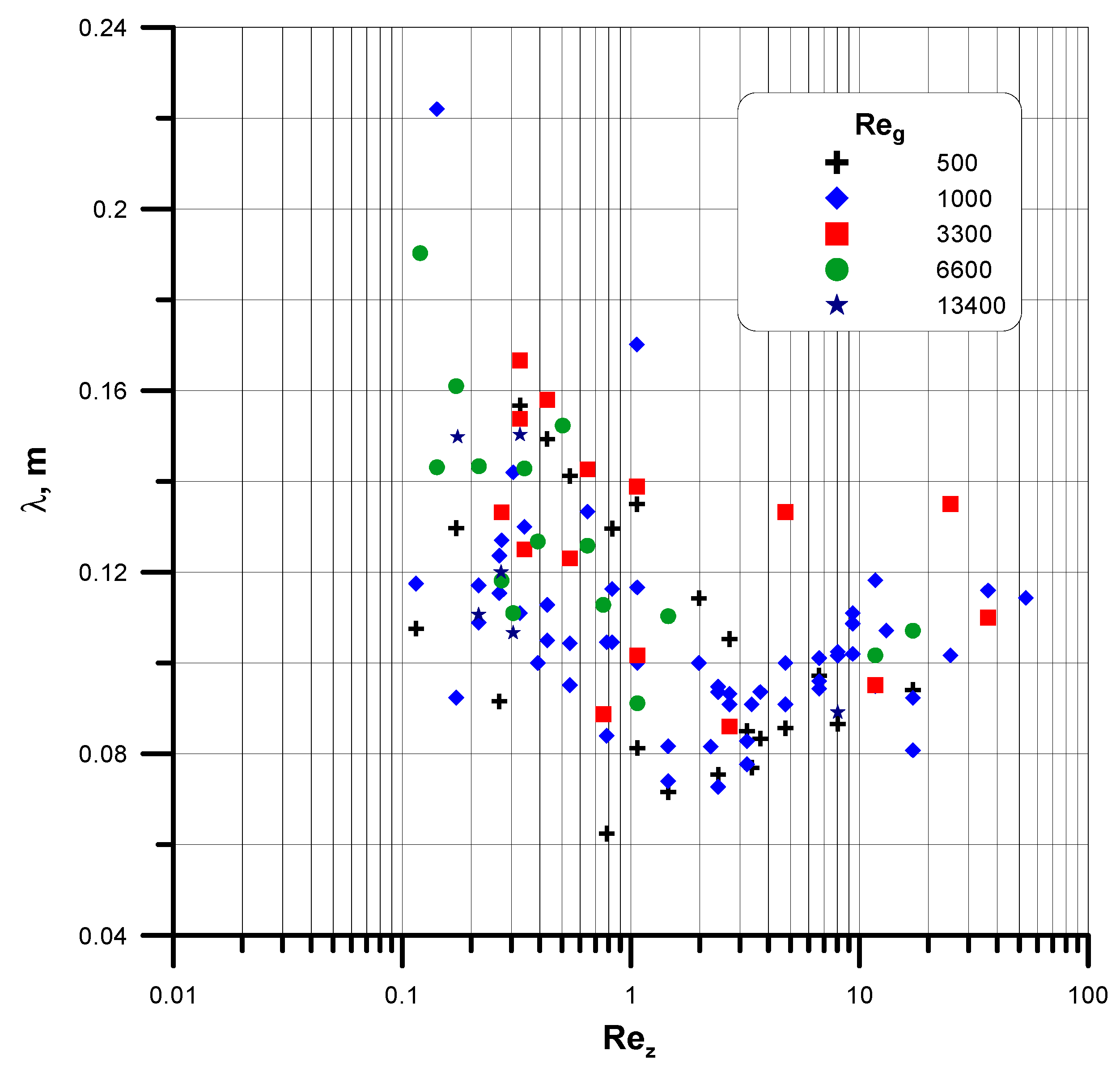
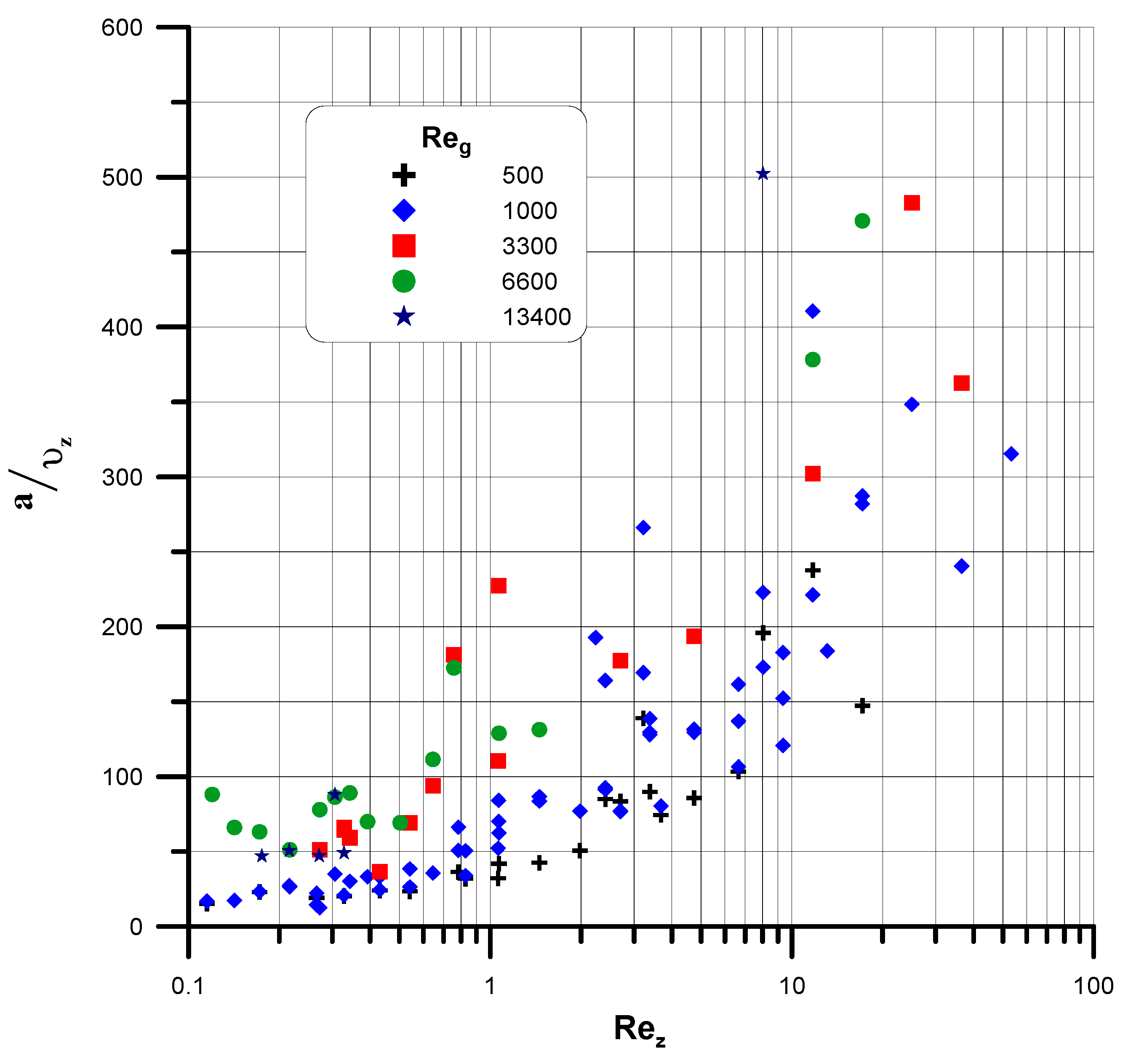
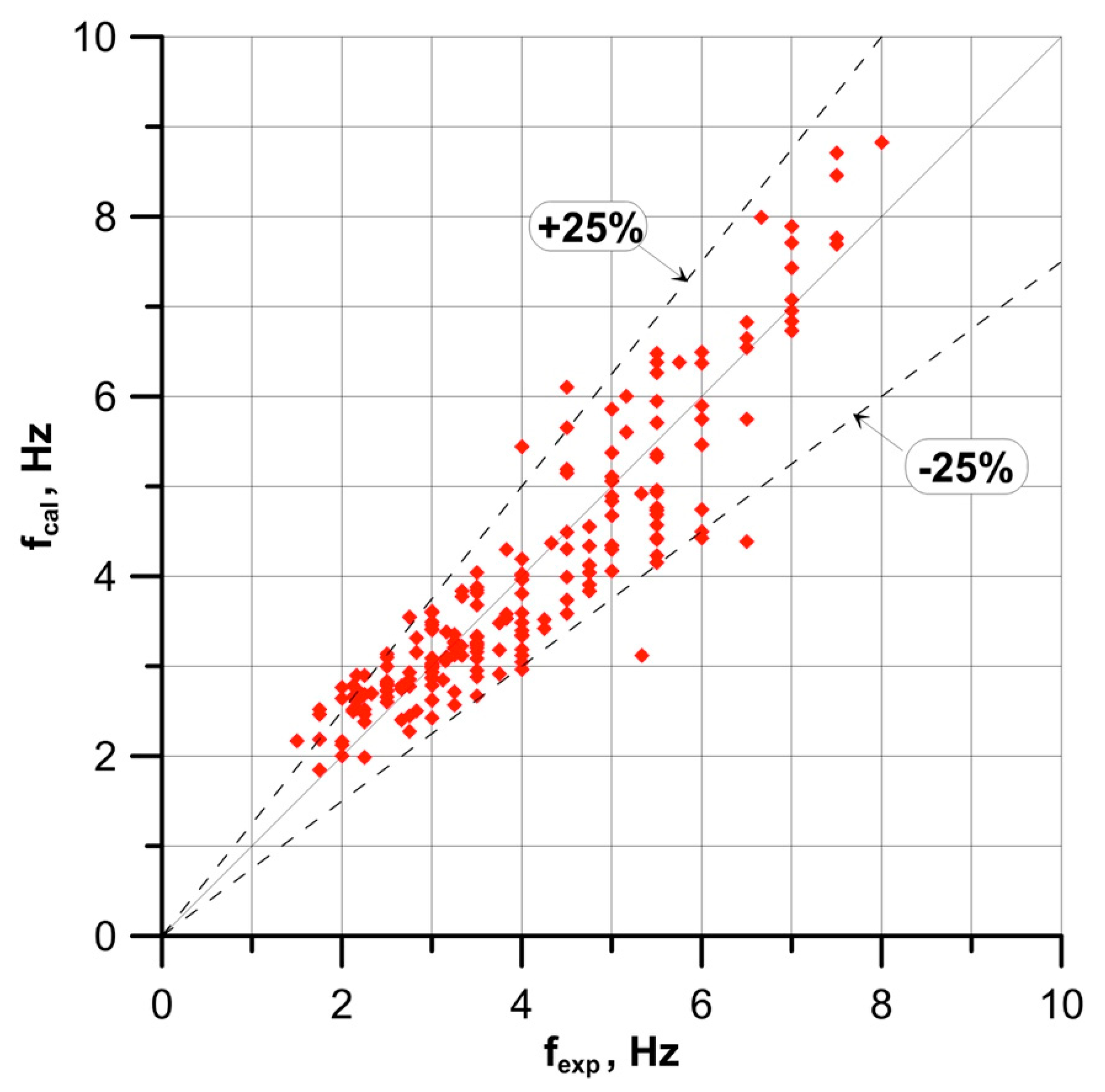
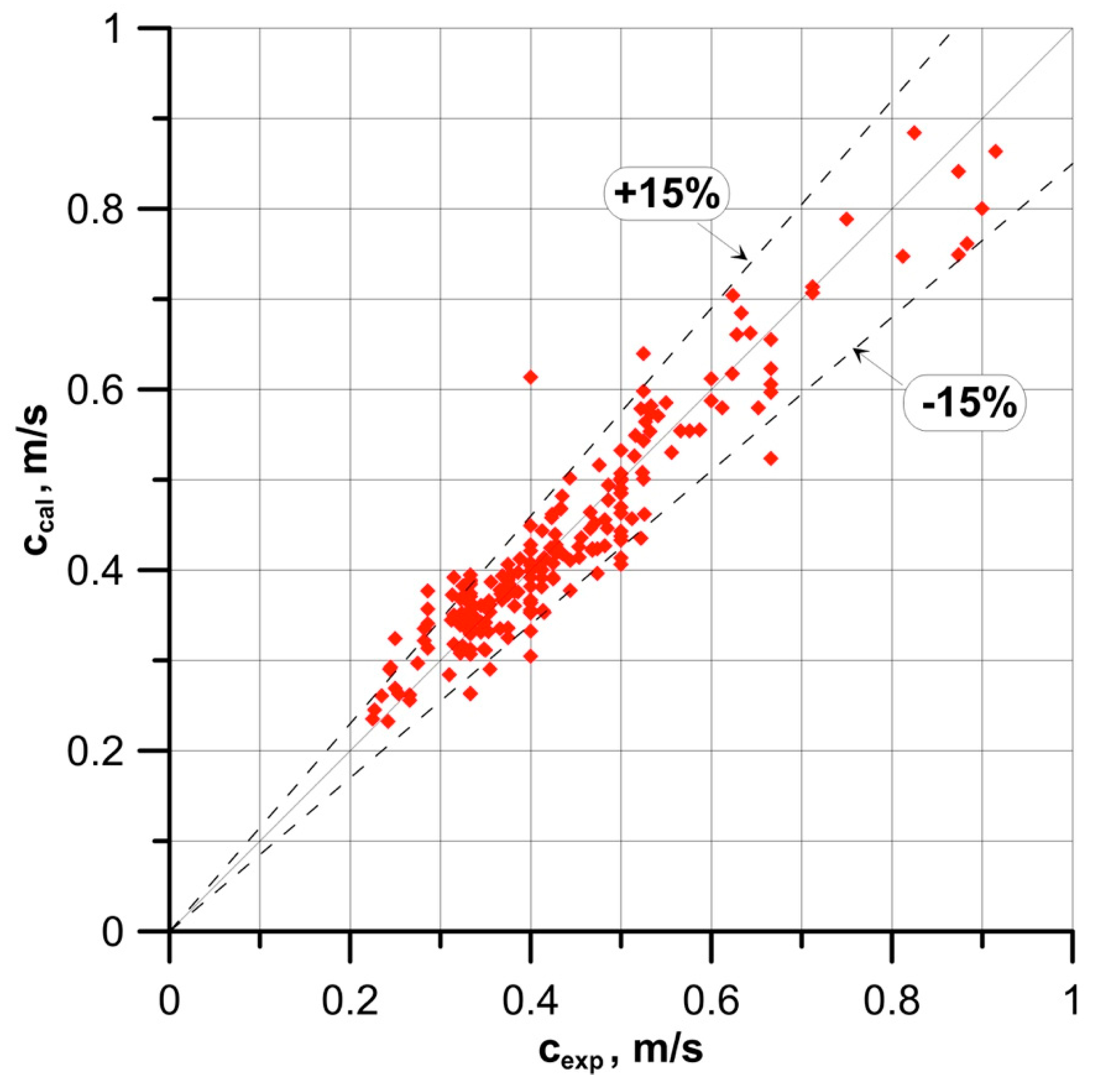

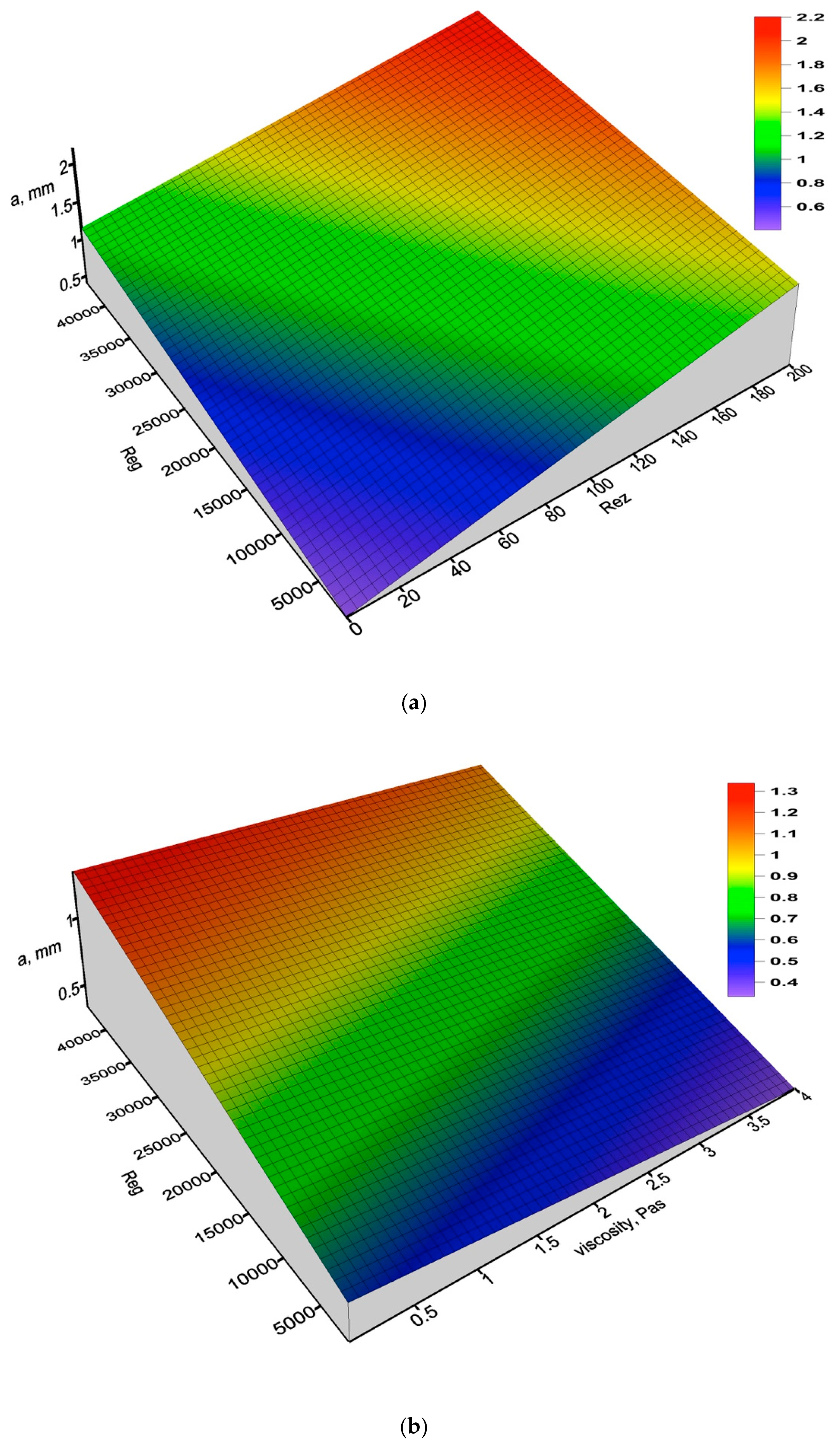



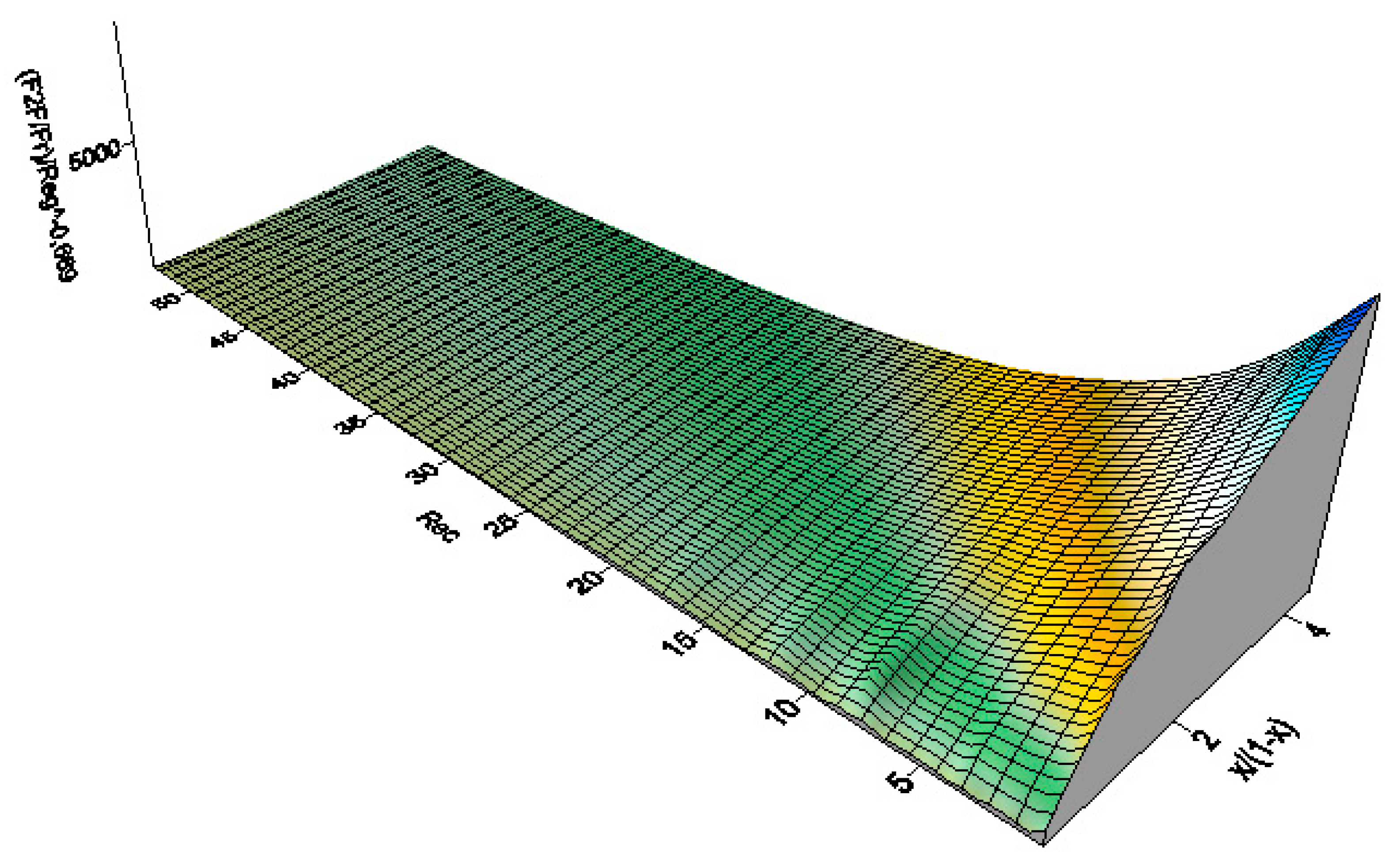
| No. | Parameter and Equation | Equation No. |
|---|---|---|
| 1. | Film thickness, s | (6) |
| 2. | Wave frequency, f | (7) |
| 3. | Wave velocity, c | (8) |
| 4. | Wave intervals, λ | (9) |
| 5. | Wave amplitude, a | (10) |
| 6. | Surface of inter-phase boundary development | (11) |
| Equation | Correlation Coefficient (r) | Values of Statistical Data (%) | ||
|---|---|---|---|---|
| MRE | MAE | MSD | ||
| (14) | 0.9866 | −0.95 | 12.3 | 15.4 |
| (15) | 0.9856 | 0.36 | 7.9 | 10.4 |
| (16) | 0.9344 | −1.08 | 14.6 | 18.6 |
| (17) | 0.9559 | −0.81 | 18.6 | 24.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czernek, K.; Witczak, S. Hydrodynamics of Two-Phase Gas-Very Viscous Liquid Flow in Heat Exchange Conditions. Energies 2020, 13, 5709. https://doi.org/10.3390/en13215709
Czernek K, Witczak S. Hydrodynamics of Two-Phase Gas-Very Viscous Liquid Flow in Heat Exchange Conditions. Energies. 2020; 13(21):5709. https://doi.org/10.3390/en13215709
Chicago/Turabian StyleCzernek, Krystian, and Stanisław Witczak. 2020. "Hydrodynamics of Two-Phase Gas-Very Viscous Liquid Flow in Heat Exchange Conditions" Energies 13, no. 21: 5709. https://doi.org/10.3390/en13215709






