Economic Impacts of the Demand Response of Electric Vehicles Considering Battery Degradation
Abstract
1. Introduction
2. Literature Review
2.1. Modeling the Degradation of Batteries
2.2. DR Evaluation of V2G Including Degradation
- The battery degradation model is combined with the EV DR evaluation model to evaluate the degradation cost due to additional charge/discharge operations.
- By modeling the degradation factors of the battery by dividing them into calendar degradation and cycle degradation, the relationship between each factor and the operation method can be clearly evaluated.
- The EV DR evaluation model uses EV fleet data using a Monte Carlo simulation based on the actual EV utilization and offers a realistic evaluation.
3. Battery Degradation Model
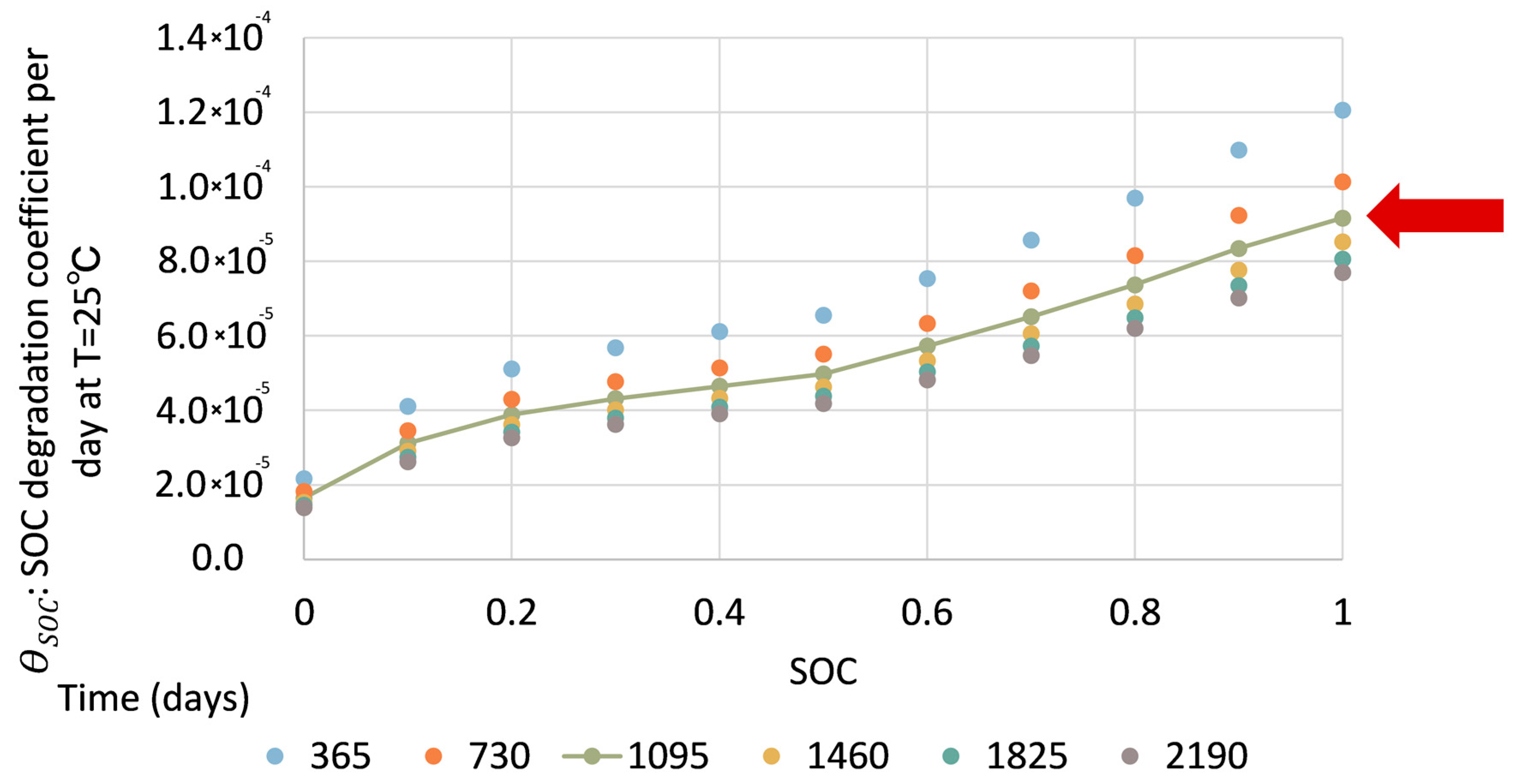
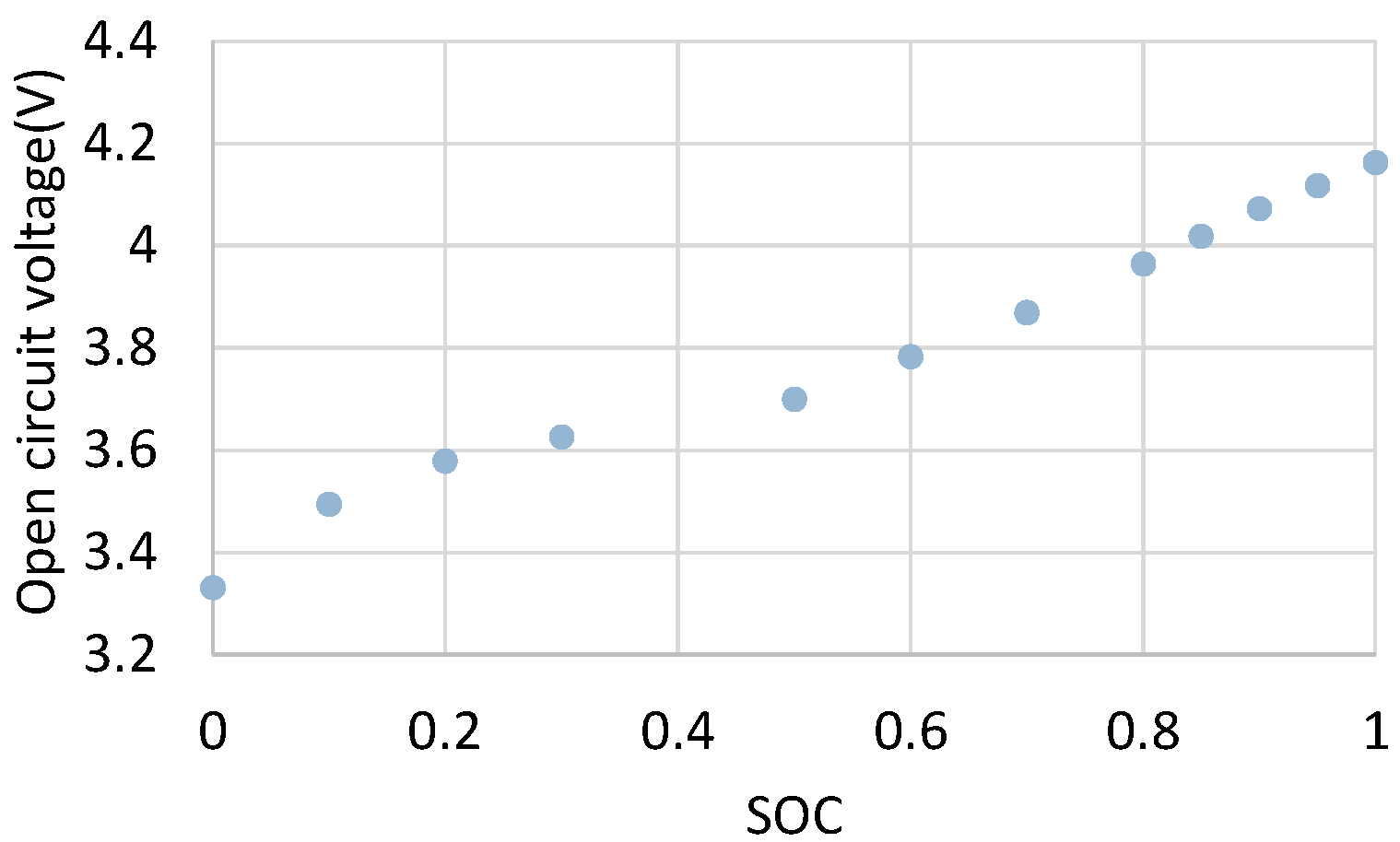
3.1. Calendar Aging
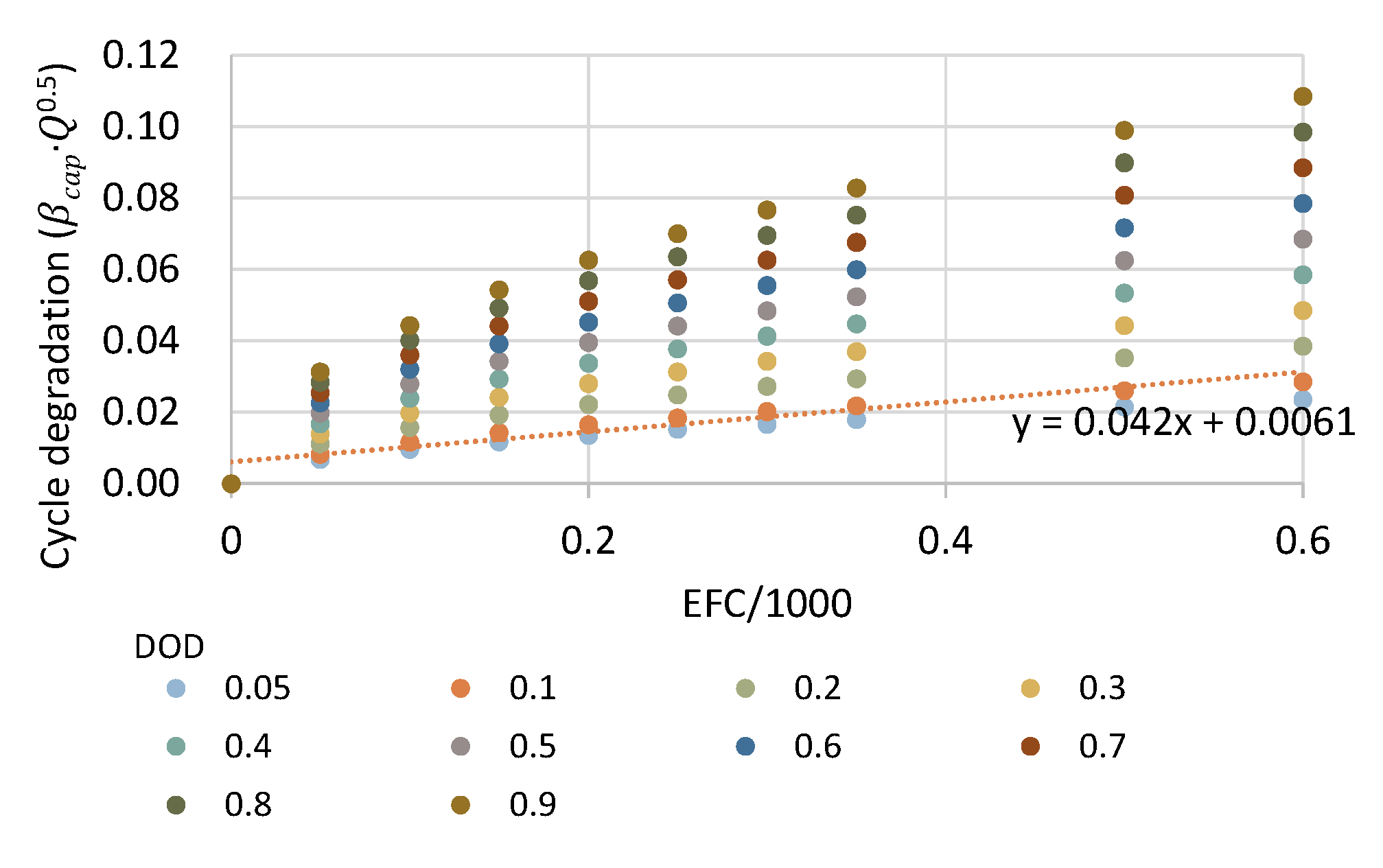
3.2. Cycling Aging
4. EV DR Evaluation Model Considering Battery Degradation
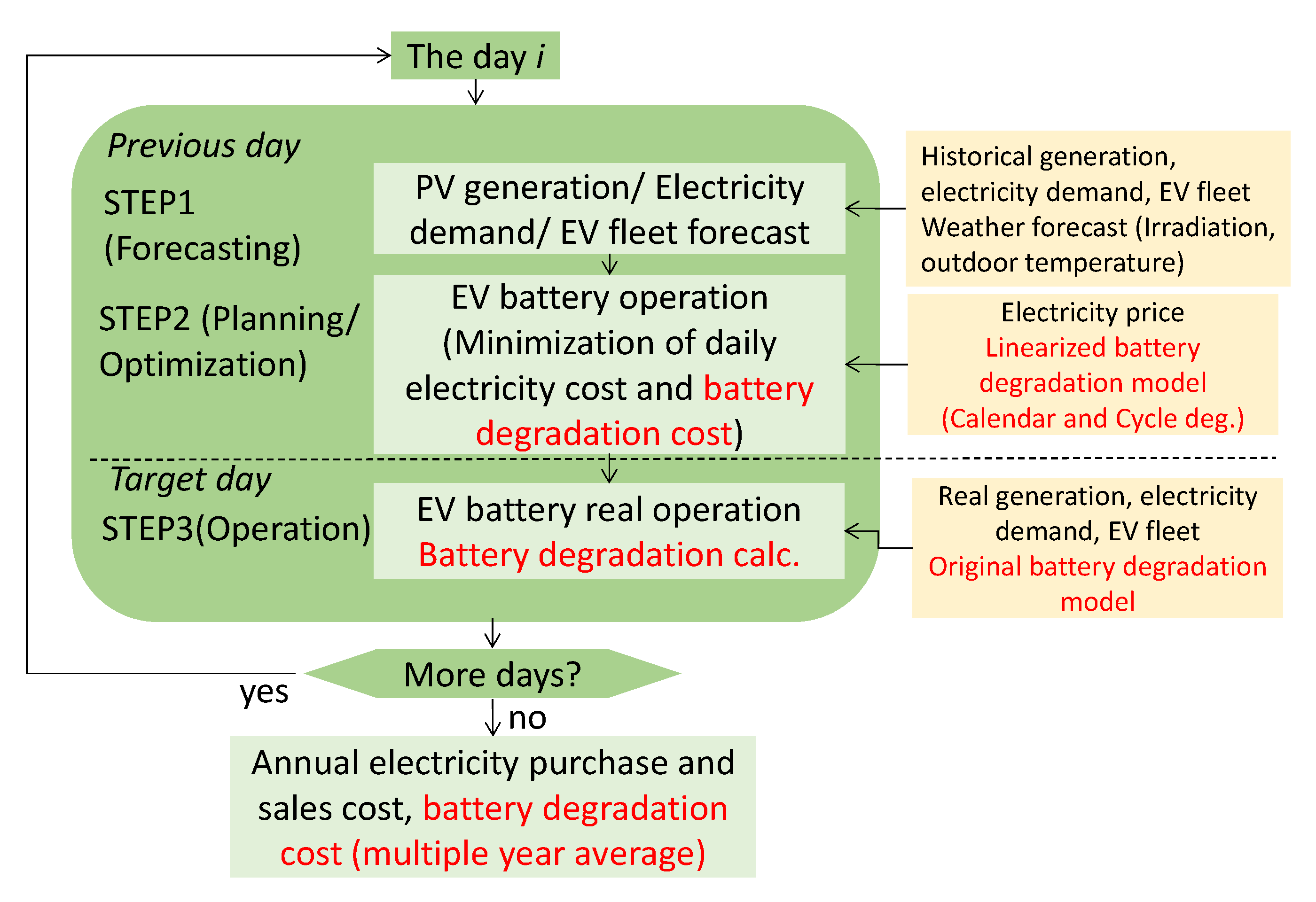
4.1. EV Battery Optimization Model (Planning Model)
| 𝑡 | time (1–24) |
| 𝑖 | number of intervals used in the linear approximation (1–10) |
| 𝑥𝑐𝑎𝑙(𝑡), 𝑥𝑐𝑦𝑐(𝑡) | calendar degradation rate (%), cycle degradation rate (%) |
| 𝑥𝑑𝑜𝑑(𝑡) | DOD (%) |
| 𝑏𝑝(𝑖) | interval step used in the linear approximation (0.1–1.0) |
| 𝑠𝑑𝑒𝑔𝑣𝑎𝑙(𝑖) | SOC degradation rate at SOC level 𝑖 |
| 𝑥𝑠𝑜𝑐𝑑𝑢(𝑖, 𝑡) | SOC level dummy variable (0 or 1) |
| 𝑥𝑠𝑜𝑐𝑑𝑒𝑔(𝑡) | SOC degradation rate |
| 𝜃𝑇 | temperature degradation coefficient (= 0.9725e0.0728⊿T) |
| 𝜃𝑑𝑜𝑑 | DOD degradation coefficient (= 0.042/1000EFS) |
| 𝑝𝑑𝑒𝑔 | unit cost of capacity degradation (US cents/%). |
4.2. Operating Model on the Target Day
5. Simulation
5.1. Simulation Conditions
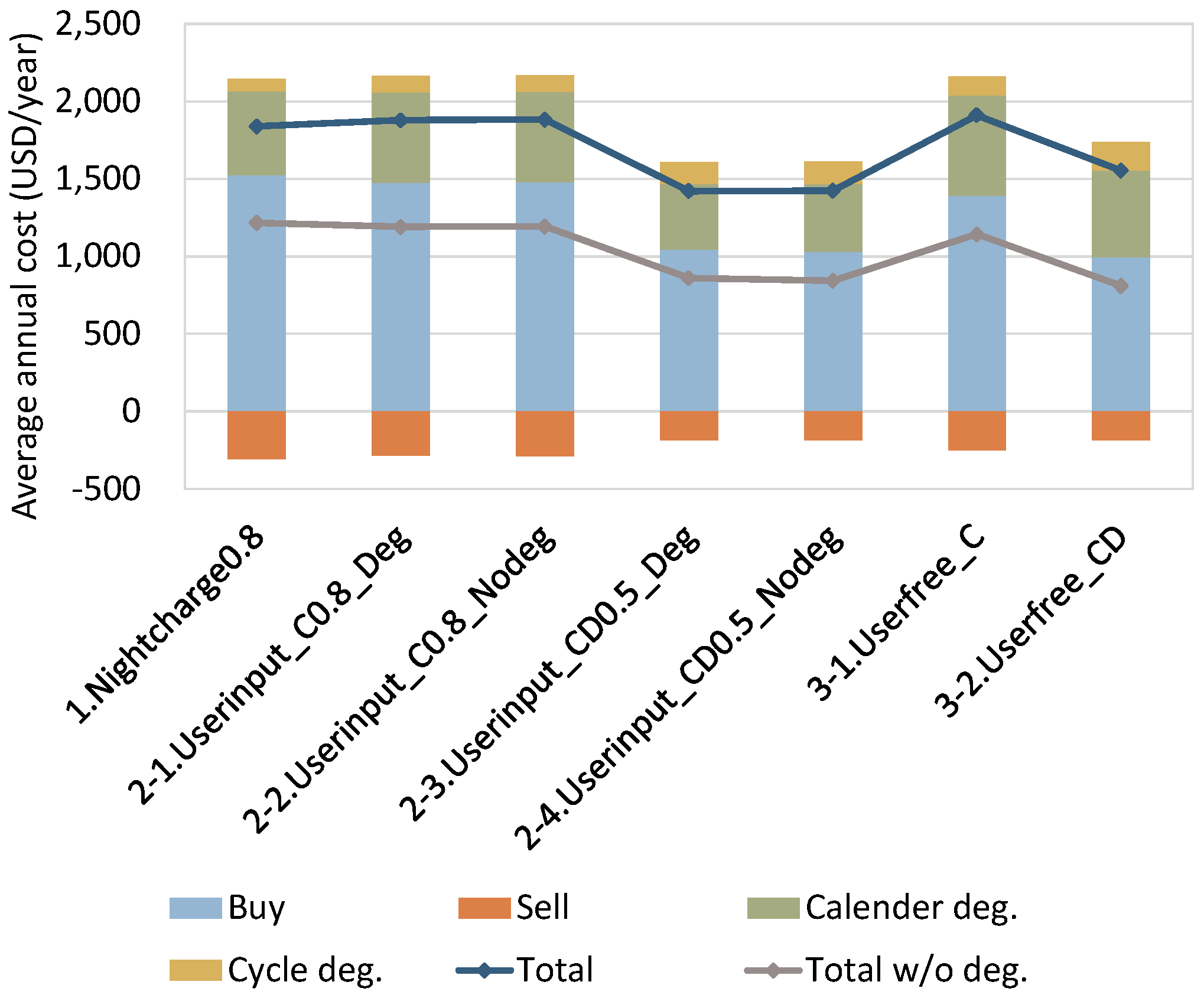
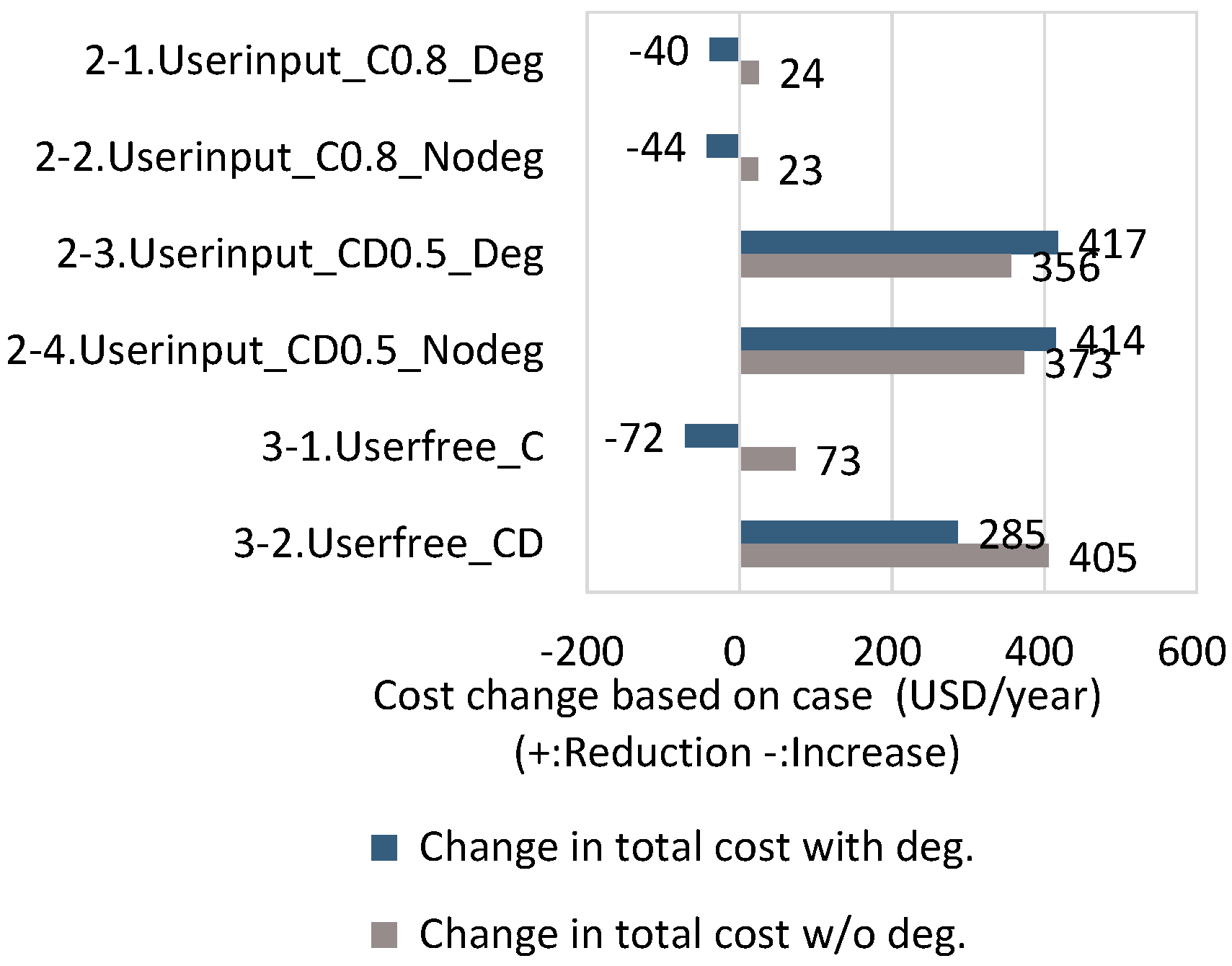
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| 𝐿𝑐𝑎𝑝 | battery degradation capacity |
| 𝐿𝑐𝑎𝑙 | battery calendar degradation |
| 𝐿𝑐𝑦𝑐 | battery cycling degradation |
| 𝑇 | cell temperature (k) |
| 𝑑𝑎𝑦 | elapsed time (days) |
| 𝑉 | open-circuit voltage (v) |
| 𝛳𝑆𝑂𝐶 | calendar degradation coefficient due to soc at the reference temperature |
| 𝛳𝑇 | calendar degradation coefficient due to temperature |
| 𝑇𝑟𝑒𝑓 | reference cell temperature (k) |
| 𝑄 | equivalent full cycles (efc) |
| 𝐷𝑂𝐷 | depth of discharge |
| 𝑡 | time (1–24) |
| 𝑖 | number intervals used in the linear approximation (1–10) |
| 𝑥𝑏𝑢𝑦 (𝑡) | electricity purchased at time t of the optimization model (kWh/h) |
| 𝑥𝑠𝑒𝑙𝑙 (𝑡) | electricity sold at time t of the optimization model (kWh/h) |
| 𝑥𝑐𝑠 (𝑡) | electricity purchased at charge stations at time t of the optimization model (kWh/h) |
| 𝑥𝑐h (𝑡) | electricity charged at time t of the optimization model (kWh/h) |
| 𝑥𝑑𝑖𝑠 (𝑡) | electricity discharged at time t of the optimization model (kWh/h) |
| 𝑥𝑠𝑜𝑐 (𝑡) | battery SOC at time t of the optimization model (kWh) |
| 𝑥𝑐h𝑑𝑢𝑚 (𝑡) | dummy variable denoting the charge time in the optimization model |
| 𝑥𝑑𝑖𝑠𝑑𝑢𝑚 (𝑡) | dummy variable denoting the discharge time in the optimization model |
| 𝑥𝑐𝑎𝑙 (𝑡) | calendar degradation rate (%) at time t in the optimization model (kWh/h) |
| 𝑥𝑐𝑦𝑐 (𝑡) | cycle degradation rate (%) at time t of the optimization model (kWh/h) |
| 𝑥𝑑𝑜𝑑 (𝑡) | DOD at time t in the optimization model |
| 𝑏𝑝 (𝑖) | interval step used in the linear approximation (0.1–1.0) |
| 𝑠𝑑𝑒𝑔𝑣𝑎𝑙 (𝑖) | SOC degradation rate at SOC level 𝑖 |
| 𝑥𝑠𝑜𝑐𝑑𝑢𝑚 (𝑖, 𝑡) | SOC level dummy variable (0 or 1) |
| 𝑥𝑠𝑜𝑐𝑑𝑒𝑔 (𝑡) | SOC degradation rate |
| 𝜃𝑇 | temperature degradation coefficient |
| 𝜃𝑑𝑜𝑑 | DOD degradation coefficient |
| 𝑝𝑏𝑢𝑦 (𝑡) | the purchase price of the electricity price at time t (US cents/kWh) |
| 𝑝𝑠𝑒𝑙𝑙 (𝑡) | the selling price of the electricity at time t (US cents/kWh) |
| 𝑝𝑐𝑠 (𝑡) | purchase price of the electricity at charge stations at time t (US cents/kWh) |
| 𝑓𝑙 (𝑡) | predicted EV fleet at time t (km) |
| 𝑑𝑒𝑚 (𝑡) | predicted electricity demand at time t (kWh/h) |
| 𝑝𝑣 (𝑡) | predicted PV power generation at time t (kWh/h) |
| 𝑝𝑑𝑒𝑔 | unit cost of capacity degradation (US cents/%) |
| h𝑜𝑚𝑒 (𝑡) | predicted index on whether EV is staying at home at time t (1: stay, 0: out) |
| 𝐵𝑘𝑊h𝟢 | initial battery SOC (kWh) |
| 𝑀 | sufficiently large constant (=10,000) |
| 𝑏𝑢𝑦 (𝑡) | final electricity purchased at time t (kWh/h) |
| 𝑠𝑒𝑙𝑙 (𝑡) | final electricity sold at time t (kWh/h) |
| 𝑐𝑠 (𝑡) | final electricity purchased at charge stations at time t (kWh/h) |
| 𝑐h (𝑡) | final electricity charged at time t (kWh/h) |
| 𝑑𝑖𝑠 (𝑡) | final electricity discharged at time t (kWh/h) |
| 𝑠𝑜𝑐 (𝑡) | final battery SOC at time t (kWh/h) |
| 𝑓𝑙𝑟𝑒𝑎𝑙 (𝑡) | real EV fleet at time t (km) |
| 𝑑𝑒𝑚𝑟𝑒𝑎𝑙 (𝑡) | real electricity demand at time t (kWh/h) |
| 𝑝𝑣𝑟𝑒𝑎𝑙 (𝑡) | real PV power generation at time t (kWh/h) |
| 𝜂𝑐h | battery charge efficiency |
| 𝜂𝑑𝑖𝑠 | battery discharge efficiency |
| 𝐸𝑉𝑒𝑓𝑓 | EV fleet efficiency (km/kWh) |
| 𝐵𝑘𝑊 | battery inverter capacity (kW) |
| 𝐵𝑘𝑊h𝑚𝑎𝑥 | upper limit of battery capacity (kWh) |
| 𝐵𝑘𝑊h𝑚𝑖𝑛 | lower limit of battery capacity (kWh) |
References
- Agency, I.E. Global EV Outlook 2019. In Scaling-Up the Transition to Electric Mobility; IEA: London, UK, 2019. [Google Scholar] [CrossRef]
- Iwafune, Y.; Ogimoto, K.; Azuma, H. Integration of Electric Vehicles into the Electric Power System Based on Results of Road Traffic Census. Energies 2019, 12, 1849. [Google Scholar] [CrossRef]
- Iwafune, Y.; Ogimoto, K.; Kobayashi, Y.; Murai, K. Driving Simulator for Electric Vehicles Using the Markov Chain Monte Carlo Method and Evaluation of the Demand Response Effect in Residential Houses. IEEE Access 2020, 8, 47654–47663. [Google Scholar] [CrossRef]
- Thompson, A.W. Economic implications of lithium ion battery degradation for Vehicle-to-Grid (V2X) services. J. Power Source 2018, 396, 691–709. [Google Scholar] [CrossRef]
- Ben-Marzouk, M.; Chaumond, A.; Redondo-Iglesias, E.; Montaru, M.; Pélissier, S. Experimental Protocols and First Results of Calendar and/or Cycling Aging Study of Lithium-Ion Batteries–the MOBICUS Project. World Electr. Veh. J. 2016, 8, 388–397. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel–cobalt–manganese oxide + spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Smith, K.; Wood, E.; Santhanagopalan, S.; Kim, G.-H.; Pesaran, A. Advanced Models and Controls for Prediction and Extension of Battery Lifetime. In Proceedings of the Large Lithium Ion Battery Technology & Application Symposia Advanced Automotive Battery Conference, Atlanta, GA, USA, 4 February 2014. [Google Scholar]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Marongiu, A.; Roscher, M.; Sauer, D.U. Influence of the vehicle-to-grid strategy on the aging behavior of lithium battery electric vehicles. Appl. Energy 2015, 137, 899–912. [Google Scholar] [CrossRef]
- Wang, D.; Coignard, J.; Zeng, T.; Zhang, C.; Saxena, S. Quantifying electric vehicle battery degradation from driving vs. vehicle-to-grid services. J. Power Sources 2016, 332, 193–203. [Google Scholar] [CrossRef]
- Neubauer, J.; Wood, E. The impact of range anxiety and home, workplace, and public charging infrastructure on simulated battery electric vehicle lifetime utility. J. Power Sources 2014, 257, 12–20. [Google Scholar] [CrossRef]
- Hoke, A.; Brissette, A.; Maksimovic, D.; Pratt, A.; Smith, K. Electric vehicle charge optimization including effects of lithium-ion battery degradation. In Proceedings of the IEEE Vehicle Power and Propulsion (VPPC), Colorado, CO, USA, 6–9 September 2011. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M.A. Optimal scheduling of electric vehicle charging and vehicle-to-grid services at household level including battery degradation and price uncertainty. IET Gener. Transm. Distrib. 2014, 8, 1007–1016. [Google Scholar] [CrossRef]
- Uddin, K.; Jackson, T.; Widanage, W.D.; Chouchelamane, G.; Jennings, P.A.; Marco, J. On the possibility of extending the lifetime of lithium-ion batteries through optimal V2G facilitated by an integrated vehicle and smart-grid system. Energy 2017, 133, 710–722. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; McKenzie, K. Durability and reliability of electric vehicle batteries under electric utility grid operations: Bidirectional charging impact analysis. J. Power Sources 2017, 358, 39–49. [Google Scholar] [CrossRef]
- Uddin, K.; Dubarry, M.; Glick, M.B. The viability of vehicle-to-grid operations from a battery technology and policy perspective. Energ. Policy 2018, 113, 342–347. [Google Scholar] [CrossRef]
- Smith, K.; Earleywine, M.; Wood, E.; Neubauer, J.; Pesaran, A. Comparison of Plug-In Hybrid Electric Vehicle Battery Life Across Geographies and Drive Cycles. In Proceedings of the 2012 SAE World Congress and Exhibition, Detroit, MI, USA, 24–26 April 2012. [Google Scholar] [CrossRef]
- BloombergNEF A Behind the Scenes Take on Lithium-ion Battery Prices. Available online: https://about.bnef.com/blog/behind-scenes-take-lithium-ion-battery-prices/ (accessed on 22 May 2020).
- Das, R.; Wang, Y.; Putrus, G.; Kotter, R.; Marzband, M.; Herteleer, B.; Warmerdam, J. Multi-objective techno-economic-environmental optimisation of electric vehicle for energy services. Appl. Energy 2020, 257, 113965. [Google Scholar] [CrossRef]




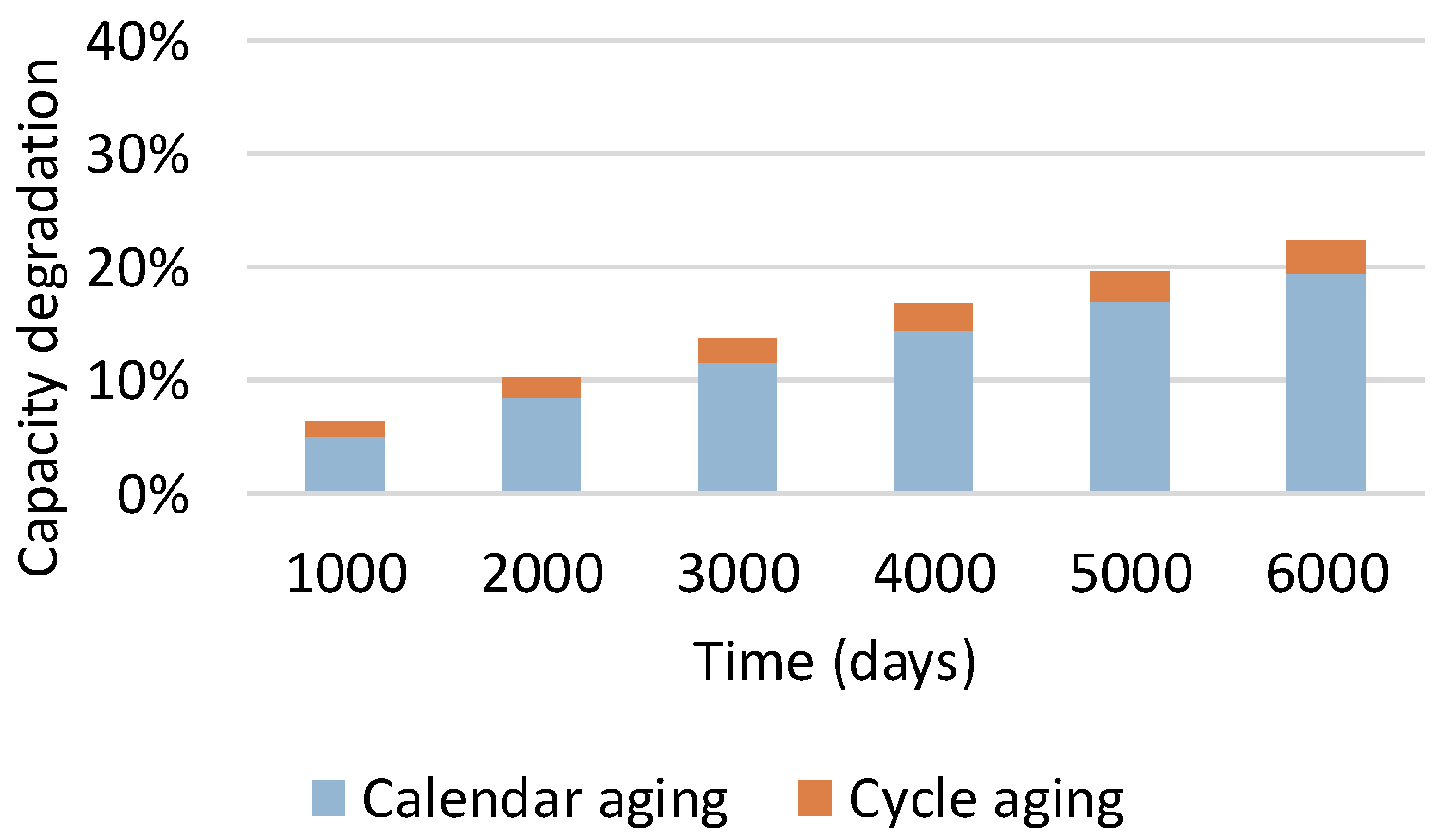





| EV Operation Case | Operation Method | Need for Forecast and Planning |
|---|---|---|
| EV night charging (base case) | The battery is charged to the reference SOC only at nighttime when the electricity is cheap | No |
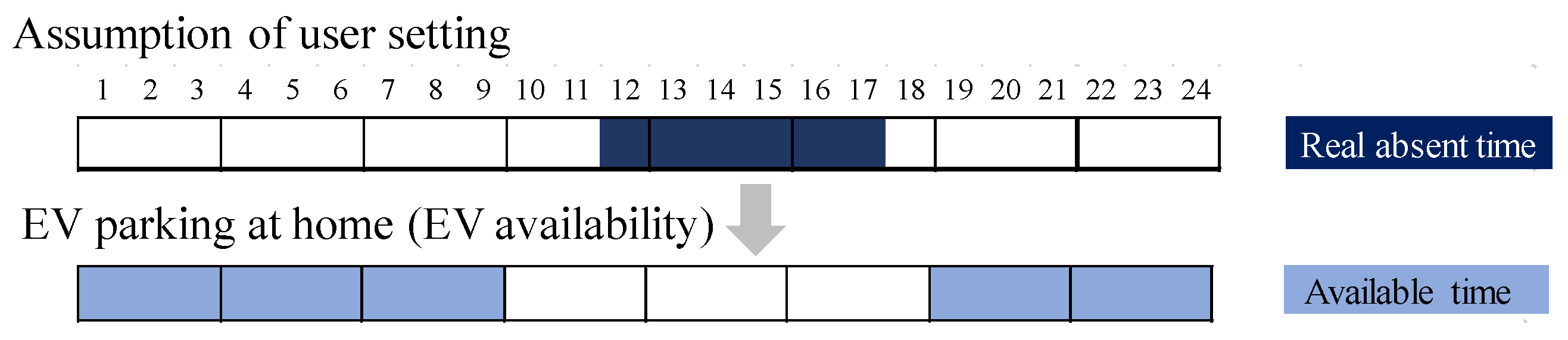
| User input case | The EV available time (the presence or absence at home in 8 periods by 3 hours) and the daily travel distance (upper-limit input in 10 km increments) are set by the user at 23:00 on the previous day, as shown in Figure 11. The daily battery operation is planned considering that the SOC at 23:00 on the target day is above the reference SOC. | Yes |
| User-free case | For the charge only control, the battery is charged up to the maximum capacity when PV surplus power is available and charged up to the reference SOC during the nighttime electricity rate period. For the charge/discharge control, the battery is discharged up to the reference SOC to supply the electricity demand that exceeds the PV generation during the daytime electricity rate period. The charging operation is the same as that for the charge only control. | No |
| Case ID | EV Operation Case | Control Method | Reference SOC of Battery | Optimization with Degradation Cost |
|---|---|---|---|---|
| 1 | EV night charging (base case) | Charge | 0.8 | - |
| 2-1 | User input case | Charge only | 0.8 | Yes |
| 2-2 | Charge only | 0.8 | No | |
| 2-3 | Charge and discharge | 0.5 | Yes | |
| 2-4 | Charge and discharge | 0.5 | No | |
| 3-1 | User-free case | Charge only | 0.8 (Charged during nighttime) 1.0 (Charged with surplus PV) | - |
| 3-2 | Charge and discharge | 0.8 (Charged during nighttime) 1.0 (Charged with surplus PV) 0.5 (Discharged when the EV is at the residence of the user) | - |
| Parameter | Value |
|---|---|
| Electricity price | The purchase price at the residence of the user: 18/33 US cents/kWh (nighttime 23:00–7:00/other time 7:00–23:00) Selling price: 8 US cents/kWh The purchase price at CSs: 50 US cents/kWh |
| Demand and PV generation profile | Data measured for 8760 h in 10 all-electric houses (PV generation 5000–6200 kWh/yr., demand other than hot water supply 6100–8400 kWh/yr.) |
| EV | Battery capacity: 40 kWh Charge and discharge capacity: 3 kW SOC lower limit: 20 kWh at V2H periods in the user-free case and 8 kWh in other cases EV fleet efficiency: 7 km/kWh Battery charge and discharge efficiency: 90% each |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwafune, Y.; Ogimoto, K. Economic Impacts of the Demand Response of Electric Vehicles Considering Battery Degradation. Energies 2020, 13, 5771. https://doi.org/10.3390/en13215771
Iwafune Y, Ogimoto K. Economic Impacts of the Demand Response of Electric Vehicles Considering Battery Degradation. Energies. 2020; 13(21):5771. https://doi.org/10.3390/en13215771
Chicago/Turabian StyleIwafune, Yumiko, and Kazuhiko Ogimoto. 2020. "Economic Impacts of the Demand Response of Electric Vehicles Considering Battery Degradation" Energies 13, no. 21: 5771. https://doi.org/10.3390/en13215771
APA StyleIwafune, Y., & Ogimoto, K. (2020). Economic Impacts of the Demand Response of Electric Vehicles Considering Battery Degradation. Energies, 13(21), 5771. https://doi.org/10.3390/en13215771




