A Decoupling Rolling Multi-Period Power and Voltage Optimization Strategy in Active Distribution Networks
Abstract
:1. Introduction
2. Modeling of Active Distribution Network
2.1. Sensitivity between Node Voltage and Power
2.2. Modeling of OLTC
2.3. Modeling of PV
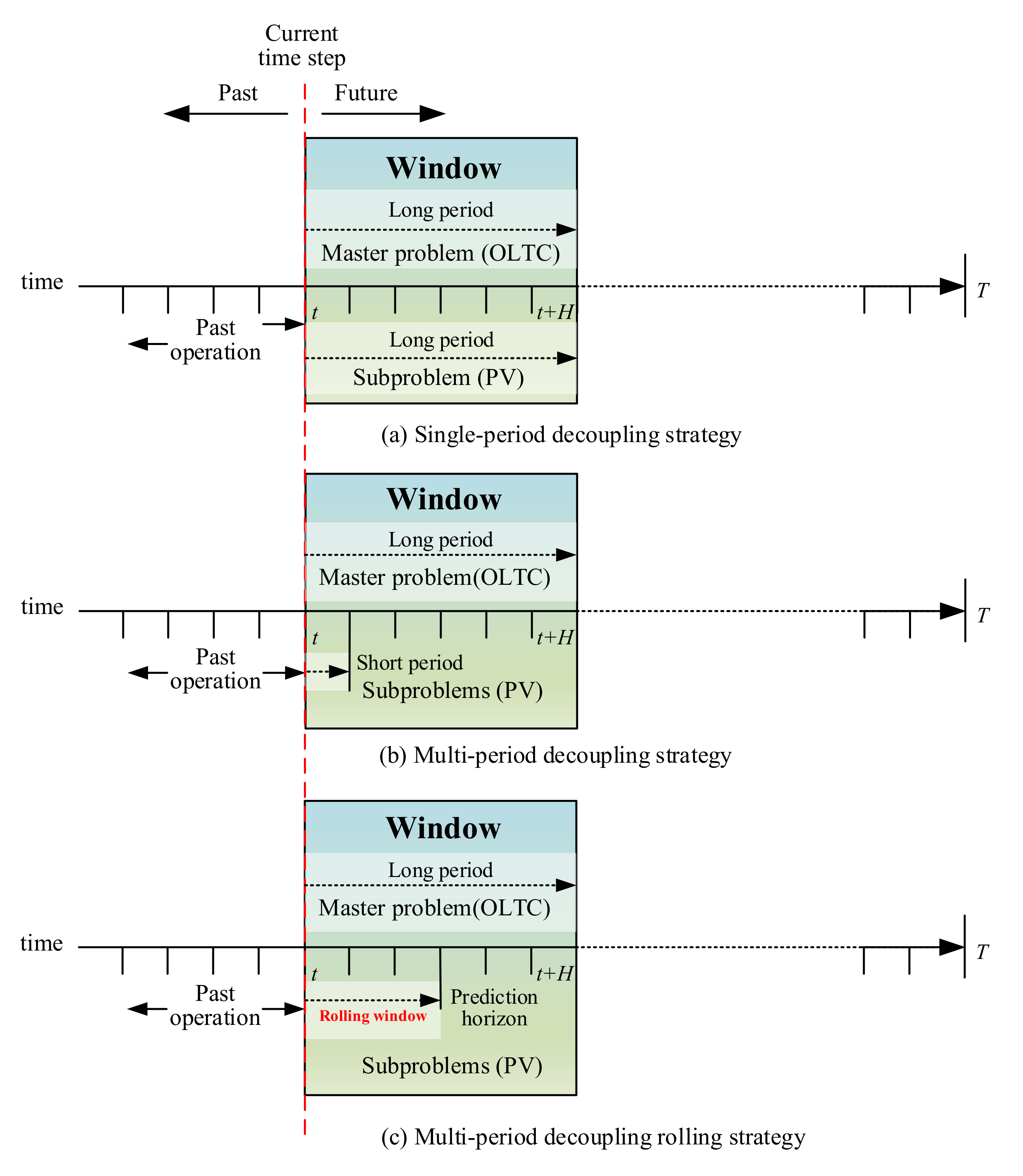
3. Decoupling Rolling Multi-Period Architecture
4. Reactive Power and Voltage Optimization Model
4.1. Objective Function
4.2. Constraints
4.2.1. Voltage Constraints
4.2.2. PV Power Constraints
4.2.3. OLTC Tap Constraints
4.3. Model Decomposition
- (1)
- MPC-Based subproblem
- (2)
- Master Problem
4.4. Solution Algorithm
5. Results and Discussion
5.1. Simulation Results of Case 1
5.1.1. Optimal Results
5.1.2. Performance Comparison
Adjustment Costs
Voltage Deviations
Active Power Losses
Computation Time
5.2. Simulation Results of Case 2
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| auxiliary variable | |
| initial lower bound of | |
| dual variable | |
| nodal voltage phase angle | |
| PV maximum power factor angle | |
| set of conductance and susceptance | |
| unit cost coefficients of OLTC | |
| , | unit cost coefficients of PV active power and reactive power |
| Elements in the Jacobian matrix | |
| Jacobian matrix from Newton Raphson power flow equation | |
| objective function of subproblems and the master problem | |
| lower and upper bound of the original problem | |
| number of iterations | |
| power-voltage sensitivity matrix | |
| OLTC tap position and OLTC tap changes | |
| , | lower and upper bound of OLTC tap position |
| PV-m capacity | |
| long-period time window | |
| rolling short-period time window | |
| total number of long periods | |
| total number of short periods in a long period | |
| nodal voltage amplitude | |
| OLTC set-point | |
| voltage variation on the low-voltage side after a OLTC tap change | |
| , | lower and upper bound of nodal voltage amplitude |
| set of nodal power and reactive power | |
| active power loss | |
| , | set of load power |
| set of PV predicted active power outputs | |
| , | set of PV actual active power and active power changes |
| , | set of PV reactive power and reactive power changes |
| , | lower and upper bound PVs reactive power |
Abbreviations
| ADN | Active distribution network |
| DG | Distributed generation |
| DRM | Decoupling rolling multi-period |
| MINP | Mixed integer nonlinear programming |
| MPC | Model predictive control |
| MPPT | Maximum power point tracking |
| OPF | Optimal power flow |
| OLTC | On-load tap changer |
| PCC | Point of common coupling |
| PV | Photovoltaic |
Appendix A
| Node | 0:00 | 1:00 | 2:00 | 3:00 | 4:00 | 5:00 | 6:00 | 7:00 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.024297 | 1.024349 | 1.024331 | 1.024316 | 1.024288 | 1.024258 | 1.024293 | 1.036911 |
| 3 | 1.024204 | 1.024308 | 1.024271 | 1.024242 | 1.024185 | 1.024126 | 1.024196 | 1.036784 |
| 4 | 1.024148 | 1.024262 | 1.024221 | 1.024190 | 1.024127 | 1.024058 | 1.024125 | 1.036702 |
| 5 | 1.023609 | 1.023882 | 1.023783 | 1.023709 | 1.023558 | 1.023374 | 1.023472 | 1.035926 |
| 6 | 1.018692 | 1.021093 | 1.020227 | 1.019572 | 1.018249 | 1.016798 | 1.018217 | 1.029404 |
| 7 | 1.013801 | 1.018310 | 1.016683 | 1.015453 | 1.012969 | 1.010310 | 1.013207 | 1.023211 |
| 8 | 1.012651 | 1.017657 | 1.015851 | 1.014486 | 1.011728 | 1.008789 | 1.012057 | 1.021791 |
| 9 | 1.012083 | 1.017339 | 1.015443 | 1.014009 | 1.011114 | 1.008026 | 1.011448 | 1.021032 |
| 10 | 1.006702 | 1.014576 | 1.011735 | 1.009588 | 1.005249 | 1.000726 | 1.006185 | 1.014380 |
| 11 | 1.005641 | 1.014019 | 1.010997 | 1.008712 | 1.004095 | 0.999267 | 1.005026 | 1.012910 |
| 12 | 1.002728 | 1.012552 | 1.009009 | 1.006330 | 1.000915 | 0.995419 | 1.002733 | 1.010033 |
| 13 | 0.999731 | 1.011142 | 1.007028 | 1.003916 | 0.997623 | 0.991292 | 0.999968 | 1.006460 |
| 14 | 0.996840 | 1.009774 | 1.005111 | 1.001584 | 0.994450 | 0.987361 | 0.997493 | 1.003277 |
| 15 | 0.994061 | 1.008450 | 1.003264 | 0.999339 | 0.991401 | 0.983635 | 0.995319 | 1.000496 |
| 16 | 0.993544 | 1.008204 | 1.002920 | 0.998923 | 0.990834 | 0.982943 | 0.994916 | 0.999981 |
| 17 | 0.992702 | 1.007805 | 1.002362 | 0.998243 | 0.989909 | 0.981711 | 0.993817 | 0.998542 |
| 18 | 0.992692 | 1.007800 | 1.002355 | 0.998235 | 0.989898 | 0.981697 | 0.993805 | 0.998526 |
| 19 | 0.992104 | 1.007527 | 1.001968 | 0.997762 | 0.989252 | 0.980857 | 0.993138 | 0.997652 |
| 20 | 0.991726 | 1.007351 | 1.001720 | 0.997459 | 0.988836 | 0.980317 | 0.992709 | 0.997090 |
| 21 | 0.991114 | 1.007067 | 1.001318 | 0.996968 | 0.988165 | 0.979445 | 0.992017 | 0.996183 |
| 22 | 0.991098 | 1.007061 | 1.001308 | 0.996955 | 0.988147 | 0.979422 | 0.992005 | 0.996166 |
| 23 | 0.990971 | 1.007007 | 1.001228 | 0.996855 | 0.988006 | 0.979268 | 0.991994 | 0.996153 |
| 24 | 0.990694 | 1.006891 | 1.001054 | 0.996637 | 0.987699 | 0.978932 | 0.991972 | 0.996124 |
| 25 | 0.990287 | 1.006732 | 1.000806 | 0.996321 | 0.987245 | 0.978513 | 0.992310 | 0.996566 |
| 26 | 0.990118 | 1.006666 | 1.000703 | 0.996190 | 0.987058 | 0.978340 | 0.992448 | 0.996748 |
| 27 | 0.990071 | 1.006648 | 1.000674 | 0.996154 | 0.987005 | 0.978325 | 0.992630 | 0.996990 |
| 28 | 1.024183 | 1.024294 | 1.024254 | 1.024224 | 1.024163 | 1.024097 | 1.024164 | 1.036745 |
| 29 | 1.023924 | 1.024122 | 1.024051 | 1.023997 | 1.023888 | 1.023744 | 1.023776 | 1.036263 |
| 30 | 1.023108 | 1.023808 | 1.023554 | 1.023363 | 1.022981 | 1.022483 | 1.022613 | 1.034712 |
| 31 | 1.022964 | 1.023752 | 1.023466 | 1.023252 | 1.022821 | 1.022260 | 1.022407 | 1.034438 |
| 32 | 1.022245 | 1.023475 | 1.023028 | 1.022693 | 1.022020 | 1.021146 | 1.021381 | 1.033068 |
| 33 | 1.020784 | 1.022891 | 1.022126 | 1.021552 | 1.020400 | 1.018958 | 1.019548 | 1.030635 |
| 34 | 1.018914 | 1.022164 | 1.020984 | 1.020098 | 1.018320 | 1.016368 | 1.018208 | 1.028856 |
| 35 | 1.018058 | 1.021818 | 1.020454 | 1.019428 | 1.017371 | 1.014905 | 1.016329 | 1.026352 |
| 36 | 1.024140 | 1.024256 | 1.024214 | 1.024182 | 1.024119 | 1.024049 | 1.024115 | 1.036691 |
| 37 | 1.023948 | 1.024097 | 1.024043 | 1.024002 | 1.023921 | 1.023823 | 1.023886 | 1.036430 |
| 38 | 1.023756 | 1.023968 | 1.023891 | 1.023833 | 1.023718 | 1.023577 | 1.023665 | 1.036159 |
| 39 | 1.023756 | 1.023968 | 1.023891 | 1.023833 | 1.023718 | 1.023582 | 1.023693 | 1.036194 |
| 40 | 1.012611 | 1.017632 | 1.015820 | 1.014451 | 1.011684 | 1.008762 | 1.012125 | 1.021888 |
| 41 | 1.012562 | 1.017610 | 1.015788 | 1.014412 | 1.011631 | 1.008803 | 1.012558 | 1.022472 |
| 42 | 1.011489 | 1.017035 | 1.015034 | 1.013521 | 1.010466 | 1.007209 | 1.010828 | 1.020245 |
| 43 | 1.010834 | 1.016694 | 1.014580 | 1.012981 | 1.009753 | 1.006323 | 1.010191 | 1.019443 |
| 44 | 1.009968 | 1.016252 | 1.013985 | 1.012271 | 1.008809 | 1.005153 | 1.009384 | 1.018424 |
| 45 | 1.009157 | 1.015845 | 1.013432 | 1.011608 | 1.007923 | 1.003963 | 1.008236 | 1.016940 |
| 46 | 1.005010 | 1.013982 | 1.010745 | 1.008298 | 1.003354 | 0.997698 | 1.002274 | 1.009103 |
| 47 | 1.002966 | 1.013065 | 1.009421 | 1.006667 | 1.001103 | 0.994611 | 0.999336 | 1.005240 |
| 48 | 1.002176 | 1.012712 | 1.008910 | 1.006037 | 1.000232 | 0.993415 | 0.998198 | 1.003744 |
| 49 | 1.001397 | 1.012402 | 1.008431 | 1.005430 | 0.999366 | 0.992225 | 0.997153 | 1.002350 |
| 50 | 1.000281 | 1.011904 | 1.007711 | 1.004541 | 0.998137 | 0.990562 | 0.995655 | 1.000383 |
| 51 | 1.000155 | 1.011843 | 1.007626 | 1.004438 | 0.997999 | 0.990358 | 0.995400 | 1.000047 |
| 52 | 1.000010 | 1.011771 | 1.007528 | 1.004320 | 0.997841 | 0.990125 | 0.995109 | 0.999666 |
| 53 | 0.999300 | 1.011419 | 1.007046 | 1.003741 | 0.997065 | 0.988985 | 0.993684 | 0.997795 |
| 54 | 0.998800 | 1.011149 | 1.006693 | 1.003326 | 0.996522 | 0.988209 | 0.992724 | 0.996549 |
| 55 | 1.005525 | 1.013973 | 1.010925 | 1.008621 | 1.003967 | 0.999069 | 1.004773 | 1.012572 |
| 56 | 1.005524 | 1.013972 | 1.010924 | 1.008620 | 1.003965 | 0.999067 | 1.004770 | 1.012568 |
| 57 | 1.002452 | 1.012400 | 1.008811 | 1.006098 | 1.000615 | 0.995266 | 1.003411 | 1.010974 |
| 58 | 1.002451 | 1.012399 | 1.008811 | 1.006098 | 1.000614 | 0.995267 | 1.003418 | 1.010982 |
| 59 | 1.024180 | 1.024291 | 1.024251 | 1.024221 | 1.024159 | 1.024093 | 1.024159 | 1.036739 |
| 60 | 1.023878 | 1.024081 | 1.024008 | 1.023952 | 1.023841 | 1.023692 | 1.023720 | 1.036201 |
| 61 | 1.023605 | 1.023920 | 1.023806 | 1.023720 | 1.023547 | 1.023337 | 1.023453 | 1.035876 |
| 62 | 1.023526 | 1.023873 | 1.023747 | 1.023652 | 1.023463 | 1.023235 | 1.023376 | 1.035782 |
| 63 | 1.023522 | 1.023871 | 1.023744 | 1.023649 | 1.023458 | 1.023229 | 1.023371 | 1.035775 |
| 64 | 1.022318 | 1.023164 | 1.022857 | 1.022626 | 1.022164 | 1.021614 | 1.021973 | 1.034042 |
| 65 | 1.021840 | 1.022876 | 1.022500 | 1.022217 | 1.021651 | 1.020987 | 1.021456 | 1.033407 |
| 66 | 1.021777 | 1.022838 | 1.022453 | 1.022163 | 1.021583 | 1.020904 | 1.021388 | 1.033324 |
| 67 | 1.021763 | 1.022830 | 1.022442 | 1.022151 | 1.021568 | 1.020885 | 1.021372 | 1.033305 |
| 68 | 1.021597 | 1.022729 | 1.022318 | 1.022009 | 1.021391 | 1.020667 | 1.021189 | 1.033080 |
| 69 | 1.021596 | 1.022729 | 1.022318 | 1.022009 | 1.021390 | 1.020667 | 1.021189 | 1.033080 |
| Node | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.036852 | 1.036862 | 1.024315 | 1.024397 | 1.024343 | 1.036919 | 1.036954 | 1.036933 |
| 3 | 1.036666 | 1.036687 | 1.024240 | 1.024404 | 1.024297 | 1.036802 | 1.036871 | 1.036829 |
| 4 | 1.036568 | 1.036587 | 1.024155 | 1.024335 | 1.024219 | 1.036715 | 1.036782 | 1.036732 |
| 5 | 1.035581 | 1.035604 | 1.023444 | 1.023862 | 1.023602 | 1.035922 | 1.036024 | 1.035891 |
| 6 | 1.026556 | 1.026987 | 1.018842 | 1.022538 | 1.020125 | 1.029691 | 1.031071 | 1.030044 |
| 7 | 1.017936 | 1.018836 | 1.014742 | 1.021711 | 1.017119 | 1.023889 | 1.026680 | 1.024804 |
| 8 | 1.015950 | 1.016969 | 1.013840 | 1.021585 | 1.016473 | 1.022574 | 1.025717 | 1.023645 |
| 9 | 1.014895 | 1.015962 | 1.013308 | 1.021438 | 1.016071 | 1.021848 | 1.025143 | 1.022966 |
| 10 | 1.005309 | 1.007076 | 1.009466 | 1.021557 | 1.013432 | 1.015780 | 1.021017 | 1.017874 |
| 11 | 1.003237 | 1.005109 | 1.008436 | 1.021274 | 1.012635 | 1.014365 | 1.019903 | 1.016555 |
| 12 | 0.998882 | 1.001331 | 1.007551 | 1.022525 | 1.012277 | 1.012055 | 1.019013 | 1.015247 |
| 13 | 0.993550 | 0.996536 | 1.005796 | 1.023012 | 1.011054 | 1.008889 | 1.017144 | 1.012866 |
| 14 | 0.988730 | 0.992296 | 1.004516 | 1.023879 | 1.010248 | 1.006183 | 1.015807 | 1.011078 |
| 15 | 0.984445 | 0.988633 | 1.003727 | 1.025137 | 1.009872 | 1.003955 | 1.015023 | 1.009905 |
| 16 | 0.983650 | 0.987954 | 1.003584 | 1.025374 | 1.009804 | 1.003543 | 1.014880 | 1.009690 |
| 17 | 0.981622 | 0.985997 | 1.002395 | 1.024774 | 1.008762 | 1.002066 | 1.013580 | 1.008200 |
| 18 | 0.981599 | 0.985975 | 1.002382 | 1.024768 | 1.008751 | 1.002049 | 1.013566 | 1.008184 |
| 19 | 0.980337 | 0.984799 | 1.001764 | 1.024554 | 1.008208 | 1.001192 | 1.012898 | 1.007405 |
| 20 | 0.979525 | 0.984043 | 1.001367 | 1.024417 | 1.007858 | 1.000642 | 1.012469 | 1.006904 |
| 21 | 0.978214 | 0.982823 | 1.000729 | 1.024199 | 1.007297 | 0.999754 | 1.011779 | 1.006099 |
| 22 | 0.978187 | 0.982801 | 1.000725 | 1.024207 | 1.007293 | 0.999740 | 1.011775 | 1.006093 |
| 23 | 0.978122 | 0.982803 | 1.000877 | 1.024435 | 1.007422 | 0.999790 | 1.011953 | 1.006275 |
| 24 | 0.977979 | 0.982808 | 1.001208 | 1.024932 | 1.007703 | 0.999898 | 1.012341 | 1.006673 |
| 25 | 0.978346 | 0.983528 | 1.002480 | 1.026416 | 1.008795 | 1.000707 | 1.013799 | 1.008226 |
| 26 | 0.978496 | 0.983825 | 1.003004 | 1.027028 | 1.009245 | 1.001040 | 1.014401 | 1.008867 |
| 27 | 0.978770 | 0.984190 | 1.003453 | 1.027482 | 1.009631 | 1.001387 | 1.014911 | 1.009420 |
| 28 | 1.036616 | 1.036636 | 1.024199 | 1.024374 | 1.024261 | 1.036759 | 1.036826 | 1.036780 |
| 29 | 1.036007 | 1.036011 | 1.023704 | 1.024009 | 1.023829 | 1.036237 | 1.036285 | 1.036188 |
| 30 | 1.033813 | 1.033828 | 1.022404 | 1.023494 | 1.022845 | 1.034629 | 1.034823 | 1.034476 |
| 31 | 1.033426 | 1.033443 | 1.022174 | 1.023404 | 1.022671 | 1.034346 | 1.034564 | 1.034174 |
| 32 | 1.031490 | 1.031516 | 1.021027 | 1.022950 | 1.021803 | 1.032927 | 1.033274 | 1.032664 |
| 33 | 1.027995 | 1.028109 | 1.019232 | 1.022549 | 1.020543 | 1.030506 | 1.031255 | 1.030249 |
| 34 | 1.025106 | 1.025629 | 1.019144 | 1.024363 | 1.021075 | 1.029215 | 1.031132 | 1.029787 |
| 35 | 1.021760 | 1.022100 | 1.016337 | 1.022310 | 1.018644 | 1.026344 | 1.027989 | 1.026271 |
| 36 | 1.036555 | 1.036574 | 1.024145 | 1.024326 | 1.024209 | 1.036705 | 1.036770 | 1.036720 |
| 37 | 1.036249 | 1.036263 | 1.023878 | 1.024115 | 1.023966 | 1.036436 | 1.036495 | 1.036419 |
| 38 | 1.035904 | 1.035916 | 1.023625 | 1.023977 | 1.023757 | 1.036177 | 1.036240 | 1.036113 |
| 39 | 1.035947 | 1.035964 | 1.023677 | 1.024036 | 1.023808 | 1.036228 | 1.036303 | 1.036174 |
| 40 | 1.016059 | 1.017113 | 1.014043 | 1.021822 | 1.016675 | 1.022726 | 1.025946 | 1.023885 |
| 41 | 1.016746 | 1.017942 | 1.015053 | 1.022911 | 1.017660 | 1.023540 | 1.027078 | 1.025086 |
| 42 | 1.013766 | 1.014893 | 1.012816 | 1.021415 | 1.015748 | 1.021114 | 1.024601 | 1.022305 |
| 43 | 1.012606 | 1.013809 | 1.012372 | 1.021483 | 1.015484 | 1.020391 | 1.024116 | 1.021697 |
| 44 | 1.011112 | 1.012429 | 1.011866 | 1.021670 | 1.015217 | 1.019494 | 1.023562 | 1.020982 |
| 45 | 1.009065 | 1.010379 | 1.010548 | 1.020985 | 1.014161 | 1.017941 | 1.022095 | 1.019299 |
| 46 | 0.998083 | 0.999397 | 1.003722 | 1.017745 | 1.008803 | 1.009754 | 1.014452 | 1.010444 |
| 47 | 0.992670 | 0.993984 | 1.000358 | 1.016151 | 1.006165 | 1.005719 | 1.010686 | 1.006080 |
| 48 | 0.990572 | 0.991887 | 0.999056 | 1.015537 | 1.005144 | 1.004157 | 1.009228 | 1.004390 |
| 49 | 0.988562 | 0.989908 | 0.997960 | 1.015183 | 1.004340 | 1.002741 | 1.007991 | 1.002923 |
| 50 | 0.985774 | 0.987154 | 0.996359 | 1.014555 | 1.003126 | 1.000731 | 1.006193 | 1.000819 |
| 51 | 0.985327 | 0.986683 | 0.995987 | 1.014281 | 1.002803 | 1.000349 | 1.005778 | 1.000355 |
| 52 | 0.984818 | 0.986149 | 0.995564 | 1.013970 | 1.002436 | 0.999914 | 1.005306 | 0.999828 |
| 53 | 0.982329 | 0.983532 | 0.993491 | 1.012444 | 1.000635 | 0.997786 | 1.002996 | 0.997247 |
| 54 | 0.980684 | 0.981805 | 0.992115 | 1.011420 | 0.999434 | 0.996374 | 1.001468 | 0.995544 |
| 55 | 1.002783 | 1.004631 | 1.008059 | 1.021000 | 1.012309 | 1.013978 | 1.019481 | 1.016082 |
| 56 | 1.002778 | 1.004625 | 1.008055 | 1.020997 | 1.012305 | 1.013973 | 1.019476 | 1.016076 |
| 57 | 0.999954 | 1.002702 | 1.009405 | 1.024638 | 1.014119 | 1.013469 | 1.021099 | 1.017444 |
| 58 | 0.999964 | 1.002714 | 1.009420 | 1.024653 | 1.014133 | 1.013481 | 1.021115 | 1.017462 |
| 59 | 1.036610 | 1.036629 | 1.024192 | 1.024368 | 1.024254 | 1.036753 | 1.036819 | 1.036772 |
| 60 | 1.035937 | 1.035933 | 1.023624 | 1.023942 | 1.023751 | 1.036176 | 1.036211 | 1.036095 |
| 61 | 1.035491 | 1.035512 | 1.023416 | 1.023922 | 1.023608 | 1.035881 | 1.035995 | 1.035829 |
| 62 | 1.035362 | 1.035390 | 1.023356 | 1.023917 | 1.023567 | 1.035796 | 1.035932 | 1.035753 |
| 63 | 1.035354 | 1.035381 | 1.023351 | 1.023914 | 1.023562 | 1.035790 | 1.035926 | 1.035746 |
| 64 | 1.033029 | 1.033100 | 1.021959 | 1.023331 | 1.022474 | 1.034086 | 1.034436 | 1.034005 |
| 65 | 1.032177 | 1.032275 | 1.021483 | 1.023170 | 1.022113 | 1.033480 | 1.033932 | 1.033410 |
| 66 | 1.032064 | 1.032166 | 1.021421 | 1.023149 | 1.022065 | 1.033400 | 1.033866 | 1.033331 |
| 67 | 1.032039 | 1.032141 | 1.021406 | 1.023144 | 1.022054 | 1.033382 | 1.033850 | 1.033313 |
| 68 | 1.031739 | 1.031850 | 1.021233 | 1.023080 | 1.021921 | 1.033166 | 1.033668 | 1.033098 |
| 69 | 1.031738 | 1.031849 | 1.021233 | 1.023080 | 1.021921 | 1.033166 | 1.033668 | 1.033098 |
| Node | 16:00 | 17:00 | 18:00 | 19:00 | 20:00 | 21:00 | 22:00 | 23:00 |
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.036920 | 1.036903 | 1.036864 | 1.036860 | 1.036840 | 1.036869 | 1.024259 | 1.024297 |
| 3 | 1.036804 | 1.036769 | 1.036690 | 1.036683 | 1.036644 | 1.036702 | 1.024128 | 1.024204 |
| 4 | 1.036712 | 1.036678 | 1.036604 | 1.036604 | 1.036566 | 1.036630 | 1.024063 | 1.024148 |
| 5 | 1.035887 | 1.035829 | 1.035720 | 1.035768 | 1.035706 | 1.035861 | 1.023406 | 1.023609 |
| 6 | 1.029617 | 1.028911 | 1.027327 | 1.027313 | 1.026493 | 1.027860 | 1.016909 | 1.018692 |
| 7 | 1.023840 | 1.022431 | 1.019198 | 1.018994 | 1.017344 | 1.019911 | 1.010451 | 1.013801 |
| 8 | 1.022540 | 1.020957 | 1.017310 | 1.017046 | 1.015190 | 1.018040 | 1.008931 | 1.012651 |
| 9 | 1.021810 | 1.020150 | 1.016331 | 1.016061 | 1.014117 | 1.017110 | 1.008178 | 1.012083 |
| 10 | 1.015870 | 1.013280 | 1.007186 | 1.006514 | 1.003433 | 1.007920 | 1.000850 | 1.006702 |
| 11 | 1.014445 | 1.011708 | 1.005280 | 1.004602 | 1.001348 | 1.006124 | 0.999413 | 1.005641 |
| 12 | 1.012369 | 1.008981 | 1.000826 | 0.999586 | 0.995489 | 1.001098 | 0.995422 | 1.002728 |
| 13 | 1.009334 | 1.005354 | 0.995684 | 0.994093 | 0.989237 | 0.995767 | 0.991236 | 0.999731 |
| 14 | 1.006813 | 1.002215 | 0.990926 | 0.988880 | 0.983224 | 0.990638 | 0.987205 | 0.996840 |
| 15 | 1.004824 | 0.999582 | 0.986566 | 0.983959 | 0.977461 | 0.985719 | 0.983336 | 0.994061 |
| 16 | 1.004457 | 0.999094 | 0.985756 | 0.983045 | 0.976390 | 0.984805 | 0.982617 | 0.993544 |
| 17 | 1.002926 | 0.997482 | 0.983994 | 0.981380 | 0.974638 | 0.983311 | 0.981442 | 0.992702 |
| 18 | 1.002910 | 0.997464 | 0.983974 | 0.981360 | 0.974617 | 0.983293 | 0.981428 | 0.992692 |
| 19 | 1.002045 | 0.996518 | 0.982836 | 0.980228 | 0.973384 | 0.982242 | 0.980605 | 0.992104 |
| 20 | 1.001490 | 0.995909 | 0.982105 | 0.979499 | 0.972591 | 0.981567 | 0.980076 | 0.991726 |
| 21 | 1.000594 | 0.994928 | 0.980923 | 0.978322 | 0.971308 | 0.980475 | 0.979219 | 0.991114 |
| 22 | 1.000583 | 0.994912 | 0.980896 | 0.978291 | 0.971272 | 0.980444 | 0.979196 | 0.991098 |
| 23 | 1.000670 | 0.994949 | 0.980775 | 0.978088 | 0.970994 | 0.980208 | 0.979014 | 0.990971 |
| 24 | 1.000862 | 0.995029 | 0.980512 | 0.977645 | 0.970387 | 0.979695 | 0.978617 | 0.990694 |
| 25 | 1.001902 | 0.995814 | 0.980473 | 0.977113 | 0.969467 | 0.978920 | 0.978022 | 0.990287 |
| 26 | 1.002331 | 0.996138 | 0.980457 | 0.976893 | 0.969088 | 0.978600 | 0.977777 | 0.990118 |
| 27 | 1.002746 | 0.996490 | 0.980595 | 0.976886 | 0.968981 | 0.978510 | 0.977708 | 0.990071 |
| 28 | 1.036758 | 1.036724 | 1.036649 | 1.036647 | 1.036609 | 1.036671 | 1.024102 | 1.024183 |
| 29 | 1.036207 | 1.036169 | 1.036137 | 1.036201 | 1.036179 | 1.036288 | 1.023779 | 1.023924 |
| 30 | 1.034527 | 1.034396 | 1.034251 | 1.034465 | 1.034374 | 1.034757 | 1.022597 | 1.023108 |
| 31 | 1.034231 | 1.034082 | 1.033918 | 1.034159 | 1.034056 | 1.034487 | 1.022388 | 1.022964 |
| 32 | 1.032749 | 1.032517 | 1.032254 | 1.032627 | 1.032464 | 1.033137 | 1.021345 | 1.022245 |
| 33 | 1.030271 | 1.029810 | 1.029149 | 1.029645 | 1.029274 | 1.030425 | 1.019243 | 1.020784 |
| 34 | 1.029216 | 1.028172 | 1.026122 | 1.026169 | 1.025144 | 1.026921 | 1.016536 | 1.018914 |
| 35 | 1.026068 | 1.025113 | 1.023519 | 1.024121 | 1.023278 | 1.025335 | 1.015306 | 1.018058 |
| 36 | 1.036701 | 1.036667 | 1.036593 | 1.036593 | 1.036556 | 1.036620 | 1.024055 | 1.024140 |
| 37 | 1.036416 | 1.036385 | 1.036317 | 1.036336 | 1.036301 | 1.036383 | 1.023839 | 1.023948 |
| 38 | 1.036125 | 1.036096 | 1.036005 | 1.036031 | 1.035987 | 1.036104 | 1.023601 | 1.023756 |
| 39 | 1.036177 | 1.036145 | 1.036031 | 1.036040 | 1.035987 | 1.036104 | 1.023601 | 1.023756 |
| 40 | 1.022723 | 1.021106 | 1.017353 | 1.017022 | 1.015119 | 1.017978 | 1.008880 | 1.012611 |
| 41 | 1.023677 | 1.021924 | 1.017737 | 1.017114 | 1.015018 | 1.017892 | 1.008812 | 1.012562 |
| 42 | 1.021079 | 1.019319 | 1.015277 | 1.014990 | 1.012937 | 1.016094 | 1.007368 | 1.011489 |
| 43 | 1.020372 | 1.018491 | 1.014169 | 1.013835 | 1.011646 | 1.014983 | 1.006479 | 1.010834 |
| 44 | 1.019507 | 1.017453 | 1.012723 | 1.012308 | 1.009922 | 1.013500 | 1.005299 | 1.009968 |
| 45 | 1.017873 | 1.015757 | 1.010974 | 1.010716 | 1.008291 | 1.012100 | 1.004186 | 1.009157 |
| 46 | 1.009258 | 1.006767 | 1.001613 | 1.002194 | 0.999517 | 1.004627 | 0.998342 | 1.005010 |
| 47 | 1.005012 | 1.002337 | 0.996999 | 0.997994 | 0.995193 | 1.000944 | 0.995462 | 1.002966 |
| 48 | 1.003367 | 1.000621 | 0.995211 | 0.996366 | 0.993517 | 0.999516 | 0.994346 | 1.002176 |
| 49 | 1.001895 | 0.999043 | 0.993465 | 0.994728 | 0.991787 | 0.998053 | 0.993219 | 1.001397 |
| 50 | 0.999801 | 0.996818 | 0.991047 | 0.992472 | 0.989420 | 0.996038 | 0.991644 | 1.000281 |
| 51 | 0.999383 | 0.996410 | 0.990696 | 0.992192 | 0.989163 | 0.995818 | 0.991470 | 1.000155 |
| 52 | 0.998909 | 0.995948 | 0.990298 | 0.991873 | 0.988870 | 0.995567 | 0.991271 | 1.000010 |
| 53 | 0.996584 | 0.993681 | 0.988344 | 0.990313 | 0.987436 | 0.994336 | 0.990295 | 0.999300 |
| 54 | 0.995046 | 0.992180 | 0.987044 | 0.989267 | 0.986470 | 0.993502 | 0.989624 | 0.998800 |
| 55 | 1.014021 | 1.011295 | 1.004927 | 1.004324 | 1.001094 | 1.005909 | 0.999246 | 1.005525 |
| 56 | 1.014016 | 1.011290 | 1.004923 | 1.004320 | 1.001091 | 1.005906 | 0.999244 | 1.005524 |
| 57 | 1.014062 | 1.010381 | 1.001305 | 0.999474 | 0.994961 | 1.000641 | 0.995052 | 1.002452 |
| 58 | 1.014076 | 1.010393 | 1.001310 | 0.999475 | 0.994960 | 1.000639 | 0.995051 | 1.002451 |
| 59 | 1.036751 | 1.036717 | 1.036643 | 1.036642 | 1.036605 | 1.036666 | 1.024098 | 1.024180 |
| 60 | 1.036126 | 1.036104 | 1.036075 | 1.036145 | 1.036125 | 1.036237 | 1.023730 | 1.023878 |
| 61 | 1.035831 | 1.035772 | 1.035645 | 1.035697 | 1.035633 | 1.035805 | 1.023374 | 1.023605 |
| 62 | 1.035746 | 1.035676 | 1.035521 | 1.035568 | 1.035490 | 1.035680 | 1.023272 | 1.023526 |
| 63 | 1.035739 | 1.035669 | 1.035514 | 1.035561 | 1.035483 | 1.035674 | 1.023267 | 1.023522 |
| 64 | 1.033974 | 1.033795 | 1.033400 | 1.033503 | 1.033307 | 1.033767 | 1.021700 | 1.022318 |
| 65 | 1.033353 | 1.033124 | 1.032607 | 1.032711 | 1.032457 | 1.033021 | 1.021083 | 1.021840 |
| 66 | 1.033271 | 1.033035 | 1.032502 | 1.032606 | 1.032345 | 1.032922 | 1.021002 | 1.021777 |
| 67 | 1.033252 | 1.033015 | 1.032479 | 1.032583 | 1.032320 | 1.032901 | 1.020984 | 1.021763 |
| 68 | 1.033030 | 1.032777 | 1.032202 | 1.032308 | 1.032027 | 1.032643 | 1.020770 | 1.021597 |
| 69 | 1.033030 | 1.032776 | 1.032201 | 1.032307 | 1.032026 | 1.032642 | 1.020769 | 1.021596 |
| Node | 0:00 | 1:00 | 2:00 | 3:00 | 4:00 | 5:00 | 6:00 | 7:00 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.024297 | 1.024349 | 1.024331 | 1.024316 | 1.024288 | 1.024258 | 1.024293 | 1.036912 |
| 3 | 1.024204 | 1.024308 | 1.024271 | 1.024242 | 1.024185 | 1.024126 | 1.024197 | 1.036786 |
| 4 | 1.024148 | 1.024262 | 1.024221 | 1.024190 | 1.024127 | 1.024058 | 1.024126 | 1.036706 |
| 5 | 1.023609 | 1.023882 | 1.023783 | 1.023709 | 1.023558 | 1.023377 | 1.023483 | 1.035945 |
| 6 | 1.018692 | 1.021093 | 1.020227 | 1.019572 | 1.018249 | 1.016822 | 1.018289 | 1.029551 |
| 7 | 1.013801 | 1.018310 | 1.016683 | 1.015453 | 1.012969 | 1.010355 | 1.013343 | 1.023488 |
| 8 | 1.012651 | 1.017657 | 1.015851 | 1.014486 | 1.011728 | 1.008840 | 1.012208 | 1.022100 |
| 9 | 1.012083 | 1.017339 | 1.015443 | 1.014009 | 1.011114 | 1.008079 | 1.011607 | 1.021357 |
| 10 | 1.006702 | 1.014576 | 1.011735 | 1.009588 | 1.005249 | 1.000800 | 1.006416 | 1.014868 |
| 11 | 1.005641 | 1.014019 | 1.010997 | 1.008712 | 1.004095 | 0.999346 | 1.005275 | 1.013435 |
| 12 | 1.002728 | 1.012552 | 1.009009 | 1.006330 | 1.000915 | 0.995514 | 1.003044 | 1.010688 |
| 13 | 0.999731 | 1.011142 | 1.007028 | 1.003916 | 0.997623 | 0.991382 | 1.000267 | 1.007153 |
| 14 | 0.996840 | 1.009774 | 1.005111 | 1.001584 | 0.994450 | 0.987447 | 0.997780 | 1.004008 |
| 15 | 0.994061 | 1.008450 | 1.003264 | 0.999339 | 0.991401 | 0.983717 | 0.995594 | 1.001267 |
| 16 | 0.993544 | 1.008204 | 1.002920 | 0.998923 | 0.990834 | 0.983024 | 0.995188 | 1.000758 |
| 17 | 0.992702 | 1.007805 | 1.002362 | 0.998243 | 0.989909 | 0.981790 | 0.994086 | 0.999330 |
| 18 | 0.992692 | 1.007800 | 1.002355 | 0.998235 | 0.989898 | 0.981775 | 0.994074 | 0.999314 |
| 19 | 0.992104 | 1.007527 | 1.001968 | 0.997762 | 0.989252 | 0.980933 | 0.993404 | 0.998449 |
| 20 | 0.991726 | 1.007351 | 1.001720 | 0.997459 | 0.988836 | 0.980392 | 0.992973 | 0.997893 |
| 21 | 0.991114 | 1.007067 | 1.001318 | 0.996968 | 0.988165 | 0.979517 | 0.992279 | 0.996996 |
| 22 | 0.991098 | 1.007061 | 1.001308 | 0.996955 | 0.988147 | 0.979495 | 0.992266 | 0.996980 |
| 23 | 0.990971 | 1.007007 | 1.001228 | 0.996855 | 0.988006 | 0.979339 | 0.992255 | 0.996970 |
| 24 | 0.990694 | 1.006891 | 1.001054 | 0.996637 | 0.987699 | 0.979000 | 0.992229 | 0.996950 |
| 25 | 0.990287 | 1.006732 | 1.000806 | 0.996321 | 0.987245 | 0.978576 | 0.992560 | 0.997412 |
| 26 | 0.990118 | 1.006666 | 1.000703 | 0.996190 | 0.987058 | 0.978401 | 0.992696 | 0.997602 |
| 27 | 0.990071 | 1.006648 | 1.000674 | 0.996154 | 0.987005 | 0.978385 | 0.992876 | 0.997848 |
| 28 | 1.024183 | 1.024294 | 1.024254 | 1.024224 | 1.024163 | 1.024097 | 1.024163 | 1.036745 |
| 29 | 1.023924 | 1.024122 | 1.024051 | 1.023997 | 1.023888 | 1.023739 | 1.023750 | 1.036234 |
| 30 | 1.023108 | 1.023808 | 1.023554 | 1.023363 | 1.022981 | 1.022473 | 1.022566 | 1.034660 |
| 31 | 1.022964 | 1.023752 | 1.023466 | 1.023252 | 1.022821 | 1.022250 | 1.022357 | 1.034382 |
| 32 | 1.022245 | 1.023475 | 1.023028 | 1.022693 | 1.022020 | 1.021133 | 1.021313 | 1.032994 |
| 33 | 1.020784 | 1.022891 | 1.022126 | 1.021552 | 1.020400 | 1.018937 | 1.019436 | 1.030514 |
| 34 | 1.018914 | 1.022164 | 1.020984 | 1.020098 | 1.018320 | 1.016331 | 1.018008 | 1.028642 |
| 35 | 1.018058 | 1.021818 | 1.020454 | 1.019428 | 1.017371 | 1.014868 | 1.016129 | 1.026138 |
| 36 | 1.024140 | 1.024256 | 1.024214 | 1.024182 | 1.024119 | 1.024049 | 1.024117 | 1.036695 |
| 37 | 1.023948 | 1.024097 | 1.024043 | 1.024002 | 1.023921 | 1.023824 | 1.023884 | 1.036434 |
| 38 | 1.023756 | 1.023968 | 1.023891 | 1.023833 | 1.023718 | 1.023579 | 1.023655 | 1.036159 |
| 39 | 1.023756 | 1.023968 | 1.023891 | 1.023833 | 1.023718 | 1.023585 | 1.023680 | 1.036193 |
| 40 | 1.012611 | 1.017632 | 1.015820 | 1.014451 | 1.011684 | 1.008813 | 1.012276 | 1.022198 |
| 41 | 1.012562 | 1.017610 | 1.015788 | 1.014412 | 1.011631 | 1.008854 | 1.012707 | 1.022784 |
| 42 | 1.011489 | 1.017035 | 1.015034 | 1.013521 | 1.010466 | 1.007265 | 1.010993 | 1.020583 |
| 43 | 1.010834 | 1.016694 | 1.014580 | 1.012981 | 1.009753 | 1.006382 | 1.010364 | 1.019796 |
| 44 | 1.009968 | 1.016252 | 1.013985 | 1.012271 | 1.008809 | 1.005216 | 1.009566 | 1.018797 |
| 45 | 1.009157 | 1.015845 | 1.013432 | 1.011608 | 1.007923 | 1.004029 | 1.008430 | 1.017331 |
| 46 | 1.005010 | 1.013982 | 1.010745 | 1.008298 | 1.003354 | 0.997778 | 1.002510 | 1.009571 |
| 47 | 1.002966 | 1.013065 | 1.009421 | 1.006667 | 1.001103 | 0.994698 | 0.999593 | 1.005746 |
| 48 | 1.002176 | 1.012712 | 1.008910 | 1.006037 | 1.000232 | 0.993505 | 0.998464 | 1.004264 |
| 49 | 1.001397 | 1.012402 | 1.008431 | 1.005430 | 0.999366 | 0.992318 | 0.997428 | 1.002887 |
| 50 | 1.000281 | 1.011904 | 1.007711 | 1.004541 | 0.998137 | 0.990660 | 0.995950 | 1.000953 |
| 51 | 1.000155 | 1.011843 | 1.007626 | 1.004438 | 0.997999 | 0.990457 | 0.995695 | 1.000617 |
| 52 | 1.000010 | 1.011771 | 1.007528 | 1.004320 | 0.997841 | 0.990224 | 0.995404 | 1.000236 |
| 53 | 0.999300 | 1.011419 | 1.007046 | 1.003741 | 0.997065 | 0.989084 | 0.993979 | 0.998366 |
| 54 | 0.998800 | 1.011149 | 1.006693 | 1.003326 | 0.996522 | 0.988308 | 0.993020 | 0.997121 |
| 55 | 1.005525 | 1.013973 | 1.010925 | 1.008621 | 1.003967 | 0.999148 | 1.005022 | 1.013097 |
| 56 | 1.005524 | 1.013972 | 1.010924 | 1.008620 | 1.003965 | 0.999145 | 1.005019 | 1.013094 |
| 57 | 1.002452 | 1.012400 | 1.008811 | 1.006098 | 1.000615 | 0.995380 | 1.003794 | 1.011736 |
| 58 | 1.002451 | 1.012399 | 1.008811 | 1.006098 | 1.000614 | 0.995381 | 1.003801 | 1.011745 |
| 59 | 1.024180 | 1.024291 | 1.024251 | 1.024221 | 1.024159 | 1.024093 | 1.024160 | 1.036741 |
| 60 | 1.023878 | 1.024081 | 1.024008 | 1.023952 | 1.023841 | 1.023693 | 1.023716 | 1.036202 |
| 61 | 1.023605 | 1.023920 | 1.023806 | 1.023720 | 1.023547 | 1.023339 | 1.023446 | 1.035877 |
| 62 | 1.023526 | 1.023873 | 1.023747 | 1.023652 | 1.023463 | 1.023236 | 1.023368 | 1.035783 |
| 63 | 1.023522 | 1.023871 | 1.023744 | 1.023649 | 1.023458 | 1.023231 | 1.023363 | 1.035777 |
| 64 | 1.022318 | 1.023164 | 1.022857 | 1.022626 | 1.022164 | 1.021618 | 1.021956 | 1.034045 |
| 65 | 1.021840 | 1.022876 | 1.022500 | 1.022217 | 1.021651 | 1.020992 | 1.021434 | 1.033411 |
| 66 | 1.021777 | 1.022838 | 1.022453 | 1.022163 | 1.021583 | 1.020909 | 1.021365 | 1.033327 |
| 67 | 1.021763 | 1.022830 | 1.022442 | 1.022151 | 1.021568 | 1.020890 | 1.021349 | 1.033308 |
| 68 | 1.021597 | 1.022729 | 1.022318 | 1.022009 | 1.021391 | 1.020673 | 1.021165 | 1.033084 |
| 69 | 1.021596 | 1.022729 | 1.022318 | 1.022009 | 1.021390 | 1.020672 | 1.021165 | 1.033084 |
| Node | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.036853 | 1.036857 | 1.024321 | 1.024400 | 1.024349 | 1.036919 | 1.036954 | 1.036930 |
| 3 | 1.036670 | 1.036678 | 1.024252 | 1.024409 | 1.024309 | 1.036801 | 1.036870 | 1.036822 |
| 4 | 1.036574 | 1.036579 | 1.024170 | 1.024343 | 1.024234 | 1.036716 | 1.036784 | 1.036729 |
| 5 | 1.035607 | 1.035603 | 1.023495 | 1.023900 | 1.023654 | 1.035937 | 1.036050 | 1.035910 |
| 6 | 1.026758 | 1.026885 | 1.019265 | 1.022851 | 1.020597 | 1.029792 | 1.031233 | 1.030090 |
| 7 | 1.018320 | 1.018626 | 1.015551 | 1.022307 | 1.018026 | 1.024077 | 1.026980 | 1.024871 |
| 8 | 1.016378 | 1.016733 | 1.014742 | 1.022249 | 1.017485 | 1.022783 | 1.026049 | 1.023716 |
| 9 | 1.015346 | 1.015716 | 1.014256 | 1.022138 | 1.017137 | 1.022070 | 1.025493 | 1.023042 |
| 10 | 1.005990 | 1.006643 | 1.010907 | 1.022712 | 1.015176 | 1.016130 | 1.021522 | 1.017915 |
| 11 | 1.003970 | 1.004652 | 1.009979 | 1.022536 | 1.014527 | 1.014751 | 1.020450 | 1.016604 |
| 12 | 0.999797 | 1.000766 | 1.009458 | 1.024176 | 1.014712 | 1.012564 | 1.019700 | 1.015300 |
| 13 | 0.994537 | 0.995704 | 1.007921 | 1.024999 | 1.014003 | 1.009410 | 1.017803 | 1.012717 |
| 14 | 0.989790 | 0.991191 | 1.006862 | 1.026209 | 1.013718 | 1.006717 | 1.016438 | 1.010723 |
| 15 | 0.985580 | 0.987252 | 1.006299 | 1.027817 | 1.013874 | 1.004503 | 1.015626 | 1.009339 |
| 16 | 0.984798 | 0.986521 | 1.006197 | 1.028120 | 1.013905 | 1.004094 | 1.015478 | 1.009085 |
| 17 | 0.982791 | 0.984497 | 1.005062 | 1.027648 | 1.013036 | 1.002630 | 1.014177 | 1.007544 |
| 18 | 0.982768 | 0.984474 | 1.005050 | 1.027644 | 1.013026 | 1.002614 | 1.014163 | 1.007528 |
| 19 | 0.981523 | 0.983240 | 1.004478 | 1.027542 | 1.012632 | 1.001769 | 1.013494 | 1.006704 |
| 20 | 0.980722 | 0.982447 | 1.004110 | 1.027477 | 1.012379 | 1.001227 | 1.013065 | 1.006175 |
| 21 | 0.979429 | 0.981166 | 1.003520 | 1.027375 | 1.011973 | 1.000351 | 1.012374 | 1.005324 |
| 22 | 0.979403 | 0.981141 | 1.003518 | 1.027388 | 1.011976 | 1.000338 | 1.012370 | 1.005316 |
| 23 | 0.979345 | 0.981116 | 1.003691 | 1.027669 | 1.012176 | 1.000394 | 1.012547 | 1.005477 |
| 24 | 0.979219 | 0.981062 | 1.004067 | 1.028283 | 1.012611 | 1.000514 | 1.012934 | 1.005829 |
| 25 | 0.979621 | 0.981655 | 1.005437 | 1.030017 | 1.014036 | 1.001350 | 1.014390 | 1.007284 |
| 26 | 0.979786 | 0.981899 | 1.006002 | 1.030733 | 1.014623 | 1.001694 | 1.014990 | 1.007884 |
| 27 | 0.980068 | 0.982235 | 1.006473 | 1.031244 | 1.015084 | 1.002046 | 1.015499 | 1.008415 |
| 28 | 1.036618 | 1.036623 | 1.024207 | 1.024375 | 1.024269 | 1.036756 | 1.036822 | 1.036769 |
| 29 | 1.035968 | 1.035947 | 1.023659 | 1.023955 | 1.023783 | 1.036190 | 1.036222 | 1.036109 |
| 30 | 1.033748 | 1.033689 | 1.022341 | 1.023393 | 1.022773 | 1.034541 | 1.034701 | 1.034311 |
| 31 | 1.033357 | 1.033291 | 1.022109 | 1.023295 | 1.022594 | 1.034250 | 1.034433 | 1.033994 |
| 32 | 1.031398 | 1.031298 | 1.020946 | 1.022800 | 1.021703 | 1.032795 | 1.033091 | 1.032408 |
| 33 | 1.027847 | 1.027733 | 1.019112 | 1.022300 | 1.020387 | 1.030284 | 1.030948 | 1.029812 |
| 34 | 1.024848 | 1.024936 | 1.018952 | 1.023917 | 1.020810 | 1.028816 | 1.030580 | 1.028987 |
| 35 | 1.021501 | 1.021404 | 1.016145 | 1.021864 | 1.018379 | 1.025944 | 1.027436 | 1.025469 |
| 36 | 1.036561 | 1.036566 | 1.024160 | 1.024334 | 1.024225 | 1.036705 | 1.036773 | 1.036717 |
| 37 | 1.036253 | 1.036252 | 1.023897 | 1.024120 | 1.023984 | 1.036431 | 1.036495 | 1.036420 |
| 38 | 1.035901 | 1.035896 | 1.023659 | 1.023976 | 1.023783 | 1.036150 | 1.036233 | 1.036124 |
| 39 | 1.035941 | 1.035942 | 1.023714 | 1.024033 | 1.023836 | 1.036195 | 1.036294 | 1.036188 |
| 40 | 1.016489 | 1.016870 | 1.014952 | 1.022485 | 1.017693 | 1.022932 | 1.026276 | 1.023951 |
| 41 | 1.017181 | 1.017672 | 1.015986 | 1.023574 | 1.018695 | 1.023739 | 1.027400 | 1.025130 |
| 42 | 1.014236 | 1.014628 | 1.013804 | 1.022132 | 1.016846 | 1.021340 | 1.024962 | 1.022374 |
| 43 | 1.013097 | 1.013524 | 1.013406 | 1.022220 | 1.016620 | 1.020620 | 1.024489 | 1.021758 |
| 44 | 1.011634 | 1.012114 | 1.012964 | 1.022433 | 1.016405 | 1.019729 | 1.023951 | 1.021032 |
| 45 | 1.009613 | 1.010056 | 1.011690 | 1.021776 | 1.015386 | 1.018190 | 1.022507 | 1.019354 |
| 46 | 0.998746 | 0.998995 | 1.005075 | 1.018643 | 1.010203 | 1.010047 | 1.014940 | 1.010472 |
| 47 | 0.993390 | 0.993543 | 1.001815 | 1.017101 | 1.007650 | 1.006034 | 1.011211 | 1.006095 |
| 48 | 0.991314 | 0.991430 | 1.000553 | 1.016506 | 1.006663 | 1.004479 | 1.009767 | 1.004399 |
| 49 | 0.989330 | 0.989431 | 0.999506 | 1.016176 | 1.005899 | 1.003072 | 1.008545 | 1.002923 |
| 50 | 0.986589 | 0.986664 | 0.997982 | 1.015596 | 1.004751 | 1.001087 | 1.006788 | 1.000828 |
| 51 | 0.986142 | 0.986193 | 0.997611 | 1.015323 | 1.004429 | 1.000705 | 1.006373 | 1.000363 |
| 52 | 0.985634 | 0.985658 | 0.997188 | 1.015012 | 1.004062 | 1.000270 | 1.005902 | 0.999837 |
| 53 | 0.983147 | 0.983040 | 0.995118 | 1.013487 | 1.002263 | 0.998142 | 1.003593 | 0.997255 |
| 54 | 0.981504 | 0.981312 | 0.993745 | 1.012465 | 1.001064 | 0.996731 | 1.002066 | 0.995552 |
| 55 | 1.003516 | 1.004174 | 1.009602 | 1.022263 | 1.014202 | 1.014364 | 1.020028 | 1.016132 |
| 56 | 1.003511 | 1.004168 | 1.009598 | 1.022260 | 1.014198 | 1.014359 | 1.020023 | 1.016126 |
| 57 | 1.001002 | 1.002215 | 1.011530 | 1.026449 | 1.016748 | 1.014093 | 1.021947 | 1.017639 |
| 58 | 1.001013 | 1.002228 | 1.011546 | 1.026466 | 1.016763 | 1.014106 | 1.021964 | 1.017657 |
| 59 | 1.036613 | 1.036619 | 1.024204 | 1.024373 | 1.024266 | 1.036752 | 1.036818 | 1.036765 |
| 60 | 1.035937 | 1.035919 | 1.023642 | 1.023944 | 1.023767 | 1.036165 | 1.036207 | 1.036094 |
| 61 | 1.035492 | 1.035485 | 1.023448 | 1.023922 | 1.023633 | 1.035862 | 1.035985 | 1.035823 |
| 62 | 1.035363 | 1.035359 | 1.023392 | 1.023915 | 1.023595 | 1.035774 | 1.035922 | 1.035744 |
| 63 | 1.035355 | 1.035351 | 1.023386 | 1.023912 | 1.023590 | 1.035767 | 1.035916 | 1.035737 |
| 64 | 1.033030 | 1.033025 | 1.022042 | 1.023322 | 1.022535 | 1.034033 | 1.034408 | 1.033979 |
| 65 | 1.032179 | 1.032180 | 1.021587 | 1.023158 | 1.022187 | 1.033413 | 1.033897 | 1.033377 |
| 66 | 1.032066 | 1.032069 | 1.021527 | 1.023137 | 1.022141 | 1.033331 | 1.033830 | 1.033297 |
| 67 | 1.032041 | 1.032044 | 1.021513 | 1.023131 | 1.022131 | 1.033313 | 1.033814 | 1.033279 |
| 68 | 1.031741 | 1.031745 | 1.021347 | 1.023065 | 1.022002 | 1.033092 | 1.033628 | 1.033061 |
| 69 | 1.031740 | 1.031745 | 1.021347 | 1.023066 | 1.022003 | 1.033092 | 1.033629 | 1.033062 |
| Node | 16:00 | 17:00 | 18:00 | 19:00 | 20:00 | 21:00 | 22:00 | 23:00 |
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.036922 | 1.036900 | 1.036866 | 1.036861 | 1.036840 | 1.036869 | 1.024259 | 1.024297 |
| 3 | 1.036808 | 1.036764 | 1.036694 | 1.036686 | 1.036644 | 1.036702 | 1.024128 | 1.024204 |
| 4 | 1.036719 | 1.036675 | 1.036609 | 1.036607 | 1.036566 | 1.036630 | 1.024063 | 1.024148 |
| 5 | 1.035920 | 1.035837 | 1.035738 | 1.035778 | 1.035706 | 1.035861 | 1.023406 | 1.023609 |
| 6 | 1.029867 | 1.028913 | 1.027475 | 1.027397 | 1.026493 | 1.027860 | 1.016909 | 1.018692 |
| 7 | 1.024314 | 1.022425 | 1.019480 | 1.019156 | 1.017344 | 1.019911 | 1.010451 | 1.013801 |
| 8 | 1.023067 | 1.020948 | 1.017625 | 1.017227 | 1.015190 | 1.018040 | 1.008931 | 1.012651 |
| 9 | 1.022365 | 1.020143 | 1.016662 | 1.016251 | 1.014117 | 1.017110 | 1.008178 | 1.012083 |
| 10 | 1.016708 | 1.013247 | 1.007682 | 1.006802 | 1.003433 | 1.007920 | 1.000850 | 1.006702 |
| 11 | 1.015347 | 1.011683 | 1.005810 | 1.004910 | 1.001348 | 1.006124 | 0.999413 | 1.005641 |
| 12 | 1.013495 | 1.008970 | 1.001479 | 0.999966 | 0.995489 | 1.001098 | 0.995422 | 1.002728 |
| 13 | 1.010545 | 1.005234 | 0.996383 | 0.994518 | 0.989237 | 0.995767 | 0.991236 | 0.999731 |
| 14 | 1.008109 | 1.001984 | 0.991671 | 0.989350 | 0.983224 | 0.990638 | 0.987205 | 0.996840 |
| 15 | 1.006209 | 0.999238 | 0.987358 | 0.984475 | 0.977461 | 0.985719 | 0.983336 | 0.994061 |
| 16 | 1.005858 | 0.998730 | 0.986557 | 0.983569 | 0.976390 | 0.984805 | 0.982617 | 0.993544 |
| 17 | 1.004353 | 0.997100 | 0.984803 | 0.981914 | 0.974638 | 0.983311 | 0.981442 | 0.992702 |
| 18 | 1.004336 | 0.997082 | 0.984783 | 0.981894 | 0.974617 | 0.983293 | 0.981428 | 0.992692 |
| 19 | 1.003494 | 0.996120 | 0.983651 | 0.980770 | 0.973384 | 0.982242 | 0.980605 | 0.992104 |
| 20 | 1.002952 | 0.995502 | 0.982923 | 0.980047 | 0.972591 | 0.981567 | 0.980076 | 0.991726 |
| 21 | 1.002080 | 0.994505 | 0.981748 | 0.978878 | 0.971308 | 0.980475 | 0.979219 | 0.991114 |
| 22 | 1.002069 | 0.994488 | 0.981721 | 0.978848 | 0.971272 | 0.980444 | 0.979196 | 0.991098 |
| 23 | 1.002167 | 0.994518 | 0.981602 | 0.978649 | 0.970994 | 0.980208 | 0.979014 | 0.990971 |
| 24 | 1.002380 | 0.994582 | 0.981345 | 0.978214 | 0.970387 | 0.979695 | 0.978617 | 0.990694 |
| 25 | 1.003466 | 0.995333 | 0.981318 | 0.977700 | 0.969467 | 0.978920 | 0.978022 | 0.990287 |
| 26 | 1.003914 | 0.995643 | 0.981306 | 0.977487 | 0.969088 | 0.978600 | 0.977777 | 0.990118 |
| 27 | 1.004340 | 0.995987 | 0.981447 | 0.977484 | 0.968981 | 0.978510 | 0.977708 | 0.990071 |
| 28 | 1.036759 | 1.036715 | 1.036651 | 1.036649 | 1.036609 | 1.036671 | 1.024102 | 1.024183 |
| 29 | 1.036153 | 1.036118 | 1.036116 | 1.036195 | 1.036179 | 1.036288 | 1.023779 | 1.023924 |
| 30 | 1.034432 | 1.034287 | 1.034220 | 1.034459 | 1.034374 | 1.034757 | 1.022597 | 1.023108 |
| 31 | 1.034128 | 1.033964 | 1.033886 | 1.034152 | 1.034056 | 1.034487 | 1.022388 | 1.022964 |
| 32 | 1.032610 | 1.032348 | 1.032213 | 1.032620 | 1.032464 | 1.033137 | 1.021345 | 1.022245 |
| 33 | 1.030045 | 1.029520 | 1.029088 | 1.029635 | 1.029274 | 1.030425 | 1.019243 | 1.020784 |
| 34 | 1.028819 | 1.027638 | 1.026021 | 1.026157 | 1.025144 | 1.026921 | 1.016536 | 1.018914 |
| 35 | 1.025669 | 1.024578 | 1.023418 | 1.024108 | 1.023278 | 1.025335 | 1.015306 | 1.018058 |
| 36 | 1.036708 | 1.036663 | 1.036598 | 1.036597 | 1.036556 | 1.036620 | 1.024055 | 1.024140 |
| 37 | 1.036423 | 1.036377 | 1.036321 | 1.036340 | 1.036301 | 1.036383 | 1.023839 | 1.023948 |
| 38 | 1.036135 | 1.036074 | 1.036005 | 1.036039 | 1.035987 | 1.036104 | 1.023601 | 1.023756 |
| 39 | 1.036188 | 1.036119 | 1.036030 | 1.036048 | 1.035987 | 1.036104 | 1.023601 | 1.023756 |
| 40 | 1.023251 | 1.021092 | 1.017670 | 1.017204 | 1.015119 | 1.017978 | 1.008880 | 1.012611 |
| 41 | 1.024211 | 1.021891 | 1.018062 | 1.017302 | 1.015018 | 1.017892 | 1.008812 | 1.012562 |
| 42 | 1.021654 | 1.019304 | 1.015624 | 1.015188 | 1.012937 | 1.016094 | 1.007368 | 1.011489 |
| 43 | 1.020970 | 1.018467 | 1.014533 | 1.014044 | 1.011646 | 1.014983 | 1.006479 | 1.010834 |
| 44 | 1.020139 | 1.017418 | 1.013114 | 1.012530 | 1.009922 | 1.013500 | 1.005299 | 1.009968 |
| 45 | 1.018533 | 1.015725 | 1.011383 | 1.010947 | 1.008291 | 1.012100 | 1.004186 | 1.009157 |
| 46 | 1.010036 | 1.006719 | 1.002113 | 1.002471 | 0.999517 | 1.004627 | 0.998342 | 1.005010 |
| 47 | 1.005848 | 1.002281 | 0.997544 | 0.998293 | 0.995193 | 1.000944 | 0.995462 | 1.002966 |
| 48 | 1.004225 | 1.000561 | 0.995773 | 0.996673 | 0.993517 | 0.999516 | 0.994346 | 1.002176 |
| 49 | 1.002779 | 0.998977 | 0.994048 | 0.995046 | 0.991787 | 0.998053 | 0.993219 | 1.001397 |
| 50 | 1.000735 | 0.996759 | 0.991664 | 0.992806 | 0.989420 | 0.996038 | 0.991644 | 1.000281 |
| 51 | 1.000318 | 0.996352 | 0.991313 | 0.992526 | 0.989163 | 0.995818 | 0.991470 | 1.000155 |
| 52 | 0.999844 | 0.995889 | 0.990915 | 0.992208 | 0.988870 | 0.995567 | 0.991271 | 1.000010 |
| 53 | 0.997521 | 0.993622 | 0.988962 | 0.990648 | 0.987436 | 0.994336 | 0.990295 | 0.999300 |
| 54 | 0.995985 | 0.992121 | 0.987664 | 0.989602 | 0.986470 | 0.993502 | 0.989624 | 0.998800 |
| 55 | 1.014923 | 1.011270 | 1.005457 | 1.004632 | 1.001094 | 1.005909 | 0.999246 | 1.005525 |
| 56 | 1.014918 | 1.011265 | 1.005453 | 1.004629 | 1.001091 | 1.005906 | 0.999244 | 1.005524 |
| 57 | 1.015356 | 1.010461 | 1.002051 | 0.999896 | 0.994961 | 1.000641 | 0.995052 | 1.002452 |
| 58 | 1.015371 | 1.010473 | 1.002057 | 0.999897 | 0.994960 | 1.000639 | 0.995051 | 1.002451 |
| 59 | 1.036755 | 1.036712 | 1.036647 | 1.036645 | 1.036605 | 1.036666 | 1.024098 | 1.024180 |
| 60 | 1.036132 | 1.036092 | 1.036077 | 1.036149 | 1.036125 | 1.036237 | 1.023730 | 1.023878 |
| 61 | 1.035839 | 1.035748 | 1.035649 | 1.035704 | 1.035633 | 1.035805 | 1.023374 | 1.023605 |
| 62 | 1.035755 | 1.035649 | 1.035526 | 1.035576 | 1.035490 | 1.035680 | 1.023272 | 1.023526 |
| 63 | 1.035748 | 1.035642 | 1.035519 | 1.035569 | 1.035483 | 1.035674 | 1.023267 | 1.023522 |
| 64 | 1.033993 | 1.033728 | 1.033412 | 1.033522 | 1.033307 | 1.033767 | 1.021700 | 1.022318 |
| 65 | 1.033377 | 1.033040 | 1.032622 | 1.032734 | 1.032457 | 1.033021 | 1.021083 | 1.021840 |
| 66 | 1.033295 | 1.032949 | 1.032518 | 1.032630 | 1.032345 | 1.032922 | 1.021002 | 1.021777 |
| 67 | 1.033277 | 1.032929 | 1.032495 | 1.032607 | 1.032320 | 1.032901 | 1.020984 | 1.021763 |
| 68 | 1.033056 | 1.032684 | 1.032218 | 1.032334 | 1.032027 | 1.032643 | 1.020770 | 1.021597 |
| 69 | 1.033056 | 1.032684 | 1.032217 | 1.032333 | 1.032026 | 1.032642 | 1.020769 | 1.021596 |
| Node | 0:00 | 1:00 | 2:00 | 3:00 | 4:00 | 5:00 | 6:00 | 7:00 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.024297 | 1.024349 | 1.024331 | 1.024316 | 1.024288 | 1.024258 | 1.024293 | 1.036913 |
| 3 | 1.024204 | 1.024308 | 1.024271 | 1.024242 | 1.024185 | 1.024126 | 1.024196 | 1.036788 |
| 4 | 1.024148 | 1.024262 | 1.024221 | 1.024190 | 1.024127 | 1.024057 | 1.024125 | 1.036711 |
| 5 | 1.023609 | 1.023882 | 1.023783 | 1.023709 | 1.023558 | 1.023373 | 1.023478 | 1.035970 |
| 6 | 1.018692 | 1.021093 | 1.020227 | 1.019572 | 1.018249 | 1.016795 | 1.018261 | 1.029687 |
| 7 | 1.013801 | 1.018310 | 1.016683 | 1.015453 | 1.012969 | 1.010304 | 1.013290 | 1.023740 |
| 8 | 1.012651 | 1.017657 | 1.015851 | 1.014486 | 1.011728 | 1.008783 | 1.012149 | 1.022379 |
| 9 | 1.012083 | 1.017339 | 1.015443 | 1.014009 | 1.011114 | 1.008020 | 1.011545 | 1.021649 |
| 10 | 1.006702 | 1.014576 | 1.011735 | 1.009588 | 1.005249 | 1.000716 | 1.006348 | 1.015232 |
| 11 | 1.005641 | 1.014019 | 1.010997 | 1.008712 | 1.004095 | 0.999258 | 1.005206 | 1.013813 |
| 12 | 1.002728 | 1.012552 | 1.009009 | 1.006330 | 1.000915 | 0.995410 | 1.002971 | 1.011108 |
| 13 | 0.999731 | 1.011142 | 1.007028 | 1.003916 | 0.997623 | 0.991263 | 1.000188 | 1.007631 |
| 14 | 0.996840 | 1.009774 | 1.005111 | 1.001584 | 0.994450 | 0.987311 | 0.997695 | 1.004542 |
| 15 | 0.994061 | 1.008450 | 1.003264 | 0.999339 | 0.991401 | 0.983564 | 0.995503 | 1.001856 |
| 16 | 0.993544 | 1.008204 | 1.002920 | 0.998923 | 0.990834 | 0.982868 | 0.995096 | 1.001358 |
| 17 | 0.992702 | 1.007805 | 1.002362 | 0.998243 | 0.989909 | 0.981631 | 0.993993 | 0.999940 |
| 18 | 0.992692 | 1.007800 | 1.002355 | 0.998235 | 0.989898 | 0.981616 | 0.993981 | 0.999924 |
| 19 | 0.992104 | 1.007527 | 1.001968 | 0.997762 | 0.989252 | 0.980772 | 0.993310 | 0.999068 |
| 20 | 0.991726 | 1.007351 | 1.001720 | 0.997459 | 0.988836 | 0.980229 | 0.992878 | 0.998517 |
| 21 | 0.991114 | 1.007067 | 1.001318 | 0.996968 | 0.988165 | 0.979351 | 0.992183 | 0.997629 |
| 22 | 0.991098 | 1.007061 | 1.001308 | 0.996955 | 0.988147 | 0.979329 | 0.992170 | 0.997613 |
| 23 | 0.990971 | 1.007007 | 1.001228 | 0.996855 | 0.988006 | 0.979172 | 0.992158 | 0.997608 |
| 24 | 0.990694 | 1.006891 | 1.001054 | 0.996637 | 0.987699 | 0.978830 | 0.992132 | 0.997596 |
| 25 | 0.990287 | 1.006732 | 1.000806 | 0.996321 | 0.987245 | 0.978401 | 0.992460 | 0.998076 |
| 26 | 0.990118 | 1.006666 | 1.000703 | 0.996190 | 0.987058 | 0.978224 | 0.992595 | 0.998274 |
| 27 | 0.990071 | 1.006648 | 1.000674 | 0.996154 | 0.987005 | 0.978206 | 0.992775 | 0.998524 |
| 28 | 1.024183 | 1.024294 | 1.024254 | 1.024224 | 1.024163 | 1.024096 | 1.024163 | 1.036748 |
| 29 | 1.023924 | 1.024122 | 1.024051 | 1.023997 | 1.023888 | 1.023736 | 1.023748 | 1.036253 |
| 30 | 1.023108 | 1.023808 | 1.023554 | 1.023363 | 1.022981 | 1.022467 | 1.022564 | 1.034689 |
| 31 | 1.022964 | 1.023752 | 1.023466 | 1.023252 | 1.022821 | 1.022244 | 1.022355 | 1.034413 |
| 32 | 1.022245 | 1.023475 | 1.023028 | 1.022693 | 1.022020 | 1.021124 | 1.021309 | 1.033033 |
| 33 | 1.020784 | 1.022891 | 1.022126 | 1.021552 | 1.020400 | 1.018922 | 1.019430 | 1.030574 |
| 34 | 1.018914 | 1.022164 | 1.020984 | 1.020098 | 1.018320 | 1.016303 | 1.017998 | 1.028743 |
| 35 | 1.018058 | 1.021818 | 1.020454 | 1.019428 | 1.017371 | 1.014840 | 1.016118 | 1.026239 |
| 36 | 1.024140 | 1.024256 | 1.024214 | 1.024182 | 1.024119 | 1.024048 | 1.024116 | 1.036701 |
| 37 | 1.023948 | 1.024097 | 1.024043 | 1.024002 | 1.023921 | 1.023820 | 1.023882 | 1.036461 |
| 38 | 1.023756 | 1.023968 | 1.023891 | 1.023833 | 1.023718 | 1.023564 | 1.023650 | 1.036259 |
| 39 | 1.023756 | 1.023968 | 1.023891 | 1.023833 | 1.023718 | 1.023567 | 1.023674 | 1.036314 |
| 40 | 1.012611 | 1.017632 | 1.015820 | 1.014451 | 1.011684 | 1.008755 | 1.012216 | 1.022481 |
| 41 | 1.012562 | 1.017610 | 1.015788 | 1.014412 | 1.011631 | 1.008794 | 1.012647 | 1.023075 |
| 42 | 1.011489 | 1.017035 | 1.015034 | 1.013521 | 1.010466 | 1.007203 | 1.010922 | 1.020891 |
| 43 | 1.010834 | 1.016694 | 1.014580 | 1.012981 | 1.009753 | 1.006317 | 1.010282 | 1.020123 |
| 44 | 1.009968 | 1.016252 | 1.013985 | 1.012271 | 1.008809 | 1.005148 | 1.009470 | 1.019152 |
| 45 | 1.009157 | 1.015845 | 1.013432 | 1.011608 | 1.007923 | 1.003960 | 1.008320 | 1.017700 |
| 46 | 1.005010 | 1.013982 | 1.010745 | 1.008298 | 1.003354 | 0.997703 | 1.002349 | 1.009989 |
| 47 | 1.002966 | 1.013065 | 1.009421 | 1.006667 | 1.001103 | 0.994619 | 0.999406 | 1.006188 |
| 48 | 1.002176 | 1.012712 | 1.008910 | 1.006037 | 1.000232 | 0.993425 | 0.998267 | 1.004716 |
| 49 | 1.001397 | 1.012402 | 1.008431 | 1.005430 | 0.999366 | 0.992237 | 0.997220 | 1.003349 |
| 50 | 1.000281 | 1.011904 | 1.007711 | 1.004541 | 0.998137 | 0.990577 | 0.995718 | 1.001441 |
| 51 | 1.000155 | 1.011843 | 1.007626 | 1.004438 | 0.997999 | 0.990373 | 0.995463 | 1.001105 |
| 52 | 1.000010 | 1.011771 | 1.007528 | 1.004320 | 0.997841 | 0.990141 | 0.995172 | 1.000724 |
| 53 | 0.999300 | 1.011419 | 1.007046 | 1.003741 | 0.997065 | 0.989001 | 0.993747 | 0.998855 |
| 54 | 0.998800 | 1.011149 | 1.006693 | 1.003326 | 0.996522 | 0.988225 | 0.992787 | 0.997611 |
| 55 | 1.005525 | 1.013973 | 1.010925 | 1.008621 | 1.003967 | 0.999060 | 1.004953 | 1.013475 |
| 56 | 1.005524 | 1.013972 | 1.010924 | 1.008620 | 1.003965 | 0.999057 | 1.004950 | 1.013471 |
| 57 | 1.002452 | 1.012400 | 1.008811 | 1.006098 | 1.000615 | 0.995272 | 1.003722 | 1.012157 |
| 58 | 1.002451 | 1.012399 | 1.008811 | 1.006098 | 1.000614 | 0.995273 | 1.003729 | 1.012166 |
| 59 | 1.024180 | 1.024291 | 1.024251 | 1.024221 | 1.024159 | 1.024092 | 1.024159 | 1.036745 |
| 60 | 1.023878 | 1.024081 | 1.024008 | 1.023952 | 1.023841 | 1.023687 | 1.023714 | 1.036239 |
| 61 | 1.023605 | 1.023920 | 1.023806 | 1.023720 | 1.023547 | 1.023329 | 1.023443 | 1.035937 |
| 62 | 1.023526 | 1.023873 | 1.023747 | 1.023652 | 1.023463 | 1.023226 | 1.023365 | 1.035850 |
| 63 | 1.023522 | 1.023871 | 1.023744 | 1.023649 | 1.023458 | 1.023220 | 1.023359 | 1.035844 |
| 64 | 1.022318 | 1.023164 | 1.022857 | 1.022626 | 1.022164 | 1.021594 | 1.021947 | 1.034195 |
| 65 | 1.021840 | 1.022876 | 1.022500 | 1.022217 | 1.021651 | 1.020961 | 1.021423 | 1.033596 |
| 66 | 1.021777 | 1.022838 | 1.022453 | 1.022163 | 1.021583 | 1.020878 | 1.021354 | 1.033517 |
| 67 | 1.021763 | 1.022830 | 1.022442 | 1.022151 | 1.021568 | 1.020859 | 1.021338 | 1.033500 |
| 68 | 1.021597 | 1.022729 | 1.022318 | 1.022009 | 1.021391 | 1.020640 | 1.021153 | 1.033289 |
| 69 | 1.021596 | 1.022729 | 1.022318 | 1.022009 | 1.021390 | 1.020639 | 1.021153 | 1.033289 |
| Node | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.036854 | 1.036862 | 1.024315 | 1.024402 | 1.024347 | 1.036920 | 1.036955 | 1.036935 |
| 3 | 1.036670 | 1.036686 | 1.024240 | 1.024414 | 1.024304 | 1.036803 | 1.036873 | 1.036832 |
| 4 | 1.036577 | 1.036587 | 1.024157 | 1.024352 | 1.024232 | 1.036719 | 1.036786 | 1.036741 |
| 5 | 1.035628 | 1.035613 | 1.023460 | 1.023938 | 1.023660 | 1.035944 | 1.036053 | 1.035936 |
| 6 | 1.026864 | 1.027041 | 1.018970 | 1.023079 | 1.020573 | 1.029849 | 1.031269 | 1.030329 |
| 7 | 1.018512 | 1.018936 | 1.014985 | 1.022727 | 1.017968 | 1.024186 | 1.027050 | 1.025331 |
| 8 | 1.016591 | 1.017081 | 1.014110 | 1.022715 | 1.017418 | 1.022905 | 1.026129 | 1.024231 |
| 9 | 1.015568 | 1.016082 | 1.013594 | 1.022625 | 1.017066 | 1.022197 | 1.025576 | 1.023580 |
| 10 | 1.006275 | 1.007258 | 1.009882 | 1.023342 | 1.015001 | 1.016355 | 1.021677 | 1.018765 |
| 11 | 1.004270 | 1.005312 | 1.008888 | 1.023192 | 1.014334 | 1.014995 | 1.020617 | 1.017509 |
| 12 | 1.000141 | 1.001599 | 1.008128 | 1.024915 | 1.014448 | 1.012878 | 1.019914 | 1.016405 |
| 13 | 0.994907 | 0.996663 | 1.006377 | 1.025848 | 1.013680 | 1.009764 | 1.018063 | 1.014021 |
| 14 | 0.990187 | 0.992279 | 1.005102 | 1.027164 | 1.013334 | 1.007112 | 1.016745 | 1.012228 |
| 15 | 0.986001 | 0.988472 | 1.004323 | 1.028877 | 1.013426 | 1.004940 | 1.015980 | 1.011046 |
| 16 | 0.985224 | 0.987767 | 1.004181 | 1.029198 | 1.013445 | 1.004538 | 1.015841 | 1.010830 |
| 17 | 0.983221 | 0.985768 | 1.003005 | 1.028746 | 1.012564 | 1.003082 | 1.014549 | 1.009327 |
| 18 | 0.983198 | 0.985745 | 1.002992 | 1.028741 | 1.012555 | 1.003066 | 1.014535 | 1.009311 |
| 19 | 0.981957 | 0.984532 | 1.002386 | 1.028656 | 1.012150 | 1.002228 | 1.013874 | 1.008520 |
| 20 | 0.981159 | 0.983753 | 1.001996 | 1.028601 | 1.011890 | 1.001689 | 1.013449 | 1.008011 |
| 21 | 0.979870 | 0.982494 | 1.001370 | 1.028517 | 1.011474 | 1.000821 | 1.012766 | 1.007193 |
| 22 | 0.979844 | 0.982470 | 1.001366 | 1.028530 | 1.011476 | 1.000808 | 1.012763 | 1.007187 |
| 23 | 0.979788 | 0.982455 | 1.001523 | 1.028819 | 1.011671 | 1.000866 | 1.012943 | 1.007363 |
| 24 | 0.979665 | 0.982422 | 1.001866 | 1.029448 | 1.012096 | 1.000994 | 1.013337 | 1.007747 |
| 25 | 0.980074 | 0.983060 | 1.003163 | 1.031217 | 1.013498 | 1.001843 | 1.014809 | 1.009269 |
| 26 | 0.980243 | 0.983323 | 1.003698 | 1.031946 | 1.014076 | 1.002193 | 1.015416 | 1.009897 |
| 27 | 0.980526 | 0.983669 | 1.004152 | 1.032466 | 1.014532 | 1.002548 | 1.015929 | 1.010443 |
| 28 | 1.036619 | 1.036631 | 1.024195 | 1.024381 | 1.024266 | 1.036758 | 1.036824 | 1.036780 |
| 29 | 1.035984 | 1.035946 | 1.023633 | 1.023985 | 1.023789 | 1.036195 | 1.036226 | 1.036131 |
| 30 | 1.033768 | 1.033712 | 1.022275 | 1.023443 | 1.022766 | 1.034553 | 1.034714 | 1.034370 |
| 31 | 1.033377 | 1.033318 | 1.022035 | 1.023348 | 1.022586 | 1.034264 | 1.034447 | 1.034060 |
| 32 | 1.031421 | 1.031346 | 1.020837 | 1.022871 | 1.021684 | 1.032815 | 1.033113 | 1.032507 |
| 33 | 1.027880 | 1.027829 | 1.018919 | 1.022412 | 1.020342 | 1.030320 | 1.030988 | 1.029988 |
| 34 | 1.024897 | 1.025133 | 1.018588 | 1.024113 | 1.020712 | 1.028884 | 1.030658 | 1.029322 |
| 35 | 1.021550 | 1.021602 | 1.015779 | 1.022060 | 1.018281 | 1.026011 | 1.027515 | 1.025805 |
| 36 | 1.036565 | 1.036573 | 1.024145 | 1.024345 | 1.024223 | 1.036708 | 1.036775 | 1.036729 |
| 37 | 1.036276 | 1.036247 | 1.023864 | 1.024162 | 1.023995 | 1.036437 | 1.036499 | 1.036446 |
| 38 | 1.035987 | 1.035852 | 1.023561 | 1.024124 | 1.023836 | 1.036169 | 1.036243 | 1.036200 |
| 39 | 1.036046 | 1.035888 | 1.023599 | 1.024211 | 1.023902 | 1.036218 | 1.036305 | 1.036279 |
| 40 | 1.016704 | 1.017221 | 1.014310 | 1.022958 | 1.017624 | 1.023056 | 1.026358 | 1.024475 |
| 41 | 1.017399 | 1.018043 | 1.015311 | 1.024062 | 1.018616 | 1.023868 | 1.027489 | 1.025684 |
| 42 | 1.014464 | 1.015011 | 1.013125 | 1.022644 | 1.016773 | 1.021461 | 1.025043 | 1.022926 |
| 43 | 1.013331 | 1.013925 | 1.012709 | 1.022762 | 1.016544 | 1.020735 | 1.024567 | 1.022325 |
| 44 | 1.011876 | 1.012543 | 1.012239 | 1.023017 | 1.016325 | 1.019834 | 1.024025 | 1.021622 |
| 45 | 1.009856 | 1.010500 | 1.010969 | 1.022380 | 1.015307 | 1.018280 | 1.022572 | 1.019937 |
| 46 | 0.998978 | 0.999548 | 1.004321 | 1.019323 | 1.010096 | 1.010087 | 1.014980 | 1.011079 |
| 47 | 0.993617 | 0.994150 | 1.001045 | 1.017818 | 1.007528 | 1.006049 | 1.011239 | 1.006713 |
| 48 | 0.991539 | 0.992057 | 0.999776 | 1.017237 | 1.006534 | 1.004485 | 1.009790 | 1.005023 |
| 49 | 0.989552 | 0.990085 | 0.998718 | 1.016923 | 1.005762 | 1.003068 | 1.008564 | 1.003555 |
| 50 | 0.986812 | 0.987345 | 0.997202 | 1.016379 | 1.004615 | 1.001055 | 1.006789 | 1.001448 |
| 51 | 0.986365 | 0.986874 | 0.996830 | 1.016106 | 1.004293 | 1.000673 | 1.006374 | 1.000984 |
| 52 | 0.985857 | 0.986340 | 0.996407 | 1.015795 | 1.003926 | 1.000239 | 1.005903 | 1.000458 |
| 53 | 0.983370 | 0.983723 | 0.994336 | 1.014272 | 1.002127 | 0.998111 | 1.003594 | 0.997878 |
| 54 | 0.981728 | 0.981997 | 0.992961 | 1.013250 | 1.000928 | 0.996700 | 1.002067 | 0.996176 |
| 55 | 1.003817 | 1.004834 | 1.008511 | 1.022918 | 1.014009 | 1.014608 | 1.020196 | 1.017036 |
| 56 | 1.003812 | 1.004828 | 1.008507 | 1.022915 | 1.014005 | 1.014604 | 1.020191 | 1.017031 |
| 57 | 1.001369 | 1.003136 | 1.010108 | 1.027194 | 1.016449 | 1.014449 | 1.022176 | 1.018808 |
| 58 | 1.001380 | 1.003150 | 1.010123 | 1.027211 | 1.016464 | 1.014462 | 1.022194 | 1.018827 |
| 59 | 1.036616 | 1.036626 | 1.024191 | 1.024380 | 1.024263 | 1.036754 | 1.036821 | 1.036777 |
| 60 | 1.035968 | 1.035909 | 1.023601 | 1.023999 | 1.023783 | 1.036173 | 1.036212 | 1.036127 |
| 61 | 1.035542 | 1.035471 | 1.023375 | 1.024013 | 1.023658 | 1.035876 | 1.035995 | 1.035883 |
| 62 | 1.035419 | 1.035344 | 1.023310 | 1.024018 | 1.023621 | 1.035790 | 1.035932 | 1.035812 |
| 63 | 1.035411 | 1.035336 | 1.023304 | 1.024015 | 1.023617 | 1.035783 | 1.035926 | 1.035805 |
| 64 | 1.033154 | 1.032997 | 1.021852 | 1.023553 | 1.022591 | 1.034069 | 1.034434 | 1.034137 |
| 65 | 1.032331 | 1.032146 | 1.021351 | 1.023443 | 1.022255 | 1.033458 | 1.033930 | 1.033574 |
| 66 | 1.032222 | 1.032034 | 1.021285 | 1.023429 | 1.022211 | 1.033378 | 1.033863 | 1.033499 |
| 67 | 1.032198 | 1.032009 | 1.021269 | 1.023425 | 1.022201 | 1.033360 | 1.033848 | 1.033482 |
| 68 | 1.031909 | 1.031708 | 1.021087 | 1.023380 | 1.022078 | 1.033142 | 1.033665 | 1.033279 |
| 69 | 1.031908 | 1.031707 | 1.021087 | 1.023381 | 1.022078 | 1.033142 | 1.033665 | 1.033279 |
| Node | 16:00 | 17:00 | 18:00 | 19:00 | 20:00 | 21:00 | 22:00 | 23:00 |
| 1 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 | 1.050000 |
| 2 | 1.036922 | 1.036901 | 1.036865 | 1.036860 | 1.036840 | 1.036869 | 1.024259 | 1.024297 |
| 3 | 1.036807 | 1.036765 | 1.036693 | 1.036684 | 1.036644 | 1.036702 | 1.024128 | 1.024204 |
| 4 | 1.036720 | 1.036671 | 1.036609 | 1.036606 | 1.036566 | 1.036630 | 1.024063 | 1.024148 |
| 5 | 1.035929 | 1.035808 | 1.035746 | 1.035777 | 1.035706 | 1.035861 | 1.023406 | 1.023609 |
| 6 | 1.029902 | 1.028795 | 1.027486 | 1.027374 | 1.026493 | 1.027860 | 1.016909 | 1.018692 |
| 7 | 1.024376 | 1.022219 | 1.019494 | 1.019110 | 1.017344 | 1.019911 | 1.010451 | 1.013801 |
| 8 | 1.023135 | 1.020722 | 1.017639 | 1.017175 | 1.015190 | 1.018040 | 1.008931 | 1.012651 |
| 9 | 1.022436 | 1.019908 | 1.016676 | 1.016197 | 1.014117 | 1.017110 | 1.008178 | 1.012083 |
| 10 | 1.016754 | 1.012994 | 1.007666 | 1.006701 | 1.003433 | 1.007920 | 1.000850 | 1.006702 |
| 11 | 1.015389 | 1.011423 | 1.005789 | 1.004801 | 1.001348 | 1.006124 | 0.999413 | 1.005641 |
| 12 | 1.013520 | 1.008702 | 1.001431 | 0.999825 | 0.995489 | 1.001098 | 0.995422 | 1.002728 |
| 13 | 1.010554 | 1.004954 | 0.996334 | 0.994350 | 0.989237 | 0.995767 | 0.991236 | 0.999731 |
| 14 | 1.008103 | 1.001695 | 0.991620 | 0.989155 | 0.983224 | 0.990638 | 0.987205 | 0.996840 |
| 15 | 1.006186 | 0.998944 | 0.987304 | 0.984253 | 0.977461 | 0.985719 | 0.983336 | 0.994061 |
| 16 | 1.005832 | 0.998435 | 0.986503 | 0.983342 | 0.976390 | 0.984805 | 0.982617 | 0.993544 |
| 17 | 1.004324 | 0.996804 | 0.984747 | 0.981681 | 0.974638 | 0.983311 | 0.981442 | 0.992702 |
| 18 | 1.004307 | 0.996786 | 0.984727 | 0.981662 | 0.974617 | 0.983293 | 0.981428 | 0.992692 |
| 19 | 1.003462 | 0.995823 | 0.983595 | 0.980533 | 0.973384 | 0.982242 | 0.980605 | 0.992104 |
| 20 | 1.002919 | 0.995204 | 0.982867 | 0.979807 | 0.972591 | 0.981567 | 0.980076 | 0.991726 |
| 21 | 1.002044 | 0.994207 | 0.981691 | 0.978634 | 0.971308 | 0.980475 | 0.979219 | 0.991114 |
| 22 | 1.002033 | 0.994190 | 0.981664 | 0.978604 | 0.971272 | 0.980444 | 0.979196 | 0.991098 |
| 23 | 1.002129 | 0.994219 | 0.981545 | 0.978402 | 0.970994 | 0.980208 | 0.979014 | 0.990971 |
| 24 | 1.002339 | 0.994283 | 0.981287 | 0.977963 | 0.970387 | 0.979695 | 0.978617 | 0.990694 |
| 25 | 1.003420 | 0.995035 | 0.981258 | 0.977439 | 0.969467 | 0.978920 | 0.978022 | 0.990287 |
| 26 | 1.003865 | 0.995345 | 0.981246 | 0.977222 | 0.969088 | 0.978600 | 0.977777 | 0.990118 |
| 27 | 1.004289 | 0.995689 | 0.981386 | 0.977217 | 0.968981 | 0.978510 | 0.977708 | 0.990071 |
| 28 | 1.036758 | 1.036715 | 1.036650 | 1.036647 | 1.036609 | 1.036671 | 1.024102 | 1.024183 |
| 29 | 1.036156 | 1.036094 | 1.036127 | 1.036195 | 1.036179 | 1.036288 | 1.023779 | 1.023924 |
| 30 | 1.034432 | 1.034262 | 1.034231 | 1.034454 | 1.034374 | 1.034757 | 1.022597 | 1.023108 |
| 31 | 1.034128 | 1.033939 | 1.033896 | 1.034146 | 1.034056 | 1.034487 | 1.022388 | 1.022964 |
| 32 | 1.032607 | 1.032323 | 1.032223 | 1.032610 | 1.032464 | 1.033137 | 1.021345 | 1.022245 |
| 33 | 1.030036 | 1.029493 | 1.029097 | 1.029615 | 1.029274 | 1.030425 | 1.019243 | 1.020784 |
| 34 | 1.028795 | 1.027611 | 1.026027 | 1.026116 | 1.025144 | 1.026921 | 1.016536 | 1.018914 |
| 35 | 1.025646 | 1.024551 | 1.023424 | 1.024068 | 1.023278 | 1.025335 | 1.015306 | 1.018058 |
| 36 | 1.036709 | 1.036658 | 1.036599 | 1.036595 | 1.036556 | 1.036620 | 1.024055 | 1.024140 |
| 37 | 1.036429 | 1.036340 | 1.036338 | 1.036341 | 1.036301 | 1.036383 | 1.023839 | 1.023948 |
| 38 | 1.036159 | 1.035928 | 1.036075 | 1.036046 | 1.035987 | 1.036104 | 1.023601 | 1.023756 |
| 39 | 1.036217 | 1.035942 | 1.036114 | 1.036058 | 1.035987 | 1.036104 | 1.023601 | 1.023756 |
| 40 | 1.023319 | 1.020863 | 1.017686 | 1.017152 | 1.015119 | 1.017978 | 1.008880 | 1.012611 |
| 41 | 1.024276 | 1.021661 | 1.018077 | 1.017245 | 1.015018 | 1.017892 | 1.008812 | 1.012562 |
| 42 | 1.021738 | 1.019063 | 1.015635 | 1.015133 | 1.012937 | 1.016094 | 1.007368 | 1.011489 |
| 43 | 1.021070 | 1.018220 | 1.014540 | 1.013987 | 1.011646 | 1.014983 | 1.006479 | 1.010834 |
| 44 | 1.020259 | 1.017162 | 1.013115 | 1.012472 | 1.009922 | 1.013500 | 1.005299 | 1.009968 |
| 45 | 1.018674 | 1.015470 | 1.011376 | 1.010891 | 1.008291 | 1.012100 | 1.004186 | 1.009157 |
| 46 | 1.010247 | 1.006497 | 1.002052 | 1.002408 | 0.999517 | 1.004627 | 0.998342 | 1.005010 |
| 47 | 1.006094 | 1.002075 | 0.997457 | 0.998228 | 0.995193 | 1.000944 | 0.995462 | 1.002966 |
| 48 | 1.004484 | 1.000362 | 0.995676 | 0.996607 | 0.993517 | 0.999516 | 0.994346 | 1.002176 |
| 49 | 1.003053 | 0.998788 | 0.993939 | 0.994978 | 0.991787 | 0.998053 | 0.993219 | 1.001397 |
| 50 | 1.001047 | 0.996571 | 0.991538 | 0.992740 | 0.989420 | 0.996038 | 0.991644 | 1.000281 |
| 51 | 1.000630 | 0.996164 | 0.991187 | 0.992460 | 0.989163 | 0.995818 | 0.991470 | 1.000155 |
| 52 | 1.000156 | 0.995701 | 0.990789 | 0.992142 | 0.988870 | 0.995567 | 0.991271 | 1.000010 |
| 53 | 0.997834 | 0.993433 | 0.988836 | 0.990582 | 0.987436 | 0.994336 | 0.990295 | 0.999300 |
| 54 | 0.996298 | 0.991932 | 0.987537 | 0.989536 | 0.986470 | 0.993502 | 0.989624 | 0.998800 |
| 55 | 1.014965 | 1.011010 | 1.005436 | 1.004523 | 1.001094 | 1.005909 | 0.999246 | 1.005525 |
| 56 | 1.014960 | 1.011005 | 1.005432 | 1.004520 | 1.001091 | 1.005906 | 0.999244 | 1.005524 |
| 57 | 1.015372 | 1.010197 | 1.001976 | 0.999742 | 0.994961 | 1.000641 | 0.995052 | 1.002452 |
| 58 | 1.015387 | 1.010209 | 1.001982 | 0.999743 | 0.994960 | 1.000639 | 0.995051 | 1.002451 |
| 59 | 1.036755 | 1.036710 | 1.036647 | 1.036643 | 1.036605 | 1.036666 | 1.024098 | 1.024180 |
| 60 | 1.036139 | 1.036042 | 1.036101 | 1.036150 | 1.036125 | 1.036237 | 1.023730 | 1.023878 |
| 61 | 1.035851 | 1.035666 | 1.035688 | 1.035706 | 1.035633 | 1.035805 | 1.023374 | 1.023605 |
| 62 | 1.035768 | 1.035558 | 1.035569 | 1.035578 | 1.035490 | 1.035680 | 1.023272 | 1.023526 |
| 63 | 1.035761 | 1.035551 | 1.035562 | 1.035571 | 1.035483 | 1.035674 | 1.023267 | 1.023522 |
| 64 | 1.034021 | 1.033528 | 1.033507 | 1.033525 | 1.033307 | 1.033767 | 1.021700 | 1.022318 |
| 65 | 1.033411 | 1.032793 | 1.032740 | 1.032739 | 1.032457 | 1.033021 | 1.021083 | 1.021840 |
| 66 | 1.033330 | 1.032696 | 1.032639 | 1.032635 | 1.032345 | 1.032922 | 1.021002 | 1.021777 |
| 67 | 1.033312 | 1.032674 | 1.032616 | 1.032612 | 1.032320 | 1.032901 | 1.020984 | 1.021763 |
| 68 | 1.033093 | 1.032411 | 1.032349 | 1.032339 | 1.032027 | 1.032643 | 1.020770 | 1.021597 |
| 69 | 1.033093 | 1.032411 | 1.032348 | 1.032338 | 1.032026 | 1.032642 | 1.020769 | 1.021596 |
References
- Cossent, R.; Gómez, T.; Olmos, L.; Gómez, T. Large-scale integration of renewable and distributed generation of electricity in Spain: Current situation and future needs. Energy Policy 2011, 39, 8078–8087. [Google Scholar] [CrossRef]
- Schonardie, M.F.; Martins, D.C. Application of the dq0 transformation in the three-phase grid-connected PV systems with active and reactive power control. In Proceedings of the 2008 IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 18–23. [Google Scholar]
- Reference Technical Rules for the Connection of Active and Passive Consumers to the HV and MV Electrical Networks of Distribution Company Issue; Italian Technical Guidelines CEI 0-16 2012-12; Comitato Elettrotecnico Italiano: Milan, Italy, 2012.
- Thomson, M.; Infield, D. Impact of widespread photovoltaics generation on distribution systems. IET Renew. Power Gener. 2007, 1, 33. [Google Scholar] [CrossRef]
- Tonkoski, R.; Lopes, L.A.C.; El-Fouly, T.H.M. Coordinated Active Power Curtailment of Grid Connected PV Inverters for Overvoltage Prevention. IEEE Trans. Sustain. Energy 2010, 2, 139–147. [Google Scholar] [CrossRef]
- Zhao, C.; Gu, C.; Li, F.; Dale, M. Understanding LV network voltage distribution- UK smart grid demonstration experience. In Proceedings of the 2015 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015; pp. 1–5. [Google Scholar]
- Dou, X.; Duan, X.; Hu, Q.; Shen, L.; Wu, Z. A nonintrusive control strategy using voltage and reactive power for distribution systems based on PV and the nine-zone diagram. Int. J. Electr. Power Energy Syst. 2019, 105, 89–97. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Adaptive power flow method for distribution systems with dispersed generation. IEEE Trans. Power Deliv. 2002, 17, 822–827. [Google Scholar] [CrossRef]
- Valverde, G.; Van Cutsem, T.H. Model Predictive Control of Voltages in Active Distribution Networks. IEEE Trans. Smart Grid 2013, 4, 2152–2161. [Google Scholar] [CrossRef]
- Robbins, B.A.; Hadjicostis, C.N.; Domínguez-García, A.D. A Two-Stage Distributed Architecture for Voltage Control in Power Distribution Systems. IEEE Trans. Power Syst. 2012, 28, 1470–1482. [Google Scholar] [CrossRef]
- Sulc, P.; Backhaus, S.; Chertkov, M. Optimal Distributed Control of Reactive Power via the Alternating Direction Method of Multipliers. IEEE Trans. Energy Convers. 2014, 29, 968–977. [Google Scholar] [CrossRef] [Green Version]
- Calderaro, V.; Galdi, V.; Massa, G.; Piccolo, A. Distributed generation management: An optimal sensitivity approach for decentralized power control. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Calderaro, V.; Conio, G.; Galdi, V.; Massa, G.; Piccolo, A. Optimal Decentralized Voltage Control for Distribution Systems with Inverter-Based Distributed Generators. IEEE Trans. Power Syst. 2013, 29, 230–241. [Google Scholar] [CrossRef]
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Options for Control of Reactive Power by Distributed Photovoltaic Generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Tang, W.; Li, L.; Zhang, B.; Zhang, L.; Wang, Y. Multi-mode adaptive local reactive power control method based on PV inverters in low voltage distribution networks. IET Gener. Transm. Distrib. 2020, 14, 542–551. [Google Scholar] [CrossRef]
- Molina-Garcia, A.; Mastromauro, R.A.; Garcia-Sanchez, T.; Pugliese, S.; Liserre, M.; Stasi, S. Reactive Power Flow Control for PV Inverters Voltage Support in LV Distribution Networks. IEEE Trans. Smart Grid 2016, 8, 447–456. [Google Scholar] [CrossRef] [Green Version]
- Dickert, J.; Domagk, M.; Schegner, P. Benchmark low voltage distribution networks based on cluster analysis of actual grid properties. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Kabir, M.N.; Mishra, Y.; Ledwich, G.; Dong, Z.Y.; Wong, K.P. Coordinated Control of Grid-Connected Photovoltaic Reactive Power and Battery Energy Storage Systems to Improve the Voltage Profile of a Residential Distribution Feeder. IEEE Trans. Ind. Inform. 2014, 10, 967–977. [Google Scholar] [CrossRef]
- Mumtaz, F.; Syed, M.H.; Al Hosani, M.; Zeineldin, H.H. A Novel Approach to Solve Power Flow for Islanded Microgrids Using Modified Newton Raphson with Droop Control of DG. IEEE Trans. Sustain. Energy 2015, 7, 493–503. [Google Scholar] [CrossRef] [Green Version]
- Biserica, M.; Berseneff, B.; Besanger, Y.; Kieny, C. Upgraded Coordinated Voltage Control for Distribution Systems. In Proceedings of the IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, B.; Lam, A.Y.S.; Dominguez-Garcia, A.D.; Tse, D. An Optimal and Distributed Method for Voltage Regulation in Power Distribution Systems. IEEE Trans. Power Syst. 2014, 30, 1714–1726. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Bhattarai, R.; Hossain, S.J.; Abdelrazek, S.; Kamalasadan, S. Coordinated voltage control strategy for voltage regulators and voltage source converters integrated distribution system. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Harbor, MD, USA, 14–17 January 2017; pp. 1–8. [Google Scholar]
- Castillo, A.; Gayme, D.F. Profit maximizing storage allocation in power grids. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 429–435. [Google Scholar]
- Bose, S.; Gayme, D.F.; Topcu, U.; Chandy, K.M.; Bose, S. Optimal placement of energy storage in the grid. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 5605–5612. [Google Scholar]
- Nasrolahpour, E.; Kazempour, S.; Zareipour, H.; Rosehart, W.D. Strategic Sizing of Energy Storage Facilities in Electricity Markets. IEEE Trans. Sustain. Energy 2016, 7, 1462–1472. [Google Scholar] [CrossRef] [Green Version]
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal siting and sizing of distributed energy storage systems via alternating direction method of multipliers. Int. J. Electr. Power Energy Syst. 2015, 72, 33–39. [Google Scholar] [CrossRef]
- Yan, W.; Yu, J.; Yu, D.; Bhattarai, K. A new optimal reactive power flow model in rectangular form and its solution by predictor corrector primal dual interior point method. IEEE Trans. Power Syst. 2006, 21, 61–67. [Google Scholar] [CrossRef]
- Esmin, A.; Lambert-Torres, G.; De Souza, A.Z. A hybrid particle swarm optimization applied to loss power minimization. IEEE Trans. Power Syst. 2005, 20, 859–866. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Wu, Q. Optimal reactive power dispatch with wind power integrated using group search optimizer with intraspecific competition and lévy walk. J. Mod. Power Syst. Clean Energy 2014, 2, 308–318. [Google Scholar] [CrossRef] [Green Version]
- Farivar, M.; Low, S.H. Branch Flow Model: Relaxations and Convexification—Part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Wang, C.; Xiang, L.; Deng, Z.; Liang, Z. Reactive Power Optimization Dispatch Strategy in Distribution Network with Distributed Generators. J. Eng. 2017, 2017, 1418–1422. [Google Scholar] [CrossRef]
- Chen, L.; Deng, Z.; Xu, X. Two-Stage Dynamic Reactive Power Dispatch Strategy in Distribution Network Considering the Reactive Power Regulation of Distributed Generations. IEEE Trans. Power Syst. 2018, 34, 1021–1032. [Google Scholar] [CrossRef]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Glavic, M.; Hajian, M.; Rosehart, W.; Van Cutsem, T.H. Receding-Horizon Multi-Step Optimization to Correct Nonviable or Unstable Transmission Voltages. IEEE Trans. Power Syst. 2011, 26, 1641–1650. [Google Scholar] [CrossRef] [Green Version]
- Fortenbacher, P.; Ulbig, A.; Andersson, G. Optimal Placement and Sizing of Distributed Battery Storage in Low Voltage Grids Using Receding Horizon Control Strategies. IEEE Trans. Power Syst. 2017, 33, 2383–2394. [Google Scholar] [CrossRef] [Green Version]
- Hug-Glanzmann, G. Coordination of intermittent generation with storage, demand control and conventional energy sources. In Proceedings of the 2010 IREP Symposium Bulk Power System Dynamics and Control—VIII (IREP), Rio de Janeiro, Brazil, 1–6 August 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Bolognani, S.; Zampieri, S. On the Existence and Linear Approximation of the Power Flow Solution in Power Distribution Networks. IEEE Trans. Power Syst. 2015, 31, 163–172. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Wu, R.; Yang, J.; Long, K.; You, P. Economical Operation of Microgrid with Various Devices Via Distributed Optimization. IEEE Trans. Smart Grid 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal Allocation of Dispersed Energy Storage Systems in Active Distribution Networks for Energy Balance and Grid Support. IEEE Trans. Power Syst. 2014, 29, 2300–2310. [Google Scholar] [CrossRef]
- Niknam, T.; Zare, M.; Aghaei, J. Scenario-Based Multiobjective Volt/Var Control in Distribution Networks Including Renewable Energy Sources. IEEE Trans. Power Deliv. 2012, 27, 2004–2019. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- GUROBI. Available online: http://www.gurobi.com (accessed on 22 February 2018).
- National Bureau of Quality Supervision. Inspection and Quarantine and National Standardization Management Committee. National Standard of the People’s Republic of China GB/T12325-2008 Power Quality and Voltage Deviation; National Bureau of Quality Supervision: Beijing, China, 2008.
- Zhang, Y.-J.; Ren, Z. Optimal Reactive Power Dispatch Considering Costs of Adjusting the Control Devices. IEEE Trans. Power Syst. 2005, 20, 1349–1356. [Google Scholar] [CrossRef]
- Wong, T. Co-ordination of transformer tap and capacitor operation for reactive power voltage control in a distribution primary substation. In Proceedings of the APSCOM 2000—5th International Conference on Advances in Power System Control, Operation and Management, Hong Kong, China, 30 October–1 November 2000; Volume 2000, pp. 479–485. [Google Scholar]
- Sun, C.; Xu, J.; Cai, B.; Yang, Z.; Li, X. Research on efficiency increase of the automatic voltage control system in Shanghai urban power grid. In Proceedings of the 8th Renewable Power Generation Conference (RPG 2019), Shanghai, China, 24–25 October 2019; pp. 1–6. [Google Scholar]
- Khan, I.; Li, Z.; Xu, Y.; Gu, W. Distributed control algorithm for optimal reactive power control in power grids. Int. J. Electr. Power Energy Syst. 2016, 83, 505–513. [Google Scholar] [CrossRef]




















| Devices | Reference | Method/Algorithm | Remarks |
|---|---|---|---|
| OLTC | [7] | Mixed integer nonlinear programming (MINP) |
|
| DG | [12,13] | Decentralized control based on voltage sensitivity |
|
| [15] | A multi-mode adaptive local control method based on Q(P) characteristics | ||
| [16] | a combination of centralized remote control and local decentralized control | ||
| DG, OLTC | [20,21,22] | Optimal power flow (OPF) calculation |
|
| [23,24] | Semi-definite relaxation | ||
| [25,26] | Benders decomposition | ||
| [27,28,29,30] | Relaxing discrete variables into continuous variables and rounding to close integers. | ||
| [31,32] | Two-stage dynamic coordination dispatch |
| |
| Storage device, OLTC, DG | [9,35,36] | Model predictive control (MPC) |
|
| Devices | Parameters | Values |
|---|---|---|
| OLTC | Tap range | −8–8 |
| PV | Capacity | 500 kWP |
| Characteristic | S1 | S2 | DRM |
|---|---|---|---|
| Decoupling of discrete/continuous device actions | √ | √ | √ |
| Subdividing optimization periods | × | √ | √ |
| MPC-based rolling optimization | × | × | √ |
| Adjustment Cost | S1 | S2 | DRM |
|---|---|---|---|
| OLTC | $24 | $24 | $24 |
| PVs | $1.17 | $1.64 | $0.63 |
| Total | $25.17 | $25.64 | $24.63 |
| Original | S1 | S2 | DRM | |
|---|---|---|---|---|
| All nodes at 11:00 | 3.4951 p.u. | 1.6899 p.u. | 1.6806 p.u. | 1.5839 p.u. |
| All nodes at 24:00 | 2.4852 p.u. | 0.9467 p.u. | 0.9467 p.u. | 0.9467 p.u. |
| Node 16 all day | 1.9247 p.u. | 1.0189 p.u. | 1.0010 p.u. | 0.9740 p.u. |
| Node 54 all day | 1.5351 p.u. | 0.6928 p.u. | 0.6899 p.u. | 0.6881 p.u. |
| All nodes all day | 299.9501 p.u. | 122.7256 p.u. | 122.0783 p.u. | 121.8496 p.u. |
| No PV | Original | S1 | S2 | DRM | |
|---|---|---|---|---|---|
| Active power losses | 4.8305 MWh | 2.0546 MWh | 2.7143 MWh | 2.6610 MWh | 2.6472 MWh |
| S1 | S2 | DRM | |
|---|---|---|---|
| Long period (1 h) optimization | 21.46 s | 48.94 s | 50.23 s |
| Short period (15 min) PV optimization | - | 9.07 s | 10.43 s |
| One day optimization | 5.33 min | 11.64 min | 14.39 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, X.; Shen, L.; Zheng, C.; Li, P.; Dou, X. A Decoupling Rolling Multi-Period Power and Voltage Optimization Strategy in Active Distribution Networks. Energies 2020, 13, 5789. https://doi.org/10.3390/en13215789
Ge X, Shen L, Zheng C, Li P, Dou X. A Decoupling Rolling Multi-Period Power and Voltage Optimization Strategy in Active Distribution Networks. Energies. 2020; 13(21):5789. https://doi.org/10.3390/en13215789
Chicago/Turabian StyleGe, Xiaohui, Lu Shen, Chaoming Zheng, Peng Li, and Xiaobo Dou. 2020. "A Decoupling Rolling Multi-Period Power and Voltage Optimization Strategy in Active Distribution Networks" Energies 13, no. 21: 5789. https://doi.org/10.3390/en13215789
APA StyleGe, X., Shen, L., Zheng, C., Li, P., & Dou, X. (2020). A Decoupling Rolling Multi-Period Power and Voltage Optimization Strategy in Active Distribution Networks. Energies, 13(21), 5789. https://doi.org/10.3390/en13215789




