Analysis of the Accelerometer Input–Output Energy Distribution Based on the Upper Bound of Absolute Dynamic Error
Abstract
:1. Introduction
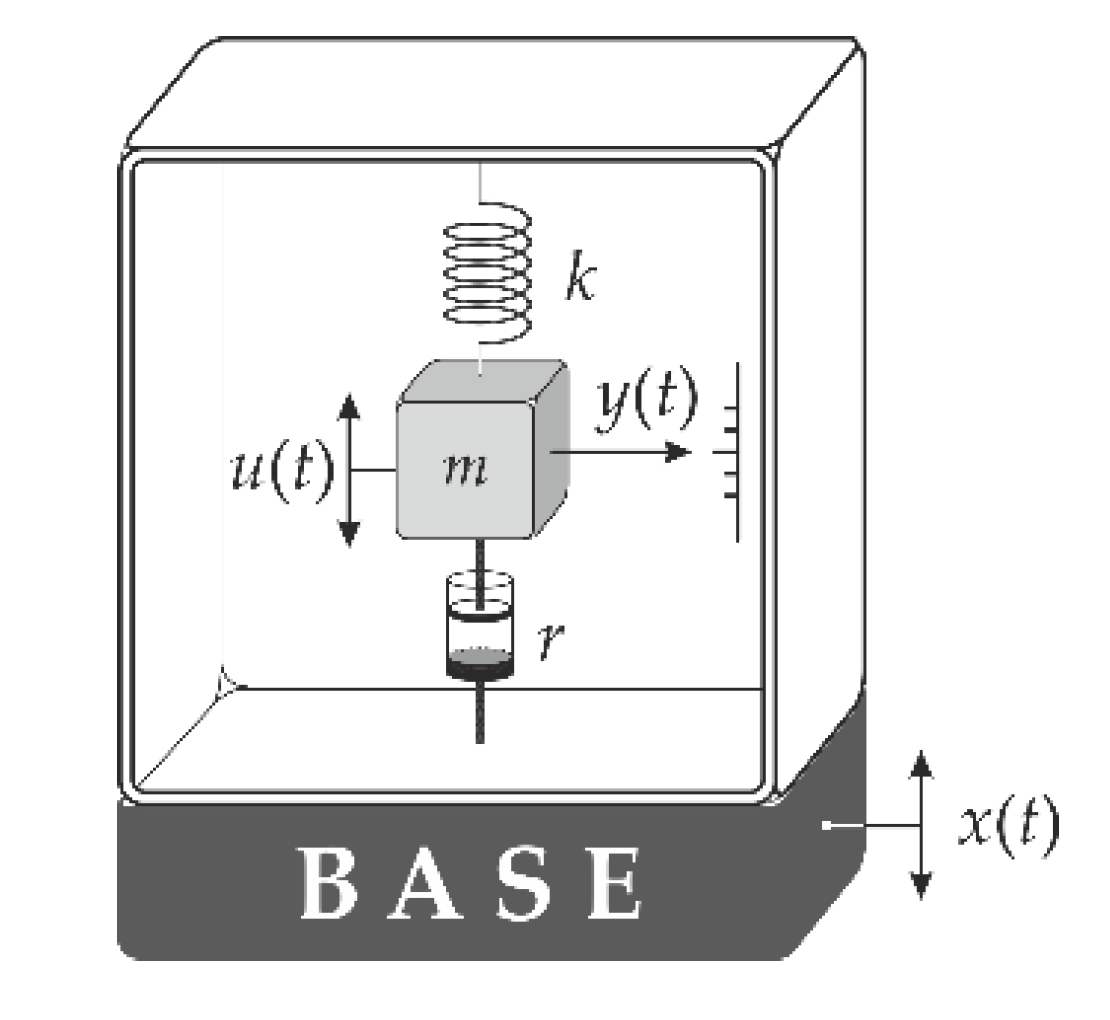
2. Theoretical Background
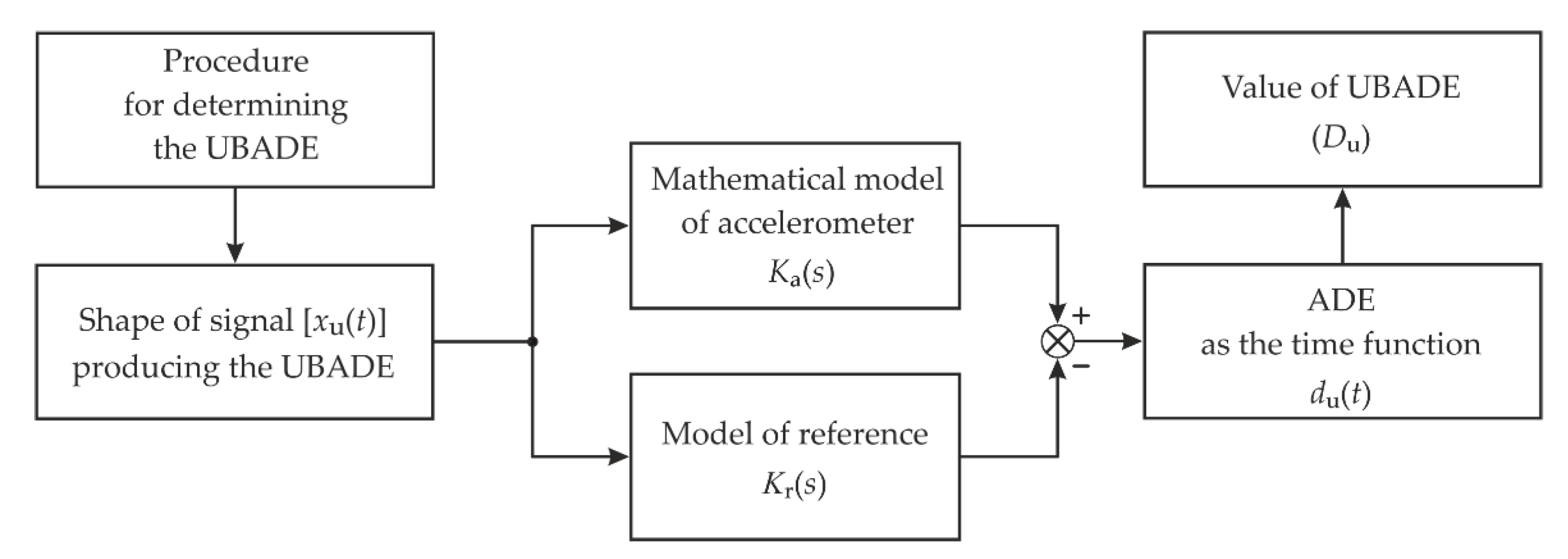
3. Procedure for Determining the UBADE
- Determine the pulse function whose duration is equal to , according to the following equation:
- 2.
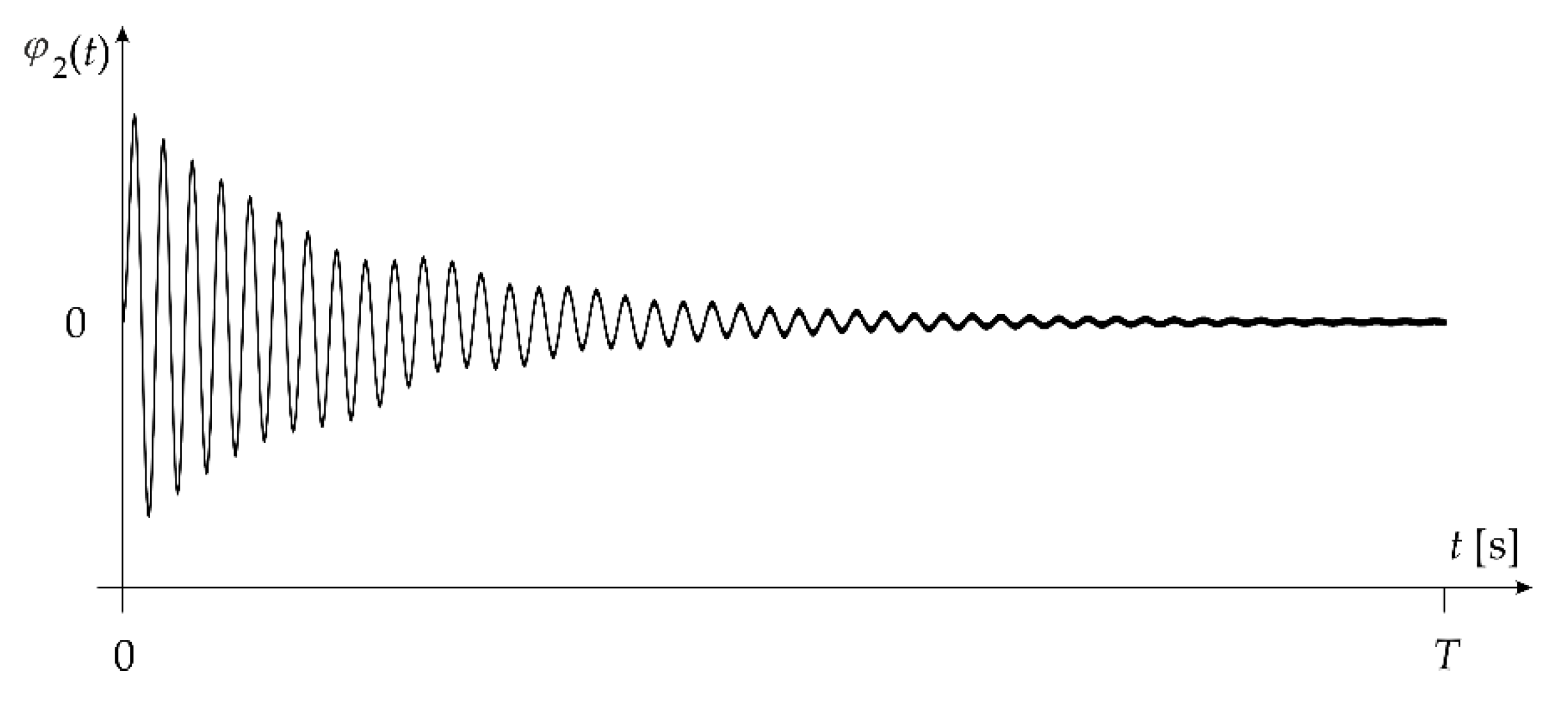
- Calculate the convolution integral based on the function and the impulse response :
- 3.
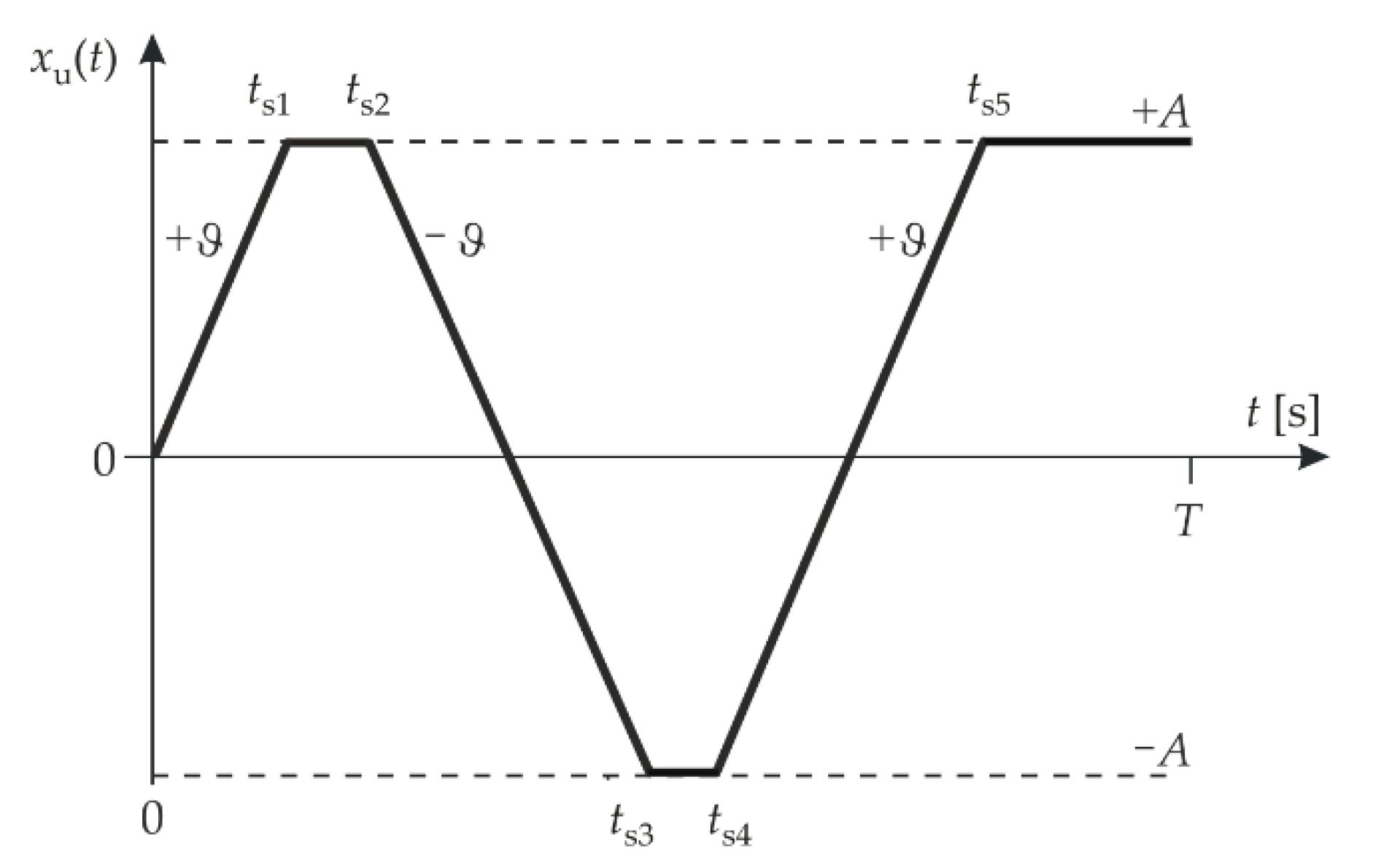
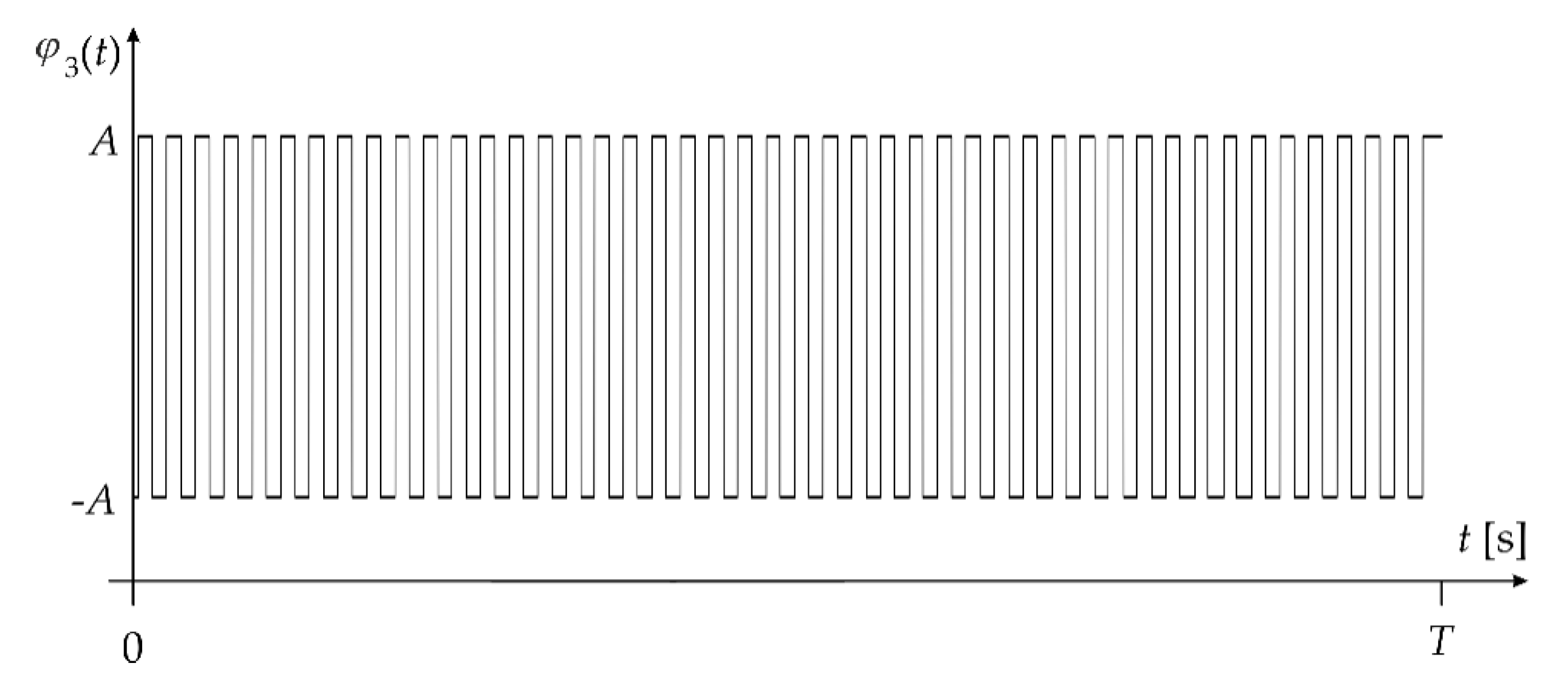
- Determine the rectangular function based on the following formula (Figure 7):
- 4.
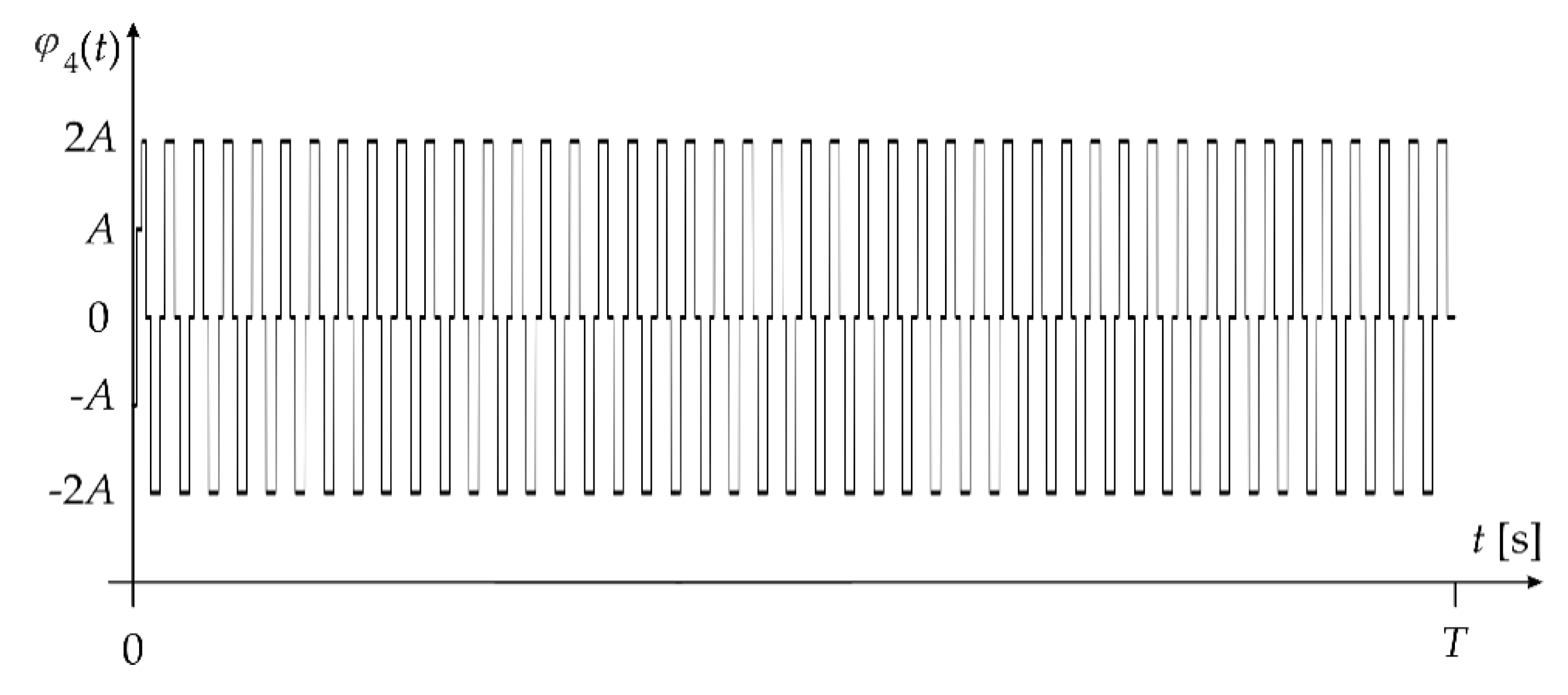
- Determine the function with value in the first interval and the values or 0 at the other intervals (Figure 8):
- 5.
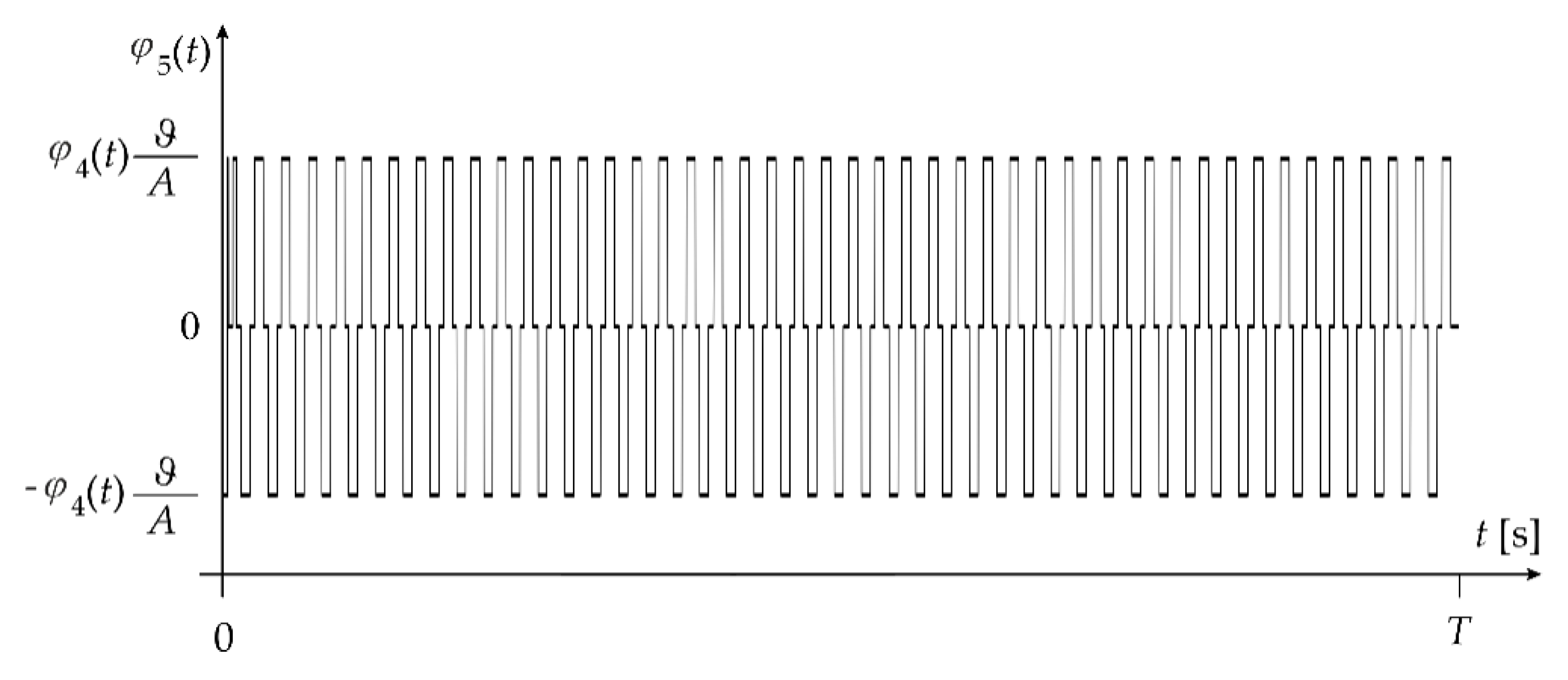
- Determine the function with the following values: 0, , or (Figure 9):
- 6.
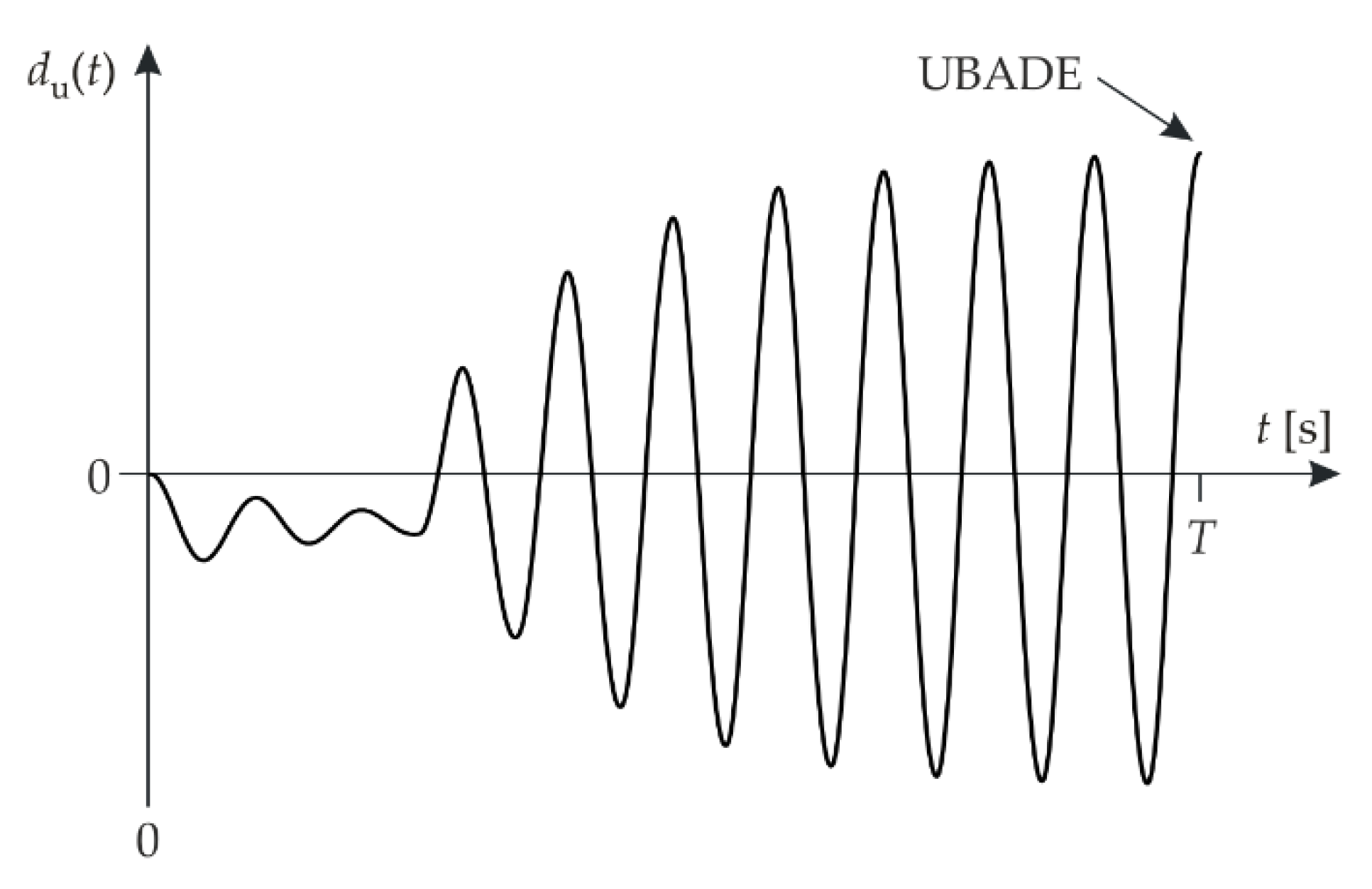
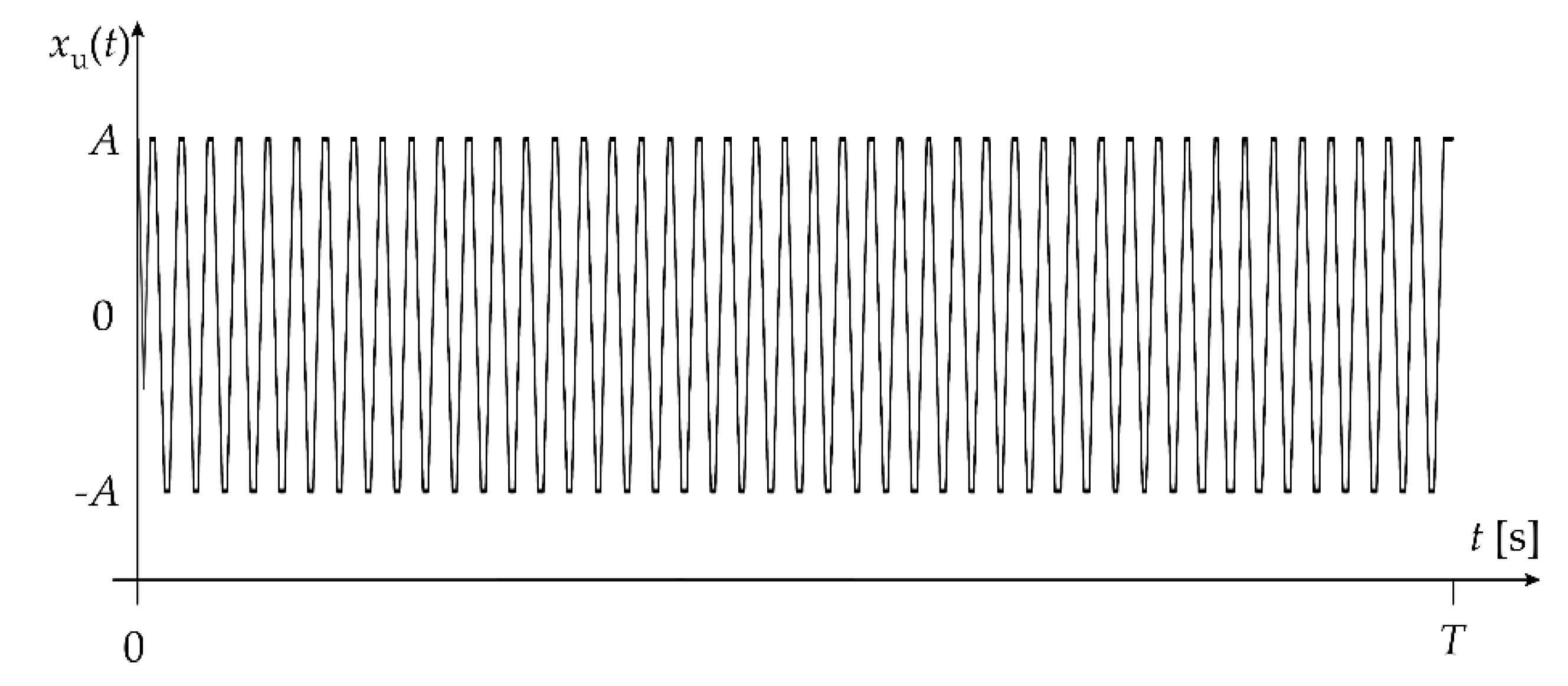
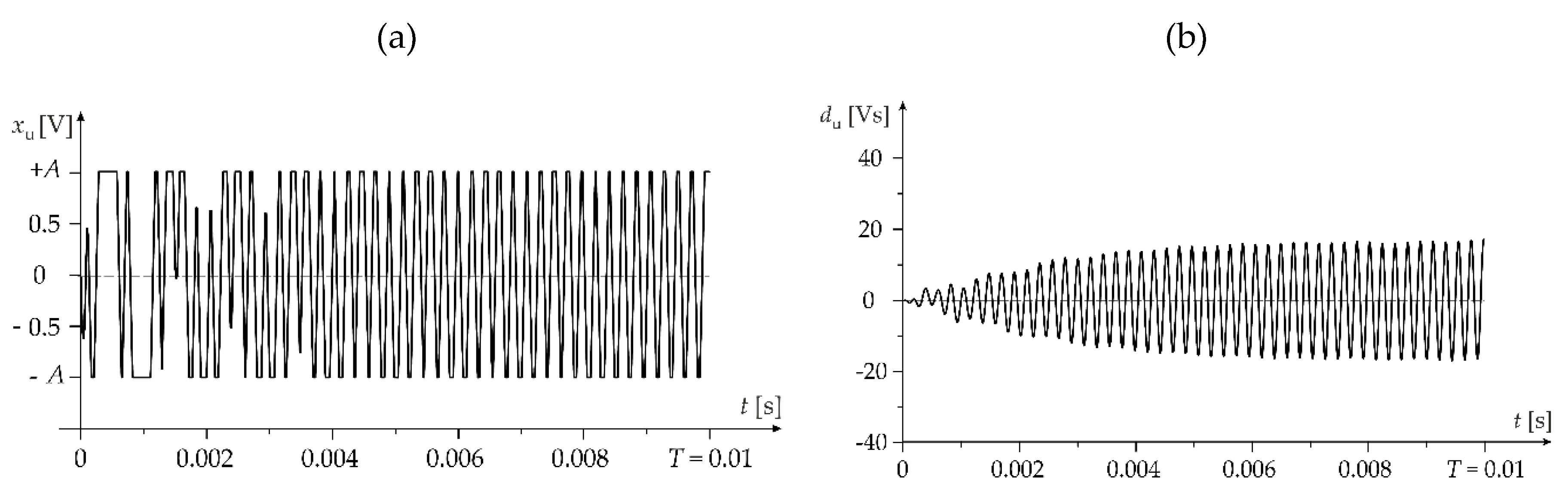
- Determine the signal with two constraints by substituting for in Equation (5) (Figure 10). This signal produces the upper bound of the absolute dynamic error.
- 7.
- Determine the absolute error as the time function:
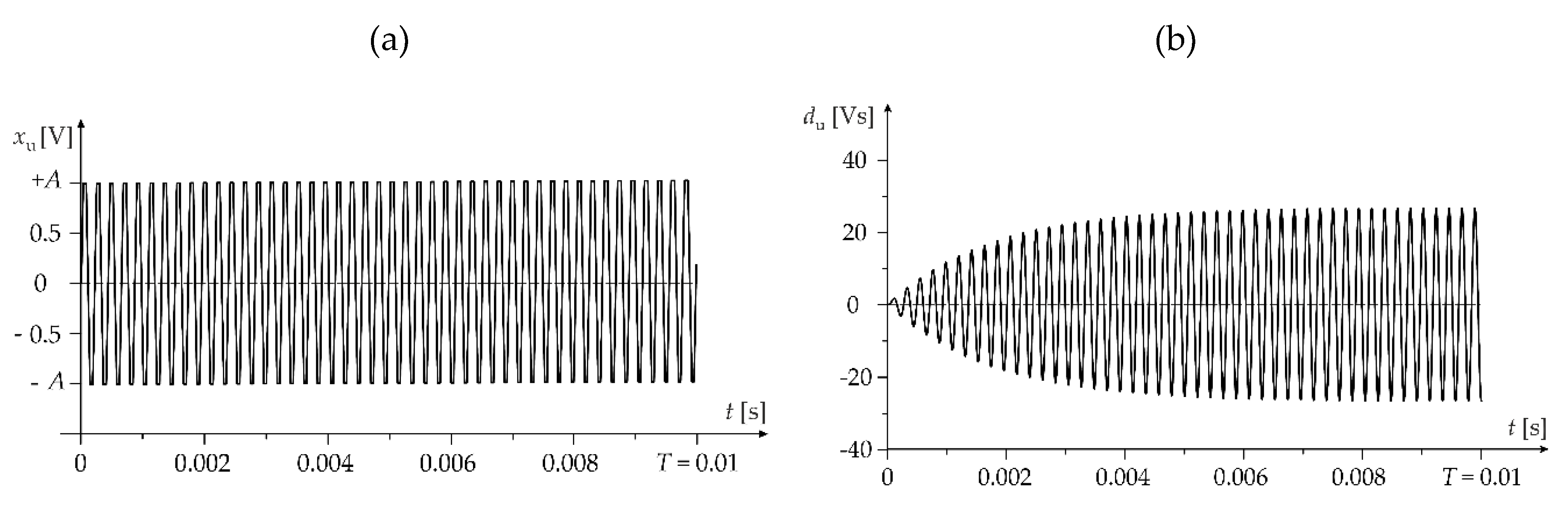
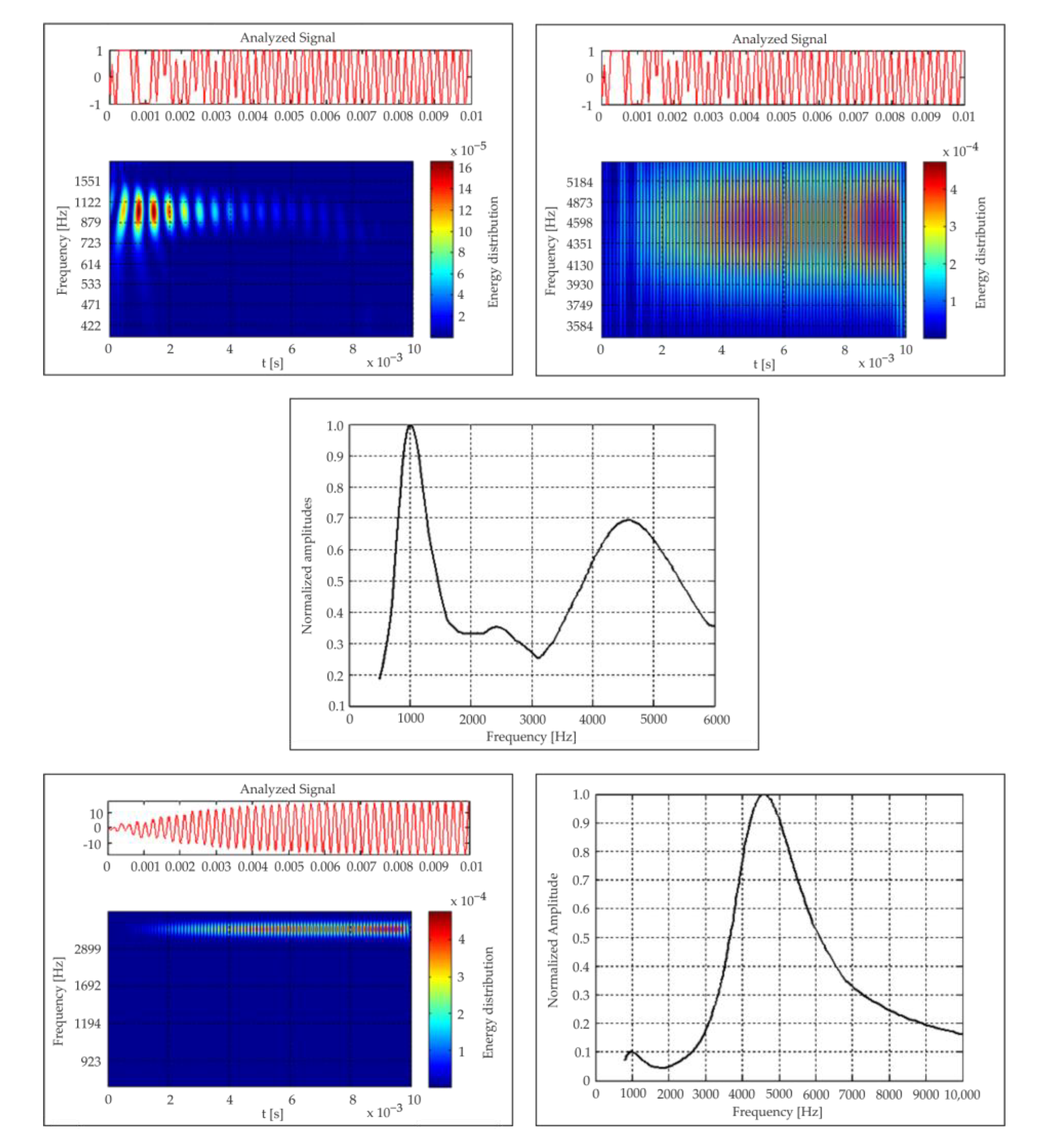
4. Analysis of the Accelerometer Input–Output Energy Distribution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Link, A.; von Martens, H.J. Accelerometers identification using shock excitation. Measurement 2004, 35, 191–199. [Google Scholar] [CrossRef]
- Link, A.; Täbner, A.; Wabinski, W.; Bruns, T.; Elster, C. Modelling accelerometers for transient signals using calibration measurement upon sinusoidal excitation. Measurement 2007, 40, 928–935. [Google Scholar] [CrossRef]
- Webster, J. The Measurement, Instrumentation and Sensors Handbook; CRC Press LLC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Evaluation of Measurement Data—Supplement 1 to the Guide to the Expression of Uncertainty in Measurement—Propagation of Distributions Using a Monte Carlo Method; JCGM: Geneva, Switzerland, 2008. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_101_2008_E.pdf (accessed on 6 November 2020).
- Evaluation of Measurement Data—Supplement 2 to the Guide to the Expression of Uncertainty in Measurement—Extension to Any Number of Output Quantities; JCGM: Geneva, Switzerland, 2011. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_102_2011_E.pdf (accessed on 6 November 2020).
- Kollar, I. On frequency-domain identification of linear systems. IEEE Trans. Instrum. Meas. 1993, 42, 2–6. [Google Scholar] [CrossRef]
- Juang, J.N. Applied System Identification; Prentice Hall: Engelwood Cliffs, NJ, USA, 1994. [Google Scholar]
- Ripper, G.P.; Dias, R.S.; Garcia, G.A. Primary accelerometer calibration problems due to vibration exciter. Measurement 2009, 42, 1363–1369. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; IEEE Press: Piscataway, NY, USA, 2001. [Google Scholar]
- Kilic, G.; Unluturk, M.S. Testing of wind turbine towers using wireless sensor network and accelerometer. Renew. Energy 2015, 75, 318–325. [Google Scholar] [CrossRef]
- Han, P.; Xue, H.; He, Q. Monitoring technique and system of hydraulic vibration of sluice gate in long distance water conservancy project. Procedia Eng. 2011, 15, 933–937. [Google Scholar] [CrossRef] [Green Version]
- Antonovskaya, G.N.; Kapustian, N.K.; Moshkunov, A.I.; Danilov, A.V.; Moshkunov, K.A. New seismic array solution for earthquake observations and hydropower plant health monitoring. J. Seismol. 2017, 21, 1039–1053. [Google Scholar] [CrossRef]
- Alenezi, A.; Abdi, A. A comparative study of multichannel and single channel accelerometer sensors for communication in oil wells. In Proceedings of the International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 6–8 April 2017. [Google Scholar]
- Ginzburg, A.A.; Manukyan, A.B.; Mironov, O.K.; Novikova, A.V.; Yushchenko, V.S. Spatial and spectral characteristics of oscillations of offshore oil and gas production platforms caused by earthquakes and other impacts. Water Resour. 2011, 38, 944–952. [Google Scholar] [CrossRef]
- Mollineaux, M.; Balafas, K.; Branner, K.; Nielsen, P.; Tesauro, A.; Kiremidjian, A.; Rajagopal, R. Damage detection methods on wind turbine blade testing with wired and wireless accelerometer sensors. In Proceedings of the 7th European Workshop on Structural Health Monitoring, Nantes, France, 8–11 July 2014. [Google Scholar]
- Layer, E.; Gawędzki, W. Theoretical principles for dynamic errors measurement. Measurement 1990, 8, 45–48. [Google Scholar] [CrossRef]
- Layer, E.; Tomczyk, K. Determination of Non-Standard Input Signal Maximizing the Absolute Error. Metrol. Meas. Syst. 2009, 17, 199–208. [Google Scholar]
- Hessling, J.P. A novel method of estimating dynamic measurement error. Meas. Sci. Technol. 2006, 17, 2740–2750. [Google Scholar] [CrossRef] [Green Version]
- Shestakov, A.L. Dynamic measuring methods: A review. Acta IMEKO 2019, 8, 64–76. [Google Scholar] [CrossRef]
- Taranow, S.; Olencki, A.; Tesik, J. Estimation of dynamic error for multi-loop measuring systems. Prz. Elektrotechniczny 2003, 79, 511–513. [Google Scholar]
- Dichev, D.; Koev, H.; Bakalova, T.; Louda, P. A Model of the Dynamic Error as a Measurement Result of Instruments Defining the Parameters of Moving Objects. Meas. Sci. Rev. 2014, 14, 183–189. [Google Scholar] [CrossRef] [Green Version]
- Shestakov, A.L. Analysis of dynamic error and selection of parameters of a measuring transducer based on step, linear and parabolic signals. Meas. Tech. 1992, 6, 13–14. [Google Scholar] [CrossRef]
- Rybin, B.S. Simple formulas for dynamic error in linear measurement systems. Meas. Tech. 1995, 38, 1319–1323. [Google Scholar] [CrossRef]
- Pinkhusovich, R.L.; Kuznetsov, B.F. Method of calculating the additional error of measurement transducers for stochastic signals. Meas. Tech. 2002, 45, 354–358. [Google Scholar] [CrossRef]
- Denisenko, V.V. The dynamic error of a multichannel measurement system. Meas. Tech. 2009, 52, 1–6. [Google Scholar] [CrossRef]
- Rutland, N.K. The Principle of Matching: Practical Conditions for Systems with Inputs Restricted in Magnitude and Rate of Change. IEEE Trans. Automat. Control 1994, 39, 550–553. [Google Scholar] [CrossRef]
- Zakian, V. Perspectives of the Matching and the Method of Inequalities. Int. J. Control 1996, 65, 147–175. [Google Scholar] [CrossRef]
- Tomczyk, K. Influence of Monte Carlo Generations Applied for Modelling of Measuring Instruments on Maximum Distance Error. Trans. Inst. Meas. Control 2019, 41, 74–84. [Google Scholar] [CrossRef]
- Layer, E.; Gawędzki, W. Time-Frequency properties of signals maximizing the dynamic errors. SAMS 1993, 11, 73–77. [Google Scholar]
- Tomczyk, K.; Layer, E. Energy density for signals maximizing the integral-square error. Measurement 2016, 90, 224–232. [Google Scholar] [CrossRef]
- Tomczyk, K.; Sieja, M. Frequency Components of Signals Producing the Upper Bound of Absolute Error Generated by the Charge Output Accelerometers. In Methods and Techniques of Signal Processing in Physical Measurement; Hanus, R., Mazur, D., Kreischer, C., Eds.; Springer: Cham, Switzerland, 2019; pp. 189–210. [Google Scholar]
- Honig, M.L.; Steiglitz, K. Maximizing the output energy of a linear channel with a time and amplitude limited input. IEEE Trans. Inf. Theory 1992, 38, 1041–1052. [Google Scholar] [CrossRef] [Green Version]
- Elia, M.; Taricco, G.; Viterbo, E. Optimal energy transfer in band-limited communication channels. IEEE Trans. Inf. Theory 1999, 45, 2020–2029. [Google Scholar] [CrossRef] [Green Version]
- Tomczyk, K. Monte Carlo-based Procedure for Determining the Maximum Energy at the Output of Accelerometers. Energies 2020, 13, 1552. [Google Scholar] [CrossRef] [Green Version]
- Yarbrough, D.W.; Bomberg, M.; Romanska-Zapala, A. On the Next Generation of Low Energy Buildings. Adv. Build. Energy Res. 2019, 1–8. [Google Scholar] [CrossRef]
- Romanska-Zapala, A.; Bomberg, M.; Yarbrough, D.W. Buildings with Environmental Quality Management: Part 4: A path to the future NZEB. J. Build. Phys. 2019, 43, 3–21. [Google Scholar] [CrossRef]
- Dudzik, M.; Stręk, A.M. ANN Architecture Specifications for Modelling of Open-Cell Aluminum under Compression. Math. Probl. Eng. 2020, 2020, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Dudzik, M.; Drapik, S.; Jagiello, A.; Prusak, J. The selected real tramway substation overload analysis using the optimal structure of an artificial neural network. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018. [Google Scholar]
- Tomczyk, K.; Piekarczyk, M.; Sokal, G. Radial basis functions intended to determine the upper bound of absolute dynamic error at the output of voltage-mode accelerometers. Sensors 2019, 19, 4154. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.C.; Lan, C.B. System modeling and robust design of microaccelerometer using piezoelectric thin film. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Taipei, Taiwan, 18 August 1999; pp. 99–104. [Google Scholar]
- Sharapov, V. Piezoceramic Sensors; Springer: Heidelberg/Berlin, Germany, 2011. [Google Scholar]
- Sánchez-Gaspariano, L.A.; Muñiz-Montero, C.; Muñoz-Pacheco, J.M.; Sánchez-López, C.; Gómez-Pavón, L.C.; Luis-Ramos, A.; Bautista-Castillo, A.I. CMOS Analog Filter Design for Very High Frequency Applications. Electronics 2020, 9, 362. [Google Scholar] [CrossRef] [Green Version]
- Raut, R.; Swamy, M.N.S. Modern Analog Filter Analysis and Design: A Practical Approach; Willey: Weinheim, Germany, 2010. [Google Scholar]
- Bialasiewicz, J.T. Wavelet-Based Approach to Evaluation of Signal Integrity. IEEE Trans. Ind. Electron. 2013, 60, 4590–4598. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.C. Wave Parameters and Functions in Wavelet Analysis. Ocean Eng. 2004, 31, 111–125. [Google Scholar] [CrossRef]
- Xiangcheng, M.; Haibao, R.; Zisheng, O.; Wei, W.; Keping, M. The use of the Mexican Hat and the Morlet Wavelets for Detection of Ecological Patterns. Plant Ecol. 2005, 179, 1–19. [Google Scholar]

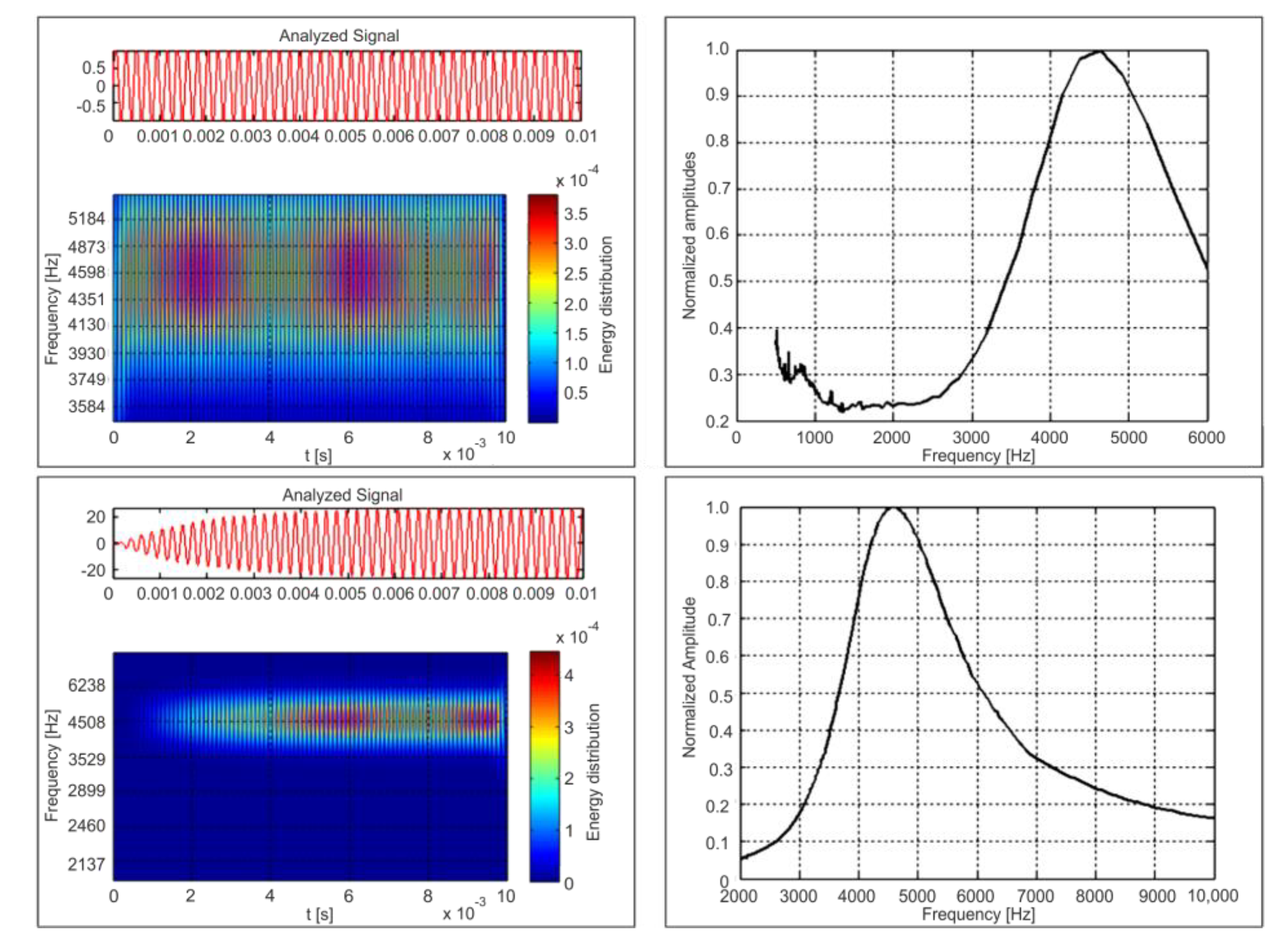

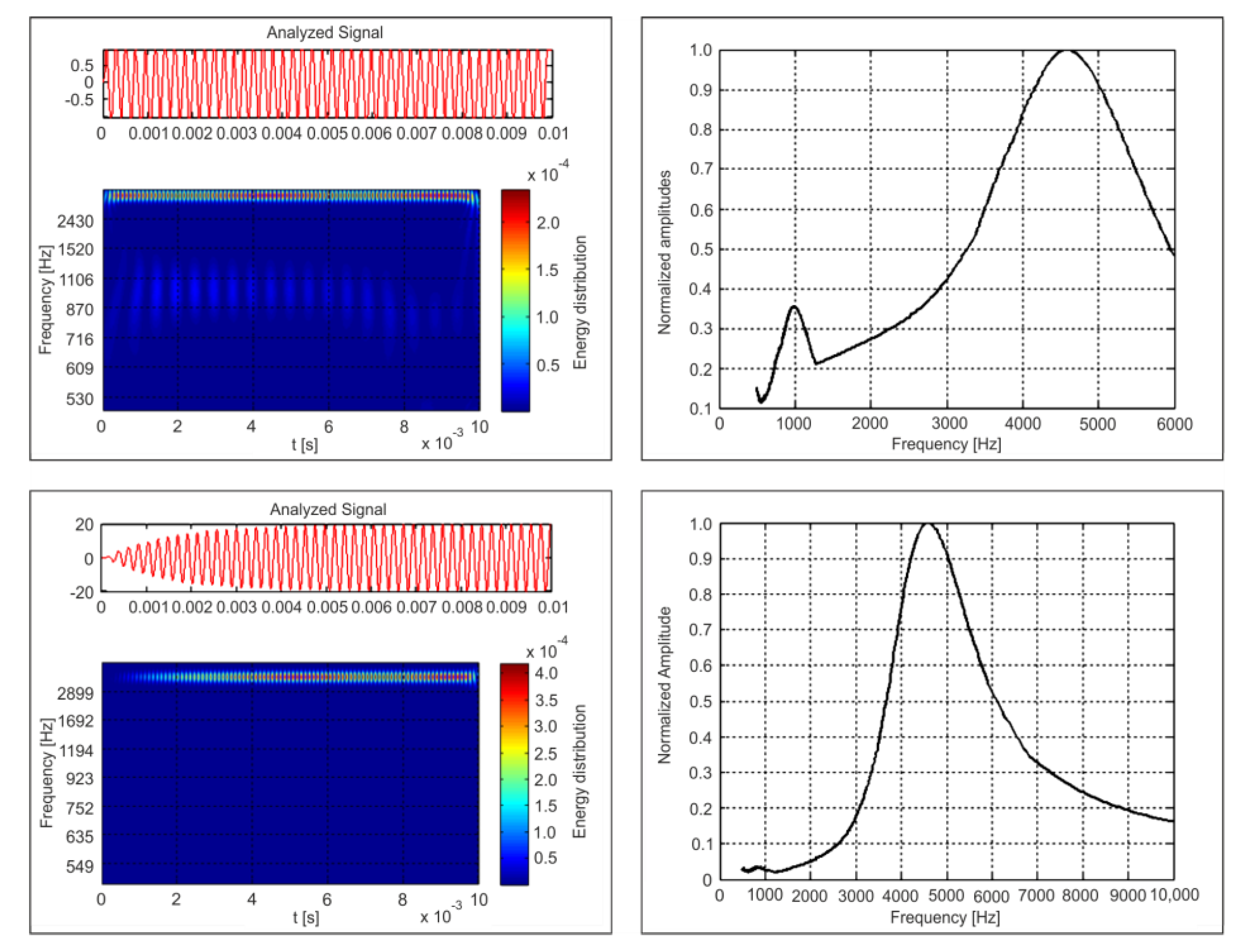
| No. | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 4581 | 0.020 | 1 | 0.01 | 27,900 | |
| 2 | 4579 | 0.026 | 27,890 | ||||
| 3 | 4678 | 0.031 | 27,430 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomczyk, K.; Sieja, M. Analysis of the Accelerometer Input–Output Energy Distribution Based on the Upper Bound of Absolute Dynamic Error. Energies 2020, 13, 5816. https://doi.org/10.3390/en13215816
Tomczyk K, Sieja M. Analysis of the Accelerometer Input–Output Energy Distribution Based on the Upper Bound of Absolute Dynamic Error. Energies. 2020; 13(21):5816. https://doi.org/10.3390/en13215816
Chicago/Turabian StyleTomczyk, Krzysztof, and Marek Sieja. 2020. "Analysis of the Accelerometer Input–Output Energy Distribution Based on the Upper Bound of Absolute Dynamic Error" Energies 13, no. 21: 5816. https://doi.org/10.3390/en13215816
APA StyleTomczyk, K., & Sieja, M. (2020). Analysis of the Accelerometer Input–Output Energy Distribution Based on the Upper Bound of Absolute Dynamic Error. Energies, 13(21), 5816. https://doi.org/10.3390/en13215816







