Modeling of Working Machines Synergy in the Process of the Hybrid Electric Vehicle Acceleration
Abstract
:1. Introduction
- ➢
- specification of the components assembled in the tests (experimental part);
- ➢
- creating a mathematical model of a power-split hybrid vehicle;
- ➢
- presentation of the results;
- ➢
- discussion of the results and conclusions.
2. Experimental Part
3. Model of a Power-Split Hybrid Drive System
3.1. Torque Transmission Dynamics and Vehicle Movement
- ➢
- all shaft connections are rigid so there is no slippage between the drive components (no power loss);
- ➢
- the moments of inertia of the internal combustion engine and electric machines are related to the moments of inertia of the yokes of satellites, sun wheels and crown gear;
- ➢
- the moment of inertia of the main gear pinion is not taken into account;
- ➢
- only longitudinal forces acting on the vehicle during travel are taken into account.
- (a)
- Angular velocities:
- (b)
- Mass moments of inertia and torques of the system:
- (c)
- Vehicle inertia:
- (d)
- Vehicle speed:
- (a)
- Angular velocities:
- (b)
- Mass moments of inertia and torques of the system (JE = 0, TE = 0):
3.2. High Voltage Battery Level
3.3. Energy Management Strategy
- (a)
- Internal combustion engine torque:
- (b)
- Angular velocity of internal combustion engine:
- (c)
- Torque of the MG1 electric machine:
- (d)
- Angular speed of the MG1 electric machine:
- (e)
- Torque of the MG2 electric machine:
- (f)
- Angular speed of the MG2 electric machine:
- (g)
- High voltage battery power:
- (h)
- Battery state of charge:
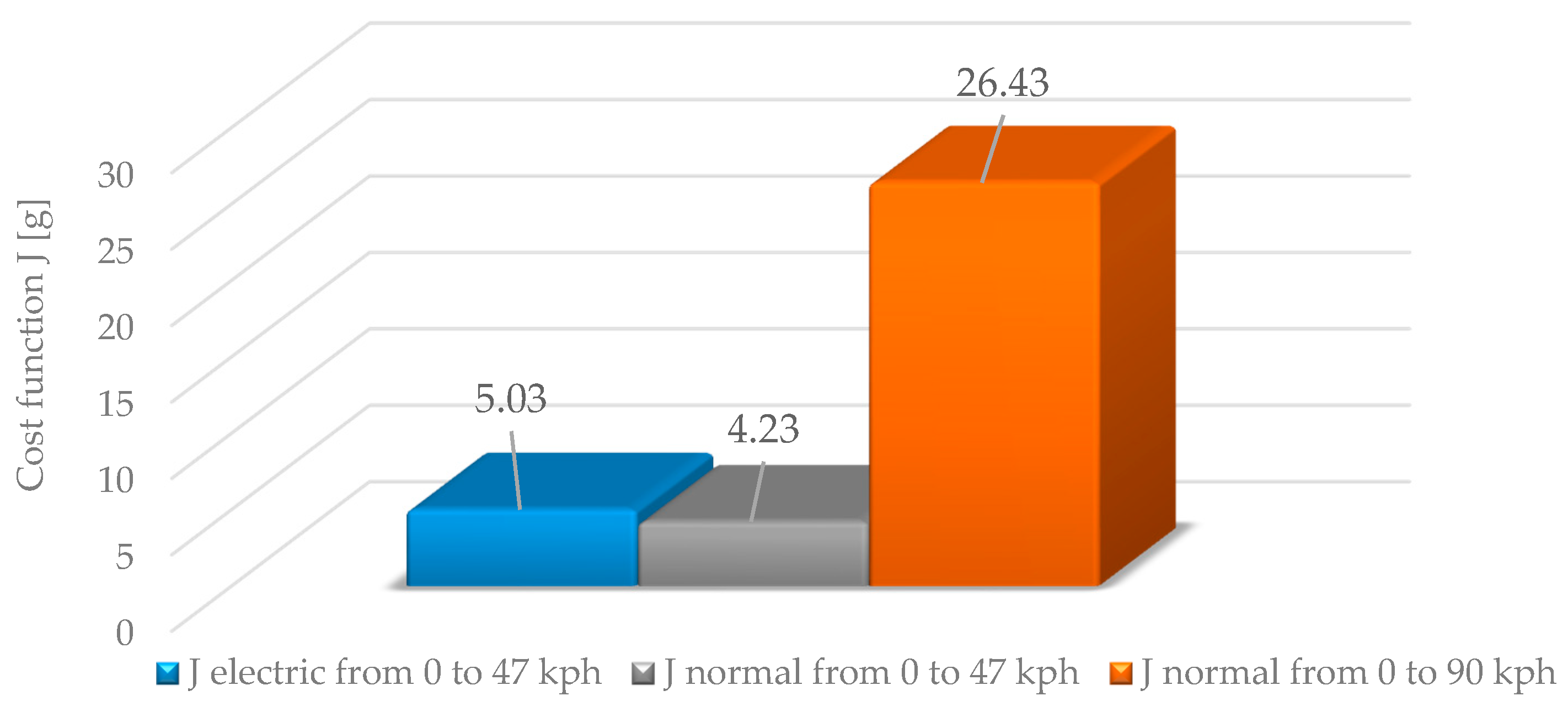
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclatures
| Af | [m2] | frontal area of vehicle |
| [kg/Ws] | specific fuel consumption | |
| Cd | [-] | air drag resistance coefficient |
| C1 | [m] | number of teeth of the first set satellites |
| C2 | [m] | number of teeth of the second set of satellites |
| fd | [-] | total gear ratio |
| fr | [-] | rolling resistance coefficient |
| fuels | [g] | fuel consumption |
| Fp | [N] | propelling force |
| F1 | [N] | internal between teeth force of the first gear |
| F2 | [N] | internal between teeth force of the second gear |
| g | [ms−2] | gravitational acceleration |
| Ibat | [A] | battery charging/discharging current |
| J | [g] | cost function |
| JE | [kgm2] | mass moment of inertia of the internal combustion engine |
| JG | [kgm2] | mass moment of inertia of the generator MG1 |
| JR | [kgm2] | mass moment of inertia of the planetary gear ring wheel |
| JM | [kgm2] | mass moment of inertia of the electric motor MG2 |
| m | [kg] | total mass of vehicle |
| [kg/s] | actual fuel consumption | |
| [kg/s] | equivalent fuel consumption (high voltage battery flow) | |
| N | [-] | number of steps |
| Pbat | [W] | power of battery |
| PE | [W] | internal combustion engine power |
| Qmax | [Ah] | maximum battery capacity |
| Qused | [Ah] | battery capacity used |
| rbat | [Ω] | internal battery resistance |
| rd | [m] | dynamic wheel radius |
| R | [m] | number of teeth of the ring gear |
| R1 | [m] | number of crown wheel teeth |
| R2 | [m] | number of ring wheel teeth on the electric motor side |
| s | [-] | step |
| SOC | [%] | state of charge |
| SOCd | [%] | desired state of charge |
| S1 | [m] | number of teeth of the first sun gear |
| S2 | [m] | number of teeth of the second sun gear |
| t | [s] | time |
| td | [-] | jump (step level) |
| Tbrk | [Nm] | brake torque |
| Tdes | [Nm] | desired torque |
| TEdes | [Nm] | desired torque of the internal combustion engine |
| TGdes | [Nm] | desired torque of the generator |
| TMdes | [Nm] | desired torque of the electric motor |
| Tpre | [Nm] | expected system torque |
| Tresis | [Nm] | resistance torque |
| TE | [Nm] | torque of the internal combustion engine |
| TG | [Nm] | generator torque |
| TM | [Nm] | electric engine torque |
| TR | [Nm] | torque of the ring gear of the planetary gear |
| Ubus | [V] | voltage in the battery circuit |
| vveh | [ms−1] | vehicle speed |
| VOC | [V] | open-circuit voltage of the battery |
| Wu | [J/kg] | calorific value of fuel |
| α | [°] | slope of elevation |
| αE | [-] | penalty factor |
| ωC1 | [1/s] | angular velocity of the satellite yoke C1 |
| ωE | [1/s] | angular speed of the internal combustion engine, |
| ωG | [1/s] | angular speed of the generator |
| ωM | [1/s] | angular velocity of the electric motor |
| ωR | [1/s] | angular velocity of the crown wheel R (ring) |
| ωs1 | [1/s] | angular velocity of the sun wheel S1 |
| ωs2 | [1/s] | angular velocity of the sun wheel S2 |
| ρ | [-] | coefficient occurring between the tracking error and the equivalent fuel consumption |
| ρA | [kgm−3] | air density |
| ηcoulomb | [-] | Coulomb efficiency |
| ηE | [-] | overall engine efficiency |
| [s] | internal combustion engine operation time | |
| [s] | generator operation time | |
| [s] | electric motor operation time |
References
- Ripaccioli, G.; Bernardini, D.; Di Cairano, S.; Bemporad, A.; Kolmanovsky, I.V. A stochastic model predictive control approach for series hybrid electric vehicle power management. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5844–5849. [Google Scholar]
- Borhan, H.; Vahidi, A.; Wei, L.; Phillips, A.; di Cairano, S.; Kuang, M.; McGee, R. Nonlinear model predictive control of a power-split hybrid electric vehicle: Influence of inclusion of powertrain dynamics. In Proceedings of the Dynamic Systems and Control Conference, Arlington, VA, USA, 31 October–2 November 2011; pp. 1–8. [Google Scholar]
- Kleimaier, A.; Schroder, D. An approach for the online optimized control of a hybrid powertrain. In Proceedings of the 7th International Workshop on Advanced Motion Control, Maribor, Slovenia, 3–5 July 2002; pp. 215–220. [Google Scholar]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems, Introduction to Modeling and Optimalization; Springer: Berlin, Germany, 2005; p. 190. [Google Scholar]
- Barsali, S.; Miulli, C.; Possenti, A. A control strategy to minimalize fuel consumption of series hybrid electric vehicles. IEEE Trans. Veh. Technol. 2004, 19, 187–195. [Google Scholar]
- Delprat, S.; Lauber, J.; Guerra, T.M.; Rimaux, J. Control of a parallel hybrid powertrain: Optimal control. IEEE Trans. Veh. Technol. 2004, 53, 872–881. [Google Scholar] [CrossRef]
- Musado, C.; Rizzoni, G.; Staccia, B. A ECMS: An adaptive algorithm for hybrid electric vehicle energy management. In Proceedings of the 44th IEEE Conference Decision Control, European Control Conference, Seville, Spain, 12–15 December 2005; pp. 1816–1823. [Google Scholar]
- Zhu, Y.; Chen, Y.; Tian, G.; Wu, H.; Chen, Q. A four-step method to design an energy management strategy for hybrid vehicles. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 156–161. [Google Scholar]
- Lin, C.C.; Peng, H.; Grizzle, J.W.; Kang, J.M. Power management strategy for a parallel hybrid electric truck. IEEE Trans. Control Syst. Technol. 2003, 11, 839–849. [Google Scholar]
- Lin, C.C.; Peng, H.; Grizzle, J.W. A stochastic control strategy for hybrid electric vehicles. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Back, M. Pradikitive Antriebregulung zum energieoptimalen Betrieb von Hybridfahrzeugen. Ph.D. Dissertation, University Karlsruhe, Karlsruhe, Germany, 2004. [Google Scholar]
- Steinmauer, G.; de Re, L. Optimal control of dual power sources. In Proceedings of the 2001 IEEE International Conference on Control Applications, Mexico City, Mexico, 7 September 2001; pp. 422–442. [Google Scholar]
- Paganelli, G.; Guezennec, Y.; Rizzoni, G. Optimizing Control Strategy for Hybrid Fuel Cell Vehicle; Tech. Rep.; SAE: Warrendale, PA, USA, 2002. [Google Scholar]
- Paganelli, G.; Delprat, S.; Guerra, T.; Rimaux, J.; Santin, J. Equivalent consumption minimization strategy for parallel hybrid powertrains. IEEE Veh. Technol. Conf. 2002, 4, 2076–2081. [Google Scholar]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal control of parallel hybrid electric vehicles. IEEE Trans. Control. Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- Gao, J.; Zhu, G.; Strangas, E.; Sun, F. Equivalent fuel consumption optimal control of a series hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2009, 23, 1003–1018. [Google Scholar] [CrossRef]
- Liu, J.; Peng, H. Modeling and control of a power-split hybrid vehicle. IEEE Trans. Control Syst. Technol. 2008, 16. [Google Scholar] [CrossRef]
- Liu, J.; Peng, H. Automated modelling of a power-split hybrid vehicles. In Proceedings of the 17th World Congress. The International Federation of Automatic Control, Seoul, Korea, 6–11 July 2008; pp. 4648–4653. [Google Scholar]
- Chen, Z.; Xiong, R.; Wang, K.; Jiao, B. Optimal energy management strategy of a plug-in hybrid electric vehicle based on a particle swarm optimization algorithm. Energies 2015, 8, 3661–3678. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Cao, B.; Wen, J.; Bian, Y. Particle Swarm Optimization for Plug-in Hybrid Electric Vehicle Control Strategy Parameter. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–5. [Google Scholar]
- Abido, M.A. Optimal power flow using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2002, 24, 563–571. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Chen, S.-Y.; Hung, Y.-H.; Wu, C.-H.; Huang, S.-T. Optimal energy management of a hybrid electric powertrain system using improved particle swarm optimization. Appl. Energy 2015, 160, 132–145. [Google Scholar]
- Hwang, H.-Y.; Chen, J.-S. Optimized fuel economy control of power—Split hybrid electric vehicle with particle swarm optimization. Energies 2020, 13, 2278. [Google Scholar] [CrossRef]
- Kim, T.S.; Manzie, C.; Sharma, R. Model predictive control of velocity and torque split in a parallel hybrid vehicle. In Proceedings of the IEEE international conference on systems, San Antonio, TX, USA, 11–14 October 2009; pp. 2014–2019. [Google Scholar]
- Borhan, H.A.; Vahidi, A. Model predictive control of a power-split hybrid electric vehicle with combined battery and ultra-capacitor energy storage. In Proceedings of the American control conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5031–5036. [Google Scholar]
- Moura, S.J.; Fathy, H.K.; Callaway, D.S.; Stein, J.L. A stochastic optimal control approach for power management in plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2011, 19, 545–555. [Google Scholar] [CrossRef] [Green Version]
- Yu, K.; Yang, J.; Yamaguchi, D. Model predictive control for hybrid vehicle ecological driving using traffic signal and road slop information. Control Theory Technol. 2015, 13, 17–28. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, G. Adaptive recursive prediction of the desired torque of hybrid powertrain. IEEE Trans. Veh. Technol. 2015, 64. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, G. Model Predictive Control of a Power Split Hybrid Powertrain. In Proceedings of the American Control Conference (ACC), Boston Marriott Copley Place, MA, USA, 6–8 July 2016. [Google Scholar]
- Shi, D.H.; Wang, S.H.; Pierluigi, P.; Chen, L.; Wang, R.; Wang, R. Modeling and optimal energy management of a power split hybrid electric vehicle. Sci. China Tech. Sci. 2017, 60, 713–725. [Google Scholar] [CrossRef]
- Cao, J.; Peng, J.; He, H. Modeling and simulation research on power-split hybrid electric vehicle. Energy Procedia 2016, 104, 354–359. [Google Scholar] [CrossRef]
- Merkisz, J.; Pielecha, I. Uklady Mechaniczne Pojazdow Hybrydowych; Wydawnictwo Politechniki Poznanskiej: Poznan, Poland, 2015. [Google Scholar]
- Ketzer, M.B.; Lima, A.M.N.; Oliveira, A.C.; Jacobina, C.B. Evaluating circuit topologies for battery charge equalization. In Proceedings of the IEEE 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 743–748. [Google Scholar]
- Lin, X.; Stefanopoulou, A.G.; Li, Y.; Anderson, R.D. State of charge imbalance estimation for battery strings under reduced voltage sensing. IEEE Trans. Control Syst. Technol. 2015, 23, 1052–1062. [Google Scholar]
- Ouyang, Q.; Chen, J.; Zheng, J.; Fang, H. Optimal cell-to-cell balancing topology design for serially connected lithium-ion battery packs. IEEE Trans. Sustain. Energy 2018, 9, 350–360. [Google Scholar] [CrossRef]
- Han, W.; Zou, C.; Zhang, L.; Zhou, C. Estimation of cell SOC evolution and system performance in module-based battery charge equalization systems. IEEE Trans. Smart Grid. 2019, 10, 4717–4727. [Google Scholar] [CrossRef]
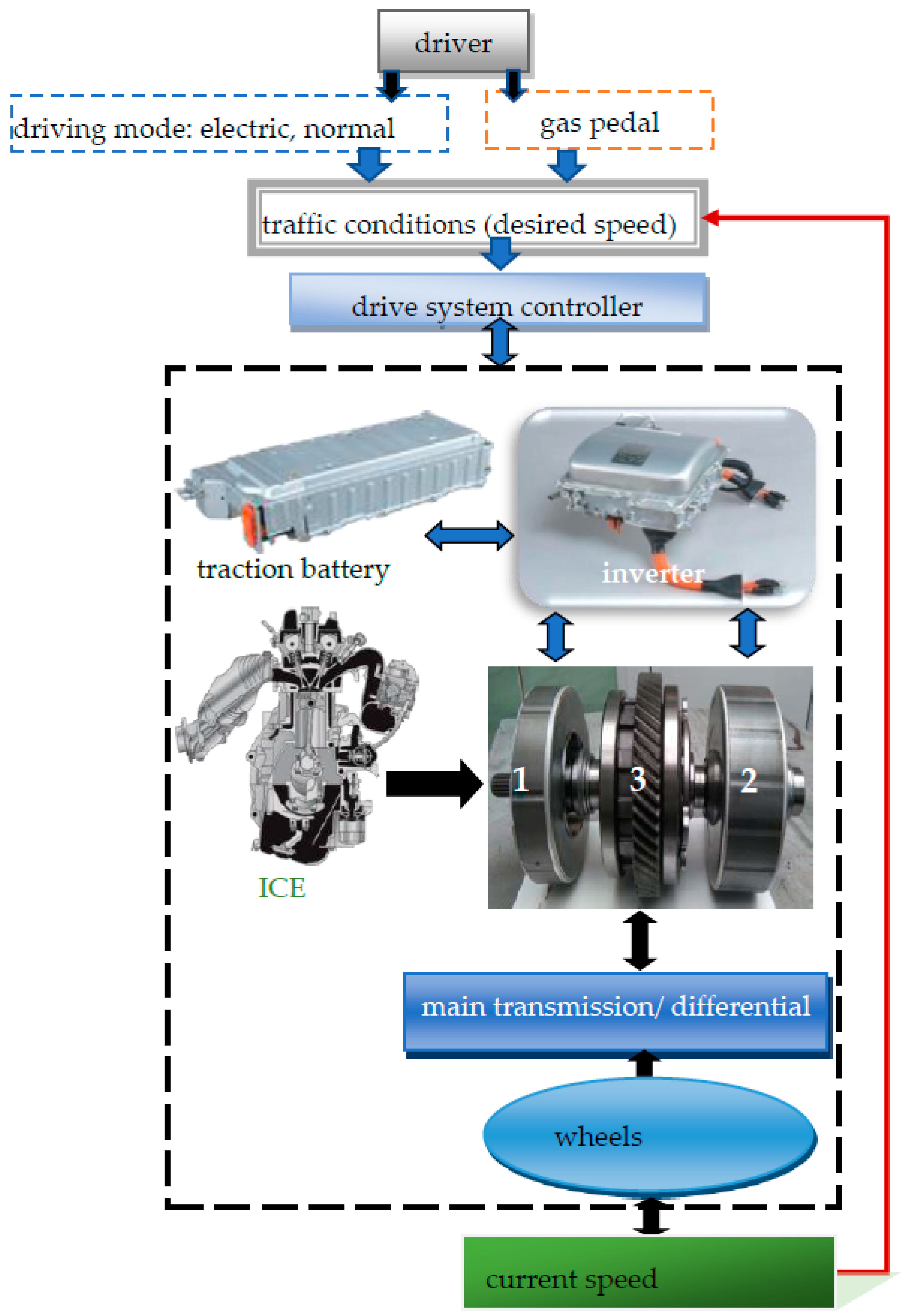

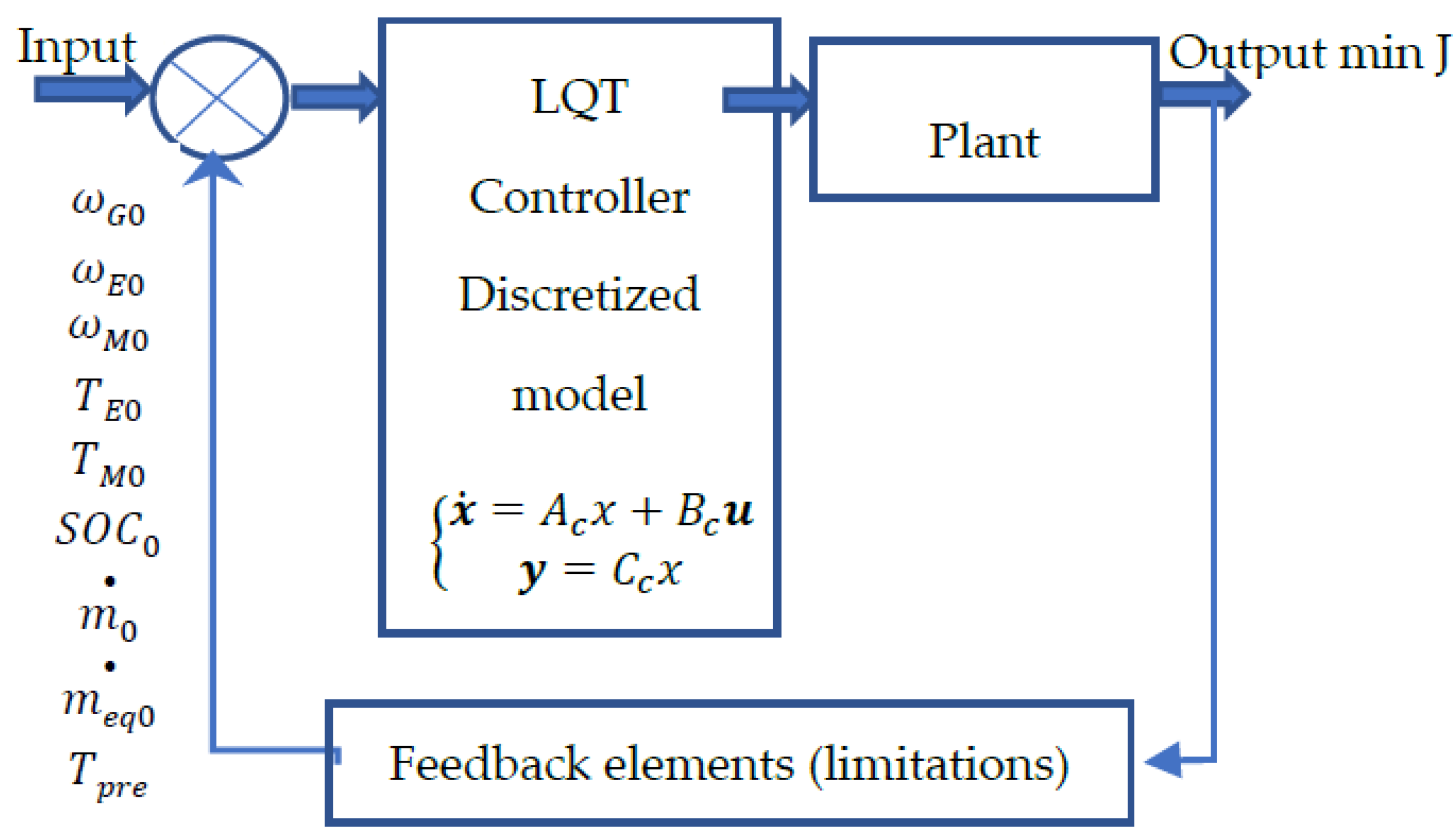




| (a) | |
| Total mass | 1630 kg (1445 kg + 185 kg—driver and passenger) |
| Dynamic wheel radius | 0.29 m |
| Frontal area | 1.62 m2 |
| Rolling resistance coefficient | 0.0084—tire energy class C |
| Air drag coefficient | 0.25 |
| Drive system type HEV | power-split hybrid |
| Internal Combustion Engine Specification | |
| Ignition type | spark ignition |
| Capacity | 1.8 dm3 |
| Number of cylinders | 4 |
| Max. power | 73 kW |
| Max. power rotational speed | 5200 rpm |
| Max. torque | 142 Nm |
| (b) | |
| Max. torque rotational speed | 4000 rpm |
| Mass moment of inertia | 0.18 kg m2 |
| Generator (MG1) Specification | |
| Type | three-phase synchronous alternating current (AC) |
| Function | generator, internal combustion engine (ICE) starter |
| Rated voltage | 500 V |
| Maximum output power | 42 kW |
| Max torque | 45 Nm |
| Current at max torque | 75 A |
| Max. rotational speed | 10,000 rpm |
| Mass moment of inertia | 0.023 kg m2 |
| Electric Motor (MG2) Specification | |
| Type | three-phase synchronous AC |
| Function | generator, wheel drive |
| Rated voltage | 500 V |
| Maximum output power | 60 kW |
| Maximum torque | 207 Nm |
| Current at max torque | 230 A |
| Max. rotational speed | 13,000 rpm |
| Mass moment of inertia | 0.012 kg m2 |
| High Voltage Battery and Inverter Specification | |
| Battery type | NiMH |
| Nom. voltage | 201.6 V |
| Capacity | 6.5 Ah |
| Item | Parameter | Value |
|---|---|---|
| Vehicle | Mass | 1630 kg |
| Engine | Start delay | 0.5 s |
| Time constant | 1 s | |
| Max torque | 142 Nm | |
| Power output | 73 kW | |
| Motor | Max torque | 207 Nm |
| Power output | 60 kW | |
| Battery | SOC upper bound | 0.75 |
| SOC lower bound | 0.45 | |
| SOC target | 0.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prajwowski, K.; Golebiewski, W.; Lisowski, M.; Abramek, K.F.; Galdynski, D. Modeling of Working Machines Synergy in the Process of the Hybrid Electric Vehicle Acceleration. Energies 2020, 13, 5818. https://doi.org/10.3390/en13215818
Prajwowski K, Golebiewski W, Lisowski M, Abramek KF, Galdynski D. Modeling of Working Machines Synergy in the Process of the Hybrid Electric Vehicle Acceleration. Energies. 2020; 13(21):5818. https://doi.org/10.3390/en13215818
Chicago/Turabian StylePrajwowski, Konrad, Wawrzyniec Golebiewski, Maciej Lisowski, Karol F. Abramek, and Dominik Galdynski. 2020. "Modeling of Working Machines Synergy in the Process of the Hybrid Electric Vehicle Acceleration" Energies 13, no. 21: 5818. https://doi.org/10.3390/en13215818
APA StylePrajwowski, K., Golebiewski, W., Lisowski, M., Abramek, K. F., & Galdynski, D. (2020). Modeling of Working Machines Synergy in the Process of the Hybrid Electric Vehicle Acceleration. Energies, 13(21), 5818. https://doi.org/10.3390/en13215818







