Design and Analysis of Second-Order Sliding Mode Controller for Active Magnetic Bearing

Abstract

An active magnetic bearing (AMB) is a kind of high-performance bearing that uses controllable electromagnetic force to levitate the rotor. Its control performance directly affects the operation characteristics of high-speed motors and other electromechanical products. The magnetic bearing control model is nonlinear and difficult to control. Sliding mode control algorithm can be used in the magnetic bearing control system, but the traditional sliding mode control has the problem of high-frequency chattering, which affects the operation stability of magnetic bearings. Based on the second-order sliding mode control algorithm, a new second-order sliding mode controller for active magnetic bearing control was designed, and the stability of the designed sliding mode control law was proven by Lyapunov criterion. On the basis of the established active magnetic bearing control model, the numerical analysis of the designed controller was carried out, and the control effect was compared with that obtained by the exponential reaching law for the sliding mode control algorithm. The experimental results show that the designed sliding mode controller has better dynamic performance and stability than the exponential reaching law for the sliding mode controller.

1. Introduction

An active magnetic bearing (AMB) is a kind of bearing structure that uses controllable electromagnetic force to make the rotor suspend stably. It has the advantages of strong antidisturbance ability, fast dynamic response, adjustable bearing capacity, and small loss. AMB has no contact with the rotor, which can realize the stable operation of the rotor at high speed, and is suitable for carrying high-speed motors [1,2]. As a precision component, the stable operation of AMB involves multidisciplinary knowledge and cross-coupling, such as electromagnetic, thermal, and rotor dynamics, and the output of electromagnetic force presents nonlinear characteristics, so it is difficult to control AMB accurately. Sliding mode control has the advantages of strong robustness and no need for an accurate control object model, making it suitable for the control of AMB [3,4,5]. However, the traditional sliding mode control has the problem of high-frequency chattering near the stable point, which may excite the unmodeled high-frequency components in the system, thus reducing the stability of AMB and weakening its ability to resist dynamic load disturbance [6,7].

In order to realize the stability control of AMB, which is a time-varying, complex, and nonlinear system, a magnetic bearing system control method based on PID surface sliding mode control was proposed in [8]. The sliding surface was designed as a PID surface to reduce the chattering phenomenon. In [9], a sliding mode controller was designed for the rotor axial position control problem. The adaptive law was used to adjust the weight parameters of an RBF network online to realize the online optimization of sliding mode controller parameters. A design method of a 5-DOF AMB controller based on sliding mode control (SMC) and neural network (NN) was proposed in [10]. The sliding mode control was used to achieve high robustness and fast response, while the neural network compensated the unmodeled uncertainties and external disturbances by an online tuning algorithm. In [11], the optimal gain matrix of the state observer and the parameters of the sliding mode controller were solved by using the linear quadratic regulator method. The designed sliding mode controller had good control performance and robustness to model parameter perturbation.

To reduce the chattering problem of traditional sliding mode control, Levant proposed a higher-order sliding mode theory [12] and gave the control accuracy estimation of several second-order sliding mode control algorithms. Higher-order sliding mode is a generalization of the traditional sliding mode, which requires the r-order sliding surface $S=\left\{x\in X|s=\dot{s}=\cdots s^{r-1}=0\right\}$ to converge in a finite time, thus eliminating the chattering problem of the traditional sliding mode. In [13], the authors discuss the definition of sliding mode order, relative degree, chattering attenuation, filtering, and implementation complexity of high-order sliding mode and introduce the application occasion and control effect of high-order sliding mode. In [14], the high-order sliding mode (HOSM) control is called quasicontinuous (QC) control. It was proven that the sliding variable and its derivatives converge to zero gradually in the HOSM set. In addition to the HOSM set, the output of the controller is continuous, so the higher-order sliding mode control has less chattering characteristics. In order to discuss the finite-time-constrained stabilization of nonlinear systems with matching uncertainties, a high-order finite-time control law was designed in [15]. When all the high-order derivatives of the output satisfy $s=\dot{s}=\cdots s^n=0$, the output of the system satisfies $s\in \left(-c,c\right)$, where c is chosen as constant. For the traditional sliding mode control algorithm applied to the control of a magnetic bearing system, there is a high-frequency chattering problem near the stable point. In this paper, a new second-order sliding mode controller is designed for the control of magnetic bearings. The first derivative information of the sliding mode variable is introduced to ensure the convergence of the sliding mode variable and its first derivative, and the high-frequency chattering problem near the stable point is eliminated theoretically. The structure of the control law is given, and the stability of the controller is proven by Lyapunov stability criterion. The control effects of the designed controller and sliding mode controller based on exponential reaching law were compared by simulation, and the experimental results were verified by the magnetic bearing control hardware experimental platform.

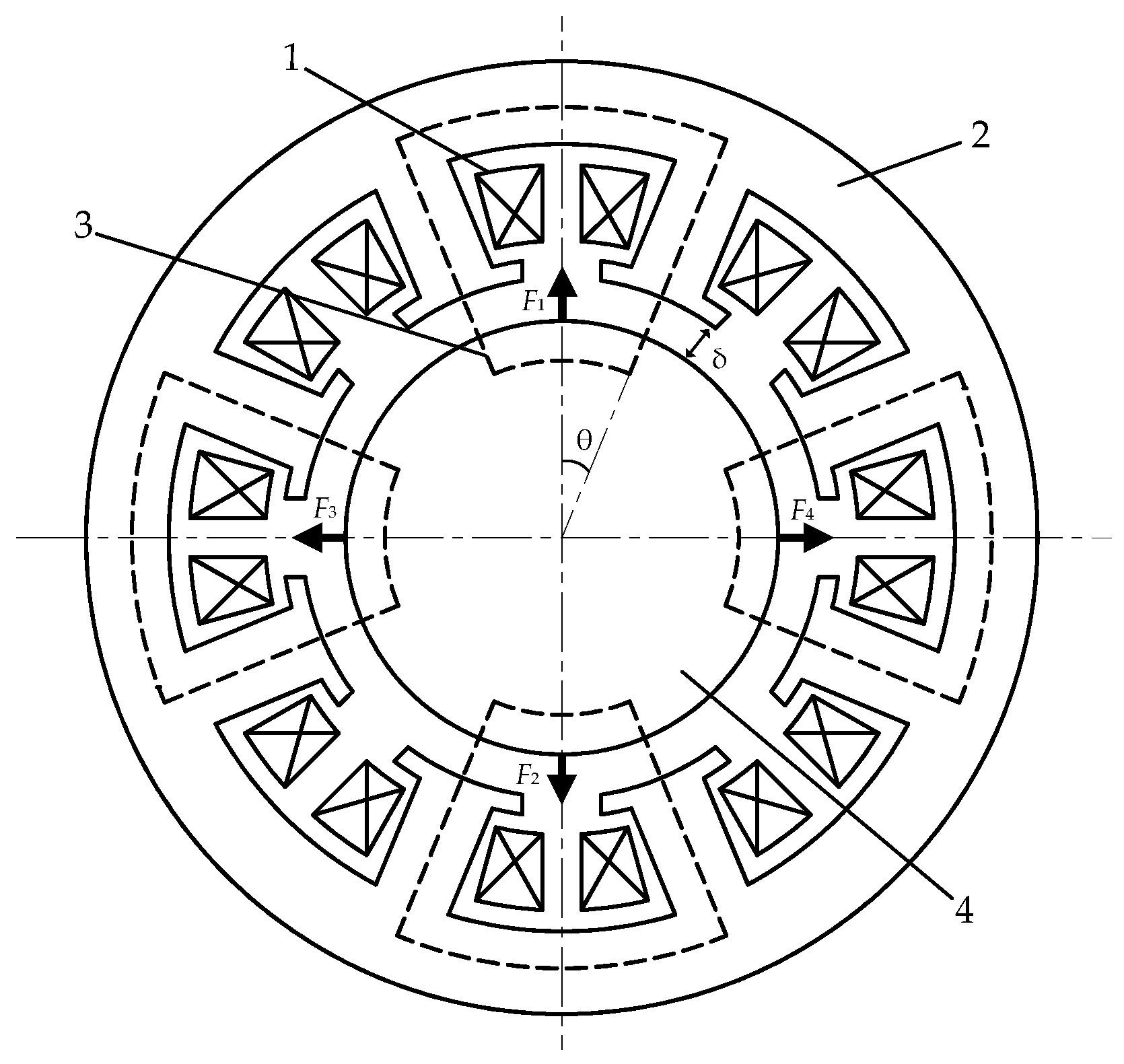
2. Model of the AMB

The structure of AMB used in this paper is shown in Figure 1 and is mainly composed of stator core, electromagnetic coil, and rotor. The eight magnetic poles of the stator core are divided into four groups according to the different magnetic line paths. The electromagnetic force F₁–F₄ in the four directions can be adjusted by controlling the corresponding electromagnetic coil current, as shown in Figure 1, so as to realize stable suspension of the rotor.

In order to obtain the model of the AMB, the magnetic circuit of the AMB was analyzed. Considering that the magnetic induction intensity of the AMB is small and the core will not be saturated, the magnetic resistance in the iron core is ignored. The electromagnetic force of a single pole can be calculated by the virtual displacement method:

$$F_m=\frac{1}{2}BHS=\frac{{\mu }_0{N}^{2}S{i}^2}{2{\delta }^2}$$

(1)

where ${\mu }_0$ is vacuum permeability, N is coil turns, S is pole area, i is current in coil, δ is air gap size, B is magnetic flux density, and H is magnetic field intensity.

Because the angle between the magnetic poles θ is small, i.e., x ≈ δ, the relationship between the magnetic force on one side of the magnetic bearing and the displacement x is obtained as follows:

$$F=2F_m\cos \theta =\frac{{\mu }_0{N}^{2}S{i}^2}{{\delta }^2}\cos \theta$$

(2)

Assuming that the upward force on the bearing is F₁ and the downward force is F₂, the resultant force on the bearing is F = F₁ − F₂. In actual operation, the position deviation of the rotor is very small. At the equilibrium point x = 0, i = i₀, Taylor expansion of Equation (2) is carried out, omitting the second-order and above higher-order small quantities:

$$F=\frac{4{\mu }_0{N}^{2}S\cos \theta i_0^2}{x_0^3}x+\frac{4{\mu }_0{N}^{2}S\cos \theta i_0}{x_0^2}i$$

(3)

Considering the external gravity as an additional disturbing force, the rotor motion equation under the action of electromagnetic force is considered:

$$m\ddot{x}=K_{x}x+K_{i}i$$

(4)

where $K_x=\frac{4{\mu }_0{N}^{2}S\cos \theta i_0^2}{x_0^3}$ is the force displacement coefficient and $K_i=\frac{4{\mu }_0{N}^{2}S\cos \theta i_0}{x_0^2}$ is the force current coefficient.

After Laplace transform of Equation (4), we can obtain

$$m{s}^2{X}_{\left(s\right)}=K_x{X}_{\left(s\right)}+K_i{I}_{\left(s\right)}$$

(5)

where I_(s) is the control current and X_(s) is the output displacement.

It can be obtained that the model of the AMB analyzed in this paper is as follows:

$$\left[\begin{array}{c}\dot{x}\\ \ddot{x}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ \frac{K_x}{m}& 0\end{array}\right]\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]+\left[\begin{array}{c}0\\ \frac{K_i}{m}\end{array}\right]\left[i\right]$$

(6)

Considering that the coil current of AMB needs to have fast dynamic response performance and provide enough high bearing capacity, the coil turns and stable point current were designed. The specific structural parameters of the AMB designed in this paper are shown in

Table 1. Design parameters of magnetic bearing.

Parameters	Designed Value
Coil turns	150
Number of poles	8
Stator out diameter	120 mm
Rotor out diameter	50 mm
Air gap length	1.4 mm
Magnetic pole area	129 mm2
Magnetic pole angle	22°

.

By substituting the structural parameters of the AMB into Equation (6), the specific model of the designed bearing can be obtained, as shown in Equation (7).

$$\left[\begin{array}{c}\dot{x}\\ \ddot{x}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 14247.7& 0\end{array}\right]\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]+\left[\begin{array}{c}0\\ 19.95\end{array}\right]\left[i\right]$$

(7)

3. Sliding Mode Control for the AMB

3.1. Principle of Sliding Mode Control and Chattering Problem

Sliding mode control is a kind of variable structure control algorithm. The fundamental difference between sliding mode control and conventional control strategy is the discontinuity of its control; that is, the output of the controller changes with time and presents switching characteristics. Since sliding mode is independent of system parameters and disturbances, the system in sliding mode has strong robustness [16].

Set the control system as

$$x\in R^n,u\in R^m,t\in R$$

(8)

by solving the control function

$$u=\{\begin{array}{cc}{u}^{+}(x)& s(x)>0\\ u^{-}(x)& s(x)<0\end{array}$$

(9)

When u⁺(x) ≠ u⁻(x), the sliding mode exists, and all the system state points except s = 0 reach the sliding surface in finite time.

Sliding mode control makes the system state point run in a small amplitude and high-frequency sliding mode along the prescribed state trajectory. When the trajectory of the system reaches the switching surface, its velocity is not zero. Therefore, the inertia makes the moving point cross the sliding surface s = 0 and move repeatedly, which will cause a chattering problem.

The existence of chattering will affect the stability of the control system and even lead to system oscillation, instability, and other serious consequences. It is necessary to optimize the traditional sliding mode control to reduce or even eliminate the chattering problem. The commonly used methods to suppress chattering include quasi-sliding mode method, filtering method, and higher-order sliding mode method [17,18]. The higher-order sliding mode is improved on the basis of the traditional sliding mode, which makes the r-order sliding surface converge in finite time. Therefore, the higher-order sliding mode control can not only keep the advantages of simple and strong robustness of the traditional sliding mode control but also greatly reduce the chattering of the system and improve the control accuracy.

3.2. Design and Stability Analysis of Second-Order Sliding Mode Controller

The second-order sliding mode control algorithm belongs to the higher-order sliding mode control algorithm. The goal is to design the control law so that the sliding mode variable s and the first derivative of the sliding mode variable can converge in finite time. Firstly, the sliding mode variable s = x − c is taken, where x is the actual position of the rotor and c is the given position of the rotor. According to the model of AMB, the control input u directly affects the sign and size of $\ddot{s}$, as shown in Equation (7). Therefore, the design of the control law can be completed by finding the switching logic that depends on s and $\dot{s}$ and ensuring that the state of the system converges to the sliding surface $s=0,\dot{s}=0$ in a finite time [19,20].

To prove the stability of the controller, the Lyapunov function should first be constructed as follows:

$$V_{\left(x\right)}=\frac{1}{2}{s}^{T}s$$

(10)

The derivation of Equation (10) is carried out, and the Lyapunov function always satisfies the following conditions:

$${\dot{V}}_{\left(x\right)}=s\dot{s}\le 0$$

(11)

Then, the state point of the system can be guaranteed to reach the sliding surface finally.

In this paper, based on the model of AMB, according to the stability requirements of Lyapunov, a second-order sliding mode controller for the control of magnetic bearing is designed by introducing the first derivative information of sliding mode variable s:

$$u=-\frac{K_x}{K_i}\left(s+c\right)+u_1-{\lambda }_2\dot{s}$$

(12)

$$u_1=\{\begin{array}{ll}{\lambda }_1\mathrm{sgn}s& \mathrm{s}{\displaystyle \int \mathrm{sgn}sdt<0} \\ 0& \mathrm{s}{\displaystyle \int \mathrm{sgn}sdt\ge 0}\end{array}$$

(13)

The basic design idea is that the λ₂$\dot{s}$ part of the control law is formed by introducing the derivative information of the sliding mode variable $\dot{s}$. The influence of the derivative of the sliding mode variable $\dot{s}$ on the output of the controller can be adjusted by changing the size of the λ₂ parameter, and the anti-interference ability of the system and the stability requirements of the system can be achieved by introducing the λ₁sgns part of the control law.

In order to prove the convergence of the algorithm, a positive definite function is constructed according to the Lyapunov stability criterion:

$$U_1=\frac{1}{2}{s}^2>0$$

(14)

By deriving the function, we can obtain

$$\begin{array}{l}{\dot{U}}_1=s\dot{s}=\left(x-c\right)\left(\dot{x}-0\right)=s\cdot {\displaystyle \int \frac{K_x}{m}x+\frac{K_i}{m}u dt}\\ =s\cdot \left\{{\displaystyle \int \frac{K_x}{m}x+\frac{K_i}{m}\left[-\frac{K_x}{K_i}\left(s+c\right)+u_1-{\lambda }_2\dot{s}\right]dt}\right\}\\ =s\cdot \left(\frac{K_i}{m}{\displaystyle \int u_1-{\lambda }_2\dot{s}dt}\right)\le -{\lambda }_2\frac{K_i}{m}{s}^2\le 0\end{array}$$

(15)

Similarly, by constructing a positive definite function for $\dot{s}$ and deriving it, we can obtain

$$\begin{array}{l}{\dot{U}}_2=\dot{s}\ddot{s}=\left(\dot{x}-0\right)\left(\ddot{x}-0\right)=\dot{s}\cdot \left(\frac{K_x}{m}x+\frac{K_i}{m}u\right)\\ =\dot{s}\cdot \left\{\frac{K_x}{m}x+\frac{K_i}{m}\left[-\frac{K_x}{K_i}\left(s+c\right)+u_1-{\lambda }_2\dot{s}\right]\right\}\\ =\dot{s}\cdot \left[\frac{K_i}{m}\left(u_1-{\lambda }_2\dot{s}\right)\right]\end{array}$$

(16)

For the stability analysis of $\dot{s}$, there are two cases:

(1) When $s{\displaystyle \int \mathrm{sgn}sdt}<0$,

$$\begin{array}{l}{\dot{U}}_2=\dot{s}\ddot{s}=\dot{s}\left[\frac{K_i}{m}\left({\lambda }_1\mathrm{sgn}s-{\lambda }_2\dot{s}\right)\right]\\ ={\lambda }_1\frac{K_i}{m}\dot{s}\cdot \mathrm{sgn}s-{\lambda }_2{\dot{s}}^2\le 0\end{array}$$

(17)

(2) When $s{\displaystyle \int \mathrm{sgn}sdt}\ge 0$,

$${\dot{U}}_2=\dot{s}\ddot{s}=\dot{s}\left[\frac{K_i}{m}\left(-{\lambda }_2\dot{s}\right)\right]\le 0$$

(18)

It is proved that the sliding mode variable s = x − c of the designed controller converges in the finite time, and the output characteristics of the controller meet the requirements of the operation stability of AMB.

The second-order sliding mode controller sets the K_X and K_i parameters of the controller according to the model of AMB and adjusts the performance of the controller by adjusting the parameters of λ₁ and λ₂. The larger the parameter λ₁ is, the stronger the anti-interference ability of the system will be. However, if the parameter λ₁ is too large, it will affect the static stability of the system. The influence of $\dot{s}$ on the output of the controller is adjusted by changing the size of λ₂ parameter. The larger λ₂ is, the stronger the feedback effect of $\dot{s}$ will be, which is beneficial to the stability of the system but may reduce the dynamic response performance of the system.

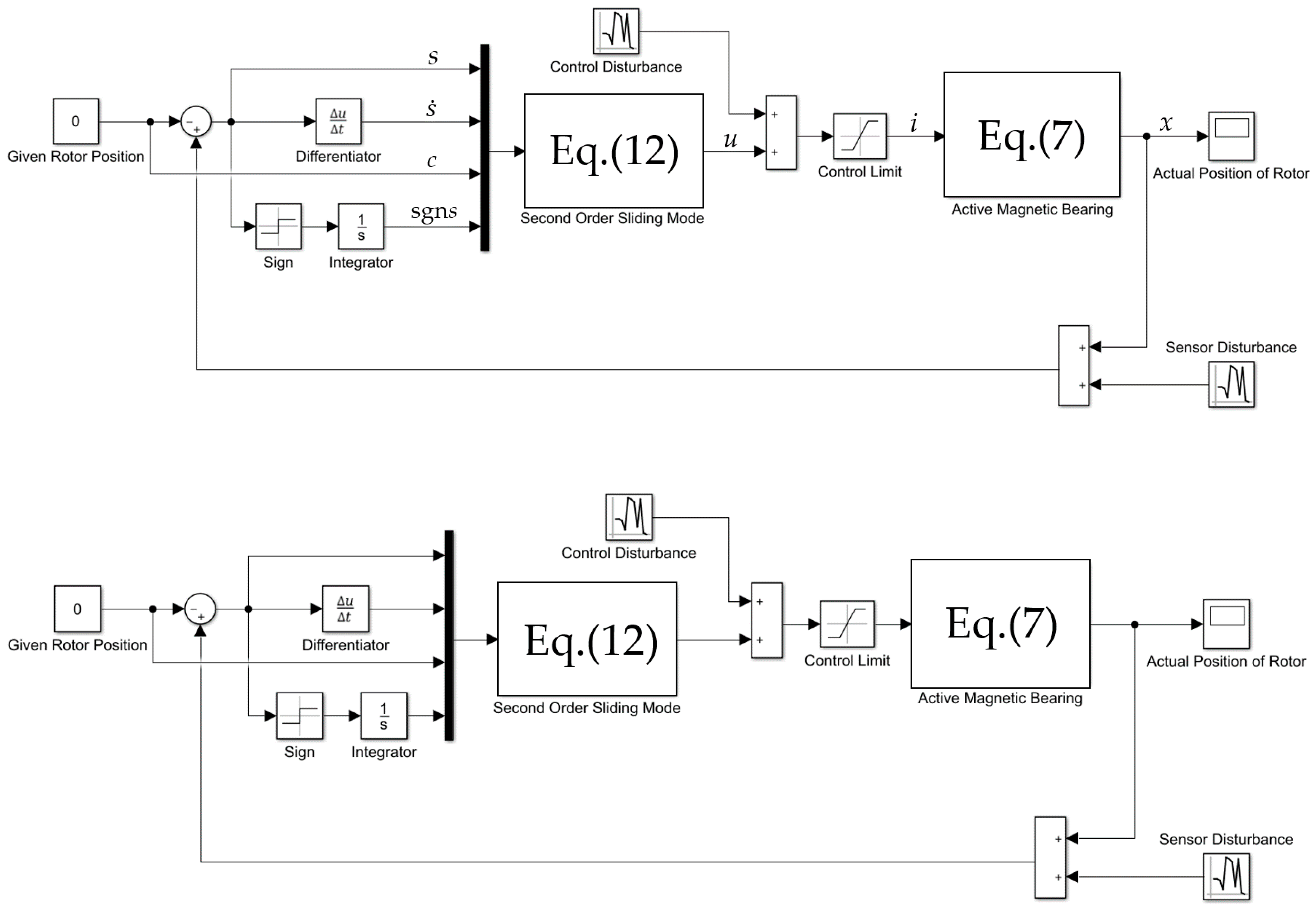
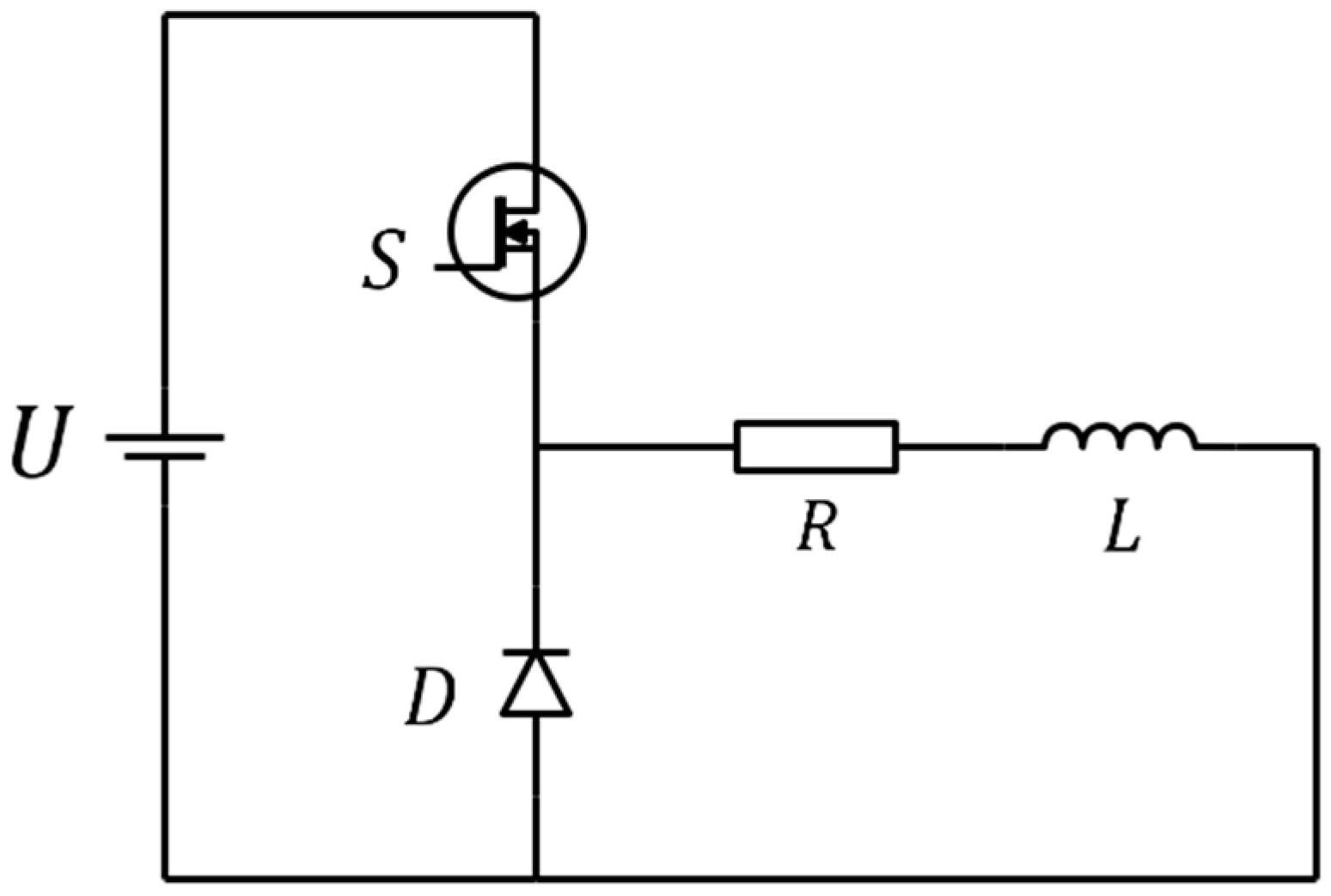
4. Modeling and Simulation of Control System

4.1. Establishment of Simulation Model

Based on the model of AMB, the sliding mode control algorithm was programmed, and the control disturbance and sensor disturbance were added. At the initial moment, the rotor does not float yet. The initial position of the rotor of the magnetic bearing was set to −1.4 mm, and the given rotor position was 0 mm. The simulation model of AMB under the second-order sliding mode control was obtained as shown in Figure 2.

In order to satisfy the stability of the controller, Equations (13), (15), and (16) should be satisfied. Therefore, in order to ensure that the controller can meet the Lyapunov stability criterion, the following equation should be satisfied:

$${\lambda }_1,{\lambda }_2>0$$

(19)

Theoretically, since the parameter λ₁ controls the size of the switching control term sgns, a greater λ₁ value results in a stronger anti-interference ability of the system. The parameter λ₂ controls the magnitude of the first derivative of the sliding mode variable, so the chattering of the controller is limited. However, the fast response performance of the system will be affected. Generally speaking, as long as the selected parameters satisfy Equation (19), then the system can eventually be stable. In the process of simulation, three levels of parameter values were selected first: λ₁ = 0.001, 0.01, and 0.1 and λ₂ = 1, 10, and 100. Combining these parameters, a group of fast response and small overshoot was selected, namely λ₁ = 0.001 and λ₂ = 10. After minor adjustment, the final selected parameters were obtained, as shown in

Table 2. Parameters of second-order sliding mode controller.

Parameters	Symbol	Value
Force-displacement coefficient	Kx	4929.7
Force-current coefficient	Ki	6.9016
Parameter1	λ1	0.001
Parameter2	λ2	18

.

The design of a sliding mode controller based on reaching law is the basic method for designing a first-order sliding mode controller. The exponential reaching law is a common form, and its structure is $\dot{s}=-\epsilon \mathrm{sgn}\left(s\right)-ks$, where ε is the constant reaching gain and k is the exponential gain. The exponential reaching law is divided into two parts: pure exponential reaching term $\dot{s}=-ks$ and constant reaching term $\dot{s}=-\epsilon \mathrm{sgn}\left(s\right)$. The simulation model of a sliding mode controller based on exponential reaching law is shown in Figure 3.

When selecting parameters ε and k, we should consider the reaching speed and the chattering of sliding mode motion. When the value of ε is too large, the chattering near the switching surface will be very large. When ε is too small, the reaching speed will be very slow and will not reach the stable point. For the selection of k value, if the selection is too small, the approaching speed of the system will be slower in the case of interference. When the k value is too high, the overall dynamic performance of the system will be poor. Therefore, in general, selecting a smaller value of ε and a larger value of k can achieve fast reaching and eliminate chattering. We selected three levels of parameters: ε = 0.01, 0.1, 1 and k = 10, 100, 1000. By combining the three levels of parameters, the control effect of the controller under different control parameters was obtained. The optimal parameter combination of ε = 0.1 and k = 100 was selected. The final parameters were obtained by adjusting the parameters slightly. The controller parameters selected in this paper are shown in

Table 3. Parameters of exponential reaching law for sliding mode controller.

Parameters	Symbol	Value
Constant reaching gain	ε	0.3
Exponential reaching gain	k	100

.

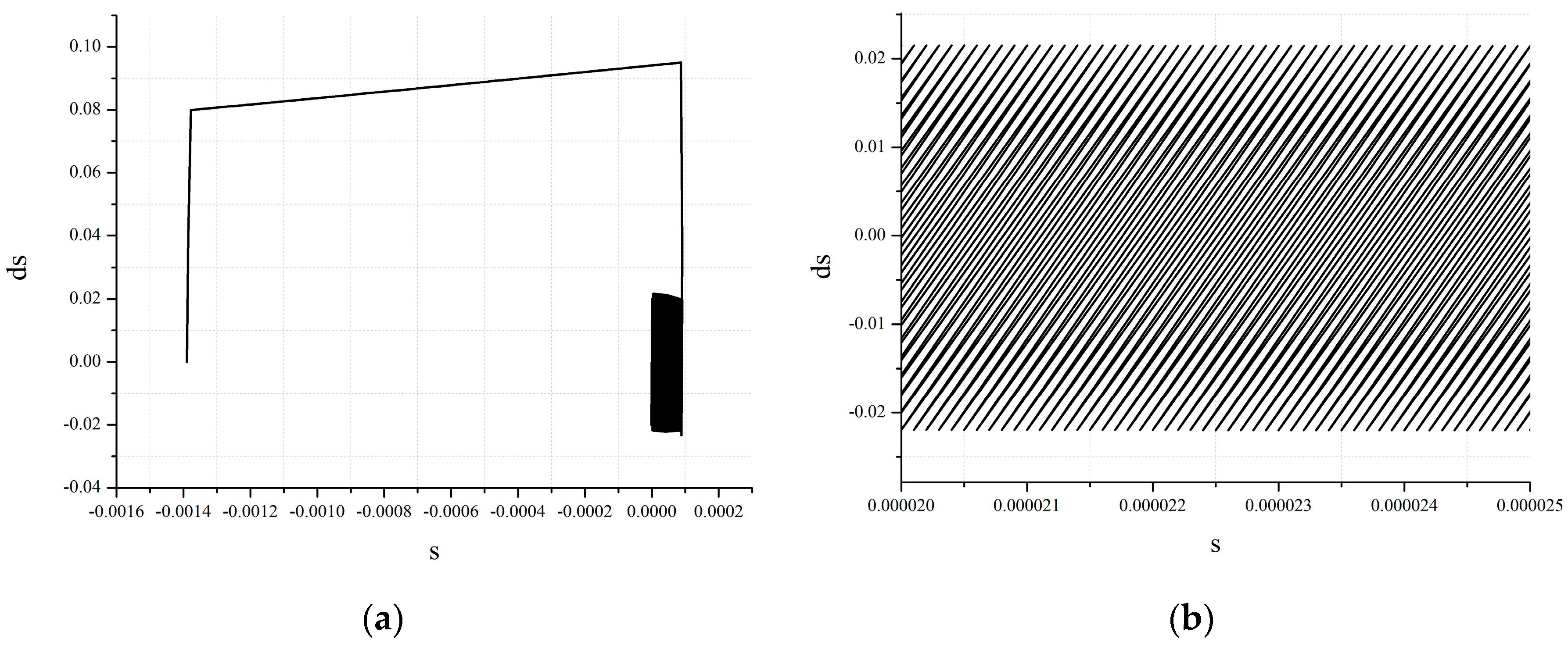
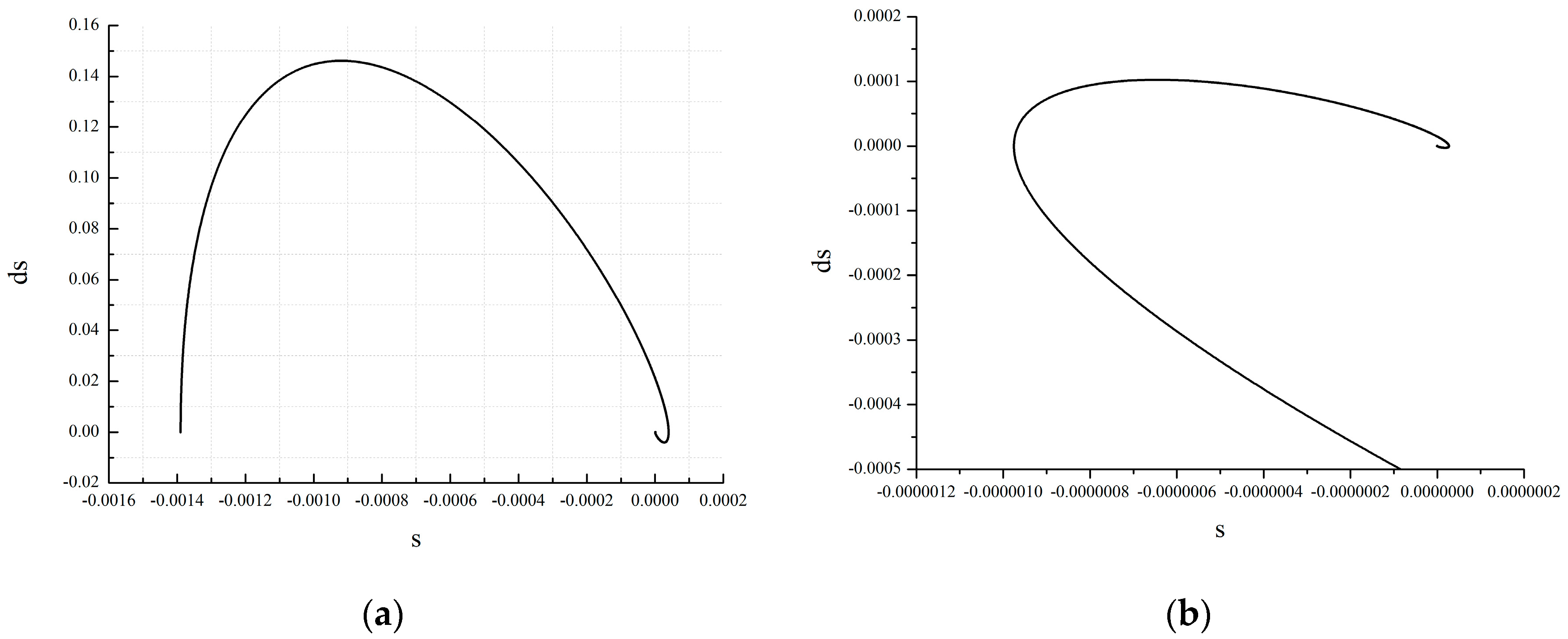
4.2. Comparison of Simulation Results

Both the exponential reaching law for sliding mode controller and the second-order sliding mode controller can realize the stability control of the AMB in Figure 4a. The rotor of the bearing quickly adjusted from the initial −1.4 mm to the fixed position and remained stable. The second-order sliding mode controller had 2.75% overshoot. Its stability time was 0.024 s, representing a 29.4% decrease when compared with the 0.034 s stability time of the exponential reaching law sliding mode control law. An enlarged view of the rotor position trajectory of 0.193–0.1936 s is shown in Figure 4b. It can be seen that in the final stable stage, the exponential reaching law for sliding mode controller had a chattering phenomenon. This was due to the fact that the first derivative of the sliding mode variable of the exponential reaching law did not converge in the reaching stage, and there was still a velocity across the sliding surface. The second-order sliding mode controller converged to the sliding surface, which can greatly reduce the chattering phenomenon.

Under the action of exponential reaching law for sliding mode controller, the phase trajectory of sliding mode variable s is shown in Figure 5a. Here, “ds” is the first derivative of sliding mode variable, i.e., $\dot{s}$. The initial speed of pure exponential reaching term $\dot{s}=-ks$ was very large in the process of reaching motion and gradually decreased, thus greatly shortening the system stability time, and the speed was not too fast when reaching the stable point. The constant reaching term $\dot{s}=-\epsilon \mathrm{sgn}\left(s\right)$ ensured that the velocity of the system near the sliding surface was not zero, and the system could converge in finite time. Therefore, in the final stable stage, the sliding mode variable s had high-frequency chattering, as shown in Figure 5b.

In Figure 6, “ds” is the first derivative of sliding mode variable, i.e., $\dot{s}$. It can be seen that the phase trajectory of sliding mode variable s converges smoothly to (0,0) point in Figure 6a; that is, the second-order sliding mode controller constrains the sliding mode variable s to the zero point while constraining the first-order variable $\dot{s}$ to the zero point. There was no chattering phenomenon during the rotor position adjustment of the AMB. This was because the design goal of the second-order sliding mode controller was to make the system converge to the sliding surface $S=\left\{x\in X|s=\dot{s}=\cdots s^{r-1}=0\right\}$. Therefore, the velocity of sliding mode variable converged to zero after the system was stable so that chattering could be eliminated while the output followed the given value.

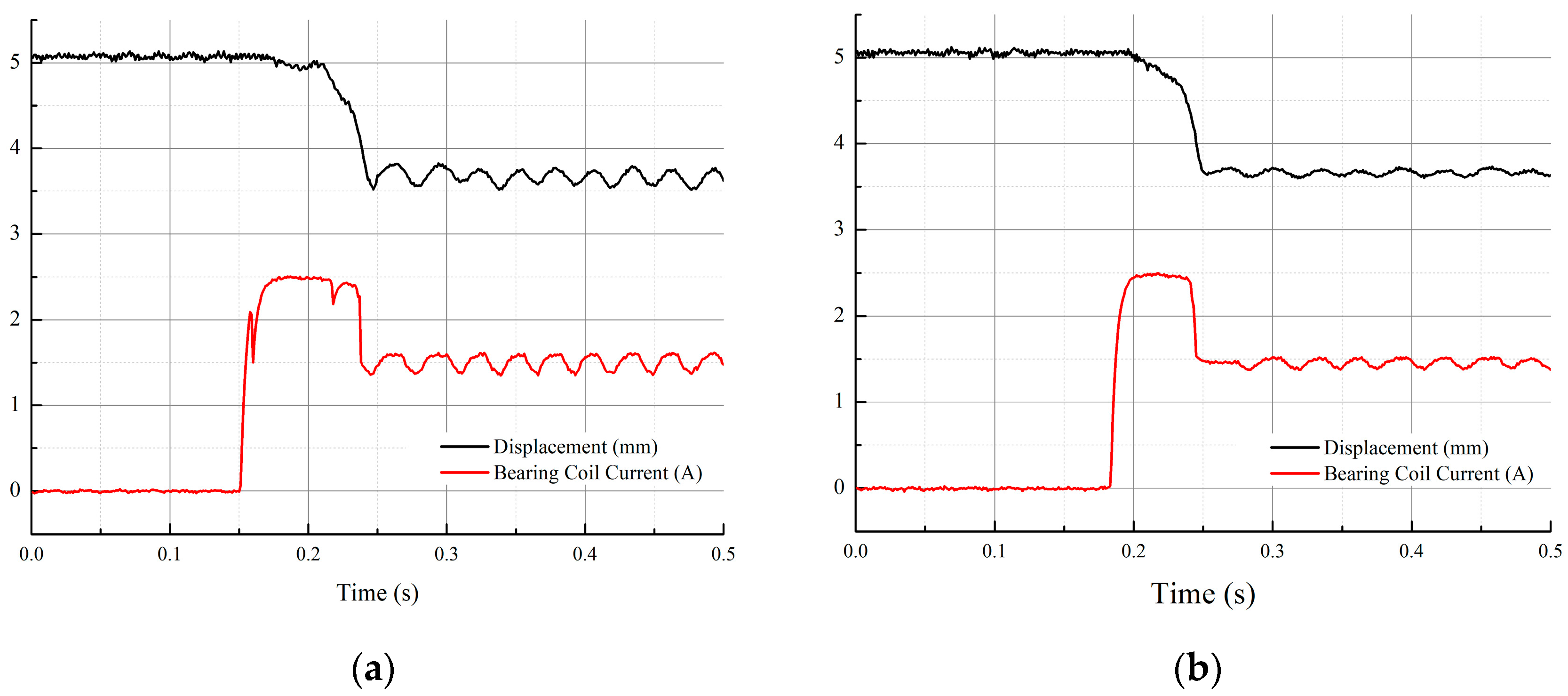
5. Experimental Verification

5.1. Establishment of Experimental Platform

The experimental platform of AMB control mainly included two parts: hardware system and software system. The hardware system consisted of AMB, displacement sensor, signal processing circuit, digital signal processor (DSP) controller, and switching power amplifier. The software system mainly refers to the programs running in the controller, including digital filter program, control algorithm program, and pulse-width modulation (PWM) output control program. The software system needs to sample the rotor position through the Active Directory (AD) interface of the controller and provide the switching signal of the power amplifier through the PWM output module to realize the stable operation of the AMB. In order to ensure the safe operation of the DSP controller, there was an optocoupler isolated driving link between the controller and the switching power amplifier. The experimental platform structure is shown in Figure 7.

The electromagnetic force of AMB is produced by the coil, and the output characteristic of electromagnetic force is determined by the output performance of power amplifier. The current in the coil on each side of AMB is controlled by a switching power amplifier. The structure of switching power amplifier is shown in Figure 8.

Here, U is DC power supply, S is MOSFET, and D is power diode; series resistor R and inductor L are used instead of coils.

When the S is on, the current flowing through the coil rises; when the S is turned off, the current on the coil is free-flowing through the power diode D. As the coil consumes energy, the current gradually decreases. The current on the coil can be controlled by the PWM control signal of the DSP controller.

In order to verify the control performance of the second-order sliding mode controller and exponential reaching law for sliding mode controller, the experimental hardware platform of the AMB control system was built. The hardware platform of the AMB and its controller are shown in Figure 9.

The voltage signal of the displacement sensor was filtered by the signal processing circuit and then sent to the DSP controller. The control algorithm was realized in the DSP controller. The switching signal of the switching power amplifier was generated by the PWM module of the DSP controller. In order to ensure the safe operation of the DSP controller, the optocoupler isolation circuit was used as the driver of the switching power amplifier.

5.2. Starting Process

When the AMB was powered on and started, it can be seen from Figure 10a that under the action of exponential reaching law for sliding mode controller, the current of coil rose to 2.5 A after being electrified, lasted for 0.1 s, and then gradually stabilized to 1.5 A. In the process of current rising, there was a big fluctuation. The voltage of the displacement sensor decreased from 2.5 V to about 1.64 V when the current of coil rose. Similarly, in Figure 10b, under the action of the second-order sliding mode controller, after the AMB was powered on, the current of the coil rose to the maximum value, about 2.5 A, lasted for about 0.05 s, and then gradually decreased to the stable state, about 1.5 A. At the same time, the voltage of the displacement sensor gradually dropped to about 1.65 V. In the whole starting process, the current fluctuation of the coil and the voltage fluctuation of the displacement sensor were less than those of the exponential reaching law for sliding mode controller.

5.3. Stable Stage

When the AMB was stable, the voltage signal of the horizontal X direction sensor was stable at about 1.8 V, while the vertical Y direction sensor was about 1.65 V under the action of exponential reaching law for sliding mode controller. According to the waveform of the steady-state displacement sensor in Figure 11b, the AMB could operate stably under the second-order sliding mode control; the sensor voltage in X direction was about 1.82 V, and that in Y direction was about 1.65 V. Moreover, the ripple size was obviously less than that seen for the exponential reaching law for sliding mode controller.

It can be seen in Figure 12a that the voltage variation range corresponding to the rotor axis trajectory under exponential reaching law for sliding mode control was basically limited to 0.24 V. As shown in Figure 12b, the fluctuation range of the shaft center trajectory under the second-order sliding mode control was obviously smaller than that of the exponential reaching law for sliding mode controller, and the voltage corresponding to the shaft orbit was limited to 0.14 V, which means that the rotor was more stable under the action of the second-order sliding mode controller.

The voltage of the displacement sensor was transformed into the actual position of the rotor, and the experimental results of the two controllers were compared. The designed second-order sliding mode controller could stabilize the AMB and was superior to the traditional exponential reaching law for sliding mode controller in terms of stability time and rotor position fluctuation, as shown in

Table 4. Comparison of experimental results.

Controller	Stabilization Time	Trajectory Range
Exponential Reaching Law	0.1 s	0.397 mm
Second-Order Sliding Mode	0.05 s	0.232 mm

.

6. Conclusions

In this paper, the second-order sliding mode controller was designed according to the magnetic bearing control model by introducing the second-order sliding mode control algorithm. The simulation analysis and experimental verification of the second-order sliding mode controller and exponential reaching law for sliding mode controller were carried out. The conclusions are as follows:

(1)

The simulation results show that the second-order sliding mode controller has no high-frequency chattering phenomenon in the stable stage of AMB. Finally, the velocity of the sliding mode variable converges to zero, and its phase trajectory converges to zero in spiral form.

(2)

The experimental results show that the second-order sliding mode controller can achieve the stability control of AMB, and compared with the exponential reaching law for sliding mode controller, the stability time of the magnetic bearing is shortened by 50%, and the axis trajectory range is reduced by 41.5%.

From the above, it can be concluded that the designed second-order sliding mode controller has a better control effect. The establishment of the proposed controller is based on the linearized model of the magnetic bearing near the balance position, and the performance of the AMB may not be in an optimal state when the working state of the AMB can be easily changed, such as in high-speed rotation or under heavy load impact.