1. Introduction
Sonic velocity and density logs provide direct in situ measurement of formation dynamic moduli and derived quantities. Given compressional-wave velocity, density, and measured or estimated shear-wave velocity, dynamic bulk, P-wave, Young’s and shear moduli and Poisson’s ratio can be directly calculated [
1]. With sufficient calibration, these dynamic moduli can potentially be used to estimate static moduli and, especially if anisotropy can also be quantified, they may be useful for hydraulic fracturing design in shale reservoirs [
2].
Dynamic bulk (
k) and shear (μ) moduli are determined directly from acoustic velocities and density by
and
while the P-wave modulus (
M) is simply
where V
p is compressional-wave velocity, V
s is shear-wave velocity, and ρ is rock bulk density. Of more direct interest in engineering applications are Poisson’s ratio, ν, and Young’s modulus,
E, given by
and
The ratio
k/μ is related to the V
p/V
s ratio by
There is a one-to-one relationship between Poisson’s ratio, the velocity ratio, and the bulk-to-shear moduli ratio. We can expect these ratios to be dependent on rock and fluid properties, such as porosity, mineralogy, total solid organic carbon (TOC), fluid compressibility, and effective pressure as well as factors less readily quantifiable from logs such as texture, pore, and inclusion shape, organic matter maturity, and degree of lithification/cementation.
As the velocities are measured at sonic frequencies with acoustic signals exhibiting small strain amplitudes, dynamic moduli are generally not equal to static (zero-frequency) elastic moduli [
3] but may provide useful indication of Young’s modulus and Poisson’s ratio variations along a borehole [
4] as well as estimation of formation brittleness [
5]. Empirical relations can be used to convert dynamic to static moduli [
6] but care must be taken to consider anisotropic and pressure effects when doing so [
7]. Deviations of these moduli from expectations, as evidenced on sonic compressional-wave and shear-wave sonic logs, may provide useful lithologic insights in formation evaluation [
8,
9,
10].
There are numerous other studies relating velocities and/or elastic moduli to rock properties in shale reservoirs (for example [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25]). Factors affecting velocities and moduli include, but are not limited to, mineral composition, porosity, solid organic volume, pore fluid content, properties and saturation, effective pressure, degree of lithification/cementation and organic maturity, structural arrangement and distribution of constituents, and pore and grain shape spectra. As a practical matter, there are generally too many unknowns to reliably predict velocities directly from rock properties and environmental conditions without local calibration. However, in conventional reservoirs and inorganic shales, it is well established that many rock properties and environmental factors, though directly having a strong effect on velocities and moduli, may have a reduced effect on relationships between velocities or moduli (see for example [
8,
26]). This enables shear-wave velocity prediction from given compressional-wave velocity and compositional volumetrics with good precision and accuracy without explicit consideration of all the factors affecting velocities listed above [
27]. In this paper, we have selected seven different shale reservoirs to empirically study, and generalize across a variety of formations, the factors controlling velocity and moduli relationships and to determine the most significant factors that cause variation in these relationships within and between formations. The objective is to arrive at more universal relationships that can be applied with good accuracy and precision without calibration by locality, formation, or degree of maturity.
2. Materials and Methods
As unconventional shale reservoirs are generally highly anisotropic [
28,
29] we here restrict our analysis to bedding normal velocities measured by sonic logs in vertical wells in formations with nearly horizontal dip. For wells or formations with different orientations, correction for anisotropy may be necessary.
Our objective is to develop an interpretive framework based on the relationships between dynamic moduli using empirical observation and regression analysis. We utilized a database consisting of full well-logging suites in single vertical pilot wells in seven different shale reservoirs including the Spraberry, Wolfcamp, Avalon, Woodford, Eagle Ford, Cline, and Bakken formations. The well logs included reliable compressional and shear-wave sonic logs and core-calibrated volumetric well log analyses (for further description of the quantitative well log analysis performed, see [
9]). These reservoirs have a wide range of rock and fluid properties as determined by volumetric well log analysis (summarized in
Figure 1,
Table 1 and
Table 2 for our dataset) yet similar relationships between compressional-wave velocity and shear-wave velocity (see
Figure 2 and
Table 3). The spread of the compositional variation by formation is indicated by the standard deviations around the mean compositions (
Table 1). Comparisons of well log volumetric analyses to core measurements for these formations are provided in prior papers [
9] and [
27] and in
Figure 3 for an interval in the Wolfcamp shale.
Table 4 shows that the V
p-V
s relationship (see
Figure 2) derived here from logs in organic shale reservoirs is close to trends from laboratory measurements for both dry organic and dry inorganic shales with low total organic content (TOC) reported in [
9]. Our dataset only samples these formations at one locality for each formation so is not meant to be representative of these formations over a wide geographic area. For our dataset, the Spraberry, Wolfcamp, Woodford, and Cline formations have similar composition and pore fluid (volatile oil). The Woodford is somewhat different in that it has no carbonate content and the lowest average porosity of all the formations. The dominant constituent of the Eagle Ford is calcite, and it is the only log in our dataset over a producing gas reservoir. The Bakken has the highest TOC and produces black oil. The Avalon has the highest average quartz content in the dataset.
We studied how variable composition impacts relationships between dynamic moduli by performing multivariate linear regression analysis and related statistical tests using the Microsoft™ EXCEL software product. The equations for statistical quantities used in this paper are provided in
Appendix A. Regressions were performed on various subsets including all wells combined, specific formations, and averages for each formation. To isolate controlling variables strictly within the shale reservoir rock while considering uncertainty in water saturation calculations, we excluded from our analysis datapoints with water saturations greater than 70% as well as low TOC intervals with weight percent of total organic content less than 1%. We also excluded datapoints within the logging tool spatial resolution of boundaries with non-reservoir layers. The resulting data spreadsheet we used to perform regressions is included in
supplementary materials Table S1.
3. Results
Given that density and compressional-wave velocity are often highly correlated [
32] the well-defined V
s − V
p relationships in
Figure 2 and
Table 3 suggest that, as V
p is a good predictor of V
s when shear sonic logs are not available [
27], dynamic elastic moduli should also be correlated. This correlation can be seen in
Figure 4 and
Figure 5 and
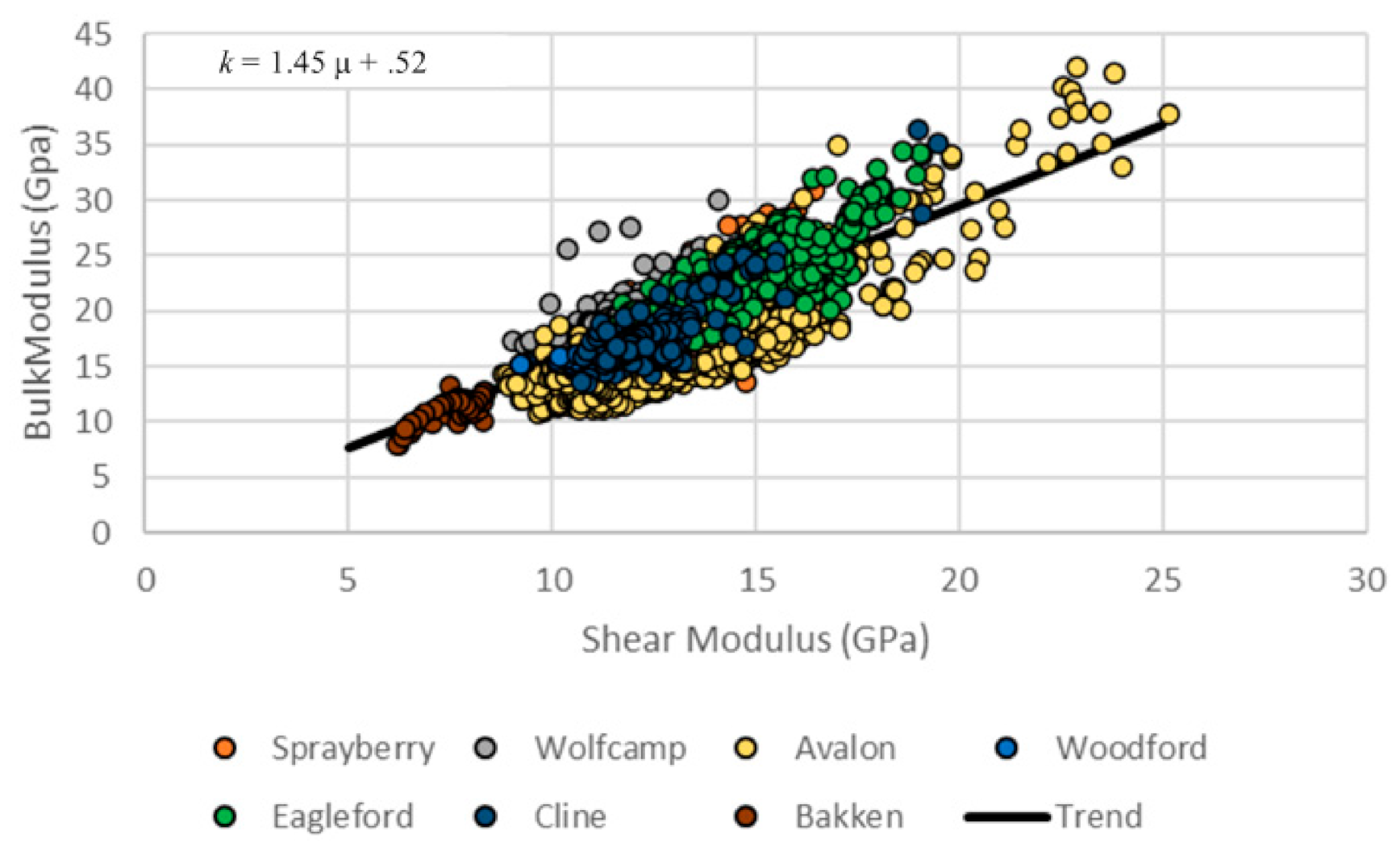
Table 5, where individual formations show similar but distinct relationships between dynamic bulk and shear moduli. In comparison to the velocity trends, which are for the most part similar and well defined, the dynamic elastic moduli trends exhibit more variation in slope and intercept, lower correlation coefficients, and greater prediction error. This may be due to the less well-defined relationship between velocities and densities that may introduce variability into the modulus trends.
To predict shear modulus when only compressional wave-velocity and density are logged, bivariate regression for shear modulus (see
Figure 6) gives
where velocity is given in km/s, density is in gm/cc, shear modulus is in GPa, and ρV
p2 is the P-wave modulus
M. The tighter fit and higher correlation than that obtained for the bulk modulus relation can be attributed in part to the greater range of P-wave modulus values.
A dominant factor determining the
k-μ or
M-μ relationships (and perhaps more importantly deviations from a single relationship for a formation in a specific locality) is the mineralogical composition. The relationships in
Table 5 are dependent to a large extent on the average composition of the formation at the well location.
The compositional dependence can be summarized statistically for the entire dataset via linear multiple regression. We regressed moduli against all lithologic parameters including mineral composition, TOC (total organic carbon), porosity, and fluid modulus, saturations, and bulk volumes. Of note, in our dataset we found no statistically significant relationship between observed bulk modulus or P-wave modulus and fluid properties. This can be explained by the exclusion of water saturations above 70%, as within reservoir rock containing hydrocarbons the variation of moduli with water saturation is small compared to the difference in moduli between fully-water saturated and partially water-saturated shales [
9].
A small improvement over Equation (7) in prediction of shear-modulus can be achieved by accounting for the compositional dependence. Multiple regression in units of GPa and decimal volume fraction yields
where, X
TOC is the volume fraction of organic matter converted from weight percent TOC using the Vernik [
30] method, X
CLAY is the volume fraction of clay minerals from log analysis as described in [
9], and X
CARB is also derived from volumetric log analysis and taken as the sum of carbonate volume fractions (calcite and dolomite) plus the volume fraction of pyrite which was too small in number or range to stand alone as a regression variable and therefore lumped with carbonates due to its high density. The correlation coefficient for the regression is 0.95 and the standard error of the predicted shear modulus is 0.77. The regression is highly significant with an F of 4424 and a sig F of 0.
Equation (8) indicates that for a given P-wave modulus, increasing TOC increases the shear modulus (corresponding to a reduced
M/μ and thus reduced V
p/V
s ratio) and the shear modulus decreases with increasing clay or carbonate content at a given P-wave modulus (corresponding to in increased
M/μ and V
p/V
s ratio). As discussed in [
9], the effects of fluid hydrocarbons and TOC are intimately intertwined and difficult to separate. To first order, those effects are apparently combined in the TOC effect evident in Equation (8).
Predicting moduli from volumetric analysis alone (without dynamic P-wave modulus as input) as a function of depth is more challenging as the P-wave modulus implicitly contains and accounts for local variation in factors such as porosity, pore shape, effective pressure, and degree of lithification. The best statistically significant correlations we could find were on the order of 0.8 for shear modulus and 0.85 for bulk modulus. We do not report those relationships here as they can be easily misapplied as they would be highly locality and formation dependent. We did, however, wish to investigate the compositional dependence of average formation properties. Perhaps surprisingly, when weighting all shale reservoir formations equally, we found excellent (and the most statistically significant) results for average formation properties using only TOC and clay volume fractions. For bulk modulus, the regression fit for average formation properties and weighting all formations equally in units of GPa and decimal volume fraction is
The correlation coefficient is a remarkable 0.99 with an F statistic (ratio of explained to unexplained variance) of 68.7, and the significance of F (probability that the correlation is spurious by random chance) being less than 0.001. The standard error in the predicted average bulk modulus is 0.75 GPa. Increasing organic content or volume of clay both decrease the bulk modulus with the dependence on TOC being about 3 times stronger. Neither porosity, carbonate content, nor fluid properties improved the regression, which is surprising given that these factors have a clear effect on compressibility. We hypothesize that this is due to the non-independence of variables such that the effects of mineral composition, porosity, and fluid properties are intertwined with average volume fractions of TOC and clay; these two compositional variables are consequently sufficient to establish a correlation between average observations and predictions that would be difficult to improve upon. The insensitivity to fluids is not contrary to the findings in [
9] which noted the difference in bulk modulus between fully-brine saturated shales and reservoir shales with appreciable fluid hydrocarbons; the difference being that in the data presented here we have excluded all water saturations above 70%. The lack of dependence on carbonate content may be in part fortuitous, as in our dataset the single formation with anomalously large volume fraction of carbonate is also the only formation that produces gas, and these factors may cancel out. However, we would not expect such cancellation to occur for average formation shear modulus (which should be insensitive to pore fluid modulus) where, the same compositional variables are dominant (in units of GPa and decimal volume fraction)
The regression yields a dependence of shear modulus with X
TOC that is no longer linear but rather varies with the square of TOC volume fraction. The regression prediction for average formation properties has a correlation coefficient of 0.93 with an F of 12 and a significance of F of 0.02. The standard error is 1 GPa. The correlation is not quite as good as in predicting bulk modulus from these same variables and there is a 2% probability that the correlation can be caused by random chance. Nevertheless, this is an acceptable result in relating shear modulus to compositional variables with the error being tolerable for many applications (see for example [
30] and [
33]) and Equations (9) and (10) are best used as an indication of the systematics of variation of moduli with composition, rather than for prediction of absolute moduli.
The cross-plot of measured versus predicted average formation moduli (
Figure 7) using Equations (9) and (10) shows some slight bias in some of the formations; suggesting that local recalibration is likely to be helpful, especially for different localities or formations. Given the other factors mentioned previously affecting moduli that are not accounted for in Equations (9) and (10) it is highly unlikely that these relations will hold far beyond the points of calibration or with very different rock properties or environmental conditions. We must emphasize that Equations (9) and (10) are intended to show relative changes in modulus that might be expected with a given change in composition rather than for the purpose of predicting moduli in absolute terms without local calibration. These trends are not expected to be universal; rather Equations (7) and (8) using the P-wave modulus should be used for predictive purposes.
Given that compressional-wave velocity is an excellent predictor of shear-wave velocity one might find it surprising that using the bulk modulus to predict shear modulus does not improve prediction of average reservoir properties. This is explained by the fact that, being so well related to volumes of organic carbon and clay via Equation (9), negligible additional information is provided by explicitly including the average bulk modulus. Consequently, including average bulk modulus as a regression variable reduces the statistical significance of the prediction of average shear modulus. As average bulk modulus is linear with XTOC and average shear modulus is non-linear, we expect the ratio of average bulk and shear moduli (and the derived Poisson’s ratio) to also vary non-linearly with total organic content.
The other dynamic elastic moduli of interest (assuming first order isotropy) can be computed directly from bulk and shear moduli using
for Young’s modulus (E), and
for Poisson’s ratio (ν). Error propagation through Equations (11) and (12) was tested by adding 10% zero-mean random white noise to all the measured dynamic bulk and shear moduli in our dataset, resulting in less than 3% standard error for Young’s modulus and 5% standard error for Poisson’s ratio.
Combining Equations (9) and (10) with (11) and (12) allows computation of Young’s modulus and Poisson’s ratio as a function of fractional organic and clay volumes (
Figure 8 and
Figure 9) as an indication of relative changes. In these plots, we have restricted the maximum X
TOC to 0.2 so as not to extrapolate the results far from the average formation properties of the entire dataset.
In agreement with laboratory measurements [
7], Young’s modulus decreases monotonically with increasing volume fractions of clay or organic matter (
Figure 8). At a given organic volume fraction, increasing the clay volume fraction from 0% to 50%, drops the Young’s modulus almost in half. The absolute change in Young’s modulus with organic matter volume is virtually independent of clay volume. As a result, for higher clay volumes the percent change in Young’s modulus with organic matter is much greater than for low clay volumes. Poisson’s ratio increases with clay volume fraction and decreases with TOC (
Figure 9) although the percent change is much smaller for Poisson’s ratio than for Young’s modulus. The magnitude of the increase in Poisson’s ratio with clay volume fraction is reduced at higher TOC where Poisson’s ratio becomes relatively insensitive to changing TOC as the curves flatten out.
Using these same equations and varying clay volume fraction from 0 to 0.7, the cross-plot of Poisson’s ratio versus Young’s modulus for lines of constant TOC volume (
Figure 10) shows that (1) the variation in Young’s modulus is much greater than that for Poisson’s ratio and (2) Young’s modulus and Poisson’s ratio both decrease with increasing TOC. For reservoir rocks with high Young’s modulus and low clay content, the relationship between Young’s modulus and Poisson’s ratio at a given TOC is almost linear.
4. Discussion
The effect of fluids (or lack thereof) is conceptually easy to understand and, to first order at least, behaves in the way physical equations suggest in shale reservoirs [
9]. Ignoring geological diagenesis and geochemical effects, the mechanics of Biot-Gassman theory [
34,
35] tells us that for a given rock frame compressibility, the more compressible the fluid, the more compressible the fluid saturated rock. Thus, all else being equal, a gas-saturated rock should have a lower
k/μ ratio than a light oil-saturated rock with high gas–oil-ratio (GOR), which in turn should have a lower
k/μ ratio than a black oil reservoir with low GOR. It is also generally accepted [
36] that Gassmann’s equations are applicable at sonic frequencies in permeable sandstones. Within the context of his assumptions, Gassmann [
35] proves that shear modulus should be unaffected by the pore fluid compressibility. This may not be entirely true if non-spherical pores are acoustically disconnected and pressures cannot equilibrate, but we will accept this as a working hypothesis with the assumption that, if the hydrocarbons are indeed flowable, then there is pressure communication between pores and Gassmann’s equations apply. It has also been shown [
37] that if similar low-aspect ratio pores are aligned, as one might expect them to be for the most part in shales, that Gassmann’s equations, which are the low frequency limit of the more general Biot theory, are applicable and shear modulus is mechanically independent of fluid compressibility. This is because the pores deform to the same degree for a given applied stress and pressure equilibration between pores is achieved without requiring actual fluid communication. In organic shales, [
9] reported bulk modulus variation with fluid saturation from fully brine-saturated to hydrocarbon saturated, but no such dependency for shear modulus. The effect of pore fluids on a
k versus μ cross-plot, should then be entirely on
k while leaving μ unchanged. This would of course change the
k versus μ relationship. However, regressions (9) and (10) for data entirely within hydrocarbon saturated reservoir rocks show no dependency of either bulk modulus or shear modulus with fluid properties and saturations. The change in bulk modulus from hydrocarbons saturated to fully brine-saturated, should be generally larger than the change in bulk modulus as hydrocarbon saturation varies within a reservoir. As we have excluded datapoints with brine-saturations greater than 70% from regression analysis, the fluid effect on rock bulk modulus as saturation varies should be small. In addition, the effects of interrelated parameters such as pore fluid saturation and TOC are not readily separated by multiple linear regression in these data and may mask any small fluid modulus effect. Controlled laboratory experiments, though difficult to perform in shales, are needed to separate the direct effect of varying fluid modulus from that of solid organic matter volume fraction.
Equations (7) and (8), both using the dynamic P-wave modulus, are the most promising for prediction of the variation of bedding normal dynamic shear modulus throughout a reservoir with limited information, and for application without local calibration. To apply Equation (7), only compressional-wave sonic and density logs are required. Equation (8) requires these and volumetric well log analysis compositions. Starting with P-wave modulus to predict shear modulus yields more universal relations because factors such as porosity, pore fluid content, effective pressure, degree of lithification and cementation, thermal maturity, pore and grain shape distribution, and structural arrangement and distribution of constituents are all reflected to some degree in the P-wave modulus. Within reservoir rock they do not apparently change the relationships between P-wave modulus and shear modulus to the extent that compositional variables do. The most important compositional variables are fractional volumes of solid organic matter, clay, and carbonates. As fractional volumes sum to one, the fractional quartz volume is reflected in the other constituent volumes and can be thought of as the background giving the regression intercept which is modified by the other compositions.
Figure 11 compares observed versus predicted shear moduli using P-wave modulus alone (Equation (7)) and using modulus and composition (Equation (8)). A perfect prediction would have a regression trendline between observation and prediction along the diagonal with a slope of 1 and an intercept of 0. Using P-wave modulus alone (
Figure 11a) gives a trendline slope of 0.85, an intercept of nearly 2 GPa, and a squared correlation coefficient (R
2) of 0.85; a good prediction with slope and intercept not far from unity and zero, but suggesting bias manifesting as an underestimation of large shear moduli and overestimation of small moduli. Adding compositional information with Equation (8) improves R
2 to 0.88 with slope of 0.95 and intercept of −0.16 indicating less bias.
The fact that a regression equation yields on average accurate predictions of shear modulus for all the calibration data across all included formations does not mean that the depth-by-depth prediction of shear modulus will be acceptable over a given logged interval. This becomes important in intervals where compositions deviate significantly from the average composition in the calibration dataset. For example,
Figure 12 shows the observed dynamic shear modulus log in an interval of the Spraberry formation. The predicted shear modulus using only P-wave modulus is clearly overestimated in the intervals of lower shear modulus while the prediction incorporating compositional information is generally better.
We performed out-of-sample validation on measurements available in the literature to test the applicability of Equations (7) and (8) in different localities, different formations, and with different measurement methods (laboratory versus log). Unfortunately, tabulated moduli and compositions are not common, so in some cases we had to read values from logs or take averages to get representative values. Compositions on lab samples are also problematical because those reported are not necessarily for the same piece of rock the measurements are made on.
Table 6 lists the samples we use for validation.
Figure 13 shows that moduli predicted for these samples using Equations (7) and (8) have standard error of around 1.5 GPa, an acceptable result especially given the variety of unknowns associated with using measurements from other sources that may result in inconsistencies. For example, the laboratory measurements were made on dry samples rather than under in situ conditions, and log compositional analysis can be variable depending on how constituents are defined or lumped. In log analysis, it is not uncommon for there to be inconsistencies in the definition of clay volume or in how feldspars of various kinds are handled. Considering these uncertainties and the small sample size for this test we do not judge the difference in standard error between the methods to be significant. The good correlation (R
2 = 0.95) between predicted and observed moduli for both Equations (7) and (8) suggests that the use of P-wave modulus is robust without local calibration.
5. Conclusions
We performed linear regression of sonic log compressional and shear-wave bedding normal velocities in single vertical wells from each of seven different unconventional shale reservoirs: the Spraberry, Wolfcamp, Avalon, Woodford, Eagle Ford, Cline, and Bakken formations.
Overall, and in each of these formations, relationships between compressional and shear-wave velocities are well defined. Compressional-wave velocity is an excellent predictor of shear-wave velocity with a correlation coefficient of 0.9 and a mean absolute error of 2.9% when using a single equation for all seven reservoirs; when regressing individually for each reservoir the mean absolute error is 1.7%.
Combined with a bulk density log, these velocities can be used to compute dynamic elastic moduli logs including bulk, shear, and Young’s moduli and Poisson’s ratio.
Using measured dynamic P-wave modulus to predict shear modulus results in a high correlation coefficient (0.92) with a standard prediction error of 0.92 GPa. Adding compositional variables to the regression improves the correlation coefficient to 0.95 and reduces the standard error to 0.77 GPa. Both regressions have high statistical significance with virtually nil probability of the correlations being spurious.
Using bulk modulus alone as a predictor of shear modulus and a single linear regression equation for all formations resulted in only a modest correlation (0.78) and relatively large error between measurements and predictions of nearly 3 GPa. The error can be improved using formation specific equations or regressing against volumetric compositional variables; the two most important being fractional volume of organic matter and volume of clay in that order.
While average formation bulk modulus was found to be linearly related to volume faction of TOC, average formation shear modulus is better predicted using the square of the volume fraction of TOC. Using a single regression equation and only compositional variables for all formations, standard prediction error was 1 GPa for average formation shear modulus and 0.75 GPa for bulk modulus. The regressions indicate that both Young’s modulus and Poisson’s ratio decrease with increasing TOC while increasing clay volume decreases Young’s modulus and increases Poisson’s ratio. Including other variables in the modulus regressions such as porosity, carbonate content, and fluid properties, and saturations did not improve the predictions appreciably and resulted in reduced statistical measures of significance. However, it is unlikely that regressions containing only compositional variables alone will remain valid outside of the calibration dataset due to variations in factors such as porosity, effective stress, fluid content, degree of lithification, and hydrocarbon maturity. Predictions using the plane-wave modulus, with or without compositional information, promise to be more universally applicable.