VPSO-SVM-Based Open-Circuit Faults Diagnosis of Five-Phase Marine Current Generator Sets
Abstract
:1. Introduction
1.1. Research Background and Motivations
- (1)
- When machine power and phase current are kept constant, increasing phase number of the machine can reduce phase voltage, resulting in large power output with lower voltage level. This can also avoid the current-sharing problem caused by power electronic devices in series and parallel connections [7].
- (2)
- An MPM can provide more control freedom than a three-phase machine; fault-tolerant operation could be achieved in an MPM if one or more phase is in fault conditions [8].
- (3)
- Compared to a traditional three-phase machine, the dynamic and static characteristics of an MPM are improved [9], making it more suitable for sustainable energy generation systems.
1.2. State of the Art of Marine Current Generation and Its Fault Detection and Diagnosis (FDD)
1.3. Organization of This Article
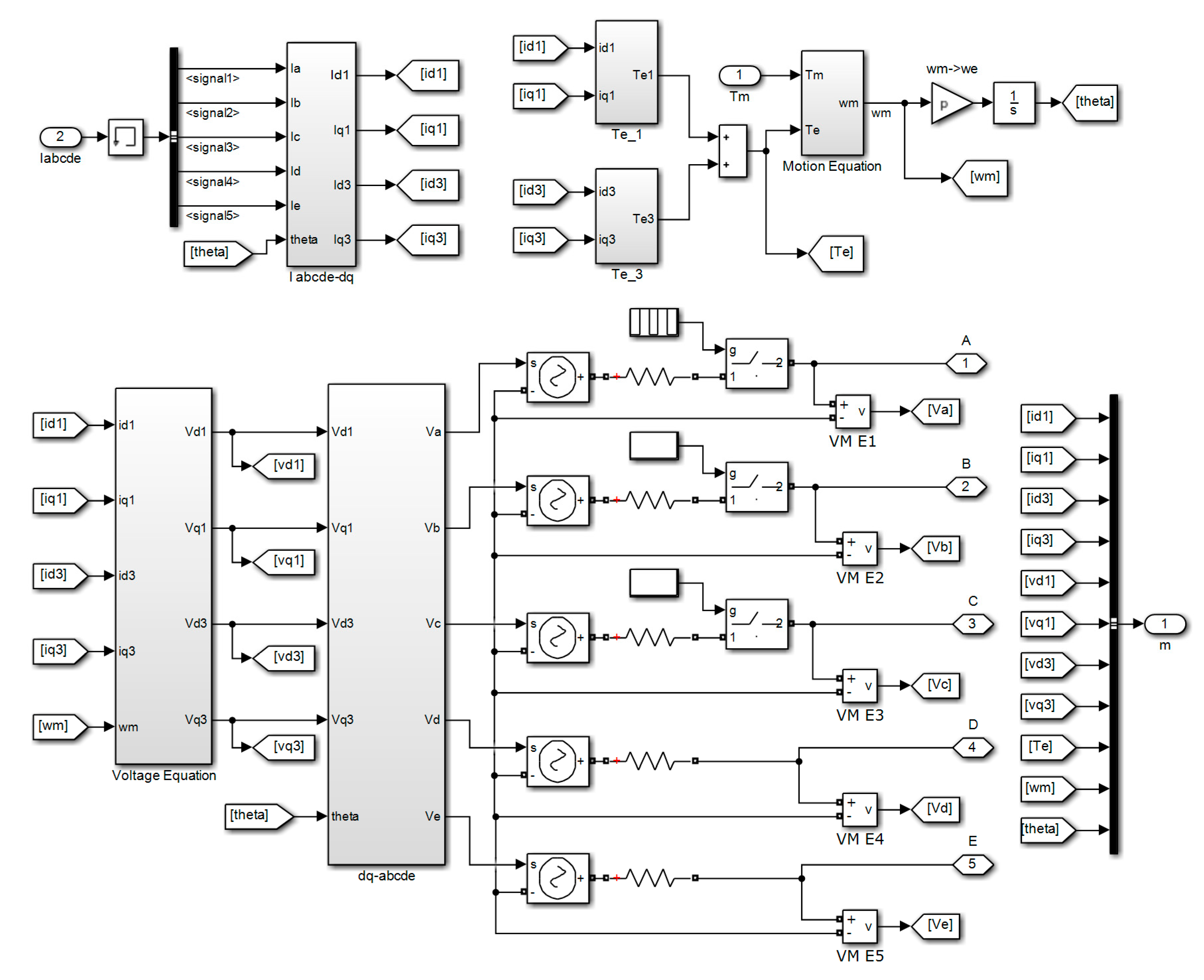
2. Mathematical Models of Five-Phase Permanent Magnet Synchronous Generator (FP-PMSG)-Based Marine Current Generator Set (MCGS)
2.1. MCGS Structure
2.2. Hydro Turbine Model
2.2.1. Tidal Speed Model
2.2.2. Hydro Turbine Model
2.3. Model of Non-Salient FP-PMSG with Third Harmonic Windings (THWs)
3. Faults Detection and Diagnosis of FP-PMSG
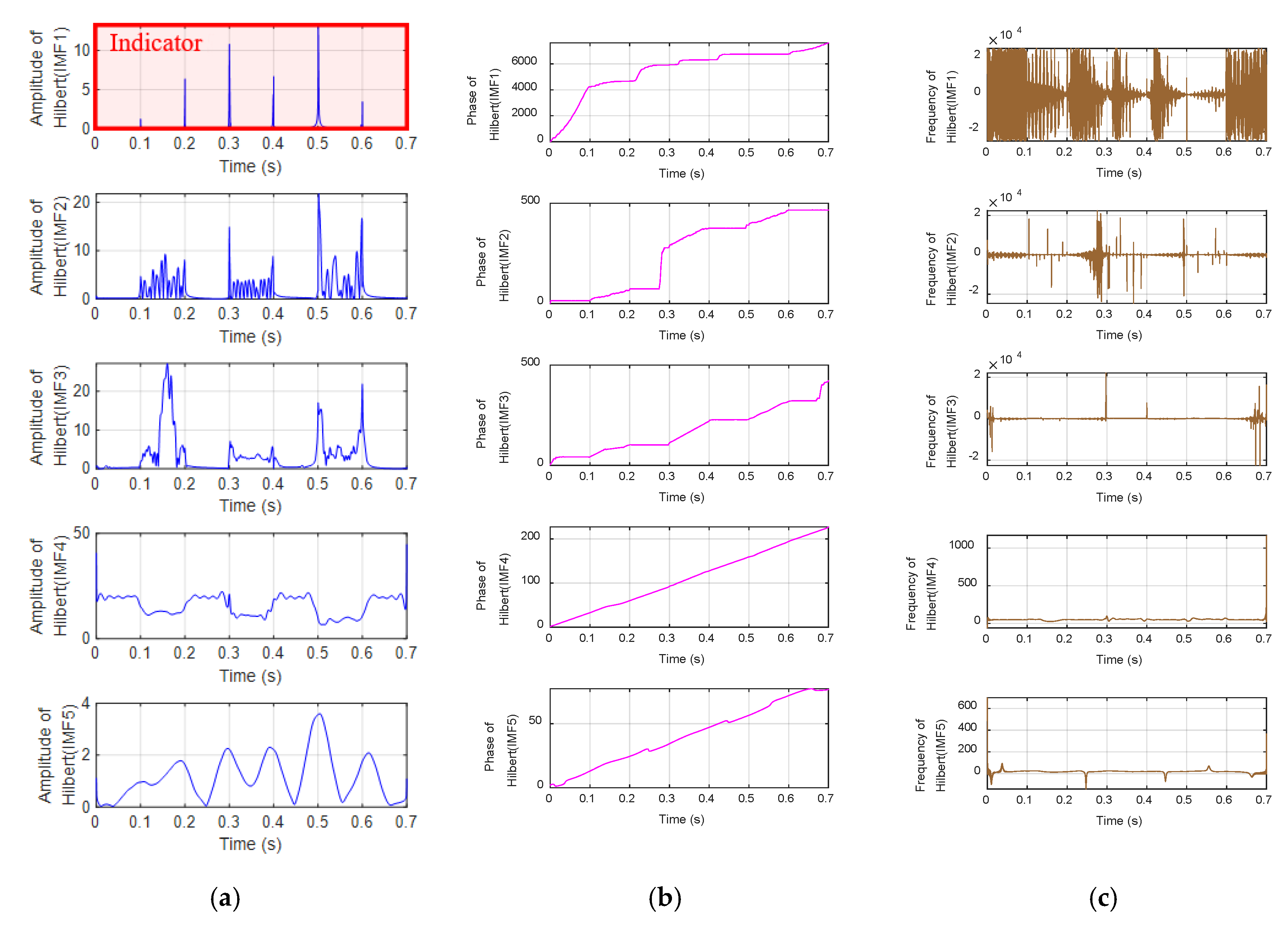
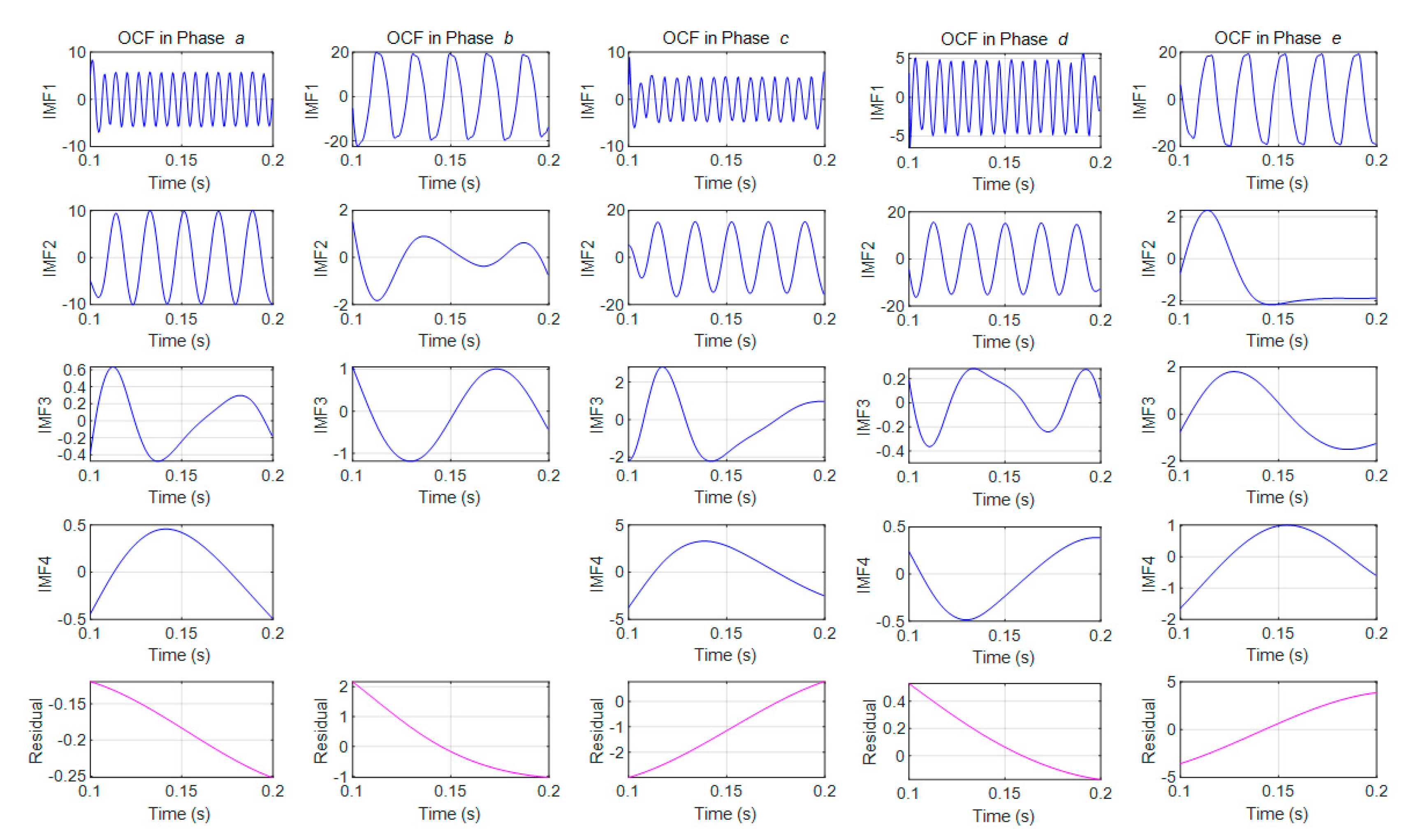
3.1. Empirical Mode Decomposition (EMD)-Hilbert Based Fault Detection and Fault Feature Parameters Extraction
3.2. Support Vector Machine (SVM)-Based Fault Classification
3.3. Variable-Parameter Particle Swarm Optimization (VPSO) for SVM Parameters Optimation
3.4. Working Flow of VPSO-SVM-Based Fault Diagnosis
4. Simulations and Results Analysis
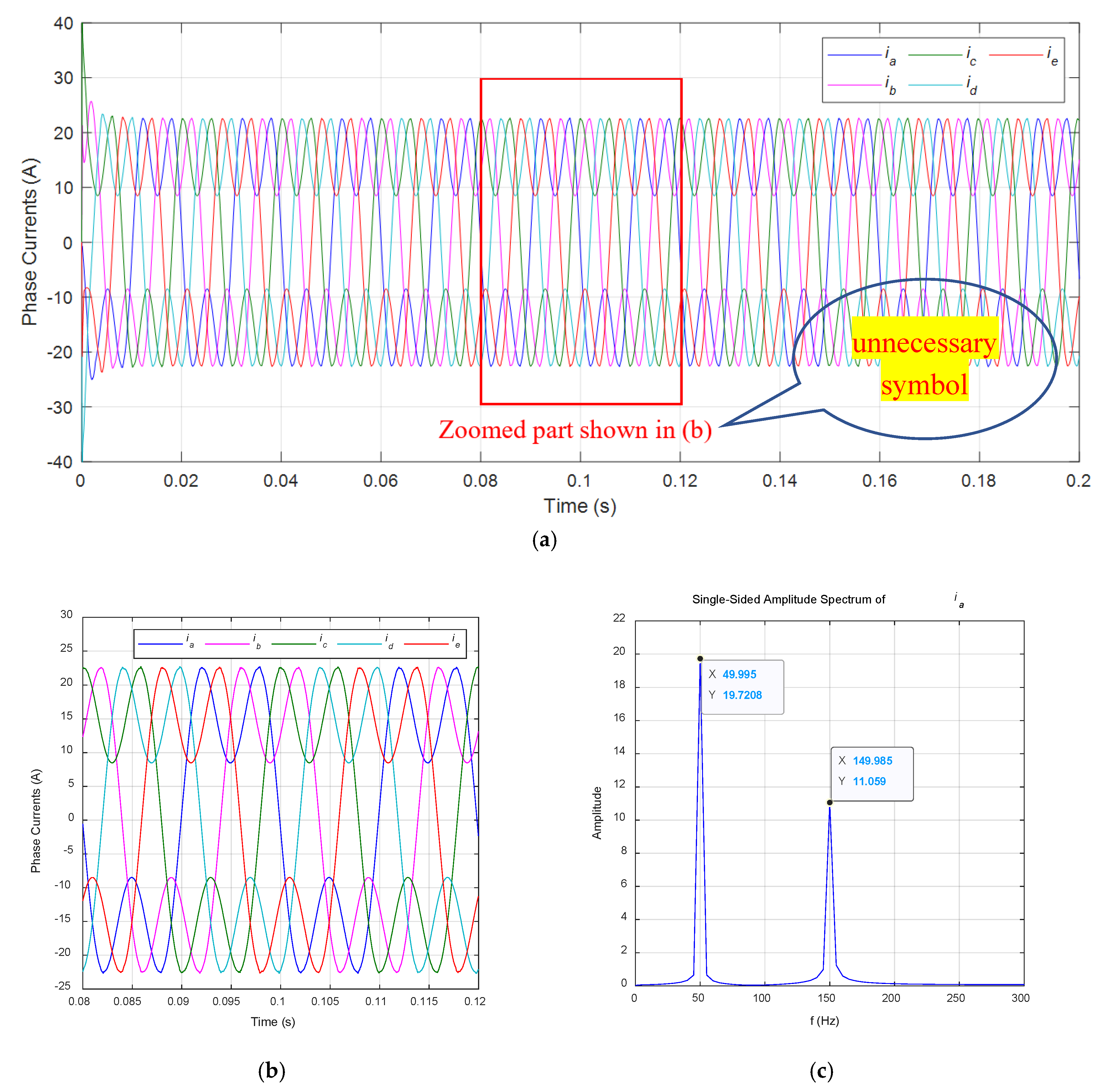
4.1. MCGS Simulation with No Faults
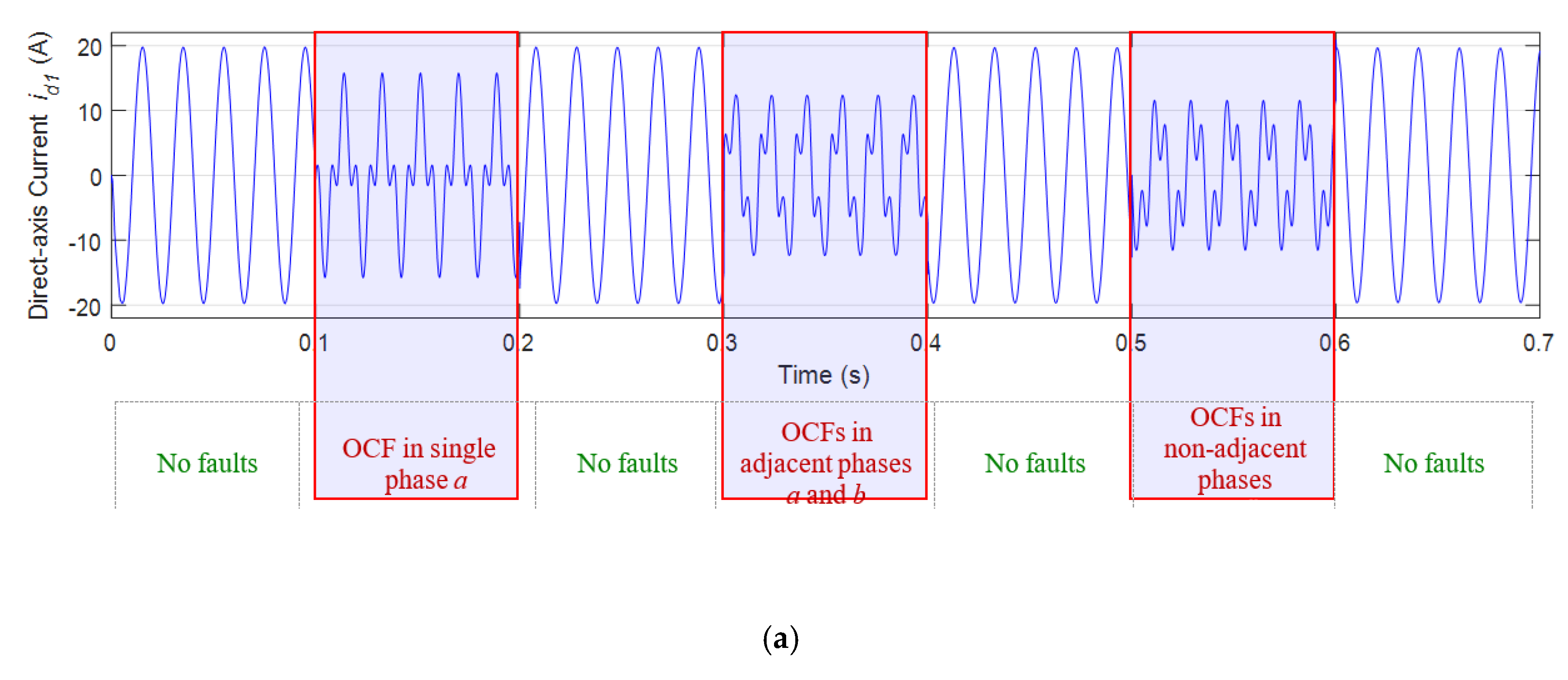
4.2. FP-PMSG Open-Circuit Faults (OCFs) Detection Simulations
- (1)
- single-phase OCFs, for example OCFs in phase a.
- (2)
- OCFs in two adjacent phases, for example OCFs concurrently in phase a and b.
- (3)
- OCFs in two non-adjacent phases, for example OCFs concurrently in phase a and c.
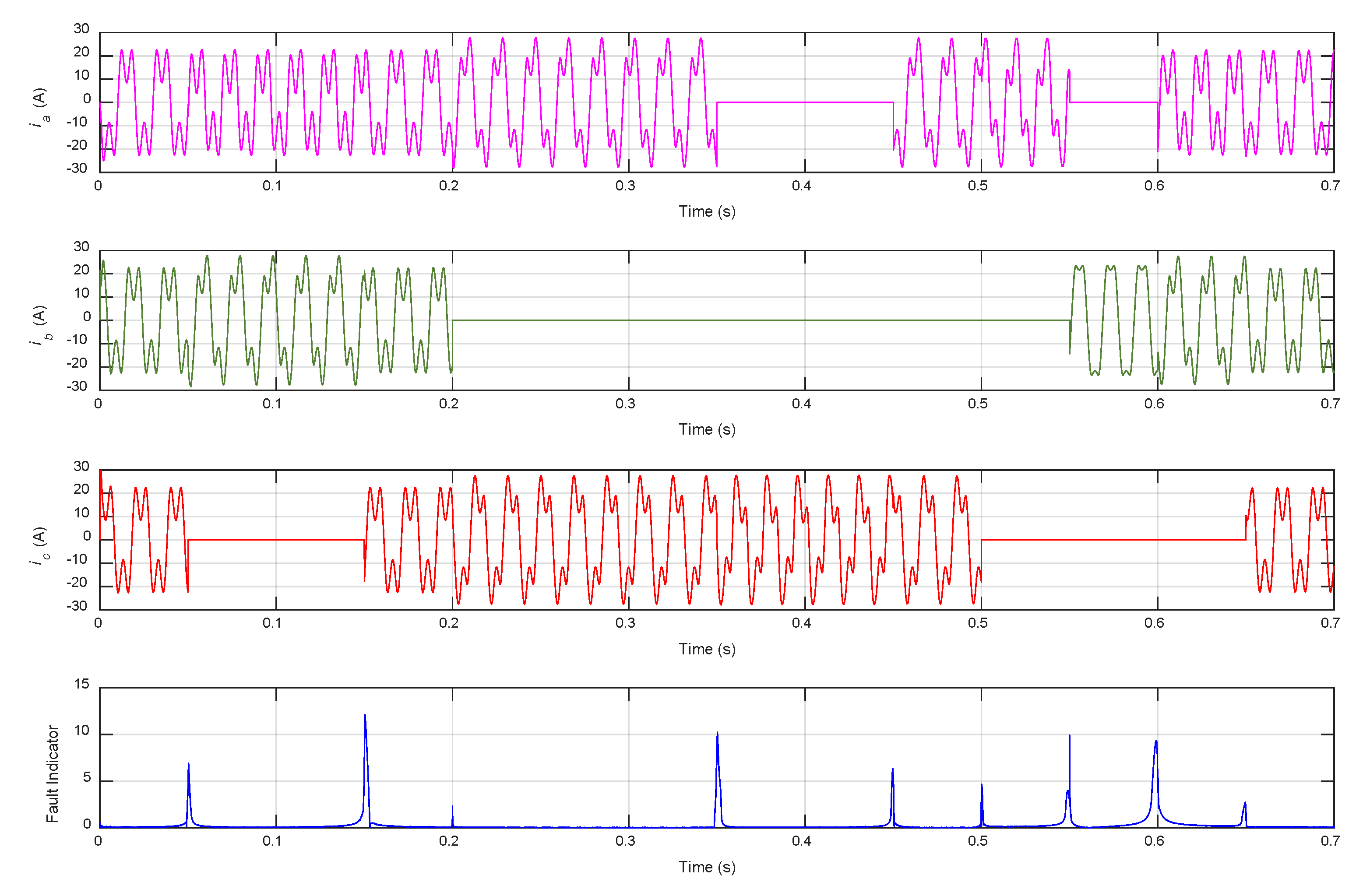
- (1)
- during the first 0.1 s of the simulation, the MCGS was running normally;
- (2)
- at 0.1 s, an OCF happened in single-phase a and was revoked at 0.2 s;
- (3)
- the MCGS was running in normal condition from 0.2 s to 0.3 s;
- (4)
- at 0.3 s, OCFs simultaneously happened in two adjacent phases a and b, and the faults were both removed at 0.4 s;
- (5)
- the MCGS was running in normal condition from 0.4 s to 0.5 s;
- (6)
- at 0.5 s, OCFs happened again concurrently in two non-adjacent phases a and c, and the faults were both revoked at 0.6 s;
- (7)
- from 0.6 s to 0.7 s, the MCGS operated with no faults.
- (1)
- during the four intervals when there were no faults (namely intervals of 0–0.1 s, 0.2–0.3 s, 0.4–0.5 s and 0.5–0.6 s), the currents of five phases had same amplitudes with peak values of 22.67 A.
- (2)
- From 0.1 s to 0.2 s, when an OCF happened in single-phase a, its current became zero, meanwhile, the currents of its two adjacent phases, b and e, increased with peak values of 27.55 A and 27.83 A, respectively. The currents of phases c and d had no obvious increments.
- (3)
- From 0.3 s to 0.4 s, when OCFs happened in two adjacent phases a and b, their currents both became zero, at the same time, the currents of its two adjacent phases, c and e, increased and reached peak values of 27.88 A and 27.78 A, respectively. The current peak value of phase d decreased to 19.74 A.
- (4)
- From 0.5 s to 0.6 s, when OCFs happened in two non-adjacent phases a and c, their currents both became zero, the current peak value of phase b decreased to 23.63 A and phases d and e increased to 25.88 A and 26.01 A, respectively.
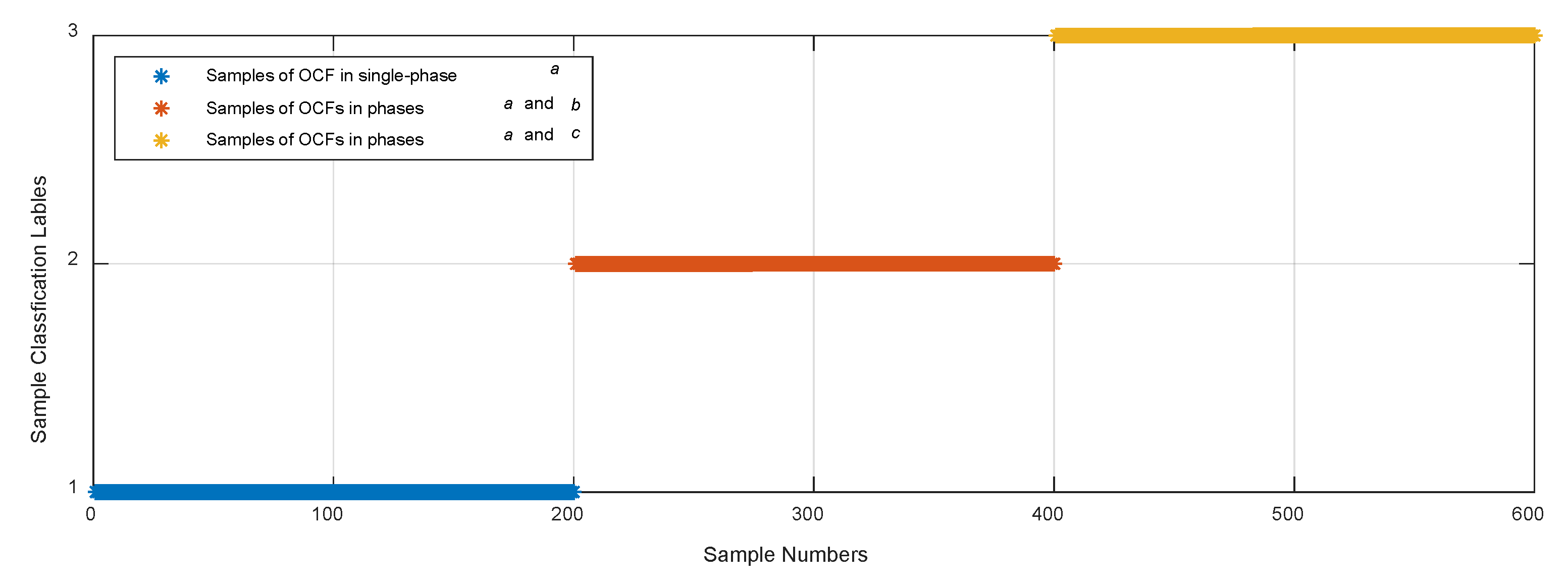
4.3. Three Different FP-PMSG OCFs Diagnosis Simulations and Results Comparison
- -
- Label “1” is for OCF in the single-phase a,
- -
- Label “2” is for OCFs in both phase a and b,
- -
- Label “3” is for OCFs in phase a and c.
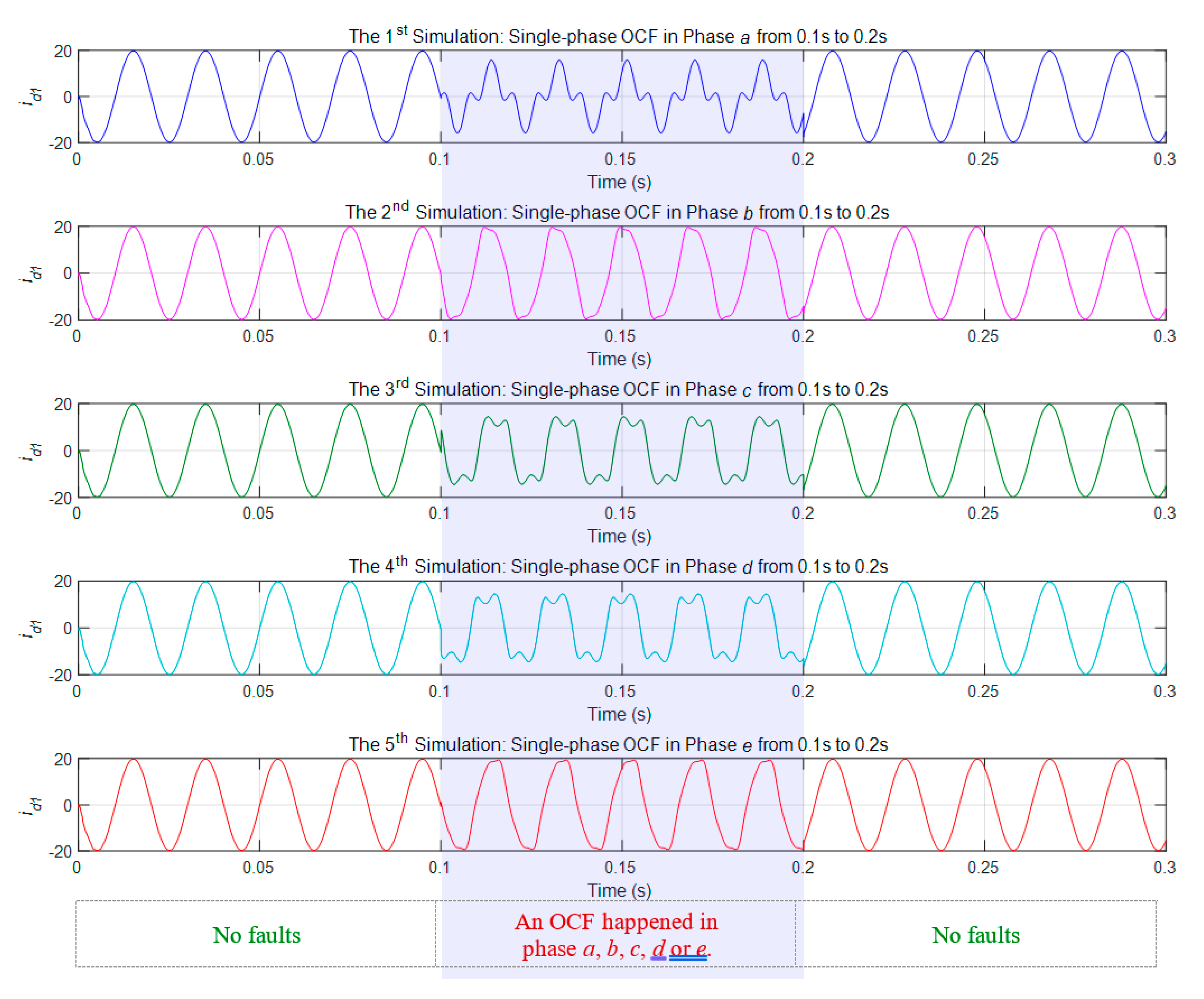
4.4. Faulty Phase Diagnosis Simulations of Single-Phase OCFs and Results Comparison
- (1)
- in the 1st simulation, from 0 to 0.1 s and from 0.2 to 0.3 s, the MCGS was running normally, while from 0.1 to 0.2 s, a single-phase OCF happened in phase a;
- (2)
- in the 2nd simulation, from 0 to 0.1 s and from 0.2 to 0.3 s, the MCGS was running normally, while from 0.1 to 0.2 s, a single-phase OCF happened in phase b;
- (3)
- in the 3rd simulation, from 0 to 0.1 s and from 0.2 to 0.3 s, the MCGS was running normally, while from 0.1 to 0.2 s, a single-phase OCF happened in phase c;
- (4)
- in the 4th simulation, from 0 to 0.1 s and from 0.2 to 0.3 s, the MCGS was running normally, while from 0.1 to 0.2 s, a single-phase OCF happened in phase d;
- (5)
- in the 5th simulation, from 0 to 0.1 s and from 0.2 to 0.3 s, the MCGS was running normally, while from 0.1 to 0.2 s, a single-phase OCF happened in phase e.
- -
- Label “1” is for single-phase OCF in phase a,
- -
- Label “2” is for single-phase OCF in phase b,
- -
- Label “3” is for single-phase OCF in phase c,
- -
- Label “4” is for single-phase OCF in phase d,
- -
- Label “5” is for single-phase OCF in phase e.
5. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Djebarri, S.; Charpentier, J.F.; Scuiller, F.; Benbouzid, M. Design and Performance Analysis of Double Stator Axial Flux PM Generator for Rim Driven Marine Current Turbines. IEEE J. Ocean. Eng. 2016, 41, 50–66. [Google Scholar] [CrossRef] [Green Version]
- Elghali, S.E.B.; Balme, R.; Le Saux, K.; Benbouzid, M.E.H.; Charpentier, J.F.; Hauville, F. A Simulation Model for the Evaluation of the Electrical Power Potential Harnessed by a Marine Current Turbine. IEEE J. Ocean. Eng. 2007, 32, 786–797. [Google Scholar] [CrossRef]
- Khan, M.J.; Iqbal, M.T.; Quaicoe, J.E. Dynamics of a vertical axis hydrokinetic energy conversion system with a rectifier coupled multi-pole permanent magnet generator. IET Renew. Power Gener. 2010, 4, 116–127. [Google Scholar] [CrossRef]
- Gong, B.; Wang, K.; You, J.; Meng, F.; Luo, Y. A novel phase-locked loop for power converters of ocean current power generation system. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 1984–1989. [Google Scholar] [CrossRef]
- Fall, O.; Charpentier, J.F.; Nguyen, N.K.; Letellier, P. Performances comparison of different concentrated-winding configurations for 5-phase PMSG in normal and faulty modes in flux weakening operation for fixed pitch tidal turbines. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 13–14 June 2016; pp. 2789–2795. [Google Scholar] [CrossRef] [Green Version]
- Fall, O.; Charpentier, J.F.; Nguyen, N.K.; Letellier, P. Maximum torque per ampere control strategy of a 5-phase PM generator in healthy and faulty modes for tidal marine turbine application. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 468–473. [Google Scholar] [CrossRef] [Green Version]
- Li, G.J.; Ren, B.; Zhu, Z.Q. Design guidelines for fractional slot multi-phase modular permanent magnet machines. IET Electr. Power Appl. 2017, 11, 1023–1031. [Google Scholar] [CrossRef]
- Abd Hafez, A.A.; Todd, R.; Forsyth, A.J.; Cross, A.M. Direct current ripple compensation for multi-phase fault-tolerant machines. IET Electr. Power Appl. 2011, 5, 28–36. [Google Scholar] [CrossRef] [Green Version]
- Zoric, I.; Jones, M.; Levi, E. Arbitrary d–q current sharing in three-phase winding sets of multi-phase machines. J. Eng. 2019, 2019, 4173–4177. [Google Scholar] [CrossRef]
- Dwari, S.; Parsa, L. Fault-Tolerant Control of Five-Phase Permanent-Magnet Motors with Trapezoidal Back EMF. IEEE Trans. Ind. Electron. 2011, 58, 476–485. [Google Scholar] [CrossRef]
- Wang, K.; Gu, Z.Y.; Liu, C.; Zhu, Z.Q. Design and Analysis of a Five-Phase SPM Machine Considering Third Harmonic Current Injection. IEEE Trans. Energy Convers. 2018, 33, 1108–1117. [Google Scholar] [CrossRef]
- Cruz, S.M.; Ferreira, M.; Mendes, A.M.; Cardoso, A.J.M. Analysis and Diagnosis of Open-Circuit Faults in Matrix Converters. IEEE Trans. Ind. Electron. 2011, 58, 1648–1661. [Google Scholar] [CrossRef]
- Ferdjallah-Kherkhachi, E.; Schaeffer, E.; Loron, L.; Benbouzid, M.E.H. Online monitoring of marine turbine insulation condition based on high frequency models: Methodology for finding the “best” identification protocol. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3374–3380. [Google Scholar] [CrossRef]
- Benelghali, S.; Benbouzid, M.E.H.; Charpentier, J.F. Generator Systems for Marine Current Turbine Applications: A Comparative Study. IEEE J. Ocean. Eng. 2012, 37, 554–563. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Lin, Y.; Lo, T. Implementation and Measurements of a Prototype Marine-Current Power Generation System on Peng-Hu Island. IEEE Trans. Ind. Appl. 2015, 51, 651–657. [Google Scholar] [CrossRef]
- Arzu, F.; Darvishi, H.H.; Hashim, R.B.; Ghazvinei, P.T.; Soeb, M.R. Numerical investigation on the hydrodynamic performance of variable length blade tidal turbine: An attribute to enhance energy capture. IET Renew. Power Gener. 2017, 11, 347–352. [Google Scholar] [CrossRef]
- Vybulkova, L.; Vezza, M.; Brown, R. Simulating the Wake Downstream of a Horizontal Axis Tidal Turbine Using a Modified Vorticity Transport Model. IEEE J. Ocean. Eng. 2016, 41, 296–301. [Google Scholar] [CrossRef] [Green Version]
- Pham, H.T.; Bourgeot, J.M.; Benbouzid, M.E.H. Comparative Investigations of Sensor Fault-Tolerant Control Strategies Performance for Marine Current Turbine Applications. IEEE J. Ocean. Eng. 2018, 43, 1024–1036. [Google Scholar] [CrossRef]
- Elghali, S.E.B.; Benbouzid, M.E.H.; Ahmed-Ali, T.; Charpentier, J.F. High-Order Sliding Mode Control of a Marine Current Turbine Driven Doubly-Fed Induction Generator. IEEE J. Ocean. Eng. 2010, 35, 402–411. [Google Scholar] [CrossRef] [Green Version]
- Benelghali, S.; Benbouzid, M.E.H.; Charpentier, J.F.; Ahmed-Ali, T.; Munteanu, I. Experimental Validation of a Marine Current Turbine Simulator: Application to a permanent magnet synchronous generator-based system second-order sliding mode control. IEEE Trans. Ind. Electron. 2011, 58, 118–126. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; At-Ahmed, N.; Machmoum, M.; Zam, M.E.H. Modeling and Vector Control of Marine Current Energy Conversion System Based on Doubly Salient Permanent Magnet Generator. IEEE Trans. Sustain. Energy 2016, 7, 409–418. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.H. Dynamic Analysis of a Grid-Connected Marine-Current Power Generation System Connected to a Distribution System. IEEE Trans. Power Syst. 2010, 25, 1798–1805. [Google Scholar] [CrossRef]
- Mekri, F.; Elghali, S.B.; Benbouzid, M.E.H. Fault-Tolerant Control Performance Comparison of Three- and Five-Phase PMSG for Marine Current Turbine Applications. IEEE Trans. Sustain. Energy 2013, 4, 425–433. [Google Scholar] [CrossRef]
- Zhou, Z.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.E.H.; Tang, T. Power Control of a Nonpitchable PMSG-Based Marine Current Turbine at Overrated Current Speed with Flux-Weakening Strategy. IEEE J. Ocean. Eng. 2015, 40, 536–545. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Wang, T.; Tang, T. A multi-mode process monitoring method based on mode-correlation PCA for Marine Current Turbine. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 286–291. [Google Scholar] [CrossRef]
- Ferdjallah-Kherkhachi, E.; Schaeffer, E.; Loron, L.; Benbouzid, M.E.H. Effect of the short-term temperature changes on Diagnostic Indicator in online insulation monitoring by parametric identification. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Buzios, Brazil, 3–5 June 2015; pp. 822–826. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, T.; Tang, T.; Benbouzid, M.; Diallo, D. Imbalance fault detection of marine current turbine under condition of wave and turbulence. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6353–6358. [Google Scholar] [CrossRef]
- Choqueuse, V.; Benbouzid, M.E.H. Non-stationary spectral estimation for wind turbine induction generator faults detection. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7376–7381. [Google Scholar] [CrossRef] [Green Version]
- Arafat, A.K.M.; Choi, S.; Baek, J. Open-Phase Fault Detection of a Five-Phase Permanent Magnet Assisted Synchronous Reluctance Motor Based on Symmetrical Components Theory. IEEE Trans. Ind. Electron. 2017, 64, 6465–6474. [Google Scholar] [CrossRef]
- Immovilli, F.; Bianchini, C.; Lorenzani, E.; Bellini, A.; Fornasiero, E. Evaluation of Combined Reference Frame Transformation for Interturn Fault Detection in Permanent-Magnet Multiphase Machines. IEEE Trans. Ind. Electron. 2015, 62, 1912–1920. [Google Scholar] [CrossRef]
- Hu, R.; Wang, J.; Sen, B.; Mills, A.R.; Chong, E.; Sun, Z. PWM Ripple Currents Based Turn Fault Detection for Multiphase Permanent Magnet Machines. IEEE Trans. Ind. Appl. 2017, 53, 2740–2751. [Google Scholar] [CrossRef] [Green Version]
- Sen, B.; Wang, J. Stator Interturn Fault Detection in Permanent-Magnet Machines Using PWM Ripple Current Measurement. IEEE Trans. Ind. Electron. 2016, 63, 3148–3157. [Google Scholar] [CrossRef] [Green Version]
- Sundaram, V.M.; Toliyat, H.A. Stator inter-turn fault detection for seamless fault-tolerant operation of five-phase induction motors. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Salehifar, M.; Arashloo, R.S.; Moreno-Equilaz, J.M.; Sala, V.; Romeral, L. Fault Detection and Fault Tolerant Operation of a Five Phase PM Motor Drive Using Adaptive Model Identification Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 212–223. [Google Scholar] [CrossRef]
- Perveen, R.; Kishor, N.; Mohanty, S.R. Fault detection for offshore wind farm connected to onshore grid via voltage source converter-high voltage direct current. IET Gener. Transm. Distrib. 2015, 9, 2544–2554. [Google Scholar] [CrossRef]
- Yue, M.; Ait-Ahmed, M.; Benkhoris, M.F.; Yao, G. A HHT based fault detection method of a multiphase generator—Diode rectifier se. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 5–8 November 2017; pp. 8311–8316. [Google Scholar] [CrossRef]
- Xie, L.; Tang, T. Modeling and control of a small marine current power generation system. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 18–20 October 2012; pp. 1438–1443. [Google Scholar] [CrossRef]
- Yao, N.; Zhang, F.; Cai, Z.; Rao, K.; Xu, M. The effect of moment of inertia on the transformation efficiency of a turbine for underwater motors. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 412–417. [Google Scholar] [CrossRef]
- Mousa, H.H.; Youssef, A.R.; Mohamed, E.E. Optimal power extraction control schemes for five-phase PMSG based wind generation systems. Eng. Sci. Technol. Int. J. 2020, 23, 144–155. [Google Scholar] [CrossRef]
- Yuan, J.; Jiang, H.; Zhao, Q.; Xu, C.; Liu, H.; Tian, Y. Dual-Mode Noise-Reconstructed EMD for Weak Feature Extraction and Fault Diagnosis of Rotating Machinery. IEEE Access 2019, 7, 173541–173548. [Google Scholar] [CrossRef]
- Alvarez-Gonzalez, F.; Griffo, A.; Wang, B. Permanent magnet synchronous machine stator windings fault detection by Hilbert–Huang transform. J. Eng. 2019, 2019, 3505–3509. [Google Scholar] [CrossRef]
- Chen, G.; Cai, X. Reconfigurable Control for Fault-Tolerant of Parallel Converters in PMSG Wind Energy Conversion System. IEEE Trans. Sustain. Energy 2019, 10, 604–614. [Google Scholar] [CrossRef]
- Zidi, S.; Moulahi, T.; Alaya, B. Fault Detection in Wireless Sensor Networks Through SVM Classifier. IEEE Sens. J. 2018, 18, 340–347. [Google Scholar] [CrossRef]
- Jan, S.U.; Lee, Y.; Shin, J.; Koo, I. Sensor Fault Classification Based on Support Vector Machine and Statistical Time-Domain Features. IEEE Access 2017, 5, 8682–8690. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Tang, Y. Clustered Hybrid Wind Power Prediction Model Based on ARMA, PSO-SVM, and Clustering Methods. IEEE Access 2020, 8, 17071–17079. [Google Scholar] [CrossRef]
- Divyajot; Kumar, R.; Fozdar, M. Optimal sizing of hybrid ship power system using variants of particle swarm optimization. In Proceedings of the 2017 International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 26–27 October 2017; pp. 527–532. [Google Scholar] [CrossRef]
- Ding, S.; Hang, J.; Wei, B.; Wang, Q. Modelling of supercapacitors based on SVM and PSO algorithms. IET Electr. Power Appl. 2018, 12, 502–507. [Google Scholar] [CrossRef]









| Parameter Tuning Method | Conditions | Comments |
|---|---|---|
| where , and are parameter adjustment coefficients, which satisfy , and . fitave is average fitness, its superscript k indicates iteration steps. is a random value between 0 and 1. | ||
| keeps same | ||
| Generator Parameter | Values |
|---|---|
| Number of pole pairs, p | 10 |
| Stator inductance, Ld1, Lq1, Ld3, Lq3 | Ld1 = Lq1 = 45 mH, Ld3 = Lq3 = 5 mH |
| Stator resistance, R | 4Ω |
| Flux of permanent magnet, φm1, φm3 | φm1 = 1 Wb, φm3 = 0.19 Wb |
| Inertia, J | 0.003 kg.m2 |
| Mechanical damping coefficient, B | 1 × 10−3 |
| Parameters | Values | |
|---|---|---|
| PSO | Size of swarm | 20 |
| Maximum number of iterations | 200 | |
| Initial value of c1 (Fixed in CPSO-SVM) | 1.5 | |
| Initial value of c2 (Fixed in CPSO-SVM) | 1.5 | |
| Initial value of ω (Fixed in CPSO-SVM) | 1 | |
| Range of penalty factor C | [0.01 10] | |
| Range of kernel function parameter g | [0.01 10] | |
| Adjustment coefficients | [1.15 1.15 0.98] | |
| SVM | penalty factor C (for SVM with fixed parameters) | 2 |
| kernel parameter g (for SVM with fixed parameters) | 1 | |
| Cross validation set number | 5 | |
| Number of training samples | 100 | |
| Number of testing samples | 100 |
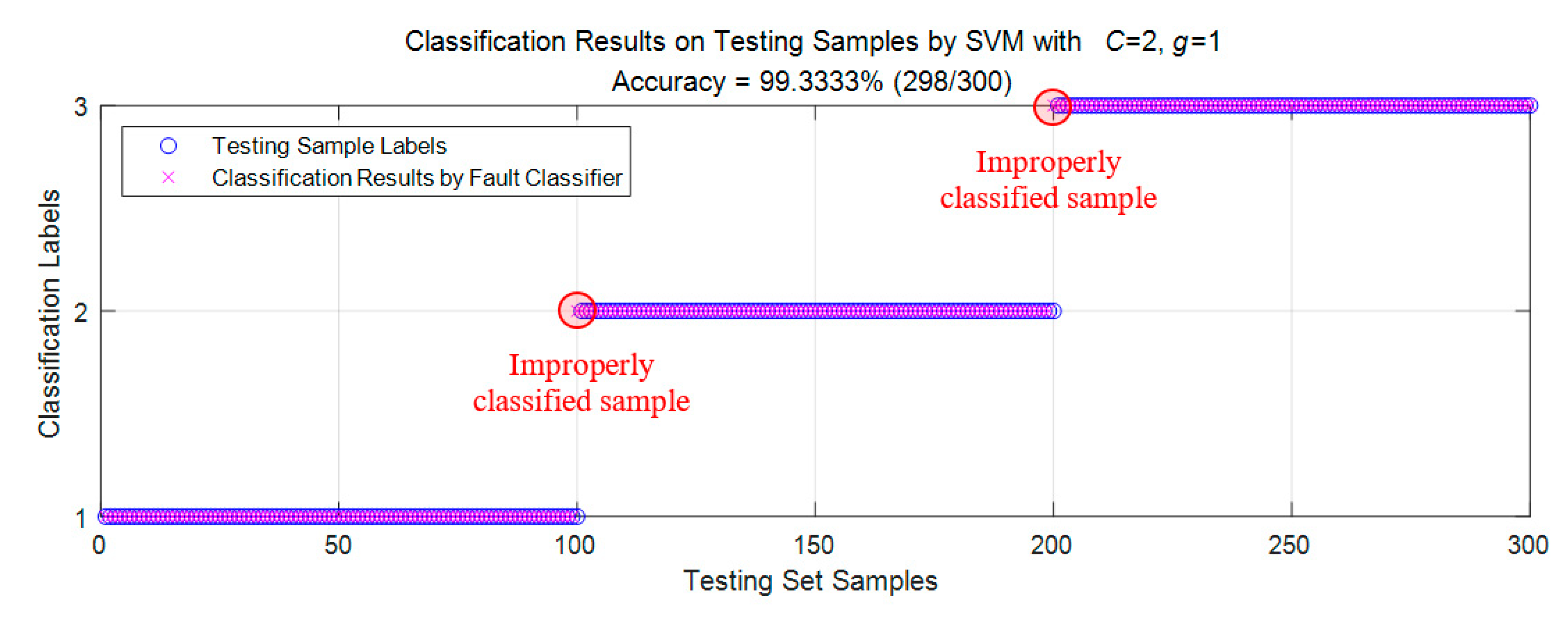
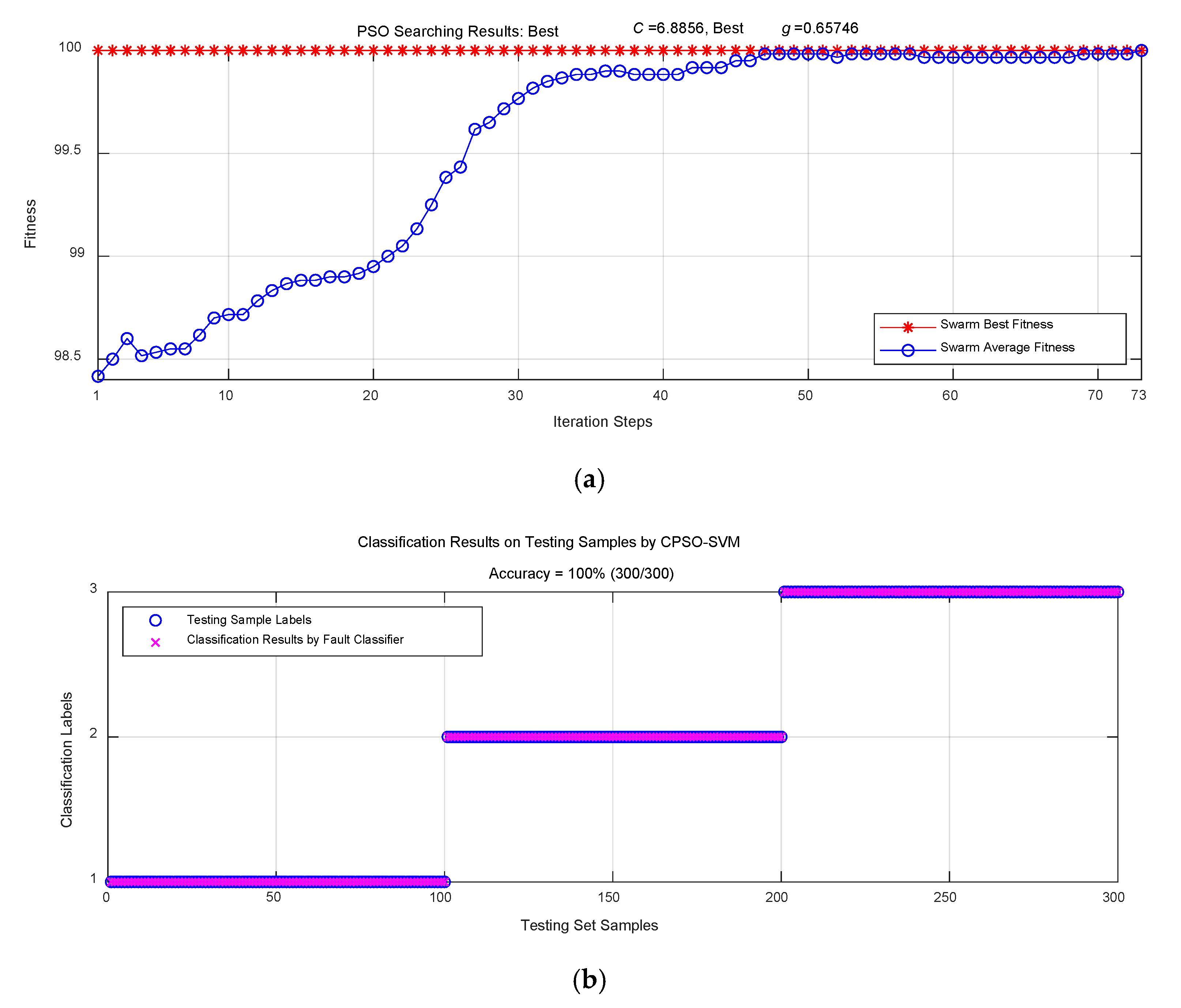
| SVM | CPSO-SVM | VPSO-SVM | |
|---|---|---|---|
| Elapsed Time on Training (s) | 0.001976 | 18.527162 | 8.469169 |
| Classification Accuracy on Testing Set Samples (correctly classified samples/total samples) | 99.33% (298/300) | 100% (300/300) | 100% (300/300) |
| PSO Iteration Steps | - | 73 | 29 |
| SVM | CPSO-SVM | VPSO-SVM | |
|---|---|---|---|
| Elapsed Time on Training (s) | 0.004017 | 83.073914 | 33.393072 |
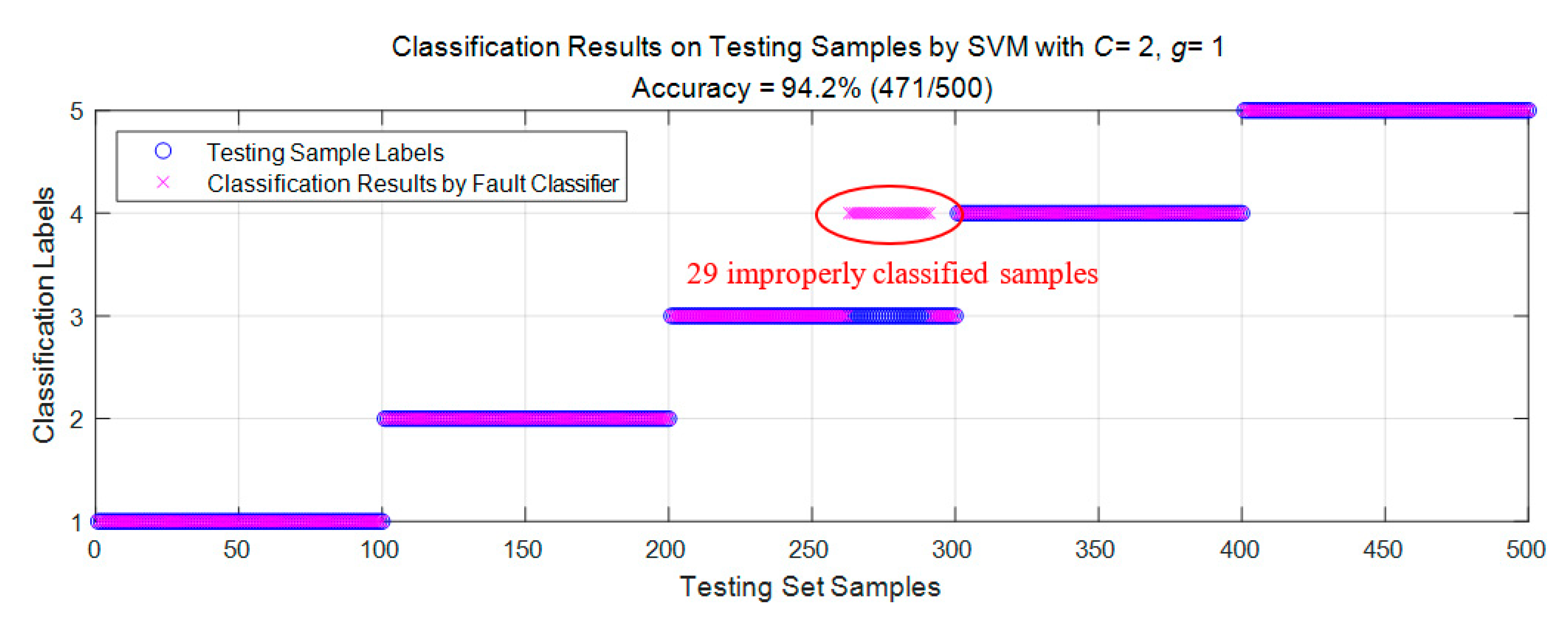
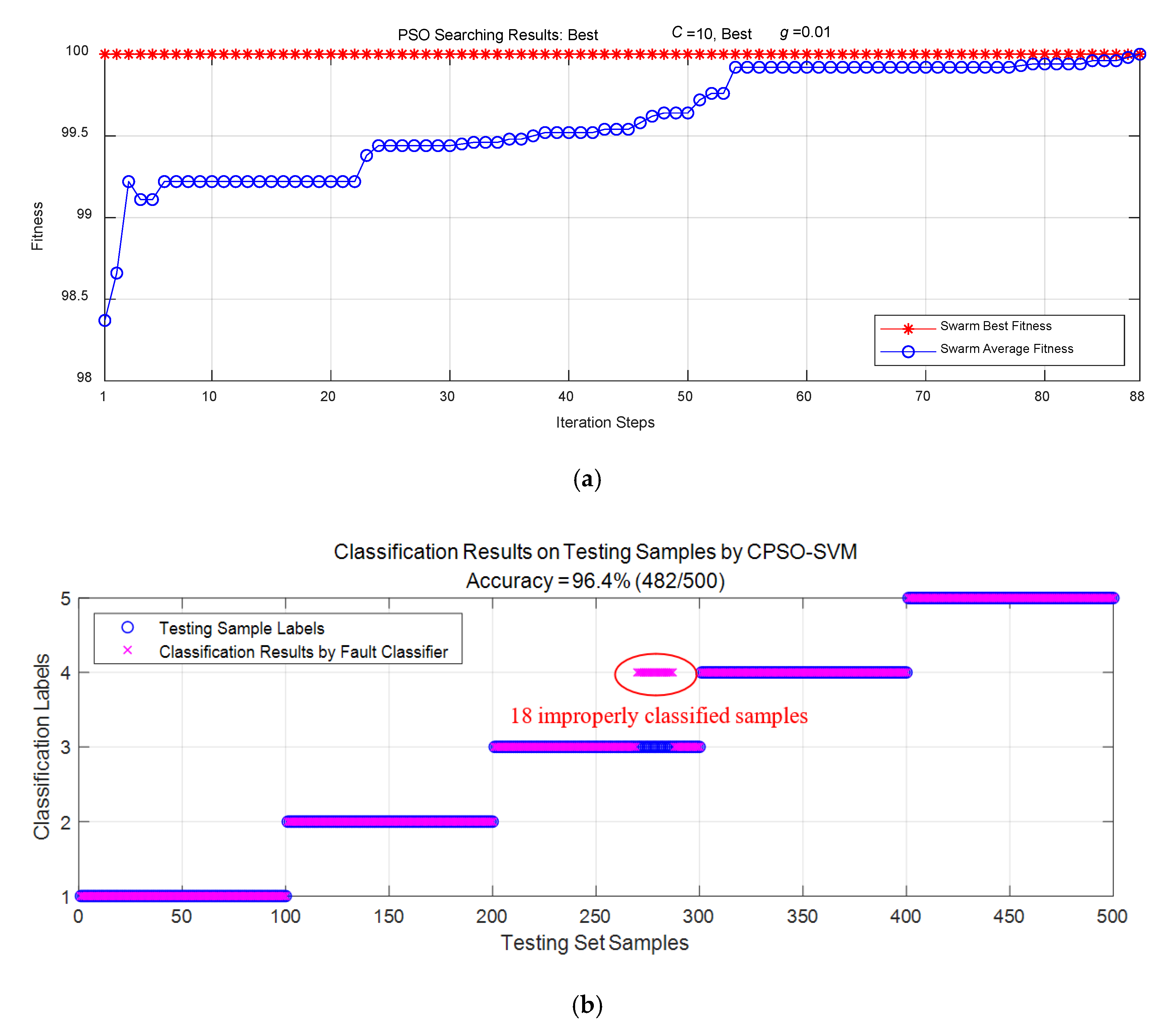
| Classification Accuracy on Testing Samples (correctly classified samples/total samples) | 94.2% (471/500) | 96.4% (482/500) | 96.4% (482/500) |
| PSO Iteration Steps | - | 88 | 33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, G.; Pang, S.; Ying, T.; Benbouzid, M.; Ait-Ahmed, M.; Benkhoris, M.F. VPSO-SVM-Based Open-Circuit Faults Diagnosis of Five-Phase Marine Current Generator Sets. Energies 2020, 13, 6004. https://doi.org/10.3390/en13226004
Yao G, Pang S, Ying T, Benbouzid M, Ait-Ahmed M, Benkhoris MF. VPSO-SVM-Based Open-Circuit Faults Diagnosis of Five-Phase Marine Current Generator Sets. Energies. 2020; 13(22):6004. https://doi.org/10.3390/en13226004
Chicago/Turabian StyleYao, Gang, Shuxiu Pang, Tingting Ying, Mohamed Benbouzid, Mourad Ait-Ahmed, and Mohamed Fouad Benkhoris. 2020. "VPSO-SVM-Based Open-Circuit Faults Diagnosis of Five-Phase Marine Current Generator Sets" Energies 13, no. 22: 6004. https://doi.org/10.3390/en13226004
APA StyleYao, G., Pang, S., Ying, T., Benbouzid, M., Ait-Ahmed, M., & Benkhoris, M. F. (2020). VPSO-SVM-Based Open-Circuit Faults Diagnosis of Five-Phase Marine Current Generator Sets. Energies, 13(22), 6004. https://doi.org/10.3390/en13226004







