A Simulation Approach for Optimising Energy-Efficient Driving Speed Profiles in Metro Lines †
Abstract
1. Introduction
2. Problem Description
3. Optimisation Model
- sp is the decision variables vector, whose generic element is term spi;
- spi is the cruising speed (m/s) that the train must not exceed when running on section i;
- sp^ is the optimal value for sp;
- ET(.) is the total traction energy used by a convoy on the metro line for each outward plus return trip;
- EiT(.) is the traction energy used by a metro train on section i;
- spmini is the minimum value of spi on section i (m/s);
- spmaxi is the maximum value of spi on section i (m/s), which depends on the features of the railway track and of rolling stock: Such values are those corresponding to a non-optimised (all-out driving style) solution;
- ti(.) is the expected running time (s) of each section i, which depends on spi;
- ot represents the set of rail sections belonging to a direction of the metro line (for instance, from terminal A to terminal B);
- rt represents the set of rail sections belonging to the other direction of the metro line (for instance, from terminal B to terminal A);
- RTot is the reserve time available at terminal B;
- RTrt is the reserve time available at terminal A.
4. Case Study
5. Solution Approaches and Numerical Results
5.1. Results with the GRG Algorithm
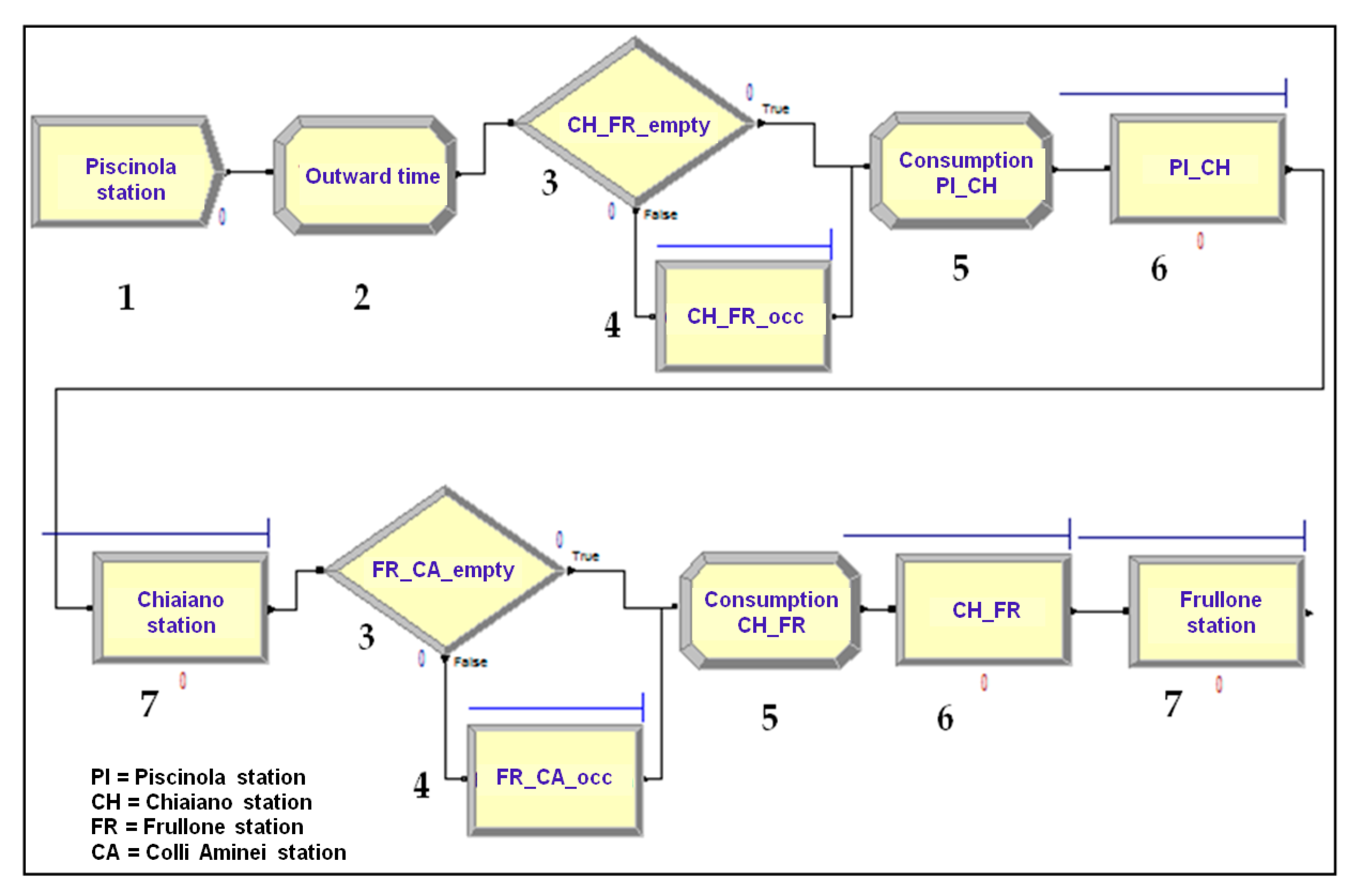
5.2. Results with Arena and Optquest
- Create. This module represents the end of the line; it was set to generate a convoy every 480 s, which is the headway of the line.
- Assign. This module is necessary to record the outward time of the convoy from the terminal to arrive at the other terminal (before arrival there is a Record module, not shown in the figure, which is used to record statistics on convoy journey times).
- Decide. This module verifies the occupation of the sections and allows the train to enter the section (module 5) only if the next two sections are empty. Otherwise, the train will have to wait, and in the simulation model, it will be directed to module 4.
- Hold. This module hosts the convoy until the next two sections are empty.
- Assign. This second assign module is used to calculate the traction energy consumption variable on the section. This expression links travel times to consumption and is obtained, on each section, by combining Equation (5) with Equation (6) to obtain a relation between consumption and travel time.
- Process. This module represents the resources, in terms of railway tracks, of the section. The capacity attributed to the module is equal to 1: Only one train can occupy the section at the same time. Moreover, a delay function is included, representing a negative exponential distribution of an average of 7.5% of the total travel time of the section.
- Process. This second process module represents the presence of the train in the station. In this case, the time the train stays in the station is represented by a normal variable of mean 20 s and a standard deviation of 0.2.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- European Environment Agency. Air Quality in Europe—2019 Report, EEA Report No. 10/2019; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- European Environment Agency. Greenhouse Gas Emissions from Transport in Europe; EEA: Copenhagen, Denmark, 2017; Available online: https://www.eea.europa.eu/data-and-maps/indicators/transport-emissions-of-greenhouse-gases/transport-emissions-of-greenhouse-gases-12 (accessed on 21 September 2020).
- European Environment Agency. Final Energy Consumption by Sector and Fuel in Europe; EEA: Copenhagen, Denmark, 2018; Available online: https://www.eea.europa.eu/data-and-maps/indicators/final-energy-consumption-by-sector-10/assessment (accessed on 21 September 2020).
- European Commission. White Paper: Roadmap to a Single European Transport Area—Towards a Competitive and Resource Efficient Transport System; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Botte, M.; D’Acierno, L. Dispatching and rescheduling tasks and their interactions with travel demand and the energy domain: Models and algorithms. Urban Rail Transit 2018, 4, 163–197. [Google Scholar] [CrossRef]
- Mo, P.; Yang, L.; Gao, Z. Energy-efficient train operation strategy with speed profiles selection for an urban metro line. Transp. Res. Rec. 2019, 2673, 348–360. [Google Scholar] [CrossRef]
- Cunillera, A.; Fernández-Rodríguez, A.; Cucala, A.P.; Fernández-Cardador, A.; Falvo, M.C. Assessment of the worthwhileness of efficient driving in railway systems with high-receptivity power supplies. Energies 2020, 13, 1836. [Google Scholar] [CrossRef]
- Yuan, W.; Frey, H.C. Potential for metro rail energy savings and emissions reduction via eco-driving. Appl. Energy 2020, 268, 1–13. [Google Scholar] [CrossRef]
- Hansen, I.; Pachl, J. Railway, Timetable and Traffic: Analysis, Modelling, Simulation; Eurailpres: Hamburg, Germany, 2008. [Google Scholar]
- Liu, R.; Golovitcher, I.M. Energy-efficient operation of rail vehicles. Transp. Res. A-Pol. 2003, 37, 917–932. [Google Scholar] [CrossRef]
- Dominguez, M.; Fernandez-Cardador, A.; Cucala, A.P.; Pecharroman, R.R. Energy savings in metropolitan railway substations through regenerative energy recovery and optimal design of ATO speed profiles. IEEE Trans. Autom. Sci. Eng. 2012, 9, 496–504. [Google Scholar] [CrossRef]
- Miyatake, M.; Ko, H. Optimization of train speed profile for minimum energy consumption. IEEJ Trans. Electr. Electr. 2010, 5, 263–269. [Google Scholar] [CrossRef]
- Lukaszewicz, P. Energy saving driving methods for freight trains. WIT Trans. Built Environ. 2004, 74, 901–909. [Google Scholar]
- Ke, B.R.; Chen, N. Signalling block layout and strategy of train operation for saving energy in mass rapid transit systems. IEE Proc. Electr. Power Appl. 2005, 152, 129–140. [Google Scholar] [CrossRef]
- Gu, Q.; Lu, X.Y.; Tang, T. Energy saving for automatic train control in moving block signalling system. In Proceedings of the 14th International IEEE Conference on Intelligent Transportation Systems (IEEE ITSC 2011), Washington, DC, USA, 5–7 October 2011. [Google Scholar]
- Howlett, P. The optimal control of a train. Ann. Oper. Res. 2000, 98, 65–87. [Google Scholar] [CrossRef]
- Khmelnitsky, E. On an optimal control problem of train operation. IEEE Trans. Autom. Control 2000, 45, 1257–1266. [Google Scholar] [CrossRef]
- Albrecht, T.; Oettich, S. A new integrated approach to dynamic schedule synchronization and energy saving train control. WIT Trans. Built Environ. 2002, 61, 847–856. [Google Scholar]
- Franke, R.; Terwiesch, P.; Meyer, M. An algorithm for the optimal control of the driving of trains. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000. [Google Scholar]
- Ko, H.; Koseki, T.; Miyatake, M. Application of dynamic programming to optimization of running profile of a train. WIT Trans. Built Environ. 2004, 74, 103–112. [Google Scholar]
- Wang, Y.; De Shutter, B.; Van der Boom, T.J.J.; Ning, B. Optimal trajectory planning for trains—A pseudospectral method and a mixed integer linear programming approach. Transp. Res. C-Emerg. 2013, 29, 97–114. [Google Scholar] [CrossRef]
- Gallo, M.; Simonelli, F.; De Luca, G.; De Martinis, V. Estimating the effects of energy-efficient driving profiles on railway consumption. In Proceedings of the 15th International Conference on Environment and Electrical Engineering (IEEE EEEIC 2015), Rome, Italy, 10–13 June 2015. [Google Scholar]
- Gallo, M.; Simonelli, F.; De Luca, G. The potential of energy-efficient driving profiles on railway consumption: A parametric approach. In Transport Infrastructure and Systems; Dell’Acqua, G., Wegman, F., Eds.; Taylor & Francis Group: London, UK, 2017; pp. 819–824. [Google Scholar]
- Simonelli, F.; Gallo, M.; Marzano, V. Kinematic formulation of energy-efficient train speed profiles. In Proceedings of the 2015 AEIT International Annual Conference, Naples, Italy, 16 October 2015. [Google Scholar]
- D’Acierno, L.; Botte, M. A passenger-oriented optimization model for implementing energy-saving strategies in railway contexts. Energies 2018, 11, 2946. [Google Scholar] [CrossRef]
- Botte, M.; D’Acierno, L. A Total Cost Approach (TCA) for optimising energy-saving measures in disruption conditions. WSEAS Trans. Environ. Dev. 2019, 15, 182–188. [Google Scholar]
- Botte, M.; D’Acierno, L.; Gallo, M. Effects of rolling stock unavailability on the implementation of energy-saving policies: A metro system application. Lect. Notes Comput. Sci. 2019, 11620, 120–132. [Google Scholar]
- Fernández-Rodríguez, A.; Su, S.; Fernández-Cardador, A.; Cucala, A.P.; Cao, Y. A multi-objective algorithm for train driving energy reduction with multiple time targets. Eng. Optim. 2020. [Google Scholar] [CrossRef]
- D’Ariano, A.; Albrecht, T. Running time re-optimization during real-time timetable perturbations. WIT Trans. Built Environ. 2006, 88, 531–540. [Google Scholar]
- Corman, F.; D’Ariano, A.; Pacciarelli, D.; Pranzo, M. Evaluation of green wave policy in real-time railway traffic management. Transp. Res. C-Emerg. 2009, 17, 607–616. [Google Scholar] [CrossRef]
- Dicembre, A.; Ricci, S. Railway traffic on high density urban corridors: Capacity, signalling and timetable. J. Rail Transp. Plan. Manag. 2011, 1, 59–68. [Google Scholar] [CrossRef]
- Krasemann, J.T. Design of an effective algorithm for fast response to the re-scheduling of railway traffic during disturbances. Transp. Res. C-Emerg. 2012, 20, 62–78. [Google Scholar] [CrossRef]
- Beugin, J.; Marais, J. Simulation-based evaluation of dependability and safety properties of satellite technologies for railway localization. Transp. Res. C-Emerg. 2012, 22, 42–57. [Google Scholar] [CrossRef]
- Albrecht, T.; Gassel, C.; Binder, A.; van Luipen, J. Dealing with operational constraints in energy efficient driving. In Proceedings of the IET Conference on Railway Traction Systems (RTS 2010), Birmingham, UK, 13–15 April 2010. [Google Scholar]
- Wang, P.; Goverde, R.M.P. Multi-train trajectory optimization for energy-efficient timetabling. Eur. J. Oper. Res. 2019, 272, 621–635. [Google Scholar] [CrossRef]
- Su, S.; Wang, X.; Cao, Y.; Yin, J. An energy-efficient train operation approach by integrating the metro timetabling and eco-driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4252–4268. [Google Scholar] [CrossRef]
- Pena-Alcaraz, M.; Fernández, A.; Cucala, P.; Ramos, A.; Pecharromán, R.R. Optimal underground timetable design based on power flow for maximizing the use of regenerative-braking energy. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 397–408. [Google Scholar] [CrossRef]
- Bocharnikov, Y.V.; Tobias, A.M.; Roberts, C. Reduction of train and net energy consumption using genetic algorithms for trajectory optimization. In Proceedings of the IET Conference on Railway Traction Systems (RTS 2010), Birmingham, UK, 13–15 April 2010. [Google Scholar]
- Iannuzzi, D.; Tricoli, P. Metro trains equipped onboard with supercapacitors: A control technique for energy saving. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM 2010), Pisa, Italy, 14–16 June 2010. [Google Scholar]
- Corapi, G.; Sanzari, D.; De Martinis, V.; D’Acierno, L.; Montella, B. A simulation-based approach for evaluating train operating costs under different signalling systems. WIT Trans. Built Environ. 2013, 130, 149–161. [Google Scholar]
- De Martinis, V.; Gallo, M.; D’Acierno, L. Estimating the benefits of energy-efficient train driving strategies: A model calibration with real data. WIT Trans. Built Environ. 2013, 130, 201–211. [Google Scholar]
- Gallo, M.; Botte, M.; Ruggiero, A.; D’Acierno, L. The optimisation of driving profiles for minimising energy consumptions in metro lines. In Proceedings of the 20th IEEE International Conference on Environment and Electrical Engineering (IEEE EEEIC 2020) and 4th Industrial and Commercial Power Systems Europe (I&CPS 2020), Madrid, Spain, 9–12 June 2020; pp. 886–891. [Google Scholar]
- D’Acierno, L.; Botte, M.; Placido, A.; Caropreso, C.; Montella, B. Methodology for determining dwell times consistent with passenger flows in the case of metro services. Urban Rail Transit 2017, 3, 73–89. [Google Scholar] [CrossRef]
- D’Acierno, L.; Botte, M.; Gallo, M.; Montella, B. Defining reserve times for metro systems: An analytical approach. J. Adv. Transp. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Rockwell Automation. Arena, User’s Guide; NYSE: ROK: Milwaukee, WI, USA, 2014. [Google Scholar]
- Rockwell Automation. OptQuest for Arena, User’s Guide; NYSE: ROK: Milwaukee, WI, USA, 2012. [Google Scholar]








| Section | a0 | a1 | a2 | R2 |
|---|---|---|---|---|
| Piscinola−Chiaiano | 382.58 | −7.3153 | 0.0494 | 0.995 |
| Chiaiano−Frullone | 311.59 | −5.9263 | 0.0412 | 0.994 |
| Frullone−Colli Aminei | 308.64 | −5.9925 | 0.0426 | 0.995 |
| Colli Aminei−Policlinico | 193.63 | −3.6940 | 0.0278 | 0.993 |
| Policlinico−Rione Alto | 137.07 | −3.4154 | 0.0346 | 0.998 |
| Rione Alto−Montedonzelli | 208.99 | −4.2972 | 0.0343 | 0.993 |
| Montedonzelli−Medaglie d’Oro | 277.64 | −7.3952 | 0.0714 | 0.999 |
| Medaglie d’Oro−Vanvitelli | 214.36 | −5.4264 | 0.0522 | 0.995 |
| Vanvitelli−Quattro Giornate | 347.22 | −7.659 | 0.0621 | 0.994 |
| Quattro Giornate−Salvator Rosa | 303.51 | −6.3979 | 0.0490 | 0.997 |
| Salvator Rosa−Materdei | 152.39 | −3.0893 | 0.0258 | 0.994 |
| Materdei−Museo | 319.45 | −6.6472 | 0.0502 | 0.996 |
| Museo−Dante | 129.67 | −2.3601 | 0.0223 | 0.997 |
| Dante−Toledo | 167.81 | −3.1315 | 0.0253 | 0.993 |
| Toledo−Municipio | 155.36 | −3.4048 | 0.0298 | 0.999 |
| Municipio−Università | 165.01 | −4.4123 | 0.0417 | 0.998 |
| Università−Garibaldi | 355.30 | −6.8061 | 0.0470 | 0.993 |
| Garibaldi−Università | 348.93 | −6.542 | 0.0440 | 0.994 |
| Università−Municipio | 165.10 | −4.200 | 0.0417 | 0.997 |
| Municipio−Toledo | 172.21 | −4.1688 | 0.0395 | 0.998 |
| Toledo−Dante | 182.46 | −3.7264 | 0.0322 | 0.998 |
| Dante−Museo * | 73 | 0 | 0 | − |
| Museo−Materdei | 307.77 | −6.5452 | 0.0507 | 0.997 |
| Materdei−Salvator Rosa | 162.36 | −3.5414 | 0.0312 | 0.993 |
| Salvator Rosa−Quattro Giornate | 296.22 | −6.2573 | 0.0486 | 0.996 |
| Quattro Giornate−Vanvitelli | 308.43 | −6.6977 | 0.0536 | 0.995 |
| Vanvitelli−Medaglie d’Oro | 228.10 | −6.2305 | 0.0631 | 0.995 |
| Medaglie d’Oro−Montedonzelli | 266.19 | −7.1081 | 0.0698 | 0.998 |
| Montedonzelli−Rione Alto | 228.22 | −4.9491 | 0.0409 | 0.996 |
| Rione Alto−Policlinico | 132.20 | −3.0712 | 0.0296 | 0.994 |
| Policlinico−Colli Aminei | 208.79 | −4.2971 | 0.0341 | 0.994 |
| Colli Aminei−Frullone | 324.50 | −6.7636 | 0.0510 | 0.997 |
| Frullone−Chiaiano | 335.00 | −6.3842 | 0.0439 | 0.994 |
| Chiaiano−Piscinola | 367.75 | −6.6808 | 0.0473 | 0.995 |
| Section | b0 | b1 | R2 |
|---|---|---|---|
| Piscinola−Chiaiano | 32.130 | 0.1714 | 0.970 |
| Chiaiano−Frullone | 21.017 | 0.1877 | 0.979 |
| Frullone−Colli Aminei | 22.536 | 0.2184 | 0.918 |
| Colli Aminei−Policlinico | 0.386 | 0.2768 | 0.986 |
| Policlinico−Rione Alto | −4.451 | 0.2200 | 0.959 |
| Rione Alto−Montedonzelli | −3.346 | 0.1890 | 0.984 |
| Montedonzelli−Medaglie d’Oro | −4.193 | 0.2142 | 0.965 |
| Medaglie d’Oro−Vanvitelli | 29.933 | 0.0333 | 0.246 ** |
| Vanvitelli−Quattro Giornate | −3.886 | 0.2088 | 0.987 |
| Quattro Giornate−Salvator Rosa | −3.645 | 0.1979 | 0.985 |
| Salvator Rosa−Materdei | −3.346 | 0.1890 | 0.984 |
| Materdei−Museo | −3.275 | 0.1877 | 0.984 |
| Museo−Dante | −4.766 | 0.2306 | 0.958 |
| Dante−Toledo | −3.823 | 0.1755 | 0.981 |
| Toledo−Municipio | −5.336 | 0.2493 | 0.958 |
| Municipio−Università | −5.366 | 0.2503 | 0.958 |
| Università−Garibaldi | −8.0533 | 0.4045 | 0.991 |
| Garibaldi−Università | −0.8627 | 0.2295 | 0.961 |
| Università−Municipio | 0.2106 | 0.2315 | 0.963 |
| Municipio−Toledo | 28.198 | 0.0046 | 0.029 |
| Toledo−Dante | 14.332 | − | − |
| Dante−Museo * | 43.570 | 0.0851 | 0.850 |
| Museo−Materdei | 23.618 | 0.0102 | 0.067 ** |
| Materdei−Salvator Rosa | 41.334 | 0.1080 | 0.957 |
| Salvator Rosa−Quattro Giornate | 31.098 | 0.0812 | 0.814 |
| Quattro Giornate−Vanvitelli | −3.403 | 0.1901 | 0.974 |
| Vanvitelli−Medaglie d’Oro | 26.093 | 0.0528 | 0.499 ** |
| Medaglie d’Oro−Montedonzelli | 34.757 | 0.0437 | 0.636 |
| Montedonzelli−Rione Alto | 17.031 | 0.0030 | 0.006 ** |
| Rione Alto−Policlinico | −5.771 | 0.2574 | 0.982 |
| Policlinico−Colli Aminei | −5.633 | 0.2520 | 0.980 |
| Colli Aminei−Frullone | −5.524 | 0.2483 | 0.991 |
| Frullone−Chiaiano | −5.029 | 0.2363 | 0.993 |
| Chiaiano−Piscinola | −8.0533 | 0.4045 | 0.991 |
| Section | spcru [km/h] | ti [s] | dt [s] | rt [s] | EiT [kWh] |
|---|---|---|---|---|---|
| Piscinola-Chiaiano | 77 | 112.19 | 20 | 240 | 45.328 |
| Chiaiano-Frullone | 77 | 99.54 | 20 | 35.470 | |
| Frullone-Colli Aminei | 77 | 99.79 | 20 | 39.353 | |
| Colli Aminei-Policlinico | 77 | 74.02 | 20 | 21.700 | |
| Policlinico-Rione Alto | 45 | 53.44 | 20 | 5.449 | |
| Rione Alto-Montedonzelli | 65 | 74.59 | 20 | 8.939 | |
| Montedonzelli-Medaglie d’Oro | 45 | 89.44 | 20 | 5.446 | |
| Medaglie d’Oro-Vanvitelli | 65 | 82.19 | 20 | 27.769 | |
| Vanvitelli-Quattro Giornate | 65 | 111.76 | 20 | 9.686 | |
| Quattro Giornate-Salvator Rosa | 65 | 94.67 | 20 | 9.218 | |
| Salvator Rosa-Materdei | 65 | 60.59 | 20 | 8.939 | |
| Materdei-Museo | 65 | 99.48 | 20 | 8.926 | |
| Museo-Dante | 45 | 68.62 | 20 | 5.611 | |
| Dante-Toledo | 77 | 76.69 | 20 | 9.691 | |
| Toledo-Municipio | 45 | 62.49 | 20 | 5.882 | |
| Municipio-Università | 77 | 87.75 | 20 | 13.907 | |
| Università-Garibaldi | 80 | 111.61 | 20 | 23.722 | |
| Garibaldi-Università | 77 | 106.07 | 20 | 240 | 23.093 |
| Università-Municipio | 77 | 88.94 | 20 | 16.809 | |
| Municipio-Toledo | 45 | 64.60 | 20 | 10.628 | |
| Toledo-Dante | 77 | 86.44 | 20 | 28.552 | |
| Dante-Museo* | 30 | 73.00 | 20 | 14.332 | |
| Museo-Materdei | 65 | 96.54 | 20 | 49.102 | |
| Materdei-Salvator Rosa | 65 | 63.99 | 20 | 24.281 | |
| Salvator Rosa-Quattro Giornate | 65 | 94.83 | 20 | 48.354 | |
| Quattro Giornate-Vanvitelli | 65 | 99.54 | 20 | 36.376 | |
| Vanvitelli-Medaglie d’Oro | 65 | 89.72 | 20 | 8.953 | |
| Medaglie d’Oro-Montedonzelli | 65 | 99.07 | 20 | 29.525 | |
| Montedonzelli-Rione Alto | 65 | 79.33 | 20 | 37.598 | |
| Rione Alto-Policlinico | 65 | 57.63 | 20 | 17.226 | |
| Policlinico-Colli Aminei | 65 | 73.55 | 20 | 10.960 | |
| Colli Aminei-Frullone | 65 | 100.34 | 20 | 10.748 | |
| Frullone-Chiaiano | 77 | 103.70 | 20 | 13.595 | |
| Chiaiano-Piscinola | 77 | 133.77 | 20 | 13.167 | |
| Total | 4129.92 | 678.335 | |||
| Section | spcru [km/h] | ti [s] | dt [s] | rt [s] | EiT [kWh] |
|---|---|---|---|---|---|
| Piscinola-Chiaiano | 60 | 121.15 | 20 | 42.458 | |
| Chiaiano-Frullone | 54 | 111.99 | 20 | 31.118 | |
| Frullone-Colli Aminei | 50 | 115.59 | 20 | 33.447 | |
| Colli Aminei-Policlinico | 30 | 107.83 | 20 | 8.690 | |
| Policlinico-Rione Alto | 30 | 65.75 | 20 | 2.149 | |
| Rione Alto-Montedonzelli | 41 | 90.84 | 20 | 4.354 | |
| Montedonzelli-Medaglie d’Oro | 40 | 96.30 | 20 | 4.345 | |
| Medaglie d’Oro-Vanvitelli | 55 | 73.67 | 20 | 28.118 | |
| Vanvitelli-Quattro Giornate | 48 | 122.16 | 20 | 6.200 | |
| Quattro Giornate-Salvator Rosa | 49 | 107.29 | 20 | 6.098 | |
| Salvator Rosa-Materdei | 31 | 81.82 | 20 | 2.462 | |
| Materdei-Museo | 51 | 110.49 | 20 | 6.363 | |
| Museo-Dante | 30 | 78.94 | 20 | 2.152 | |
| Dante-Toledo | 34 | 90.13 | 20 | 2.201 | |
| Toledo-Municipio | 30 | 80.04 | 20 | 2.143 | |
| Municipio-Università | 30 | 76.11 | 20 | 2.143 | |
| Università-Garibaldi | 37 | 168.76 | 20 | 5.457 | |
| Garibaldi-Università | 30 | 192.27 | 20 | 4.082 | |
| Università-Municipio | 30 | 76.63 | 20 | 6.022 | |
| Municipio-Toledo | 30 | 82.70 | 20 | 7.156 | |
| Toledo-Dante | 57 | 74.67 | 20 | 28.460 | |
| Dante-Museo* | 30 | 73.00 | 20 | 14.332 | |
| Museo-Materdei | 55 | 101.19 | 20 | 48.247 | |
| Materdei-Salvator Rosa | 55 | 61.97 | 20 | 24.178 | |
| Salvator Rosa-Quattro Giornate | 52 | 102.65 | 20 | 46.915 | |
| Quattro Giornate-Vanvitelli | 54 | 103.22 | 20 | 35.468 | |
| Vanvitelli-Medaglie d’Oro | 32 | 92.99 | 20 | 2.710 | |
| Medaglie d’Oro-Montedonzelli | 47 | 86.53 | 20 | 28.553 | |
| Montedonzelli-Rione Alto | 54 | 80.03 | 20 | 37.134 | |
| Rione Alto-Policlinico | 51 | 52.54 | 20 | 17.185 | |
| Policlinico-Colli Aminei | 30 | 110.57 | 20 | 1.951 | |
| Colli Aminei-Frullone | 38 | 140.93 | 20 | 3.961 | |
| Frullone-Chiaiano | 40 | 148.76 | 20 | 4.505 | |
| Chiaiano-Piscinola | 42 | 170.41 | 20 | 4.912 | |
| Total | 4129.92 | 505.669 | |||
| Reserve Time [s] | Consumption [kWh] | Train Cycle Time [s] | Running Travel Time [s] | Vehicle Number [#] |
|---|---|---|---|---|
| Non-optimised | 678.332 | 4130 | 3650 | 11 |
| 240 (480) | 505.668 | 4130 | 4130 | 11 |
| 260 (520) | 501.513 | 4170 | 4170 | 11 |
| 280 (560) | 497.567 | 4250 | 4250 | 11 |
| 300 (600) | 493.805 | 4290 | 4290 | 11 |
| 320 (640) | 490.214 | 4330 | 4330 | 11 |
| 340 (680) | 486.813 | 4370 | 4370 | 11 |
| 360 (720) | 483.602 | 4410 | 4410 | 11 |
| 380 (760) | 480.640 | 4450 | 4450 | 11 |
| 400 (800) | 477.958 | 4490 | 4490 | 12 |
| Before Optimisation | After Optimisation | |||
|---|---|---|---|---|
| Section | EiT [kWh] | spcru [km/h] | EiT [kWh] | spcru [km/h] |
| Piscinola-Chiaiano | 44.92 | 77 | 44.32 | 69 |
| Chiaiano-Frullone | 35.50 | 77 | 31.61 | 53 |
| Frullone-Colli Aminei | 38.80 | 77 | 30.83 | 44 |
| Colli Aminei-Policlinico | 19.80 | 77 | 12.95 | 45 |
| Policlinico-Rione Alto | 5.59 | 45 | 2.45 | 31 |
| Rione Alto-Montedonzelli | 7.68 | 65 | 4.58 | 41 |
| Montedonzelli-Medaglie d’Oro | 5.60 | 45 | 4.72 | 40 |
| Medaglie d’Oro-Vanvitelli | 27.85 | 65 | 16.82 | 34 |
| Vanvitelli-Quattro Giornate | 8.89 | 65 | 6.46 | 48 |
| Quattro Giornate-Salvator Rosa | 8.23 | 65 | 2.92 | 34 |
| Salvator Rosa-Materdei | 8.44 | 65 | 1.21 | 35 |
| Materdei-Museo | 7.67 | 65 | 5.69 | 50 |
| Museo-Dante | 5.20 | 45 | 4.79 | 40 |
| Dante-Toledo | 7.83 | 77 | 2.65 | 40 |
| Toledo-Municipio | 5.36 | 45 | 3.50 | 36 |
| Municipio-Università | 13.75 | 77 | 2.86 | 33 |
| Università-Garibaldi | 20.97 | 80 | 3.98 | 39 |
| Garibaldi-Università | 25.44 | 77 | 11.78 | 39 |
| Università-Municipio | 16.42 | 77 | 5.80 | 31 |
| Municipio-Toledo | 10.93 | 45 | 10.83 | 44 |
| Toledo-Dante | 28.08 | 77 | 15.94 | 32 |
| Dante-Museo* | 14.22 | 30 | 14.19 | 32 |
| Museo-Materdei | 48.17 | 65 | 46.71 | 44 |
| Materdei-Salvator Rosa | 24.05 | 65 | 20.24 | 37 |
| Salvator Rosa-Quattro Giornate | 48.45 | 65 | 48.15 | 59 |
| Quattro Giornate-Vanvitelli | 35.49 | 65 | 35.20 | 47 |
| Vanvitelli-Medaglie d’Oro | 8.80 | 65 | 2.07 | 34 |
| Medaglie d’Oro-Montedonzelli | 28.20 | 65 | 28.09 | 40 |
| Montedonzelli-Rione Alto | 36.55 | 65 | 36.53 | 48 |
| Rione Alto-Policlinico | 16.25 | 65 | 13.24 | 36 |
| Policlinico-Colli Aminei | 10.52 | 65 | 2.89 | 34 |
| Colli Aminei-Frullone | 11.48 | 65 | 10.74 | 48 |
| Frullone-Chiaiano | 12.84 | 77 | 8.78 | 53 |
| Chiaiano-Piscinola | 13.61 | 80 | 2.11 | 40 |
| Total | 661.54 | 495.67 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallo, M.; Botte, M.; Ruggiero, A.; D’Acierno, L. A Simulation Approach for Optimising Energy-Efficient Driving Speed Profiles in Metro Lines. Energies 2020, 13, 6038. https://doi.org/10.3390/en13226038
Gallo M, Botte M, Ruggiero A, D’Acierno L. A Simulation Approach for Optimising Energy-Efficient Driving Speed Profiles in Metro Lines. Energies. 2020; 13(22):6038. https://doi.org/10.3390/en13226038
Chicago/Turabian StyleGallo, Mariano, Marilisa Botte, Antonio Ruggiero, and Luca D’Acierno. 2020. "A Simulation Approach for Optimising Energy-Efficient Driving Speed Profiles in Metro Lines" Energies 13, no. 22: 6038. https://doi.org/10.3390/en13226038
APA StyleGallo, M., Botte, M., Ruggiero, A., & D’Acierno, L. (2020). A Simulation Approach for Optimising Energy-Efficient Driving Speed Profiles in Metro Lines. Energies, 13(22), 6038. https://doi.org/10.3390/en13226038







