Camera-Driven Probabilistic Algorithm for Multi-Elevator Systems
Abstract
:1. Introduction
2. Model Description
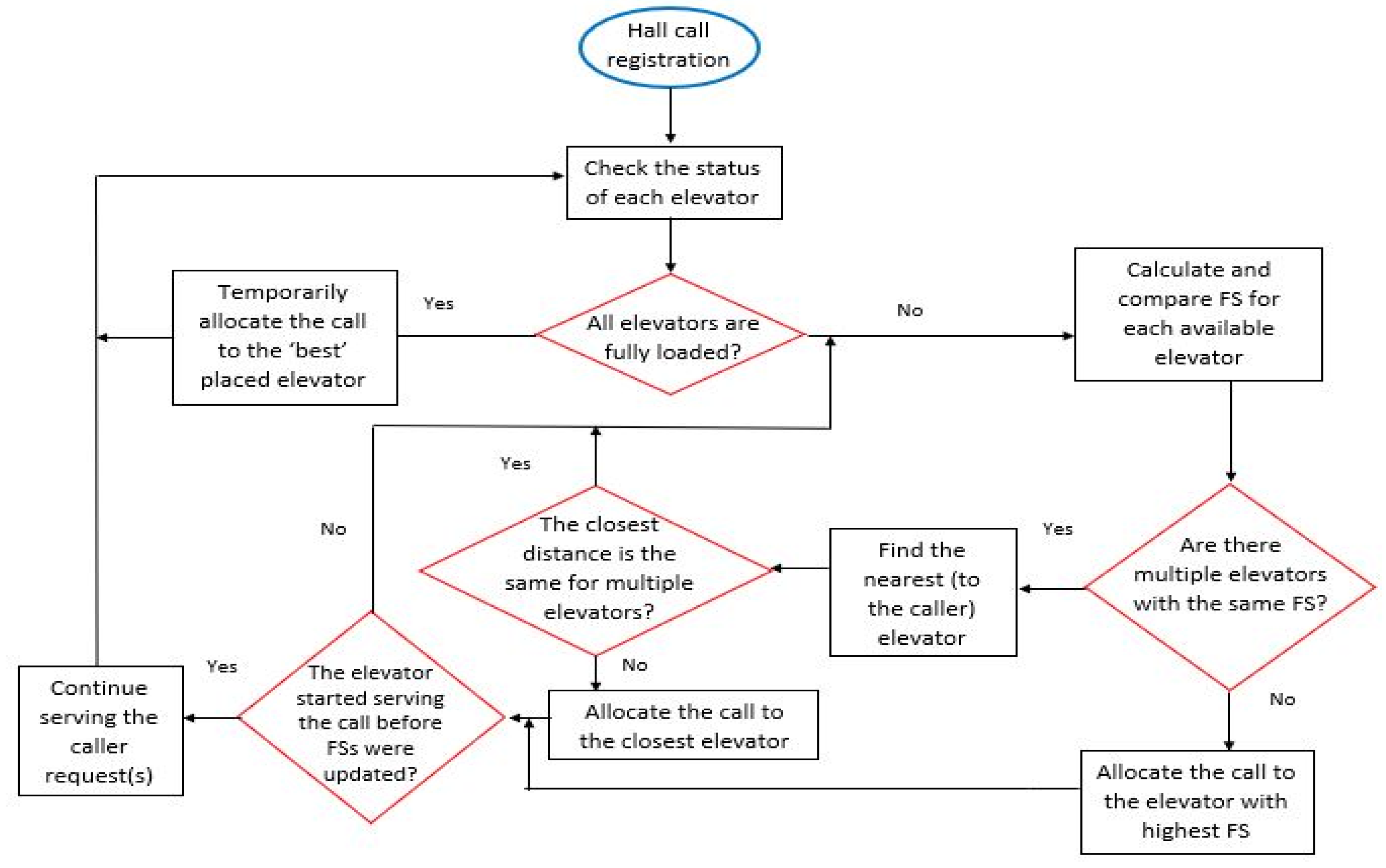
2.1. EGC with Conventional Nearest Car Algorithm
- (1)
- When the elevator is moving towards the passenger and its’ direction as well as the passenger’s desired direction are the same, the algorithm gives a position bias to this elevator, as if the elevator was one floor nearer to the passenger. In this case, the FS is calculated as follows:where (N + 1) is the number of floors in a building, and d is the number of floors between the passenger and the elevator car.FS = (N + 1) − (d − 1) = (N + 2) − d
- (2)
- If the elevator is committed to moving towards the passenger whose desired direction is opposite to that of the elevator, thenSimilarly, Equation (2) can be applied to calculate FS for an idle elevator car.FS = (N + 1) − d
- (3)
- If the elevator is committed to moving away from the passenger, the algorithm sets FS to a value that does not depend on the distance.
2.2. Proposed EGC with Modified NC Algorithm
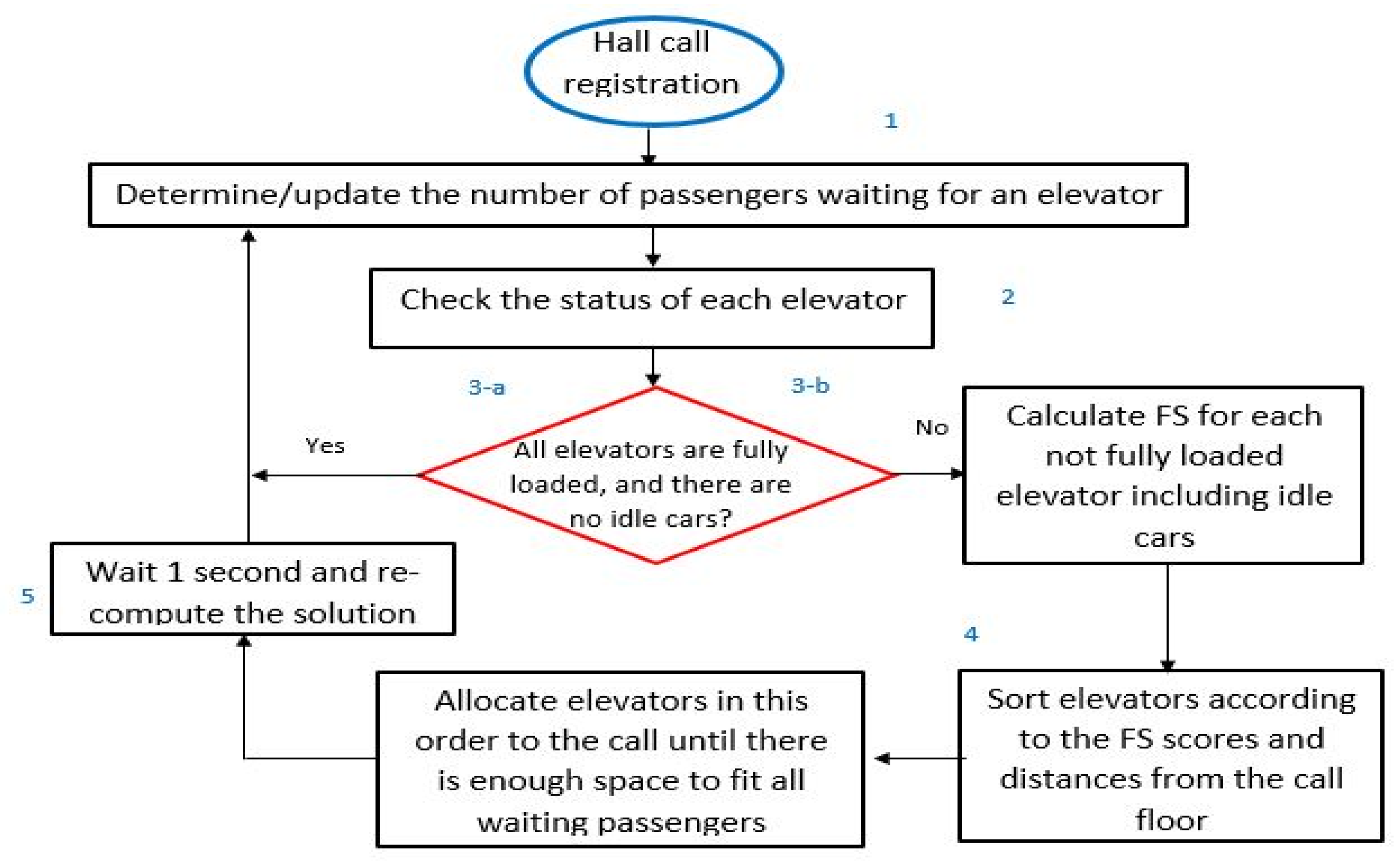
- Once the call is registered, the system determines how many passengers are waiting on the floor where the call was made.
- Next, the system checks the status of each elevator car (location, available capacity, movement direction).
- (a) When all elevator cars are fully loaded, the system checks the status of each elevator car again after 1 second.(b) When there is at least one elevator car available, the system orders elevators from highest FS to lowest; elevators with equal FS are ordered by distance to the landing floor, with the closest first.
- The system allocates the call to the elevators according to the order in 3B (Figure 2) until all passengers of the registered floor fit into the elevator cars.
- The system will loop through the whole elevator allocation procedure every second looking for a better solution until all passengers get inside the elevator cars.
2.3. Proposed EGC with BN Subroutine
- Number of Adults (A)
- -
- for the cameras on each floor—21 states from 0 to 20;
- -
- for the cameras inside an elevator car—11 states from 0 to 10.
- Number of Children (C)
- -
- for the cameras on each floor—21 states from 0 to 20;
- -
- for the cameras inside an elevator car—11 states from 0 to 10.
- Number of Small Items (SI)
- -
- for the cameras on each floor—21 states from 0 to 20;
- -
- for the cameras inside an elevator car—11 states from 0 to 10.
- Number of Big Items (BI)
- -
- for the cameras on each floor—21 states from 0 to 20;
- -
- for the cameras inside an elevator car—11 states from 0 to 10.
3. Results
3.1. Elevator Performance Metrics and Traffic Patterns
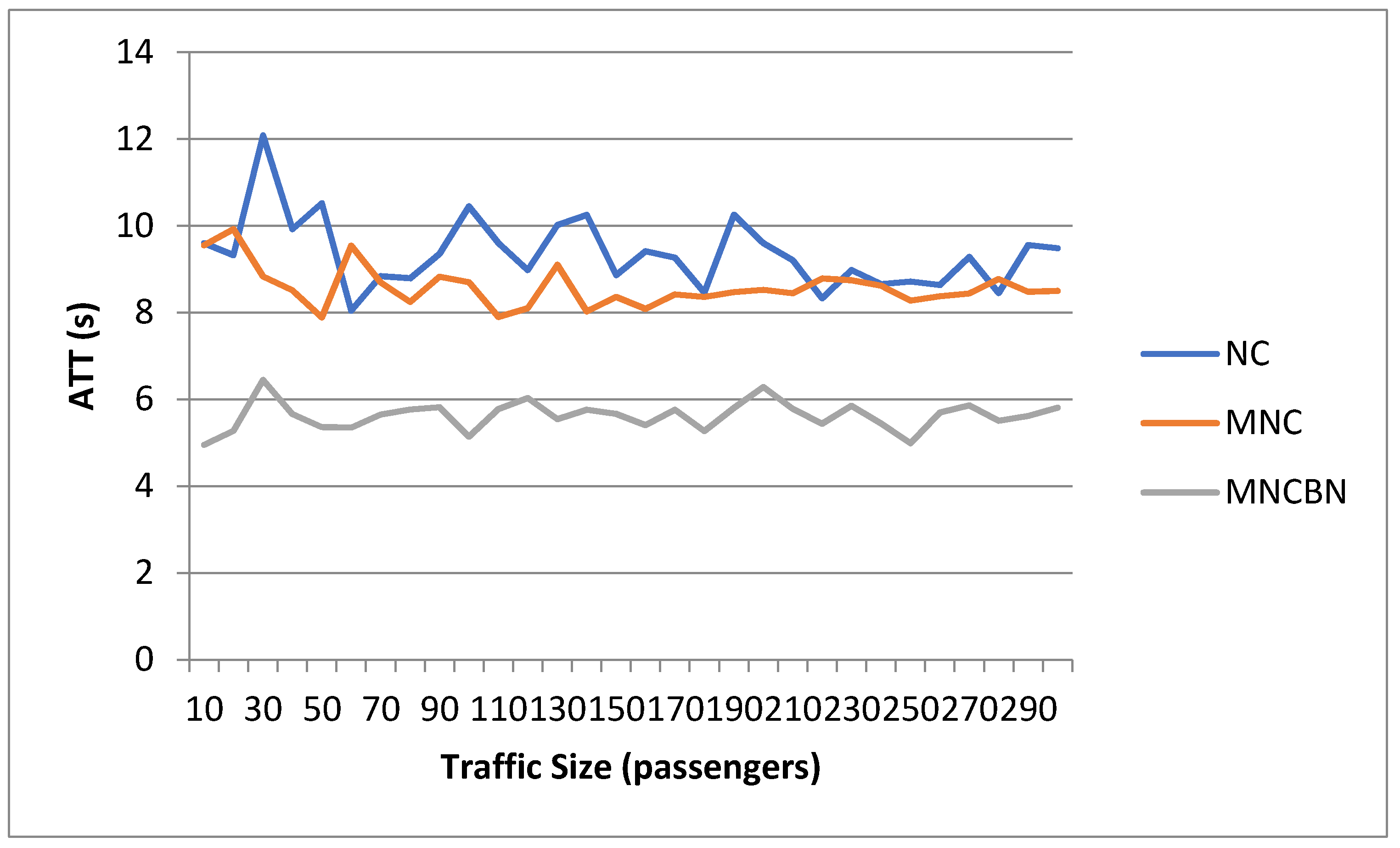
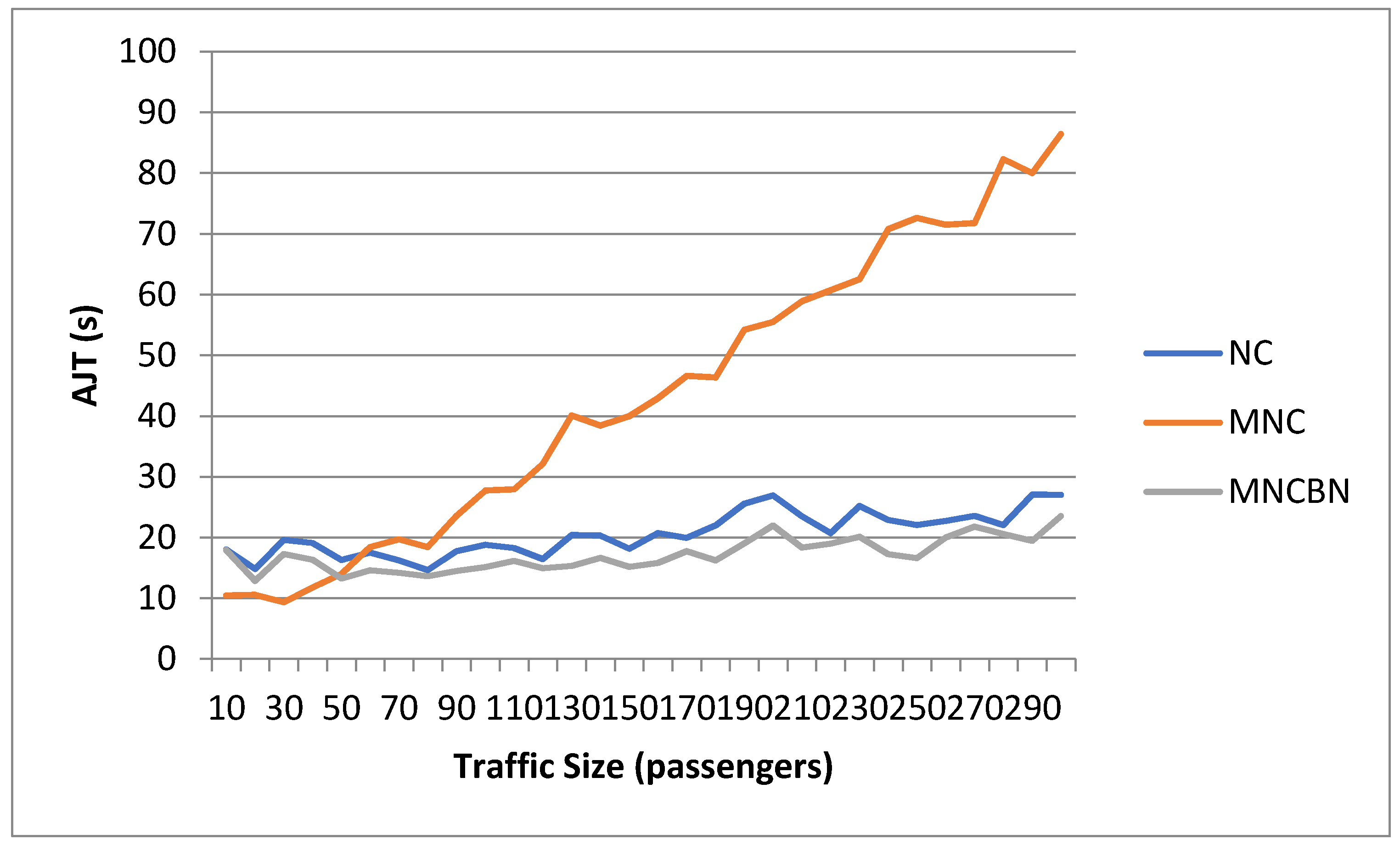
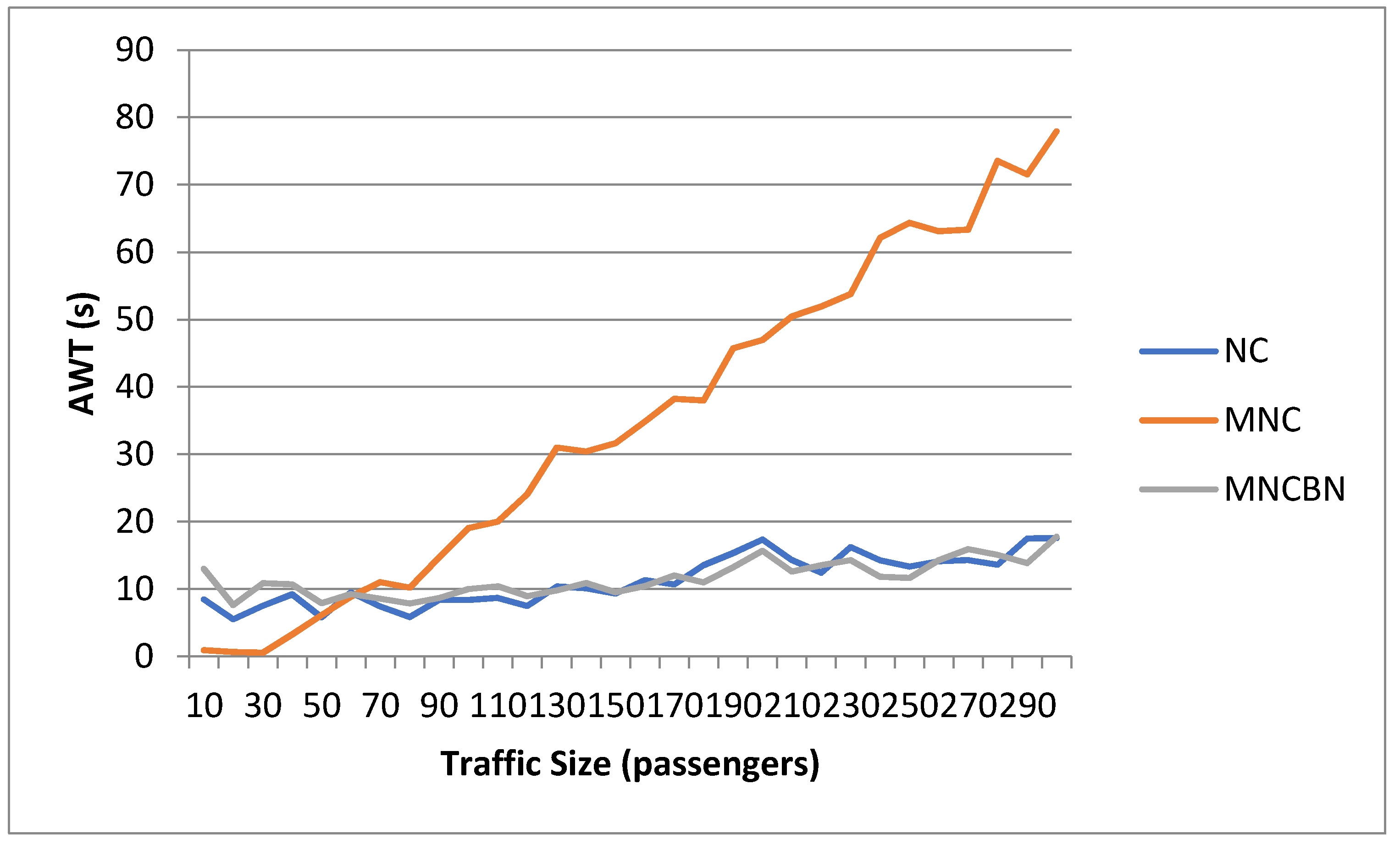
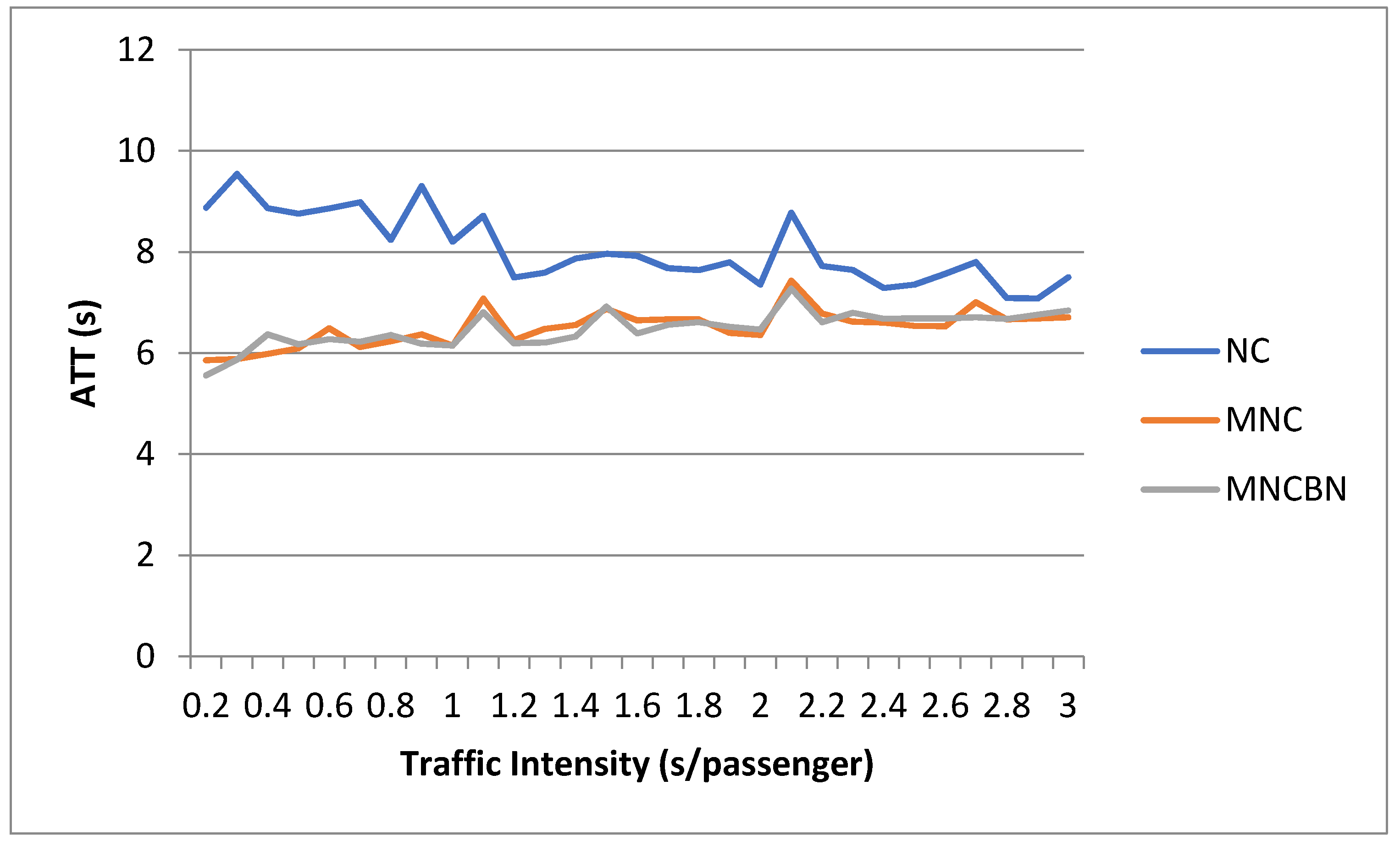
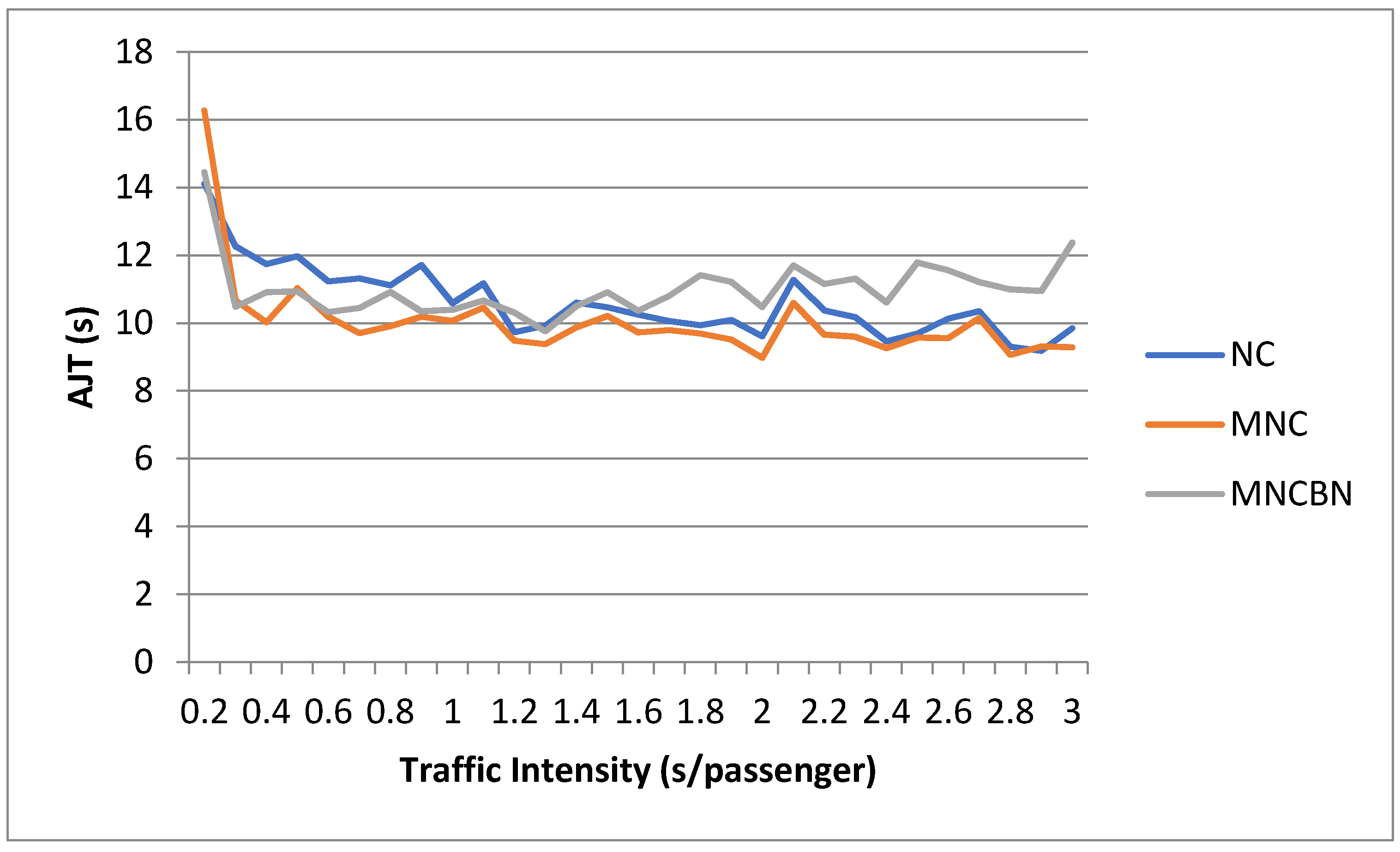
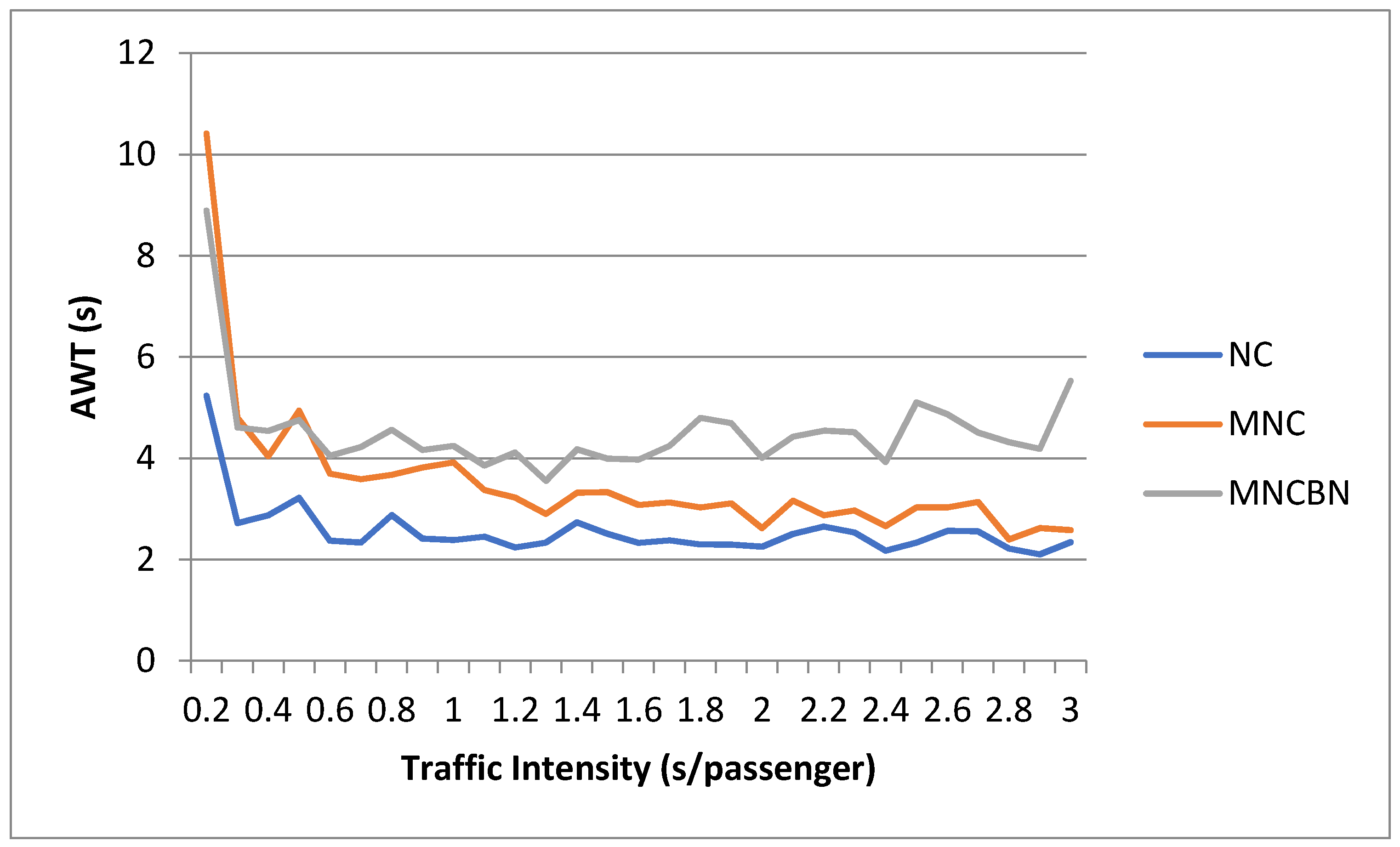
3.2. Dependence on Traffic Size and Intensity
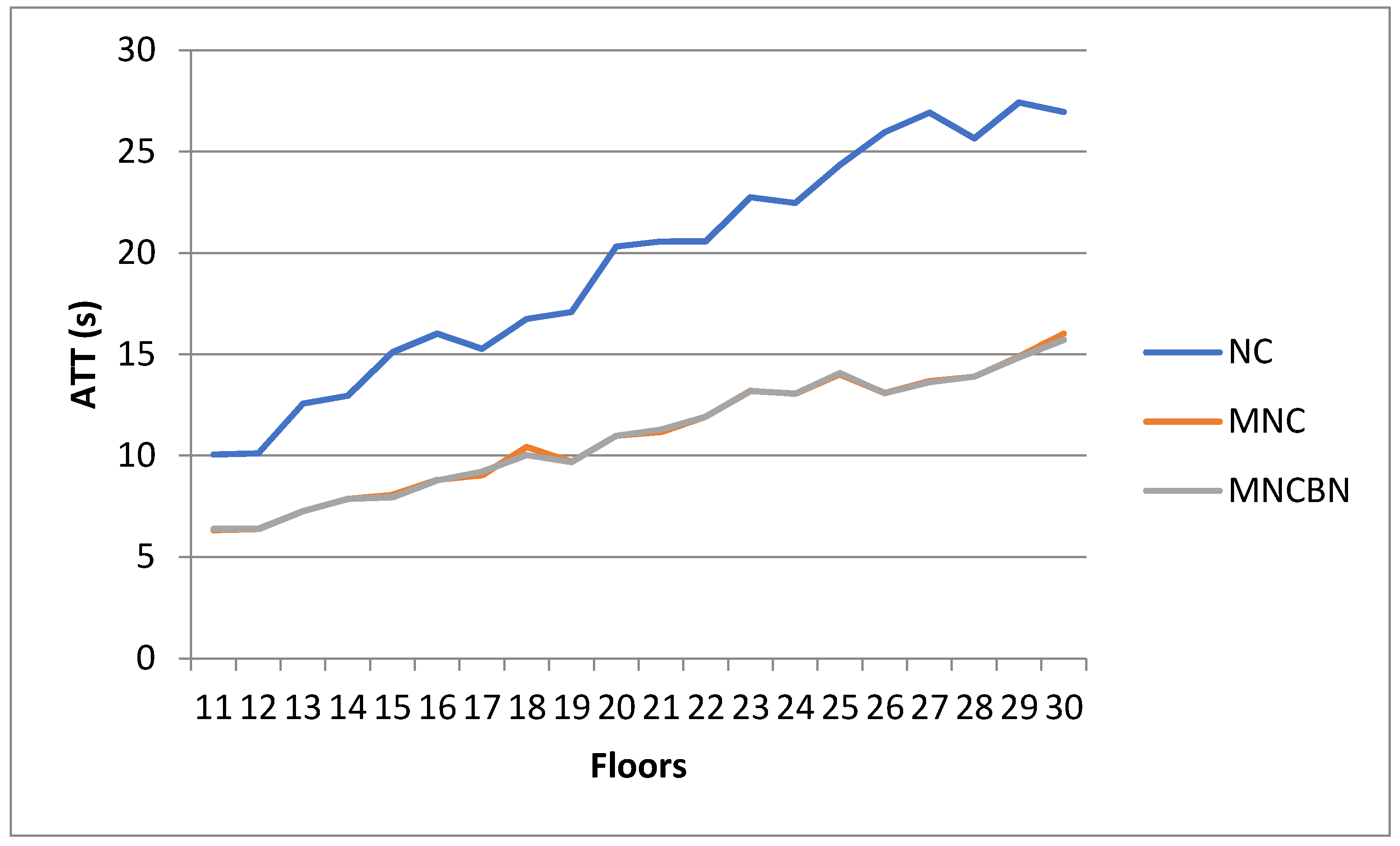
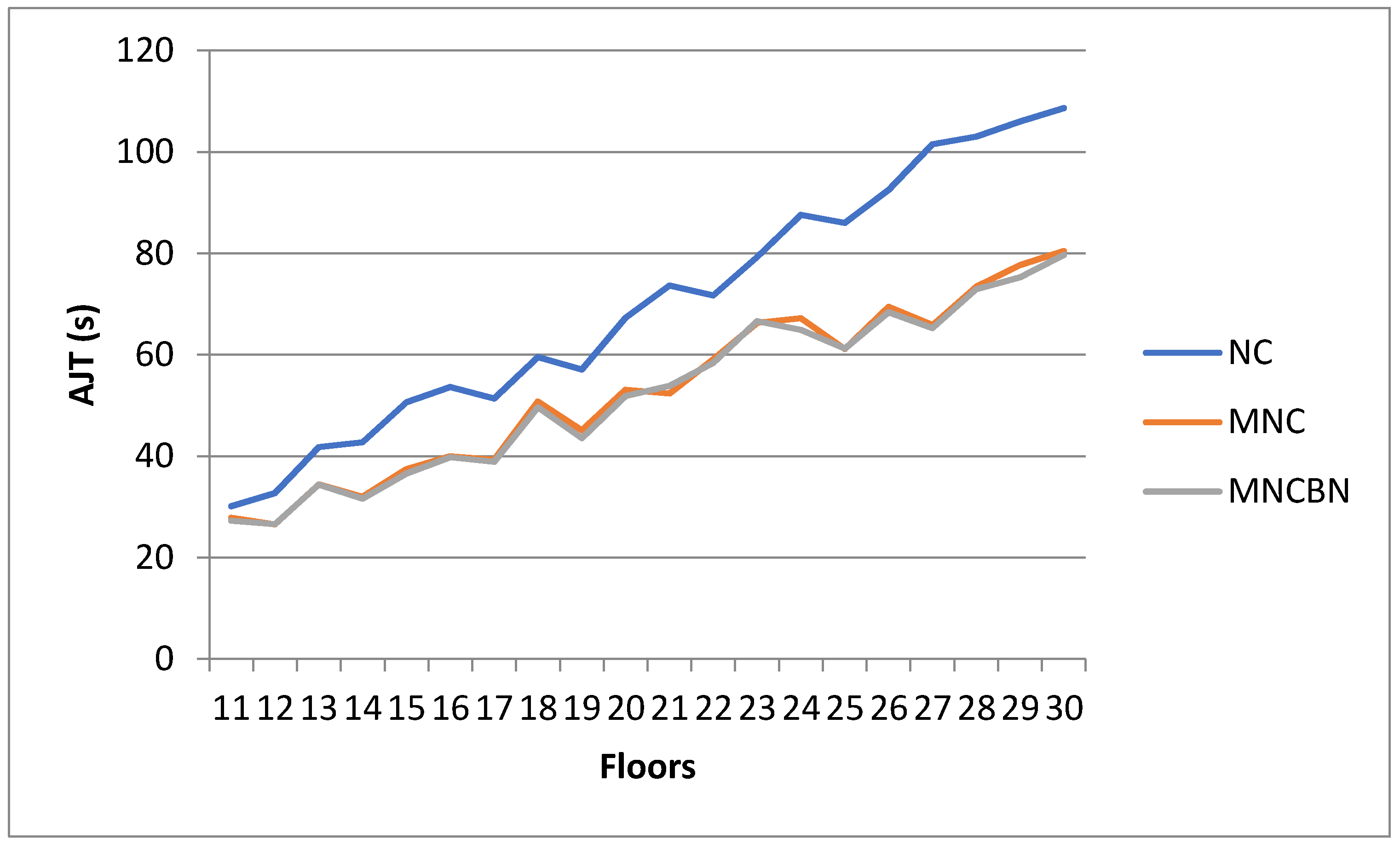
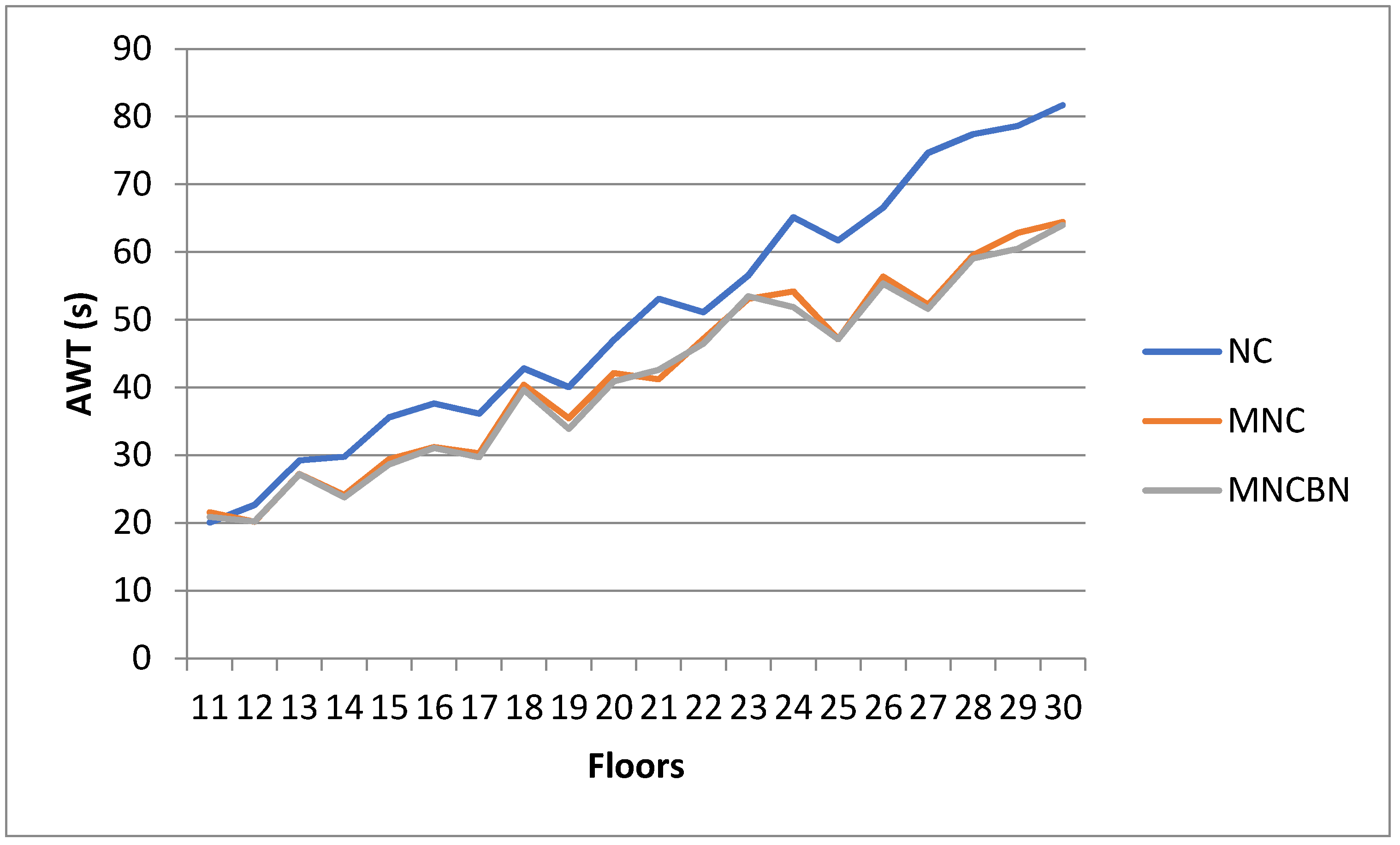
3.3. Dependence on the Building Height
3.4. Comparison of Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations Organization. World Urbanization Prospects: The 2018 Revision (Key Facts); United Nations: New York, NY, USA, 2019. [Google Scholar]
- Smith, S.F.; Barlow, G.J.; Xie, X.-F.; Rubinstein, Z.B. SURTRAC: Scalable Urban Traffic Control. In Proceedings of the TRB 2013 Annual Meeting, Washington, DC, USA, 13–17 January 2013. [Google Scholar]
- Rapid Flow Technologies LLC. RAPID FLOW BLOG. Rapid Flow Technologies LLC, 30 August 2018. Available online: https://www.rapidflowtech.com/blog/surtrac-deployment-at-urban-grid-networks-in-pittsburgh-neighborhoods (accessed on 5 August 2020).
- Bapin, Y.; Zarikas, V. Smart building’s elevator with intelligent control algorithm based on Bayesian networks. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 16–24. [Google Scholar] [CrossRef] [Green Version]
- Amrin, A.; Zarikas, V.; Spitas, C. Reliability analysis and functional design using Bayesian networks generated automatically by an “Idea Algebra” framework. Reliab. Eng. Syst. Saf. 2018, 180, 211–225. [Google Scholar] [CrossRef]
- Zarikas, V.; Papageorgiou, E.; Pernebayeva, D.; Tursynbek, N. Medical decision support tool from a fuzzy-rules driven Bayesian network. In Proceedings of the 10th International Conference on Agents and Artificial Intelligence, Funchal, Portugal, 16–18 January 2018. [Google Scholar]
- Yu, D.C.; Nguyen, T.; Haddawy, P. Bayesian Network Model for Reliability Assessment of Power Systems. IEEE Trans. Power Syst. 1999, 14, 426–432. [Google Scholar] [CrossRef] [Green Version]
- Yongli, Z.; Limin, H.; Liguo, Z.; Yan, W. Bayesian Network Based Time-sequence Simulation for Power System Reliability Assessment. In Proceedings of the Seventh Mexican International Conference on Artificial Intelligence, Atizapan de Zaragoza, Mexico, 27–31 October 2008. [Google Scholar]
- Ebrahimi, A.; Daemi, T. A Novel Method for Constructing the Bayesian Network for Detailed Reliability Assessment of Power Systems. In Proceedings of the International Conference on Electric Power and Energy Conversion Systems, Sharjah, UAE, 10–12 November 2009. [Google Scholar]
- Shofield, A.; Stonham, T.; Mehta, P. Automated people counting to aid lift control. Autom. Constr. 1997, 6, 437–445. [Google Scholar] [CrossRef]
- Shao, H.; Li, L.; Xiao, P.; Leung, M.K. ELEVIEF: An Active Elevator Video Surveillance System. In Proceedings of the Workshop on Human Motion, Austin, TX, USA, 7–8 December 2000. [Google Scholar]
- Lee, Y.; Song, T.; Kim, H.; Han, D.K.; Ko, H. Hostile Intent and Behaviour Detection in Elevators. In Proceedings of the 4th International Conference on Imaging for Crime Detection and Prevention 2011 (ICDP 2011), London, UK, 3–4 November 2011. [Google Scholar]
- Zou, J.; Zhao, Q. Occupancy Detection in Elevator Car by Fusing Analysis of Dual Videos. In Proceedings of the 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017. [Google Scholar]
- Sun, Z.; Xu, B.; Wu, D.; Lu, M.; Cong, J. A real-time video surveillance and state detection approach for elevator cabs. In Proceedings of the International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 23–26 October 2019. [Google Scholar]
- Ding, N.; Luh, P.B.; Chen, T.; Zhang, H. Optimization of Elevator Evacuation Considering Potential Over-Crowding. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014. [Google Scholar]
- Barney, G.; Al-Sharif, L. Elevator Traffic Handbook Theory and Practice; Routledge: New York, NY, USA, 2016. [Google Scholar]
- Python 3.7–Python Releases for Windows. Available online: https://www.python.org/downloads/windows/ (accessed on 16 August 2020).
- Bayesialab 8–Bayesian Networks for Research, Analytics, and Reasoning. Available online: https://www.bayesia.com/introduction?__hstc=221168007.d6327a006492fd03c47179bdedf277c4.1549810675300.1549810675300.1565871411196.2&__hssc=221168007.17.1565871411196&__hsfp=1049575405 (accessed on 24 August 2020).


| Traffic Size | Interval | NC 1 | MNC 2 | MNCBN 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ATT | AJT | AWT | ATT | AJT | AWT | ATT | AJT | AWT | ||
| 100 | 0.01 | 8.58 | 35.20 | 26.62 | 8.66 | 29.36 | 20.70 | 8.68 | 29.30 | 20.62 |
| 200 | 0.01 | 8.86 | 100.94 | 92.08 | 9.03 | 59.99 | 50.96 | 9.03 | 59.87 | 50.84 |
| 300 | 0.01 | 7.79 | 171.52 | 163.73 | 8.05 | 94.98 | 86.93 | 8.05 | 94.98 | 86.93 |
| 100 | 0.1 | 8.54 | 35.83 | 27.30 | 8.59 | 28.72 | 20.13 | 8.53 | 28.47 | 19.94 |
| 200 | 0.1 | 7.87 | 100.02 | 92.15 | 8.02 | 50.49 | 42.47 | 8.04 | 50.20 | 42.16 |
| 300 | 0.1 | 8.24 | 167.53 | 159.29 | 8.50 | 86.88 | 78.38 | 8.45 | 86.33 | 77.88 |
| 200 | 1 | 8.14 | 24.18 | 16.05 | 8.20 | 21.19 | 12.99 | 8.20 | 18.84 | 10.64 |
| 100 | 2 | 8.45 | 15.89 | 7.44 | 8.51 | 16.21 | 7.71 | 8.42 | 15.93 | 7.52 |
| 200 | 2 | 8.28 | 18.27 | 9.99 | 8.30 | 18.40 | 10.11 | 8.29 | 17.24 | 8.95 |
| 300 | 2 | 8.10 | 19.56 | 11.47 | 8.13 | 18.28 | 10.16 | 8.07 | 17.81 | 9.74 |
| Traffic Size | Interval | NC 1 | MNC 2 | MNCBN 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ATT | AJT | AWT | ATT | AJT | AWT | ATT | AJT | AWT | ||
| 100 | 0.01 | 10.61 | 51.00 | 40.39 | 9.01 | 39.80 | 30.78 | 8.54 | 35.72 | 27.18 |
| 200 | 0.01 | 9.61 | 78.49 | 68.89 | 8.47 | 54.38 | 45.91 | 8.37 | 55.58 | 47.21 |
| 300 | 0.01 | 9.35 | 107.15 | 97.80 | 7.90 | 86.09 | 78.19 | 7.92 | 81.68 | 73.76 |
| 100 | 0.1 | 9.64 | 36.00 | 26.36 | 8.89 | 34.72 | 25.84 | 7.65 | 32.24 | 24.60 |
| 200 | 0.1 | 9.99 | 68.28 | 58.29 | 8.56 | 59.44 | 50.88 | 8.70 | 61.18 | 52.48 |
| 300 | 0.1 | 9.82 | 92.94 | 83.12 | 8.14 | 75.63 | 67.49 | 8.17 | 75.45 | 67.27 |
| 200 | 1 | 13.31 | 18.35 | 5.04 | 9.97 | 17.69 | 7.72 | 9.27 | 16.56 | 7.29 |
| 100 | 2 | 11.03 | 15.84 | 4.81 | 8.36 | 14.67 | 6.31 | 8.08 | 16.58 | 8.50 |
| 200 | 2 | 11.40 | 16.06 | 4.66 | 8.14 | 14.24 | 6.10 | 8.21 | 15.67 | 7.46 |
| 300 | 2 | 11.20 | 16.34 | 5.15 | 8.27 | 14.77 | 6.50 | 8.46 | 16.74 | 8.28 |
| Traffic Size | Interval | NC 1 | MNC 2 | MNCBN 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ATT | AJT | AWT | ATT | AJT | AWT | ATT | AJT | AWT | ||
| 100 | 0.01 | 9.24 | 20.94 | 11.70 | 6.07 | 15.73 | 9.67 | 6.32 | 16.51 | 10.20 |
| 200 | 0.01 | 9.14 | 29.34 | 20.20 | 5.82 | 23.75 | 17.94 | 5.70 | 22.35 | 16.65 |
| 300 | 0.01 | 8.79 | 37.49 | 28.70 | 6.21 | 32.87 | 26.66 | 5.93 | 31.11 | 25.18 |
| 100 | 0.1 | 8.99 | 16.72 | 7.73 | 6.00 | 14.84 | 8.85 | 5.60 | 14.27 | 8.67 |
| 200 | 0.1 | 8.93 | 20.75 | 11.82 | 5.75 | 16.92 | 11.18 | 5.26 | 15.92 | 10.67 |
| 300 | 0.1 | 8.91 | 26.32 | 17.41 | 5.38 | 19.60 | 14.22 | 5.54 | 20.35 | 14.80 |
| 200 | 1 | 7.59 | 10.08 | 2.49 | 6.06 | 9.19 | 3.13 | 5.88 | 10.49 | 4.60 |
| 100 | 2 | 7.31 | 9.85 | 2.54 | 6.03 | 9.16 | 3.13 | 6.47 | 10.13 | 3.66 |
| 200 | 2 | 7.37 | 9.67 | 2.30 | 6.13 | 9.13 | 3.00 | 6.22 | 10.50 | 4.29 |
| 300 | 2 | 7.79 | 10.44 | 2.65 | 6.49 | 9.77 | 3.28 | 6.58 | 10.97 | 4.39 |
| # | Null Hypothesis | Test | Significance 1 | Decision |
|---|---|---|---|---|
| 1 | Distribution of ATT_NC, ATT_MNC, and ATT_MNCBN are the same | Related samples Friedman’s two-way analysis of variance by ranks | 0.001 | Reject the null hypothesis |
| 2 | Distribution of AJT_NC, AJT_MNC, and AJT_MNCBN are the same | 0.027 | ||
| 3 | Distribution of AWT_NC, AWT_MNC, and AWT_MNCBN are the same | 0.905 | Retain the null hypothesis |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bapin, Y.; Alimanov, K.; Zarikas, V. Camera-Driven Probabilistic Algorithm for Multi-Elevator Systems. Energies 2020, 13, 6161. https://doi.org/10.3390/en13236161
Bapin Y, Alimanov K, Zarikas V. Camera-Driven Probabilistic Algorithm for Multi-Elevator Systems. Energies. 2020; 13(23):6161. https://doi.org/10.3390/en13236161
Chicago/Turabian StyleBapin, Yerzhigit, Kanat Alimanov, and Vasilios Zarikas. 2020. "Camera-Driven Probabilistic Algorithm for Multi-Elevator Systems" Energies 13, no. 23: 6161. https://doi.org/10.3390/en13236161
APA StyleBapin, Y., Alimanov, K., & Zarikas, V. (2020). Camera-Driven Probabilistic Algorithm for Multi-Elevator Systems. Energies, 13(23), 6161. https://doi.org/10.3390/en13236161





