Analysis on the Thermal Balance and Operational Parameters for the District Heating System with Peak Load Boilers in Heating Substations
Abstract
:1. Introduction
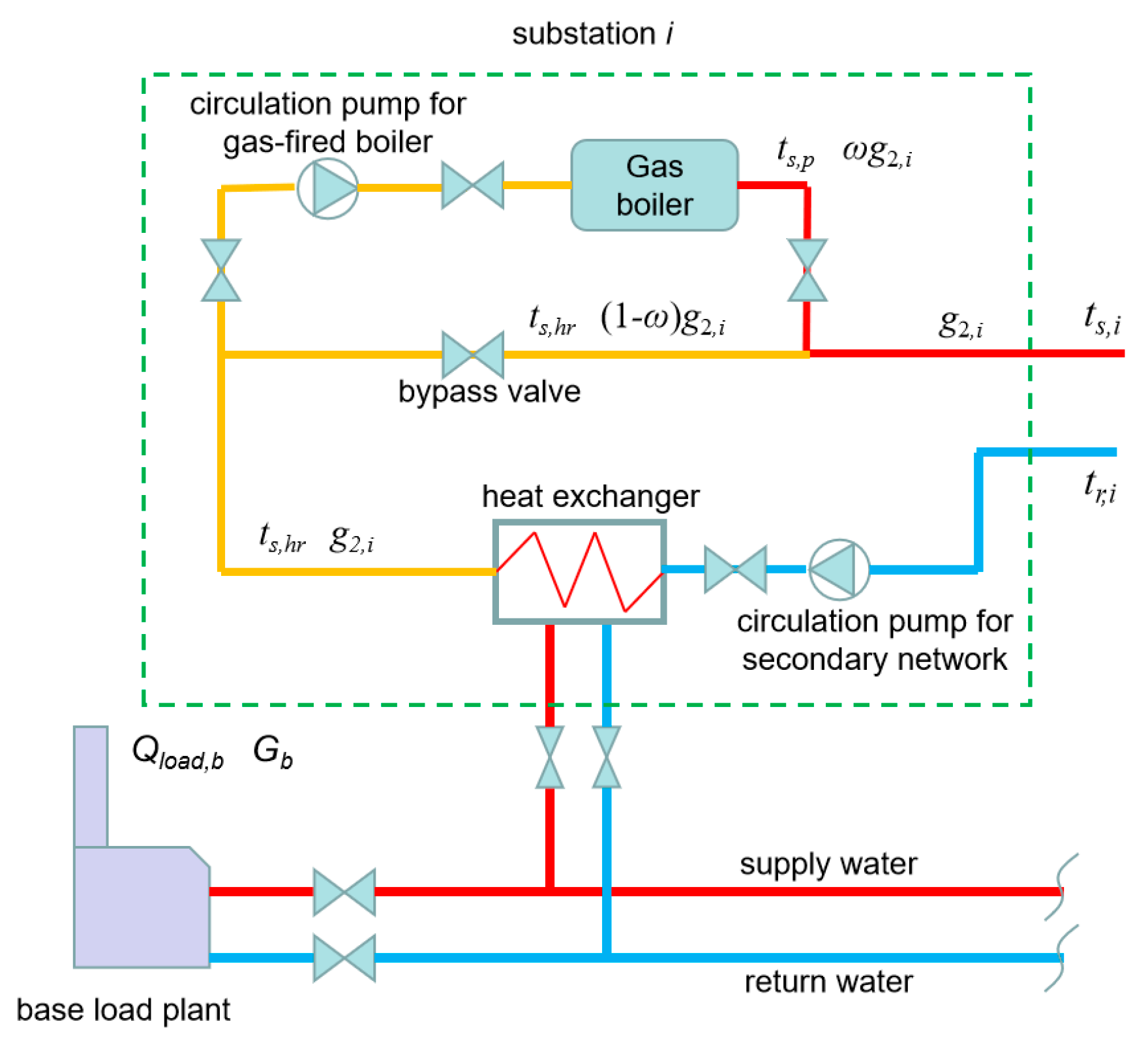
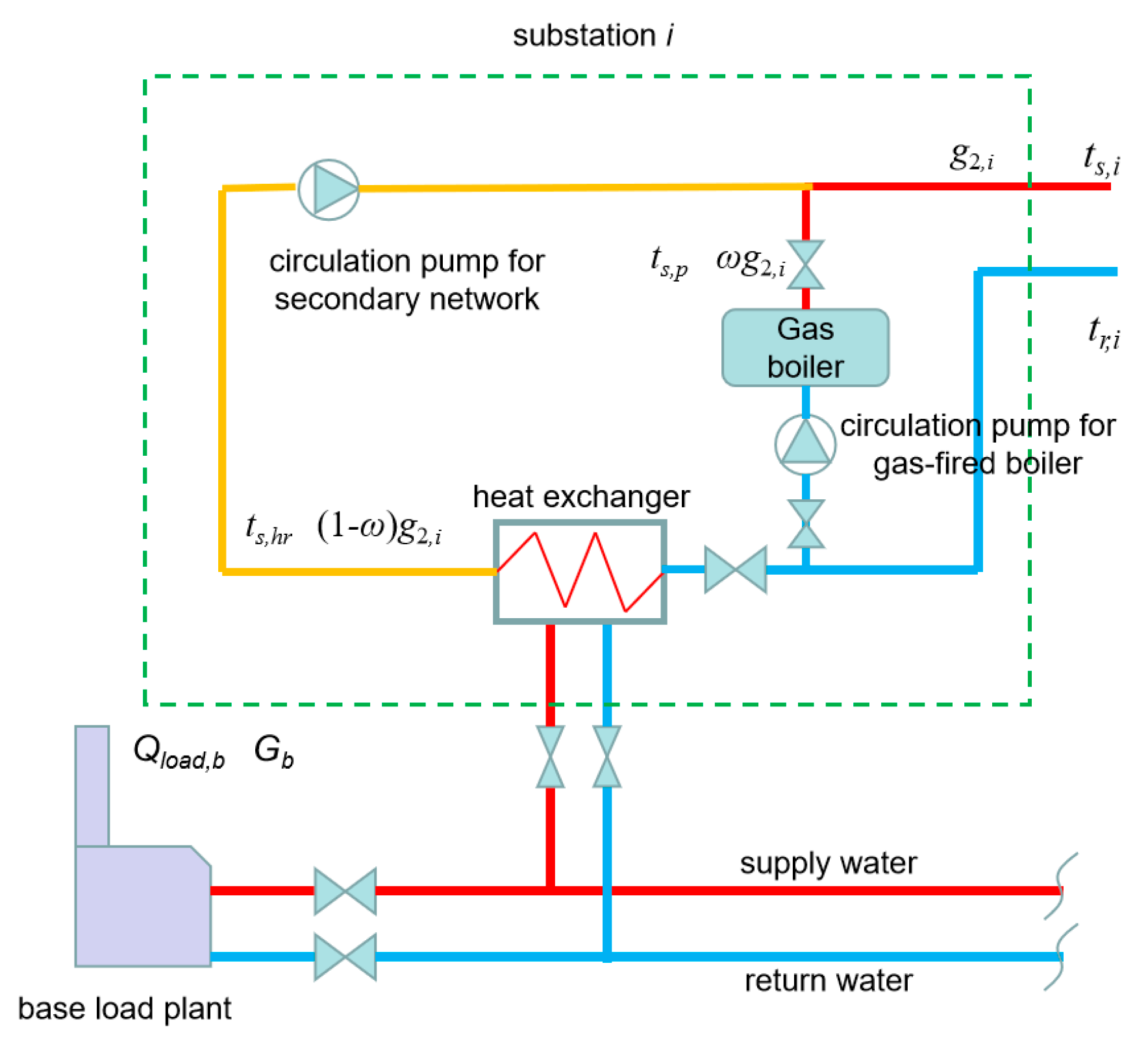
2. Connection Modes of the Peak Boilers and System Characteristics
2.1. Connection Modes between Peak Boilers (PB) and Heat Exchangers
2.2. Base Load Ratio
2.3. System Characteristics
3. Thermal Balance of the DH System with Peak Shaving Gas-Fired Boilers in Heating Substations
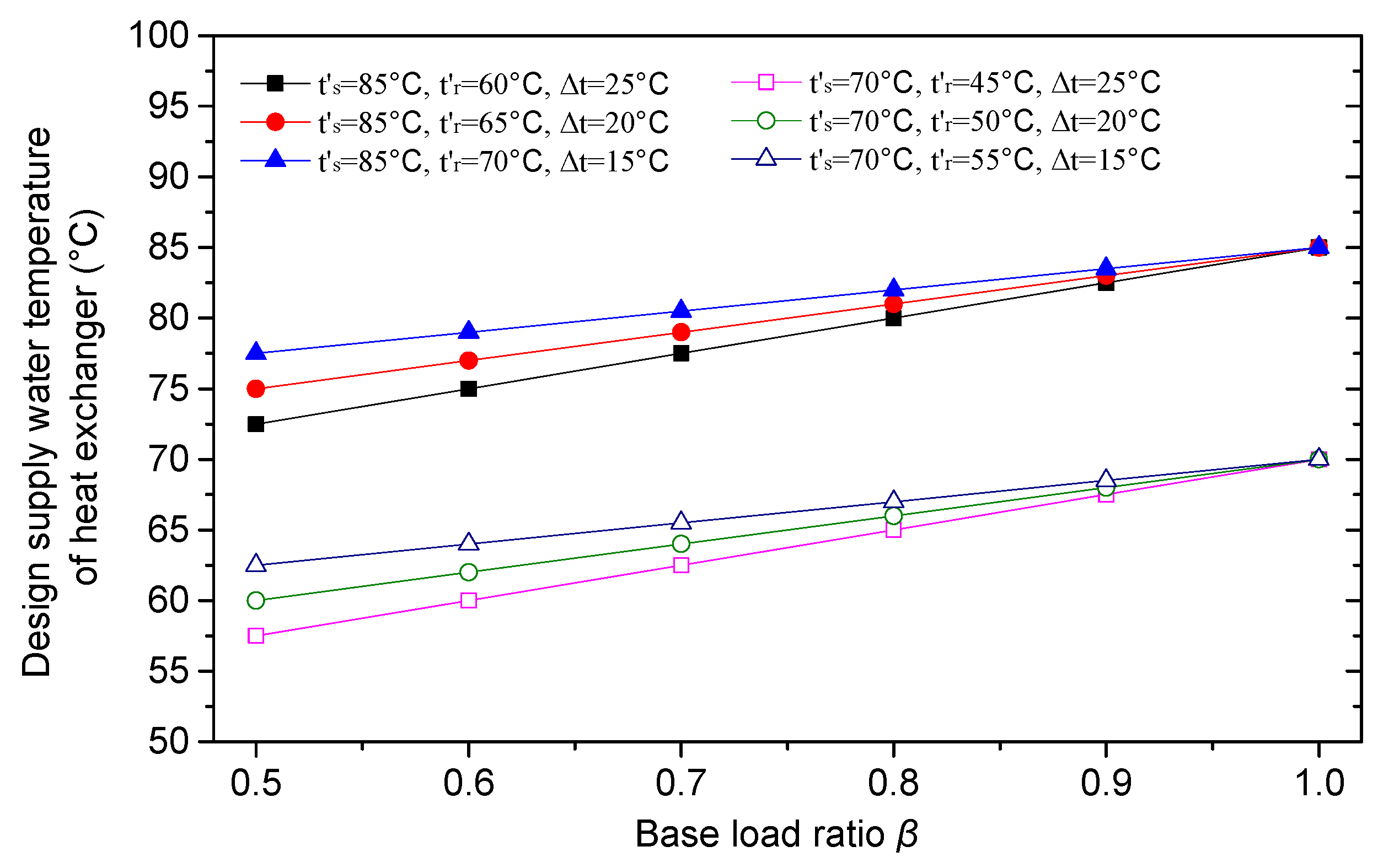
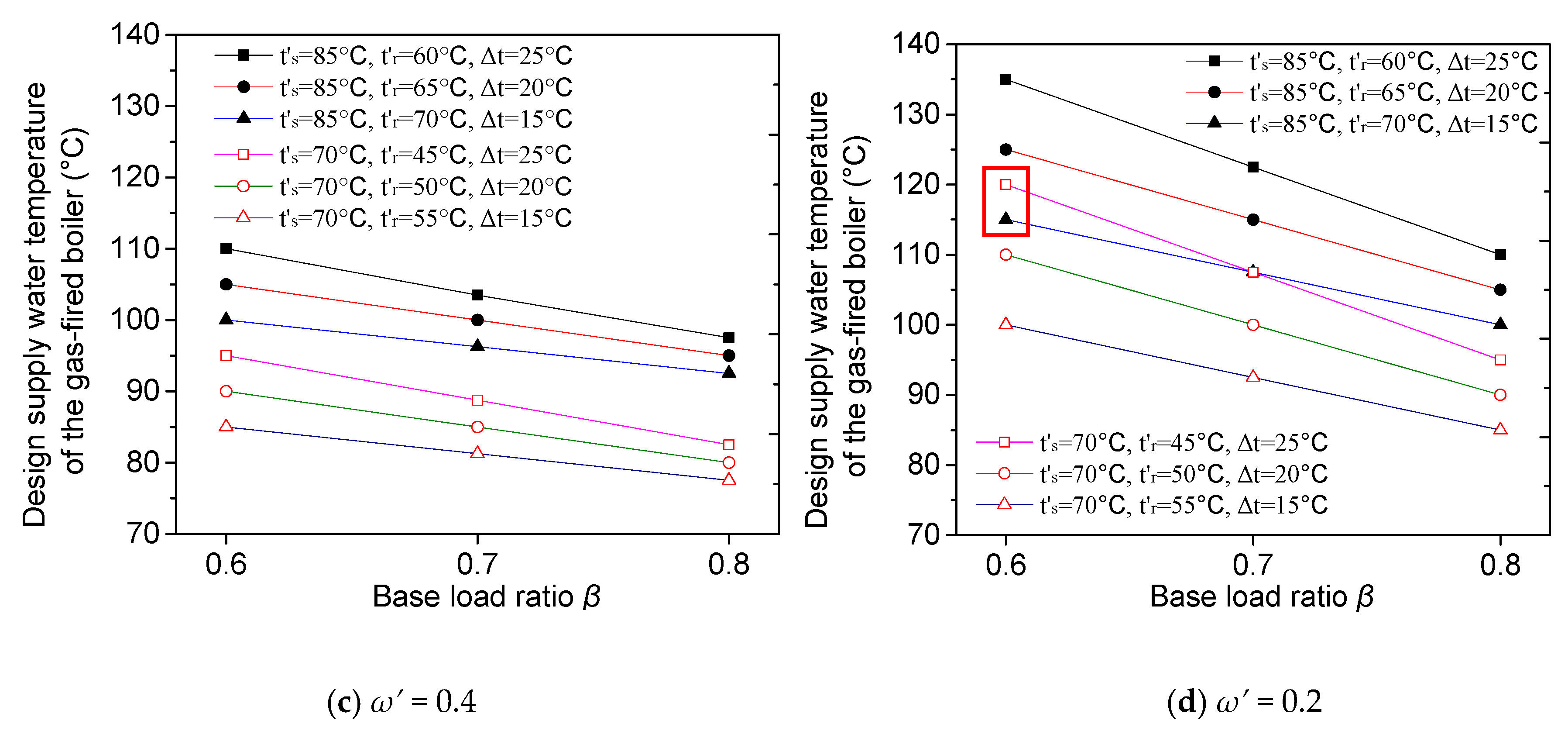
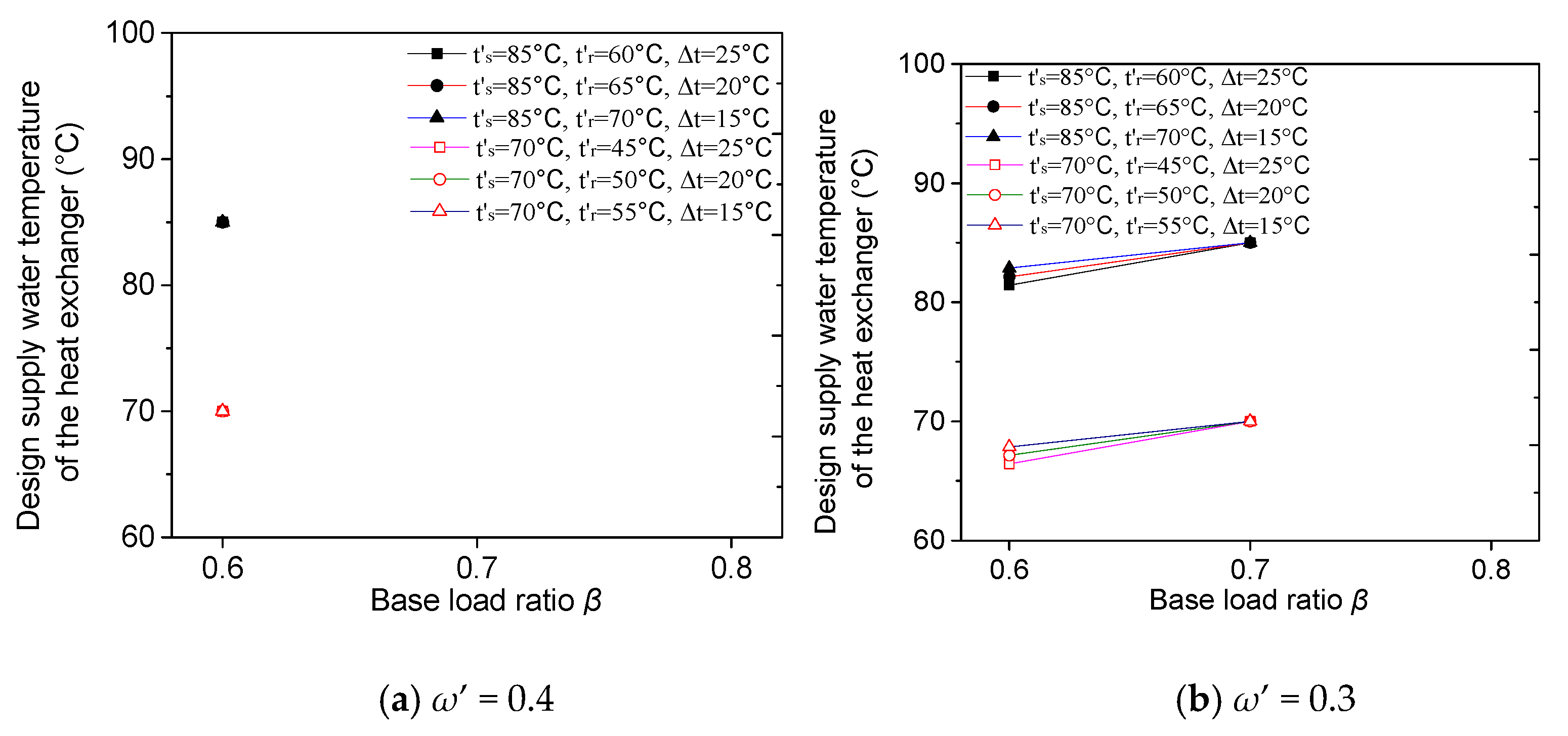
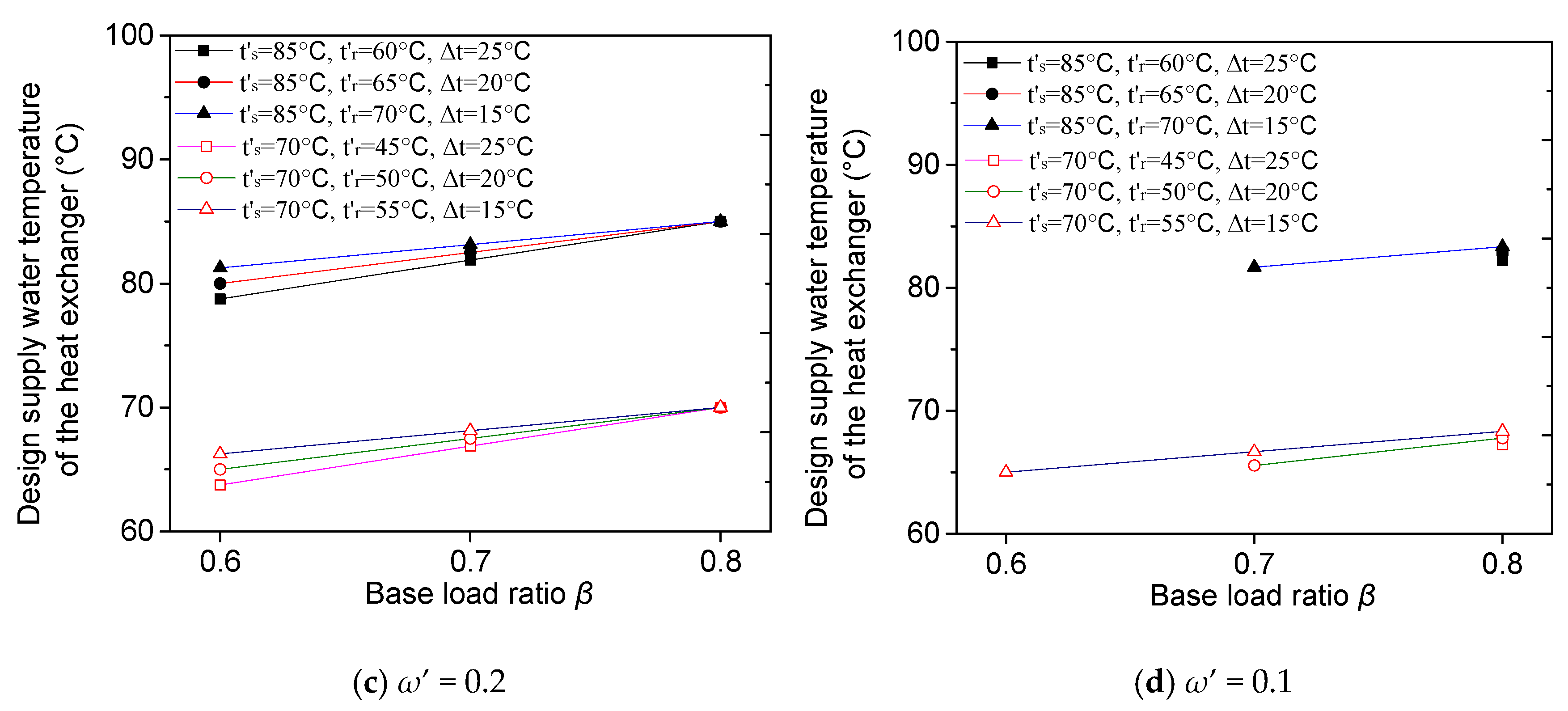
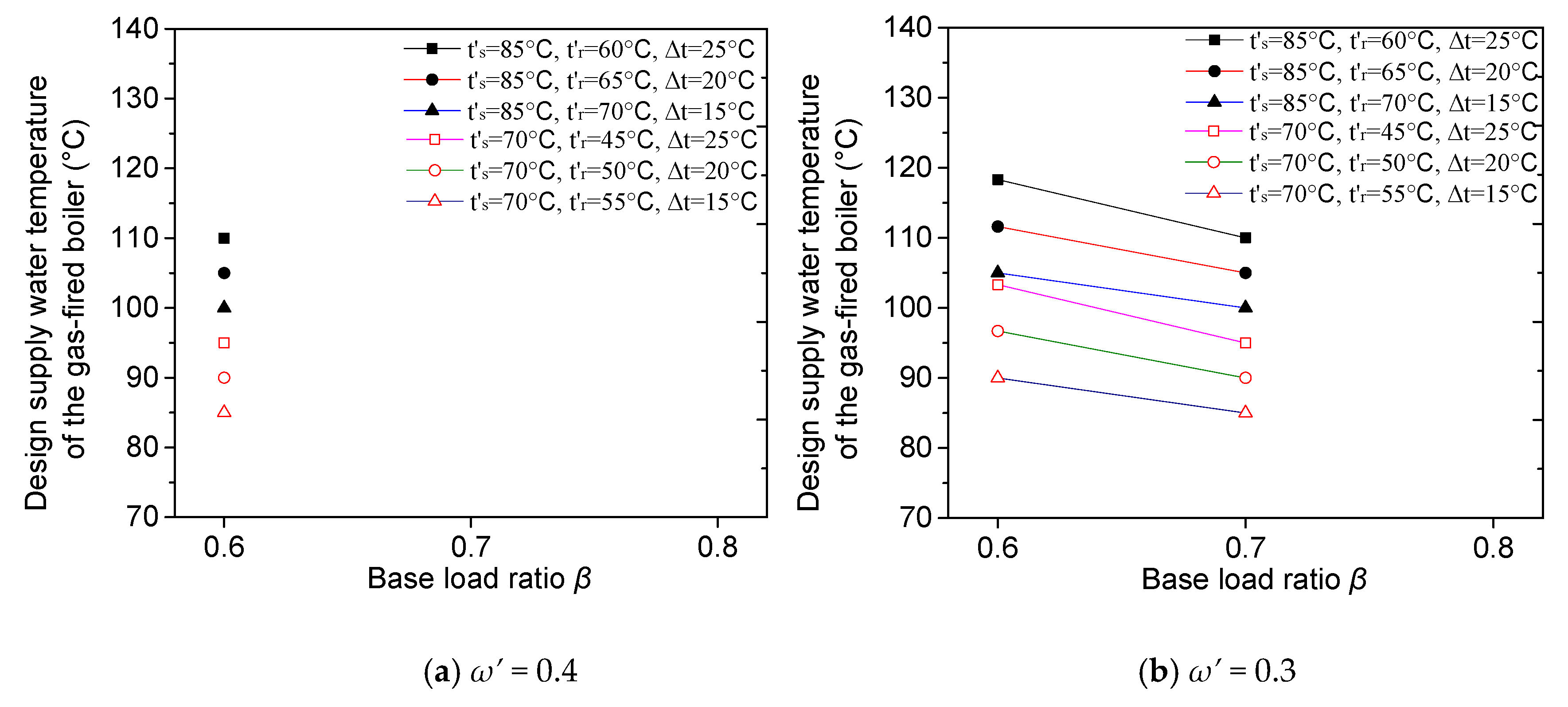
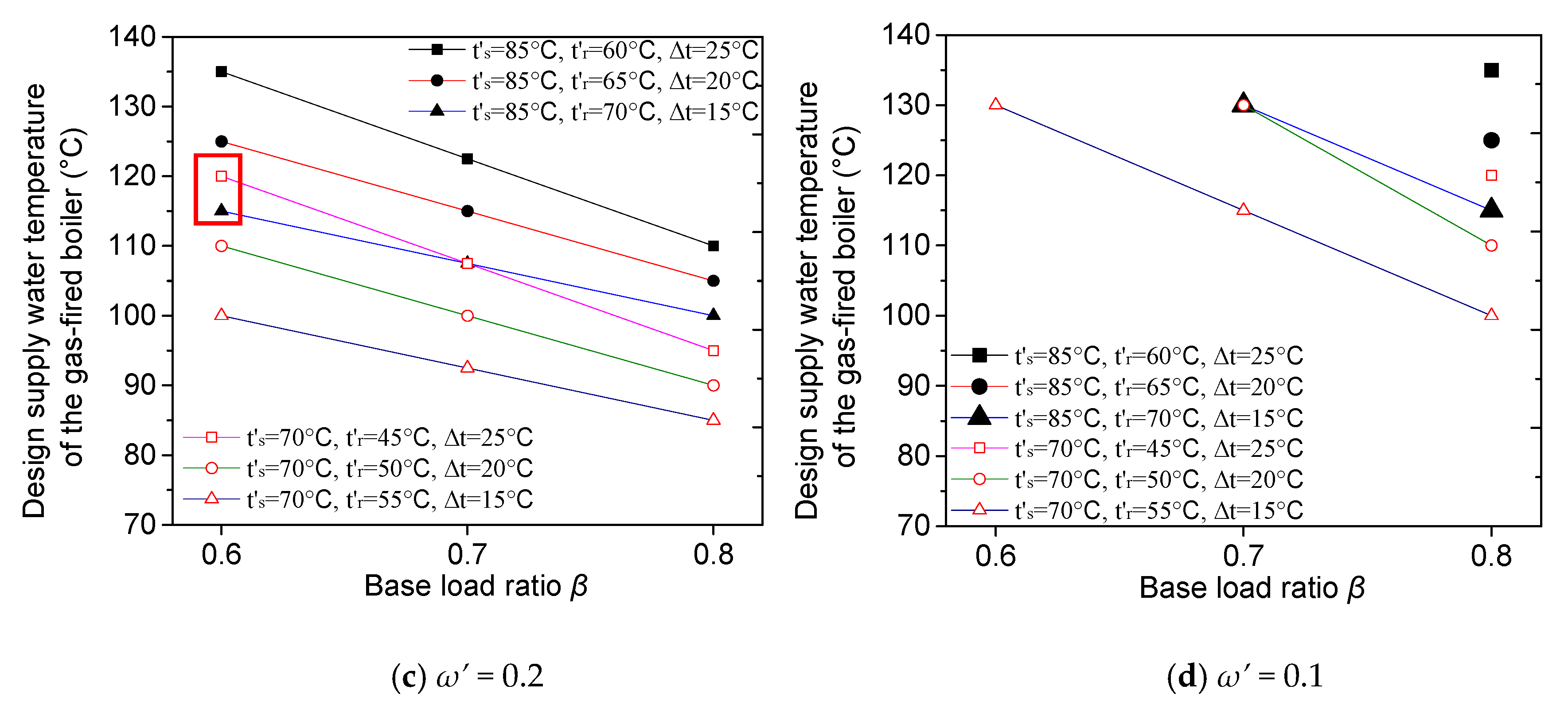
3.1. Design Supply Water Temperatures of Heat Exchanger and the Gas-Fired Boiler
3.2. Supply Water Temperatures of Heat Exchanger and Gas-Fired PB under Working Conditions
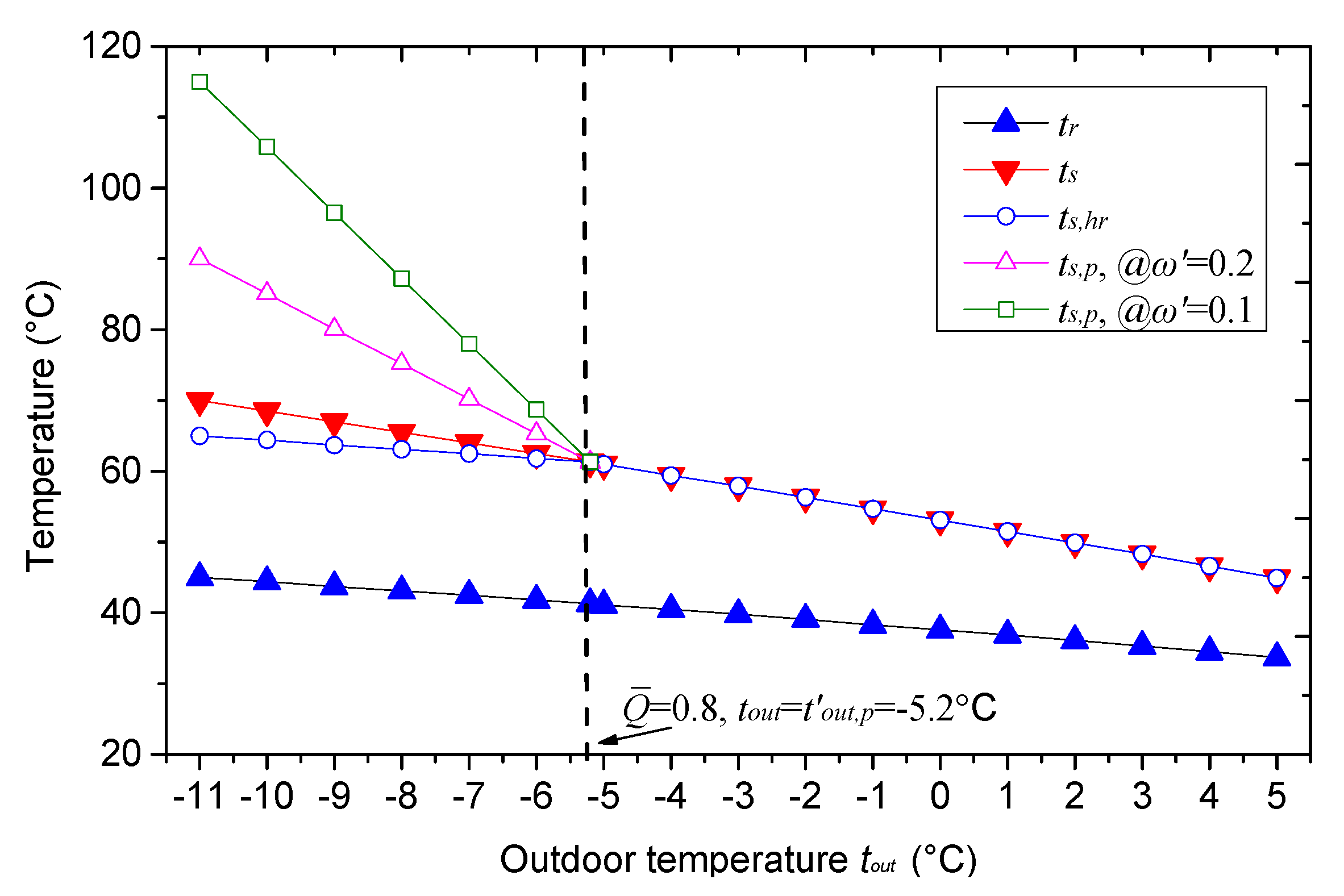
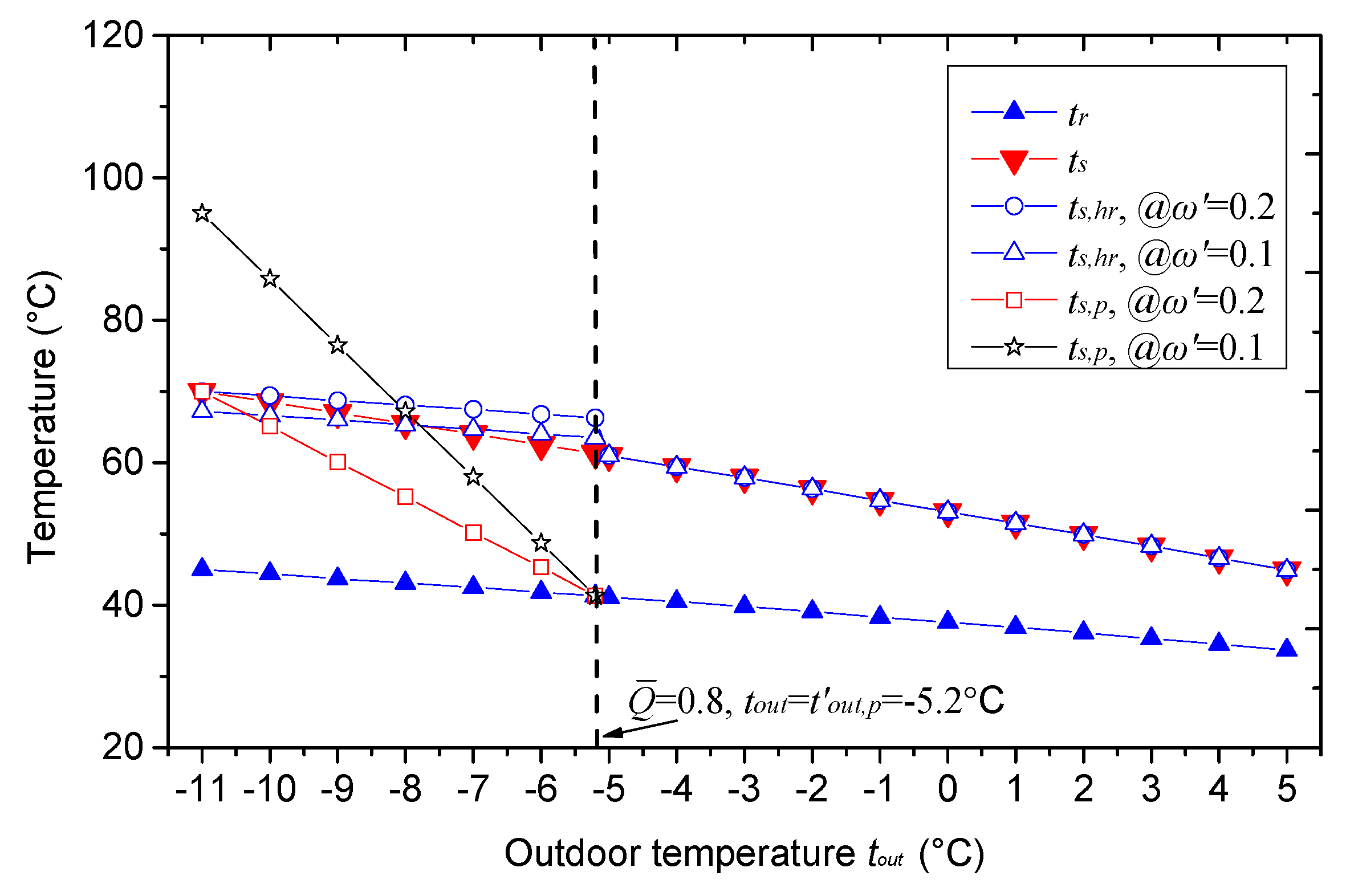
3.2.1. During the Peak Heating Period
3.2.2. During the Heating Period When Peak Heating Is Not Needed
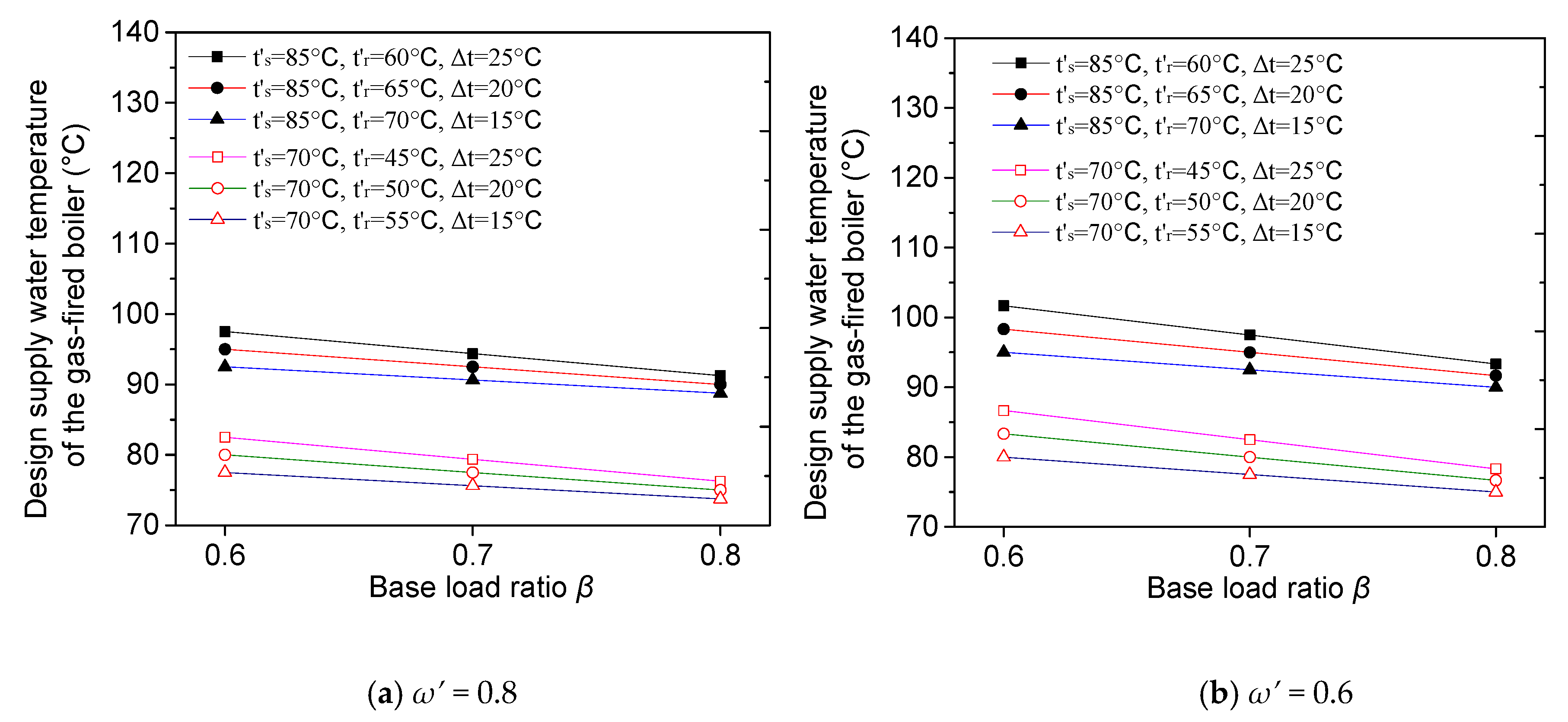
3.3. Discussion on the Design Peak-Shaving Flow Ratio
4. Conclusions
- Under series connection mode, the design supply temperature of heat exchangers decreases linearly while the design supply temperature of increases linearly with decreasing value of β; and their variation speeds are only proportional to the network temperature difference (Δt) but has no relation to the network temperature levels. This makes with low DH temperature level but at bigger Δt can even be higher than that with high temperature level at smaller Δt.
- For the parallel connection mode, when the design peak shaving flow ratio ω′ = 1 − β, are equal to the design supply water temperature of the DHN and irrelevant to the Δt. Unlike the , varies with different Δt even when ω′ = 1 − β. When ω′ < 1 − β (Note that ω′ can not be larger than 1 − β according to the thermal balance), decreases linearly but increases linearly when β is smaller, and the increasing speed is faster for the system with the bigger Δt. This also makes it possible for with lower temperature level to exceed that with higher temperature level.
- After examining the variation of those parameters under working conditions with arbitrary tout, an important property for both series and parallel connection modes was revealed, i.e., the temperature difference between the supply water temperature of the heat exchanger ts,hr and the return water temperature tr is a constant which equals to ( − ).
- This study proposed a very important variable called the design peak shaving flow ratio ω′, which heavily affects the system from the perspective of the pumping energy consumption. If the value of ω′ is too large, the pumping energy consumption of the peak-shaving circulation pump will be increased, otherwise the supply temperature of gas-fired boilers will be dramatically increased due to the small flow rate at a certain heat output. There exists an upper and lower limit of ω′ for both connection modes. The upper limits of ω′ are 1 and (1 − β) for series and parallel connection modes, but the lower limits should be determined according to the chosen of other parameters, e.g., , , and . It is recommended to use the smallest possible peak shaving flow ratio for both series or parallel connection modes in order to save pumping energy.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a, coefficient of the heat transfer equation of radiators. |
| b, index of the heat transfer equation of radiators. |
| cwater, specific heat capacity of water; 4186.8 J/(kg·°C). |
| F, radiation area of the radiators; m2. |
| Fhr, heat exchange area; m2. |
| Gb, flow rate of the base load heat plant; kg/s. |
| Gp, flow rate of the circulation pump for peak shaving gas-fired boiler; kg/s. |
| G1, flow rate in the primary network; kg/s. |
| G2, flow rate of the circulation pump for secondary network; kg/s. |
| g2,i, flow rate in the ith heating substation; kg/s. |
| , relative flow rate ratio in primary network. |
| , relative flow rate ratio in secondary network. |
| , relative flow rate ratio of primary side in the ith substation. |
| , relative flow rate ratio of secondary side in the ith substation. |
| , relative flow rate ratio in the secondary side of the heat exchanger. |
| , relative heat transfer coefficient of water-water heat exchanger. |
| , relative heat transfer coefficient of the heat exchanger in the ith substation. |
| Q′, design heat load of the whole DH system; W. |
| qload,b,i, heat load supplied from the base load heat plant to the ith substation; W. |
| qload,i, heat load of the ith substation; W. |
| Qload,b, heat load of the base load heat plant; W. |
| Qload,p, peak shaving heat load during the peak heating period; W. |
| Qhr, heat load of all heat exchangers; W. |
| Qnetwork, heat load that users receive from the network; W. |
| Qbuilding, heat load of the buildings in the network; W. |
| Qradiator, heat releasing load of radiators in the network; W. |
| q, volumetric heat index of the buildings; W/m3. |
| qhr,i, heat laod of heat exchanger in the ith substation; W. |
| , relative heat load ratio in primary network. |
| , relative heat load ratio in secondary network. |
| ts, supply water temperature of the secondary network; °C. |
| ts,hr, supply water temperature of the heat exchanger; °C. |
| tr, return water temperatures of the secondary network; °C. |
| ts,p, supply water temperature of the peak shaving gas-fired boiler; °C. |
| tout, outdoor temperature; °C. |
| tin, indoor temperature; °C. |
| Δt, logarithmic mean temperature difference of the heat exchanger; °C. |
| V, peripheral volume of the buildings; m3. |
| α, peak load ratio. |
| β, base load ratio of a DH system. |
| βi, base load ratio for the ith substation. |
| ω, peak shaving flow ratio. |
| τs, supply water temperature of the primary network; °C. |
| τr, return water temperature of the primary network; °C. |
| Note: parameters with “ ′ ” means design value. |
References
- Wang, H.C.; Lahdelma, R.; Wang, X.; Jiao, W.L.; Zhu, C.Z.; Zou, P.H. Analysis of the location for peak heating in CHP based district heating systems. Appl. Therm. Eng. 2015, 87, 402–411. [Google Scholar] [CrossRef]
- Zhang, D.G. The Operation Analysis and Best Project Confirm in Many Heat Sources Joint Operation of Heat Supply Networks. Master’s Thesis, Harbin Engineering University, Harbin, China, 2005. [Google Scholar]
- Helen. Finland. Reliable District Heat from Helen. Available online: https://www.helen.fi/en/heating/ (accessed on 19 September 2019).
- Kauko, H.; Kvalsvik, K.H.; Rohde, D.; Hafner, A.; Nord, N. Dynamic modelling of local low-temperature heating grids: A case study for Norway. Energy 2017, 139, 289–297. [Google Scholar] [CrossRef] [Green Version]
- Barelli, L.; Bidini, G.; Pinchi, E.M. Implementation of a Cogenerative District Heating: Optimization of a Simulation Model for the Thermal Power Demand. Energy Build. 2006, 38, 1434–1442. [Google Scholar] [CrossRef]
- He, P.; Tao, Y.C.; Xu, M.Z. Analysis of multi-source combined heating condition. Gas Heat 1990, 10, 34–40. [Google Scholar]
- He, P.; Tao, Y.C.; Sun, G. Analysis of the design principle and method of multi-heat source combined heating system pipe network. Gas Heat 1990, 10, 43–48. [Google Scholar]
- Jiang, Y.; Lin, F.; Liu, L.F. The Utility Model Relates to a Method for Combined Heating of Coal and Gas. Chinese Patent Number CN 1952493A, 14 January 2009. [Google Scholar]
- Huang, J. Comprehensive Evaluation for the Setup of Peak Heating Using Gas Fired Boiler. Master’s Thesis, Beijing University of Civil Engineering and Architecture, Beijing, China, 2011. [Google Scholar]
- Wang, H.C.; Jiao, W.L.; Lahdelma, R.; Zou, P.H. Techno-economic analysis of a coal-fired CHP based DH system with gas-fired boilers for peak load compensation. Energy Policy 2011, 39, 7950–7962. [Google Scholar] [CrossRef]
- Wang, H.C.; Jiao, W.L.; Zou, P.H.; Liu, J.C. Analysis of an effective solution to excessive heat supply in a city primary heating network using gas-fired boilers for peak load compensation. Energy Build. 2010, 42, 2090–2097. [Google Scholar] [CrossRef]
- Han, W.G.; Jiang, Y.; Guo, F. Analysis of energy consumption of various heating methods. J. HVAC 2005, 35, 106–110. [Google Scholar]
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelplund, F.; Mathiesen, B. 4th Generation District Heating (4GDH): Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Zheng, X.J.; You, S.J.; Jiang, N. Operation and regulation scheme of central heating system with two-level network peak regulation. J. Tianjin Univ. 2008, 40, 1511–1516. [Google Scholar]
- Zheng, X.J. Optimization design of gas peak-regulating central heating system for secondary network. J. Tianjin Univ. 2007, 40, 948–951. [Google Scholar]
| Parameters | Series Connection | Parallel Connection | ||
|---|---|---|---|---|
| Design Parameters | ||||
| Operating Parameters | ts,hr | Gas-fired boilers operating | ||
| Gas-fired boilers closed | ts,hr = ts | |||
| ts,p | Gas-fired boilers operating | |||
| Gas-fired boilers closed | ||||
| Design peak shaving flow ratio ω′ | ≤ ω′ ≤ 1 | ≤ ω′ ≤ 1 − β | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, H.; Wu, X.; Duanmu, L.; Teppo, E.; Lahdelma, R.; Li, J.; Yu, L. Analysis on the Thermal Balance and Operational Parameters for the District Heating System with Peak Load Boilers in Heating Substations. Energies 2020, 13, 6180. https://doi.org/10.3390/en13236180
Li X, Wang H, Wu X, Duanmu L, Teppo E, Lahdelma R, Li J, Yu L. Analysis on the Thermal Balance and Operational Parameters for the District Heating System with Peak Load Boilers in Heating Substations. Energies. 2020; 13(23):6180. https://doi.org/10.3390/en13236180
Chicago/Turabian StyleLi, Xiangli, Haichao Wang, Xiaozhou Wu, Lin Duanmu, Esa Teppo, Risto Lahdelma, Ji Li, and Li Yu. 2020. "Analysis on the Thermal Balance and Operational Parameters for the District Heating System with Peak Load Boilers in Heating Substations" Energies 13, no. 23: 6180. https://doi.org/10.3390/en13236180





