A Novel Equivalent Continuum Approach for Modelling Hydraulic Fractures
Abstract
1. Introduction
2. Literature Review on Hydraulic Fracturing Modelling Methods
2.1. Analytical Models
2.2. Cohesive Zone Method (CZM)
2.3. Extended Finite Element Modelling (XFEM)
2.4. Discrete Element Method (DEM)
2.5. FEM-DEM
2.6. Equivalent Continuum Methods (ECM)
3. Methodology
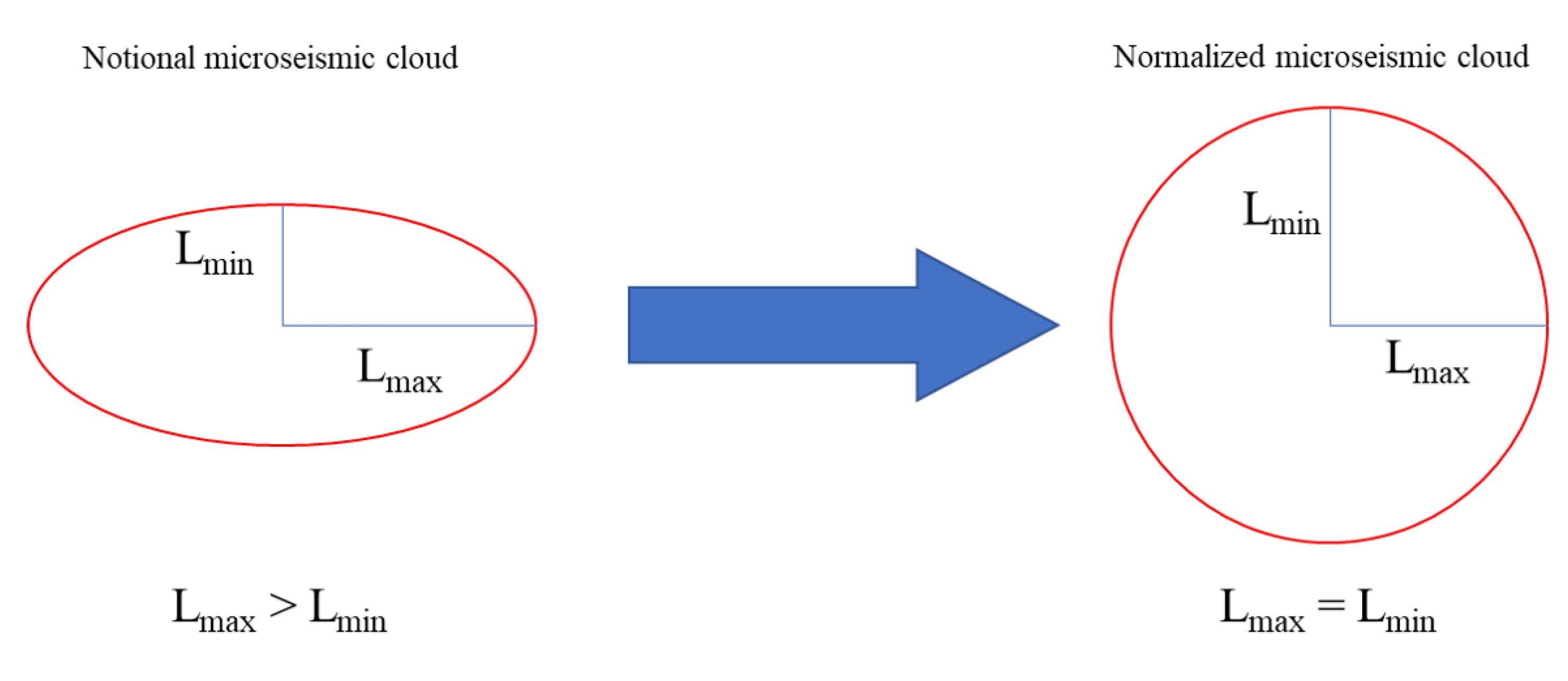
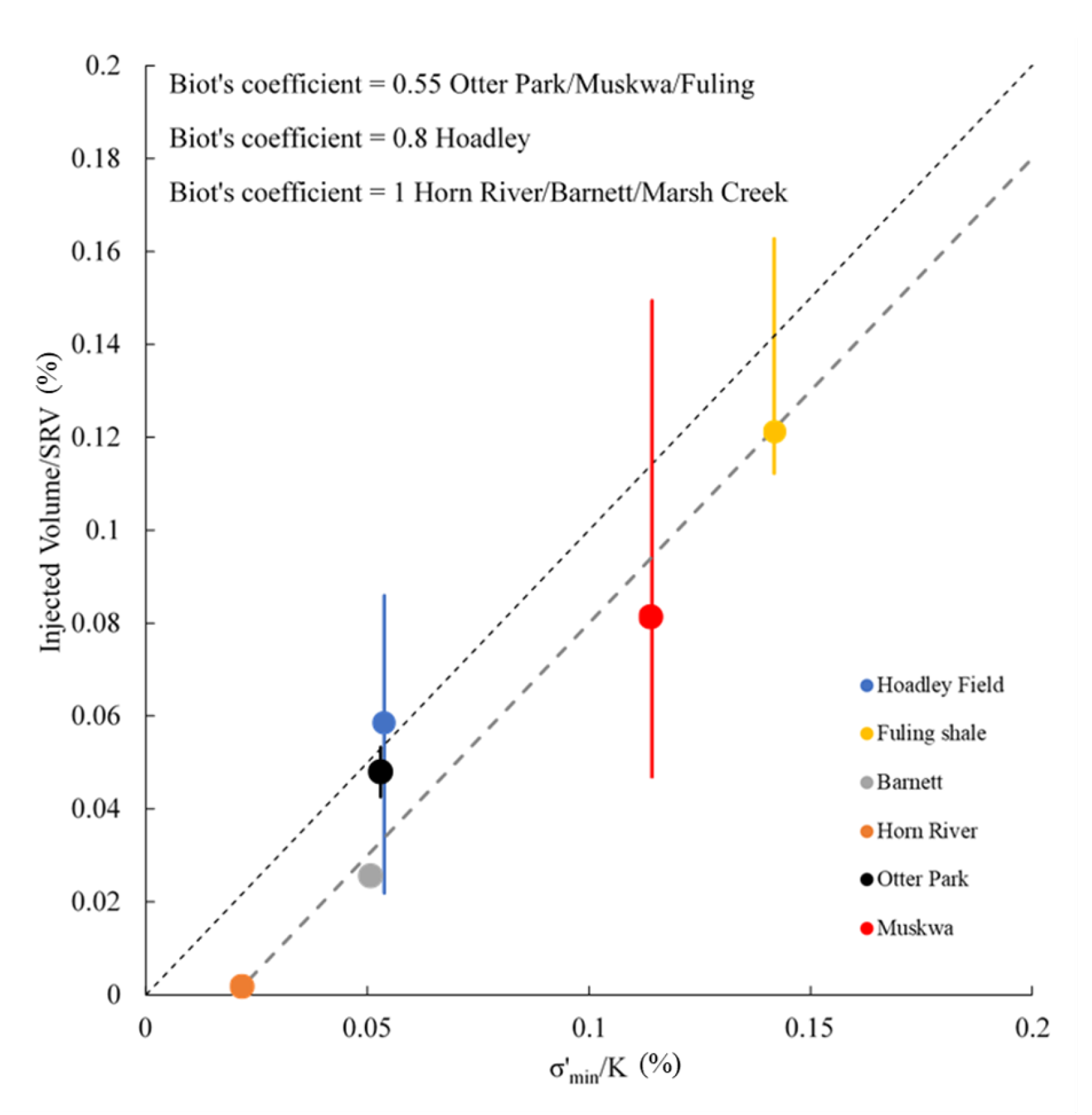
3.1. Average Volumetric Strain in Fractured Zone
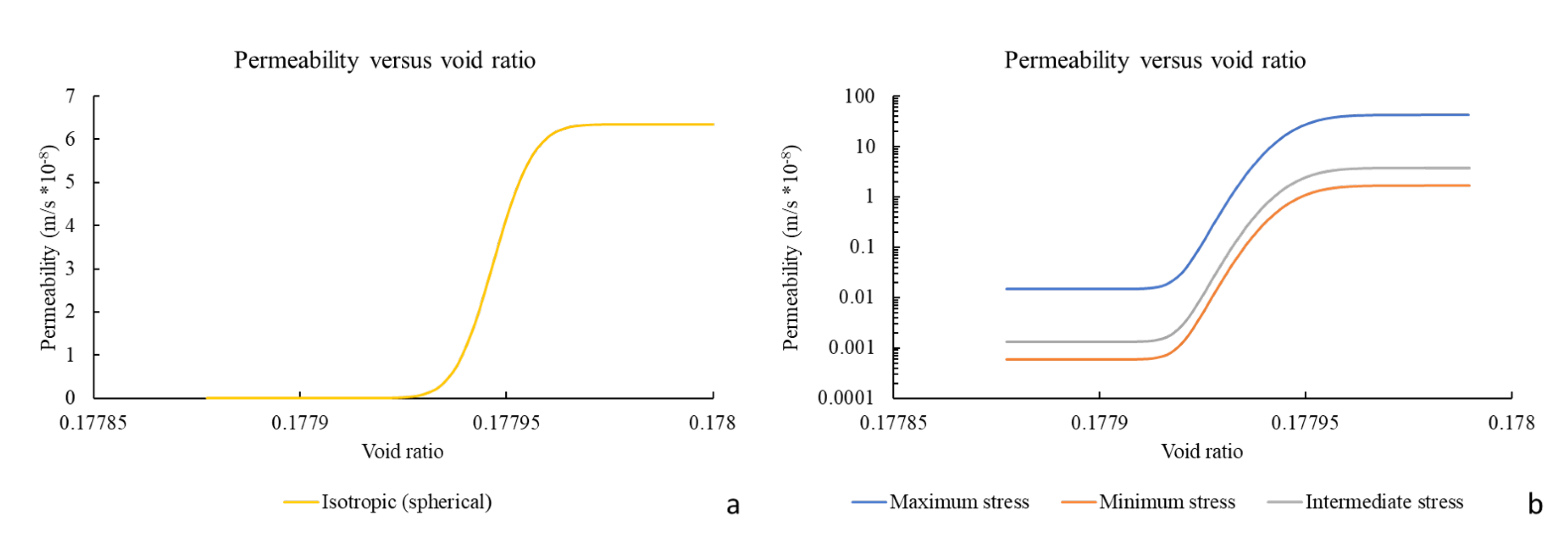
3.2. Void Ratio Dependent Permeability
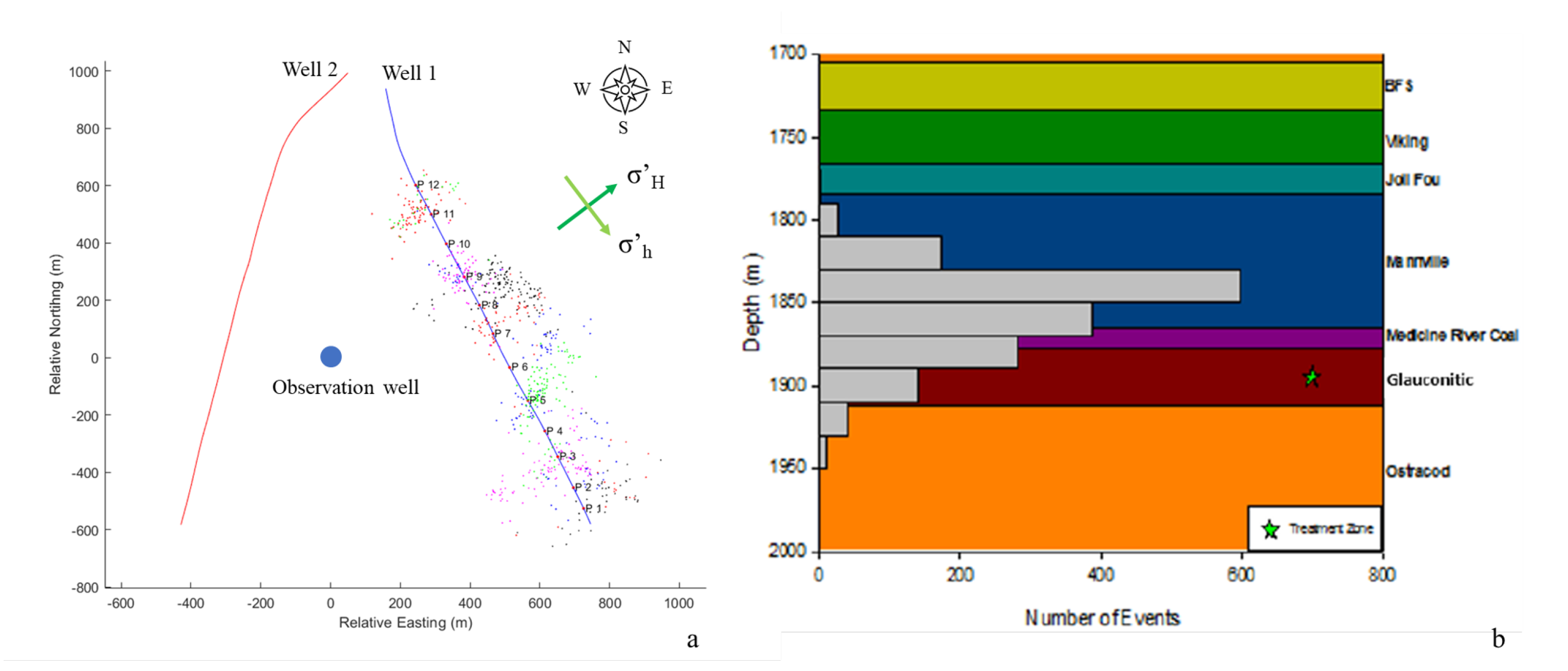
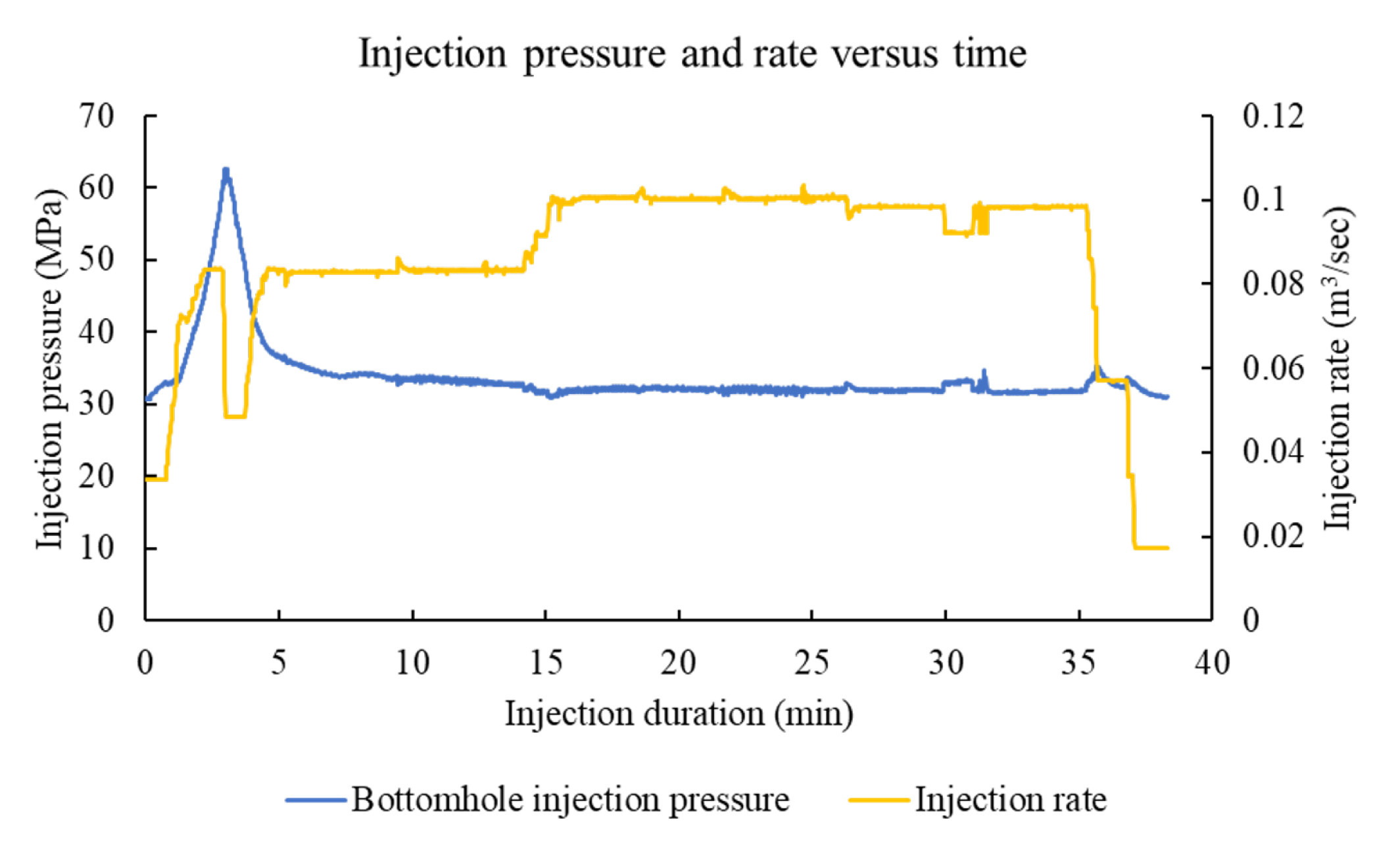
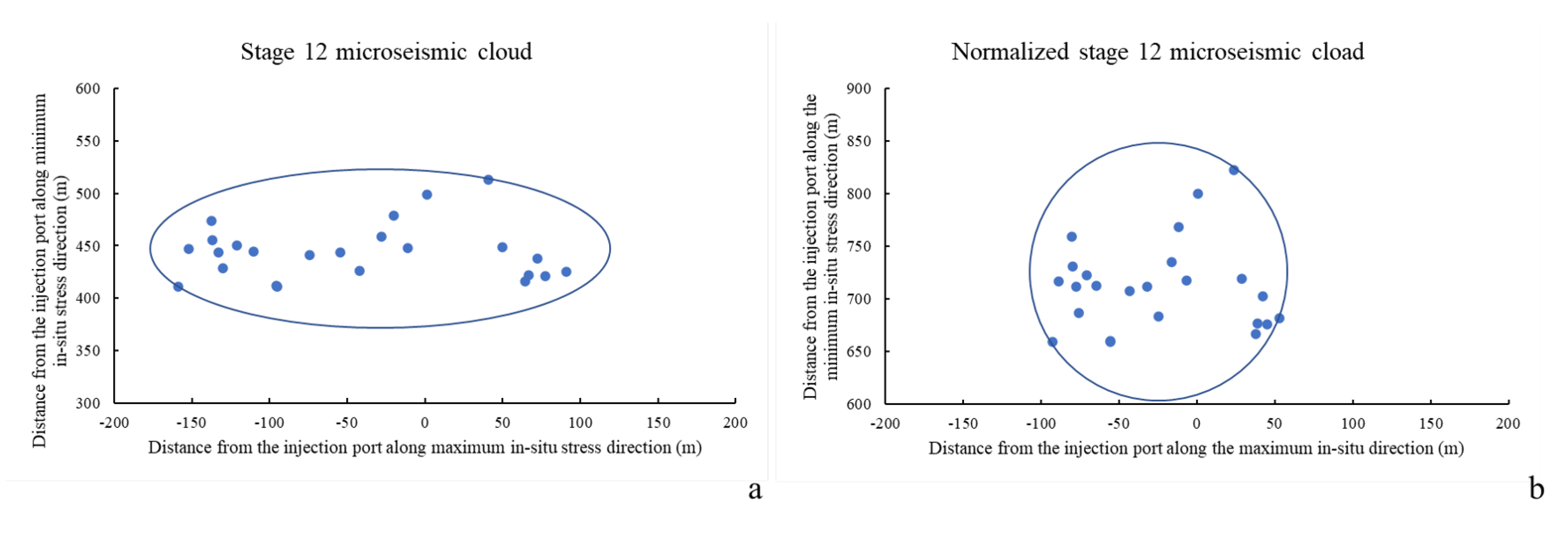
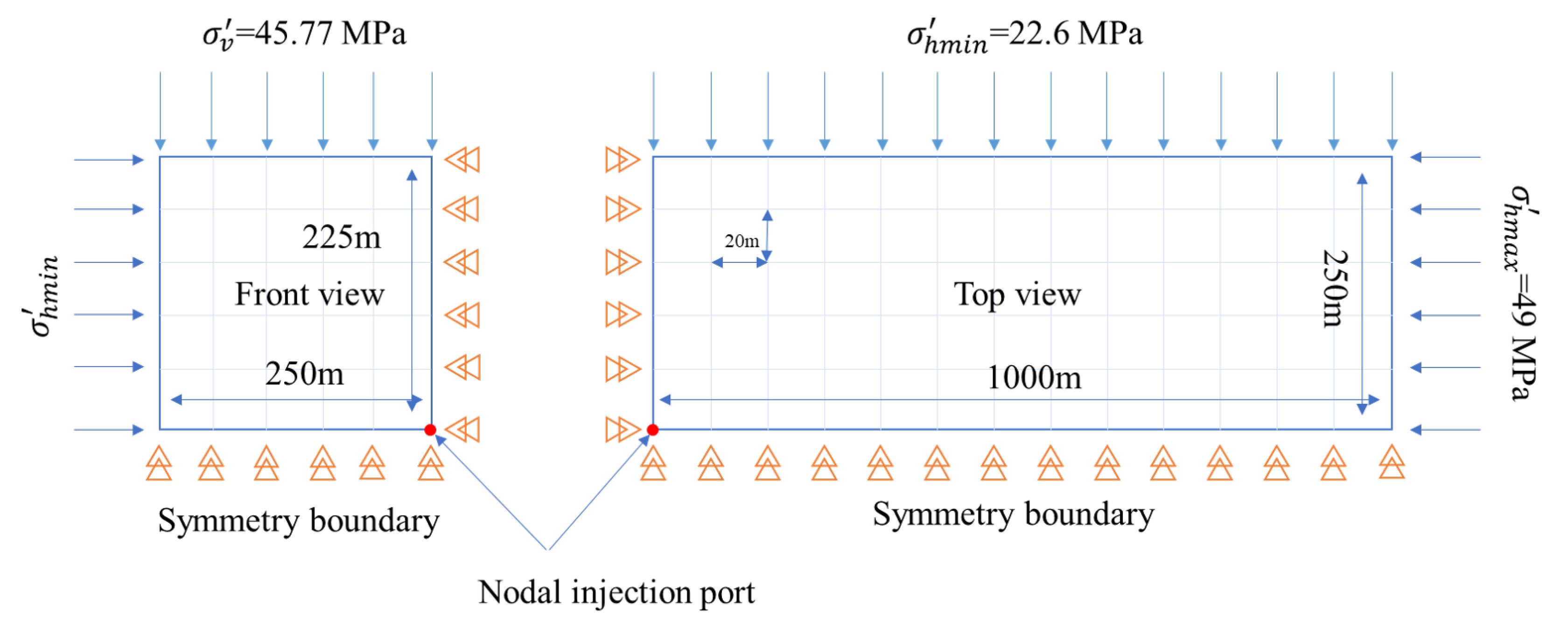
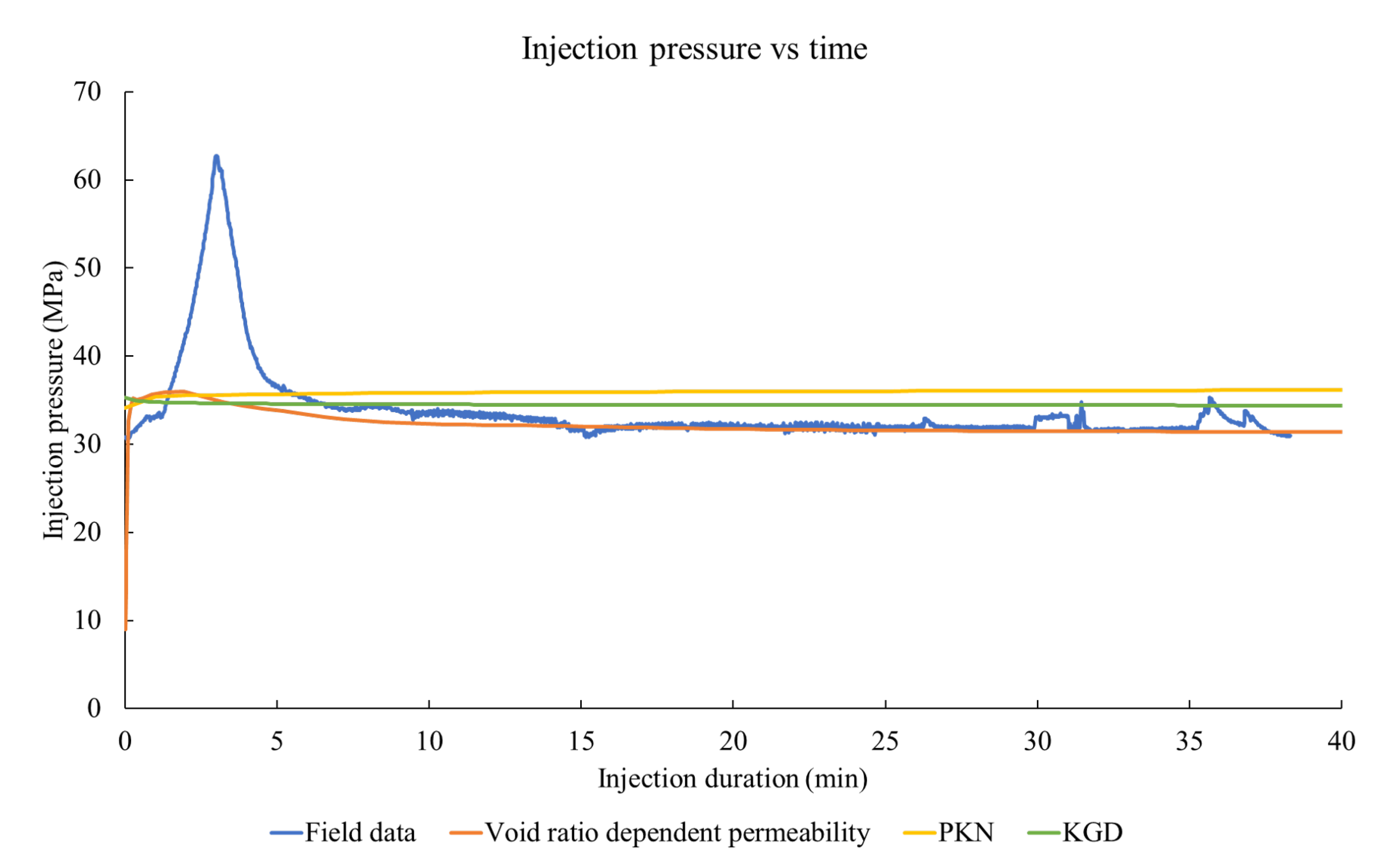
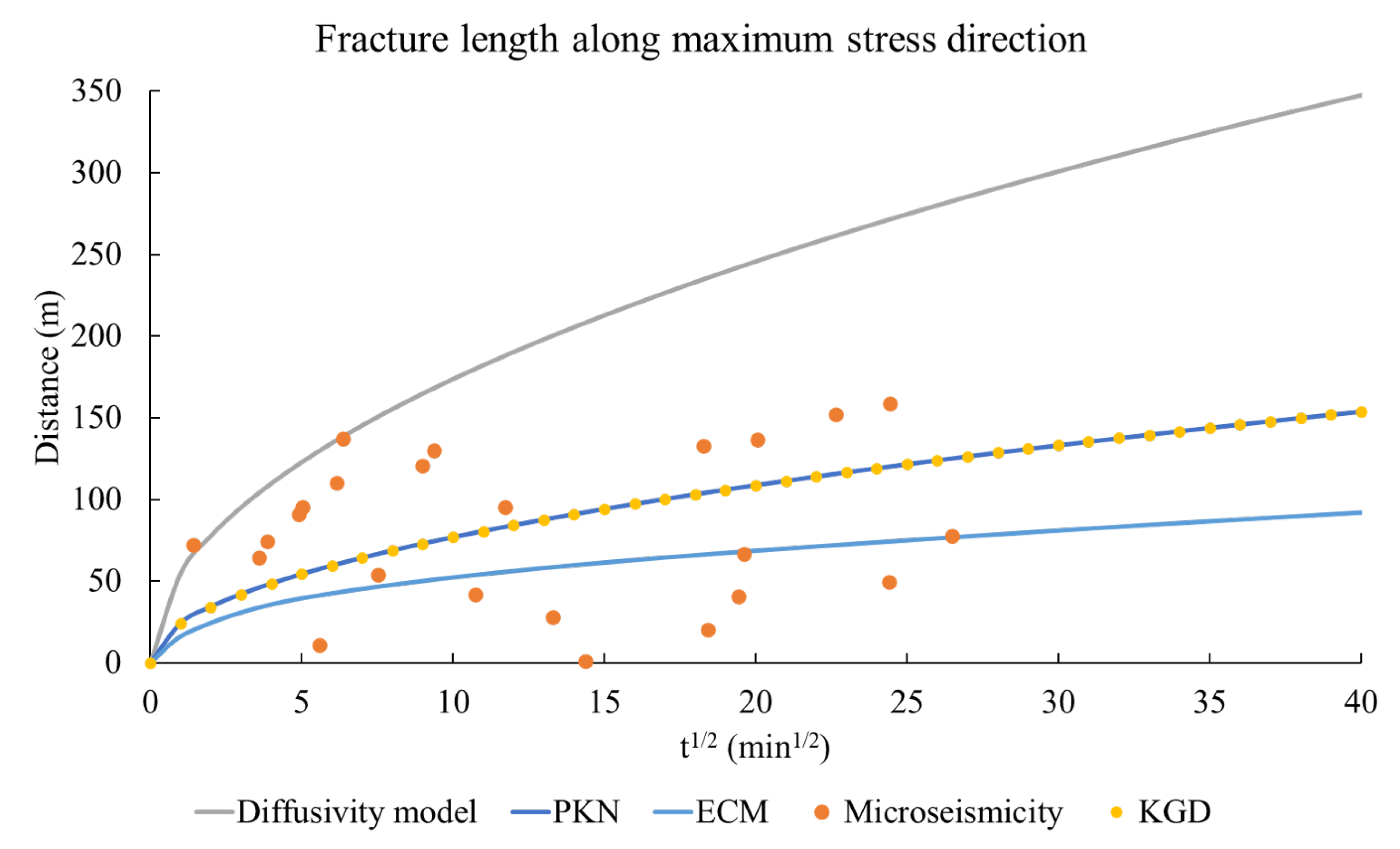
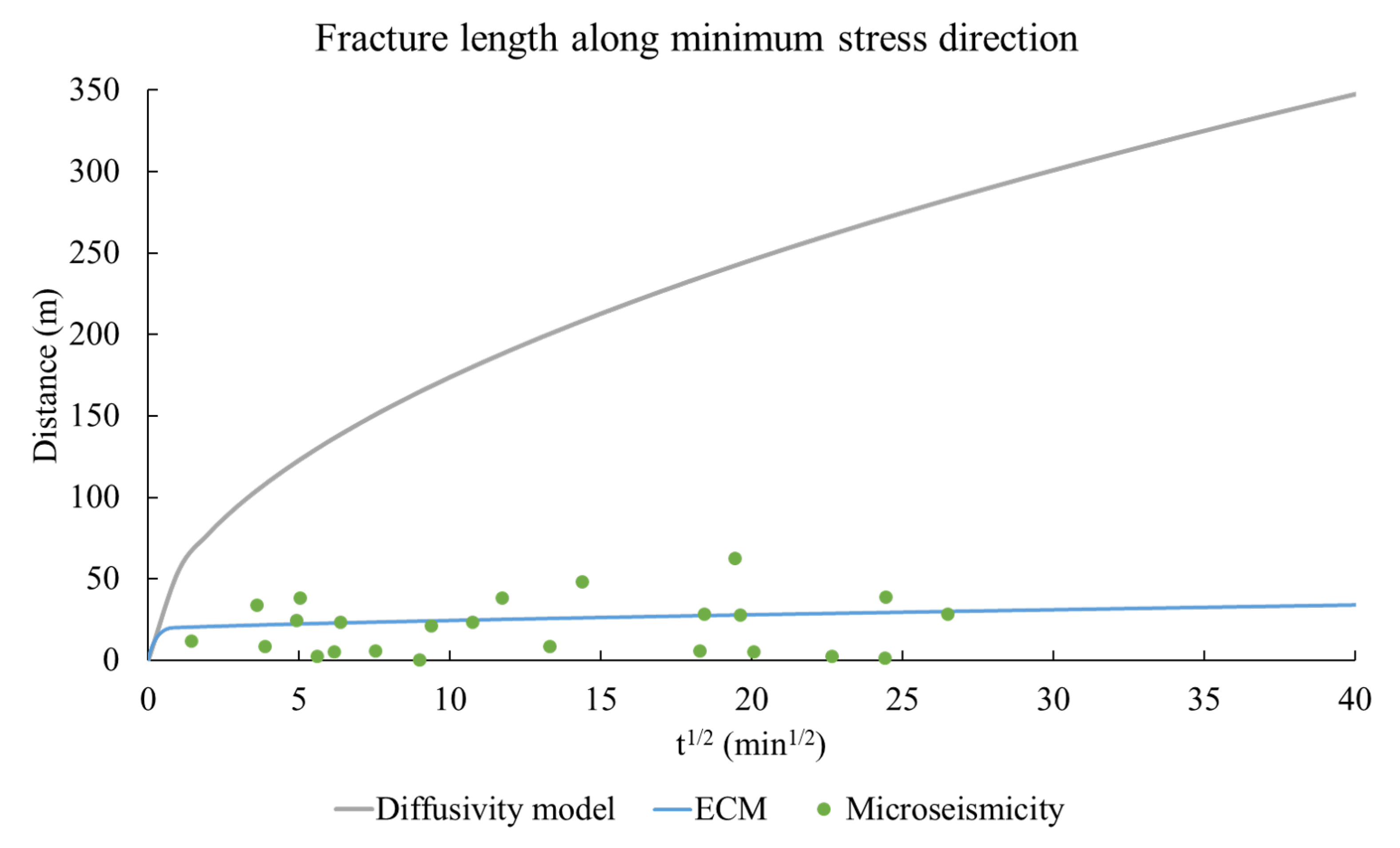
3.3. Case Study—Hoadley Tight Sand Reservoir
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite Element Modelling |
| CZM | Cohesive Zone Modelling |
| XFEM | Extended Finite Element Modelling |
| ECM | Equivalent Continuum Method |
| SRV | Stimulated Reservoir Volume |
References
- Li, Q.; Xing, H.; Liu, J.; Liu, X. A review on hydraulic fracturing of unconventional reservoir. Petroleum 2015, 1, 8–15. [Google Scholar] [CrossRef]
- Montgomery, C.T.; Smith, M.B. Hydraulic fracturing: History of an enduring technology. JPT J. Pet. Technol. 2010, 62, 26–32. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. A simplified three-dimensional displacement discontinuity method for multiple fracture simulations. Int. J. Fract. 2015, 193, 191–204. [Google Scholar] [CrossRef]
- Warpinski, N. A review of hydraulic-fracture induced microseismicity. In Proceedings of the 48th US Rock Mechanics/Geomechanics Symposium, Minneapolis, MN, USA, 1–4 June 2014; American Rock Mechanics Association. Available online: https://www.onepetro.org/conference-paper/ARMA-2014-7774 (accessed on 24 November 2020).
- Yao, Y.; Gosavi, S.V.; Searles, K.H.; Ellison, T.K. Cohesive fracture mechanics based analysis to model ductile rock fracture. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Haddad, M.; Sepehrnoori, K. Simulation of multiple-stage fracturing in quasibrittle shale formations using pore pressure cohesive zone model. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014; pp. 1777–1792. [Google Scholar] [CrossRef]
- Haddad, M.; Sepehrnoori, K. Integration of XFEM and CZM to model 3D multiple-stage hydraulic fracturing in quasi-brittle shale formations: Solution-dependent propagation direction. In Proceedings of the AADE National Technical Conference and Exhibition, San Antonio, TX, USA, 8–9 April 2015; pp. 8–9. [Google Scholar]
- Haddad, M.; Sepehrnoori, K. Simulation of hydraulic fracturing in quasi-brittle shale formations using characterized cohesive layer: Stimulation controlling factors. J. Unconv. Oil Gas Resour. 2015, 9, 65–83. [Google Scholar] [CrossRef]
- Wang, H. Numerical modeling of non-planar hydraulic fracture propagation in brittle and ductile rocks using XFEM with cohesive zone method. J. Pet. Sci. Eng. 2015, 135, 127–140. [Google Scholar] [CrossRef]
- Zielonka, M.G.; Searles, K.H.; Ning, J.; Buechler, S.R. Development and validation of fully-coupled hydraulic fracturing simulation capabilities. In Proceedings of the SIMULIA Community Conference, Providence, RI, USA, 20–22 May 2014; pp. 19–21. [Google Scholar]
- Arndt, S.; Zee, W.V.D.; Hoeink, T.; Hughes, B.; Nie, J. Hydraulic fracturing simulation for fracture networks. In Proceedings of the SIMULIA Community Conference, Berlin, Germany, 18–21 May 2015; Volume 4. [Google Scholar]
- Nasirisavadkouhi, A. A comparison study of KGD. PKN Modif. P3D Model 2015. [Google Scholar] [CrossRef]
- Yu, G.; Aguilera, R. 3D analytical modeling of hydraulic fracturing stimulated reservoir volume. In SPE Latin America and Caribbean Petroleum Engineering Conference, Mexico City, Mexico, 16–18 April, 2012; Society of Petroleum Engineers, SPE-153486-MS, SPE; Available online: https://www.onepetro.org/conference-paper/SPE-153486-MS (accessed on 24 November 2020).
- Bouteca, M.J. 3D analytical model for hydraulic fracturing: Theory and field test. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, USA, 27–30 September 1984. [Google Scholar] [CrossRef]
- Stalgorova, E.; Mattar, L. Analytical model for unconventional multifractured composite systems. SPE Reserv. Eval. Eng. 2013, 16, 246–256. [Google Scholar] [CrossRef]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 2007, 21, 1571–1581. [Google Scholar] [CrossRef]
- Nordgren, R. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Maulianda, B. On Hydraulic Fracturing of Tight Gas Reservoir Rock. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2016. [Google Scholar] [CrossRef]
- Gonzalez, D.; Holman, R.; Richard, R.; Xue, H.; Morales, A.; Kwok, C.K.; Judd, T. Accounting for production shadow in infill/DUC well hydraulic fracturing modeling and calibration. In SPE Liquids-Rich Basins Conference-North America, Midland, Texas, USA, 13–14 September, 2017; Society of Petroleum Engineers; Available online: https://www.onepetro.org/conference-paper/SPE-187479-MS (accessed on 24 November 2020).
- Valiullin, A.; Makienko, V.; Yudin, A.; Overin, A.; Gromovenko, A. Channel fracturing technique helps to revitalize brown fields in langepas area. In Society of Petroleum Engineers—SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 24–26 November 2015; Society of Petroleum Engineers; Available online: https://www.onepetro.org/conference-paper/SPE-178131-MS (accessed on 24 November 2020). [CrossRef]
- Chen, Z.; Bunger, A.P.; Zhang, X.; Jeffrey, R.G. Cohesive zone finite element-based modeling of hydraulic fractures. Acta Mech. Solida Sin. 2009, 22, 443–452. [Google Scholar] [CrossRef]
- Wang, X.L.; Liu, C.; Wang, H.; Liu, H.; Wu, H.A. Comparison of consecutive and alternate hydraulic fracturing in horizontal wells using XFEM-based cohesive zone method. J. Pet. Sci. Eng. 2016, 143, 14–25. [Google Scholar] [CrossRef]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, L.; Keer, L.M. Pore pressure cohesive zone modeling of hydraulic fracture in quasi-brittle rocks. Mech. Mater. 2015, 83, 17–29. [Google Scholar] [CrossRef]
- Carrier, B.; Granet, S. Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model. Eng. Fract. Mech. 2012, 79, 312–328. [Google Scholar] [CrossRef]
- Yao, Y. Linear elastic and cohesive fracture analysis to model hydraulic fracture in brittle and ductile rocks. Rock Mech. Rock Eng. 2012, 45, 375–387. [Google Scholar] [CrossRef]
- Lavrov, A.; Larsen, I.; Holt, R.M.; Bauer, A.; Pradhan, S. Hybrid FEM/DEM simulation of hydraulic fracturing in naturally-fractured reservoirs. In Proceedings of the 48th US Rock Mechanics/Geomechanics Symposium, Minneapolis, MN, USA, 1–4 June 2014; pp. 626–633. [Google Scholar]
- Munjiza, A.; John, N.W. Mesh size sensitivity of the combined FEM/DEM fracture and fragmentation algorithms. Eng. Fract. Mech. 2001, 69, 281–295. [Google Scholar] [CrossRef]
- Min, K.B. Fractured Rock Masses as Equivalent Continua—A Numerical Study. Ph.D. Thesis, Mark Och Vatten, Stockholm, Sweden, 2004. [Google Scholar]
- Oda, M. An equivalent continuum model for coupled stress and fluid flow analysis in jointed rock masses. Water Resour. Res. 1986, 22, 1845–1856. [Google Scholar] [CrossRef]
- Villeneuve, M.C.; Heap, M.J.; Kushnir, A.R.; Qin, T.; Baud, P.; Zhou, G.; Xu, T. Estimating in situ rock mass strength and elastic modulus of granite from the Soultz-sous-Forêts geothermal reservoir (France). Geotherm. Energy 2018, 6, 1–29. [Google Scholar] [CrossRef]
- JianPing, Y.; WeiZhong, C.; DianSen, Y.; JingQiang, Y. Numerical determination of strength and deformability of fractured rock mass by FEM modeling. Comput. Geotech. 2015, 64, 20–31. [Google Scholar] [CrossRef]
- Mack, M.G.; Warpinski, N.R. Mechanics of hydraulic fracturing. In Reservoir Stimulation; Wiley: New York, NY, USA, 2000; pp. 1–6. [Google Scholar]
- SIMULIA. ABAQUS 6.16-1. 2016. Available online: http://130.149.89.49:2080/v2016/index.html (accessed on 24 November 2020).
- Youn, D.J.; Griffiths, D.V. Hydro-Mechanical Coupled Simulation of Hydraulic Fracturing Using the Extended Finite Element Method (XFEM). Ph.D Thesis, Colorado School of Mines, Golden, GO, USA, 2016. [Google Scholar]
- Kang, Y.; Yu, M.; Miska, S.; Takach, N.E. Wellbore stability: A critical review and introduction to DEM. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009; Volume 4, pp. 2689–2712. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, H.; Mattson, E.; Wang, H.F.; Haimson, B.C.; Doe, T.W.; Oldenburg, C.M.; Dobson, P.F. Modeling of Hydraulic Fracture Propagation at the kISMET Site Using a Fully Coupled 3D Network-Flow and Quasi-Static Discrete Element Model; Technical Report; Idaho National Lab (INL): Idaho Falls, ID, USA, 2017. [Google Scholar]
- Nguyen, T.K.; Combe, G.; Caillerie, D.; Desrues, J. FEM x DEM modelling of cohesive granular materials: Numerical homogenisation and multi-scale simulations. Acta Geophys. 2014, 62, 1109–1126. [Google Scholar] [CrossRef]
- Maulianda, B.; Savitri, C.D.; Prakasan, A.; Atdayev, E.; Yan, T.W.; Yong, Y.K.; Elrais, K.A.; Barati, R. Recent comprehensive review for extended finite element method (XFEM) based on hydraulic fracturing models for unconventional hydrocarbon reservoirs. J. Pet. Explor. Prod. Technol. 2020. [Google Scholar] [CrossRef]
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Oda, M. Similarity rule of crack geometry in statistically homogeneous rock masses. Mech. Mater. 1984, 3, 119–129. [Google Scholar] [CrossRef]
- Mayerhofer, M.; Lolon, E.; Warpinski, N.; Cipolla, C.; Walser, D.; Rightmire, C. What Is Stimulated Rock Volume? In Proceedings of the SPE Shale Gas Production Conference, Fort Worth, TX, USA, 16–18 November 2009. [Google Scholar]
- Ahmed, T. Reservoir Engineering Handbook; Gulf Professional Publishing: Oxford, UK, 2018. [Google Scholar]
- Shapiro, S.; Hummel, N. Nonlinear diffusion-based interpretation of hydraulic fracturing induced seismicity. In Proceedings of the 75th EAGE Conference & Exhibition-Workshops, London, UK, 10–13 June 2013. cp–349–00028. [Google Scholar]
- Eaton, D.; Caffagni, E.; van der Baan, M.; Matthews, L. Passive seismic monitoring and integrated geomechanical analysis of a tight-sand reservoir during hydraulic-fracture treatment, flowback and production. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014; pp. 1537–1545. [Google Scholar]
- Ren, L.; Lin, R.; Zhao, J. Stimulated reservoir volume estimation and analysis of hydraulic fracturing in shale gas reservoir. Arab. J. Sci. Eng. 2018, 43, 6429–6444. [Google Scholar] [CrossRef]
- Li, Q.; Aguilera, R. Parametric probabilistic models for fluid diffusivity inversion and forward microseismic generation using seismicity rates. SPE West. Reg. Meet. 2018. [Google Scholar] [CrossRef]
- Xu, Y.; Adefidipe, O.; Dehghanpour, H. Estimating fracture volume using flowback data from the Horn River Basin: A material balance approach. J. Nat. Gas Sci. Eng. 2015, 25, 253–270. [Google Scholar] [CrossRef]
- Reynolds, M.; Thomson, S.; Peyman, F.; Hung, A.; Quirk, D.; Chen, S. A Direct Comparison of Hydraulic Fracture Geometry and Well Performance between Cemented Liner and Openhole Packer Completed Horizontal Wells in a Tight Gas Reservoir. In Proceedings of the PSPE Hydraulic Fracturing Technology Conference, Woodlands, TX, USA, 6–8 February 2012; pp. 1–19. [Google Scholar] [CrossRef]
- Broger, E.K.; Syhlonyk, G.E.; Zaitlin, B.A. Glauconite Sandstone Exploration: A Case Study from the Lake Newell Project, Southern Alberta. In Petroleum Geology of the Cretaceous Mannville Group Western Canada—Memoir 18; American Association of Petroleum Geologists, AAPG: Tulsa, OK, USA, 1997; pp. 140–168. Available online: http://archives.datapages.com/data/cspg_sp/data/018/018001/140_cspgsp0180140.htm (accessed on 24 November 2020).
| Property | Value |
|---|---|
| Porosity | 8–20% [49] [18] |
| Permeability | 0.001–0.01 mD [49] 0.07 mD [18] |
| Density | 2220 kg/m [50] |
| Depth | 2075 m [49] 1900 m [18] |
| Pore pressure gradient | 8.5–16.1 kPa/m [49] kPa/m [18] |
| gradient | kPa/m [18] |
| gradient | kPa/m [18] |
| gradient | kPa/m [18] |
| Young’s modulus | GPa [18] |
| Poisson’s ratio | [18] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atdayev, E.; Wong, R.C.K.; Eaton, D.W. A Novel Equivalent Continuum Approach for Modelling Hydraulic Fractures. Energies 2020, 13, 6187. https://doi.org/10.3390/en13236187
Atdayev E, Wong RCK, Eaton DW. A Novel Equivalent Continuum Approach for Modelling Hydraulic Fractures. Energies. 2020; 13(23):6187. https://doi.org/10.3390/en13236187
Chicago/Turabian StyleAtdayev, Eziz, Ron C. K. Wong, and David W. Eaton. 2020. "A Novel Equivalent Continuum Approach for Modelling Hydraulic Fractures" Energies 13, no. 23: 6187. https://doi.org/10.3390/en13236187
APA StyleAtdayev, E., Wong, R. C. K., & Eaton, D. W. (2020). A Novel Equivalent Continuum Approach for Modelling Hydraulic Fractures. Energies, 13(23), 6187. https://doi.org/10.3390/en13236187





