Substation Related Forecasts of Electrical Energy Storage Systems: Transmission System Operator Requirements

Abstract

The growth in volatile renewable energy (RE) generation is accompanied by an increasing network load and an increasing demand for storage units. Household storage systems and micro power plants, in particular, represent an uncertainty factor for distribution networks, as well as transmission networks. Due to missing data exchanges, transmission system operators cannot take into account the impact of household storage systems in their network load and generation forecasts. Thus, neglecting the increasing number of household storage systems leads to increasing forecast inaccuracies. To consider the impact of the storage systems on forecasting, this paper presents a new approach to calculate a substation-specific storage forecast, which includes both substation-specific RE generation and load forecasts. For the storage forecast, storage systems and micro power plants are assigned to substations. Based on their aggregated behavior, the impact on the forecasted RE generation and load is determined. The load and generation are forecasted by combining several optimization approaches to minimize the forecasting errors. The concept is validated using data from the German transmission system operator, 50 Hertz Transmission GmbH. This investigation demonstrates the significance of using a battery storage forecast with an integrated load and generation forecast.

1. Introduction

The steadily growing share of renewable energy (RE) in power generation is being accompanied by increasing uncertainty in the estimation of power system conditions in system and operational management. This uncertainty overlaps with uncertainty in the estimation of the power system load. Furthermore, the increasing share of prosumers in the low voltage system means that the load and generation can no longer be separated at network hand-over points. Additionally, the number of storage systems is greatly increasing [1] and becoming a relevant part of power system operations for transmission system operators (TSOs). Thus, forecasts of generation, consumption and storage are essential for current and future power network planning and management and, in general, for the European interconnected power system (the day-ahead congestion forecast, DACF, as well as the intraday congestion forecast, IDCF). The importance of forecasting is emphasized by the processes for which the forecasts are used, including the following:

• Horizontal load compensation: The remuneration of renewable energy generation will be distributed according to the demand of the consumers in the control areas between the TSOs based on the results of the close to real time (C2RT) load forecast and the renewable energy act (EEG) [2];
• Week ahead planning process: This process serves as the basis for reserve power plant operational planning;
• System Monitoring: This process enables C2RT power system state monitoring and stability monitoring;
• RE-Marketing: According to the renewable energy act, the generation from every small RE (every unit that was not directly traded) must be marketed by TSOs at the spot market. Consequently, the TSOs need a precise RE generation forecast;
• Day-ahead congestion forecast (DACF): With the forecast of RE, the power plant schedules and the load forecast a power flow calculation is applied to the control area and the interconnections to neighboring TSOs. The aim is to identify congestions;
• Intraday congestion forecast (IDCF): The day-ahead applied power flow calculation is updated with the latest forecasts and power plant schedules.

The forecast-related information exchange is carried out between different stakeholders such as TSOs, distribution system operators (DSOs), balancing groups, large loads and large generation units. Supplementary to these exchanges, TSO and first-level DSO exchange observable area data for the joint handover substations. However, this is not suitable for a TSO to determine an accurate control area or substation-related forecast. The photovoltaic (PV) system generation influences the load profiles for small consumers in the case of rooftop systems or, in the worst predictable case, for additional battery storage systems. Currently, to forecast the load, RE-generation and storage behavior, German TSOs only have precise information access to the following:

• Measured data for:
  • Large loads and conventional power plants at high, up to the highest, voltage levels and the corresponding schedules;
  • The vertical load at TSO-DSO substations;
  • A few very large windfarms and solar parks and their corresponding schedules;
• Installed power and the according postal codes of RE and battery storage systems;
• The historical sum of the measurements (at least one month old) for RE in the control area.

Based on these data, the TSO’s goal is to establish a precise control area load and a generation forecast to achieve the above processes. In this way, a huge number of loads, generation units and storages have no direct assignment to substations. Another current challenge for TSOs is to develop substation-specific forecasts.

This paper focuses on the 50 Hertz control area in Germany, which is characterized by a large proportion of renewable energy systems. The installed capacity of wind turbines here is currently 19.8 GW (as of December 2019), and the installed capacity for PV systems is 12.2 GW (as of December 2019) [2,3]. Thus, the 50Hertz control area already contributes 32% and 25% of the installed wind and PV power in Germany [4,5]. The increasing number of installed PV systems is challenging for TSOs since these systems include a particularly large number of micro-plants, as every second micro-plant (photovoltaic system below 30 kW) in Germany had an additional battery storage system installed in 2017 [1]. At the end of 2017, the system portfolio comprised 85′000 decentralized solar storage systems with a storage capacity of around 600 MWh and an estimated total power of around 280 MW; these systems are installed at the German low voltage level [1]. Furthermore, in 2050, 16 to 45 GW of installed household storage capacity is estimated to be connected to the German grid [6]. Both the household storage systems and the connected micro-plants are difficult to assign to nodes. However, the increase in household storage systems and the connected micro-systems will essentially lead to a change in electricity consumption, which will be noticeable in the network and operational management of the TSOs.

Due to the growth of volatile generation and storage systems in the distribution system and the resulting changes of power flows at the hand-over points to the TSO’s system, the importance of the substation-related load, generation and storage forecasts is increasing. Researchers have already developed several short-term forecasting models for RE, load and net demand [7,8,9,10,11,12,13,14]. The net demand is the resulting deviation between RE power generation and load. Distinctions between direct and indirect net demand forecast approaches were made in [7,8,9,10,11]. Direct methods forecast the net demand itself, whereas indirect methods forecast the RE generation and load to subsequently subtract them. In this way, an indirect forecast achieves greater results and is especially recommended for applications with an increasing share of volatile RE [7,9]. Indirect net demand forecasts, such as those developed in [7,8,9,10], only consider the generation and load behavior and focus on the distribution level. Thus, these models do not consider the storage behavior and are not suitable for TSO requirements. The investigations in [15,16,17,18,19,20] focused on optimizing the scheduling strategies of storage systems to improve either the system stability [15,16,17,18] or the battery efficiency [19,20], taking into account the load or RE forecasts. These models actively intervene in storage behavior by optimizing the storage strategy. However, to the best of the authors’ knowledge, no work has forecasted the impact of unknown storage strategies aggregated to TSO’s handover points. Additionally, different forecasting models have emerged from diverse approaches to create a RE power generation forecast and can be divided into two groups: physical models and statistical models [12,14,21]. The weaknesses and strengths of these models differ due to their diversity. So far, there is no overall dominant forecast model [22]. To make optimal use of these models, the idea is to combine them. Combining forecasts could yield positive and negative errors that compensate for each other, thus improving the forecasting quality [23]. Although combining forecasts is already a well-known method for improving forecast accuracy, with a wide range of approaches such as simple average and Bayesian methods, this approach is still underdeveloped [24]. The disadvantage of several combined forecast models is the missing dynamic adjustment of the combination weights, which can miss the real-time changes in RE generation [25]. A corresponding dynamic combination forecast yielded improved results in [25,26]. However, these were forecast models at the distribution level. Challenges that occur during the aggregation at a TSO substation, e.g., missing measurements and a shift in the generation and load between substations, were not considered.

To solve the increase in fluctuating RE power generation and connected household storage, as well as the occurring challenges for TSOs, this paper introduces a new concept—integrated load, generation and storage forecast (ILEP). A substation-related forecast is proposed, which dynamically calculates the RE power generation, as well as the load, using combination methods. The previously non-existent storage forecast aims to forecast the behavior of household storage systems, aggregated per substation. The resulting behavior is then used to estimate the changes in the curve of the substation-specific load and generation forecast. Thus, this forecast will improve the DACF, IDCF and RE-marketing processes and meet short-term and medium-term power system needs.

The rest of the paper is structured as follows. Section 2 presents the determination of the input parameters for the substation-specific storage forecast. Section 3 introduces the ILEP concept based on three aspects: the methodological improvements developed for substation-specific generation and load forecasting and the developed storage forecast. The verification and discussion of the results are presented in Section 4. A conceptual power system integration of the new algorithm is drawn in Section 5. Finally, in Section 6, a conclusion of the approach is given.

2. Determination of Substation-Specific Model Parameters

The storage forecast is intended to improve the forecasts of load, generation and residual load at the TSO substations. For this purpose, the influence of households with PV and battery storages systems is forecasted. To determine the influence at the individual TSO substations, the households have to be modeled. This requires technical parameters of the plants and information on the energy consumption of the households. Installations of PV and battery systems are recorded in Germany in a central and publicly accessible register. This register allows the spatial allocation of plants to municipal areas or postal code areas. For population figures, spatial high-resolution data is also available.

Problematically, households are not connected to the high-voltage network of the TSO but instead to low-voltage networks of the subordinate distribution networks. A direct allocation of households to TSO substations is not possible due to the meshed high- and medium-voltage networks and the lack of information available to the TSO on how the distribution networks are currently switched and how they will be switched in the following hours (topology changes). The allocation of PV systems, storage systems and consumers to map households must, therefore, be based on certain assumptions (static distribution network model).

This Section describes how the model parameters used in Section 3 are determined for each TSO substation. This methodology comprises the following steps:

• Preprocessing of the data for the register of installations;
• Allocation of PV systems, battery systems and inhabitants to DSO substations;
• Determination of sensitivities reflecting the influence of DSO substations on TSO substations;
• Allocation of PV systems, battery systems and inhabitants to TSO substations.

2.1. Household PV and Battery Storage System Units

The core energy market data register (MaStR) of the Federal Network Agency serves as the database for PV and battery storage systems [27]. MaStR is an official register in which all German plants and market players in the electricity and gas sector have had to be registered since 1 July 2017. Plants that were commissioned before that date can still be registered by the operator until 31 January 2021. However, registers for installed renewable energy systems already existed before 2017. The data from these registers were subsequently moved to the new central register. The MaStR is currently the best available data source for information on PV and storage installations. This register distinguishes between single power plants (units) and clusters of power plants formed by these units. In this investigation, the data from the units are used. The version of the register extract used here (as of 4 November 2019) comprises more than 2.4 million units with various types of generation, storage and consumption. The 50 Hertz control area has 141′823 PV systems and 7′743 battery storage systems with a typical household featuring a rated electrical power of less than or equal to 10 kW.

Geographical coordinates are required to assign the units to distribution network substations. Since these coordinates are not published for units with a rated electrical power of less than 30 kW for data protection reasons, the first step in using the register data is to geocode all units without coordinates. If a municipality key is assigned to the unit, then the center of the municipality is determined by a spatial data set of the Federal Agency for Cartography and Geodesy (BKG) [28]. If the unit includes location information only in the form of a name and a postal code, the program tries to geocode this information. For this purpose, the first step is to look up an extensive locally stored data set (EnergyMap [29], as of 2015). If there is no hit, a web service (OSM Nominatim [30]) is used. The locally stored data set is then used to reduce the number of queries to the web service. The results of the first step are summarized in

Table 1. Units and rated electric power—results from geocoding and filtering.

	Photovoltaic Plants	Battery Storage Systems
50 Hertz control area	211′967	8′052
Geocoded	211′890	8′041
Filtered by rated electric power	141′823	7′743
Overall electric power (households)	803.2 MW	30.0 MW

for all PV and battery storage units in the 50Hertz control area. Due to spelling mistakes in place names and unknown postal codes, a small proportion of the units could not be geocoded.

2.2. Distribution Grid Model and DSO Substation Allocation

A 110 kV distribution network model including all substations of the transmission network (provided by 50 Hertz) is used for the allocation of the units. This model contains 56 transmission network substations, 942 distribution network substations and 1′133 110 kV power lines. The power lines have a length of up to 139 km, up to six circuits, and are constructed as overhead lines (998 lines) or, especially in urban areas, as cables (135 lines).

The PV and battery storage units are assigned to the nearest distribution network substation by applying Voronoi polygons for efficient computation. These polygons reproduce the 1D property “shortest distance” as a 2D object by simplifying the assignment and intersection operations in the geographical information system (GIS). EPSG 25832 (UTM Zone 32N) is used as the geographic reference system for these operations. Subsequently, Voronoi polygons are referred to as catchment areas.

The number of inhabitants required to model the domestic energy demand is determined by intersecting the catchment areas with the municipal areas of the control area. A publicly accessible spatial data set with census information is used for this purpose [28]. The number of inhabitants $PO{P}_i$, assigned to a distribution network substation i, is calculated as the sum of the population of the municipalities m, which are intersected by the catchment area i, weighted by the area shares of intersection area/to the area of municipalities $A_m$:

$$PO{P}_i={\displaystyle \sum \frac{A_{i,m}}{A_m}}PO{P}_m$$

(1)

The spatial allocation of consumption and generation is of great importance in the modeling of energy systems and has been used, for example, in studies on grid expansion [31]. Voronoi polygons around the substations of the high-voltage network were also used for modeling the distribution network areas in [32].

Figure 1 shows an excerpt of the 110 kV distribution network model, where the blue lines and dots represent the distribution network lines and substations. Using the catchment areas guarantees consistency in mapping the generation and consumption for both the system allocation and the number of inhabitants.

2.3. Power-Flow-Based Allocation Factors

In the following, sensitivities are determined for the aggregation of the PV and battery storage systems, as well as for the number of inhabitants, in the 56 TSO substations. For this purpose, a sub-network is first created for each distribution network substation that contains all the TSO substations that can be reached by the network. A power flow calculation is then carried out for each sub-network, where 1 MW is fed in at the respective distribution network node, and the sensitivities are determined based on the flow into the connected TSO substations (slack nodes). In the following step, there is no direct allocation of units and residents to TSO substations. The sensitivities instead serve to determine the TSO substation-related characteristic values with the help of weighted sums and weighted mean values.

To create the sub-networks, the network model is treated as a universal graph consisting of nodes and edges. Starting from the distribution network substation, all paths that end in a TSO substation are determined. The set of nodes and edges determined in this way form the sub-network. Figure 2 shows such a sub-network, which is enclosed by three TSO substations.

The software pandapower is used for the power flow calculations [33,34]. Here, the DSO substations are modeled as PQ-busses, while the TSO substations are modeled as PU-busses. Power lines are modeled by their π-equivalent circuit models. The parameters of the overhead lines and cables are based on the standard library of pandapower [35]. The calculation is carried out using the Newton-Raphson method. The initial values are determined with a DC power flow calculation. Network losses are compensated during the calculation of the sensitivities, i.e., all sensitivities of one DSO substation sum to one. As a result, there are/sensitivities/for each of the 942 distribution network nodes i, which represent the effect of a feed in or withdrawal from the respective transmission network station k from the set of all connected TSO substations $K_i$.

$$a_{i,k}=\frac{\left|P_k\right|}{{\displaystyle {\sum }_{l\in K_i}\left|P_l\right|}}k\in K_i$$

(2)

2.4. TSO Substation Allocation

The sensitivities $a_{i,k}$ are used for the allocation of the PV and battery storage system’s technical parameters and the population to the 56 transmission network substations. For each of these substations k, all connected distribution network substations $i\in I_k$ and the assignable sensitivities $a_{i,k}$ are known. From the DSO substation allocation, the number of units $N_i$ and the summed rated electrical power $P_i$ of the PV and battery storage units, as well as the population inside the catchment area $PO{P}_i$, are known. The TSO substation-specific parameters are then calculated as follows:

$$N_k={\displaystyle {\sum }_{i\in I_k}{a}_{i,k}{N}_i}$$

(3)

$$P_k={\displaystyle {\sum }_{i\in I_k}{a}_{i,k}{P}_i}$$

(4)

$$PO{P}_k={\displaystyle {\sum }_{i\in I_k}{a}_{i,k}PO{P}_i}$$

(5)

The results of the aggregation are summarized for five exemplary TSO substations in

Table 2. Photovoltaic (PV) and battery storage (BAT) parameters determined by TSO substation allocation.

TSO Substation	${\mathit{N}}_{\mathit{k},\mathbf{PV}}$	$$\begin{gathered} {\mathit{P}}_{\mathit{k},\mathbf{PV}} \\ \mathbf{in} \mathbf{kW} \end{gathered}$$	${\mathit{N}}_{\mathit{k},\mathbf{BAT}}$	$$\begin{gathered} {\mathit{P}}_{\mathit{k},\mathbf{BAT}} \\ \mathbf{in} \mathbf{kW} \end{gathered}$$	$\mathit{P}\mathit{O}{\mathit{P}}_{\mathit{k}}$
Altenfeld	2′967.3	17′211.2	139.3	501.0	240′703
Dresden Süd	4′976.4	27′928.9	314.4	1′178.5	837′522
Klostermansfeld	4′163.7	23′980.8	124.9	464.4	392′933
Wolmirstedt	3′589.6	21′843.5	148.7	653.7	368′775
Wuhlheide	917.7	4′610.3	39.1	164.6	628′337

. These substations are characterized by a high rated PV capacity or a high load.

3. The ILEP Concept

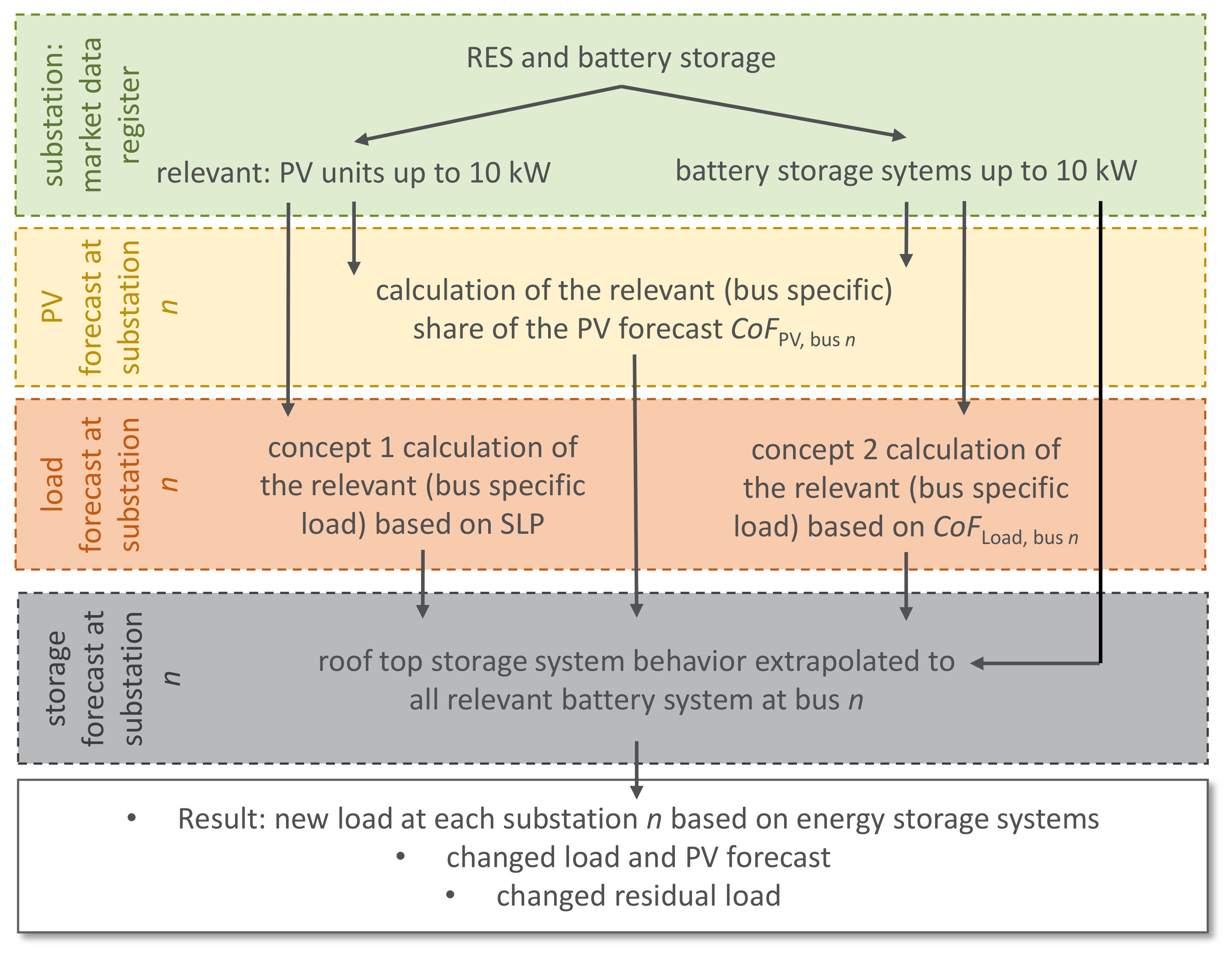
The ILEP concept focuses on household battery systems in combination with rooftop PV systems with a rated power up to 10 kW. Figure 3 presents the general concept used to calculate a substation-related storage forecast to deduce the impact of household battery systems on the load, PV and residual load forecasts at each TSO substation. This concept can be applied for two days ahead up to, and including, real-time system operator operational processes and includes:

•

Allocation of relevant PV and battery systems to TSO substations (Figure 3, green block);

•

Determination of relevant PV forecasts based on existing substation-related PV forecasts ($Co{F}_{\mathrm{PV}}$) (Figure 3, yellow block);

•

Two approaches to determine the relevant load forecast (Figure 3, orange block):

• Using standard load profiles (SLP);
• Using a dynamic load forecast ($CO{F}_{\mathrm{load}}$);

•

Implementation of a battery management concept (Figure 3, grey block).

This concept enables TSOs to automatically identify the impact of battery storage systems in operational processes and helps prepare for an increase in the share of distributed battery storage systems. According to the focus of this paper, only PV systems with a rated power of up to 10 kW are considered relevant. This means that the load and battery storage systems are also assigned to these systems and designated as relevant.

In the following, a model for forecasting substation-specific RE generation is introduced, and a dynamic load forecasting approach is presented. Based on these models, a TSO substation storage forecast is developed.

3.1. Substation-Specific Generation Forecast

As demonstrated in Section 1, a reliable and uniform generation forecast (GF) is essential for various market participants. Sufficiently accurate GFs are already being offered by a large number of providers using different approaches, methods and information sources, leading to different results. To minimize the deviation of the RE generation forecast from the actual generation and thus optimally use these provider forecasts, a method for combining these forecasts is introduced below. In this way, the weighting of individual providers has a decisive influence on the quality of the combined forecast (CoF) and thus on the safe network operations as well as the profits of energy traders and producers [23]. According to equation (6), the CoF $p_{\mathrm{c}}$ is calculated by multiplying the provider time-series $P_{\mathrm{pro}}$(the matrix with a column per provider and a row per power value) and the dynamic and optimal weightings w (the vector with a row per provider).

$$p_{\mathrm{c}}=P_{\mathrm{pro}}\cdot \mathit{w}$$

(6)

The aim of the optimal weightings w is to minimize the deviation of the overall CoF $p_{\mathrm{c}}$ from the actual generation. Dynamic and optimal weighting is achieved by using historical provider time-series and historical actual generation power $p_{\mathrm{act}}$ to minimize the magnitude of the loss function $v(p_{\mathrm{c}})$. Using a loss function allows to quantify the quality of the combination forecast. Both $p_{\mathrm{act}}$ and $P_{\mathrm{pro}}$ are fixed time-series; thus, the value of the loss function is defined by the dimension of the weightings. This leads to the following definition of the optimal weighting matrix ${\mathit{W}}_{\mathrm{opt}}$ [22]:

$${\mathit{W}}_{\mathrm{opt}}\in \arg \underset{\mathit{W}\in {ℝ}^{S\times T}}{\min }v(\mathit{W})$$

(7)

where the sum of the weights is not limited to 1. Combination forecast models vary in the design of their loss functions and their determination of ${\mathit{W}}_{\mathrm{opt}}$ [22]. In this paper, a two-step combination forecast is introduced, which considers the fluctuations in the GF quality of the individual providers.

3.1.1. Input Data

This subsection provides a description of the dataset used to determine the combination forecast for RE power generation. Historical data of provider generation forecasts and historical data on the extrapolated actual power generation of RE are used to determine the weightings for the substation-specific generation forecast. The historical data of the provider forecasts and the latest provider forecasts must be provided by the respective system operators, and it is assumed that the latest forecasts are provided the day before. The extrapolated regional generation is publicly available due to legal obligations according to § 23a, Annex 1, paragraph 3.1 of the EEG 2017. This generation is determined by extrapolating the current measured values from the selected wind and PV farms and is updated online once an hour [36,37]. The substation-specific extrapolated generation is not publicly available, so it needs to be provided by the respective system operator. Both types of time-series provide the mean capacity values per 15 min in Megawatts and are available separately for wind and PV power generation for each substation.

3.1.2. Methodology

Here, the developed regional forecast method in [23] is extended by the weighted least square method, developed in [38], and applied and adjusted to a substation-specific forecast (see Figure 4). Furthermore, the focus of system operators has shifted from forecasting actual generation measurements to forecasting extrapolated generation time-series. Since the actual generation measurements are provided with a delay of one month, whereas the extrapolated generation time series are provided 15 min after the fulfillment time, in contrast to [23,38], a data gap of one month is no longer required. As indicated in Figure 4, first, the Genetic Algorithm (GA), Particle Swarm Optimization (PSO) and the Weighted Least Square method (WLS) are used simultaneously to determine the weights w for combining the provider generation forecasts. Historical provider power generation forecasts, as well as the extrapolated actual power generation of RE, serve as input data, and two types of loss functions are considered. Since quality depends only on the magnitude of the forecast error, it is suitable to use the error ε as the loss function to determine the deviation between the extrapolated actual generation pact and the forecasted generation [22]. This loss function is, per its definition, part of the WLS method [38]. To assign a high weight to high deviations, the normalized Root Mean Square Error (RMSE) in (8), which is related to the installed wind and PV power, is used as the fitness function in the GA and PSO, whereas the fitness function is equated with the loss function [23].

$$v({\mathit{w}}_i)=RMS{E}_{\mathrm{i}}=\frac{\sqrt{\frac{1}{N}{\displaystyle \sum _{t=1}^N{\left({\mathit{p}}_{\mathrm{pre} t}\cdot {\mathit{w}}_i-p_{\mathrm{act} t}\right)}^2}}}{P_{\mathrm{installed} \mathrm{wind}}}$$

(8)

Compared to the method developed in [23], the results of the optimizations are substation-specific weightings for each day, where t in $w_t$ stands for the corresponding day. The calculated weights are multiplied with the current provider forecasts according to (6) to obtain the desired combination forecast for each method—GA, PSO, and LS.

As outlined in [23], the resulting combination forecasts are combined to mutually balance the positive and negative forecast errors. Using the RMSE as per (8), the combination forecasts are weighted according to their forecast quality on the previous day. By multiplying the derived weights by the prior combination forecasts, the final combination forecast is determined.

3.2. Substation-Specific Load Forecast

To improve the forecast processes in system management, the transformer-measured values and forecasts are decomposed. The aim of this split is to determine and calculate any necessary curtailments (or other measures) in the planning processes to plan as cost-effectively as possible, while not jeopardizing network security. In the first step, wind and PV are incorporated as substation-specific forecasts. In the next step, the remaining generation (e.g., conventional generation) and end-consumer load are provided as a forecast. At the same time, an aggregated transformer forecast is created based on the transformer-measured values to verify the results of the individual forecasts.

3.2.1. Determination of Input Data

This subsection provides a description of the determination of suitable input data for the dynamic load forecast. An initial rough analysis of the influencing factors related to the load showed that weather data, day/hour types and the active power at the transformers correlate with the load. Power plants or other modes of generation (except for combined heat and power systems) have only a small influence on the total load. Combined heat and power systems show effects in the heating period (a Pearson correlation factor from around 0.8 to 0.9) but are indirectly dependent on temperature and can, therefore, be mapped using weather data. The resulting influencing factors were then examined in more detail by means of a simple correlation analysis using the Pearson correlation coefficient (significance level 5% when using the 95% confidence interval). In this way, the correlation between substation-specific historical interpolated weather data (global radiation, wind speed, and temperature from service providers) and the historically calculated total load value per substation was analysed. The period considered here was 6 months, and a weekly evaluation was carried out. The analysis showed that global radiation, temperature and wind speed are suitable as input parameters for the load forecast. The Pearson correlation factors here range from 0.016 to 0.498 (temperature), 0.064 to 0.609 (global radiation) and 0.0152 to 0.8191 (wind speed). The results of the correlation analysis are used here as the load base value for each individual data point.

The base value of the total load forecast is calculated using measured values (sum of the transformers, power plant measured values, network losses, etc.) and extrapolations (based on measured values obtained internally and from service providers). The measured values and projections used are available online. The weather data identified by the correlation analysis as suitable input data for the total load forecast are purchased from service providers. In addition, vertical network load forecasts (forecast based on transformer measurements) and generation forecasts are used here as input variables. These are created internally or from other TSO processes. All time series (measured values, projections and forecasts) contain mean values for every 15 min.

In addition to the input data mentioned above, a distinction is also made between day types. These are saved as numerical time series, which are differentiated according to Monday, Friday, Saturday, Sunday, public holidays and school holidays. The load behavior on these days differs significantly from those on standard days (i.e., Tuesdays, Wednesdays, and Thursdays). For example, the daily maximum load drops sharply on the weekend.

3.2.2. Methodology

Two types of algorithms are used for the total load forecasting: neural networks and multiple linear regression. Due to the criticality of the subsequent processes, stable and simple calculation methods are primarily used for system management. Since the current dependencies and causal relationships for the end-consumer load are known, reliable and comprehensible results can be calculated using neural networks and regression algorithms. Both resulting forecasts are combined based on a regression analysis using historical data from the last three months. This is a static combination, where the quality of the last hours or days is currently not considered. A dynamic combination is currently not feasible (for technical reasons) since the forecasts must be calculated in a stable and comprehensible manner.

One problem, especially in the regression algorithm, is handling global radiation. In the transition period from winter to summer, the number of dark hours changes. If the chosen calibration period is too short during the transition period, unwanted peaks can occur during sunrise or sunset. To reduce these forecast errors for very changeable base values, thus avoiding frequent calibration, the daily pattern model is used. Here, every quarter of an hour is numbered consecutively to create a model for each. This produces 96 models. The advantage of this approach is that certain phenomena, such as lunch at noon are well represented. For reasons of comparison, this daily sample model is used for both algorithms, i.e., the regression and the neural networks. In the subsequent processes, only hourly values, as shown in Figure 5, are currently required, but these are also expected to change to improve the forecast quality.

3.3. Substation-Specific Storage Forecast

In this subsection, a model to calculate the effects of battery systems with rated power up to 10 kW is presented. For this process, a database and suitable assumptions, as well as a method to calculate substation-specific impacts, are introduced. This development is necessary because there is still no concept for TSOs to determine the impact of battery storage at TSO substations.

3.3.1. Database and Assumptions

The main database used to calculate the substation-specific storage impact is given by the results in Section 2, Section 3.1 and Section 3.2. This includes time-series for load and generation, which must be recalculated according to the relevant share of battery systems at a TSO substation. In this way, only the impact of rooftop PV generation up to 10 kW on battery systems and the load is relevant. Furthermore, the market data register evaluation and the calculation of substation-specific parameters deliver the number and rated power for the PV and battery units. Further data used to perform these calculations are statistical data, such as average consumption and household size, which are based on public references [39,40,41,42,43,44,45,46].

Table 3. Database for the substation-related battery storage forecast.

Variables	Data Source
PV forecast for TSO substation k (CoFk,PV)	Time-series (Section 3.1)
load forecast for TSO substation k (CoFk,Load)	Time-series (Section 3.2)
number of all PV units at substation k (Nk,PV)	determined value (Section 2)
number of all battery units at substation k (Nk,BAT)	determined value (Section 2)
number of all PV units at substation k with rated power up to 10 kW (Nk,PV,10KW)	determined value (Section 2)
number of all battery units at substation k with rated power up to 10 kW (Nk,BAT,10KW)	determined value (Section 2)
number of inhabitants at substation k (POPk)	determined value (Section 2)
rated power of PV units at substation k (Pk,PV)	determined value (Section 2)
rated power of battery units at substation k (Pk,BAT)	determined value (Section 2)
rated power of PV units at substation k with rated power up to 10 kW (Pk,PV,10kW)	determined value (Section 2)
rated power of battery units at substation k with rated power up to 10 kW (Pk,BAT,10kW)	determined value (Section 2)
population in a federal state fst (POPfst)	statistical data [39]
number of households in Germany by number of persons Pers (Pers = 1, 2,3,4, 5 and more) in the household (NPers,hh)	statistical data [40]
number of single and multi-person households in Germany by federal state fst (Nhh, fst)	statistical data [41]
average annual energy consumption for single and multi-person (2, 3 and more) households in Germany (Eaverage,hh)	statistical data [42]
Distribution of electricity consumption in Germany by consumer groups (group=industry, households (hh), traffic, business) (percentagegroup)	statistical data [43]
Standardized load profiles for households and type of day type (SLPhh,type)	statistical data [44]
Share of homeowners with their own homes (single homes or double family homes) in the east of Germany (Sho,east = 0.1786)	statistical data [45,46]

presents a summary of the database, as well as the used variables.

Besides the fixed database, logical and practice-based assumptions were made due to missing detailed data for complete control areas. These assumptions are as follows:

• Battery systems up to 10 kW are always used in combination with PV systems;
• Battery systems are only located in houses used by the owner and not rented;
• Relevant houses are inhabited by two or more persons;
• The number of battery systems at a substation (identified in Section 2) corresponds to the number of houses;
• The inverter is shared by the PV and battery system;
• The ratio of inverter capacity to battery capacity to rated power is 1 to 1 to 1

  -

  The inverter capacity $P_{k,\mathrm{inv}}$ is determined by the rated power of the battery units at a substation;

  -

  The battery capacity $C_{k,\mathrm{BAT}}$ is determined by the rated power of the battery units at a substation;

• The maximum state of charge (SoC_max) is 0.98;
• The minimum state of charge (SoC_min) is 0.2;
• All battery units at a substation have the same battery management behavior;
• Neglected: The PV system may not feed more than 50% of its rated power into the grid

  -

  This effect might be considered by the forecast data provider for calculating $Co{F}_{\mathrm{PV},\hspace{0.33em}k}.$

To model the battery management system, the following aspects are considered. There are three different charging strategies: maximizing the self-consumption rate, the fixed feed-in limit and the daily dynamic feed-in limit [47]. The most commonly used battery-charging concept is maximization of the self-consumption rate [48] because of its easy implementation and financial suitability for house owners. This concept is used here and was programmed in MATLAB based on [49].

The main objective of installing battery storage systems is to increase the self-consumption rates by optimally using and storing the excess energy generated by solar cells during peak hours. Generally, the charging system is designed to increase its self-sufficiency by storing the excess generated power during the day and using it when needed. However, if all PV systems connected to the grid inject their excess power into the grid simultaneously, the grid will lose its stability. According to [47], the charging cycle of a battery starts as soon as the PV generation is greater than the consumption. Excess energy generated after the battery is completely charged will be fed to the grid. The discharging cycle will be initiated as soon as the consumption is greater than generation. The excess energy required after battery is completely discharged will be fulfilled by the grid. The state of charge at the beginning of the day (SoC_start) is set as equal to 0.2, which represents an empty storage. In summary, based on the database, the following key aspects are used to implement the battery management in MATLAB for each substation:

• The maximum discharging and charging power are limited by the inverter capacity $P_{k,\mathrm{inv}}$;
• Discharging is only used to fulfill the load;
• If the demand of discharging and charging is bigger than $P_{k,\mathrm{inv}}$, there will be a remaining residual load;
• If $P_{\mathrm{load},k,relevant}$>$F_{k, \mathrm{BAT} \mathrm{PV}}$ then discharge the battery as long as enough capacity is remaining in the battery;
• If $P_{\mathrm{load},k,relevant}$<$F_{k, \mathrm{BAT} \mathrm{PV}}$ then charge the battery as long as enough capacity is remaining in the battery;
• The state of charge is recalculated for each time step (15-min power value) according to [50].

3.3.2. Methodology

This subsection presents the method used to calculate the battery storage impact and the resulting new residual load at TSO substations based on the presented methods, data and assumptions. In this paper, the relevant share of load and generation for storage calculation is defined as load and generation, which have a direct impact on the identified battery systems with rated power up to 10 kW. At the beginning, the relevant share of PV generation forecast at each substation is calculated.

The battery-relevant PV generation forecast is based on the profiles from Section 3.1. This forecast must be reduced according to the identified substation-specific battery characteristics. Therefore, only a portion of up to 10 kW PV systems is relevant of the starting forecast time-series. Additionally, the assumption is that one battery unit is directly correlated with one 10 kW PV unit and that only the share of these units is of interest for the remaining forecast. The resulting equation to identify the battery-relevant PV forecast $F_{k, \mathrm{BAT} \mathrm{PV}}$ at each substation k is

$$F_{k, \mathrm{BAT} \mathrm{PV}}=\frac{P_{k,\hspace{0.33em}\mathrm{PV},10\mathrm{kW}}}{P_{k,\hspace{0.33em}\mathrm{PV}}}\cdot \frac{N_{k,\hspace{0.33em}\mathrm{BAT},10kW}}{N_{k,\hspace{0.33em}\mathrm{PV},10\mathrm{kW}}}\cdot Co{F}_{k,\mathrm{PV}}.$$

(9)

Two new concepts to determine the battery-relevant load $P_{\mathrm{load},k,relevant}$ at TSO substation k are presented next. It is assumed that battery systems are currently only installed in multi-person households. This leads directly to standardized load profiles, which can be used to determine the substation-specific loads in concept 1. On the other hand, there is a proven concept from Section 3.2 that gives a good indication of the load of a substation ($Co{F}_{k,\mathrm{load}}$). This is used and tested in concept 2 because known substation-specific load characteristics can be used for storage forecasts. However, the problem lies in determining the proportion of the load of households with battery and PV systems without any measurement data from these households.

Concept 1 is mainly based on statistical data for multi-person households listed in Table 3 and the standardized load profiles (SLP). The average annual energy consumption for single- and multi-person (2, 3 and more) households in Germany ($E_{\mathrm{average},\hspace{0.33em}\mathrm{hh},\mathrm{pers}}$) is the starting point for the calculation. According to the assumptions made, two-person households ($E_{\mathrm{average},\hspace{0.33em}\mathrm{hh},2\mathrm{pers}}=3205\hspace{0.33em}\mathrm{kWh}$ annual energy demand) and three(or more) person households ($E_{\mathrm{average},\hspace{0.33em}\mathrm{hh},3\mathrm{pers}}=4856\hspace{0.33em}\mathrm{kWh}$ annual energy demand) are selected [42]. In addition, the statistical shares of two-person households $N_{Pers=2,\mathrm{hh}}$ and 3 to 5 person households ${\displaystyle \sum _{Pers=3}^5{N}_{Pers,\mathrm{hh}}}$ in Germany are considered individually. The number of battery systems at a substation $N_{k,\mathrm{BAT}}$ corresponds to the number of multi-person houses and is used to calculate the final battery-relevant energy demand $E_{k,\mathrm{load},\mathrm{relevant}}$ at a substation:

$$E_{k,\mathrm{load},\mathrm{relevant}}=N_{k,\mathrm{BAT}}\cdot E_{\mathrm{average},\hspace{0.33em}\mathrm{hh},2\mathrm{pers}}\cdot \frac{N_{Pers=2,\mathrm{hh}}}{{\displaystyle \sum _{Pers=1}^5{N}_{Pers,\mathrm{hh}}}}+N_{k,\mathrm{BAT}}\cdot E_{\mathrm{average},\hspace{0.33em}\mathrm{hh},3\mathrm{pers}}\cdot \frac{{\displaystyle \sum _{Pers=3}^5{N}_{Pers,\mathrm{hh}}}}{{\displaystyle \sum _{Pers=1}^5{N}_{Pers,\mathrm{hh}}}}.$$

(10)

The relevant load at each substation is calculated by normalizing the relevant energy demand, multiplied by the standardized load profile. The result is a daily substation-specific load profile with household characteristics depending on the number of battery units at a substation.

$$P_{\mathrm{load},k,relevant,con1}=\frac{E_{k,\mathrm{load},\mathrm{relevant}}}{1000\hspace{0.33em}\mathrm{kWh}}\cdot SLP$$

(11)

Concept 2 uses the known time-series to determine loads at a substation. The aim is to identify the relevant load portion from the time-series, which represents the sum of the load including, for example, industry, business, households and more. First, the share of households $percentag{e}_{\mathrm{hh}}$, and only multi-person households therefrom, is of interest to identify the battery-relevant share of the load. Therefore, for each substation, the federal state-specific distribution of single and multi-person households $N_{\mathrm{hh},fst}$ is considered with respect to the number of battery units and the location of the TSO substation. Moreover, the share of homeowners with their own homes (single homes or double family homes) in Eastern Germany are considered ($S_{\mathrm{ho}, \mathrm{east}}$). The following equation presents the complete calculations for each substation.

$$P_{\mathrm{load},k,relevant,con2}=Co{F}_{k,\mathrm{load}}\cdot percentag{e}_{\mathrm{hh}}\cdot \frac{N_{\mathrm{hh},fst,multiperson}}{{\displaystyle \sum _{i=single}^{multi}{N}_{\mathrm{hh},fst,i}}}\cdot \frac{N_{k,\mathrm{BAT}}}{N_{\mathrm{hh},fst,multiperson}}\cdot S_{\mathrm{ho}, \mathrm{east}}$$

(12)

With the presented calculations, the battery-relevant load and generation can be calculated for each substation. Based on the identified battery management concept for maximizing the self-consumption rate and the assumptions made, the battery storage behavior can be calculated.

The battery management is based on the residual load of load $P_{\mathrm{load},k,relevant,con2}$ and generation $F_{k, \mathrm{BAT} \mathrm{PV}}$, where a negative sign represents a PV generation larger than the load and battery charge.

$$P_{k,\mathrm{BAT},\mathrm{residual}}=P_{\mathrm{load},k,relevant,con2}-F_{k, \mathrm{BAT} \mathrm{PV}}$$

(13)

Comparing the two concepts, the relevant PV generation and battery behavior are shown to be the same. Only the determination of the substation-specific load is different. Concept 1 is purely based on statistical load data with SLP and the calculation of energy demand. This demand can become negative due to fast-changing consumer behavior that cannot be represented by statistical data as quickly as it emerges. Concept 2 shows a preliminary, not final, way to use the load forecast and substation, as well as consumer specific characteristics.

4. Case Study

To verify the developed methods, five example substations in the 50Hertz area are chosen, each representing different load and generation situations. Moreover, the substations represent different types of regions (city and country) and vary in the amount of their installed power.

Table 4. Installed RE capacity and load situation of the example substations in 2019.

		Altenfeld	Dresden-Sued	Klostermansfeld	Wolmirstedt	Wuhlheide
Installed	Wind	0.17 GW	0.15 GW	0.85 GW	0.91 GW	0.00 GW
Capacity	PV	0.19 GW	0.18 GW	0.57 GW	0.40 GW	0.02 GW
Max load		0.34 GW	0.69 GW	0.69 GW	0.74 GW	0.00 GW

summarizes the situations for each studied substation in 2019. To map the current state of the network situation, the time-series of 2018 and 2019 were applied as input data in the developed methodologies.

4.1. Substation-Specific Generation Forecast

4.1.1. Evaluation of the Results

The investigations in this work revealed that the best result in the day-ahead forecast is achieved with an input of historical time-series from the previous three months. To quantify the forecast accuracy, the normalized RMSE is used based on the installed power in 2019. In addition to the results of the developed model, the forecast accuracies of three providers (Pro1, Pro2, and Pro3) are listed in

Table 5. Forecast accuracies of substation-specific wind and photovoltaic (PV) generation forecasts: RMSE in %.

	Altenfeld	Dresden-Sued	Klostermansfeld	Wolmirstedt	Wuhlheide
ForecastType	Wind
CoF	5.28	4.87	5.01	5.18	-
Pro1	5.32	5.00	5.08	5.24	-
Pro2	6.58	6.04	6.70	6.01	-
Pro3	10.94	9.54	10.70	10.21	-
	PV
CoF	4.18	4.48	4.43	4.58	4.94
Pro1	4.20	4.51	4.46	4.63	5.07
Pro2	6.64	6.78	5.96	6.19	6.48
Pro3	17.95	19.31	18.77	18.12	17.95

.

Table 6. Forecast improvements of substation-specific wind and PV generation forecasts (in %).

RE Type	Altenfeld	Dresden-Sued	Klostermansfeld	Wolmirstedt	Wuhlheide
Wind	0.60	2.72	1.45	1.14	-
PV	0.45	0.55	0.82	1.12	2.48

shows the improvements achieved by the introduced substation-specific generation forecast compared to the best provider forecast. There are no results for wind at the substation Wuhlheide, as no wind turbine is connected to this substation. The results illustrate that improvements can be achieved for each substation regardless of the location, the amount of installed power, or the type of generation. According to Table 6, the forecast combination model indicates improvements in the range of 0.6 to 2.72% for wind and 0.42 to 2.48% for PV in comparison to the best provider (provider 1). Compared to the worst provider forecast, an enhancement of up to 76.9% can be obtained. However, since decisions led to a replacement of the worst provider at the beginning of 2019, it is more representative to compare the combined forecast with provider 2. Thus, in 2019, improvements up to 36.93% can be achieved.

Due to the poor forecasts of provider 3 and the aforementioned provider exchange, in Figure 6, only providers 1 and 2 are given. The figures show that the combination forecast curve is very close to the extrapolated generation and thus closer than the provider forecasts. Even though the combination forecast has larger discrepancies, at certain points in time, with the extrapolated generation compared to one of the individual provider forecasts, the combination forecast is consistently better than the worst individual forecast. Thus, the overall forecast accuracy of the combination forecast exceeds that of the provider forecast.

4.1.2. Further Improvement Possibilities

Even though the results of the dynamic substation-specific combination forecast for wind and PV generation showed an improvement, there are still areas for improvement. The investigations in this work showed that there are switching operations in the subordinate network from time to time that are not communicated to the transmission system operator. These switching operations lead to a shift in the generation between substations and must be considered in future analyses. As stated in the introduction, the mutual influence between storage, load and generation situations must also be investigated and included. Furthermore, there will always be uncertainty associated with RE forecasts. However, additionally estimating and preparing quantiles for the forecasts provides excellent information for all applications that require risk management, such as load balancing and RE marketing [51,52,53]. Thus, to develop an all-encompassing forecast model, quantiles must also be considered.

4.2. Substation-Specific Load Forecast

4.2.1. Evaluation of the Results

The forecast error is described by the RMSE and is currently between 20 and 250 MW for the Neural Network and between 17 and 239 for the regression model (based on weekly calculations). What needs to be discussed at this point is whether the RMSE is a well-chosen measure (common in the area of forecasts for TSOs), or if the correlation factors provide a better description of quality. The RMSE shows the average error over a selected period. However, extreme outliers that affect the quality of the subsequent processes (e.g., those in difficult network situations) may not be identified.

Figure 7 shows the comparison and error development of the calculated total load forecasts for two example substations. The regression algorithm performs best in this case, but detailed analyses indicate that during certain calendar days or events, the neural network achieves superior results. This indicates that a combination of the two algorithms, even if only a static one, has advantages. As mentioned above, the calibration period plays a major role. The first calibration spanned two years (2017 to 2019). In some local forecasts, due to changes in the structure of the network, forecast errors increased. Recalibration yielded an improvement. If there are changes/modifications in the network structure, adjustments must be made, as both the input parameters and the base value will change. The load distribution for, e.g., industries or localities, depends on the switching status of the subordinate network and has an impact on the transmission network.

4.2.2. Further Improvement Possibilities

The main problem in forecasting the load is the missing measurements for the total load per time step, especially from households. Historical values, which are also used to calibrate and train the forecast models, must be calculated in real-time based on the available forecasts for the subsequent processes. For an evaluation, snapshots of the current network situation in comparison to the planned situation must be used. However, these measurements and calculations entail a combination of all types of consumption and generation, so these measurements must be disaggregated. This simplifies troubleshooting on days with extreme network situations and the necessary adjustments of performance values in the event of multiple forecast errors.

According to the current combination of the two forecast methods mentioned above, individual situation-related advantages of individual algorithms are not considered in the case of situation-related short-term changes; thus, a static combination leads to large deviations. This must be dynamically adapted to the current value. Additionally, in the future, the consumer load profile will change. With an increase in electric mobility and further developments in smart home technology, the classic total load curve that is still visible today will change more and more. Comparing normal households with those that have a combination of PV and household storage systems, a significantly stronger dependency on the price of electricity and the weather (especially solar radiation) can be seen. This creates new challenges for the forecast algorithms. It is to be expected that several algorithms will must be combined to address these challenges. One possible combination approach is to carry out classification using a decision tree algorithm. Depending on the result, the appropriate forecast algorithm can be applied. Given a corresponding history, the forecast algorithm can be selected depending on the input parameters. The main advantage of this approach is its computation time. This approach is already in the development phase. Integration of the forecasted time series into current forecast processes for a better comparison is also in progress.

4.3. Substation-Specific Storage Forecast

4.3.1. Evaluation of the Results

The day of 17 July 2019 is used to show the functionality of this concept.

Table 7. Substation-specific data for example substations.

Example Substations	Battery Rated Power	10 kW PV-Systems, Rated Power	Concept 1 Energy Demand Example Day	Concept 2 Energy Demand Example day	Max Pload Difference between Concepts
Altenfeld	0.50 MW	17.21 MW	1.53 MWh	25.16 MWh	1.24 MW
Dresden Süd	1.18 MW	27.93 MW	3.46 MWh	68.98 MWh	3.37 MW
Klostermansfeld	0.46 MW	23.98 MW	1.37 MWh	22.81 MWh	1.13 MW
Wolmirstedt	0.65 MW	21.84 MW	1.63 MWh	25.19 MWh	1.72 MW
Wuhlheide	0.16 MW	4.61 MW	0.43 MWh	3.78 MWh	0.18 MW

presents the identified and calculated substation-specific characteristics for the five example substations. Table 7 highlights first that the rated power of the battery systems is not very high and second that the difference between the two load concepts is very high. According to the results, the most realistic and suitable concept is concept 1. As stated in Table 7, the substation Dresden Süd has the highest rated power for PV and battery. This substation is, therefore, used to analyze the results of the storage forecast concept.

Figure 8 presents the results for the battery storage forecast. The diagram represents one day with 96 quarterly hour values and compares the residual load with and without considering storage systems. The results show that the battery storage leads to the following:

• A reduced PV generation forecast, especially at the beginning of the day when the sun rises (residual load dashed black), for time steps 22–34,
• A steep PV generation ramp after the battery storage is fully loaded and the PV generation covers the load (i.e., residual load dashed black),
• A reduced load for some time steps when the sun goes down and the storage discharges (residual load, dashed black), for time steps 67–90.

Figure 9 presents the results for the battery storage forecast using concept 2. This diagram indicates a much higher load based on concept 2 for relevant load determination. The results show that the load is higher than the PV generation and that the use of the battery forecast calculation is not necessary. This might not be realistic because the PV generation for the example day is high. Furthermore, the battery seems to be unused with a permanent SoC of 0.2 because only loads with storage are focused upon. From this result, it can be concluded that the load prediction still needs to be revised according to the usage of additional or different data to apply a household storage forecast and determine the household-specific load.

4.3.2. Further Improvement Possibilities

The developed and presented concept based on load determination with concept 1 (usage of SLP) provides very good and realistic results for a day with high PV generation (Figure 8). By summarizing the facts, the impact and relevance of the battery storage forecast is highlighted very clearly in Figure 8. However, the impact may be lower for days with less PV production. Under the current circumstances, with a low proportion of distributed battery systems, there might be no problems for grid operations. However, with more battery units, the very steep ramps will be especially challenging for system operators to handle. Figure 9 displays this problem using substation load forecast data, showing that the load forecast needs further improvements. Ongoing analyses must improve concept 2 to use substation-specific load characteristics. Determination of the relevant load needs to be especially focused upon in the future.

5. The Conceptual System’s Integration of New Algorithms

The existing structure of the processes and system components is able to apply a conventional forecast, as described in Section 1. Figure 10 shows a scheme for the existing components, the adapted components, and the components that need to be added.

Since it is usually difficult to adapt existing components, the ILEP functionality is provided by a widely independent component (labeled as ILEP in the component model) that is integrated into the existing forecast system with a connector. Due to this modular addition, the conventional forecasting methods remain available and can be used if necessary. To change the forecasting method, only a thin abstraction layer is required in the forecasting system. The tasks of the different components are as follows:

•

Business IT

• Forecast system (adapted): a professional forecast system used to create a control area and substation-related load and generation forecasts, adapted for the use of alternative methods;
• Load and generation forecasts: uses conventional forecast algorithms;
• ILEP Connector (new): transfers provider forecast data and execution commands to the ILEP component and the generated forecast back to the forecast system;
• Provider forecasts: data source of the provider forecasts;
• Market: marketing of renewable energy not directly traded by the producer;
• Disclosure requirements: makes general power network data, feed-in quantities and redispatch costs available to the public;
• Archive: archiving of relevant data in accordance with legal regulations;
• PV extrapolation: determines the actual feed-in from PV systems, the data source for training, and the evaluation of generation forecast algorithms;

•

ILEP (new)

• ILEP framework: MATLAB environment and interfaces;
• ILEP algorithms: MATLAB-based forecast algorithms;
• ILEP database: stores configuration, training and evaluation data;
• ILEP GUI: configuration and evaluation of forecasts;

•

Control center

• SCADA: supervisory control and data acquisition system;
• Congestion forecasts: power-flow-based forecast system for different processes (IDCF, DACF, etc.) using the load and generation forecasts;
• Redispatch: planning, execution, and accounting of redispatch measures;
• Energy curtailment: according to German law EnWG § 13.2;
• Wind energy extrapolation: determines the actual feed-in from wind power systems, the data source for training, and the evaluation of generation forecast algorithms.

A distinction can be made between the two main operating modes: training of the forecast system and using the forecasts during operation. The basic information flows that occur in these modes are also shown in Figure 10 using arrows. Training starts with the acquisition of provider forecast data and the corresponding PV and wind energy extrapolations, as well as additional data describing relevant conditions during the respective time horizon. Using the new ILEP, this information is transferred by the ILEP connector to the ILEP component. Training ends when reconfiguration of the forecasting parameters (e.g., weightings) is done.

During operation, a scheduler triggers forecast generation multiple times a day. The latest provider forecasts and additional data for the respective time horizon are then transferred to the Forecast System. The forecasted time-series are then used for marketing renewable energies (Market) and for ensuring safe network operations (Congestion Forecasts, Redispatch, Energy Curtailment).

For practical system integration and testing the developed algorithms, the system needs the following features:

• Comparison of a conventional forecast and ILEP on the basis of error measures;
• Assessment of the influence of an improved forecast on required redispatch measures and their economic effects;
• Evaluation of the ILEP with different proportions of renewable energy in the energy mix (scenarios);
• Spatial and interactive presentation of the results.

To further develop an architectural functionality demonstrator, algorithms are embedded in the Python environment. For this purpose, an HTTP-based interface (Representational State Transfer, REST) is being developed, which allows a bidirectional flow of information for the transfer of function calls and data. On the Python side, the functionality of the ILEP algorithms is encapsulated by an API, which, among other things, allows the execution of training, forecasting and evaluation. The MATLAB-based algorithms encapsulated by the Python API are merged into the ILEP Framework. Together with data management (ILEP Database, PostgreSQL and PostGIS) and visualization (ILEP GUI, flask/dash and OpenLayers), these components have the same functionality as the ILEP component proposed for the productive system (see Figure 10).

Figure 11 shows the component model of the demonstrator and an example mockup of the user interface. The demonstrator’s calculations are performed using the Demonstrator Engine component. This model uses the Python API and already-proven alternatives for the components of the productive system congestion forecast, redispatch, energy curtailment and market (depicted in blue in Figure 11).

6. Conclusions

One of the largest identified power system operational challenges is forecasting the load, generation and impact of household battery systems while considering distributed volatile RE. This paper provides a detailed overview of the relevance of the developed ILEP-concept. This overview was done from the point of view of the system operators interacting with other market participants and internal processes. Based on the definition of the problem and its high relevance to power system stability, this paper offers defined answers to many objectives focused on battery storage in power system operator processes. In this way, the different forecast methods are applied differently in real system operator processes and indicate different technology readiness levels (TRLs). The TSO process environment is the basis for developing improved forecast algorithms and transferring them into system operator processes, as well as software applications. In preparation of substation-specific storage forecasting, one achievement is the determination of TSO substation-specific model parameters using first-level DSO substation allocation. This concept can be applied by TSOs to all small RE and storage units, which are installed under low and medium voltage levels and are more precise than using the shortest distance between units and TSO substations, which is currently applied. The only restriction is understanding and modelling the TSO-subordinated high voltage grid structure. This concept, when applied, indicates a TRL 4, so the next step should involve integration in a TSO test environment.

Through the successful optimization of TSO substation-specific generation forecasting for wind and PV, the forecast accuracy can be optimized and thus network stability and reliability, as well as the volume and cost-reductions in redispatch and feed-in management, can be ensured. Based on provider time-series and using the Genetic Algorithm, Particle Swarm Optimization and Weighted Least Square method, a combination forecast was developed. Improvements of up to 2.72% in wind forecasting and 2.48% in PV forecasting were achieved.

Furthermore, the regression method and neuronal networks were introduced and used for a new algorithm, which ensures flexible and enhanced TSO substation-specific load forecasting. The presented methods were tested in a TSO system environment and indicate that a combination of forecast methods on certain days will lead to improvements. However, the final combination concept must be improved. Ultimately, this concept indicates a TRL of five but still needs some refinement.

A concept for substation-specific storage forecasting is the main achievement of this paper. This is a completely new concept that will be needed in TSO processes with an increasing number of household storage systems. This complete concept indicates a TRL 3. The forecast is based on the presented concept for the determination of substation-specific model parameters and substation-specific load and generation forecasting. In this way, a realistic idea of how battery impacts on substations can be calculated using the relevant load under concept 1 based on statistical data and statistical consumer behavior was presented. Furthermore, the results show that a battery storage system can lead to large ramps at substations on days with high PV generation when the storage system is fully charged. As a result, those using this developed TSO concept should include certain factors in their processes. These include concepts to calculate the rated power of PV and storage systems for each substation and calculations of the relevant share of PV generation forecasts and loads. Finally, the results from the battery behavior with the residual load and remaining load should be considered in substation-specific forecasts. An essential restriction of this concept is that storage systems should have the same form of battery management; otherwise, it will not be possible to predict the storage behavior at the substation. Because of this, guidelines should be developed in a way that always specifies the type of battery management in the market master data register, and the algorithms must always be disclosed. Only with these policies will TSOs be able to proceed to substation-specific storage forecasting. In subsequent analyses, electric vehicles should be considered for households, based on scientific concepts to improve battery storage forecasts.