Optimal Sizing of On-Board Energy Storage Systems and Stationary Charging Infrastructures for a Catenary-Free Tram

Abstract

This paper introduces an optimal sizing method for a catenary-free tram, in which both on-board energy storage systems and charging infrastructures are considered. To quantitatively analyze the trade-off between available charging time and economic operation, a daily cost function containing a whole life-time cost of energy storage and an expense of energy supplies is formulated for the optimal sizing problem. A mixed particle swarm optimization algorithm is utilized to find optimal solutions for three schemes: (1) ultracapacitors storage systems with fast-charging at each station; (2) battery storage systems with slow-charging at starting and final stations; (3) battery storage systems with fast-swapping at swapping station. A case study on an existing catenary-free tramline in China is applied to verify the effectiveness of the proposed method. Results show that a daily-cost reduction over 30% and a weight reduction over 40% can be achieved by scheme 2, and a cost saving of 34.23% and a weight reduction of 32.46% can be obtained by scheme 3.

1. Introduction

Traffic congestion has become an increasingly prominent barrier to the social developments of metropolis due to the resource shortage and concentrated population during urbanization. Comparing to other urban public transports, tram is a promising alternative for reducing traffic congestion and pollution owing to its large passenger capacity and no local emissions [1].

Traditional tram powered by catenary has been used for years due to its continuous access to the energy supply, performance independent of the weather, power extraction on demand according to the numbers of travelers, and so forth. However, it has the shortcomings of voltage fluctuation, low efficiency and restricted operation regions [2,3]. To improve the energy efficiency and meet the operation area without catenary, an on-board energy storage systems (OESS) has been utilized in urban transit [4,5,6]. For the tram powered by OESS, namely catenary-free tram, the overhead power cables between stations are removed. Instead, the catenary-free tram is powered by OESS and recharged by the stationary charging equipment within a predetermined dwell time [6,7]. Therefore, in order to ensure the stable operation of the tram, the capacity of the stationary charging equipment needs to match charging demands of the OESS, including charging power and charging energy [8,9]. Hence, the stationary energy supply, that is, charging the OESS to a high (or full) state-of-charge (SOC) by stationary charging equipment when the tram docks at charging stations, is one of the key components of the energy conversions for the catenary-free tram. To evaluate the practicability and benefits of OESSs originated from different sizes and different energy supply modes, an optimal sizing method that considers both OESSs and stationary energy supplies needs to be established. To the best of our knowledge, such research has not been quantitatively discussed for the catenary-free tram.

Recently, many studies have been carried out on the applications of OESSs in rail transit. Most of them focused on the improvement of the energy management strategies under a predefined size of OESS, such as References [1,10,11,12]. An empirical sizing method for hybrid OESS (ultracapacitors (UC) and battery) was proposed in Reference [13]. The series number of energy storage elements (ESEs) was determined by dividing an expected voltage of power equipment by a rated voltage of energy storage elements (ESEs), and the parallels number of ESEs was achieved by maximizing the calculation of a peak traction power divided by a power density of ESEs and the calculation of a total energy consumption divided by a energy density of ESEs [13]. Although a feasible size can be obtained by this method, it cannot be an optimal solution. The optimization that optimizes both the size and power allocation of OESS for the tram was discussed by References [14,15]. For the hybrid OESS of the traditional tram, References [14,15] formulated an objective function in term of a whole life-time cost of the OESS for the OESS optimization. Results showed that operation regions of trams can be extended to catenary-free zones and a daily operation cost of the tram can be achieved a considerable saving after installing the hybrid OESS. Unfortunately, these studies focused on the traditional tram and they did not take the cost of stationary energy supplies into consideration. To realize the economic operation of the catenary-free tram, the whole life-time cost of OESS and the cost of stationary energy supplies need to be considered together while optimizing the OESS.

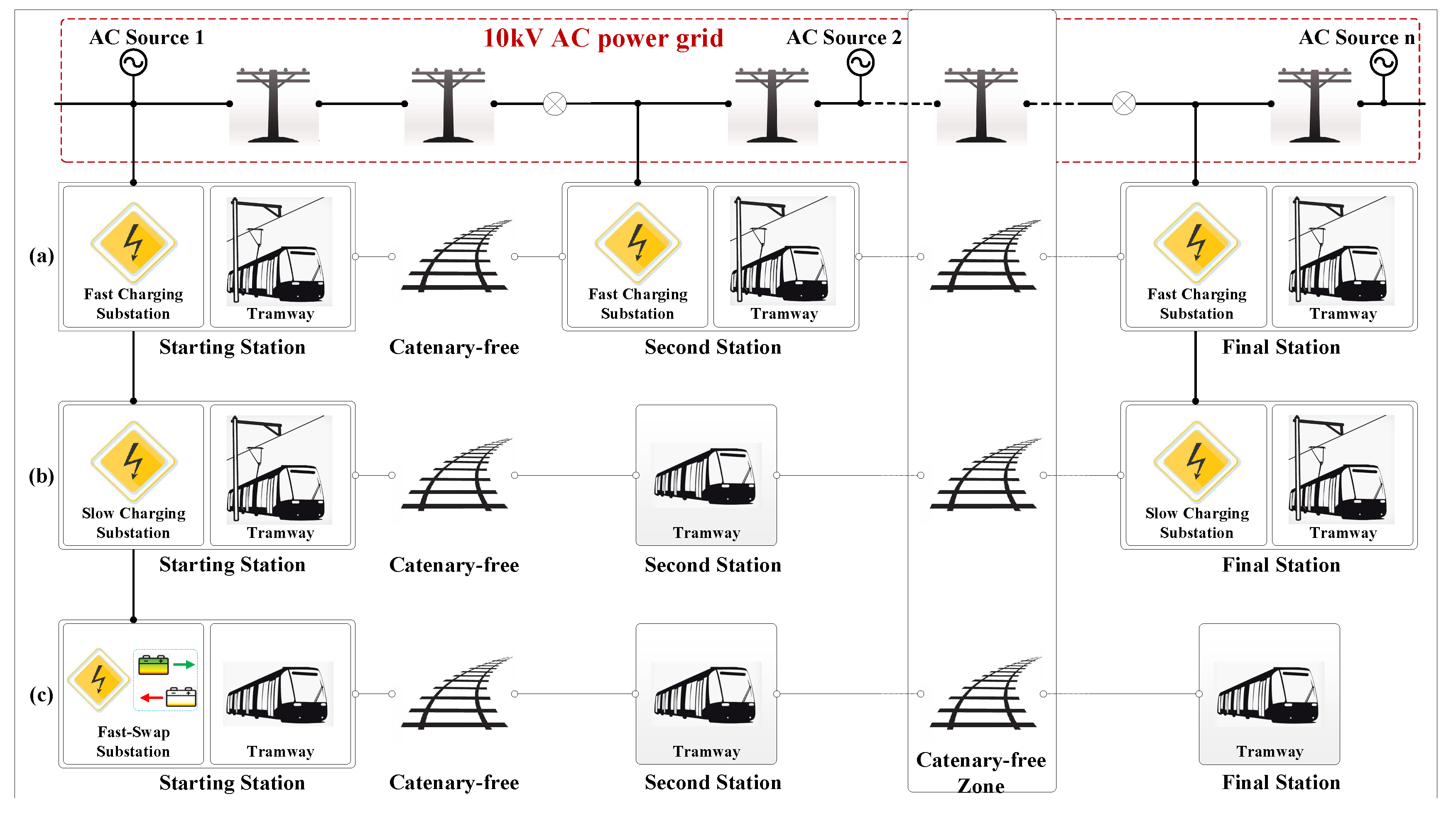
UC and battery are favored as a leading selection of ESEs for the OESS [15,16,17]. Because of a significant difference in the time scale of voltage responses, the charging time of UC and battery is different, where a fast-charging for UC (seconds-level) and a slow-charging for battery (minutes-level). As shown in Figure 1, three schemes are considered in this paper for comparing the feasibility and economy of the catenary-free tram under different energy storage types and different energy supplies: (1) UC storage systems with fast-charging at each station (US-FC); (2) battery storage systems with slow-charging at starting and final stations (BS-SC); (3) battery storage systems with fast-swapping at the swapping station (BS-FS).

Existing catenary-free tramlines in China, such as Haizhu line in Guangzhou and Huaian line in Huaian, are powered by the on-board UC system and fast-charged at each station along the tramline [3,9,18]. The US-FC has been applied in existing scenarios since the OESS energy can satisfy the operating demands at two adjacent stations. However, this scheme has high charging power requirement for the charging stations, resulting in an increment for the costs of construction and operation of charging stations [3].

The battery is appropriate to be utilized in the catenary-free tram due to its great technical improvement of charging and discharging capability and management reliability [1,6]. In particular, the lithium titanate battery, which uses ${\mathrm{Li}}_4{\mathrm{Ti}}_5{\mathrm{O}}_{12}$ (LTO) instead of graphite as its anode, is capable of being high-rate charged even at low temperature without causing any safety issues [19,20]. Thus, LTO battery has become a promising candidate for OESS application in rail transit, such as BS-SC scheme and BS-FS scheme. To improve the energy efficiency of the catenary-free tramline, a battery storage based OESS was explored in Reference [21], in which the energy supply mode named fast-swapping was applied. This energy supply is implemented by replacing the on-board battery systems with stationary battery systems when the tram arrives at swapping station, and then recharging the swapped battery systems at night. It is noted that although a centralized charging mode can greatly reduce the electricity cost, the number of the stationary battery systems increases as well. Moreover, it is essential to consider the station dwell time for a battery based OESS since the charging process of battery is much slower than the UC. Consequently, available charging time (ACT) which is defined as the remainder of station dwell time after deducting other miscellaneous processes, requires to be involved in the optimal sizing problem of OESS.

Three contributions are made:

• An optimal sizing method which considers the OESS and stationary energy supplies is proposed for the catenary-free tram, where an objective function is formulated in term of a daily cost.
• To highlight the economic operation of different schemes, i.e., US-FC, BS-SC, BS-FS, a trade-off between the ACT and the economic operation is analyzed quantitatively.
• A mixed particle swarm optimization (PSO) is used to solve the introduced optimal sizing problem and a case study on an catenary-free tramline in Foshan city, China, is applied to verify the effectiveness of the introduced method.

The remainder of this paper is organized as follows: Section 2 describes the catenary-free tram model, including the energy supply modes, the dynamic model of OESS and the efficiency model of energy supply. Section 3 formulates the proposed optimal sizing problem in detail. Section 4 introduces the PSO algorithms. In Section 5, a case study is given. Finally, Section 6 concludes this paper.

2. Catenary-Tram Model

To emphasize the difference between our work and existing researches, we address the size optimization of OESS by quantitative comparing the economy of different energy storage types and different energy supply modes. The UC-only and battery-only based OESSs are introduced, where the OESS is directly connected to the traction converter of the tram. According to the operation regimes of US-FC, BS-SC and BS-FS, three energy supplies are defined:

• Fast-charging mode (FC mode): OESSs are charged to a rated voltage within 30 s through the stationary charging equipment while the tram docks at each station.
• Slow-charging mode (SC mode): OESSs are charged to a predefined SOC within a reasonable time through the stationary charging equipment while the tram docks at the starting and final stations.
• Fast-swapping mode (FS mode): OESSs are swapped by stationary energy storage systems (ESSs) while the tram docks at the swapping station, and then the swapped OESSs are charged following a time-of-use strategy.

2.1. ESEs Modeling

To fully match the operating demands of the catenary-free tram, ESEs with characteristics of high energy density, high power density, wide temperature and long life cycle should be selected. In this paper, the LTO battery and the UC are finally chosen due to their attractive performances.

After grouping, the rated energy of battery system and UC system can be calculated as follows

$$\begin{array}{cc}\hfill & E_{\mathrm{b}}=\frac{N_{\mathrm{b},\mathrm{s}}{N}_{\mathrm{b},\mathrm{p}}{V}_{\mathrm{b},\mathrm{c}}{Q}_{\mathrm{b},\mathrm{c}}}{1000}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & E_{\mathrm{uc}}=\frac{N_{\mathrm{uc},\mathrm{s}}{N}_{\mathrm{uc},\mathrm{p}}{C}_{\mathrm{uc},\mathrm{c}}{V}_{\mathrm{uc},\mathrm{c}}^2}{2\times 3600\times 1000},\hfill \end{array}$$

(2)

where $E_{\mathrm{b}}$ [kWh] and $E_{\mathrm{uc}}$ [kWh] are the rated energy of battery system and UC system, respectively. In (1), $N_{\mathrm{b},\mathrm{s}}$, $N_{\mathrm{b},\mathrm{p}}$, $V_{\mathrm{b},\mathrm{c}}$ [V] and $Q_{\mathrm{b},\mathrm{c}}$ [Ah] are series number, parallels number, nominal voltage and nominal capacity of the LTO cell, respectively. In (2), $N_{\mathrm{uc},\mathrm{s}}$, $N_{\mathrm{uc},\mathrm{p}}$, $V_{\mathrm{uc},\mathrm{c}}$ [V] and $C_{\mathrm{uc},\mathrm{c}}$ [F] are series number, parallels number, nominal voltage and nominal capacity of the UC cell, respectively.

To simulate the power transmission between OESS and powertrain, the state equations of UC and battery need to be derived respectively. A RC model is chosen for UC, and its discrete state equation is formulated at iteration k [21]:

$$\begin{array}{cc}\hfill & I_{\mathrm{uc},\mathrm{c}}\left(k\right)=\frac{V_{\mathrm{uc},\mathrm{c}}\left(k\right)-\sqrt{V_{\mathrm{uc},\mathrm{c}}^2\left(k\right)-4R_{\mathrm{uc},\mathrm{c}}{P}_{\mathrm{uc},\mathrm{c}}\left(k\right)}}{2R_{\mathrm{uc},\mathrm{c}}}\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill & V_{\mathrm{uc},\mathrm{c}}(k+1)=V_{\mathrm{uc},\mathrm{c}}\left(k\right)-\frac{I_{\mathrm{uc},\mathrm{c}}\left(k\right)T_{\mathrm{s}}}{C_{\mathrm{uc},\mathrm{c}}}\hfill \end{array}$$

(3b)

$$\begin{array}{cc}\hfill & {soc}_{\mathrm{uc},\mathrm{c}}\left(k\right)={\left(\frac{V_{\mathrm{uc},\mathrm{c}}\left(k\right)}{V_{\mathrm{uc},\mathrm{r}}\left(k\right)}\right)}^2\times 100\%,\hfill \end{array}$$

(3c)

where $k\in \{0,1,\cdots ,T\}$ is discrete time and T [s] is final time, $I_{\mathrm{uc},\mathrm{c}}$ [A], $R_{\mathrm{uc},\mathrm{c}}$ [$\mathsf{\Omega }$], $V_{\mathrm{uc},\mathrm{r}}$ [V], $P_{\mathrm{uc},\mathrm{c}}$ [W] and ${soc}_{\mathrm{uc},\mathrm{c}}$ [%] are operation current, internal resistance, rated voltage, operation power and SOC of the UC cell, respectively, $T_{\mathrm{s}}$ is a discrete-sampling period which is set to 1 s in this paper. Under a certain cell power $P_{\mathrm{uc},\mathrm{c}}$ at each sample time k, the values of $V_{\mathrm{uc},\mathrm{c}}$, $I_{\mathrm{uc},\mathrm{c}}$ and ${soc}_{\mathrm{uc},\mathrm{c}}$ can be updated by (3a)–(3c).

Based on the LTO modelling in Reference [20], a data-driven Thevenin model for the LTO battery is established, and its mathematical expressions can be derived as follows:

$$\begin{array}{cc}\hfill & I_{\mathrm{b},\mathrm{c}}\left(k\right)=\frac{V_{\mathrm{ocv},\mathrm{c}}\left(k\right)-V_{\mathrm{p},\mathrm{c}}\left(k\right)-\sqrt{{\left(V_{\mathrm{ocv},\mathrm{c}}\left(k\right)-V_{\mathrm{p},\mathrm{c}}\left(k\right)\right)}^2-4R_{\mathrm{b},\mathrm{c}}\left(k\right)P_{\mathrm{b},\mathrm{c}}\left(k\right)}}{2R_{\mathrm{b},\mathrm{c}}\left(k\right)}\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill & V_{\mathrm{p},\mathrm{c}}(k+1)=\frac{I_{\mathrm{b},\mathrm{c}}\left(k\right)T_{\mathrm{s}}}{C_{\mathrm{p},\mathrm{c}}}+\left(1-\frac{T_{\mathrm{s}}}{R_{\mathrm{p},\mathrm{c}}{C}_{\mathrm{p},\mathrm{c}}}\right)V_{\mathrm{p},\mathrm{c}}\left(k\right)\hfill \end{array}$$

(4b)

$$\begin{array}{cc}\hfill & V_{\mathrm{b},\mathrm{o}}\left(k\right)=V_{\mathrm{ocv},\mathrm{c}}\left(k\right)-I_{\mathrm{b},\mathrm{c}}\left(k\right)R_{\mathrm{b},\mathrm{c}}\left(k\right)-V_{\mathrm{p},\mathrm{c}}\left(k\right)\hfill \end{array}$$

(4c)

$$\begin{array}{cc}\hfill & {soc}_{\mathrm{b},\mathrm{c}}(k+1)={soc}_{\mathrm{b},\mathrm{c}}\left(k\right)-\frac{I_{\mathrm{b},\mathrm{c}}\left(k\right)T_{\mathrm{s}}}{Q_{\mathrm{b},\mathrm{c}}\times 3600},\hfill \end{array}$$

(4d)

where $V_{\mathrm{ocv},\mathrm{c}}$ [V], $R_{\mathrm{b},\mathrm{c}}$ [$\mathsf{\Omega }$], $R_{\mathrm{p},\mathrm{c}}$ [$\mathsf{\Omega }$], $C_{\mathrm{p},\mathrm{c}}$ [F], $V_{\mathrm{p},\mathrm{c}}$ [V], $P_{\mathrm{b},\mathrm{c}}$ [W], $I_{\mathrm{b},\mathrm{c}}$ [A], $V_{\mathrm{b},\mathrm{o}}$ [V], ${soc}_{\mathrm{b},\mathrm{c}}$ [%] and $Q_{\mathrm{b},\mathrm{c}}$ [Ah] are open-circuit voltage, internal resistance, polarization resistance, polarization capacitor, polarization voltage, operation power, operation current, terminal voltage, SOC and rated capacity of the LTO cell, respectively. Detailed model parameters of the LTO-20Ah cell, that is, $V_{\mathrm{ocv},\mathrm{c}}$, $R_{\mathrm{b},\mathrm{c}}$, $R_{\mathrm{p},\mathrm{c}}$, $C_{\mathrm{p},\mathrm{c}}$, are reported in Reference [20]. It is similar to the UC model, under the time-varying cell power $P_{\mathrm{b},\mathrm{c}}\left(k\right)$, the values of $I_{\mathrm{b},\mathrm{c}}$, $V_{\mathrm{b},\mathrm{o}}$, $V_{\mathrm{p},\mathrm{c}}$ and ${soc}_{\mathrm{b},\mathrm{c}}$ can be updated by (4a)–(4b).

2.2. Life Cycle Model of ESEs

The life cycle of batteries and UCs is influenced by many factors, such as current rate, temperature rise, SOC range and depth of discharge (DOD). Here, the effect of DODs on the life cycle is mainly considered because the temperature and current of OESSs exhibit stable evolution trends after repeated and regular operations [22]. Since the counting process of load cycle reflects the memory characteristics of the materials, rain-flow method is commonly used in the calculation of fatigue life [23]. Therefore, it is effective to use this method to analyze the whole life-time DODs of OESSs [15,17]. Then, the remaining life cycle of OESSs is calculated based on the corresponding relationship between the specific DODs and cycle number.

Combining the experimental cycle data of the LTO in Reference [24] and the functional relationship between DOD and life cycle of LTO battery in Reference [15], the cycle number of LTO-20Ah can be calculated. To calculate the life cycle of the LTO battery in a convenient way, the data of its DOD and life cycle are fitted by an exponential function ($R^2=0.9999$) [21]

$$\begin{array}{c}\hfill N_{\mathrm{b},\mathrm{life}}\left(i\right)=675,200\times e^{-0.1424\times {DOD}_{\mathrm{b}}\left(i\right)}+161,500\times e^{-0.03195\times {DOD}_{\mathrm{b}}\left(i\right)},\end{array}$$

(5)

where ${DOD}_{\mathrm{b}}$ [%] is battery DOD, i is an index number of a specific ${DOD}_{\mathrm{b}}$, $N_{\mathrm{b},\mathrm{life}}\left(i\right)$ is the cycle number of the battery under ${DOD}_{\mathrm{b}}\left(i\right)$. For the UC, its life cycle can be almost 1 million times due to a physical process for its charging and discharging.

Then, the life cycle of OESS can be formulated as

$$\begin{array}{c}\hfill {Life}_j=1/\sum _{i=1}^{N_{j,\mathrm{DOD}}}\frac{1}{N_{j,\mathrm{life}}\left(i\right)},j\in \{\mathrm{b},\mathrm{uc}\},\end{array}$$

(6)

where $N_{j,\mathrm{DOD}}$ is total number of $DO{D}_j$ based on rain-flow method for the OESS $j\in \{\mathrm{b},\mathrm{uc}\}$.

2.3. Peak Charging Power of OESS

In US-FC scheme, the UC based OESSs need to be charged to a rated voltage within a limited time at each station. Under constant charging power and required charging time, the peak power of the charging equipment for the UC system, ($P_{\mathrm{uc},\mathrm{ch}}^{\mathrm{peak}}$ [W]) can be calculated as following

$$\begin{array}{c}\hfill P_{\mathrm{uc},\mathrm{ch}}^{\mathrm{peak}}=N_{\mathrm{uc},\mathrm{s}}{N}_{\mathrm{uc},\mathrm{p}}\times \frac{C_{\mathrm{uc},\mathrm{c}}\left(V_{\mathrm{uc},\mathrm{r}}^2-V_{\mathrm{uc},0}{V}_{\mathrm{uc},\mathrm{r}}\right)}{T_{\mathrm{uc},\mathrm{ch}}},\end{array}$$

(7)

where $V_{\mathrm{uc},0}$ [V] is the initial charging voltage of the UC cell and $T_{\mathrm{uc},\mathrm{ch}}$ [s] is corresponding charging time.

For the battery based OESS, it cannot be charged as fast as UC system probably defects caused by power density. According to the database of the constant current and constant voltage (CCCV) charging process, a minute-level charging power matrix ($P_{\mathrm{C}}$ [W]) for battery system is formulated

$$\begin{array}{c}\hfill P_{\mathrm{C}}=\left[P_{\mathrm{C}}^1,P_{\mathrm{C}}^2,\cdots ,P_{\mathrm{C}}^{t_{\mathrm{b}-1}},P_{\mathrm{C}}^{t_{\mathrm{b}}}\right],\end{array}$$

(8)

where $t_{\mathrm{b}}$ [min] is an integer which refers to the total charging duration from the return SOC to a certain cut-off SOC. Under CCCV charging regime, the peak charging power of the battery system, $P_{\mathrm{uc},\mathrm{ch}}^{\mathrm{peak}}$ [W], can be obtained when the terminal voltage of battery rises to its upper cut-off point

$$\begin{array}{c}\hfill P_{\mathrm{uc},\mathrm{ch}}^{\mathrm{peak}}=N_{\mathrm{uc},\mathrm{s}}{N}_{\mathrm{uc},\mathrm{p}}{V}_{\mathrm{b},\mathrm{cv}}{I}_{\mathrm{b},\mathrm{char}},\end{array}$$

(9)

where $V_{\mathrm{b},\mathrm{cv}}$ [V] and $I_{\mathrm{b},\mathrm{char}}$ [A] are the upper cut-off voltage and charging current of the battery cell, respectively.

2.4. Efficiency Model of Power Flow

In this work, the construction expense of charging stations is evaluated by the peak charging power, including the cost of transformers, charging equipment and basic tariff.

As shown in Figure 2, the black arrow indicates the efficiency diagram of power flow from AC gird to OESS and also from OESS to tram loads, where ${\eta }_{\mathrm{tr}}$ is the efficiency of transformer, ${\lambda }_{\mathrm{tr}}$ is the load rate, $cos\theta$ is the power factor, ${\eta }_{\mathrm{ce}}$ is the efficiency of charging equipment, and ${\eta }_{\mathrm{line}}$ is the efficiency of DC cables. The OESS satisfies the power demand of the tram loads directly when the tram is running between stations or docking at the station without charge. The power demand of the tram loads, $P_{\mathrm{t}}$, includes traction power of powertrain and auxiliary power of auxiliary load. Particularly, this paper mainly considers the efficiency of charging equipment and transformers, as the red dotted box in Figure 2 indicates, and the efficiency of DC cables ${\eta }_{\mathrm{line}}$ is ignored. Moreover, this work use the power flow to simulate the repeated charge and discharge of the OESS, in which constant values are taken into consideration for the above parameters in order to simplify model calculation, as: ${\lambda }_{\mathrm{tr}}$ = 0.8, $cos\theta$ = 0.9, ${\eta }_{\mathrm{tr}}$ = 0.98, ${\eta }_{\mathrm{ce}}$ = 0.95 [25].

Then, based on the peak charging power ($P_{\mathrm{ch},\max }$ [W]) determined by (7) and (9),

$$P_{\mathrm{ch},\max }=\left\{\begin{array}{c}{P}_{\mathrm{uc},\mathrm{ch}}^{\mathrm{peak}}\mathrm{for}\mathrm{UC-FC}\mathrm{scheme}\hfill \\ P_{\mathrm{uc},\mathrm{ch}}^{\mathrm{peak}}\mathrm{for}\mathrm{BS-SC}\mathrm{and}\mathrm{BS-FS}\mathrm{schemes}\hfill \end{array}\right.$$

the rated active power of charging equipment ($P_{\mathrm{ce}}$ [W]) and rated capacity of transformer ($S_{\mathrm{tr}}$ [VA]) can be calculated as (10).

$$\begin{array}{c}\hfill P_{\mathrm{ce}}=P_{\mathrm{ch},\max }/{\eta }_{\mathrm{ce}},S_{\mathrm{tr}}=P_{\mathrm{ce}}/\left({\lambda }_{\mathrm{tr}}cos\theta \right)\end{array}$$

(10)

3. Problem Formulation

To quantitatively analyze the feasibility and economy of the catenary-free tram in different energy storage types and different energy supply modes, that is, US-FC, BS-SC and BS-FS, an optimization problem for the OESS and charging infrastructure is proposed in this section, as

$$\begin{array}{c}\hfill \underset{X^p\in \mathsf{\Omega }}{min}{f}_{\mathrm{ob}}^p\left(X^p\right)\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\},\end{array}$$

(11)

where X is a set of decision variables including the series and parallels of the ESEs; superscript $p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\}$ corresponds to the US-FC scheme, BS-SC scheme and BS-FS scheme; $\mathsf{\Omega }$ are boundary conditions which can be given as following

$$\begin{array}{cc}\hfill & {soc}_{\mathrm{uc}}^{\min }\le {soc}_{\mathrm{uc},\mathrm{c}}\le {soc}_{\mathrm{uc}}^{\max },N_{\mathrm{uc},\mathrm{s}}^{\min }\le N_{\mathrm{uc},\mathrm{s}}\le N_{\mathrm{uc},\mathrm{s}}^{\max },E_{\mathrm{uc}}{m}_{\mathrm{uc}}\le M_{\max }\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill & {soc}_{\mathrm{b}}^{\min }\le {soc}_{\mathrm{b},\mathrm{c}}\le {soc}_{\mathrm{b}}^{\max },N_{\mathrm{b},\mathrm{s}}^{\min }\le N_{\mathrm{b},\mathrm{s}}\le N_{\mathrm{b},\mathrm{s}}^{\max },E_{\mathrm{b}}{m}_{\mathrm{b}}\le M_{\max },\left|C_{\mathrm{b}}\right|\le C_{\mathrm{b},\max },\hfill \end{array}$$

(12b)

where (12a) limits the SOC range, cell number and system mass of the UC based OESS, ${soc}_{\mathrm{uc}}^{\min }$ [%] and ${soc}_{\mathrm{uc}}^{\max }$ [%] are minimum and maximum SOC for the UC, respectively, $N_{\mathrm{uc},\mathrm{s}}^{\min }$ and $N_{\mathrm{uc},\mathrm{s}}^{\max }$ are minimum and maximum series number for the UC, respectively, $E_{\mathrm{uc}}$ [kWh] and $m_{\mathrm{uc}}$ [kWh/kg] are rated energy and energy density of the UC system, respectively.

The SOC range, cell number, system mass and operating rate $C_{\mathrm{b}}$ (that is, $I_{\mathrm{b},\mathrm{c}}/Q_{\mathrm{b},\mathrm{c}}$) of the battery based OESS are limited by (12b), where ${soc}_{\mathrm{b}}^{\min }$ [%] and ${soc}_{\mathrm{b}}^{\max }$ [%] are minimum and maximum SOC for the battery, respectively, $N_{\mathrm{b},\mathrm{s}}^{\min }$ and $N_{\mathrm{b},\mathrm{s}}^{\max }$ are minimum and maximum series number for the battery, respectively, $E_{\mathrm{b}}$ [kWh], $m_{\mathrm{b}}$ [kWh/kg] and $C_{\mathrm{b},\max }$ are rated energy, energy density and maximum rate of the battery system, respectively, and $M_{\max }$ [kg] is the maximum acceptable value of OESS weight. Note that $\left|·\right|$ function returns the absolute value for the current rate $C_{\mathrm{b}}$. Generally, $m_{\mathrm{uc}}$ and $m_{\mathrm{b}}$ are given by the cell manufacturer, while $M_{\max }$ is decided by the tram manufacturer.

The objective function $f_{\mathrm{ob}}^p\left(X^p\right)$ in (11) is defined in term of a daily cost containing a whole life-time cost of the OESS (${Cost}_{\mathrm{wlbc}}$ [RMB/day]) and a cost of energy supply (${Cost}_{\mathrm{es}}$ [RMB/day])

$$\begin{array}{c}\hfill f_{\mathrm{ob}}^p={Cost}_{\mathrm{wlbc}}^p+{Cost}_{\mathrm{es}}^p\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\},\end{array}$$

(13)

Formulation of ${Cost}_{\mathrm{wlbc}}$ and ${Cost}_{\mathrm{es}}$ is described in following subsections.

3.1. Whole Life-Time Cost of OESS

As expressed in (14), the whole life-time cost of OESS ${Cost}_{\mathrm{wlbc}}^p$ includes initial cost (${Cost}_{\mathrm{i}}$ [RMB]), replacement cost (${Cost}_{\mathrm{r}}$) and maintenance cost (${Cost}_{\mathrm{m}}$ [RMB]) of the OESS.

$$\begin{array}{c}\hfill {Cost}_{\mathrm{wlbc}}^p=\left({Cost}_{\mathrm{i}}^p+{Cost}_{\mathrm{r}}^p+{Cost}_{\mathrm{m}}^p\right)/(Y\times 365)\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\},\end{array}$$

(14)

where Y is service years.

3.1.1. The Initial Cost of OESS

The initial costs of OESS under the US-FC scheme and BS-SC scheme can be calculated as

$$\begin{array}{c}\hfill {Cost}_{\mathrm{i}}^{\mathrm{usfc}}=c_{\mathrm{e},\mathrm{uc}}{E}_{\mathrm{uc}}{N}_{\mathrm{t}},{Cost}_{\mathrm{i}}^{\mathrm{bssc}}=c_{\mathrm{e},\mathrm{b}}{E}_{\mathrm{b}}{N}_{\mathrm{t}},\end{array}$$

(15)

where $c_{\mathrm{e},\mathrm{uc}}$ [RMB/kWh] and $c_{\mathrm{e},\mathrm{b}}$ [RMB/kWh] are energy prices of the UC and battery, respectively, and $N_{\mathrm{t}}$ is the number of trams.

For the BS-FS scheme, the initial cost of OESS includes both on-board and stationary ESSs. As defined in (16), the number of stationary ESSs, $N_{\mathrm{b}}^{\mathrm{s}}$, needs to satisfy the operation conditions under maximum departure density [26]

$$\begin{array}{cc}\hfill & N_{\mathrm{b}}^{\mathrm{s}}=\frac{T_{\mathrm{b},\mathrm{ch}}+T_{\mathrm{R}}}{T_{\mathrm{hr}}},T_{\mathrm{b},\mathrm{ch}}\le T_{\mathrm{h}}\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill & N_{\mathrm{b}}^{\mathrm{s}}=\frac{T_{\mathrm{h}}}{T_{\mathrm{hr}}}+\frac{T_{\mathrm{b},\mathrm{ch}}-T_{\mathrm{h}}+T_{\mathrm{R}}}{T_{\mathrm{cr}}},T_{\mathrm{b},\mathrm{ch}}>T_{\mathrm{h}},\hfill \end{array}$$

(16b)

where $T_{\mathrm{b},\mathrm{ch}}$ [s] is charging time for the swapped battery system, $T_{\mathrm{R}}$ [s] is fast-swapping time, $T_{\mathrm{h}}$ [s] is daily rush hour, $T_{\mathrm{hr}}$ [s] is a departure interval at rush hour and $T_{\mathrm{cr}}$ [s] is a departure interval at daily off-rush hour. After determining $N_{\mathrm{b}}^{\mathrm{s}}$ by (16), the initial cost ${Cost}_{\mathrm{i}}^{\mathrm{bsfs}}$ can be formulated as

$$\begin{array}{c}\hfill {Cost}_{\mathrm{i}}^{\mathrm{bsfs}}=c_{\mathrm{e},\mathrm{b}}{E}_{\mathrm{b}}(N_{\mathrm{t}}+N_{\mathrm{b}}^{\mathrm{b}}).\end{array}$$

(17)

3.1.2. The Replacement Cost of OESSs

Based on the life cycle model derived from Section 2, the calculation of the replacement times of UC system and battery system can be referred to the following formula

$$\begin{array}{c}\hfill N_{j,\mathrm{R}}^{\mathrm{n}}=\mathrm{ceil}\left(\frac{Y}{{Life}_j^n/(N_{\mathrm{w}}^n\times 365)}\right)\mathrm{for}n\in \{1,2,\cdots ,N_{\mathrm{t}}\}\mathrm{and}j\in \{\mathrm{uc},\mathrm{b}\}\end{array}$$

(18)

where $n\in \{1,2,\cdots ,N_{\mathrm{t}}\}$ is an index number of tram, $N_{j,\mathrm{R}}^{\mathrm{n}}$ is the replacement times of the OESS, ceil function returns an round-up value for $N_{j,\mathrm{R}}^{\mathrm{n}}$, and $N_{\mathrm{w}}^n$ is daily operation times of tram n which is depended on operating timetable.

Then, the replacement cost of OESS can be calculated as follows

$$\begin{array}{c}\hfill {Cost}_{j,\mathrm{r}}=c_{\mathrm{e},j}{E}_j\times \sum _{n=1}^{N_{\mathrm{t}}}{N}_{j,\mathrm{R}}^{\mathrm{n}}\mathrm{for}j\in \{\mathrm{uc},\mathrm{b}\}.\end{array}$$

(19)

This way, the replacement costs of the aforementioned three schemes can be achieved after substituting their dynamic SOC curve into (6), (18) and (19).

3.1.3. The Maintenance Cost of OESS

Regular maintenance of OESS can ensure its durability, and the corresponding maintenance cost is considered as

$$\begin{array}{c}\hfill {Cost}_{\mathrm{m}}^p=c_{\mathrm{m}}{N}_{\mathrm{t}}\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\},\end{array}$$

(20)

where $c_{\mathrm{m}}$ [RMB/day] is an daily maintenance price for the OESSs.

3.2. Cost of Energy Supply

To improve the effectiveness of the optimal sizing problem for the catenary-free tram, the cost of energy supply (${Cost}_{\mathrm{es}}^p$) is considered in this work and described as

$$\begin{array}{c}\hfill {Cost}_{\mathrm{es}}^p={Cost}_{\mathrm{e}}^p+{Cost}_{\mathrm{s}}^p+{Cost}_{\mathrm{ms}}^p\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\}.\end{array}$$

(21)

In (21), ${Cost}_{\mathrm{es}}^p$ includes electricity cost (${Cost}_{\mathrm{e}}^p$ [RMB/day]), construction cost (${Cost}_{\mathrm{s}}^p$ [RMB/day]) and maintenance cost ${Cost}_{\mathrm{ms}}^p$ [RMB/day] of charging stations.

3.2.1. The Electricity Cost

The electricity cost of the US-FC scheme and BS-SC scheme can be calculated by multiplying the energy consumption of a single trip with the corresponding electricity price. The trip number of each tram which runs within the time window of specific electricity price can be counted by analyzing the operating timetable, as

$$N_{\mathrm{e}}=\left[\begin{array}{ccccc}{N}_{1,1}& N_{1,2}& N_{1,3}& \cdots & N_{1,N_{\mathrm{t}}}\\ N_{2,1}& N_{2,2}& N_{2,3}& \cdots & N_{2,N_{\mathrm{t}}}\\ & & & \ddots & \\ N_{L,1}& N_{L,2}& N_{L,3}& \cdots & N_{L,N_{\mathrm{t}}},\end{array}\right]$$

(22)

where $N_{\mathrm{e}}$ is a statistic matrix of trip number of all trams and each element stands for the cumulative trips of particular vehicle running within the correlative time window of electric price; L is the number of segments of the daily electricity price $c_{\mathrm{e}}$ [RMB/kWh]

$$\begin{array}{c}\hfill c_{\mathrm{e}}=\left[c_{\mathrm{e},1},c_{\mathrm{e},2},c_{\mathrm{e},3},\cdots ,c_{\mathrm{e},L}\right].\end{array}$$

(23)

Then, according to the energy consumption of a single trip, the daily electricity costs of the US-FC scheme and BS-SC scheme can be calculated as

$$\begin{array}{c}\hfill {Cost}_{\mathrm{e}}^p=E_{\mathrm{t}}^p\times \frac{\mathrm{sum}\left(c_{\mathrm{e}}{N}_{\mathrm{e}}\right)}{{\eta }_{\mathrm{ce}}{\eta }_{\mathrm{tr}}}\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc}\},\end{array}$$

(24)

where $E_{\mathrm{t}}^p$ [kWh] is energy consumption of the tram in a single trip; sum is a summation function.

For the BS-FS scheme, the stationary ESSs are charged to a predefined SOC by the CCCV regime and then waiting for the new swapping tasks if the charge is completed [27]. Therefore, in order to calculate the electricity cost under BS-FS scheme, a daily charging power matrix for the swapping station, P [kW], is established in minute-level as following (25),

$$\begin{array}{c}\hfill P=A\times B=\left[P_1,P_2,P_3,\cdots ,P_{1439},P_{1440}\right],\end{array}$$

(25)

where

$$A=\left[\begin{array}{ccccccc}{P}_{\mathrm{c},1}& 0& 0& \cdots & 0& 0& 0\\ P_{\mathrm{c},2}& P_{\mathrm{c},1}& 0& \cdots & 0& 0& 0\\ & & & \ddots & & & \\ 0& 0& P_{\mathrm{c},\mathrm{tb}}& \cdots & P_{\mathrm{c},2}& P_{\mathrm{c},1}& 0\\ 0& 0& 0& \cdots & P_{\mathrm{c},3}& P_{\mathrm{c},2}& P_{\mathrm{c},1}\end{array}\right],$$

(26)

$$\begin{array}{c}\hfill B=\left[B_1,B_2,B_3,\cdots ,B_{1439},B_{1440}\right].\end{array}$$

(27)

In (26), A [kW] is a charging sequence matrix, in which each column stands for the charging power vector of particular battery system per minute. The initial value of the charging power vector in A can be determined by the return SOC of the battery system and the minute-level charging power matrix (8) [26]. In (27), B is a charging instruction matrix which is depended on the departure timetable and charging strategy. Each element in B is a Boolean variable (1 or 0), where 1 means charge and 0 means no charge.

Then, a time-of-use electricity price is used to calculate a long-term electricity cost for the BS-FS scheme, as following

$$\begin{array}{c}\hfill {Cost}_{\mathrm{e}}^{\mathrm{bsfs}}=\left(\sum _{k=1}^{t_1}P\left(k\right)+\sum _{k=t_1+1}^{t_2}P\left(k\right)\right)\times \frac{c_{\mathrm{e},1}{T}_{\mathrm{s}}}{3600}+\cdots +\left(\sum _{k=t_{L-1}+1}^{t_L}P\left(k\right)+\sum _{k=t_L+1}^{1440}P\left(k\right)\right)\times \frac{c_{\mathrm{e},\mathrm{L}}{T}_{\mathrm{s}}}{3600},\end{array}$$

(28)

where $t_1$, $t_2$,...,$t_L$ are moments under the pointwise electricity prices.

3.2.2. The Construction Cost of Charging Stations

In this work, the peak charging power is adopted to evaluate the construction cost of charging stations. Therefrom, the costs of charging equipment and basic tariff are mainly considered and calculated as follows

$$\begin{array}{cc}\hfill & {Cost}_{\mathrm{ce}}=\left(\frac{c_{\mathrm{tr}}}{{\eta }_{\mathrm{ce}}{\lambda }_{\mathrm{tr}}cos\theta }+\frac{c_{\mathrm{ce}}}{{\eta }_{\mathrm{ce}}}\right)P_{\mathrm{ch}}^{\max }/\left(Y\times 365\right)\hfill \end{array}$$

(29a)

$$\begin{array}{cc}\hfill & {Cost}_{\mathrm{bt}}=\frac{c_{\mathrm{bt}}}{{\eta }_{\mathrm{ce}}cos\theta }\times P_{\mathrm{ch}}^{\max },\hfill \end{array}$$

(29b)

where ${Cost}_{\mathrm{ce}}$ [RMB/day] is the cost of charging equipment; ${Cost}_{\mathrm{bt}}$ [RMB/day] is the costs of basic tariff which is calculated by the maximum operation capacity; $c_{\mathrm{ce}}$ [RMB/W], $c_{\mathrm{tr}}$ [RMB/VA] and $c_{\mathrm{bt}}$ [RMB/(VA · day)] are the prices of charging equipment, transformers and peak operating capacity of the grid, respectively.

Since the energy supply modes are different, the peak charging power and the number of charging stations of aforementioned three schemes are different as well. Thus, the construction costs of charging stations can be defined by

$$\begin{array}{c}\hfill {Cost}_{\mathrm{s}}^p=\left({Cost}_{\mathrm{ce}}+{Cost}_{\mathrm{bt}}\right)\times N_{\mathrm{s}}^p\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\},\end{array}$$

(30)

where $N_{\mathrm{s}}^p$ is the number of charging stations for the three schemes. Based on the three energy supply modes, $N_{\mathrm{s}}^{\mathrm{usfc}}$ is equal to the number of stops along the tramline ($N_{\mathrm{s}}$); $N_{\mathrm{s}}^{\mathrm{bssc}}$ is equal to 2; $N_{\mathrm{s}}^{\mathrm{bsfs}}$ is equal to 1.

3.2.3. The Maintenance Cost of Charging Stations

Similarly, the maintenance cost of the charging stations is also considered and expressed as follow

$$\begin{array}{c}\hfill {Cost}_{\mathrm{m},\mathrm{s}}^p=c_{\mathrm{m},\mathrm{s}}{N}_{\mathrm{s}}^p\mathrm{for}p\in \{\mathrm{usfc},\mathrm{bssc},\mathrm{bsfs}\},\end{array}$$

where $c_{\mathrm{m},\mathrm{s}}$ is the daily maintenance price of charging stations.

4. Methodology

It can be found that the introduced objective function (13) is a superposition of multiple costs, in which some cost functions are discontinuities and cannot be directly described by the decision variables. This way, the analytical method is not suitable for the proposed optimization problem (11). For this kind of optimization problems, heuristic algorithm, such as genetic algorithm and particle swarm optimization (PSO), can not only achieve good results, but also save development time [15,25]. Noted that the introduced objective function only has two decision variables for each problem, but three cases that is, US-FC, BS-SC and BS-FS are discussed in this work. Finally, the PSO is quite consistent with our development requirements due to its fast convergence and high precision. This way, a mixed particle swarm optimization based on natural selection is utilized to solve the introduced optimization problem, where the global optimal approximation is conducted by sorting and replacing the fitness values of particles.

5. Case Study and Optimization Results

In this section, to quantitatively compare different energy storage types and different energy supply modes from the economic point of view, operating conditions of an existing catenary-free tramline in China are used to verify the effectiveness of the introduced optimization method.

5.1. Parameter Selection for the Case Study

The parameters of the catenary-free tramline in Gaoming district, Foshan city, China, are applied in this work. The length of this catenary-free tramline is about $6.5$ km [28]. The operating profiles and station positions of the tram are illustrated in Figure 3 [21,28]. It can be seen that the maximum speed is 70 km/h. Moreover, in addition to the traction power in Figure 3, the power demand of the catenary-free tram also includes an on-board auxiliary power which is considered as a constant in this work, that is, 55 kW [28]. The daily departure timetable of the tramline is listed in

Table 1. Operating timetable of the catenary-free tram.

Day Hour [h]	Departure Interval [s]	Number of Operating Trams
07:30–12:41	606	5
12:41–17:35	505	6
17:35–22:00	837	4

.

Table 2. Daily electricity price of the grid.

Day Hour [h]	10:00–15:00, 18:00–21:00	7:00–10:00, 15:00–18:00, 21:00–23:00
$c_{\mathrm{e}}$ [RMB/kWh]	$1.2682$	$0.8745$

provides a daily time-of-use electricity price in China [26]. The capacity selection of 10 kV transformer (250–2000 kVA) is referenced to JB/T 2426-2004. According to actual operating experience of the swapping stations for the pure electric buses [26], the swapping time can be from 8 to 12 min. Thus, the swap time for BS-FS scheme is set to 10 min in this work, that is, $T_{\mathrm{R}}$ = 10 min. In addition, the OESS needs to fulfill a service life of at less 12 years (Y = 12 year) until next technological reformation [29]. For the parameters of the stationary charging equipment, $c_{\mathrm{ce}}=1\mathrm{RMB}/\mathrm{W}$, $c_{\mathrm{tr}}=0.3\mathrm{RMB}/\mathrm{VA}$, $c_{\mathrm{m}}=8.2\mathrm{RMB}/\mathrm{day}$, $c_{\mathrm{m},\mathrm{s}}=8.2\mathrm{RMB}/\mathrm{day}$, $c_{\mathrm{bt}}=0.0011\mathrm{RMB}/\left(\mathrm{VA}·\mathrm{day}\right)$ [15,30,31].

The LTO-20Ah battery [24] and UC-7500F [32] are selected and their main specifications are summarized in

Table 3. Specifications of LTO-20Ah and UC-7500F.

Parameters	LTO-20 Ah	UC-7500 F
Nominal voltage	$2.3$ V	$2.7$ V
Nominal capacity	20 Ah	7500 F
Energy density	86 Wh/kg	$5.71$ Wh/kg
Power density	$2.2$ kW/kg	$6.85$ kW/kg
Operating temperature range	[−30 ${}^{\circ }$C, 65 ${}^{\circ }$C]	[−40 ${}^{\circ }$C, 65 ${}^{\circ }$C]
Operating voltage range	[ $1.5$ V, $2.7$ V]	[ 0 V, $2.7$ V]
SOC range	$[0.3,0.9]$	$[0.25,1]$
Energy price	10,000 RMB/kWh	50,000 kWh

. To preserve the optimal solutions feasible, (1) the maximum current rate of the LTO-20Ah is set to $C_{\mathrm{b},\max }=5$; (2) the minimum and maximum number of the series cell for the UC based OESS and battery based OESS are set to 186 and 351, respectively, due to an operating voltage range from 500 V to 950 V for the powertrain (from Reference [32]) and the same upper cut-off voltage for the UC and battery cell (see operating voltage range in Table 3); (3) the maximum mass of OESS ($M_{\max }$) is set to 4000 kg.

The proposed optimziaiton problem is computed by Matlab on a PC (Intel Core i5-2450M [email protected]). After many tests, the values of iterations and populations of PSO are set to 20 and 40, respectively. Moreover, a feasibility and effectiveness analysis is accomplished by repeating the optimization 50 times with the same configuration parameters due to random characteristics of PSO.

5.2. US-FC Scheme

For US-FC scheme, UC systems is charged to a rated voltage within 30s at each station. The optimization results under US-FC scheme are shown in Figure 4 and

Table 4. Optimization results of US-FC scheme.

OESS Size	OESS Mass [t]	${\mathit{f}}_{\mathbf{ob}}$	${\mathit{Cost}}_{\mathbf{i}}$	${\mathit{Cost}}_{\mathbf{r}}$	${\mathit{Cost}}_{\mathbf{e}}$	${\mathit{Cost}}_{\mathbf{s}}$	${\mathit{Cost}}_{\mathbf{m}}$	${\mathit{S}}_{\mathbf{tr}}$ [kVA]	${\mathit{P}}_{\mathbf{ce}}$ [kW]
300S/7P	3.99	3.0489	0.1092	0.1092	1.0068	1.8105	0.0132	2000	1253
351S/6P	4.00	3.0482	0.1095	0.1095	1.0066	1.8093	0.0132	2000	1252

The OESS size is described by [number of series cell/number of parallel branch]. This description is applied for the OESS size in the below tables as well. The unit of $f_{\mathrm{ob}}$, ${Cost}_{\mathrm{i}}$, ${Cost}_{\mathrm{r}}$, ${Cost}_{\mathrm{e}}$, ${Cost}_{\mathrm{s}}$, ${Cost}_{\mathrm{m}}$ is ${10}^4\mathrm{RMB}$.

. It can be seen that there are two solutions in the 50 independent optimizations: solution 1 is 300 series and 7 parallels, simplified as 300S/7P (the following descriptions for the sizes of OESS are the same), and solution 2 is 351S/6P. The computational time of each optimization is less than 20 s. From the first two rows in Table 4, we can find that sizes for solution 1 and solution 2 are almost obtained on the weight boundary, which means that the solutions of PSO can converge to the vicinity of an optimal value. Solution 2 is preferred due to a minimum daily cost, where 6 UC systems are installed on 6 trams and another 6 UC systems need to be prepared for future replacement.

The simulation results of 351S/6P are shown in Figure 5. Throughout the simulation curves, the minimum SOC and voltage of the UC system are 48.4% and 654 V, respectively. In this case, due to a large capacity demand and multiple charging sites, the construction cost of US-FC scheme is still high, accounting for 59% of the total daily cost.

5.3. BS-SC Scheme

To investigate the effect of different charging time on the introduced objective function under BS-SC scheme, the size of LTO battery is optimized with different charging rates and different charging time. The selected charging rates are 1C, 3C and 5C (the maximum operating rate of LTO-20Ah is 5C) and the charging time is set to 0–10 min after considering the average departure period of the tramline (almost 11 min). By denoting with a cut-off charging SOC at 90%, the returned SOC of battery systems cannot be lower than a definite value due to the limitation of charging rate and charging time.

The optimization results of BS-SC scheme under different charging rates and charging time are presented in

Table 5. Optimization results of BS-SC scheme under a current rate of 5C.

${\mathit{t}}_{\mathbf{b}}$ [min]	OESS Size	OESS Mass [t]	${\mathit{f}}_{\mathbf{ob}}$	${\mathit{soc}}_{\mathbf{b},\mathbf{r}}$ [%]	${\mathit{Life}}_{\mathbf{b}}$ [year]	${\mathit{S}}_{\mathbf{tr}}$ [kVA]	${\mathit{P}}_{\mathbf{ce}}$ [kW]	WorStd			${\mathit{T}}_{\mathbf{ct}}$ [s]
								Worst	Mean	Std.
2	339/20	4.00	2.9321	74.71 (74.70)	5.61	2000	1927	-	-	-	-
3	290/16	2.74	2.3782	67.12 (66.71)	4.48	2000	1319	2.3808	2.3789	9.7 × 10${}^{-4}$	41.51
4	235/17	2.30	2.2097	63.11 (58.46)	4.00	1600	1135	2.2120	2.2103	8.6 × 10${}^{-4}$	38.42
5–7	235/17	2.36	2.2097	63.11 (50–34)	4.00	1600	1135	-	-	-	-

The unit of $f_{\mathrm{ob}}$ is ${10}^4\mathrm{RMB}$.

,

Table 6. Optimization results of BS-SC scheme under a current rate of 3C.

${\mathit{t}}_{\mathbf{b}}$ [min]	OESS Size	OESS Mass [t]	${\mathit{f}}_{\mathbf{ob}}$	${\mathit{soc}}_{\mathbf{b},\mathbf{r}}$ [%]	${\mathit{Life}}_{\mathbf{b}}$ [Year]	${\mathit{S}}_{\mathbf{tr}}$ [kVA]	${\mathit{P}}_{\mathbf{ce}}$ [kW]	WorStd			${\mathit{T}}_{\mathbf{ct}}$ [s]
								Worst	Mean	Std.
3.24	339/20	4.00	2.7207	74.71 (74.70)	5.61	1600	1156	-	-	-	-
4	312/18	3.31	2.4535	71.34 (71.00)	5.08	1600	958	2.4563	2.4542	9.8 × 10${}^{-4}$	72.52
5	251/18	2.66	2.1997	66.45 (66.03)	4.40	1250	770	2.2020	2.2003	7.0 × 10${}^{-4}$	73.00
6	235/17	2.36	2.0802	63.11 (61.10)	4.00	1000	681	2.0824	2.0811	9.1 × 10${}^{-4}$	70.10
7–10	235/17	2.36	2.0802	63.11 (56–41)	4.00	1000	681	-	-	-	-

The unit of $f_{\mathrm{ob}}$ is ${10}^4\mathrm{RMB}$.

and

Table 7. Optimization results of BS-SC scheme under a current rate of 1C.

${\mathit{t}}_{\mathbf{b}}$ [min]	OESS Size	OESS Mass [t]	${\mathit{f}}_{\mathbf{ob}}$	${\mathit{soc}}_{\mathbf{b},\mathbf{r}}$ [%]	${\mathit{Life}}_{\mathbf{b}}$ [Year]	${\mathit{S}}_{\mathbf{tr}}$ [kVA]	${\mathit{P}}_{\mathbf{ce}}$ [kW]	WorStd			${\mathit{T}}_{\mathbf{ct}}$ [s]
								Worst	Mean	Std.
9.30	339/20	4.00	2.4952	74.71 (74.70)	5.61	500	369	-	-	-	-
10	279/23	3.78	2.4229	73.79 (73.50)	5.46	500	349	2.4247	2.4234	5.4 × 10${}^{-4}$	40.29

The unit of $f_{\mathrm{ob}}$ is ${10}^4\mathrm{RMB}$.

. It is similar to the optimizations for US-FC scheme, the standard deviations of the objective values by PSO are quite small. Comparing Table 5, Table 6 and Table 7, it shows that an optimal size grouping with 339S/20P is obtained on the vicinity of weight constraint while seeking the shortest charging time of each charging rate: 2.00 min, 3.24 min and 9.30 min. To satisfy the short charging time, the optimization model outputs a large size of battery system to achieve a feasible return SOC. This way, the initial cost of OESS plays a leading role in the objective function and then the optimal solutions can be found near the feasible region of returned SOC, see ${soc}_{\mathrm{b},\mathrm{r}}$ in Table 5, Table 6 and Table 7. Noted that the values outside parentheses are returned SOC of the optimal sizes and the values inside parentheses are the boundary values of returned SOC.

When the charging time is prolonged, the boundary values of return SOC gradually decrease. In this case, to reduce the objective function value, the optimization model also needs to output a large size of battery system to reduce the replacement times. Here, the optimization results in Table 5 are utilized to illustrate. When the charging time is less than 4 min, the returned SOC and corresponding limit are close due to the optimal sizes are achieved near the boundary of returned SOC (see Table 5). When the charging time is higher than 4 min, the objective function can converge to a small value, regardless of the returned SOC. In this case, both the initial cost and replacement cost of OESS play the leading role in the objective function. Besides, because of a demand of the integer multiple of replacement times, the same optimization results can be found under the cases of a high charging rate with a long charging time. For example: the charging rate of 5C with the charging time from 4 min to 7 min in Table 5). Such evolution trends can be found in other cases in Table 6 and Table 7 as well.

A size configuration in 235S/17P under a 5C charging rate is selected to simulate the power flow under BS-SC. As shown in Figure 6, after a single trip, the voltage, current and SOC of the battery system are within the predefined range, and the return SOC at the final station is 63.11%. With a long docking time (e.g., 4 min) at the final station, the battery system can be charged to an SOC of 90% with a charging rate of 5C, see in Figure 6. Moreover, under the operating demand of 12 years, 6 battery systems are installed on 6 trams in the early stages and the other 12 battery systems are used for two times replacement in the future.

5.4. BS-FS Scheme

Under FS mode, an executable charging strategy is presented with following rules: (1) charging the swapped battery systems to 90% SOC with a 1C rate and the CCCV regime; (2) charging the on-board battery systems immediately after they are swapped; (3) charging the on-board battery systems of daily last trip at midnight due to a lowest electricity price. Because of the battery swap mode and centralized charging method, the charging time can be extended and the charging power then can be significantly decreased.

The PSO results for BS-FS scheme are presented in Figure 7. It can be seen from Figure 7 that three solutions are obtained among the 50 independent optimizations for BS-FS scheme: solution 1 is 335S/14P, solution 2 is 346S/12P and solution 3 is 343S/13P. The computational time for each optimization is between 150 s and 250 s.

For BS-FS scheme, the optimal sizing problem is a cost balance between the whole life-time cost of OESS and the construction cost of charging station, due to a very slight changes in the electricity cost and maintenance cost. Detailed optimal sizing results are summarized in

Table 8. Optimization results of BS-FS schemel.

OESS Size	${\mathit{N}}_{\mathbf{b},\mathbf{R}}$	OESS Mass [t]	${\mathit{f}}_{\mathbf{ob}}$	${\mathit{Cost}}_{\mathbf{i}}$	${\mathit{Cost}}_{\mathbf{r}}$	${\mathit{Cost}}_{\mathbf{e}}$	${\mathit{Cost}}_{\mathbf{s}}$	${\mathit{Cost}}_{\mathbf{m}}$	${\mathit{S}}_{\mathbf{tr}}$ [kVA]	${\mathit{P}}_{\mathbf{ce}}$ [kW]
335S/14P	4	2.77	2.1021	0.4926	0.4926	0.9758	0.1395	0.0016	1600	962
346S/12P	5	2.45	2.0622	0.4797	0.4797	0.9788	0.1224	0.0016	1250	852
343S/13P	4	2.63	2.0587	0.4683	0.4683	0.9897	0.1308	0.0016	1250	915

The unit of $f_{\mathrm{ob}}$, ${Cost}_{\mathrm{i}}$, ${Cost}_{\mathrm{r}}$, ${Cost}_{\mathrm{e}}$, ${Cost}_{\mathrm{s}}$, ${Cost}_{\mathrm{m}}$ is ${10}^4\mathrm{RMB}$.

. Comparing the initial cost ${Cost}_{\mathrm{i}}$, the replacement cost ${Cost}_{\mathrm{i}}$ and the cost of charging station ${Cost}_{\mathrm{i}}$ in Table 8, it illustrates the whole life-time cost of OESS is the leading role of the objective function under BS-FS scheme. This is because the whole life-time cost of OESS is obviously higher than the construction cost of charging station under BS-FS scheme. After calculating the service life of above three sizes, that is, 335S/14P, 346S/12P and 343S/13P, by rain-flow method, the corresponding replacement time is 6.3300, 6.0834 and 6.0048 years, respectively.

Moreover, the size of 343S/13P is almost the optimal size for BS-FS scheme and corresponding simulation is shown in Figure 8. After a round trip, the voltage, current and SOC of battery system are within the predefined range, and the return SOC is 38%. In addition, 10 battery systems are required for the solution of 343S/13P, where 6 systems are equipped on 6 trams and the other 4 systems are placed on the swapping station for swapping tasks.

5.5. Discussion

Considering the station dwell time of vehicles is limited, it is necessary to take the available charging time (ACT) as a sensitive variable to evaluate the economy of the catenary-free tram under different schemes. To quantitative analysis of the trade-off between the ACT and economic operation, the optimal scheme is divided into 6 cases: case-1, the ACT is set to $[0,2\min ]$; case-2, the ACT is set to $(2\min ,4\min ]$; case-3, the ACT is is set to $(4\min ,6\min ]$; case-4, the ACT is is set to $(6\min ,8\min ]$; case-5, the ACT is is set to $(8\min ,10\min ]$; case-6, the ACT is larger than 10 min. This way, a high level of defined case means a large compression to the ACT.

The cost distribution of optimal solutions under different ACT is provided in Figure 9. Obviously, US-FC scheme is the only choice under case-1 due to the superior power characteristic of UCs, but its daily cost is the highest. With the prolonged ACT, the demand for peak charging power of OESS weakens gradually, resulting in the application of battery systems possible. The evolution trend of the optimal solutions and cost distribution under different charging time is exhibited in the form of histogram. It can be intuitively seen that BS-SC scheme is optimal if the ACT is between 2 min and 10 min, and BS-FS scheme has the very impressive economy if the ACT is more than 10 min. Here, it is worth mentioning that the case-level of BS-FS scheme can be adjusted to a lower grade if the swap time is decreased.

To quantitatively evaluate the benefits of the different energy storage types and different energy supplies, the daily cost and OESS weight of the optimal solutions are examined simultaneously. By taking the optimal solution of US-FC scheme as the benchmark, comparison of the optimal solutions under different ACTs is shown in Figure 10. Note that the cost-saving for BS-SC and BS-FS has been calculated in terms of a relative cost reduction from US-FC scheme, respectively. For the battery storage based OESS, although an excessive pursuit of the least charging time has a 3.8% cost saving under case-2, its weight is almost equal to that of US-FC scheme. Under case-3, case-4 and case-5, the benefit of prolonging the charging time is considerable, where a reduction over 30% in daily cost and a reduction over 40% in weight can be obtained simultaneously, see in Figure 10. For the BS-FS scheme, a 32.46% cost saving and a 34.23% weight loss are achieved due to the FS mode.

6. Conclusions

This paper provides a novel optimal sizing model for the catenary-free tram, in which both the on-board energy storage system and stationary energy supplies are considered. To study the feasibility and economy of different energy storage types and energy supply modes utilized for the catenary-free tram, three schemes are discussed from the economic point of view.

The optimization results of the case study on the catenary-free tramline in Foshan city shows that: (1) the US-FC scheme is preferred for the application of high departure density and short station dwell time; (2) the BS-SC scheme is preferred for the application of a medium length of the station dwell time; (3) the BS-FS scheme is preferred for the application of a long length of the station dwell time. Moreover, comparing to US-FC scheme, a cost saving more than 30% and a weight reduction over 40% can be obtained by BS-SC scheme, while a cost saving of 34.23% and a weight loss of 32.46% can be achieved by BS-FS scheme. In addition, the benefits of installing the battery system and prolonging the charging time are not only the cost saving and weight loss, but also the reduction of charging sites. Based on this work, an online energy management strategy of the on-board energy storage system for the catenary-free tramline may be investigated in the future.