The Effects of the Presence of a Kitchen House on the Wind Flow Surrounding a Low-Rise Building
Abstract
1. Introduction
2. Research Methodology
2.1. Post Windstorm Site-Survey
2.2. Numerical Modeling
2.3. Validation Model
- (i)
- Tominaga et al. [9] conducted both experiments and CFD.
- (ii)
- Their isolated low-rise model has strong resemblance of a Malaysian rural house.
- (iii)
- They conducted their CFD work using the ANSYS Fluent software package, which was used in the current study.
2.4. Numerical Methods for the House Model
2.4.1. Preprocessing for the House Model
2.4.2. Post-Processing for the House Model
3. Experimental Results and Discussions
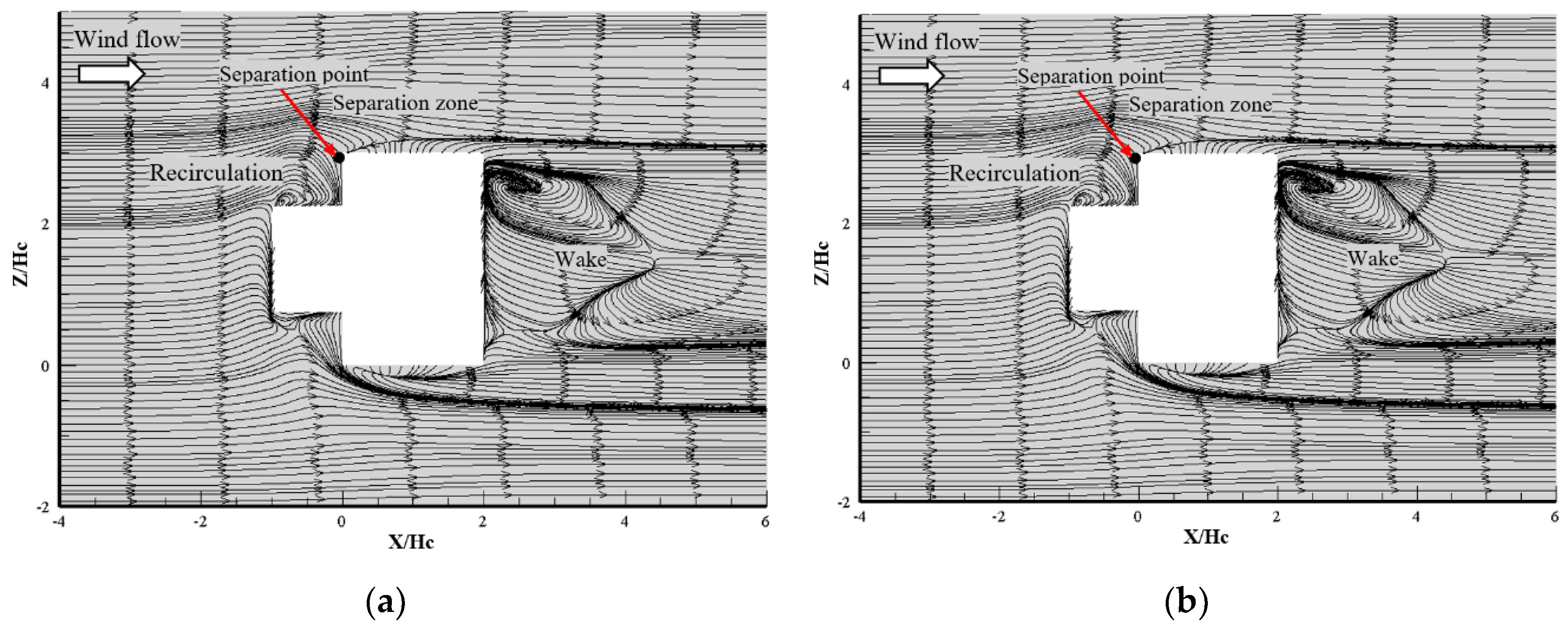
3.1. Validation Model
3.1.1. Comparison of Pressure Coefficient
3.1.2. Comparison of Pressure Coefficient
3.2. Numerical Simulation of the Rural House Using CFD
3.2.1. Grid Sensitivity Analysis
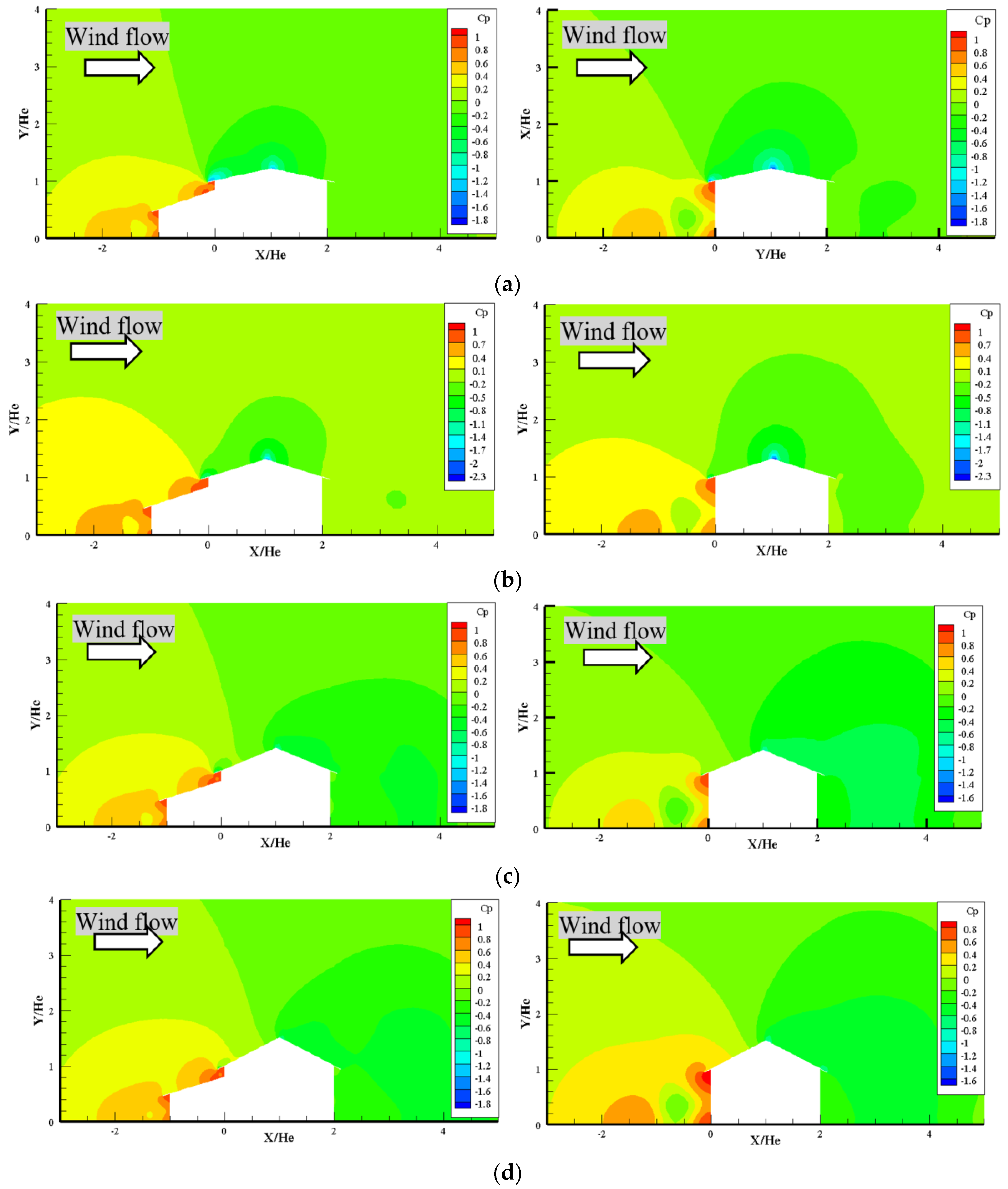
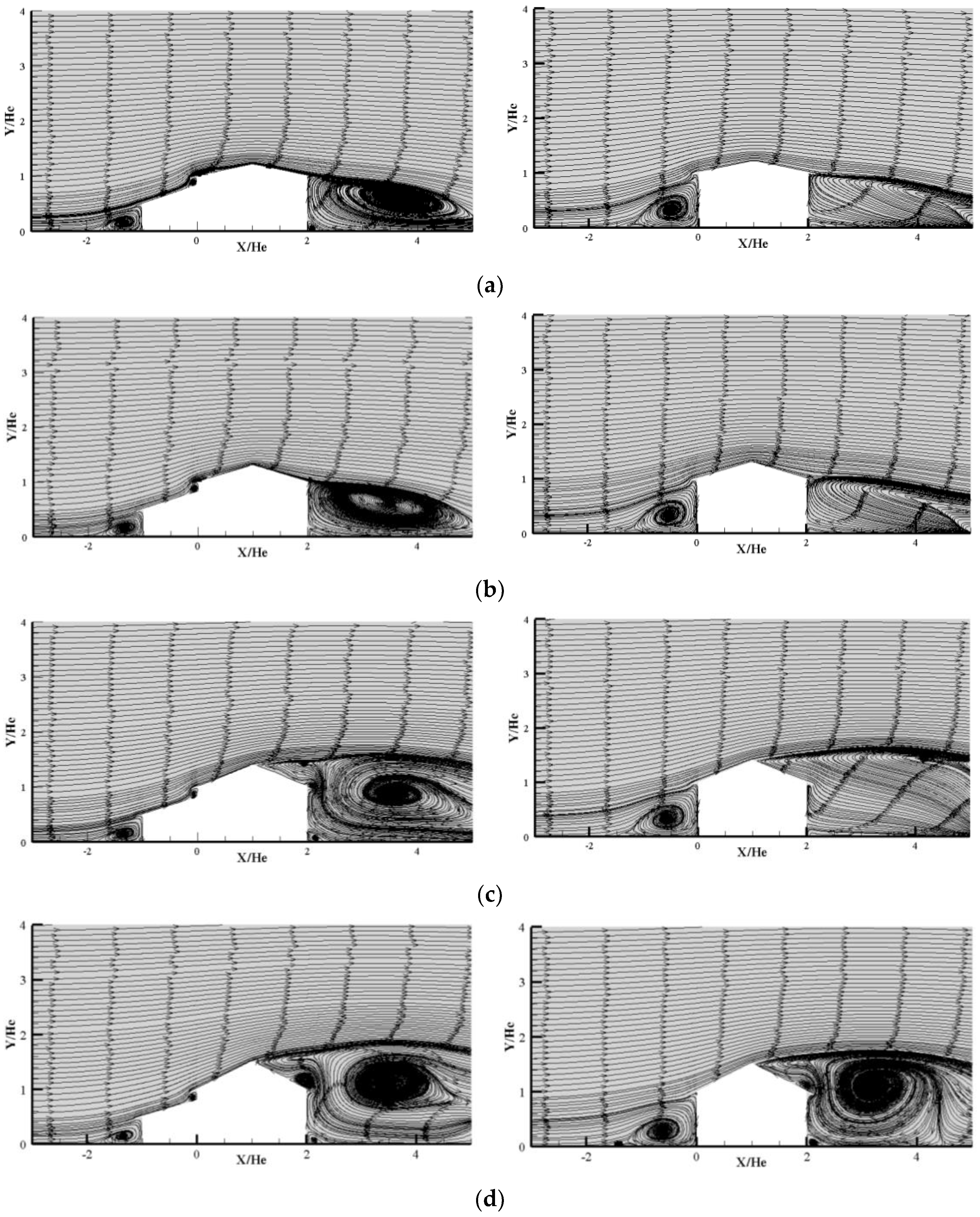
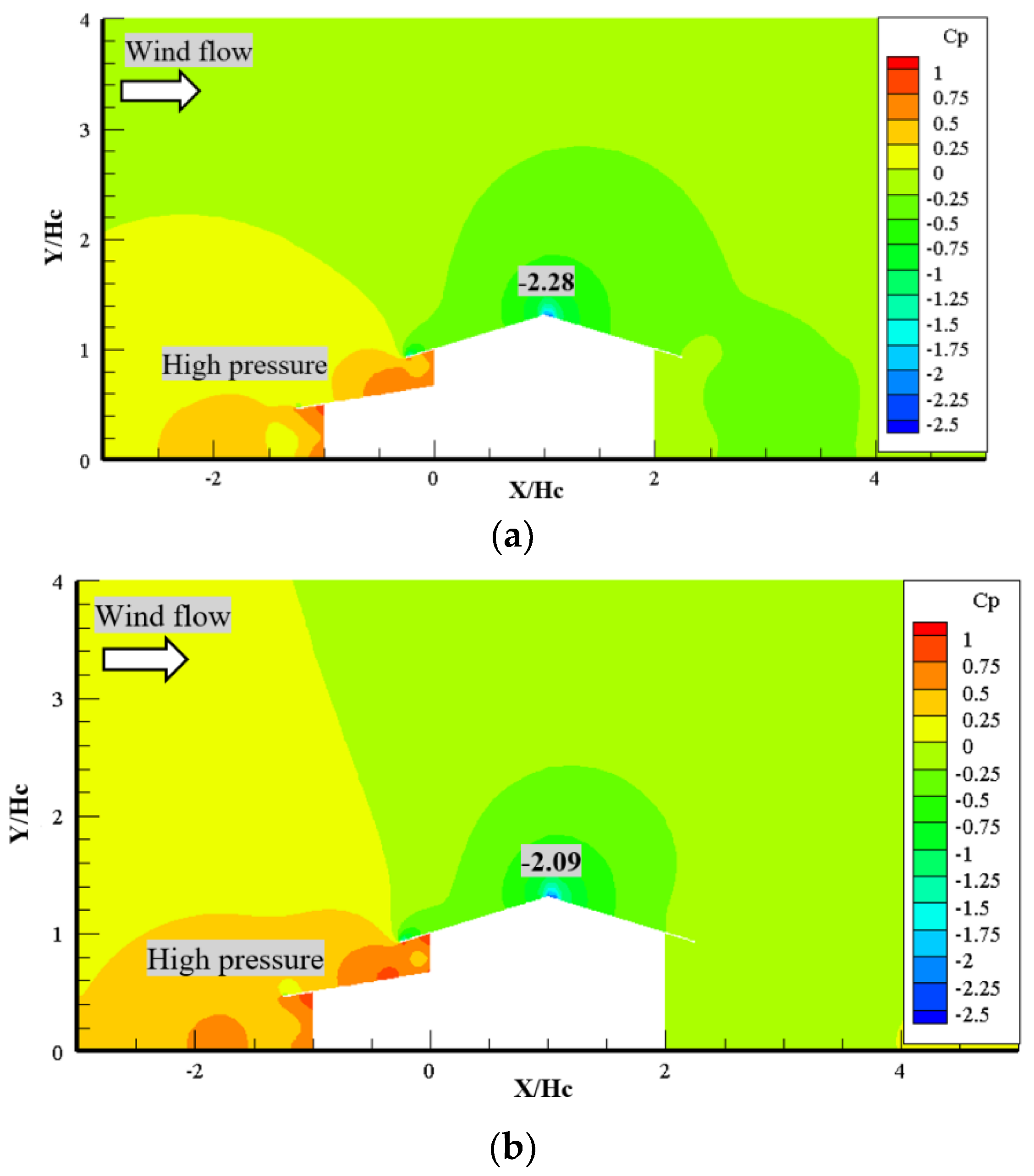
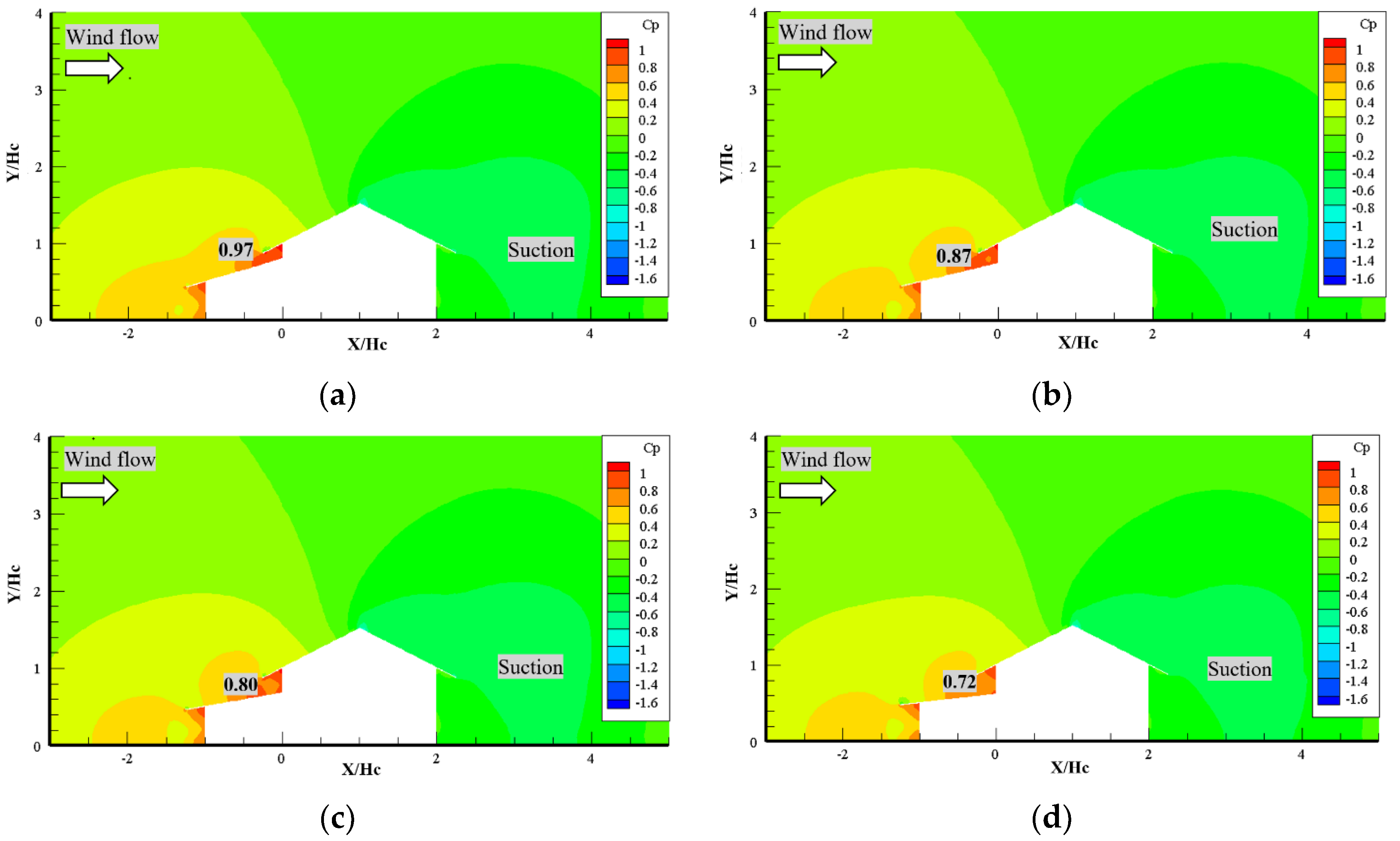
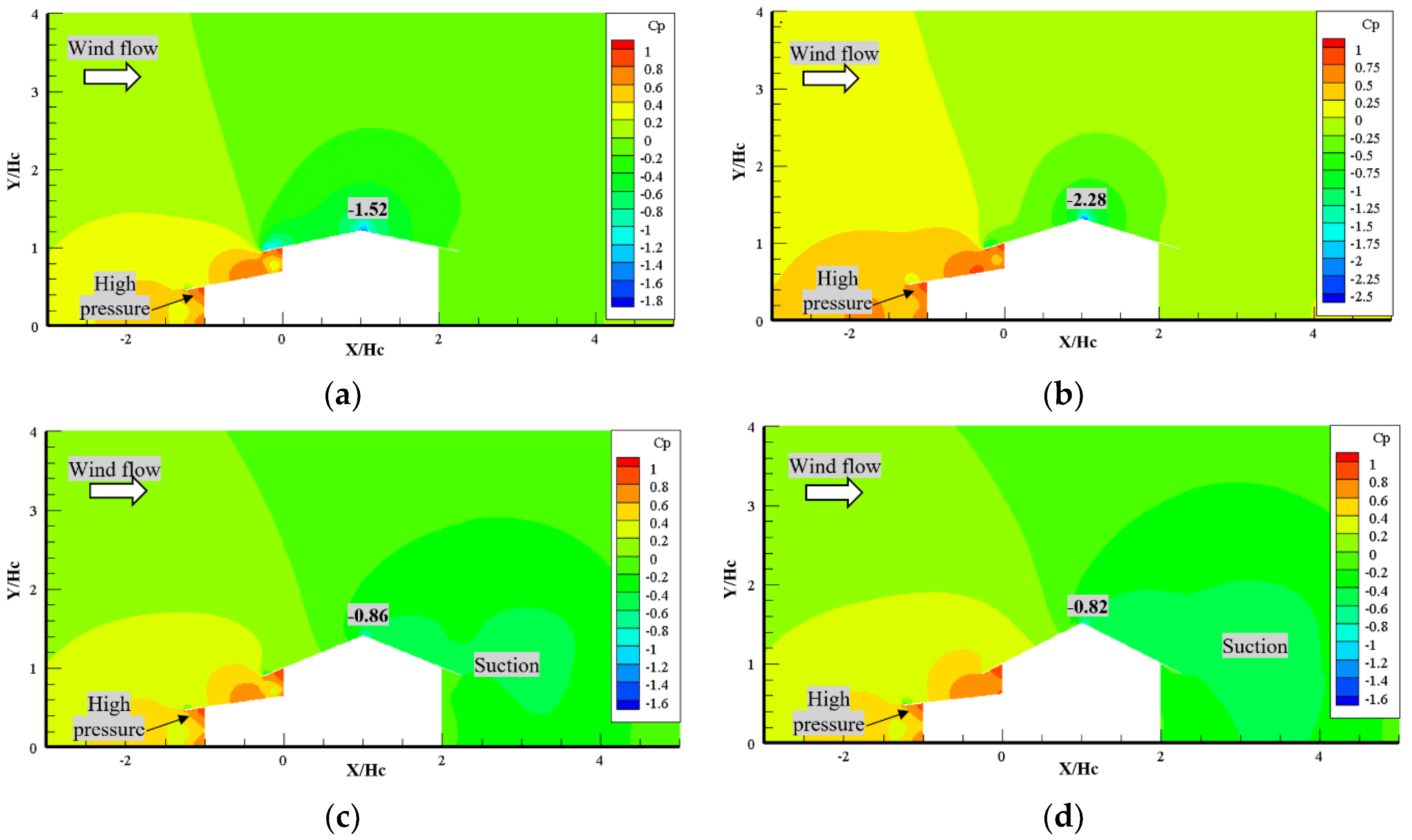
3.2.2. Rural House with and without Kitchen House
3.3. Factors Affecting the Wind Flow Around a Rural House
3.3.1. Kitchen Position
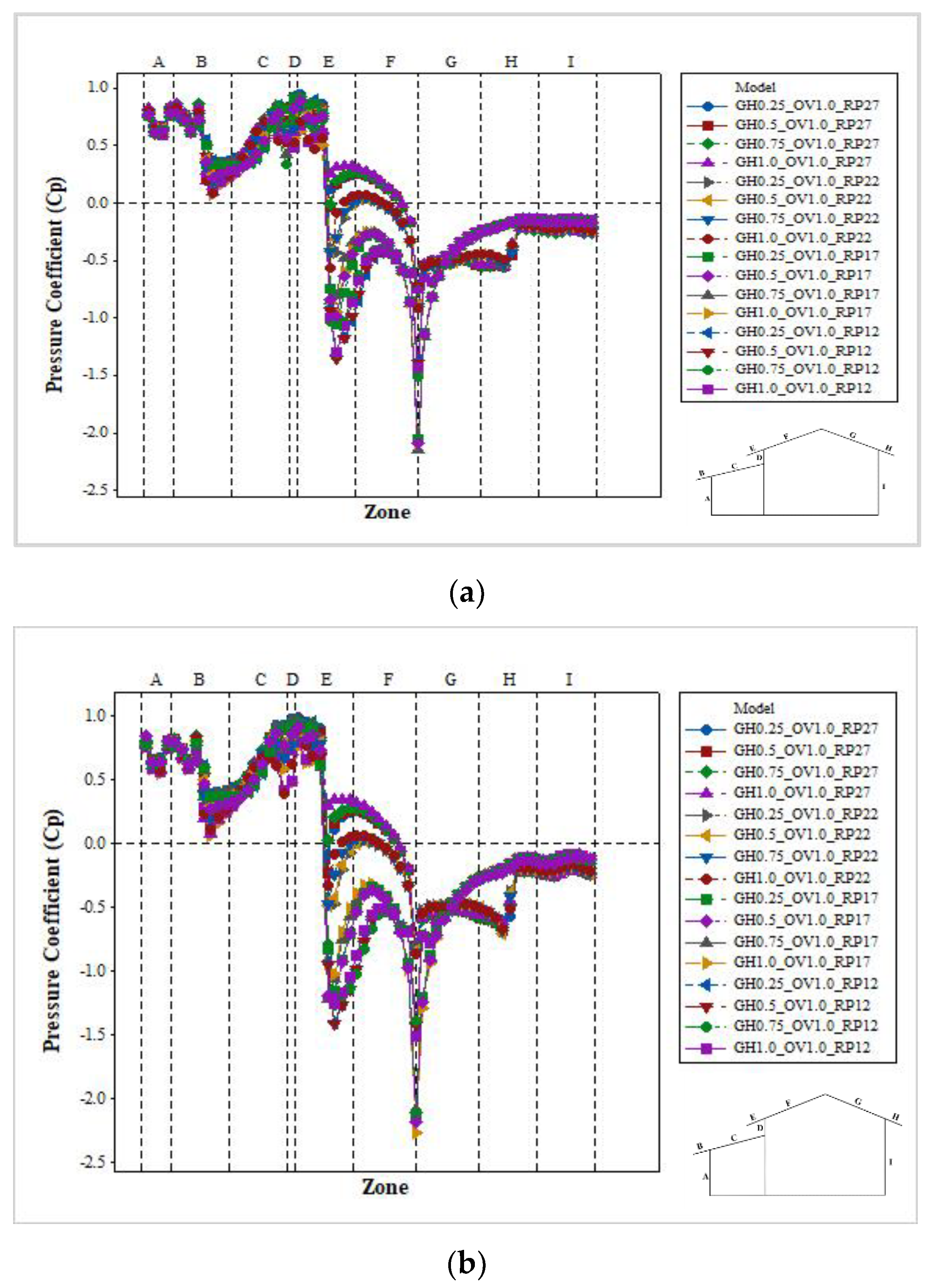
3.3.2. Gap Height
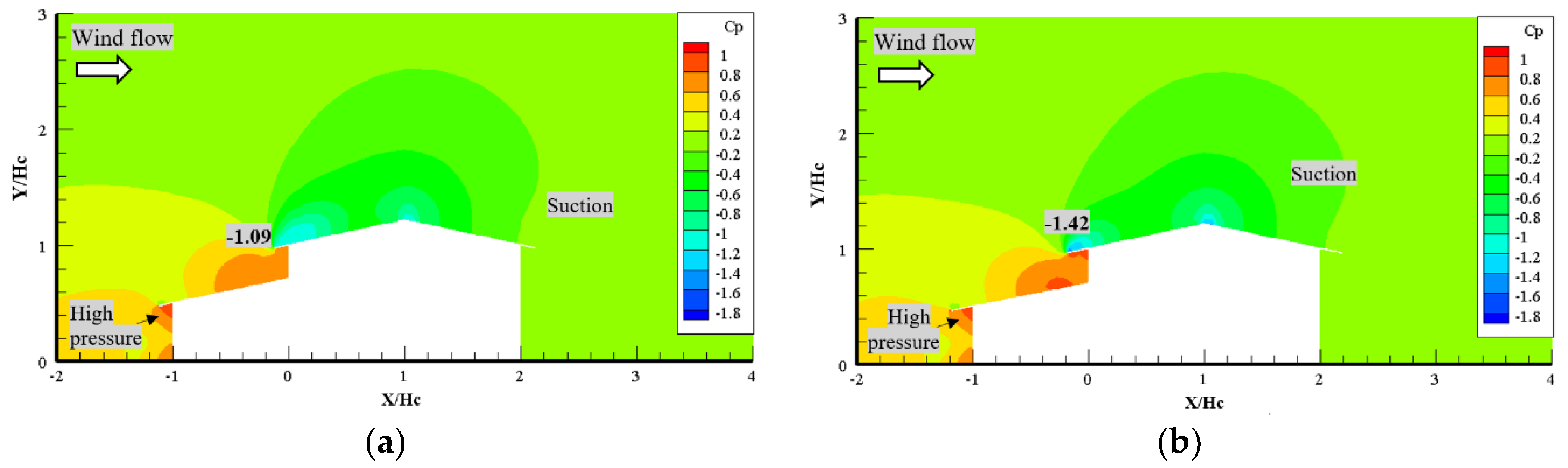
3.3.3. Roof Pitch
3.3.4. Roof Overhang
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Henry, L. Wind Engineering: A Handbook for Structural Engineers; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Henderson, D.; Ginger, J. Role of building codes and construction standards in windstorm disaster mitigation. Aust. J. Emerg. Manag. 2008, 23, 40. [Google Scholar]
- Xing, F.; Mohotti, D.; Chauhan, K. Experimental and numerical study on mean pressure distributions around an isolated gable roof building with and without openings. Build. Environ. 2018, 132, 30–44. [Google Scholar] [CrossRef]
- Aly, A.M. Atmospheric boundary-layer simulation for the built environment: Past, present and future. Build. Environ. 2014, 75, 206–221. [Google Scholar] [CrossRef]
- Fisk, W.J. Review of some effects of climate change on indoor environmental quality and health and associated no-regrets mitigation measures. Build. Environ. 2015, 86, 70–80. [Google Scholar] [CrossRef]
- Xing, F.; Mohotti, D.; Chauhan, K. Study on localised wind pressure development in gable roof buildings having different roof pitches with experiments, RANS and LES simulation models. Build. Environ. 2018, 143, 240–257. [Google Scholar] [CrossRef]
- Irtaza, H.; Javed, M.; Jameel, A. Effect on wind pressures by variation of roof pitch of low-rise hip-roof building. Asian J. Civ. Eng. 2015, 16, 869–889. [Google Scholar]
- Ozmen, Y.; Baydar, E.; Van Beeck, J. Wind flow over the low-rise building models with gabled roofs having different pitch angles. Build. Environ. 2016, 95, 63–74. [Google Scholar] [CrossRef]
- Tominaga, Y.; Akabayashi, S.-I.; Kitahara, T.; Arinami, Y. Air flow around isolated gable-roof buildings with different roof pitches: Wind tunnel experiments and CFD simulations. Build. Environ. 2015, 84, 204–213. [Google Scholar] [CrossRef]
- Meecham, D.; Surry, D.; Davenport, A. The magnitude and distribution of wind-induced pressures on hip and gable roofs. J. Wind Eng. Ind. Aerodyn. 1991, 38, 257–272. [Google Scholar] [CrossRef]
- Ahmad, S.; Kumar, K. Effect of geometry on wind pressures on low-rise hip roof buildings. J. Wind Eng. Ind. Aerodyn. 2002, 90, 755–779. [Google Scholar] [CrossRef]
- Ahmad, S.; Kumar, K. Wind pressures on low-rise hip roof buildings. Wind Struct. 2002, 5, 493–514. [Google Scholar] [CrossRef]
- Xu, Y.; Reardon, G. Variations of wind pressure on hip roofs with roof pitch. J. Wind Eng. Ind. Aerodyn. 1998, 73, 267–284. [Google Scholar] [CrossRef]
- Takano, Y.; Moonen, P. On the influence of roof shape on flow and dispersion in an urban street canyon. J. Wind Eng. Ind. Aerodyn. 2013, 123, 107–120. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Murakami, S.; Mochida, A.; Kondo, K.; Ishida, Y. Development of a new k− ε model for flow and pressure fields around bluff body. J. Wind Eng. Ind. Aerodyn. 1997, 67, 169–182. [Google Scholar] [CrossRef]
- Holmes, J.D. Wind pressures on tropical housing. J. Wind Eng. Ind. Aerodyn. 1994, 53, 105–123. [Google Scholar] [CrossRef]
- Surry, D.; Lin, J. The effect of surroundings and roof corner geometric modifications on roof pressures on low-rise buildings. J. Wind Eng. Ind. Aerodyn. 1995, 58, 113–138. [Google Scholar] [CrossRef]
- Chang, C.-H.; Meroney, R.N. The effect of surroundings with different separation distances on surface pressures on low-rise buildings. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1039–1050. [Google Scholar] [CrossRef]
- Wan Chik, F.; Che Deraman, S.; Noram, I.R.; Muhammad, M.; Majid, T.; Zulkarnain, N. Development of Windstorm Database System for Wind Damages in Malaysia. J. Civ. Eng. Res. 2014, 4, 214–217. [Google Scholar]
- Bachok, M.F.; Shamsudin, S.; Abidin, R.Z. Effectiveness of Windstorm-Producing Thunderstorms Early Warning Issues in Peninsular Malaysia. Int. J. Environ. Sci. Dev. 2015, 6, 635. [Google Scholar] [CrossRef]
- MS 1553:2002. Malaysia Standard Code of Practise on Wind Loading for Building; Department of Standards Malaysia: Selangor, Malaysia, 2002. [Google Scholar]
- GhaffarianHoseini, A.; Berardi, U.; Dahlan, N.D.; GhaffarianHoseini, A. What can we learn from Malay vernacular houses? Sustain. Cities Soc. 2014, 13, 157–170. [Google Scholar] [CrossRef]
- Ghaffarianhoseini, A.; Berardi, U.; Ghaffarianhoseini, A. Thermal performance characteristics of unshaded courtyards in hot and humid climates. Build. Environ. 2015, 87, 154–168. [Google Scholar] [CrossRef]
- Kubota, T.; Zakaria, M.A.; Abe, S.; Toe, D.H.C. Thermal functions of internal courtyards in traditional Chinese shophouses in the hot-humid climate of Malaysia. Build. Environ. 2017, 112, 115–131. [Google Scholar] [CrossRef]
- Kyritsi, E.; Michael, A. An assessment of the impact of natural ventilation strategies and window opening patterns in office buildings in the mediterranean basin. Build. Environ. 2019, 175, 106384. [Google Scholar] [CrossRef]
- Roosli, R.; Bakar, A.H.A.; Abas, N.F.; Ismail, M.; Abdullah, S.; Yusuf, M.N. Criteria and determinants for assessing the sustainability of conservation management and process of Malay Vernacular House. Adv. Environ. Biol. 2015, 59–63. [Google Scholar]
- Lim, J.Y. The Malay House: Rediscovering Malaysia’s Indigenous Shelter System; Institut Masyarakat: Kuala Lumpur, Malaysia, 1987. [Google Scholar]
- Majid, T.; Ramli, N.I.; Ali, M.; Saad, M.S.H. Malaysia Country Report 2012: Wind Related Disaster Risk Reduction and Wind Environmental Issues. In 7th Workshop on Regional Harmonization of Wind Loading and Wind Environmental Specifications in Asia-Pacific Economies; Universiti Malaysia Pahang: Kuantan, Pahang, Malaysia, 2012; pp. 12–13. [Google Scholar]
- Ai, Z.; Mak, C.; Niu, J.; Li, Z.; Zhou, Q. The effect of balconies on ventilation performance of low-rise buildings. Indoor Built Environ. 2011, 20, 649–660. [Google Scholar] [CrossRef]
- Kumar, K.S.; Stathopoulos, T. Computer Simulation of fluctuating wind pressures on low building roofs. Concordia University. J. Wind Eng. Ind. Aerodyn. 1997, 69, 485–495. [Google Scholar] [CrossRef]
- Ginger, J.; Letchford, C. Pressure factors for edge regions on low rise building roofs. J. Wind Eng. Ind. Aerodyn. 1995, 54, 337–344. [Google Scholar] [CrossRef]
- Alemu, A.T.; Saman, W.; Belusko, M. A model for integrating passive and low energy airflow components into low rise buildings. Energy Build. 2012, 49, 148–157. [Google Scholar] [CrossRef]
- Pietrzyk, K.; Hagentoft, C.-E. Probabilistic analysis of air infiltration in low-rise buildings. Build. Environ. 2008, 43, 537–549. [Google Scholar] [CrossRef]
- Khanduri, A.; Morrow, G. Vulnerability of buildings to windstorms and insurance loss estimation. J. Wind Eng. Ind. Aerodyn. 2003, 91, 455–467. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical simulation of dispersion around an isolated cubic building: Comparison of various types of k–ɛ models. Atmos. Environ. 2009, 43, 3200–3210. [Google Scholar] [CrossRef]
- Zaini, S.S.; Majid, T.A.; Deraman, S.N.C.; Chik, F.A.W.; Muhammad, M.K.A. Post Windstorm Evaluation of Critical Aspects Causing Damage to Rural Houses in the Northern Region of Peninsular Malaysia. In MATEC Web of Conferences, 2017; EDP Sciences: Ulis, France, 2017; p. 03016. [Google Scholar]
- Zhang, X. CFD Simulation of Neutral ABL Flows; Risø National Laboratory: Roskilde, Denmark, 2009. [Google Scholar]
- Richards, P.; Hoxey, R. Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. J. Wind Eng. Ind. Aerodyn. 1993, 46, 145–153. [Google Scholar] [CrossRef]
- Montazeri, H.; Blocken, B. CFD simulation of wind-induced pressure coefficients on buildings with and without balconies: Validation and sensitivity analysis. Build. Environ. 2013, 60, 137–149. [Google Scholar] [CrossRef]



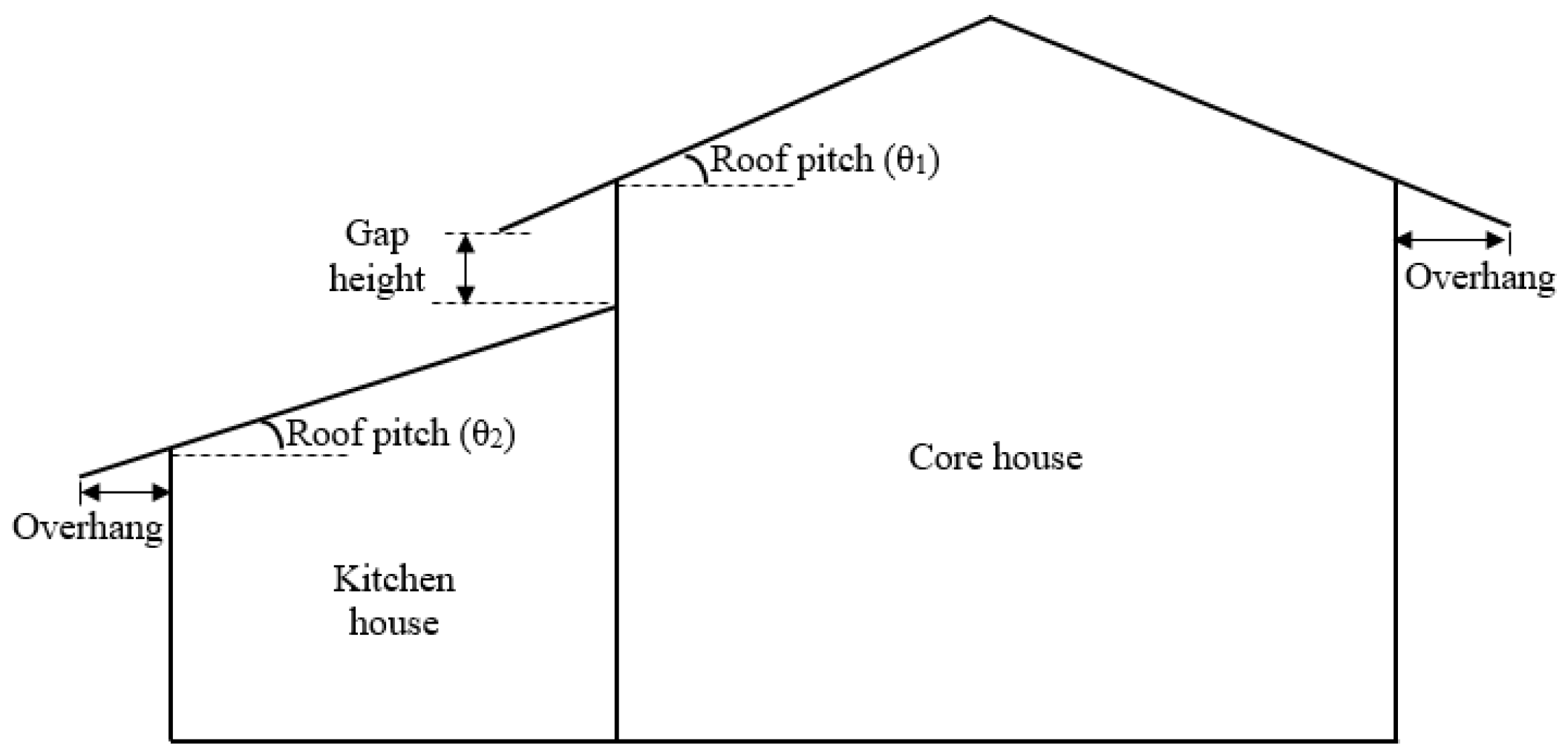
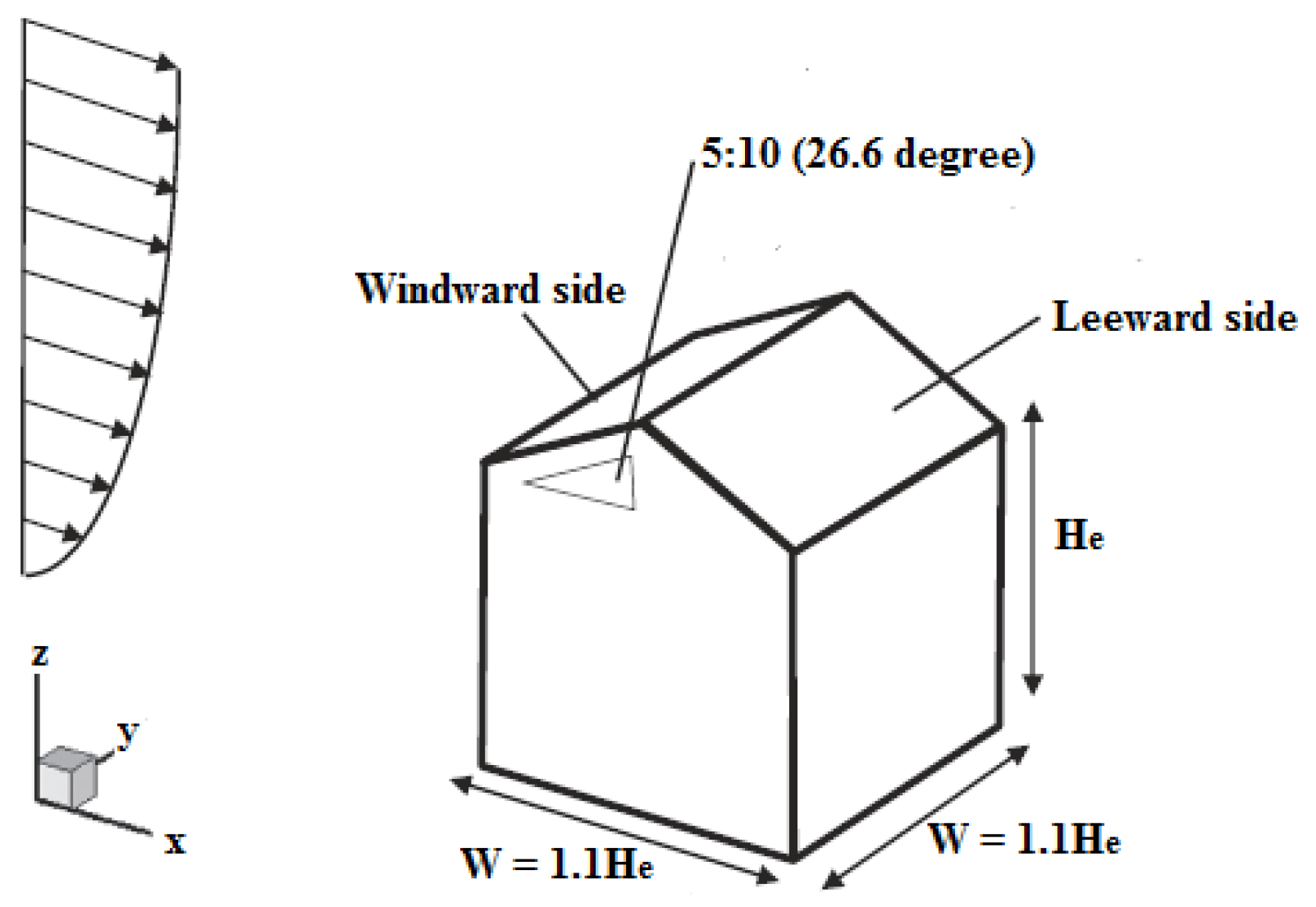
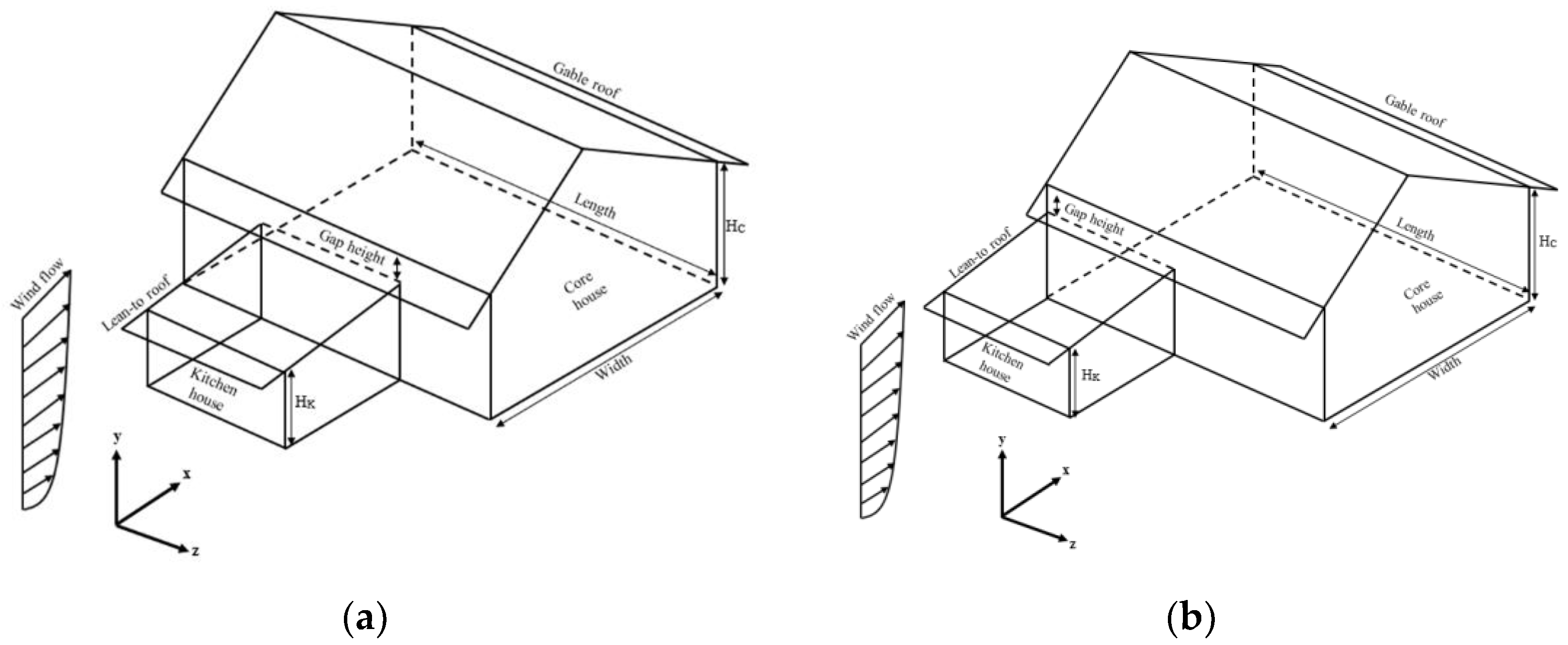





| Parameters | Core House | Kitchen House |
|---|---|---|
| House dimension | 12 m (L) × 8 m (W) × 4 m (HC) | 6 m (L) × 4 m (W) × 2 m (HK) |
| Overhang (OV) | 0.5 m, 0.75 m, 1.0 m | 0.5 m, 0.75 m, 1.0 m |
| Gap height (GH) | 0.25 m, 0.5 m, 0.75 m, 1.0 m | - |
| Roof pitch (RP) | 12°, 17°, 22°, 27° | Varies with gap height |
| Parameters | Value |
|---|---|
| Air density, ρ | 1.172 kg/m3 |
| Dynamic viscosity, μ | 1.8628 × 10−5 kg/m.s |
| Reference temperature, T | 28 °C |
| Wind speed, V | 26.4 m/s |
| (I) Group | (J) Group | Mean Difference (I-J) | p | |
|---|---|---|---|---|
| Games–Howell | Current study | WTT [9] CFD [9] | −0.0938 −0.0246 | 0.891 0.987 |
| WTT [9] | Current study CFD [9] | 0.0692 0.0938 | 0.891 0.837 | |
| CFD [9] | Current study WTT [9] | −0.0246 −0.0938 | 0.987 0.837 |
| WTT [9]–CFD [9] | WTT [9]–Current Study | CFD [9]–Current Study | |
|---|---|---|---|
| MAE | 0.112917 | 0.098984 | 0.130353 |
| NAE | 0.221949 | 0.233659 | 0.307706 |
| RMSE | 0.182149 | 0.112218 | 0.154472 |
| Overhang Length (m) | Percentage Difference CP (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Zone B | Zone D | Zone E | Zone F | Ridge | ||||||
| Position of Kitchen House | Position of Kitchen House | Position of Kitchen House | Position of Kitchen House | Position of Kitchen House | ||||||
| Center | Edge | Center | Edge | Center | Edge | Center | Edge | Center | Edge | |
| 0.5 | 0 | −340.0 | 0 | −8.0 | 0 | −27.3 | 0 | 31.6 | 0 | −9.0 |
| 0.75 | 0 | −118.0 | 0 | −20.6 | 0 | 43.8 | 0 | 25.0 | 0 | 1.0 |
| 1.0 | 0 | −9.0 | 0 | 16.7 | 0 | 7.4 | 0 | 21.2 | 0 | 8.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che Deraman, S.N.; Abo Sabah, S.H.; Zaini, S.S.; Majid, T.A.; Al-Fakih, A. The Effects of the Presence of a Kitchen House on the Wind Flow Surrounding a Low-Rise Building. Energies 2020, 13, 6243. https://doi.org/10.3390/en13236243
Che Deraman SN, Abo Sabah SH, Zaini SS, Majid TA, Al-Fakih A. The Effects of the Presence of a Kitchen House on the Wind Flow Surrounding a Low-Rise Building. Energies. 2020; 13(23):6243. https://doi.org/10.3390/en13236243
Chicago/Turabian StyleChe Deraman, Siti Noratikah, Saddam Hussein Abo Sabah, Shaharudin Shah Zaini, Taksiah A. Majid, and Amin Al-Fakih. 2020. "The Effects of the Presence of a Kitchen House on the Wind Flow Surrounding a Low-Rise Building" Energies 13, no. 23: 6243. https://doi.org/10.3390/en13236243
APA StyleChe Deraman, S. N., Abo Sabah, S. H., Zaini, S. S., Majid, T. A., & Al-Fakih, A. (2020). The Effects of the Presence of a Kitchen House on the Wind Flow Surrounding a Low-Rise Building. Energies, 13(23), 6243. https://doi.org/10.3390/en13236243







