Flow Characteristics of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes
Abstract
1. Introduction
2. Methodology and Computational Model
2.1. Actuator Line Model
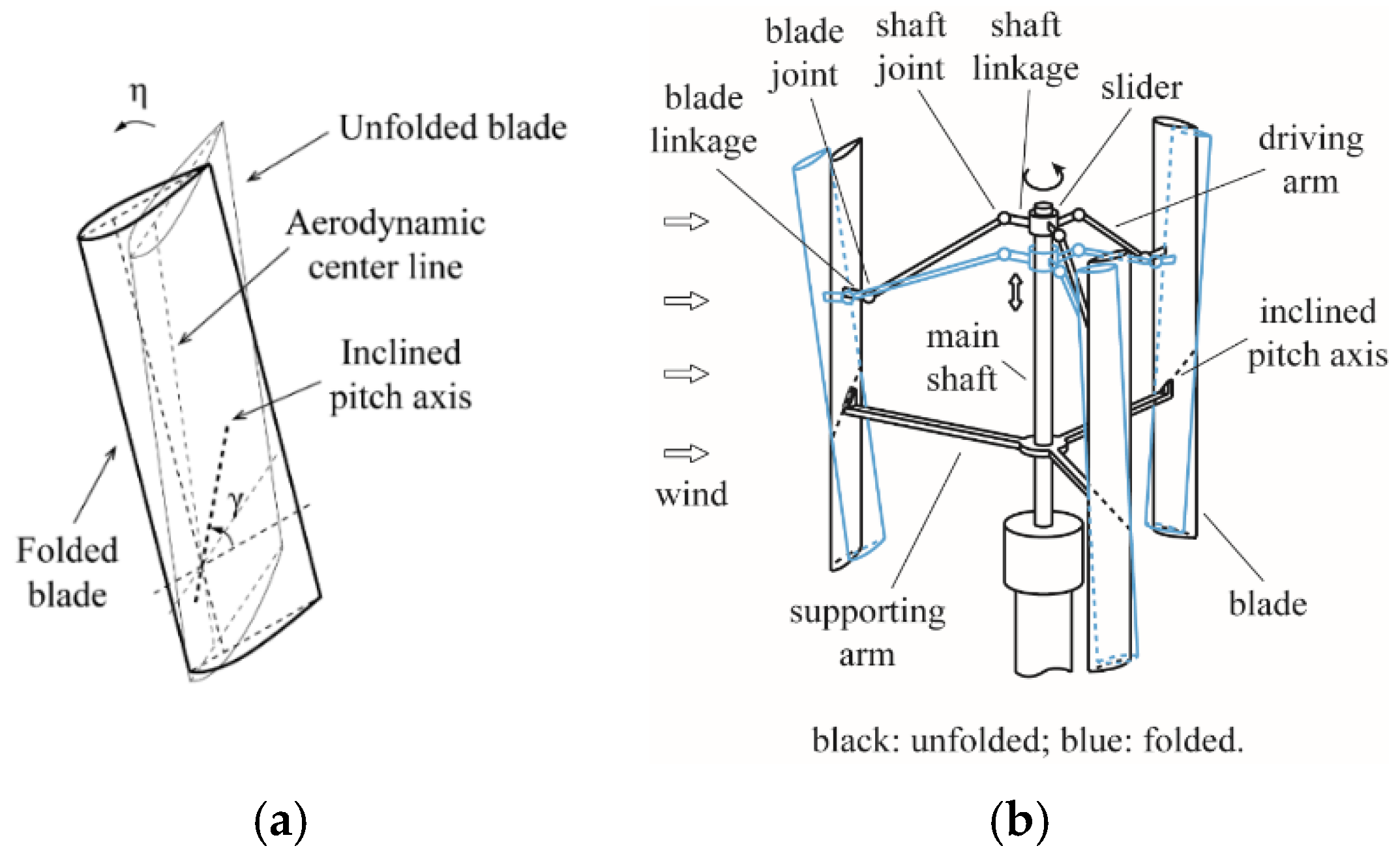
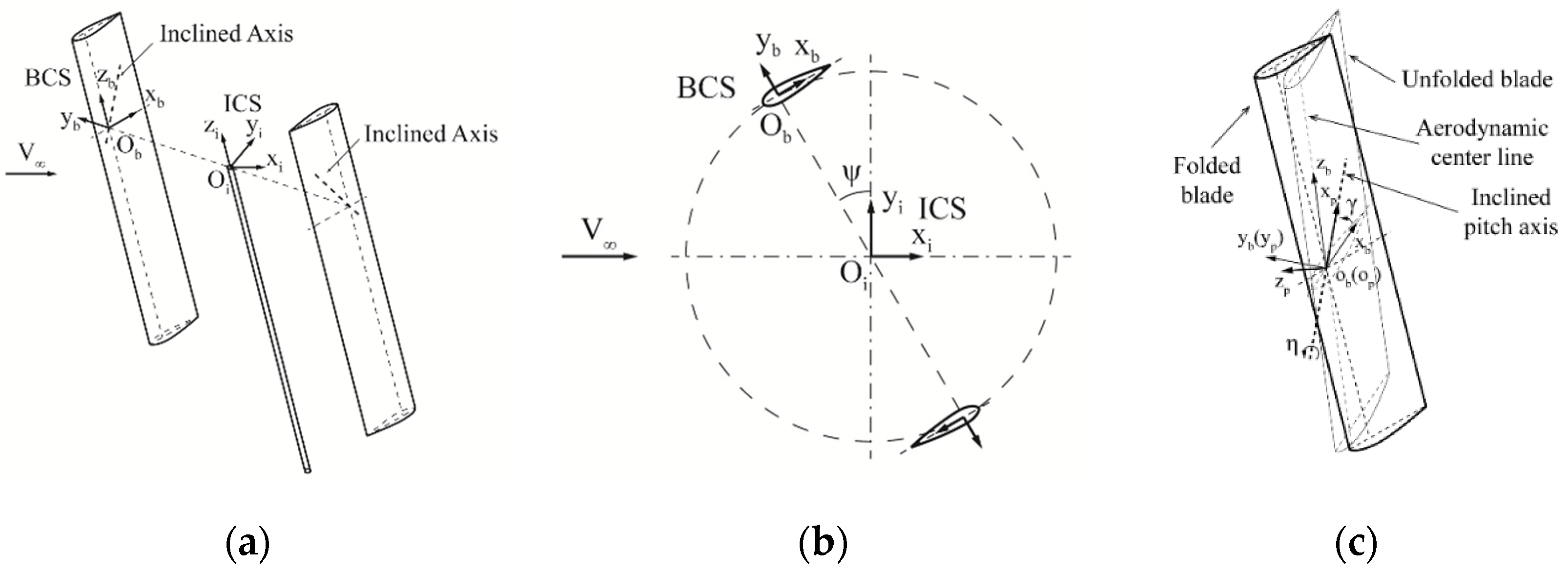
2.2. Wind Turbine Model and Coordinate Systems
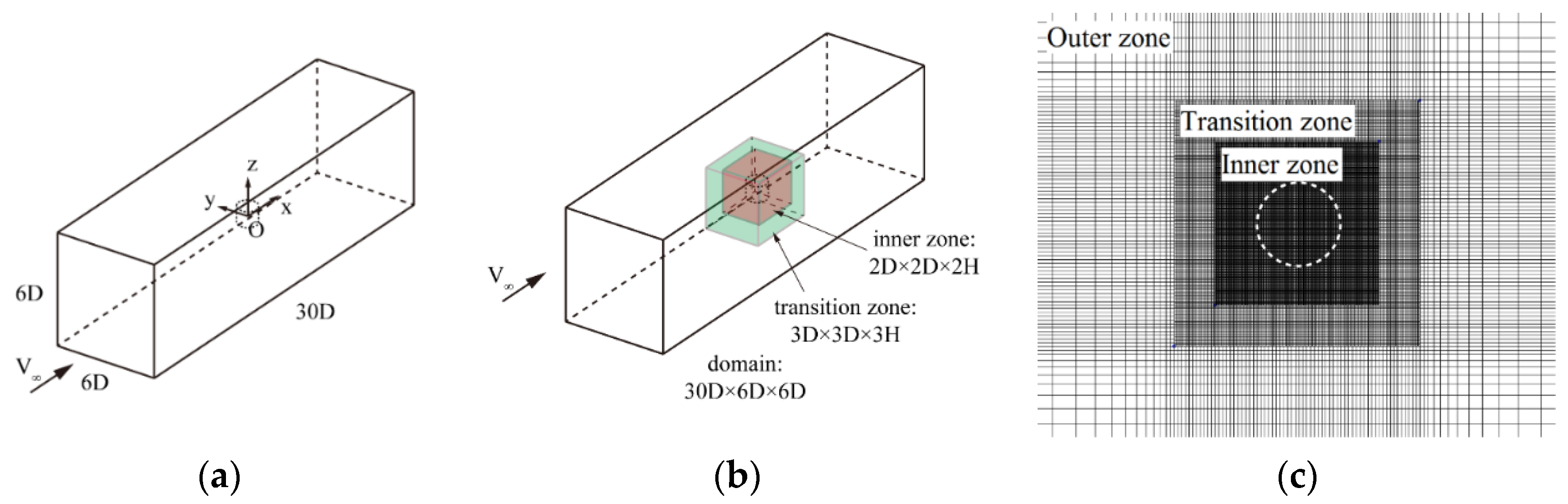
2.3. Computational Setup
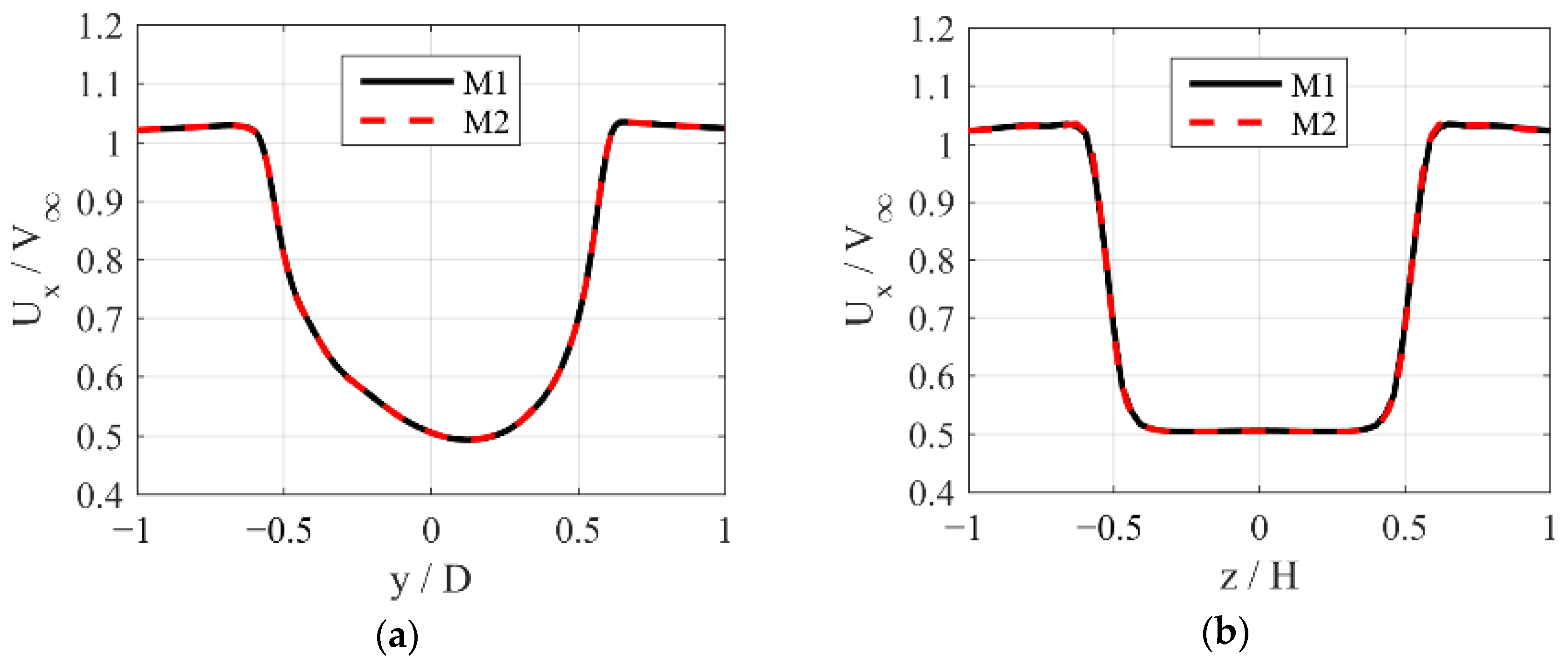
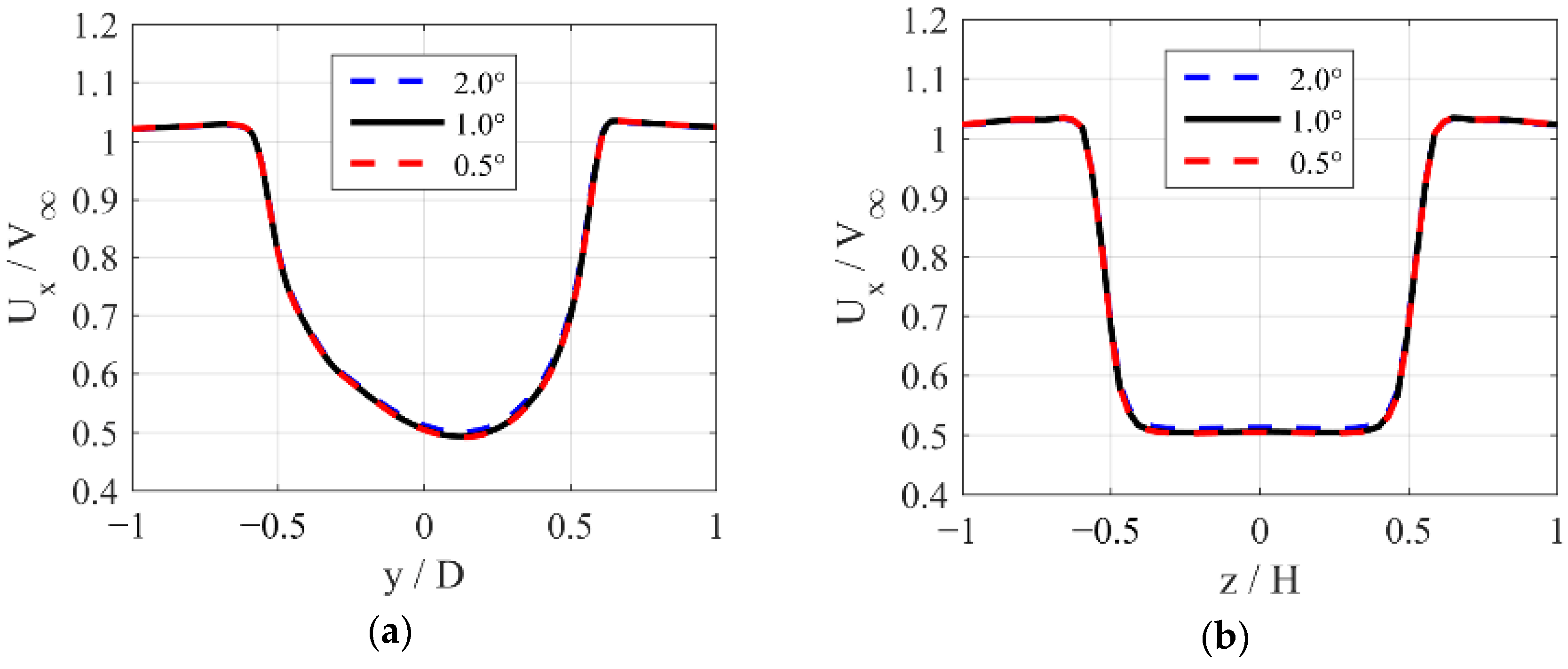
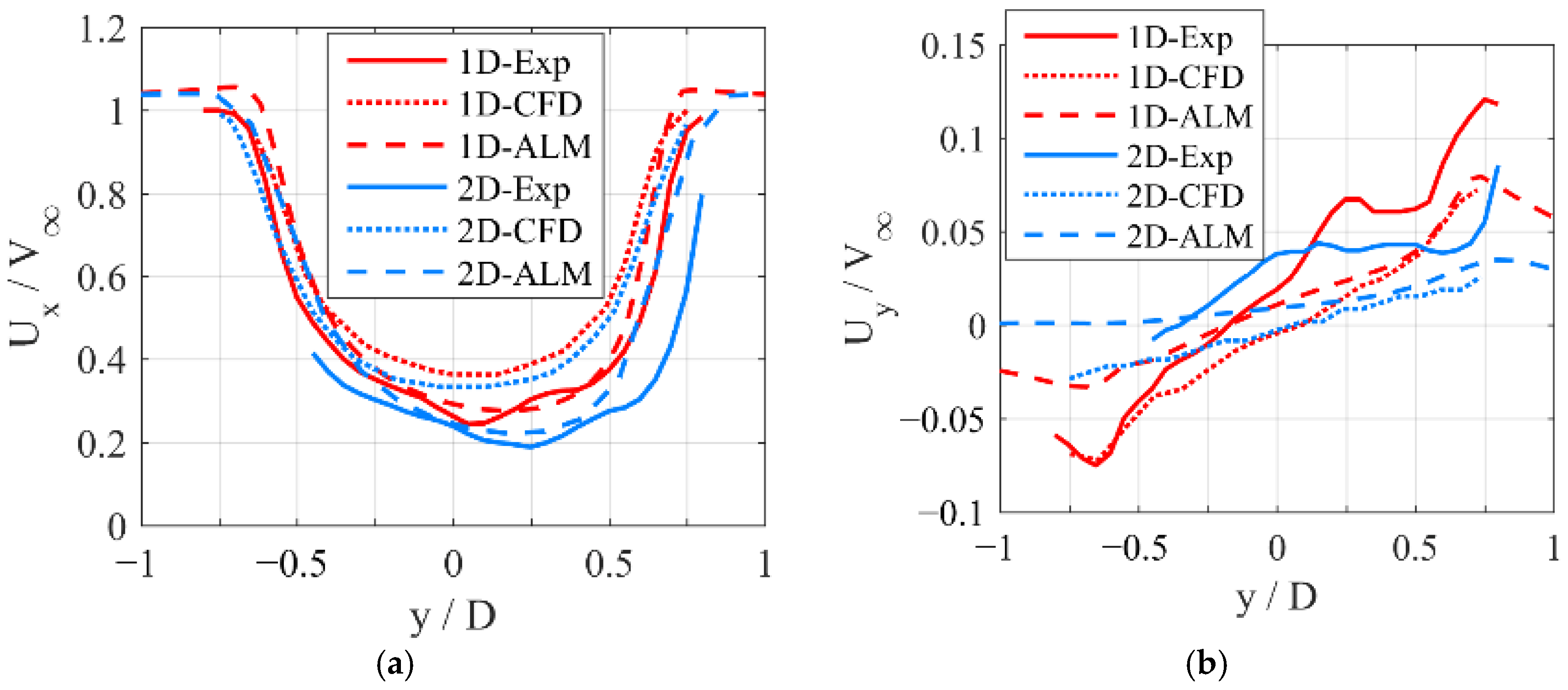
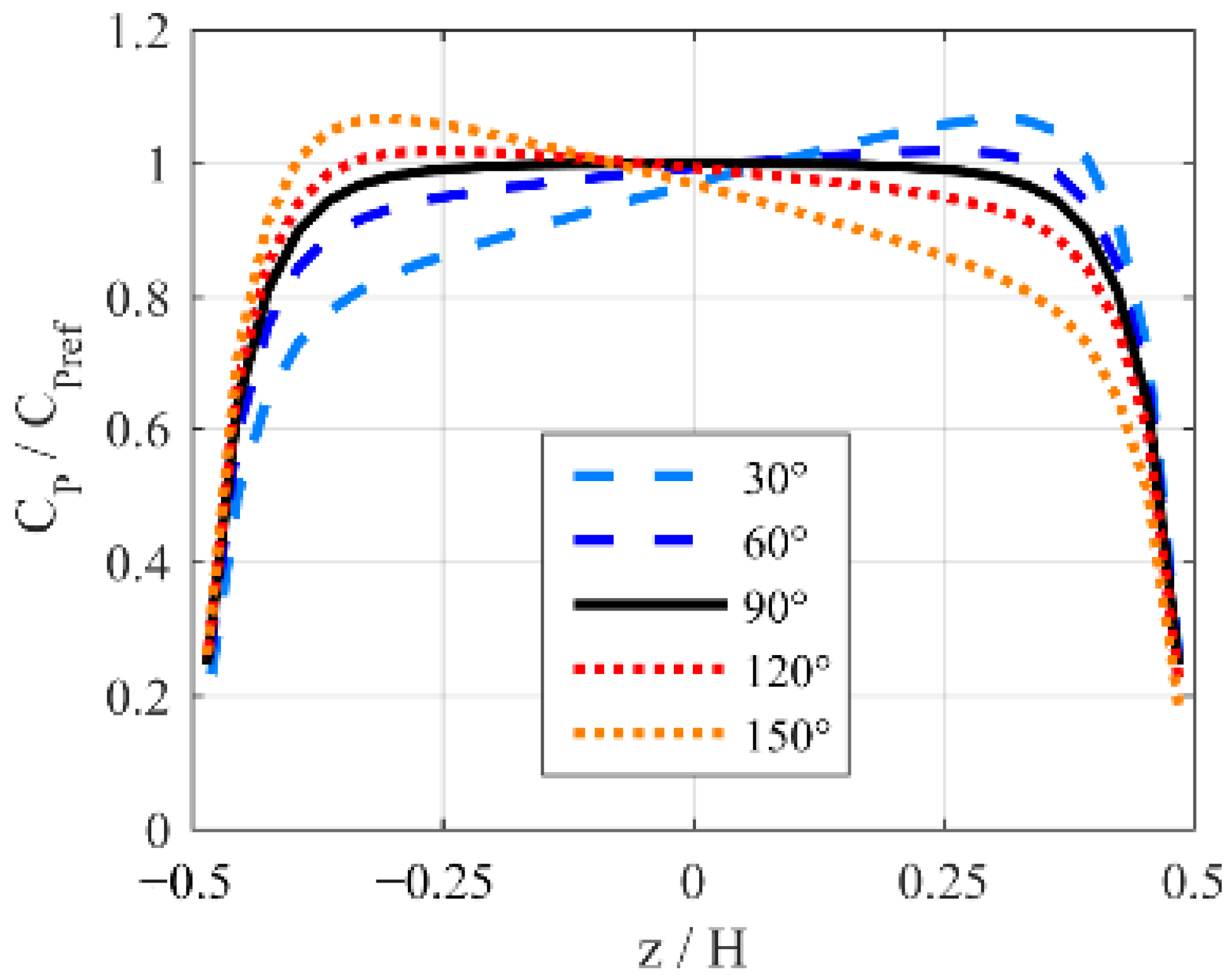
3. Validation
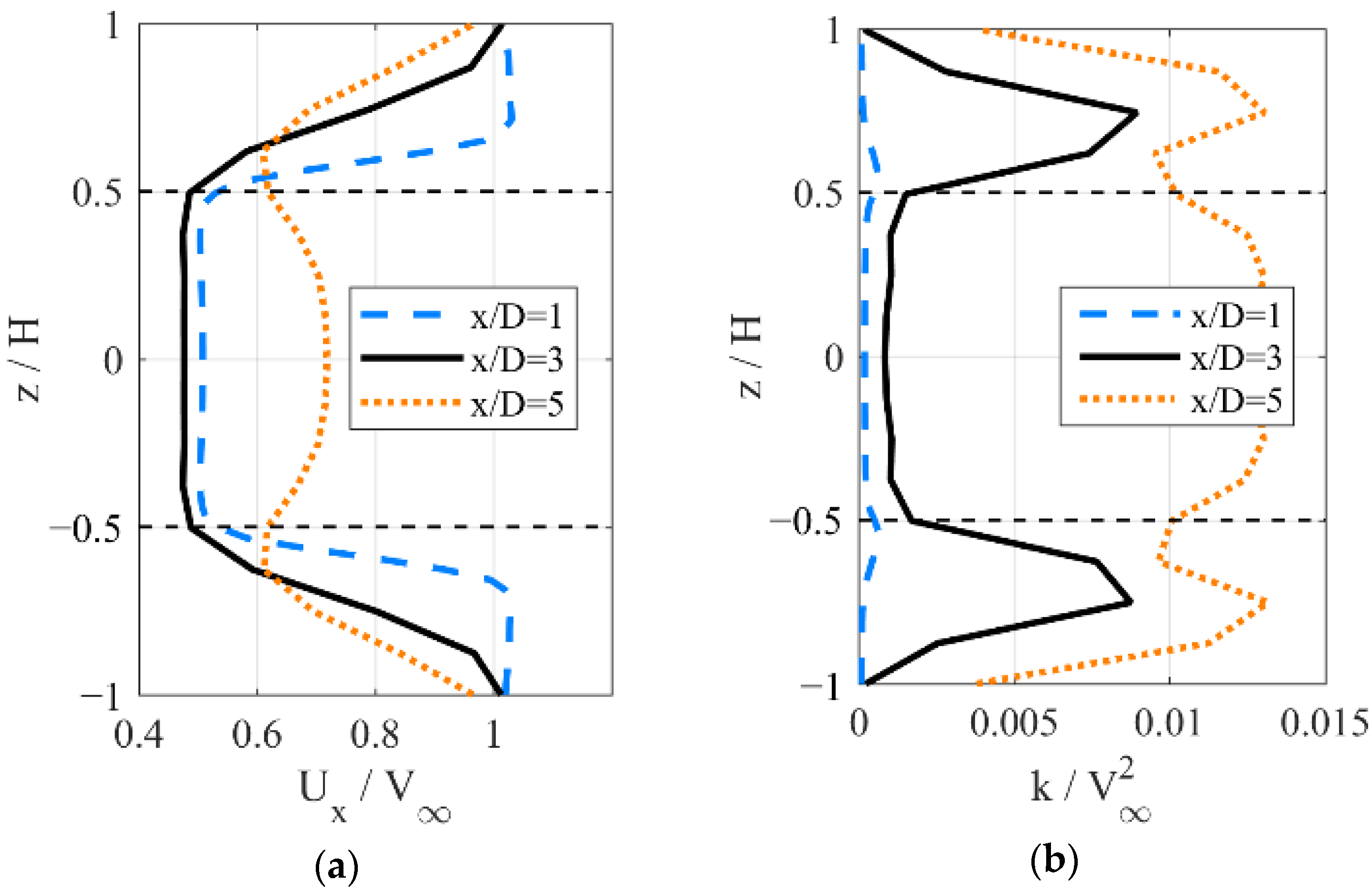
4. Results and Discussion
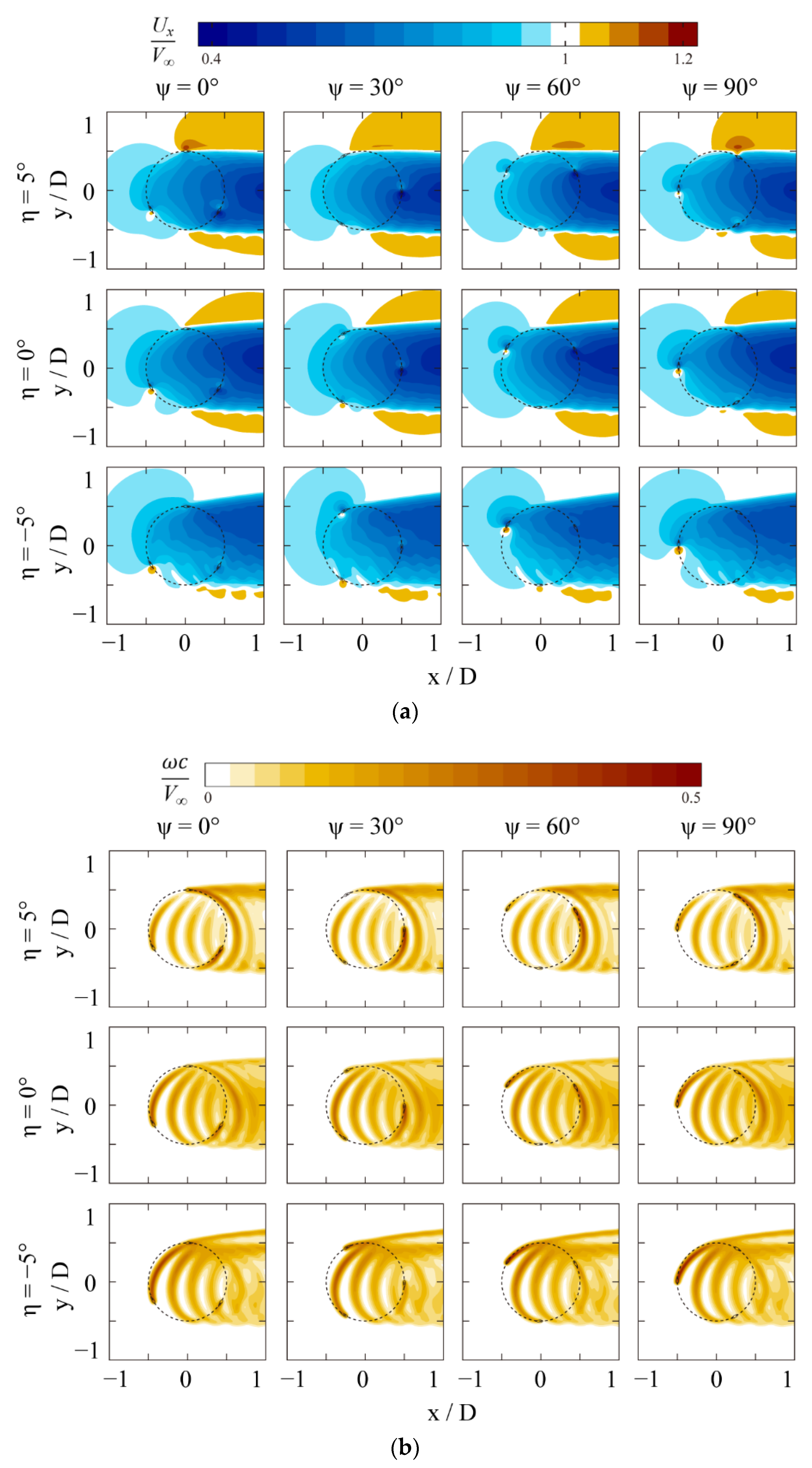
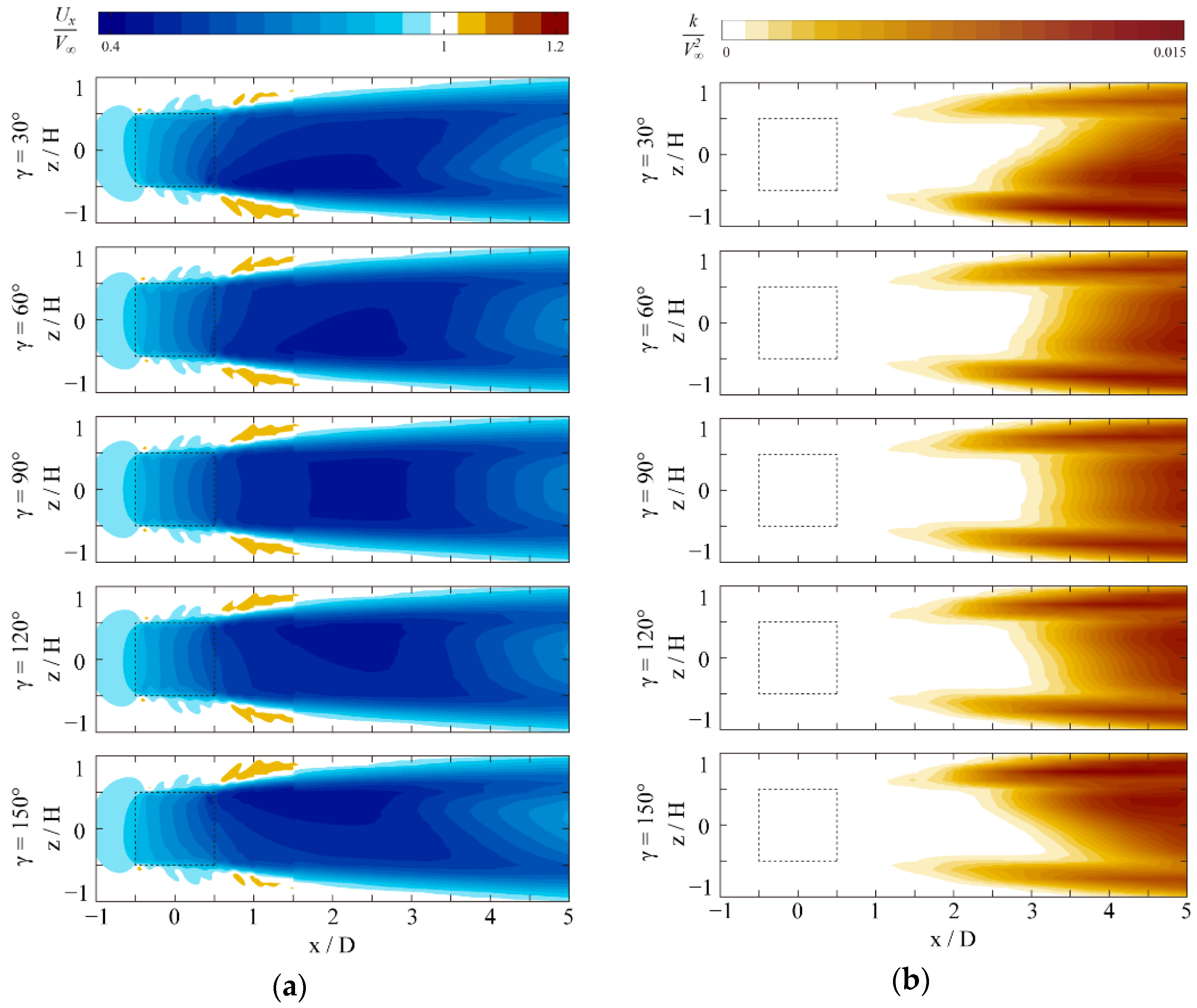
4.1. Unsteady Flow Fields around the Wind Turbine with Various Fold Angles
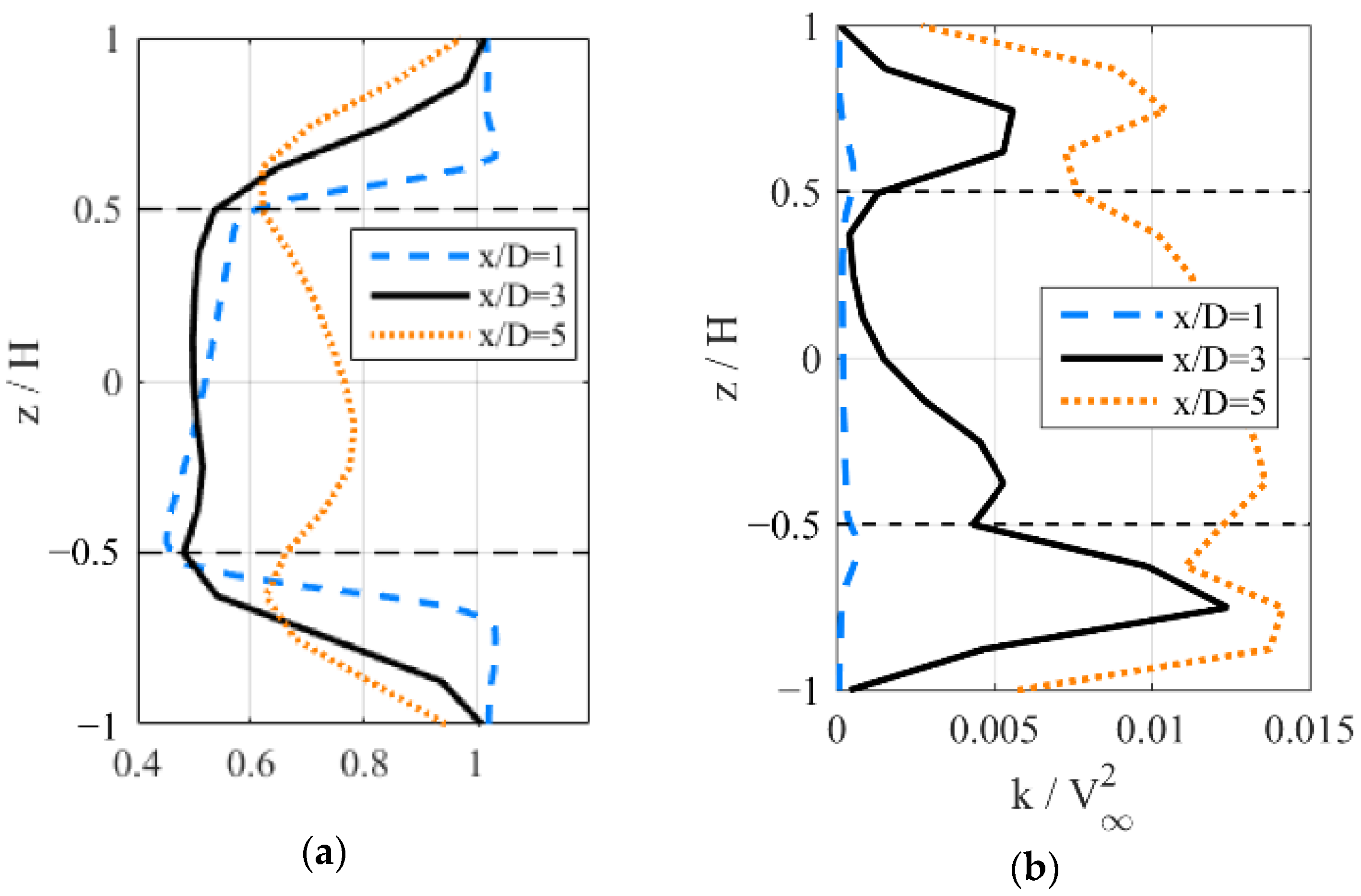
4.2. Instantaneous Flow Fields Downstream with Various Fold Angles
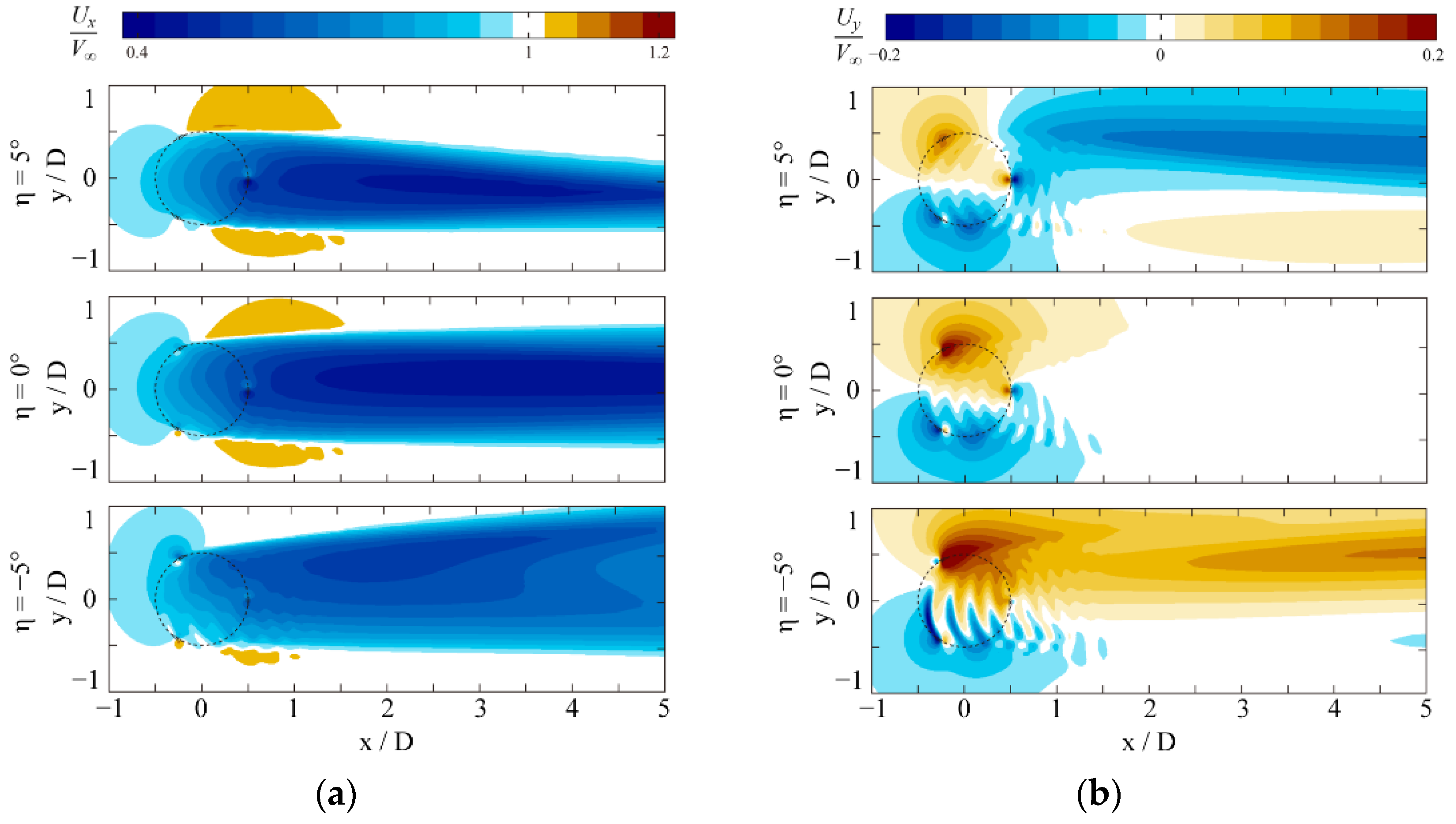
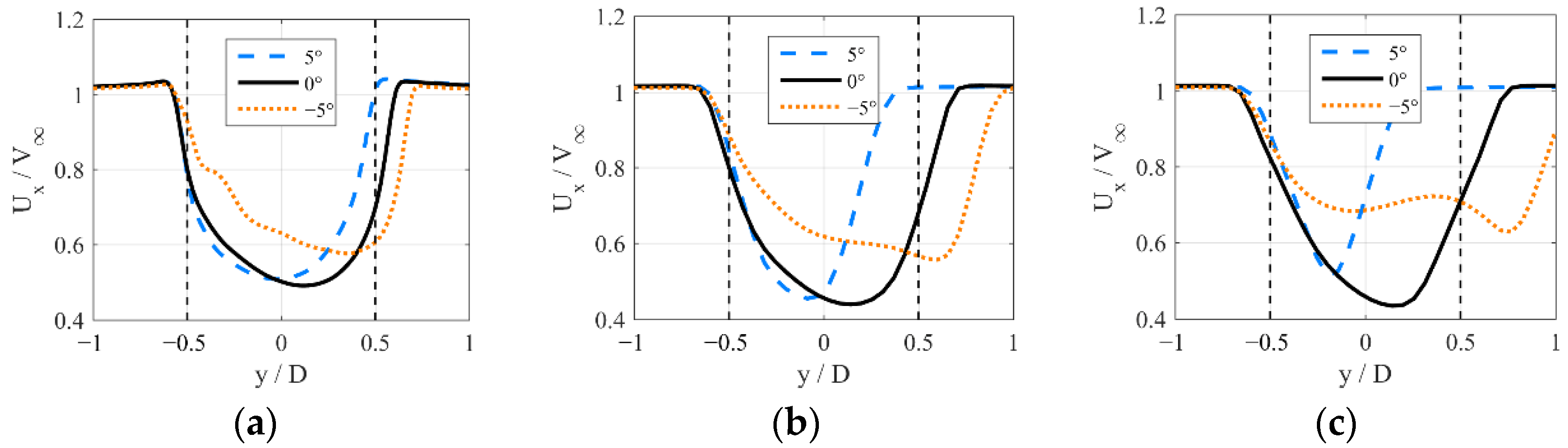
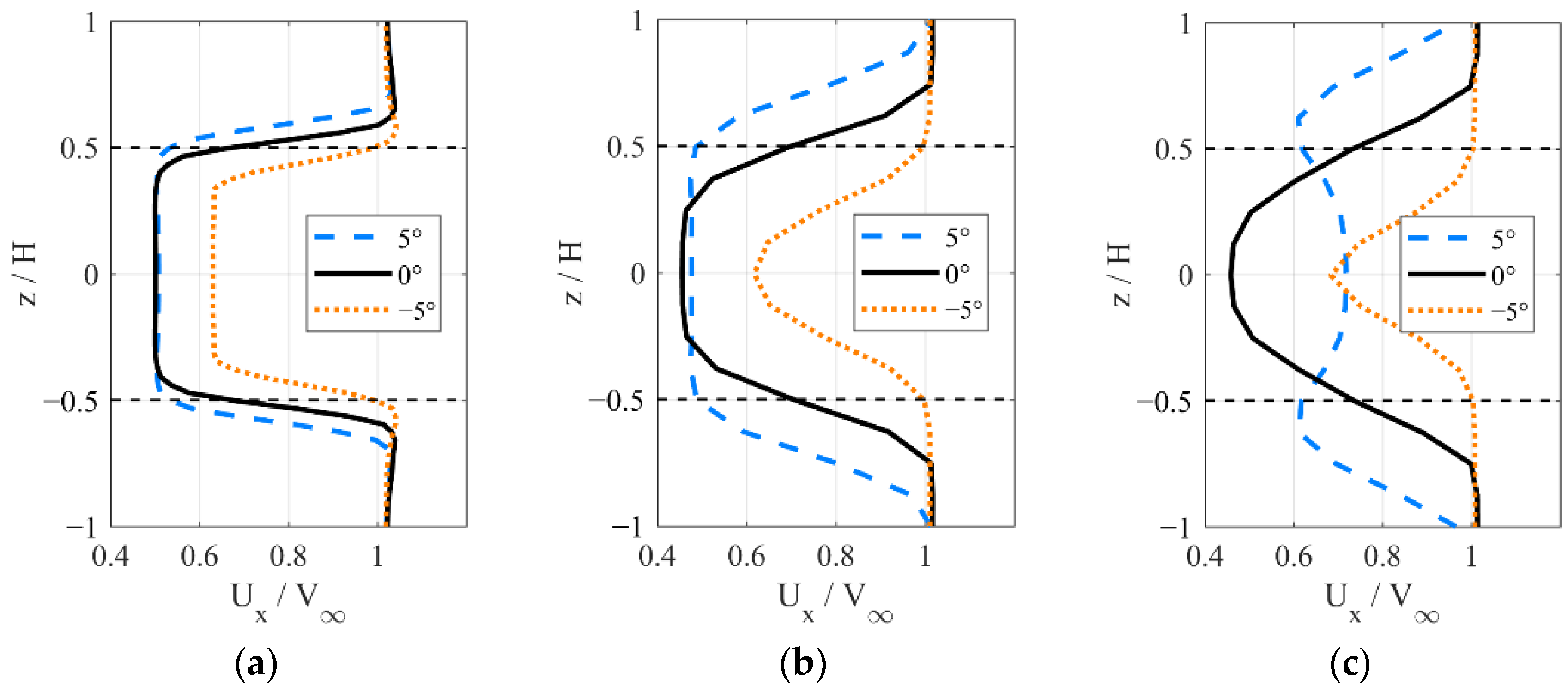
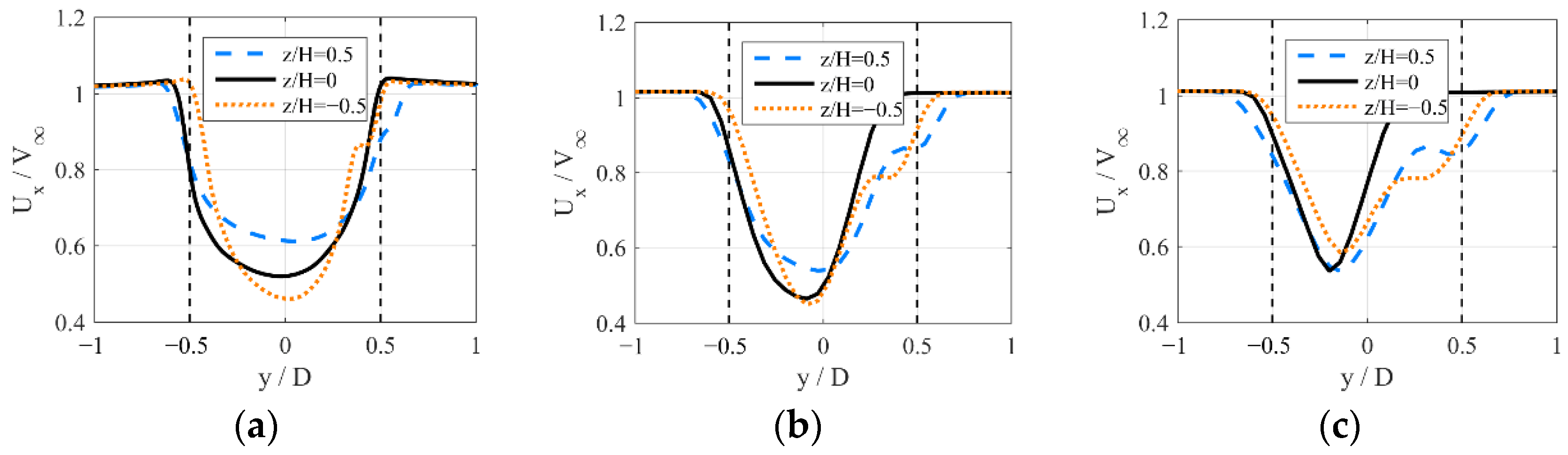
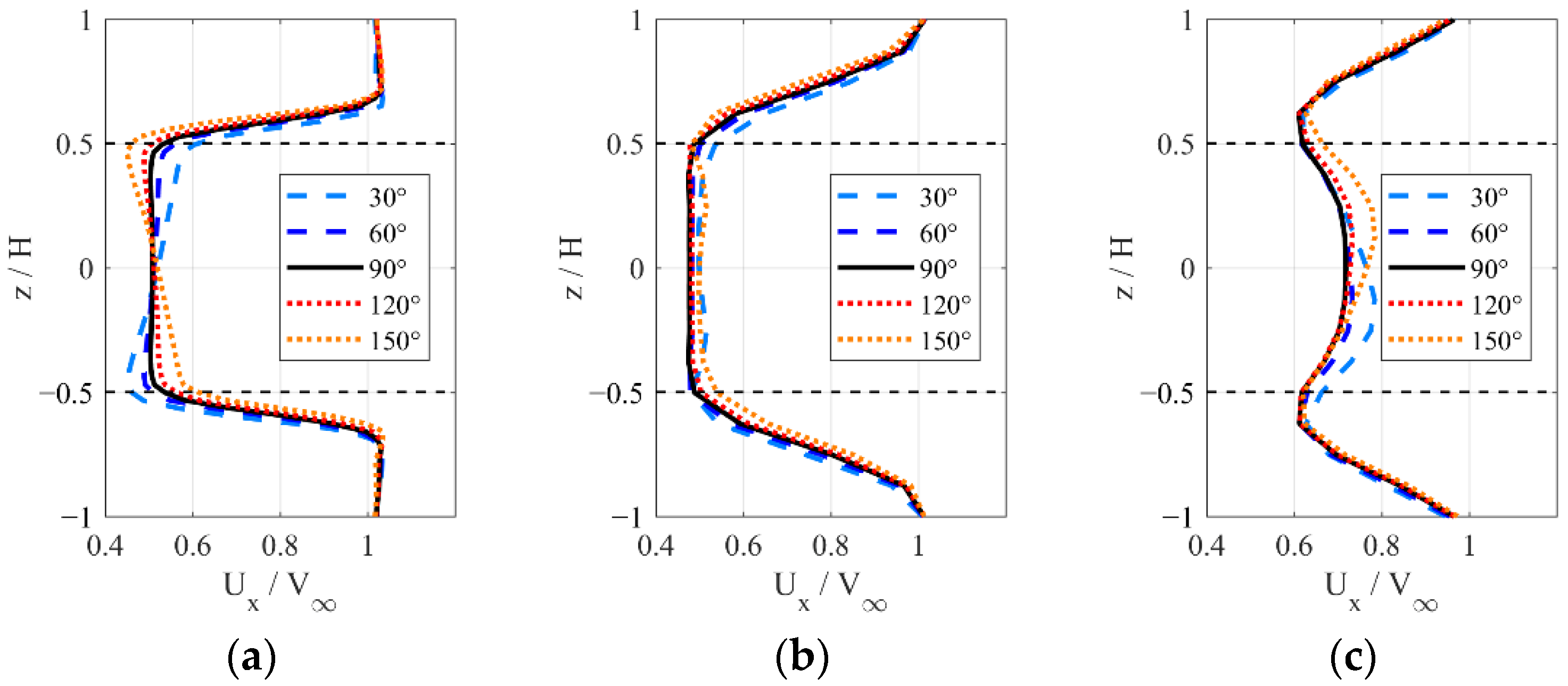
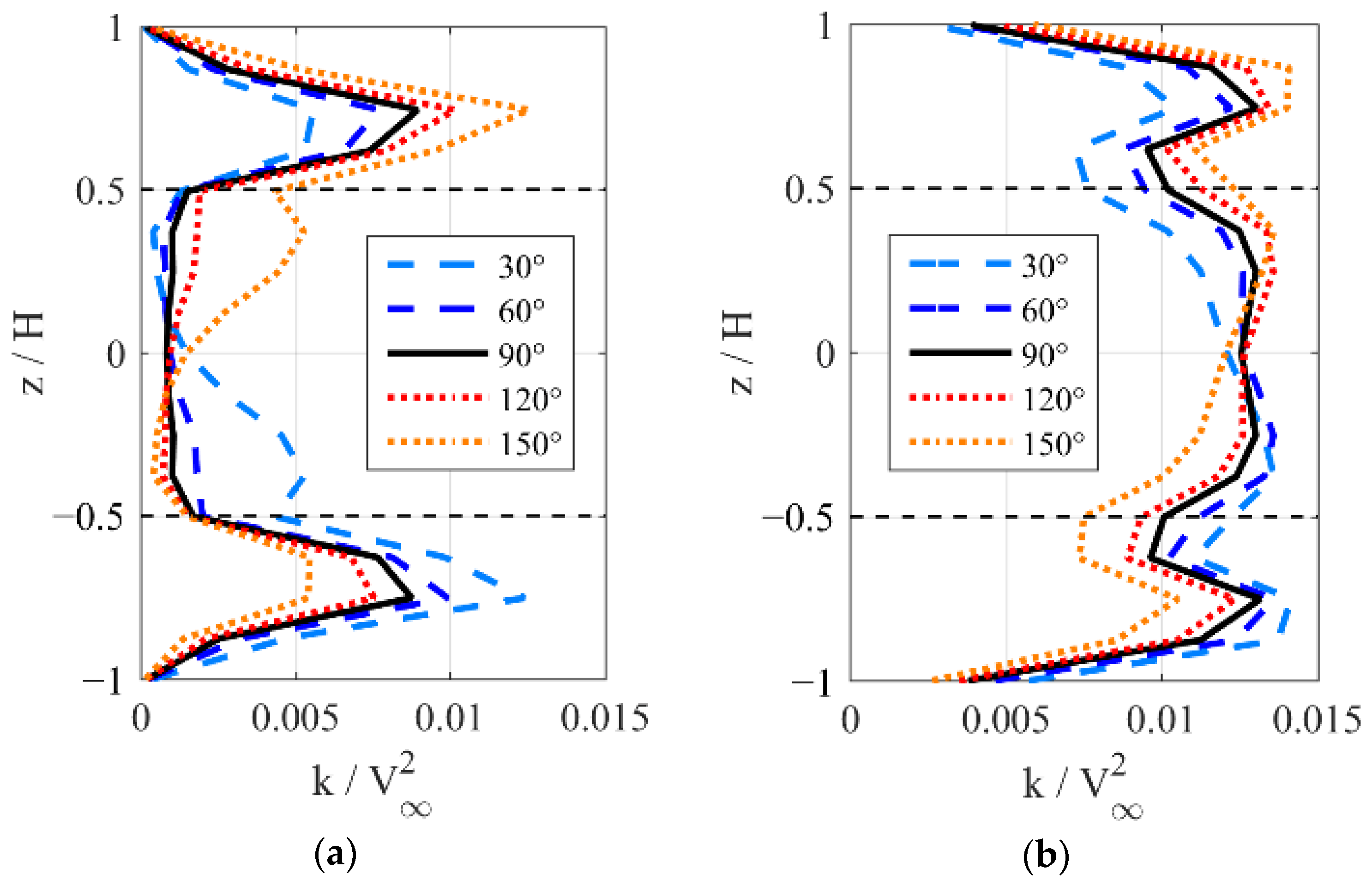
4.3. Instantaneous Flow Fields Downstream with Various Incline Angles
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hezaveh, S.H.; Bou-Zeid, E.; Lohry, M.W.; Martinelli, L. Simulation and wake analysis of a single vertical axis wind turbine. Wind Energy 2017, 20, 713–730. [Google Scholar] [CrossRef]
- Tescione, G.; Ragni, D.; He, C.; Simão Ferreira, C.J.; van Bussel, G.J.W. Near wake flow analysis of a vertical axis wind turbine by stereoscopic particle image velocimetry. Renew. Energy 2014, 70, 47–61. [Google Scholar] [CrossRef]
- Parker, C.M.; Araya, D.B.; Leftwich, M.C. Effect of chord-to-diameter ratio on vertical-axis wind turbine wake development. Exp. Fluids 2017, 58, 168. [Google Scholar] [CrossRef]
- Franchina, N.; Persico, G.; Savini, M. 2D-3D Computations of a Vertical Axis Wind Turbine Flow Field: Modeling Issues and Physical Interpretations. Renew. Energy 2019, 136, 1170–1189. [Google Scholar] [CrossRef]
- Brochier, G.; Fraunie, P.; Beguier, C.; Paraschivoiu, I. Water channel experiments of dynamic stall on Darrieus wind turbine blades. J. Propuls. Power 1986, 2, 445–449. [Google Scholar] [CrossRef]
- Rolin, V.; Porté-Agel, F. Wind-tunnel study of the wake behind a vertical axis wind turbine in a boundary layer flow using stereoscopic particle image velocimetry. J. Phys. Conf. Ser. 2015, 625, 012012. [Google Scholar] [CrossRef]
- Li, Q.A.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. The influence of flow field and aerodynamic forces on a straight-bladed vertical axis wind turbine. Energy 2016, 111, 260–271. [Google Scholar] [CrossRef]
- Li, Q.A.; Maeda, T.; Kamada, Y.; Murata, J.; Yamamoto, M.; Ogasawara, T.; Shimizu, K.; Kogaki, T. Study on power performance for straight-bladed vertical axis wind turbine by field and wind tunnel test. Renew. Energy 2016, 90, 291–300. [Google Scholar] [CrossRef]
- Ryan, K.J.; Coletti, F.; Elkins, C.J.; Dabiri, J.O.; Eaton, J.K. Three-dimensional flow field around and downstream of a subscale model rotating vertical axis wind turbine. Exp. Fluids 2016, 57, 38. [Google Scholar] [CrossRef]
- Abkar, M.; Dabiri, J.O. Self-similarity and flow characteristics of vertical-axis wind turbine wakes: An LES study. J. Turbul. 2017, 18, 373–389. [Google Scholar] [CrossRef]
- Kadum, H.; Friedman, S.; Camp, E.H.; Cal, R.B. Development and scaling of a vertical axis wind turbine wake. J. Wind Eng. Ind. Aerodyn. 2018, 174, 303–311. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Effect of aspect ratio on vertical-axis wind turbine wakes. J. Fluid Mech. 2020, 889, R1-1-12. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. A large-eddy simulation study of vertical axis wind turbine wakes in the atmospheric boundary layer. Energies 2016, 9, 366. [Google Scholar] [CrossRef]
- Posa, A. Influence of Tip Speed Ratio on wake features of a Vertical Axis Wind Turbine. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104076. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, Z.; Zhang, Y.; Jinyama, H.; Li, Q. Numerical Investigation of the Tip Vortex of a Straight-Bladed Vertical Axis Wind Turbine with Double-Blades. Energies 2017, 10, 1721. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Performance and near-wake measurements for a vertical axis turbine at moderate Reynolds number. In Proceedings of the ASME 2013 Fluids Engineering Division Summer Meeting, Incline Village, NV, USA, 7–11 July 2013. [Google Scholar]
- Bachant, P.; Wosnik, M. Effects of Reynolds Number on the Energy Conversion and Near-Wake Dynamics of a High Solidity Vertical-Axis Cross-Flow Turbine. Energies 2016, 9, 73. [Google Scholar] [CrossRef]
- Orlandi, A.; Collu, M.; Zanforlin, S.; Shires, A. 3D URANS analysis of a vertical axis wind turbine in skewed flows. J. Wind Eng. Ind. Aerodyn. 2015, 147, 77–84. [Google Scholar] [CrossRef]
- Mendoza, V.; Chaudhari, A.; Goude, A. Performance and wake comparison of horizontal and vertical axis wind turbines under varying surface roughness conditions. Wind Energy 2018, 22, 458–472. [Google Scholar] [CrossRef]
- Souaissa, K.; Ghiss, M.; Chrigui, M.; Bentaher, H.; Maalej, A. A comprehensive analysis of aerodynamic flow around H-Darrieus rotor with camber-bladed profile. Wind Eng. 2019, 43, 459–475. [Google Scholar] [CrossRef]
- Xu, W.; Li, G.; Wang, F.; Li, Y. High-resolution numerical investigation into the effects of winglet on the aerodynamic performance for a three-dimensional vertical axis wind turbine. Energy Convers. Manag. 2020, 205, 112333. [Google Scholar] [CrossRef]
- Villeneuve, T.; Boudreau, M.; Dumas, G. Improving the efficiency and the wake recovery rate of vertical-axis turbines using detached end-plates. Renew. Energy 2020, 150, 31–45. [Google Scholar] [CrossRef]
- Su, J.; Chen, Y.; Han, Z.; Zhou, D.; Bao, Y.; Zhao, Y. Investigation of V-shaped blade for the performance improvement of vertical axis wind turbines. Appl. Energy 2020, 260, 114326. [Google Scholar] [CrossRef]
- Brownstein, I.D.; Wei, N.J.; Dabiri, J.O. Aerodynamically Interacting Vertical-Axis Wind Turbines Performance Enhancement and Three-Dimensional Flow. Energies 2019, 12, 2724. [Google Scholar] [CrossRef]
- Jakubowski, M.; Starosta, R.; Fritzkowski, P. Kinematics of a vertical axis wind turbine with a variable pitch angle. In Proceedings of the AIP Conference Proceedings 1922, Lublin, Poland, 13–16 September 2017; p. 110012. [Google Scholar]
- Kiwata, T.; Yamada, T.; Kita, T.; Takata, S.; Komatsu, N.; Kimura, S. Performance of a Vertical Axis Wind Turbine with Variable-Pitch Straight Blades utilizing a Linkage Mechanism. J. Environ. Eng. 2010, 5, 213–225. [Google Scholar] [CrossRef]
- Abdalrahman, G.; Melek, W.; Lien, F.-S. Pitch angle control for a small-scale Darrieus vertical axis wind turbine with straight blades (H-Type VAWT). Renew. Energy 2017, 114, 1353–1362. [Google Scholar] [CrossRef]
- Guo, J.; Zeng, P.; Lei, L. Performance of a straight-bladed vertical axis wind turbine with inclined pitch axes by wind tunnel experiments. Energy 2019, 174, 553–561. [Google Scholar] [CrossRef]
- Guo, J.; Zeng, P.; Lei, L. Structure Analysis of an Innovative Vertical Axis Wind Turbine with Inclined Pitch Axes using Finite Element Method. IOP Conf. Ser. Mater. Sci. Eng. 2020, 825, 012004. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z. Computation of wind turbine wakes using combined Navier-Stokes/actuator-line methodology. In Proceedings of the 1999 European Wind Energy Conference and Exhibition, Nice, France, 1–5 March 1999; pp. 156–159. [Google Scholar]
- Mendoza, V.; Goude, A. Improving farm efficiency of interacting vertical-axis wind turbines through wake deflection using pitched struts. Wind Energy 2019, 22, 538–546. [Google Scholar] [CrossRef]
- Zhao, R.; Creech, A.C.W.; Borthwick, A.G.L.; Venugopal, V.; Nishino, T. Aerodynamic Analysis of a Two-Bladed Vertical-Axis Wind Turbine Using a Coupled Unsteady RANS and Actuator Line Model. Energies 2020, 13, 776. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Large eddy simulation of vertical axis wind turbine wakes. Energies 2014, 7, 890–912. [Google Scholar] [CrossRef]
- Bachant, P.; Goude, A.; Wosnik, M. Actuator line modeling of vertical-axis turbines. arXiv 2018, arXiv:1605.01449. [Google Scholar]
- Mendoza, V.; Bachant, P.; Ferreira, C.; Goude, A. Near-wake flow simulation of a vertical axis turbine using an actuator line model. Wind Energy 2019, 22, 171–188. [Google Scholar] [CrossRef]
- Mendoza, V.; Goude, A. Validation of Actuator Line and Vortex Models Using Normal Forces Measurements of a Straight-Bladed Vertical Axis Wind Turbine. Energies 2020, 13, 511. [Google Scholar] [CrossRef]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; SAND-80-2114; Sandia National Laboratories: Albuquerque, NM, USA, 1981.
- Martínez-Tossas, L.A.; Churchfield, M.J.; Meneveau, C. Optimal smoothing length scale for actuator line models of wind turbine blades based on Gaussian body force distribution. Wind Energy 2017, 20, 1083–1096. [Google Scholar] [CrossRef]
- Dyachuk, E.; Goude, A.; Bernhoff, H. Dynamic Stall Modeling for the Conditions of Vertical Axis Wind Turbines. AIAA J. 2014, 52, 72–81. [Google Scholar] [CrossRef]
- Guo, J.; Meng, H.; Zeng, P.; Lei, L. Several Modifications to Improve Numerical Stability of Leishmen-Beddoes Dynamic Stall Model. In Proceedings of the ASME 2020 Fluids Engineering Division Summer Meeting collocated with the ASME 2020 Heat Transfer Summer Conference and the ASME 2020 18th International Conference on Nanochannels, Microchannels, and Minichannels, Virtual Conference, Online. 13–15 July 2020. [Google Scholar]
- Mendoza, V.; Bachant, P.; Wosnik, M.; Goude, A. Validation of an Actuator Line Model Coupled to a Dynamic Stall Model for Pitching Motions Characteristic to Vertical Axis Turbines. J. Phys. Conf. Ser. 2016, 753, 22043. [Google Scholar] [CrossRef]
- Dyachuk, E.; Goude, A.; Berhnoff, H. Simulating Pitching Blade With Free Vortex Model Coupled With Dynamic Stall Model for Conditions of Straight Bladed Vertical Axis Turbines. J. Sol. Energy Eng. 2015, 137, 041008. [Google Scholar] [CrossRef]
- Bianchini, A.; Balduzzi, F.; Ferrara, G.; Ferrari, L. Virtual incidence effect on rotating airfoils in Darrieus wind turbines. Energy Convers. Manag. 2016, 111, 329–338. [Google Scholar] [CrossRef]
- Goude, A. Fluid Mechanics of Vertical Axis Turbines: Simulations and Model Development; Uppsala University: Uppsala, Sweden, 2012. [Google Scholar]
- Castelli, M.R.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. Effect of pitch angle on power performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2017, 197, 132–150. [Google Scholar] [CrossRef]
- Rogowski, K. CFD Computation of the H-Darrieus Wind Turbine—The Impact of the Rotating Shaft on the Rotor Performance. Energies 2019, 12, 2506. [Google Scholar] [CrossRef]










| Parameters | Case 1 | Case 2 |
|---|---|---|
| Airfoil | NACA 0021 | NACA 0018 |
| Blade number | 3 | 2 |
| Diameter/m | 1.03 | 1 |
| Blade span/m | 1.4564 | 1 |
| Chord length/m | 0.0858 | 0.06 |
| Freestream velocity/(m/s) | 9 | 9.3 |
| TSR | 1.43~3.29 | 4.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Lei, L. Flow Characteristics of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes. Energies 2020, 13, 6281. https://doi.org/10.3390/en13236281
Guo J, Lei L. Flow Characteristics of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes. Energies. 2020; 13(23):6281. https://doi.org/10.3390/en13236281
Chicago/Turabian StyleGuo, Jia, and Liping Lei. 2020. "Flow Characteristics of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes" Energies 13, no. 23: 6281. https://doi.org/10.3390/en13236281
APA StyleGuo, J., & Lei, L. (2020). Flow Characteristics of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes. Energies, 13(23), 6281. https://doi.org/10.3390/en13236281





