Residential Buildings’ Foundations as a Ground Heat Exchanger and Comparison among Different Types in a Moderate Climate Country †
Abstract
:1. Introduction
2. Residential Dwellings with Nearly Zero Energy Characteristics in Cyprus
2.1. Typical Construction with Heating and Cooling Loads in Cyprus
2.2. Selected Dwelling with Tyical Load for a nZEB
3. Computational Modeling
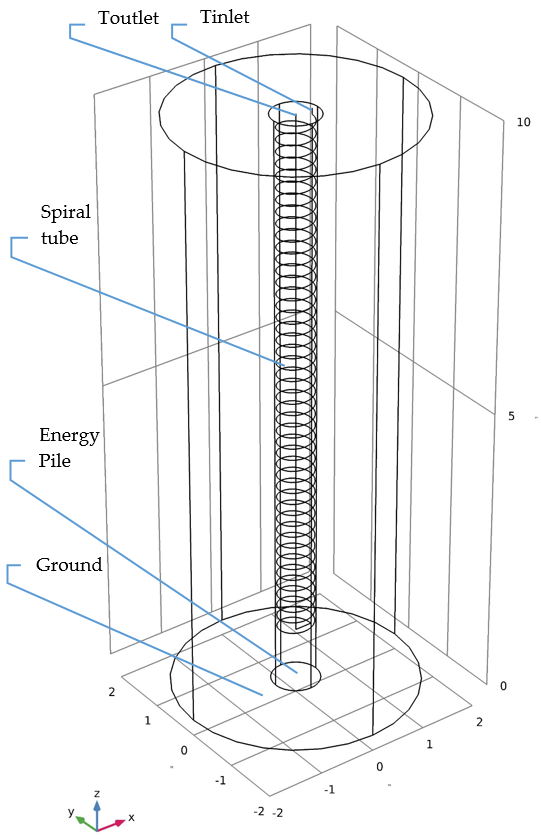
3.1. Energy Pile
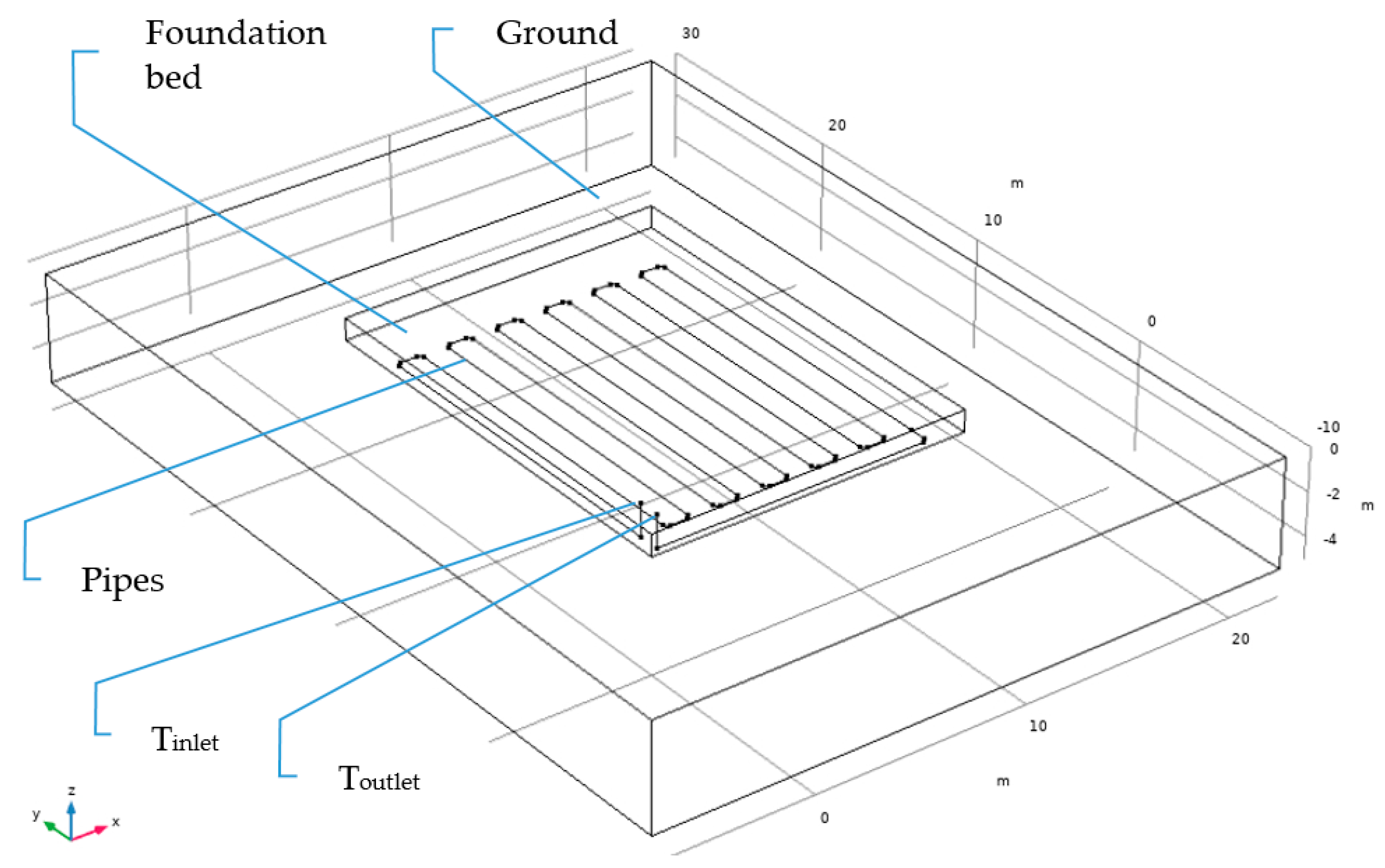
3.2. Foundation Bed GHE
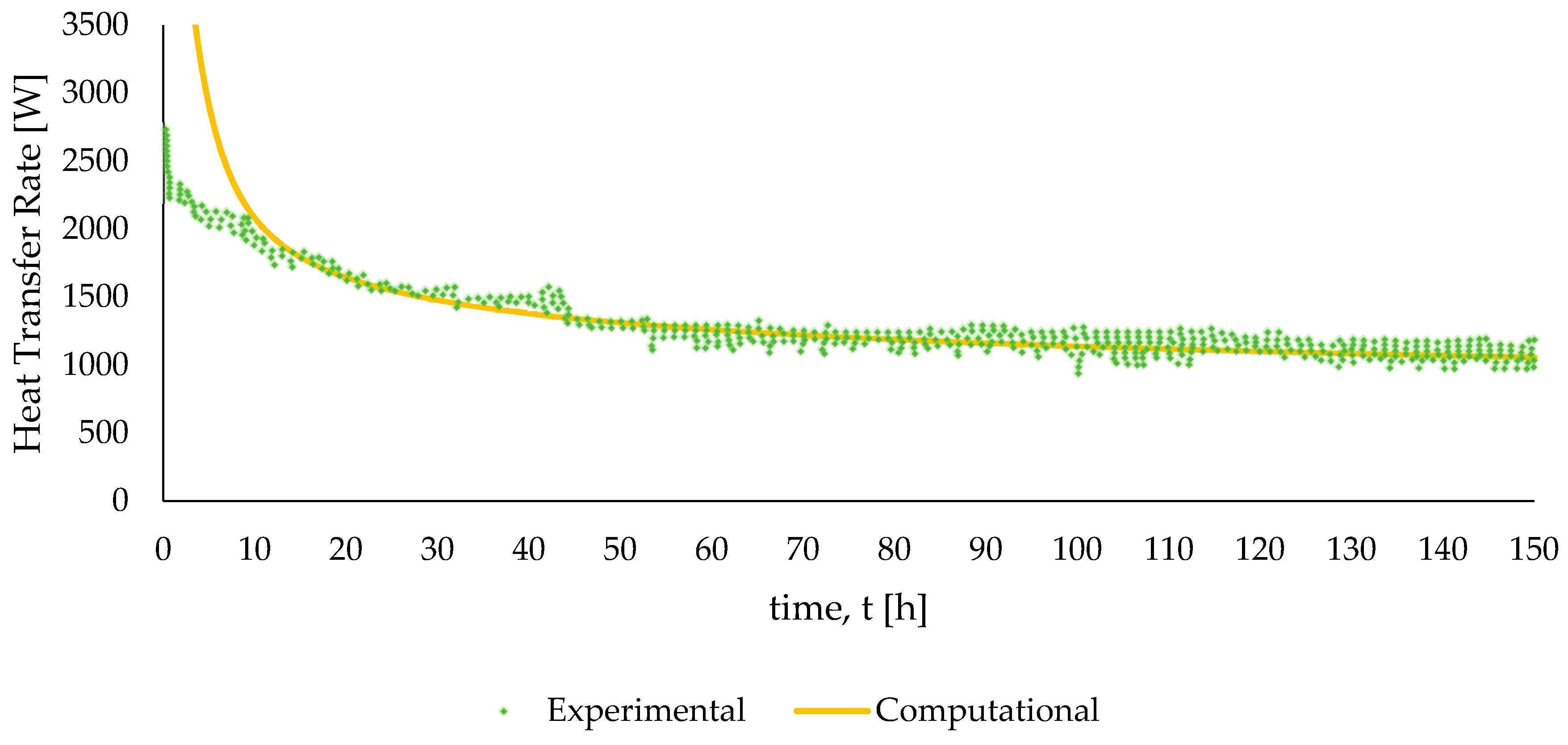
3.3. Computational Verification and Validation
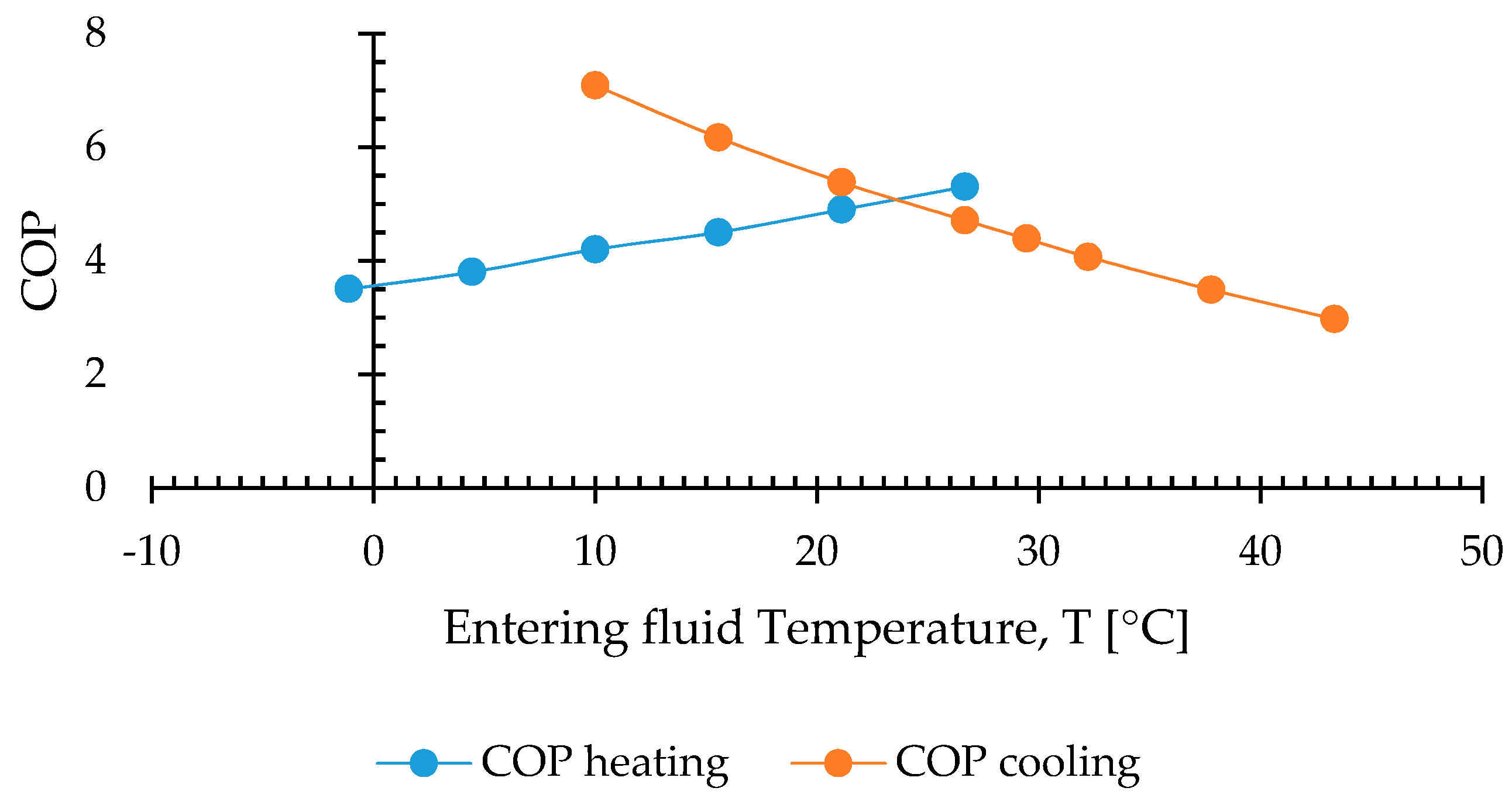
4. Computational Results and Discussion
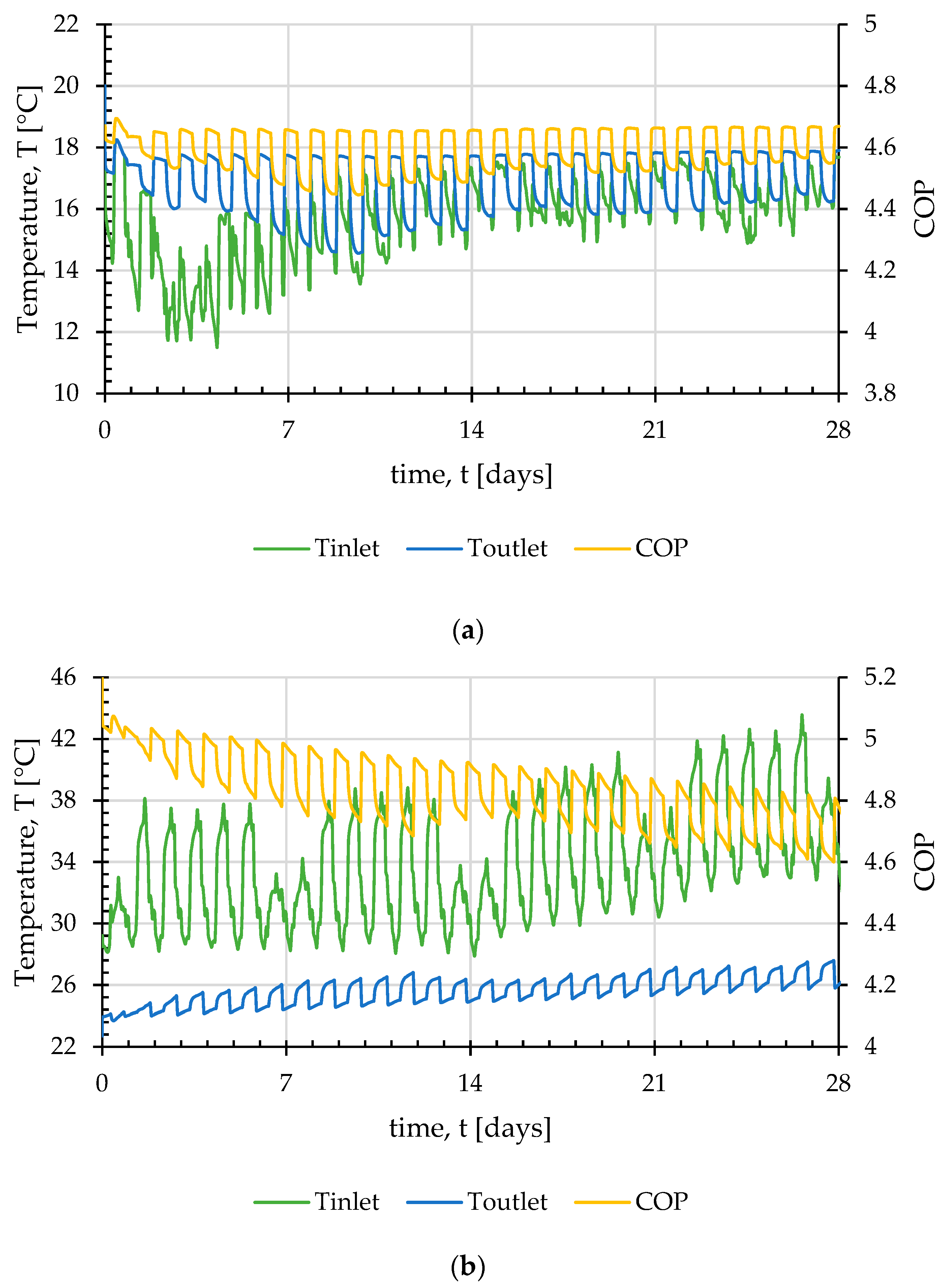
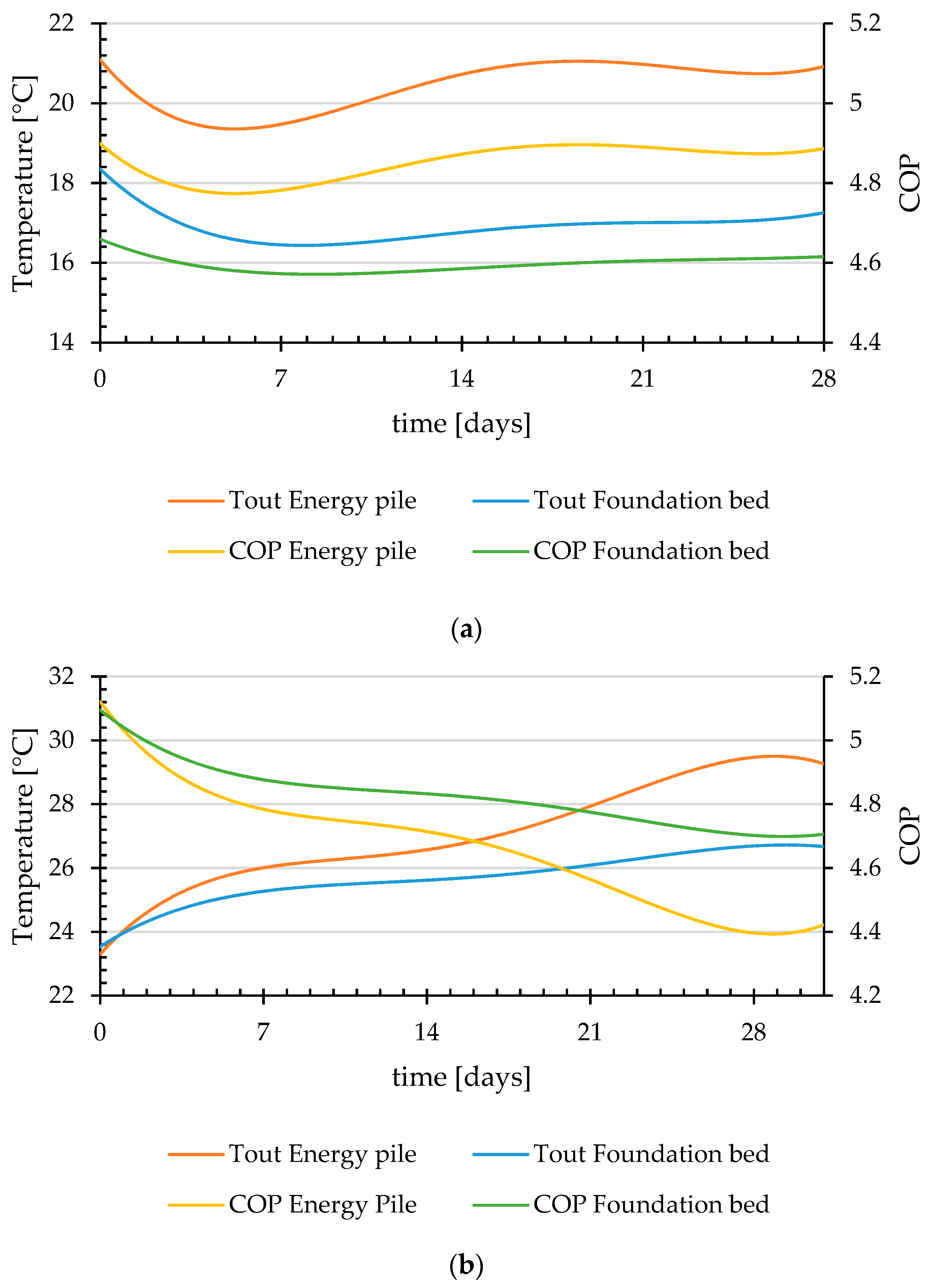
4.1. Energy Piles
4.2. Foundation Bed
5. Economic Evaluation
Economic Evaluation of a Residential Building as a GHE Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Fuel | CO2 Emissions (kgCO2/kWh) | Primary Energy (kWh) |
|---|---|---|
| Diesel oil | 0.266 | 1.1 |
| Grid supplied electricity | 0.794 | 2.7 |
| Grid displaced electricity | 0.794 | 2.7 |
| LPG | 0.249 | 1.1 |
| Biomass | 0.025 | 1.1 |
References
- EuroStat. Energy Consumption and Use by Household. Available online: https://ec.europa.eu/eurostat/web/products-eurostat-news/-/DDN-20190620-1 (accessed on 10 February 2019).
- EU Parliament. Directive 2010/31/Eu of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings; EU Parliament: Brussels, Belgium, 2010. [Google Scholar]
- Lund, J.W.; Toth, A.N. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2020, 60, 66–93. [Google Scholar] [CrossRef]
- Aresti, L.; Christodoulides, P.; Florides, G. A review of the design aspects of ground heat exchangers. Renew. Sustain. Energy Rev. 2018, 92, 757–773. [Google Scholar] [CrossRef]
- Bezyan, B.; Porkhial, S.; Mehrizi, A.A. 3-D simulation of heat transfer rate in geothermal pile-foundation heat exchangers with spiral pipe configuration. Appl. Therm. Eng. 2015, 87, 655–668. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, B.; Liu, F. Study on the thermal performance of several types of energy pile ground heat exchangers: U-shaped, W-shaped and spiral-shaped. Energy Build. 2016, 133, 335–344. [Google Scholar] [CrossRef]
- Fadejev, J.; Simson, R.; Kurnitski, J.; Haghighat, F. A review on energy piles design, sizing and modelling. Energy 2017, 122, 390–407. [Google Scholar] [CrossRef]
- Brandl, H. Thermo-active Ground-Source Structures for Heating and Cooling. Procedia Eng. 2013, 57, 9–18. [Google Scholar] [CrossRef] [Green Version]
- De Moel, M.; Bach, P.M.; Bouazza, A.; Singh, R.M.; Sun, J.O. Technological advances and applications of geothermal energy pile foundations and their feasibility in Australia. Renew. Sustain. Energy Rev. 2010, 14, 2683–2696. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Zhang, X.; Liu, J.; Li, K.; Yang, J. Numerical and experimental assessment of thermal performance of vertical energy piles: An application. Appl. Energy 2008, 85, 901–910. [Google Scholar] [CrossRef]
- Gashti, E.H.N.; Uotinen, V.-M.; Kujala, K. Numerical modelling of thermal regimes in steel energy pile foundations: A case study. Energy Build. 2014, 69, 165–174. [Google Scholar] [CrossRef]
- Suryatriyastuti, M.; Mroueh, H.; Burlon, S. Understanding the temperature-induced mechanical behaviour of energy pile foundations. Renew. Sustain. Energy Rev. 2012, 16, 3344–3354. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.-R.; Xue, J.; Zosseder, K.; Go, G.-H.; Park, H. Evaluation of the thermal efficiency and a cost analysis of different types of ground heat exchangers in energy piles. Energy Convers. Manag. 2015, 105, 393–402. [Google Scholar] [CrossRef]
- Sterpi, D.; Tomaselli, G.; Angelotti, A. Energy performance of ground heat exchangers embedded in diaphragm walls: Field observations and optimization by numerical modelling. Renew. Energy 2020, 147, 2748–2760. [Google Scholar] [CrossRef] [Green Version]
- Loveridge, F. The Thermal Performance of Foundation Piles used as Heat Exchangers in Ground Energy Systems. Ph.D Thesis, University of Southhampton, Southhampton, UK, June 2012. [Google Scholar]
- Sani, A.K.; Singh, R.M.; Amis, T.; Cavarretta, I. A review on the performance of geothermal energy pile foundation, its design process and applications. Renew. Sustain. Energy Rev. 2019, 106, 54–78. [Google Scholar] [CrossRef]
- Carotenuto, A.; Marotta, P.; Massarotti, N.; Mauro, A.; Normino, G. Energy piles for ground source heat pump applications: Comparison of heat transfer performance for different design and operating parameters. Appl. Therm. Eng. 2017, 124, 1492–1504. [Google Scholar] [CrossRef]
- Zarrella, A.; De Carli, M.; Galgaro, A. Thermal performance of two types of energy foundation pile: Helical pipe and triple U-tube. Appl. Therm. Eng. 2013, 61, 301–310. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, F.; Liu, C.; Tian, M.; Chen, B. Influence of spiral pitch on the thermal behaviors of energy piles with spiral-tube heat exchanger. Appl. Therm. Eng. 2017, 125, 1280–1290. [Google Scholar] [CrossRef]
- Saeidi, R.; Noorollahi, Y.; Esfahanian, V. Numerical simulation of a novel spiral type ground heat exchanger for enhancing heat transfer performance of geothermal heat pump. Energy Convers. Manag. 2018, 168, 296–307. [Google Scholar] [CrossRef]
- Dehghan, B.; Sisman, A.; Aydin, M. Parametric investigation of helical ground heat exchangers for heat pump applications. Energy Build. 2016, 127, 999–1007. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.; Yoon, S.; Shin, H.; Lee, D.-S. Case study of heat transfer behavior of helical ground heat exchanger. Energy Build. 2012, 53, 137–144. [Google Scholar] [CrossRef]
- Kim, M.-J.; Lee, S.; Yoon, S.; Jeon, J.-S. Evaluation of geometric factors influencing thermal performance of horizontal spiral-coil ground heat exchangers. Appl. Therm. Eng. 2018, 144, 788–796. [Google Scholar] [CrossRef]
- Cui, P.; Li, X.; Man, Y.; Fang, Z. Heat transfer analysis of pile geothermal heat exchangers with spiral coils. Appl. Energy 2011, 88, 4113–4119. [Google Scholar] [CrossRef]
- Park, S.; Lee, D.; Choi, H.-J.; Jung, K.; Choi, H. Relative constructability and thermal performance of cast-in-place concrete energy pile: Coil-type GHEX (ground heat exchanger). Energy 2015, 81, 56–66. [Google Scholar] [CrossRef]
- Park, S.; Lee, S.; Lee, D.; Lee, S.S.; Choi, H. Influence of coil pitch on thermal performance of coil-type cast-in-place energy piles. Energy Build. 2016, 129, 344–356. [Google Scholar] [CrossRef]
- Fan, R.; Jiang, Y.; Yao, Y.; Shiming, D.; Ma, Z. A study on the performance of a geothermal heat exchanger under coupled heat conduction and groundwater advection. Energy 2007, 32, 2199–2209. [Google Scholar] [CrossRef]
- Stylianou, I.I.; Tassou, S.; Christodoulides, P.; Aresti, L.; Florides, G. Modeling of vertical ground heat exchangers in the presence of groundwater flow and underground temperature gradient. Energy Build. 2019, 192, 15–30. [Google Scholar] [CrossRef]
- Aresti, G.A.L.; Florides, P. Christodoulides, “Computational modelling of a ground heat exchanger with groundwater flow. Bulg. Chem. Commun. 2016, 48, 55–63. [Google Scholar]
- Huang, G.; Yang, X.; Liu, Y.; Zhuang, C.; Zhang, H.; Lu, J. A novel truncated cone helix energy pile: Modelling and investigations of thermal performance. Energy Build. 2018, 158, 1241–1256. [Google Scholar] [CrossRef]
- Mehrizi, A.A.; Porkhial, S.; Bezyan, B.; Lotfizadeh, H. Energy pile foundation simulation for different configurations of ground source heat exchanger. Int. Commun. Heat Mass Transf. 2016, 70, 105–114. [Google Scholar] [CrossRef]
- Kayaci, N.; Demir, H. Comparative performance analysis of building foundation Ground heat exchanger. Geothermics 2020, 83, 101710. [Google Scholar] [CrossRef]
- Aresti, L.; Christodoulides, P.; Lazari, L.; Florides, G. Computational Investigation on the Effect of Various Parameters of a Spiral Ground Heat Exchanger. In Proceedings of the 12th International Workshop on Applied Modeling & Simulation (WAMS 2019), NUSS Kent Ridge Guild House, Singapore, 30–31 October 2019. [Google Scholar]
- Ministry of Commerce Industry and Energy Tourism. 2nd National Plan for Increasing the Number of Nearly Zero-Energy Buildings (NZEBs); European Commission: Athens, Greece, 2017.
- Panayiotou, G.P.; A Kalogirou, S.; Florides, G.; Maxoulis, C.; Papadopoulos, A.M.; Neophytou, N.; Fokaides, P.A.; Georgiou, G.; Symeou, A.; Georgakis, G. The characteristics and the energy behaviour of the residential building stock of Cyprus in view of Directive 2002/91/EC. Energy Build. 2010, 42, 2083–2089. [Google Scholar] [CrossRef]
- CYSTAT. Construction and Housing Statistics; Statistical Service of the Republic of Cyprus: Nicosia, Cyprus, 2016.
- European Committee. Eurostat Database; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- Cyprus Energy Service. Thermal Insulation Guide, 2nd ed.; Ministry of Energy Commerce Industry and Tourism: Nicosia, Cyprus, 2009.
- Fokaides, P.A.; Christoforou, E.A.; Kalogirou, S.A. Legislation driven scenarios based on recent construction advancements towards the achievement of nearly zero energy dwellings in the southern European country of Cyprus. Energy 2014, 66, 588–597. [Google Scholar] [CrossRef]
- Christodoulides, P.; Aresti, L.; Florides, G. Air-conditioning of a typical house in moderate climates with Ground Source Heat Pumps and cost comparison with Air Source Heat Pumps. Appl. Therm. Eng. 2019, 158, 113772. [Google Scholar] [CrossRef]
- Pouloupatis, P.D. Determination of the Thermal Characteristics of the Ground in Cyprus and Their Effect on Ground Heat; Brunel University: London, UK, 2014. [Google Scholar]
- Pouloupatis, P.; Tassou, S.; Christodoulides, P.; Florides, G. Parametric analysis of the factors affecting the efficiency of ground heat exchangers and design application aspects in Cyprus. Renew. Energy 2017, 103, 721–728. [Google Scholar] [CrossRef]
- Serghides, D.K.; Dimitriou, S.; Katafygiotou, M.C.; Michaelidou, M. Energy Efficient Refurbishment towards Nearly Zero Energy Houses, for the Mediterranean Region. Energy Procedia 2015, 83, 533–543. [Google Scholar] [CrossRef] [Green Version]
- Alexandri, E.; Androutsopoulos, A. Energy Upgrade of Existing Dwellings in Greece; Embodied Energy Issues. Procedia Environ. Sci. 2017, 38, 196–203. [Google Scholar] [CrossRef]
- Manganelli, B.; Morano, P.; Tajani, F.; Salvo, F. Affordability Assessment of Energy-Efficient Building Construction in Italy. Sustainability 2019, 11, 249. [Google Scholar] [CrossRef] [Green Version]
- Aresti, L.; Christodoulides, P.; Panayiotou, G.P.; Florides, G. The Potential of Utilizing Buildings’ Foundations as Thermal Energy Storage (TES) Units from Solar Plate Collectors. Energies 2020, 13, 2695. [Google Scholar] [CrossRef]
- Dehghan, B. Experimental and computational investigation of the spiral ground heat exchangers for ground source heat pump applications. Appl. Therm. Eng. 2017, 121, 908–921. [Google Scholar] [CrossRef]
- Christodoulides, P.; Florides, G.; Pouloupatis, P. A practical method for computing the thermal properties of a Ground Heat Exchanger. Renew. Energy 2016, 94, 81–89. [Google Scholar] [CrossRef]
- Pouloupatis, P.; Florides, G.; Tassou, S. Measurements of ground temperatures in Cyprus for ground thermal applications. Renew. Energy 2011, 36, 804–814. [Google Scholar] [CrossRef]
- Florides, G.; Pouloupatis, P.; Kalogirou, S.A.; Messaritis, V.; Panayides, I.; Zomeni, Z.; Partasides, G.; Lizides, A.; Sophocleous, E.; Koutsoumpas, K.; et al. The geothermal characteristics of the ground and the potential of using ground coupled heat pumps in Cyprus. Energy 2011, 36, 5027–5036. [Google Scholar] [CrossRef]
- Ramos, R.; Aresti, L.; Yiannoukos, L.; Tsiolakis, E.; Pekris, J.; Vieira, A.; Florides, G.; Christodoulides, P. Thermal and physical characteristics of soils in Cyprus for use in shallow geothermal energy applications. Energy Ecol. Environ. 2019, 4, 300–309. [Google Scholar] [CrossRef]
- Blum, P.; Campillo, G.; Kölbel, T. Techno-economic and spatial analysis of vertical ground source heat pump systems in Germany. Energy 2011, 36, 3002–3011. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, J.; Meng, F. Techno-economic evaluation of multiple energy piles for a ground-coupled heat pump system. Energy Convers. Manag. 2018, 178, 200–216. [Google Scholar] [CrossRef]
- Zhang, W.; Cui, P.; Liu, J.; Liu, X. Study on heat transfer experiments and mathematical models of the energy pile of building. Energy Build. 2017, 152, 643–652. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.; Go, G.-H.; Park, S. An experimental and numerical approach to derive ground thermal conductivity in spiral coil type ground heat exchanger. J. Energy Inst. 2015, 88, 229–240. [Google Scholar] [CrossRef]
- Suzuki, M.; Yoneyama, K.; Amemiya, S.; Oe, M. Development of a Spiral Type Heat Exchanger for Ground Source Heat Pump System. Energy Procedia 2016, 96, 503–510. [Google Scholar] [CrossRef] [Green Version]
- Akrouch, G.A.; Sanchez, M.; Briaud, J.-L. Thermal performance and economic study of an energy piles system under cooling dominated conditions. Renew. Energy 2020, 147, 2736–2747. [Google Scholar] [CrossRef]
- Michopoulos, A.; Voulgari, V.; Tsikaloudaki, A.; Zachariadis, T. Evaluation of ground source heat pump systems for residential buildings in warm Mediterranean regions: The example of Cyprus. Energy Effic. 2016, 9, 1421–1436. [Google Scholar] [CrossRef]
- Lu, Q.; Narsilio, G.A.; Aditya, G.R.; Johnston, I.W. Economic analysis of vertical ground source heat pump systems in Melbourne. Energy 2017, 125, 107–117. [Google Scholar] [CrossRef]
- Tassou, S.; Marquand, C.; Wilson, D. Energy and economic comparisons of domestic heat pumps and conventional heating systems in the British climate. Appl. Energy 1986, 24, 127–138. [Google Scholar] [CrossRef]
- Ouyang, X.; Lin, B. Levelized cost of electricity (LCOE) of renewable energies and required subsidies in China. Energy Policy 2014, 70, 64–73. [Google Scholar] [CrossRef]
- Tsagarakis, K.P. Optimal number of energy generators for biogas utilization in wastewater treatment facility. Energy Convers. Manag. 2007, 48, 2694–2698. [Google Scholar] [CrossRef]
- Sullivan, W.G.; Wicks, E.M.; Koelling, P.C. Engineering Economy, 16th ed.; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Gabrielli, L.; Bottarelli, M. Financial and economic analysis for ground-coupled heat pumps using shallow ground heat exchangers. Sustain. Cities Soc. 2016, 20, 71–80. [Google Scholar] [CrossRef]
- Li, W.X.; Li, X.; Wang, Y.; Tu, J. An integrated predictive model of the long-term performance of ground source heat pump (GSHP) systems. Energy Build. 2018, 159, 309–318. [Google Scholar] [CrossRef]
- Zhou, S.; Cui, W.; Tao, J.; Peng, Q. Study on ground temperature response of multilayer stratums under operation of ground-source heat pump. Appl. Therm. Eng. 2016, 101, 173–182. [Google Scholar] [CrossRef]
- Aresti, L.; Christodoulides, P.; Panayiotou, G.P.; Florides, G. An investigation on the environmental impact of various GHEs configurations. Renew. Energy 2020. under review. [Google Scholar]

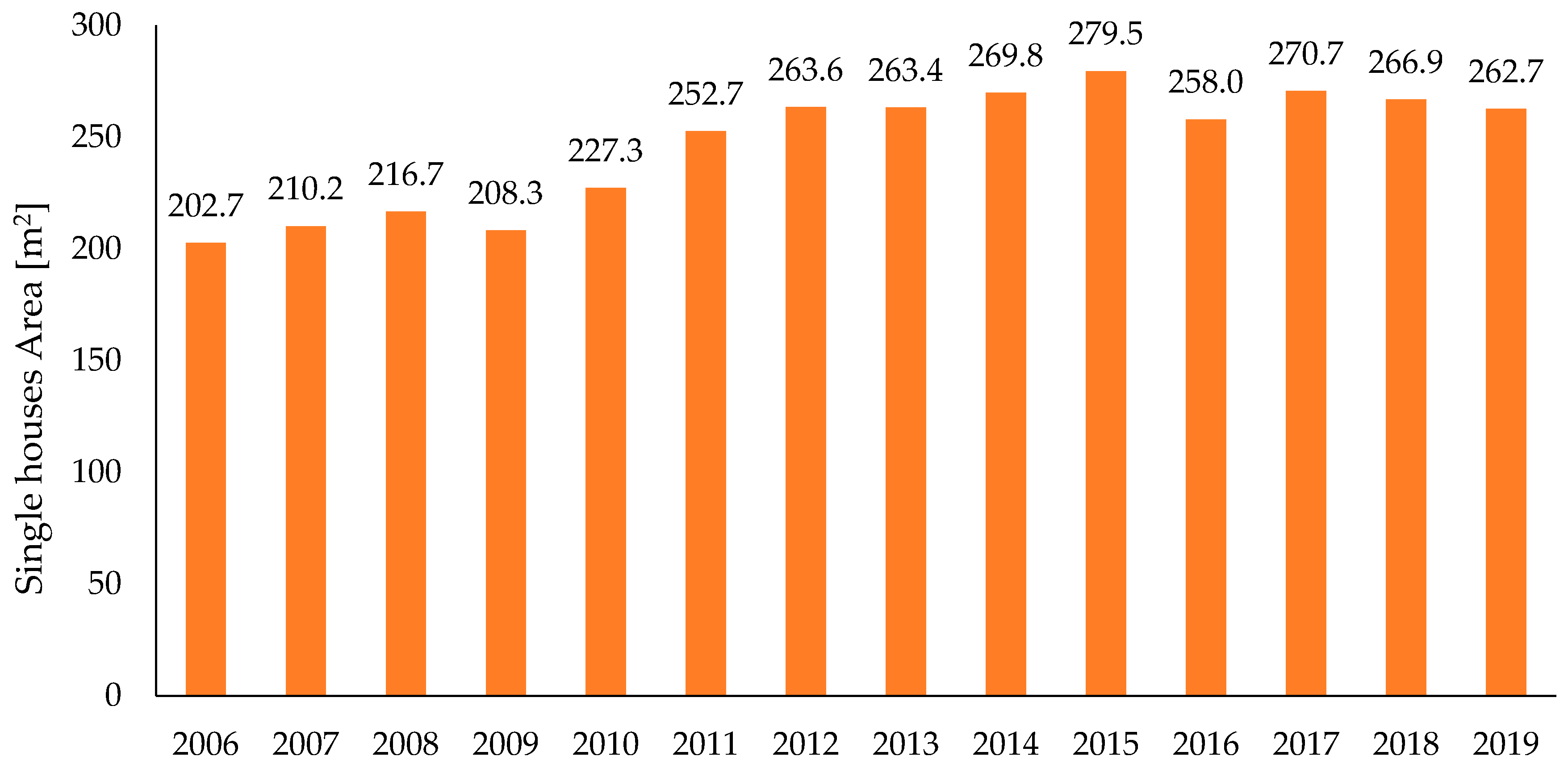



| Requirements | Minimum Value |
| Energy performance certificate of a building | A |
| Maximum primary energy consumption in residential buildings | 100 kWh per m2 per year |
| Maximum energy demand for heating for residential buildings | 15 kWh per m2 per year |
| Renewable Energy Sources percentage of the total primary energy consumption | 25% |
| Construction elements | Maximum U-value |
| External walls and load-carrying elements (pillars, beams and load-carrying walls) that are part of the building envelope | 0.4 W m−2 K−1 |
| Horizontal building elements (floors in a pilotis, floors in a cantilever, terraces, roofs) and ceilings that are part of the building envelope | 0.4 W m−2 K−1 |
| Door and Window frames that are part of the building envelope | 2.25 W m−2 K−1 |
| Material | Thickness (mm) | U-Values (W m−2 K−1) | |
|---|---|---|---|
| External Wall | |||
| Typical External Wall before EPBD | Plaster | 25 | 1.388 |
| Brick | 200 | ||
| Plaster | 25 | ||
| Typical External Wall after EPBD— Configuration [1] | Plaster | 25 | 0.581 |
| Perforated Thermal brick | 300 | ||
| Plaster | 25 | ||
| Typical External Wall after EPBD— Configuration [2] | Plaster | 25 | 0.318 |
| Insulation material (polystyrene) | 50 | ||
| Perforated Thermal brick | 250 | ||
| Plaster | 25 | ||
| Roof | |||
| Typical Roof before EPBD | Trowel | 10 | 3.252 |
| Reinforced concrete | 150 | ||
| Screed | 100 | ||
| Waterproofing layer | 5 | ||
| Typical Roof after EPBD | Trowel | 10 | 0.274 |
| Reinforced concrete | 150 | ||
| Insulation material (polystyrene) | 100 | ||
| Screed | 100 | ||
| Waterproofing layer | 5 |
| Energy Pile Model Characteristics | |
|---|---|
| Energy Pile length | 10 m |
| Energy Pile diameter | 0.8 m |
| Spiral Coil diameter | 0.6 m |
| Spiral Coil length | 9 m |
| Spiral Coil pitch | 0.2 m |
| Coil tube diameter | 32 mm |
| Coil tube thickness | 3 mm |
| Domain/Ground diameter | 4 m (5 × Energy Pile diameter) |
| Flow rate | 10 L/min |
| Total Pipe length | 85.3 m |
| Foundation Bed Model Characteristics | |
|---|---|
| Foundation bed (length × width) | 15 × 10 m |
| Foundation bed depth | 1 m |
| Pipe diameter | 32 mm |
| Pipe thickness | 3 mm |
| Flow rate | 10 L/min |
| Total pipe length | 220 m |
| Material | k W m−1 K−1 | ρ kg m−3 | cp J Kg−1 K−1 | Description |
|---|---|---|---|---|
| Ground | 1.4 | 2300 | 950 | Marl, chalk, and gravel |
| Grout/foundation | 1.628 | 2500 | 837 | Reinforced concrete |
| Pipes | 0.42 | 1100 | 1465 | HDPE |
| Circulating Fluid | 0.6 | 998.2 | 4182 | Water |
| Item | Energy Pile Single | Energy Pile × 4 | Foundation Bed |
|---|---|---|---|
| U-tube GHE Φ 32 mm (6 €/m) | 341 | 1365 | 1320 |
| Header-flowmeters-valve | 400 | ||
| Horizontal pipe circuits | 300 | ||
| Difference from a high-efficiency ASHP price (low-efficiency ASHP) | −2000 (+2000) | ||
| General expenses/Labour | 250 | 1000 | 1000 |
| Total (€) compared to high-efficiency ASHP | −709 | 1065 | 1020 |
| Total (€) compared to low-efficiency ASHP | 3291 | 5065 | 5020 |
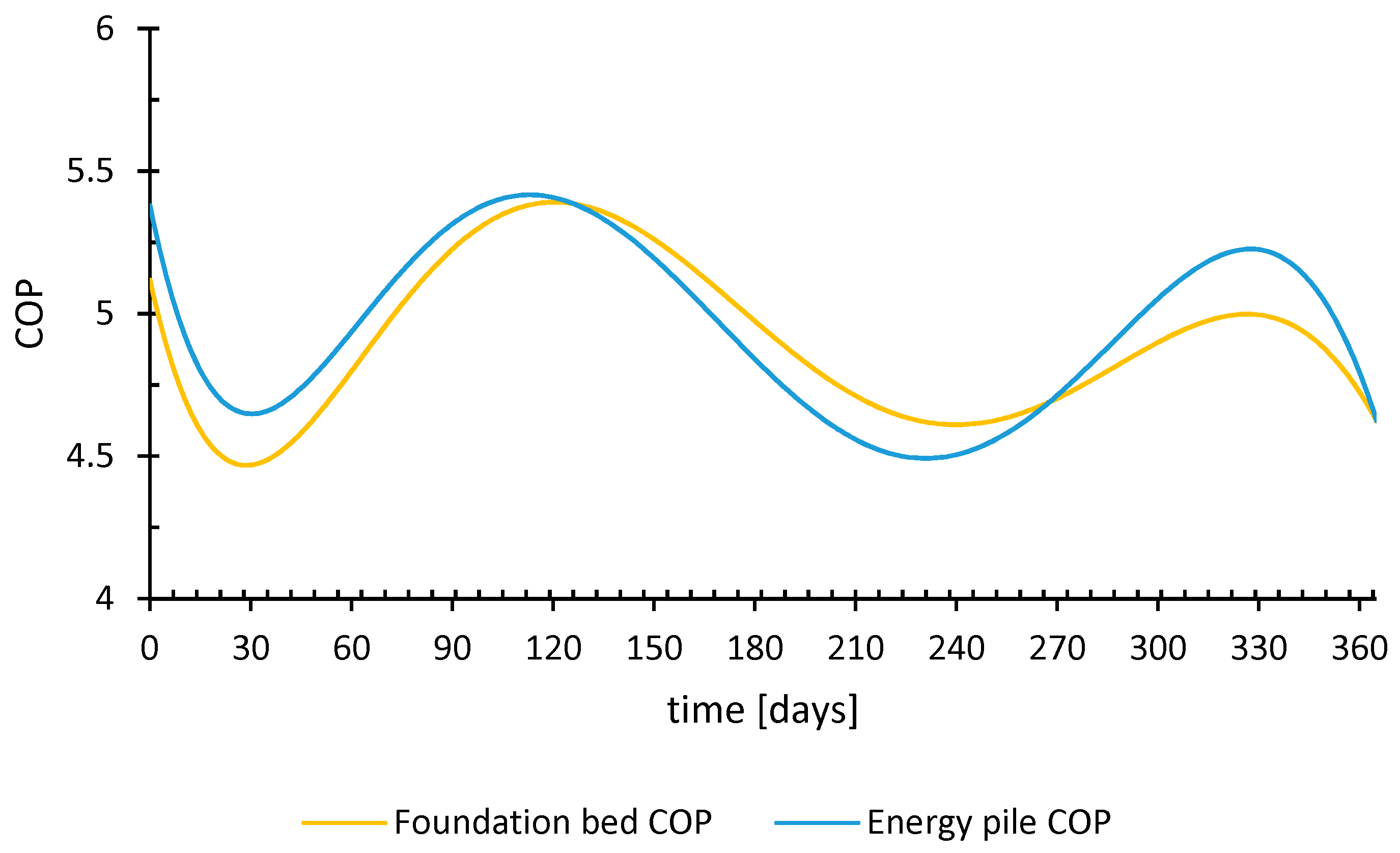
| Heating (kWh) | Cooling (kWh) | Foundation Bed COP (average) | Foundation Bed Input Electrical Energy (kWh) | Energy Pile COP (Average) | Energy Pile Input Electrical Energy (kWh) | |
|---|---|---|---|---|---|---|
| January | 709 | 0 | 4.71 | 151 | 4.91 | 144 |
| February | 712 | 0 | 4.60 | 155 | 4.76 | 150 |
| March | 205 | 7 | 4.75 | 43 | 4.73 | 43 |
| April | 0 | 376 | 5.63 | 67 | 5.67 | 66 |
| May | 0 | 809 | 5.33 | 152 | 5.45 | 148 |
| June | 0 | 2076 | 5.07 | 409 | 4.86 | 427 |
| July | 0 | 2882 | 4.83 | 597 | 4.66 | 618 |
| August | 0 | 2733 | 4.61 | 593 | 4.51 | 606 |
| September | 0 | 1909 | 4.64 | 411 | 4.56 | 419 |
| October | 0 | 687 | 4.88 | 141 | 5.06 | 136 |
| November | 9 | 121 | 4.96 | 24 | 5.19 | 23 |
| December | 514 | 0 | 4.85 | 106 | 4.96 | 104 |
| Total (kWh) | 2150 | 11600 | 2849 | 2885 |
| Type | Cost to Cover (€) | Total Savings per Year (€) | SPP (Years) | SPP with 2% EP Inflation (Years) | DPP 2% (Years) | DPP 2%, with 2% EP Inflation (Years) | DPP 2%, with 5% EP Inflation (Years) | Cash Flow Return Rate per Year (%) |
|---|---|---|---|---|---|---|---|---|
| Energy Piles GSHP system compared to ASHP with high COP (3852 kWh) | 1065 | 517 | 2.06 | 2.04 | 2.12 | 2.10 | 2.06 | 48.11 |
| Foundation Bed GSHP system compared to ASHP with high COP (3852 kWh) | 1020 | 524 | 1.95 | 1.93 | 2.01 | 1.99 | 1.95 | 51.01 |
| Energy Piles GSHP system compared to ASHP with low COP (4727 kWh) | 5065 | 683 | 7.41 | 6.97 | 8.10 | 7.56 | 6.89 | 8.31 |
| Foundation Bed GSHP system compared to ASHP with low COP (4727 kWh) | 5020 | 690 | 7.27 | 6.85 | 7.94 | 7.42 | 6.77 | 8.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aresti, L.; Christodoulides, P.; Panayiotou, G.P.; Florides, G. Residential Buildings’ Foundations as a Ground Heat Exchanger and Comparison among Different Types in a Moderate Climate Country. Energies 2020, 13, 6287. https://doi.org/10.3390/en13236287
Aresti L, Christodoulides P, Panayiotou GP, Florides G. Residential Buildings’ Foundations as a Ground Heat Exchanger and Comparison among Different Types in a Moderate Climate Country. Energies. 2020; 13(23):6287. https://doi.org/10.3390/en13236287
Chicago/Turabian StyleAresti, Lazaros, Paul Christodoulides, Gregoris P. Panayiotou, and Georgios Florides. 2020. "Residential Buildings’ Foundations as a Ground Heat Exchanger and Comparison among Different Types in a Moderate Climate Country" Energies 13, no. 23: 6287. https://doi.org/10.3390/en13236287
APA StyleAresti, L., Christodoulides, P., Panayiotou, G. P., & Florides, G. (2020). Residential Buildings’ Foundations as a Ground Heat Exchanger and Comparison among Different Types in a Moderate Climate Country. Energies, 13(23), 6287. https://doi.org/10.3390/en13236287






