Heating Performance of Solar Building Integrated Wall under Natural Circulation
Abstract
1. Introduction
2. Experimental
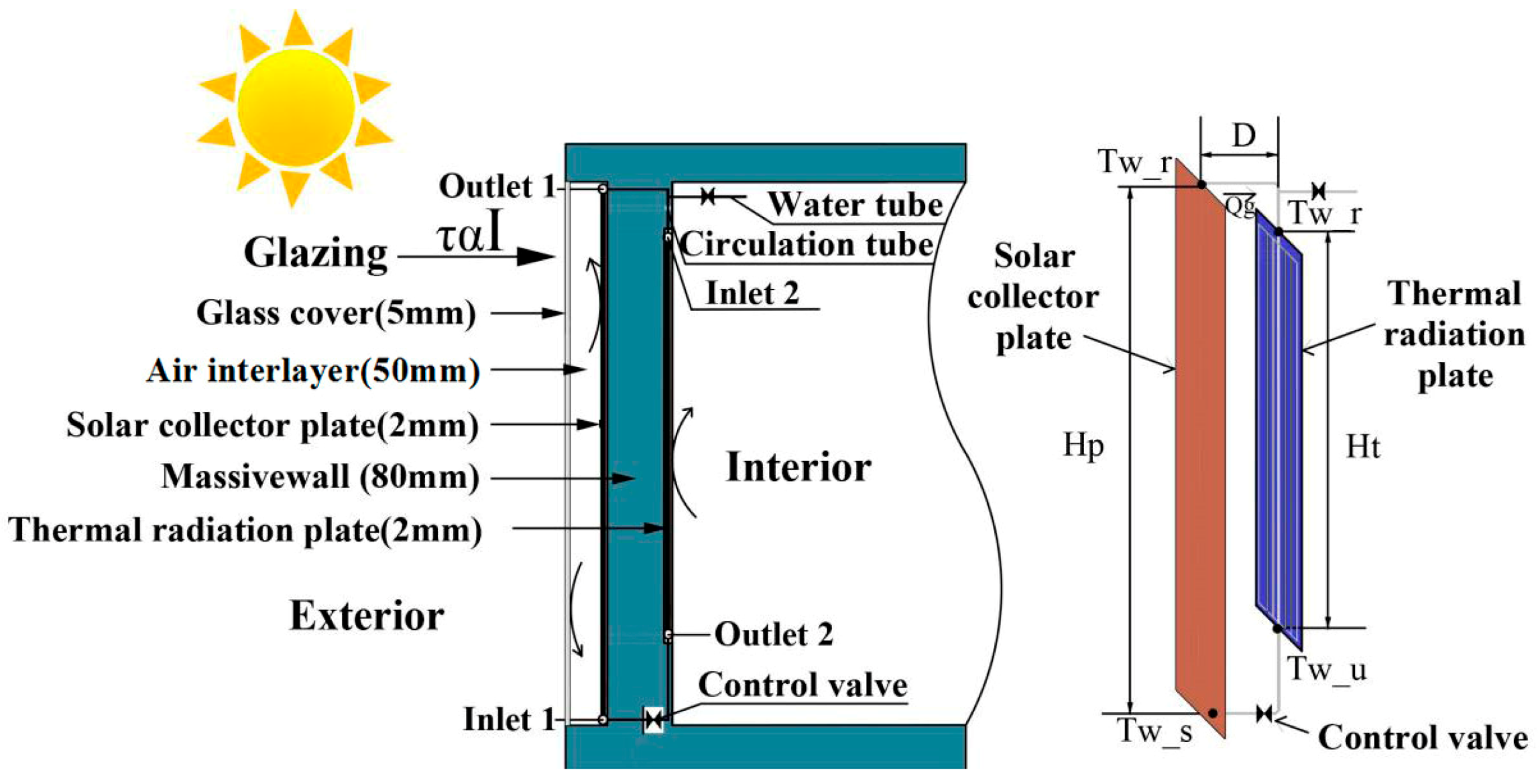
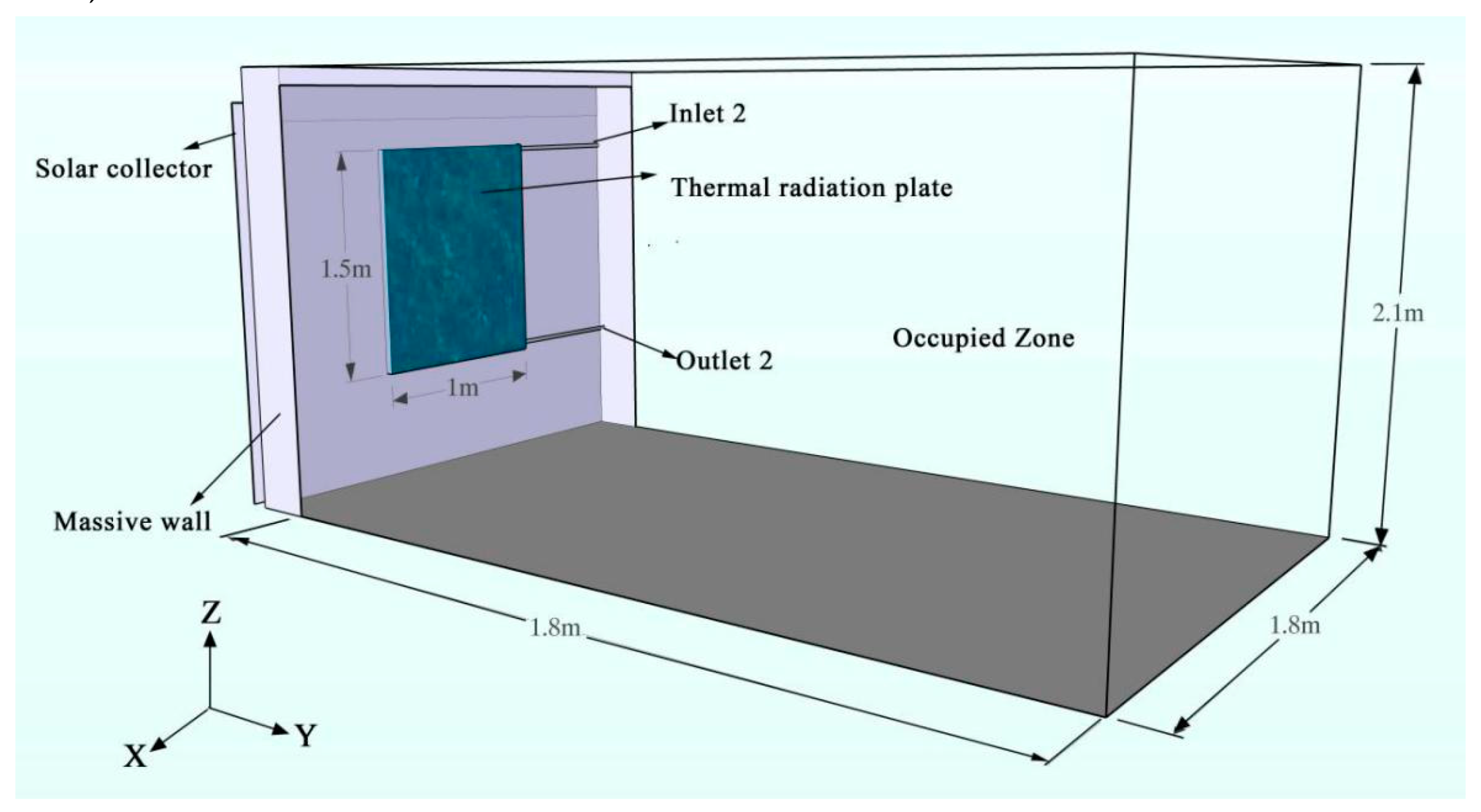
2.1. Description of the Façade System
2.2. Experimental Methods
2.3. Experimental Results
2.3.1. Pipe Impedance
2.3.2. Parameter Uncertainty Analysis
2.3.3. Experimental Test of Natural Circulation
3. Numerical Model
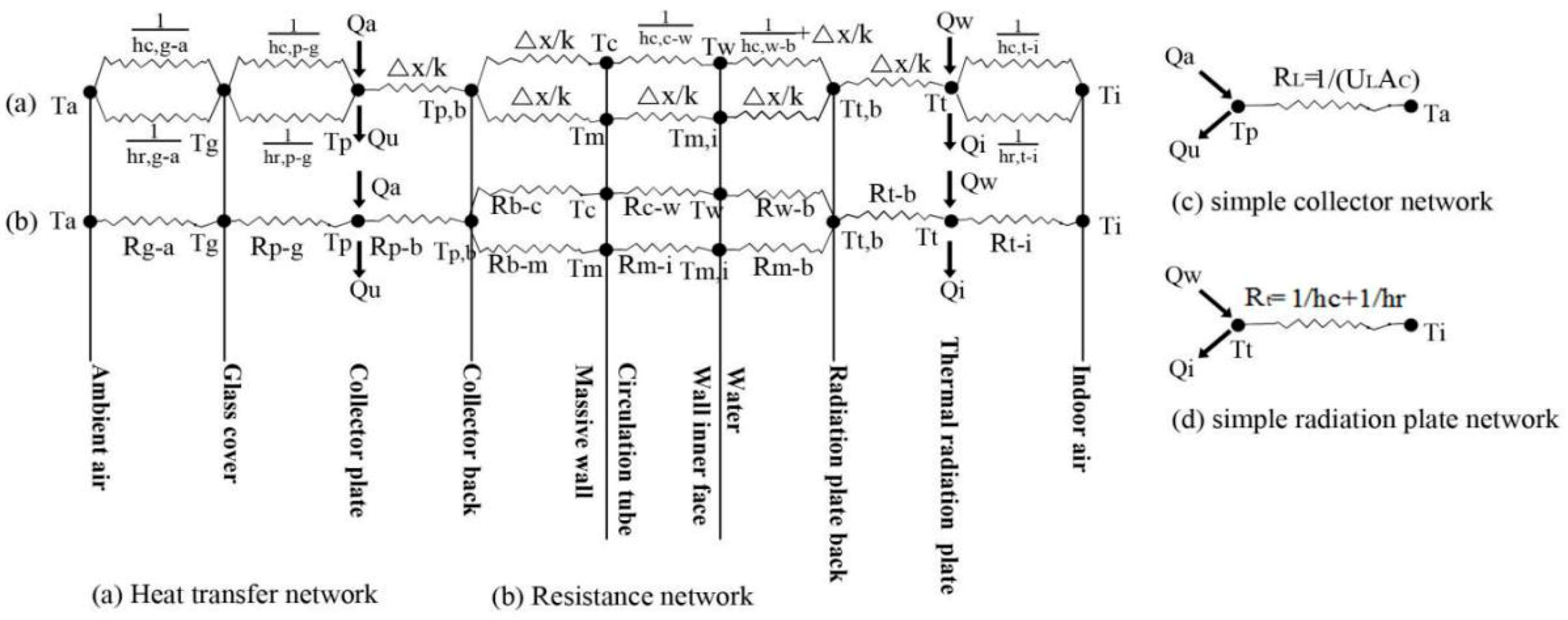
3.1. Analysis of Heat Transfer Process
- The natural circulation loop was a single-phase system, which did not involve the study of two-phase natural circulation conditions.
- There was no heat conduction and heat exchange in the axial direction of the pipe wall.
- The fluid was an incompressible Newtonian fluid, and the density and viscosity characteristics of the fluid were linear functions of temperature.
- No inner heat source in this system.
- The circulating pipe in system was adiabatic, while the water temperatures at inlet 1 and outlet 1 were equal to the temperatures at the outlet 2 and inlet 2, respectively.
3.1.1. Heating Side
3.1.2. Cooling Side
3.1.3. Wall Circulation System
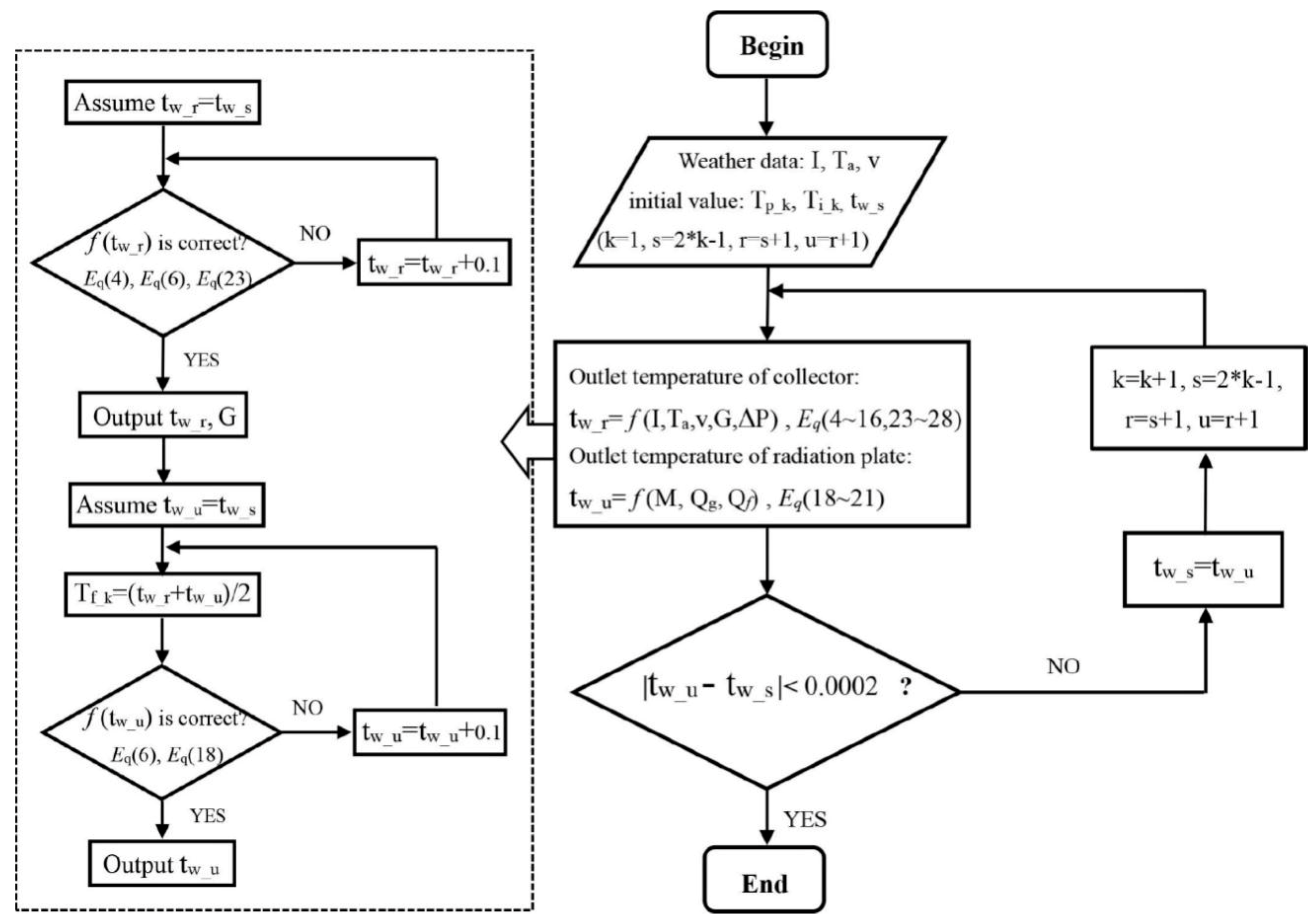
3.2. Simulation Methods
- At the beginning of the program, refer to the experimental data and input the necessary parameters, such as solar radiation (I), wind speed (v), and ambient air temperature (Ta). Set the initial values of the solar collector temperature (Tp_k), the inlet water temperature (tw_s), and the indoor temperature (Ti_k).
- Solve the water temperature at the collector outlet 1 (tw_r). Assume that outlet water temperature of the solar collector (tw_r) is equal to its inlet water temperature (tw_s) at the k-th cycle, superpose iterations in steps of 0.001, and combine Equations (4)–(16) and (23)–(28), until tw_r with the required accuracy is found.
- Take the collector’s water temperature (tw_r) as the radiation plate’s inlet water temperature at the k-th cycle.
- Solve the radiation plate’s outlet water temperature (tw_u) in the k-th cycle. Assume the water temperature at radiation plate outlet (tw_u) is equal to the water temperature at collector’s inlet (tw_s). Based on the fact that the mass flow on the cooling side is equal to that on the heating side, combining Equations (6) and (18)–(21), determine whether f (tw_u) is equal to 0 within the accuracy range.
- If f (tw_u) is equal to 0 within the accuracy range, then tw_u is the water temperature at radiation plate’s outlet at the k-th cycle and outputs tw_u.
- If not, the iteration is continued with a step size of 0.0001 until tw_u with the required accuracy is found. In this process, the surface temperature of radiation plate is seen as the average temperature of the outlet and inlet water temperature of radiation plate.
- According to the actual water temperature at collector inlet (tw_s) at the k-th cycle and the outlet water temperature of radiation plate (tw_u) obtained from the calculation at the k-th cycle, determine whether the cycle can be terminated or not. That is, within the precision range (±0.0002), is the tw_u equal to the tw_s?
- If it is, output the thermal supply from thermal radiation plate to indoor, and calculate the façade’s solar heat efficiency according to Equation (28).
- If not, take the water temperature at the radiation plate outlet 2 (tw_u) obtained at k-th cycle as the inlet water temperature of the solar collector (tw_s) at k+1-th cycle, return to step 2, and continue the cycle until the heat balance condition is satisfied, and finally obtain the solar heat efficiency of the system.
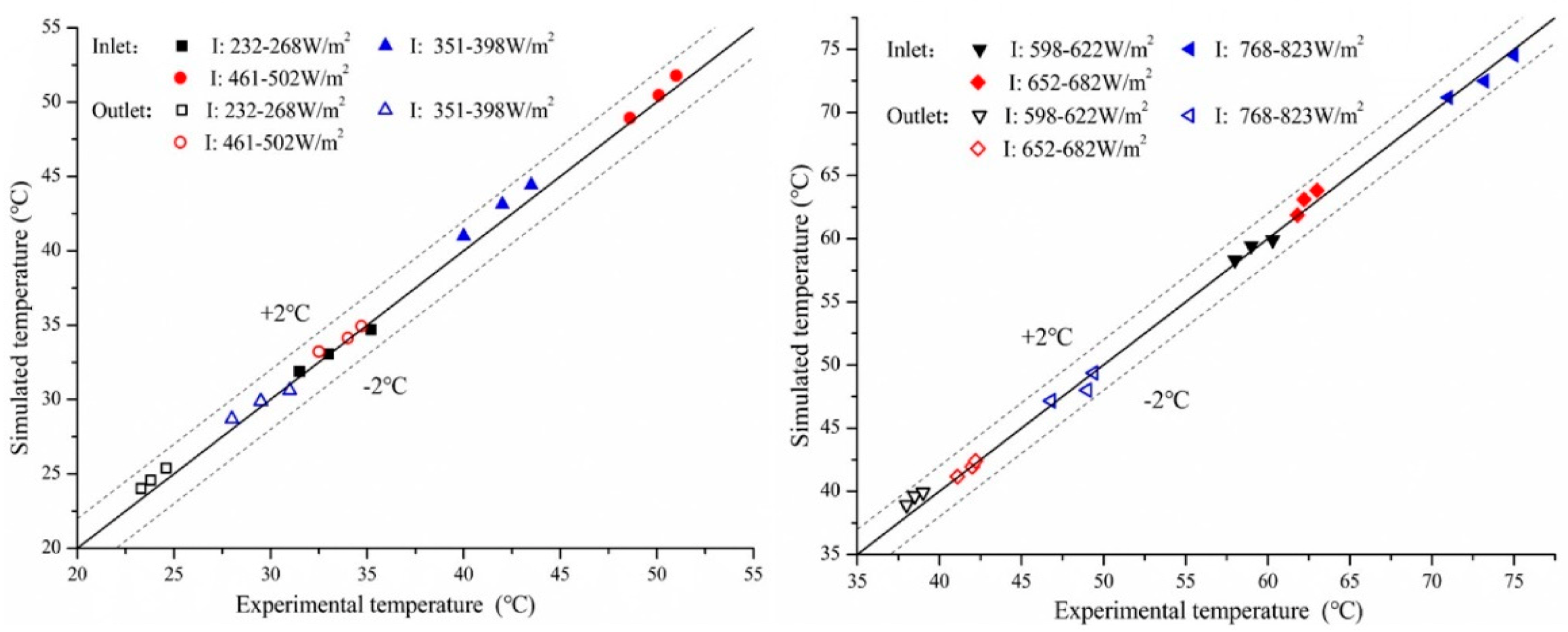
4. Simulation Validation
5. Discussion and Analysis
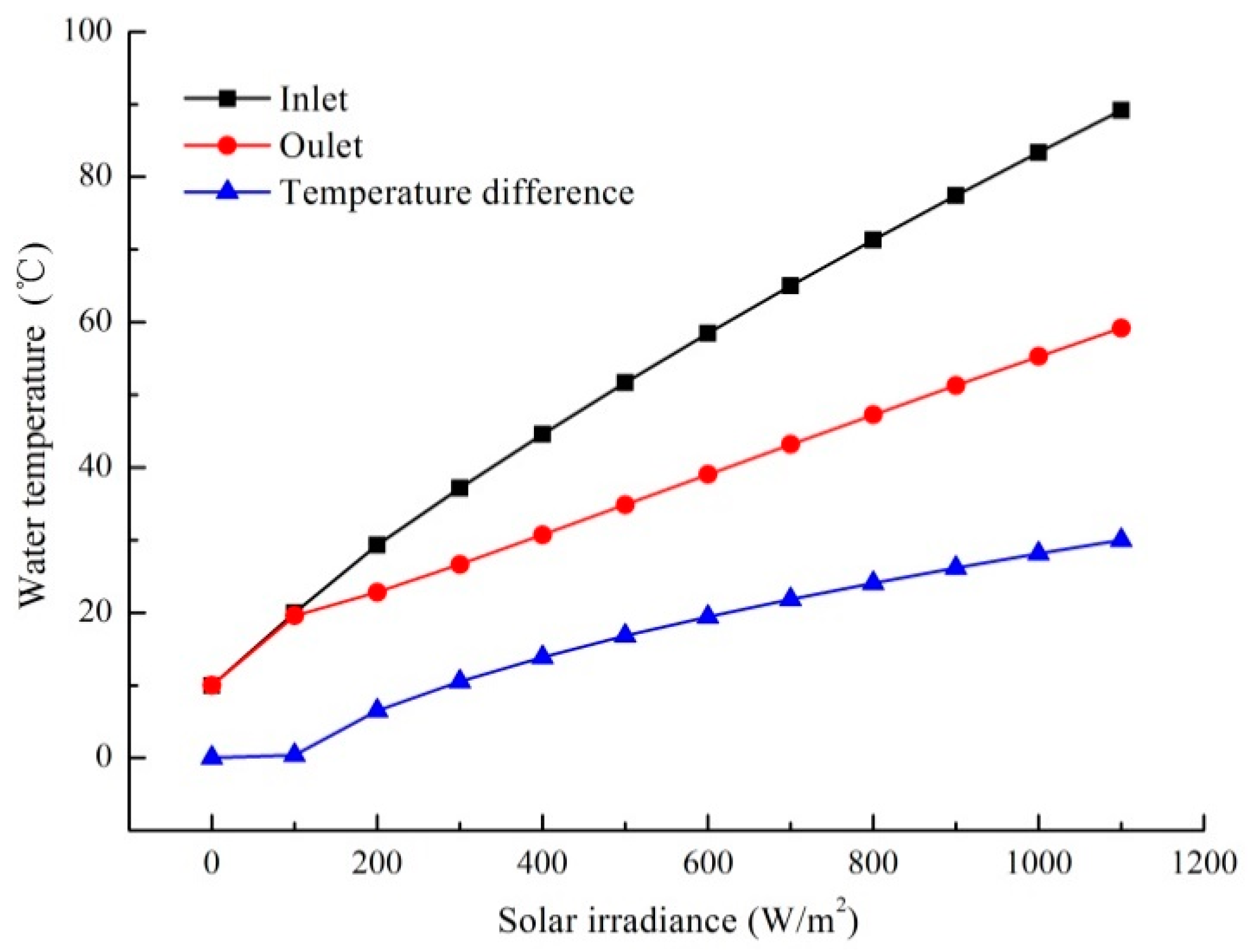
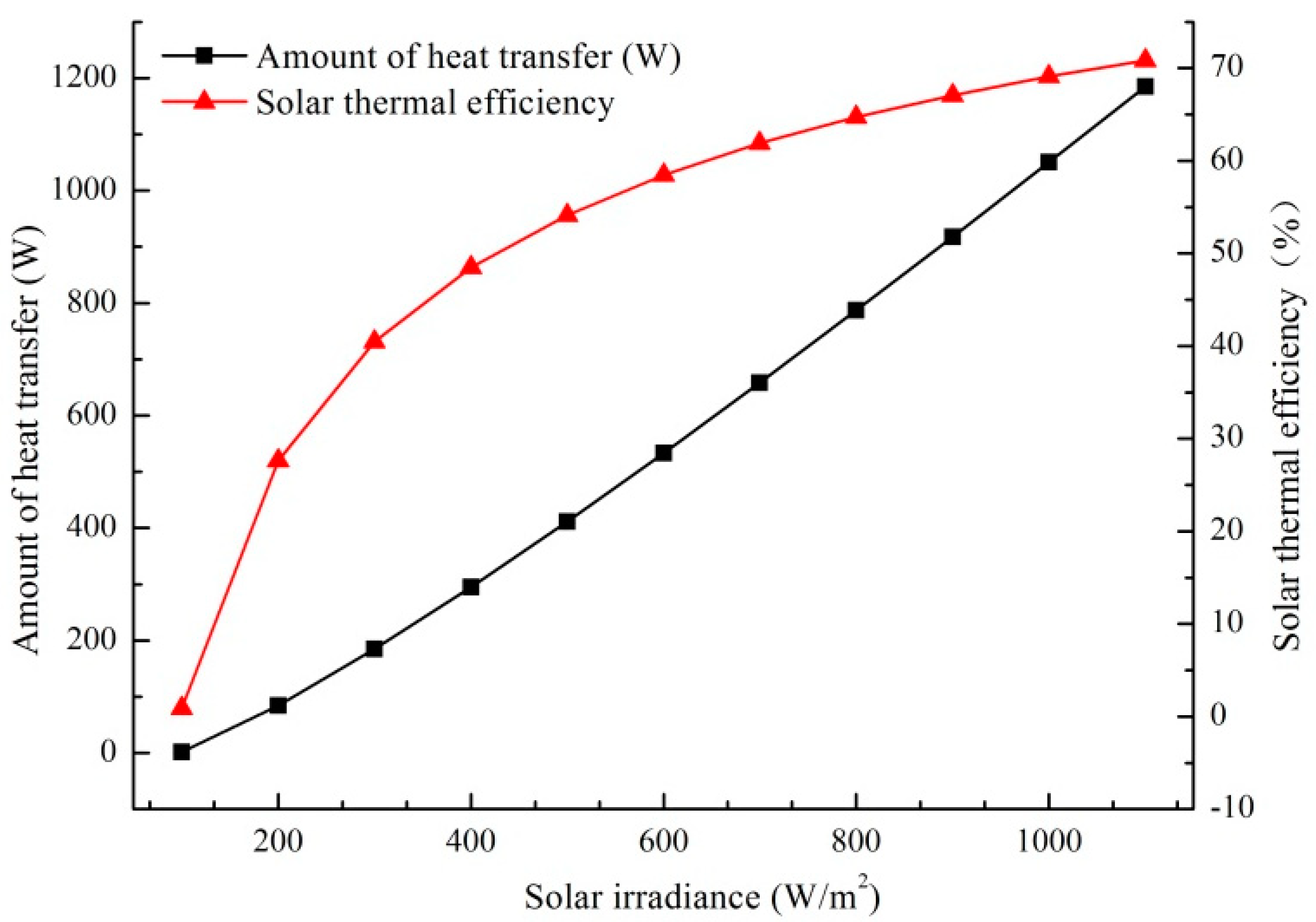
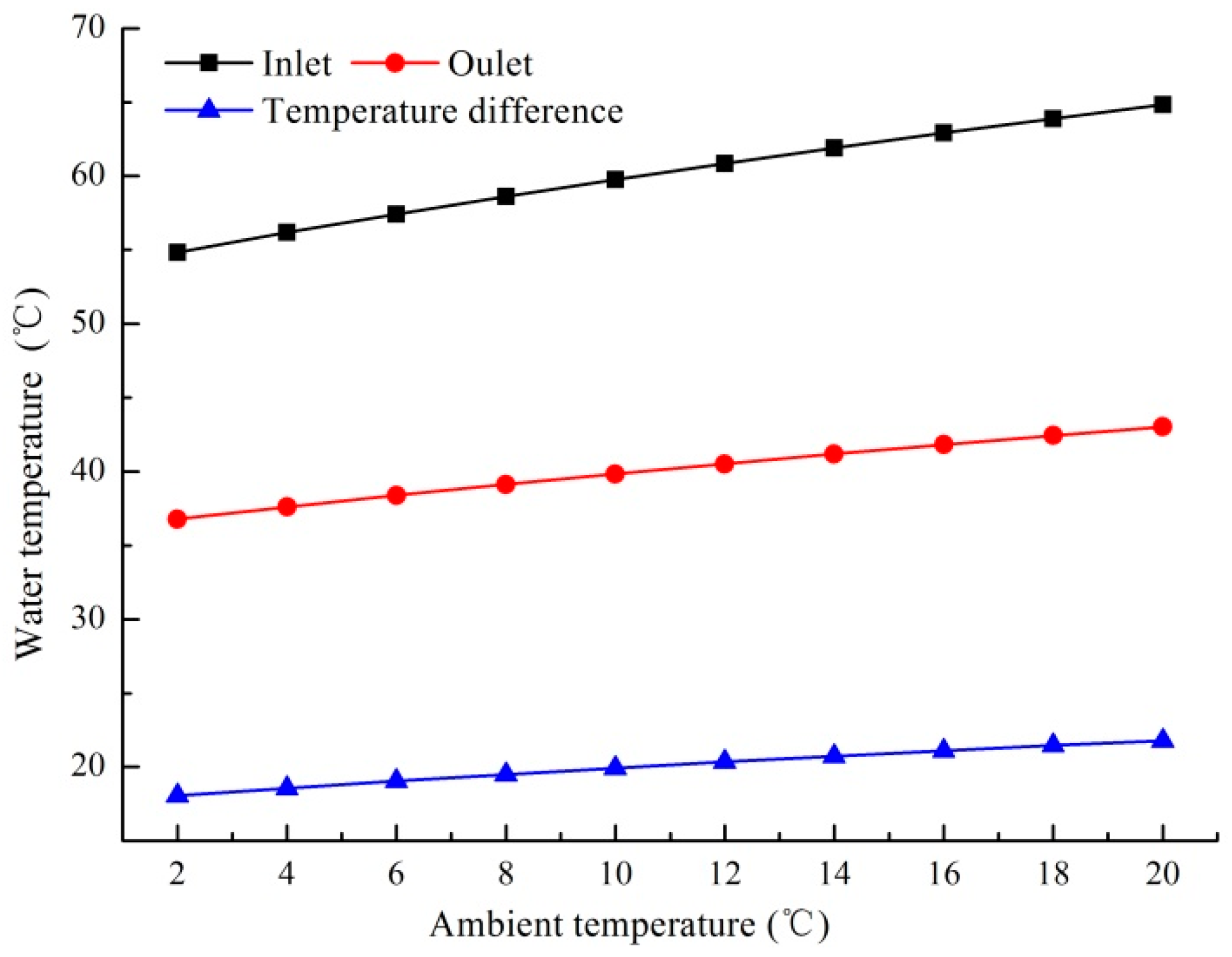
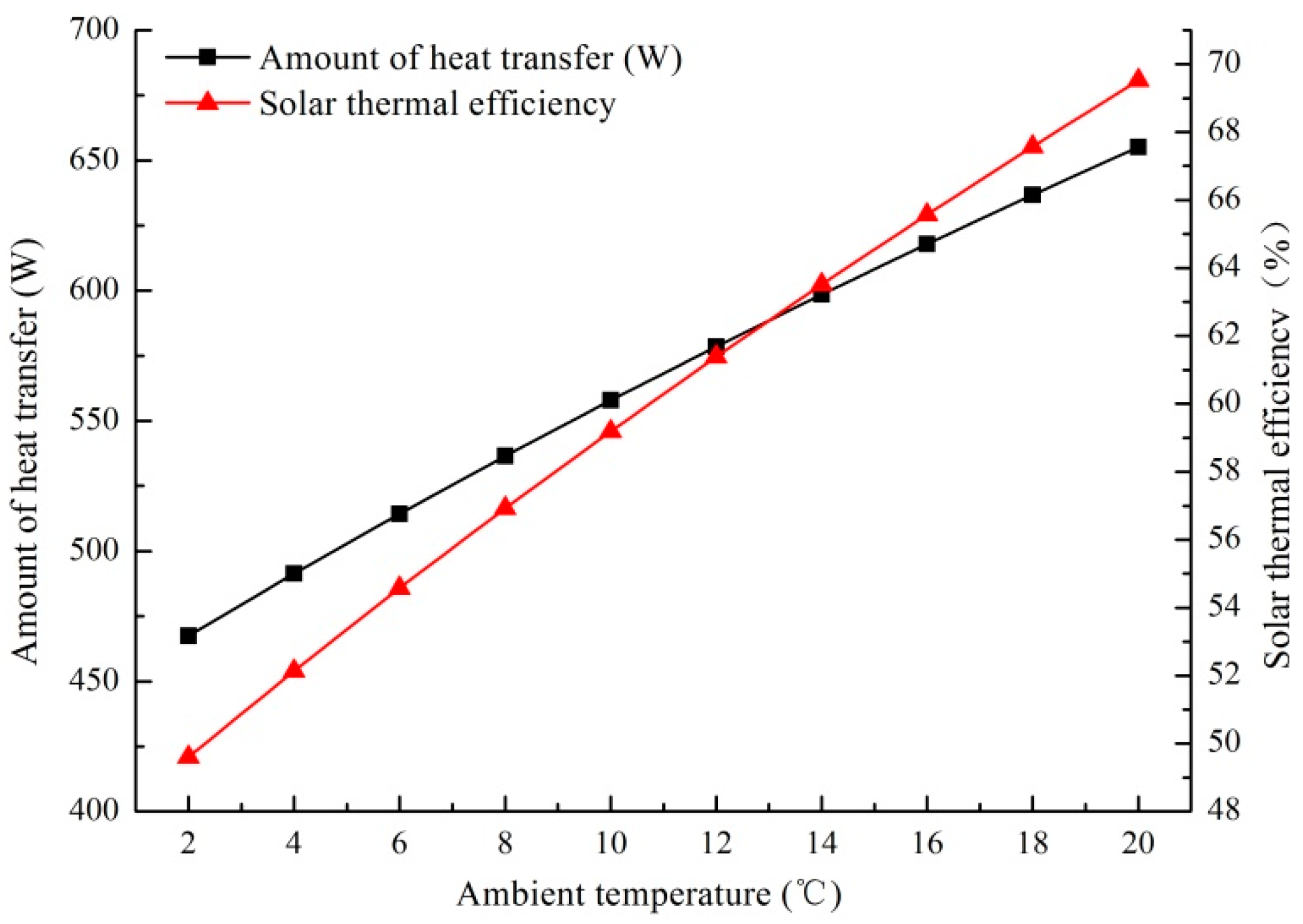
5.1. Effect of Outdoor Thermal Environment Parameters
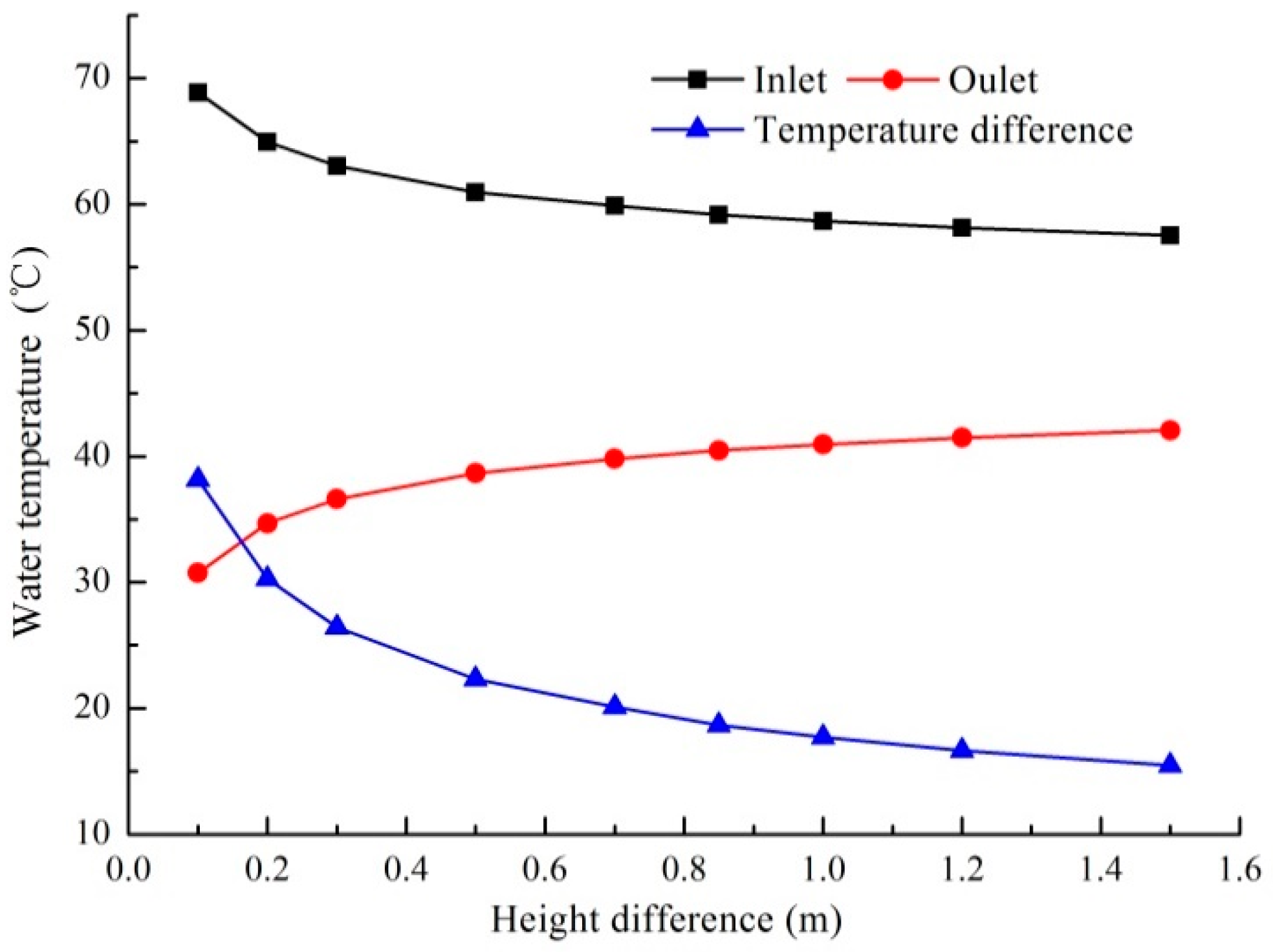
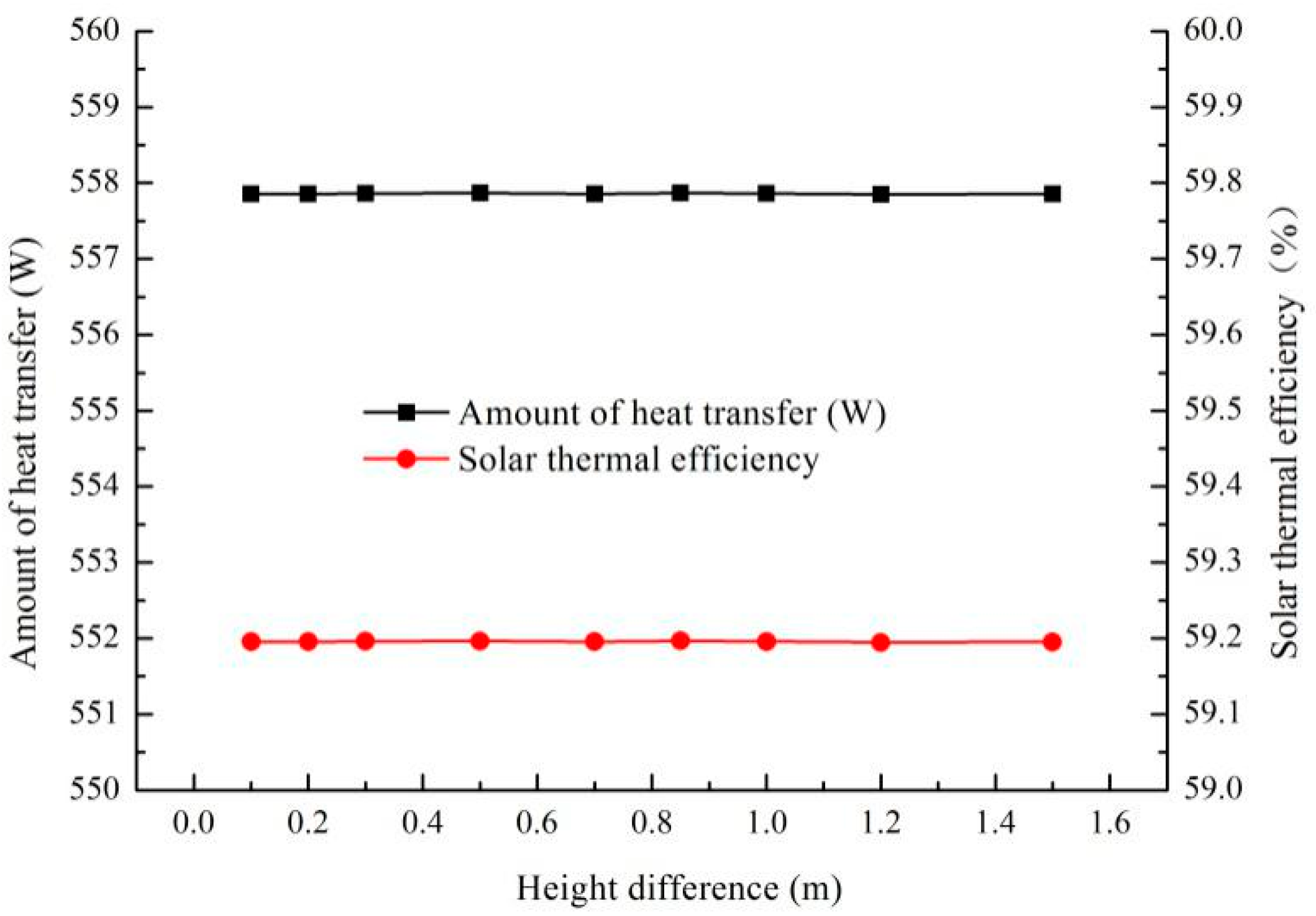
5.2. Effect of the Height Difference between the Thermal Radiation Plate Center and Solar Collector Center
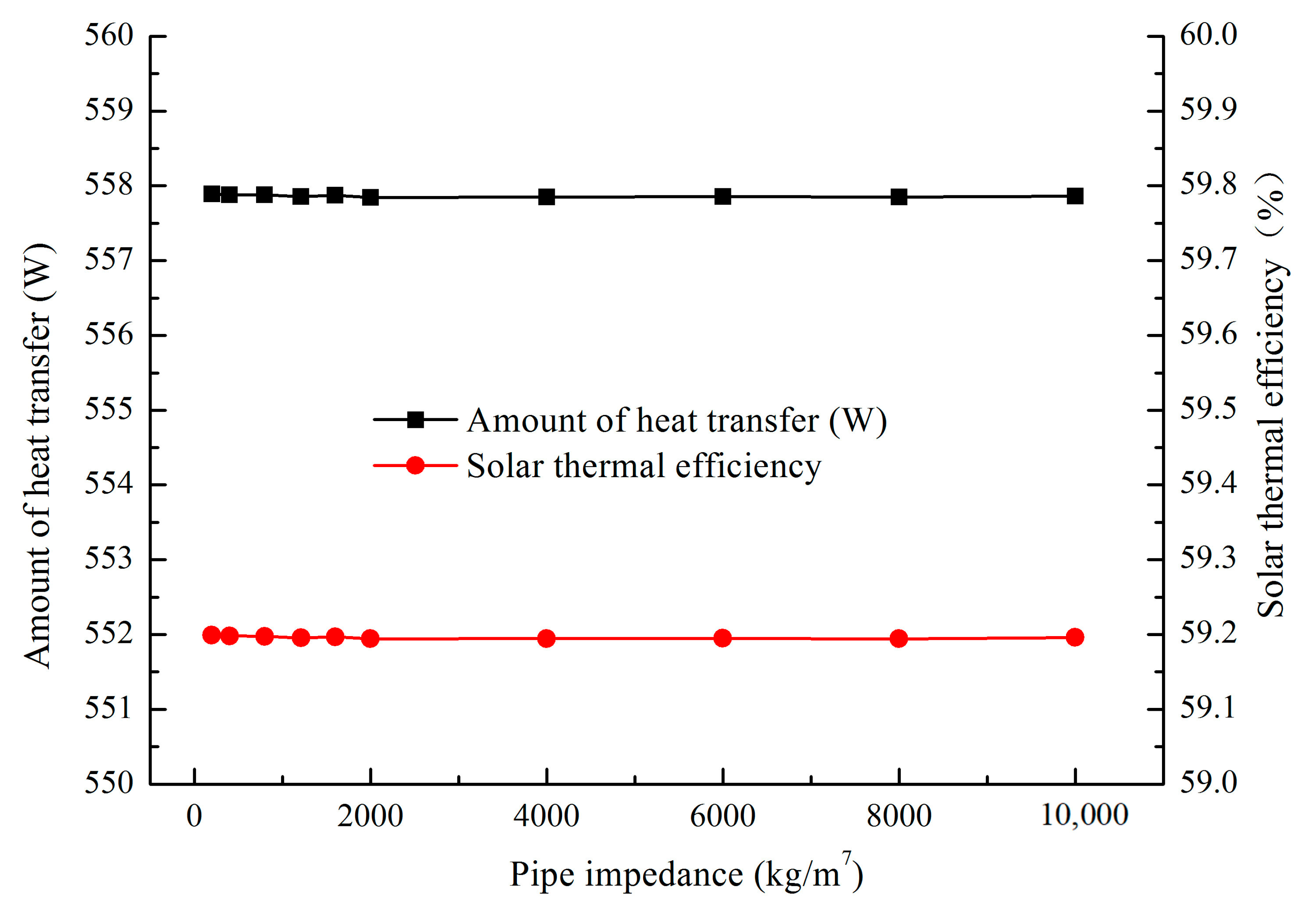
5.3. Effect of the Pipeline Impedance of the System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Area, m2 |
| c | Heat capacity, J/(kg·K) |
| d | Circulation tube diameter, m |
| F | Radiation angle coefficient |
| f | Friction factor |
| G | Mass flow rate, kg/s |
| g | Gravitational acceleration, m2/s |
| h | Heat transfer coefficient, W/(m2·K) |
| I | Solar radiation illumination, W/m2 |
| k | Thermal conductivity, W/(m·K) |
| L | The length of collector plate, m |
| M | Mass, kg |
| N | The number of glass cover |
| Nu | Nusselt number |
| P | Pressure, Pa |
| Q | Heat flux, W |
| R | Thermal resistance, (m2·K)/W |
| Ra | Rayleigh number |
| S | Pipe impedance, kg/m7 |
| T | Temperature, °C |
| t | Time, s |
| UL | Heat loss coefficient, W/(m2·K) |
| v | Velocity, m/s |
Greek Letters
| τ | Glass cover transmittance |
| α | Absorptivity |
| σ | Stefan Boltzmann constant, W/(m2·K4) |
| ε | Emissivity |
| θ | Incidence angle, ° |
| γ | kinematic viscosity of air, m2/s |
| β | Volumetric expansion coefficient, 1/K |
| Ψ | Thermal diffusivity of air, m2/s |
| δ | Thickness, m |
| ρ | Density, kg/m3 |
| η | Solar heat efficiency of the circulation system |
Subscripts
| a | Air, ambient |
| p | Solar collector plate |
| w | Water |
| g | Glass cover |
| r | Radiation |
| i | Inlet, inside |
| o | Outlet |
| t | Thermal radiation plate |
| j | Non-heated surface |
References
- Tian, Z.; Zhang, X.; Jin, X.; Zhou, X.; Si, B.; Shi, X. Towards adoption of building energy simulation and optimization for passive building design: A survey and a review. Energy Build. 2018, 158, 1306–1316. [Google Scholar] [CrossRef]
- Daigle, Q.; O’Brien, P.G. Heat Generated Using Luminescent Solar Concentrators for Building Energy Applications. Energies 2020, 13, 5574. [Google Scholar] [CrossRef]
- Zarrella, A.; Zecchin, R.; Pasquier, P.; Guzzon, D.; Prataviera, E.; Vivian, J.; De Carli, M.; Emmi, G. Analysis of Retrofit Solutions of a Ground Source Heat Pump System: An Italian Case Study. Energies 2020, 13, 5680. [Google Scholar] [CrossRef]
- Wang, D.; Hu, L.; Du, H.; Liu, Y.; Huang, J.; Xu, Y.; Liu, J. Classification, experimental assessment, modeling methods and evaluation metrics of Trombe walls. Renew. Sustain. Energy Rev. 2020, 124, 178–191. [Google Scholar] [CrossRef]
- Chang, C.; Zhu, N.; Yang, K.; Yang, F. Data and analytics for heating energy consumption of residential buildings: The case of a severe cold climate region of China. Energy Build. 2018, 172, 104–115. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, Q.; Tian, Z.; He, B.-J.; Jin, G. A comprehensive analysis on definitions, development, and policies of nearly zero energy buildings in China. Renew. Sustain. Energy Rev. 2019, 114, 109314. [Google Scholar] [CrossRef]
- Omrany, H.; GhaffarianHoseini, A.; GhaffarianHoseini, A.; Raahemifar, K.; Tookey, J. Application of passive wall systems for improving the energy efficiency in buildings: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 62, 1252–1269. [Google Scholar] [CrossRef]
- Ali, I.; Shafiullah, G.; Urmee, T. A preliminary feasibility of roof-mounted solar PV systems in the Maldives. Renew. Sustain. Energy Rev. 2018, 83, 18–32. [Google Scholar] [CrossRef]
- Brito, M.; Freitas, S.; Guimarães, S.; Catita, C.; Redweik, P. The importance of facades for the solar PV potential of a Mediterranean city using LiDAR data. Renew. Energy 2017, 111, 85–94. [Google Scholar] [CrossRef]
- Liang, R.; Wang, P.; Zhou, C.; Pan, Q.; Riaz, A.; Zhang, J. Thermal performance study of an active solar building façade with specific PV/T hybrid modules. Energy 2020, 191, 116532. [Google Scholar] [CrossRef]
- Yu, B.; Liu, X.; Li, N.; Liu, S.; Ji, J. The performance analysis of a purified PV/T-Trombe wall based on thermal catalytic oxidation process in winter. Energy Convers. Manag. 2020, 203, 112262. [Google Scholar] [CrossRef]
- Hu, Z.; He, W.; Ji, J.; Hu, D.; Lv, S.; Chen, H.; Shen, Z. Comparative study on the annual performance of three types of building integrated photovoltaic (BIPV) Trombe wall system. Appl. Energy 2017, 194, 81–93. [Google Scholar] [CrossRef]
- Briga-Sá, A.; Boaventura-Cunha, J.; Lanzinha, J.C.G.; Paiva, A. An experimental analysis of the Trombe wall temperature fluctuations for high range climate conditions: Influence of ventilation openings and shading devices. Energy Build. 2017, 138, 546–558. [Google Scholar] [CrossRef]
- Hu, Z.; He, W.; Hong, X.; Ji, J.; Shen, Z. Numerical analysis on the cooling performance of a ventilated Trombe wall combined with venetian blinds in an office building. Energy Build. 2016, 126, 14–27. [Google Scholar] [CrossRef]
- Abbassi, F.; Dehmani, L. Experimental and numerical study on thermal performance of an unvented Trombe wall associated with internal thermal fins. Energy Build. 2015, 105, 119–128. [Google Scholar] [CrossRef]
- Chen, W.; Liu, W. Numerical analysis of heat transfer in a passive solar composite wall with porous absorber. Appl. Therm. Eng. 2008, 28, 1251–1258. [Google Scholar] [CrossRef]
- Chen, W.; Liu, W. Numerical analysis of heat transfer in a composite wall solar-collector system with a porous absorber. Appl. Energy 2004, 78, 137–149. [Google Scholar] [CrossRef]
- Zhu, N.; Li, S.; Hu, P.; Lei, F.; Deng, R. Numerical investigations on performance of phase change material Trombe wall in building. Energy 2019, 187, 116057. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Design Optimization of a Composite Solar Wall Integrating a PCM in a Individual House: Heating Demand and Thermal Comfort Considerations. Energies 2020, 13, 5640. [Google Scholar] [CrossRef]
- Pasquay, T. Natural ventilation in high-rise buildings with double facades, saving or waste of energy. Energy Build. 2004, 36, 381–389. [Google Scholar] [CrossRef]
- Chan, A.; Chow, T.; Fong, K.; Lin, Z. Investigation on energy performance of double skin façade in Hong Kong. Energy Build. 2009, 41, 1135–1142. [Google Scholar] [CrossRef]
- Su, Z.; Li, X.; Xue, F. Double-skin façade optimization design for different climate zones in China. Sol. Energy 2017, 155, 281–290. [Google Scholar] [CrossRef]
- Lee, K.O.; Medina, M.A.; Raith, E.; Sun, X. Assessing the integration of a thin phase change material (PCM) layer in a residential building wall for heat transfer reduction and management. Appl. Energy 2015, 137, 699–706. [Google Scholar] [CrossRef]
- Radhi, H. Viability of autoclaved aerated concrete walls for the residential sector in the United Arab Emirates. Energy Build. 2011, 43, 2086–2092. [Google Scholar] [CrossRef]
- Shen, C.; Li, X. Energy saving potential of pipe-embedded building envelope utilizing low-temperature hot water in the heating season. Energy Build. 2017, 138, 318–331. [Google Scholar] [CrossRef]
- Ibrahim, M.; Wurtz, E.; Biwole, P.H.; Achard, P. Transferring the south solar energy to the north facade through embedded water pipes. Energy 2014, 78, 834–845. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Z.; Duan, C. A new type of passive solar energy utilization technology—The wall implanted with heat pipes. Energy Build. 2014, 84, 111–116. [Google Scholar] [CrossRef]
- Sakhaei, S.A.; Valipour, M.S. Performance enhancement analysis of The flat plate collectors: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 102, 186–204. [Google Scholar] [CrossRef]
- Shi, Q.; Lv, J.; Guo, C.; Zheng, B. Experimental and simulation analysis of a PV/T system under the pattern of natural circulation. Appl. Therm. Eng. 2017, 121, 828–837. [Google Scholar] [CrossRef]
- Kalogirou, S. Solar Energy Engineering: Processes and Systems; Elsevier/Academic Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Klein, S. Calculation of flat-plate collector loss coefficients. Sol. Energy 1975, 17, 79–80. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook 2016, HVAC Systems and Equipment: American Society of Heating, Refrigerating, and Air-Conditioning Engineers; ASHRAE: Atlanta, GA, USA, 2016. [Google Scholar]



| Material Layers | Thickness (mm) | Length (mm) | Height (mm) | Density kg/m3 | Specific Heat Capacity J/(kg·K) | Thermal Conductivity W/(m·K) |
|---|---|---|---|---|---|---|
| Glass cover | 5 | 2000 | 2000 | 2500 | 840 | 0.76 |
| Air interlayer | 50 | 2000 | 2000 | 1.205 | 1005 | - |
| Solar collector | 2 | 2000 | 2000 | 2719 | 871 | 202.4 |
| Massive wall | 80 | 2000 | 2300 | 50 | 1380 | 0.037 |
| Copper pipe | 8 | 8 | 2000 | 8978 | 381 | 387.6 |
| Thermal radiation plate | 2 | 2000 | 1500 | 2719 | 871 | 202.4 |
| Test Parameters | Test Instrument | Type | Accuracy |
|---|---|---|---|
| Solar radiation intensity | Solar pyrometer | TBQ-2 | ≤0.2% |
| Temperature | Thermocouple | Ni-Cr and Ni-Si | ≤0.2% |
| Data acquisition unit | XSR-70 A | ≤0.2% | |
| Air velocity | Multi-parameter ventilator | TSI-9555 A | ±0.015 m/s |
| Water flow | Water meter | LXS | ±2% |
| Rotameter | LZB-15 | ±1.5% | |
| Differential pressure | U-tube liquid pressure gauge | BYY-100 | ±2.5% |
| Water Flow (m3/s) | Differential Pressure (Pa) | Pipe Impedance (kg/m7) |
|---|---|---|
| 3.5 × 10−3 | 1.2 × 10−2 | 980.2 |
| 3.8 × 10−3 | 1.5 × 10−2 | 1038.8 |
| 4.3 × 10−3 | 2.2 × 10−2 | 1189.8 |
| 7.6 × 10−3 | 6.9 × 10−2 | 1211.2 |
| 9.9 × 10−3 | 13.3 × 10−2 | 1359.9 |
| 12.7 × 10−2 | 21.4 × 10−2 | 1486.1 |
| Variable | T | v | I | Qv | ΔP | ρ | G | S | η |
|---|---|---|---|---|---|---|---|---|---|
| Ur | 0.08% | 1.70% | 1.82% | 3.24% | 2.04% | 1.02% | 2.98% | 6.47% | 3.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Li, N.; Lu, J.; A, Y. Heating Performance of Solar Building Integrated Wall under Natural Circulation. Energies 2020, 13, 6288. https://doi.org/10.3390/en13236288
Shen X, Li N, Lu J, A Y. Heating Performance of Solar Building Integrated Wall under Natural Circulation. Energies. 2020; 13(23):6288. https://doi.org/10.3390/en13236288
Chicago/Turabian StyleShen, Xiaohang, Nianping Li, Jiao Lu, and Yongga A. 2020. "Heating Performance of Solar Building Integrated Wall under Natural Circulation" Energies 13, no. 23: 6288. https://doi.org/10.3390/en13236288
APA StyleShen, X., Li, N., Lu, J., & A, Y. (2020). Heating Performance of Solar Building Integrated Wall under Natural Circulation. Energies, 13(23), 6288. https://doi.org/10.3390/en13236288





