An Exact Algorithm for the Optimal Chiller Loading Problem and Its Application to the Optimal Chiller Sequencing Problem

Abstract

The optimal management of multiple chiller systems calls for the solution of the so-called optimal chiller loading (OCL) problem. Due to the interplay of continuous and logical constraints, OCL is an NP-hard problem, so that a variety of heuristic algorithms have been proposed in the literature. Herein, an algorithm for its exact solution, named X-OCL, is developed under the assumption that the chillers’ power consumption curves are quadratic. The proposed method hinges on a decomposition of the solution space so that the overall OCL problem is decomposed to a set of equality constrained quadratic programming problems that can be solved in closed form. By applying the new X-OCL solver to well known case studies, we assess and compare the performances of several literature algorithms, highlighting also some errors in the published results. Moreover, X-OCL is used to design a greedy optimal chiller sequencing (OCS) solver, called X-OCS. The X-OCS is tested on two literature benchmarks and on the model of the heating, ventilation and air-conditioning (HVAC) system of a semiconductor plant, over a two-year period. The performances of X-OCS are remarkably close to the theoretical optimal performance.

1. Introduction

Heating, ventilation and air-conditioning (HVAC) systems typically utilize a large percentage of the total building energy consumption, amounting to approximately 25–30% for dwellings [1] and up to more than 50% in industries relying on clean-rooms [2]. Between 40% and 60% of this requirement is due to chillers, which are therefore responsible for a significant fraction of total energy use. Such numbers indicate that the efficiency of HVAC systems is closely dependent on the efficiency of the chiller unit. Since a multiple chiller system typically employs machines, there are usually several combinations of chillers’ part loads that are able to satisfy the load demand. The problem of determining the load fraction that each chiller has to deliver in order to minimize the system power consumption is known as optimal chiller loading (OCL) problem. In the last decade, several methods have been proposed to solve the OCL problem [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Chang et al. [3] assume that the chillers’ efficiency is a quadratic function of the partialization and maximize the sum of chillers’ coefficients of performance (COP) using the Lagrangian method. Of course, maximizing the sum of the efficiencies is not equivalent to the “canonical” OCL problem, where system power consumption is instead minimized. In a second paper, Chang [4] has addressed the canonical OCL problem again by the Langrangian multipliers methods, assuming that all the chiller power consumption curves are convex and cubic in the part load ratio. The poor convergence properties of the lambda iteration at low cooling load demand were obviated by a suitable gradient method.

Nevertheless, it is well-known that the chillers’ power consumption could be a concave function, which makes OCL an NP-hard mixed-integer problem and poses a further challenge to the search of the optimal solution as global convergence of iterative methods cannot be guaranteed. This has motivated the development of several heuristic methods which do not guarantee optimality, but are effective to obtain a fair solution in a viable execution time.

Assuming quadratic models of power consumption, Geem [5] resorts to the generalized reduced gradient (GRG) method. Salari et al. [6] show that the mixed integer problem can be solved using the general algebraic modeling system (GAMS). In parallel, many nature-inspired heuristic algorithms have been proposed, namely, genetic algorithm (GA) [7,8], simulated annealing (SA) [9,10], particle swarm optimization (PSO) [11,12], evolution strategy (ES) [13], differential evolution (DE) [14], cuckoo search algorithm using differential operator (DCSA) [15], differential search (DS) [16], improved firefly algorithm (IFA) [17], teaching-learning-based optimization (TLBO) [18], improved invasive weed optimization (EIWO) [19], distributed chaotic estimation of distribution algorithm (DCEDA) [20], imperialist competitive algorithm (ICA) [21] and wild goat’s algorithm (WGA) [22].

Many of these algorithms have been tested on the Hsinchu benchmark, a widely used case study consisting of a six-chiller system installed in a semiconductor factory located in the Hsinchu Scientic Garden (Taiwan). Hence, it is therefore natural to use the performances achieved on this benchmark to compare and rank alternative solution methods. A selection consisting of the six best algorithms is reported in

Table 1. Comparison of the results of IFA, DCSA, GAMS, TLBO, EIWO and DCEDA on Hsinchu benchmark.

${\mathit{Q}}_{\mathit{load}}$ [kW]	i	IFA (2013)		DCSA (2014)		GAMS (2015)		TLBO (2017)		EIWO (2018)		DCEDA (2020)
		${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]
$\mathbf{6858}(\mathbf{90}\%)$	1	0.812774	-	0.812726	-	0.8127	808.9736	0.8186	-	0.8127	-	0.8126	-
	2	0.749527	-	0.749619	-	0.7496	740.7275	0.7523	-	0.7492	-	0.7489	-
	3	1.000000	-	1.000000	-	1.0000	903.3450	1.0000	-	1.0000	-	1.0000	-
	4	1.000000	-	1.000000	-	1.0000	781.4890	1.0000	-	1.0000	-	1.0000	-
	5	1.000000	-	1.000000	-	1.0000	755.2010	1.0000	-	1.0000	-	1.0000	-
	6	0.838603	-	0.838559	-	0.8386	748.8392	0.8297	-	0.8390	-	0.8395	-
	∑		$\mathbf{4738.576}$		$\mathbf{4738.575}$		$\mathbf{4738.5753}$		$\mathbf{4738.54}$		$\mathbf{4738.575}$		$\mathbf{4738.58}$
$\mathbf{6477}(\mathbf{85}\%)$	1	0.727803	-	0.727731	-	0.7277	718.5040	0.727731	-	0.7275	-	0.7280	-
	2	0.656174	-	0.656132	-	0.6561	641.1960	0.656132	-	0.6563	-	0.6564	-
	3	1.000000	-	1.000000	-	1.0000	903.3450	1.000000	-	1.0000	-	1.0000	-
	4	1.000000	-	1.000000	-	1.0000	781.4890	1.000000	-	1.0000	-	1.0000	-
	5	1.000000	-	1.000000	-	1.0000	755.2010	1.000000	-	1.0000	-	1.0000	-
	6	0.716408	-	0.716524	-	0.7165	621.9135	0.716524	-	0.7166	-	0.7160	-
	∑		$\mathbf{4421.649}$		$\mathbf{4421.649}$		$\mathbf{4421.6486}$		$\mathbf{4421.65}$		$\mathbf{4421.649}$		$\mathbf{4421.65}$
$\mathbf{6096}(\mathbf{80}\%)$	1	0.642725	-	0.642735	-	0.6427	639.1411	0.6431	-	0.6427	-	0.6431	-
	2	0.562642	-	0.562645	-	0.5626	553.8955	0.5621	-	0.5628	-	0.5622	-
	3	1.000000	-	1.000000	-	1.0000	903.3450	1.000000	-	1.0000	-	1.0000	-
	4	1.000000	-	1.000000	-	1.0000	781.4890	1.000000	-	1.0000	-	1.0000	-
	5	1.000000	-	1.000000	-	1.0000	755.2010	1.000000	-	1.0000	-	1.0000	-
	6	0.594504	-	0.594490	-	0.5945	510.6347	0.5946	-	0.5944	-	0.5946	-
	∑		$\mathbf{4143.706}$		$\mathbf{4143.706}$		$\mathbf{4143.7064}$		$\mathbf{4143.64}$		$\mathbf{4143.706}$		$\mathbf{4143.71}$
$\mathbf{5717}(\mathbf{75}\%)$	1	0.842218	-	0.843697	-	0.0000	0.0000	0.55765	-	0.0000	-	0.0000	-
	2	0.781365	-	0.783794	-	0.7150	702.4809	0.46918	-	0.7151	-	0.7144	-
	3	0.000002	-	0.000001	-	1.0000	903.3450	0.99995	-	1.0000	-	1.0000	-
	4	0.999995	-	1.000000	-	1.0000	781.4890	1.00000	-	1.0000	-	1.0000	-
	5	1.000000	-	1.000000	-	1.0000	755.2010	1.00000	-	1.0000	-	1.0000	-
	6	0.887053	-	0.883049	-	0.7934	700.0373	0.47250	-	0.7933	-	0.7941	-
	∑		${\mathbf{3840.063} }^{*}$		${\mathbf{3840.055} }^{*}$		$\mathbf{3842.5532}$		$\mathbf{3904.70}$		$\mathbf{3842.553}$		$\mathbf{3843.07}$
$\mathbf{5334}(\mathbf{70}\%)$	1	0.759350	-	0.749969	-	0.0000	0.0000	0.64179	-	0.0000	-	0.0000	-
	2	0.691121	-	0.682477	-	0.5835	572.3074	0.66219	-	0.5834	-	0.5831	-
	3	0.000021	-	0.000012	-	1.0000	903.3450	0.33009	-	1.0000	-	1.0000	-
	4	1.000000	-	1.000000	-	1.0000	781.4890	0.99059	-	1.0000	-	1.0000	-
	5	1.000000	-	1.000000	-	1.0000	755.2010	0.99900	-	1.0000	-	1.0000	-
	6	0.757897	-	0.776363	-	0.6217	534.0950	0.58047	-	0.6218	-	0.6221	-
	∑		${\mathbf{3507.286} }^{*}$		${\mathbf{3507.270} }^{*}$		$\mathbf{3546.4375}$		$\mathbf{3642.51}$		$\mathbf{3546.438}$		$\mathbf{3546.48}$

. In order of publication, they are IFA (2013), DCSA (2014), GAMS (2015), TLBO (2017), EIWO (2018), DCEDA (2020). Two recent algorithms, ICA (2020) and WGA (2020), claim to have improved over the existing literature. However, an inspection of the chillers’ cooling capacities used in these two papers shows that they are different from those of the standard benchmark so that the claim of improvement is void. It is worth noting that, since an exact solver of the Hsinchu benchmark is not available, the final word on the optimality of solutions found by heuristic algorithms still needs to be had.

In the practical management of a real chiller system, solving the OCL is not sufficient, because there exist further dynamic constraints, namely minimum up-time and down-time requirements on chillers’ operation. When these constraints are accounted for, the power consumption minimization problem goes under the name of optimal chiller sequencing (OCS). Again, this is a problem that is hardly tractable without resorting to some heuristics. In particular, the knowledge of all future cooling loads is required, which raises the problem of forecasting it with reasonable accuracy, a task that can be successfully addressed only on a finite prediction horizon. In the literature, OCS solvers resulting from the combination of heuristic OCL algorithms with dynamic programming schemes have been proposed [8,23,24,25].

The present paper addresses both the OCL and OCS problems. Concerning the former one, two main issues are investigated. First of all, we derive an exact algorithm when the chillers’ power consumption is a quadratic function of the partial load ratio (PLR), as it happens for the Hsinchu benchmark. Our X-OCL algorithm allows one to have the final word on the existing heuristic methods, highlighting also some erroneous results reported in the literature. The second issue has to do with the practical applicability of X-OCL to real-world plants. In particular, the execution time is compared with a state-of-art mixed integer solver and the adequacy of the quadratic power consumption model is discussed.

Concerning the OCS problem, we exploit the X-OCL algorithm to derive a lower bound on the minimum power consumption achievable by any OCS solver. Second, a greedy OCS algorithm leveraging on X-OCL is proposed and compared with [23]. Finally, the lower bound is used to quantitatively assess the degree of suboptimality ensuing from the lack of preview implicit in the greedy approach.

Literature benchmarks, i.e., the Hsinchu one and two OCS benchmarks are used for test and comparison. Moreover, an extensive dataset collected during two years in a semiconductor fab is used to build and demonstrate a comprehensive solution of both OCL and OCS, including the data-based estimation of the chillers’ power consumption models. In particular, the potential energy saving with respect with the current HVAC energy management is assessed.

2. The Optimal Chiller Loading Problem

Assuming n chillers operated in parallel, let $Q_i$$,i=1,\dots ,n$, denote the cooling power delivered by the i-th chiller and $P_i$$=P_i\left(Q_i\right),i=1,\dots ,n$ the associated power consumption. For a prescribed overall cooling load demand $Q_{load}$, the goal of the OCL problem is finding the cooling powers $Q_i,i=1,\dots ,n$ that the n chillers have to deliver in order to minimize the system total energy consumption $P_{tot}$:

$$\underset{Q_1,\dots ,Q_n}{min}\sum _{i=1}^n{P}_i\mathrm{s}.\mathrm{t}.Q_{load}=\sum _{i=1}^n{Q}_i$$

For each chiller, PLR (part load ratio) denotes the cooling load fraction, given by

$$PL{R}_i=\frac{Q_i}{Q_{100\%,i}}$$

where $Q_{100\%,i}$ is the maximum power supplied under full capacity operation. The vector of all PLRs is denoted by

$$\mathbf{PLR}={[PL{R}_1,\dots ,PL{R}_n]}^T$$

When the i-th chiller is turned on, it should not operate under a minimum $PLR$, denoted by $PL{R}_{min,i},1$. For the subsequent derivations, it is convenient to introduce a binary variable ${\delta }_i$ that indicates the status of the i-th chiller and a real-valued variable $x_i$, such that:

$$PL{R}_i={\delta }_i·x_i,{\delta }_i\in \{0,1\},x_i\in [PL{R}_{min,i},1]$$

The power consumption $P_i$ of the i-th chiller is assumed to depend mainly on $PL{R}_i$ and the condenser inlet water temperature $T_i$, that is $P_i=P_i(PL{R}_i,T_i)$.

The consumption surface $P_i(PL{R}_i,T_i)$ is either obtained from laboratory experiments or field data collected during operation.

Note that the problem of finding the optimal part load ratios ${\mathbf{PLR}}^{*}$ can be formulated as a mixed-integer nonlinear program (MINLP):

$$\begin{array}{cccc}\hfill {\mathbf{PLR}}^{*}:=& arg\underset{\mathbf{PLR}}{min}\hfill & \hfill & \sum _{i=1}^n{P}_i\left(PL{R}_i\right)\hfill \end{array}$$

(1a)

$$\begin{array}{cccc}& \mathrm{subject} \mathrm{to}\hfill & & \sum _{i=1}^{n}PL{R}_i·Q_{100\%,i}=Q_{load}\hfill \end{array}$$

(1b)

$$\begin{array}{cccc}& & & PL{R}_i={\delta }_i·x_i\hfill \end{array}$$

(1c)

$$\begin{array}{cccc}& & & PL{R}_{min}\le x_i\le 1\hfill \end{array}$$

(1d)

$$\begin{array}{cccc}& & & {\delta }_i\in \{0,1\}\hfill \end{array}$$

(1e)

In the above problem, two types of constraints are present: the cooling demand constraint, Equation (1b) and a set of operational constraints Equation (1c–e) regarding the admissible operating regions of the chillers.

In the following, it is implicitly assumed that the cooling demand constraint is such that the admissible solutions set is nonempty. Then, given that the constraints define a closed set of admissible solution, the cost function admits a minimum.

2.1. Quadratic Power Consumption Model

With the exception of particular structures, mixed-integer programming problems are classified as NP-hard, which means that in the worst case, the solution time grows at least exponentially with the problem size. Although its combinatorial nature might suggest the use of heuristics, we will show that a significant subclass of industrial OCL problems, characterized by a quadratic power consumption model quadratic in $PL{R}_i$, may still be successfully attacked by a carefully designed exact method. It is worth asking whether the quadratic assumption of the power consumption is more or less realistic. We will discuss this point later. Even if the consumption is not quadratic, a good quadratic approximation is likely computable. Moreover, in the case in which it is not easy to workout a good quadratic approximation, it can still be addressed by means piece-wise quadratic model, as suggested in Section 6.

Assumption 1.

The power consumption $P_i$ of the i-th chiller obeys the following model:

$$P_i(PL{R}_i,T_i)=\left\{\begin{array}{cc}{\beta }_{0,i}+{\beta }_{1,i}PL{R}_i+{\beta }_{2,i}PL{R}_i^2+f\left(T_i\right),\hfill & \mathit{if}PL{R}_{min}\le PL{R}_i\le 1\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

(2)

where ${\beta }_{p,i}$ are the model parameters and $f(·)$ is a suitable function. Moreover, it is assumed that ${\beta }_{2,i}\ne 0$.

When the OCL problem is solved in a given time slot, the condenser inlet water temperature $T_i$ can be assumed to be known. Then, for a given $T_i$, in the interval $[PL{R}_{min},1]$, the consumption surface is a quadratic function of $PL{R}_i$ alone:

$$P_i(PL{R}_i,T_i)=\left\{\begin{array}{cc}{a}_i+c_{i}PL{R}_i+q_{i}PL{R}_i^2,\hfill & \mathrm{if}PL{R}_{min}\le PL{R}_i\le 1\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(3)

with $a_i={\beta }_{0,i}+f\left(T_i\right)$, $c_i={\beta }_{1,i}$, and $q_i={\beta }_{2,i}$.

In view of the quadratic nature of the cost function, the system total energy consumption can be expressed in matrix form as follows:

$$\begin{array}{c}\hfill P_{tot}=\sum _{i=1}^n{P}_i=\frac{1}{2}{\mathbf{x}}^T\mathbf{Q}\mathbf{x}+{\mathbf{c}}^T\mathbf{x}+\mathbf{a}\end{array}$$

(4a)

where

$$\begin{array}{cc}\hfill \mathbf{x}& =\left\{PL{R}_i\right\},\mathbf{x}\in {\mathbb{R}}^{n\times 1}\hfill \\ \hfill \mathbf{a}& =\left\{a_i\right\},\mathbf{a}\in {\mathbb{R}}^{n\times 1}\hfill \\ \hfill \mathbf{c}& =\left\{c_i\right\},\mathbf{c}\in {\mathbb{R}}^{n\times 1}\hfill \\ \hfill \mathbf{Q}& =diag\left\{2q_i\right\},\mathbf{Q}\in {\mathbb{R}}^{n\times n}\hfill \end{array}$$

Moreover, the equality constraint (1b) can be rewritten as

$$\begin{array}{c}\hfill \mathbf{E}\mathbf{x}=d\end{array}$$

(4b)

where

$$\begin{array}{cc}\hfill \mathbf{E}& =\left\{Q_{100\%,i}\right\},\mathbf{E}\in {\mathbb{R}}^{1\times n}\hfill \\ \hfill d& =Q_{load},d\in \mathbb{R}\hfill \end{array}$$

Equation (4a,b) represent the standard OCL problem with quadratic power consumption, that so far has been attacked by either mixed integer programming solvers or a variety of heuristic algorithms. Differently from these approaches, below we derive an algorithm that computes the exact solution.

2.2. Partition of the Solution Space

In view of (4), the admissible set $\mathcal{F}$ for $PL{R}_i$ is

$$\begin{array}{ccc}\hfill PL{R}_i& \in & \mathcal{F},\mathcal{F}=\bigcup _{s=0}^3{\mathcal{F}}_{\sigma }\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_0& =& \left\{0\right\},{\mathcal{F}}_1=\left\{PL{R}_{min}\right\},\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_2& =& \left\{1\right\},{\mathcal{F}}_3=(PL{R}_{min},1)\hfill \end{array}$$

(7)

where each subset ${\mathcal{F}}_{\sigma }$ is associated with one of the following operating conditions: switched off ($\sigma =0$), minimum part load ($\sigma =1$), maximum part load ($\sigma =2$), intermediate part load ($\sigma =3$). In the sequel, ${\sigma }_i\in \{0,1,2,3\}$ will denote the state of the $i\text{-}$th chiller.

In order to satisfy the operational constraints of a multiple chiller system, the solution of the OCL problem must be searched within the cartesian product of the chillers’ admissible sets, i.e., 

$$\mathbf{PLR}\in \mathcal{S},\mathcal{S}={\mathcal{F}}^n$$

Since the admissible set $\mathcal{F}$ of a single chiller can be partitioned in four subsets, the overall admissible set $\mathcal{S}$ can be partitioned in $4^n$ subsets ${\mathcal{S}}_j,j=1,\dots ,4^n$, each of which is in a one-to-one correspondence with the $n-$digit multichiller code

$${\mathbf{s}}_j=\left[\begin{array}{ccc}{s}_{j1}& \dots & s_{jn}\end{array}\right],s_{ji}\in \{0,1,2,3\}$$

formed by the state codes ${\sigma }_i,i=1,\dots ,n$, of the n chillers.

To make an example, consider the case of $n=3$ chillers. Then, the possible $4^n=64$ subsets ${\mathcal{S}}_j$ are associated to the multi-chiller codes as follows:

$$\begin{array}{ccc}\hfill {\mathcal{S}}_1& =& {\mathcal{F}}_0\times {\mathcal{F}}_0\times {\mathcal{F}}_0\leftrightarrow {\mathbf{s}}_1=[0,0,0]\hfill \\ \hfill {\mathcal{S}}_2& =& {\mathcal{F}}_0\times {\mathcal{F}}_0\times {\mathcal{F}}_1\leftrightarrow {\mathbf{s}}_2=[0,0,1]\hfill \\ \hfill {\mathcal{S}}_3& =& {\mathcal{F}}_0\times {\mathcal{F}}_0\times {\mathcal{F}}_2\leftrightarrow {\mathbf{s}}_3=[0,0,2]\hfill \\ \hfill {\mathcal{S}}_4& =& {\mathcal{F}}_0\times {\mathcal{F}}_0\times {\mathcal{F}}_3\leftrightarrow {\mathbf{s}}_4=[0,0,3]\hfill \\ \hfill {\mathcal{S}}_5& =& {\mathcal{F}}_0\times {\mathcal{F}}_1\times {\mathcal{F}}_0\leftrightarrow {\mathbf{s}}_5=[0,1,0]\hfill \\ \hfill {\mathcal{S}}_6& =& {\mathcal{F}}_0\times {\mathcal{F}}_1\times {\mathcal{F}}_1\leftrightarrow {\mathbf{s}}_6=[0,1,1]\hfill \\ \hfill {\mathcal{S}}_7& =& {\mathcal{F}}_0\times {\mathcal{F}}_1\times {\mathcal{F}}_2\leftrightarrow {\mathbf{s}}_7=[0,1,2]\hfill \\ \hfill {\mathcal{S}}_8& =& {\mathcal{F}}_0\times {\mathcal{F}}_1\times {\mathcal{F}}_3\leftrightarrow {\mathbf{s}}_8=[0,1,3]\hfill \\ \hfill {\mathcal{S}}_9& =& {\mathcal{F}}_0\times {\mathcal{F}}_2\times {\mathcal{F}}_0\leftrightarrow {\mathbf{s}}_9=[0,2,0]\hfill \\ \hfill \dots & =& \dots \hfill \\ \hfill {\mathcal{S}}_{64}& =& {\mathcal{F}}_3\times {\mathcal{F}}_3\times {\mathcal{F}}_3\leftrightarrow {\mathbf{s}}_{64}=[3,3,3]\hfill \end{array}$$

The n elements of the set ${\mathcal{S}}_j$ are in a one-to-one correspondence with the chiller number $i,1\le i\le n$. Given the chiller number i, the notation ${\mathcal{S}}_j\left[i\right]$ will denote the operating condition, either a point or a range, of the i-th chiller. For instance, within ${\mathcal{S}}_8$, whose multi-chiller code is ${\mathbf{s}}_8=[0,1,3]$, the three chillers $i=1,2,3$ will operate at the following conditions:    

$$\begin{array}{ccc}\hfill {\mathcal{S}}_8\left[1\right]& =& 0\hfill \\ \hfill {\mathcal{S}}_8\left[2\right]& =& PL{R}_{min}\hfill \\ \hfill {\mathcal{S}}_8\left[3\right]& =& (PL{R}_{min},1)\hfill \end{array}$$

2.3. Divide and Conquer Strategy

For $j=1,\dots ,4^n$, let $\mathbf{QP}\left(j\right)$ indicate the OCL problem (4) restricted to the subset ${\mathcal{S}}_j$.

Problem 1.

$\mathbf{QP}\left(j\right)$

$$\begin{array}{ccc}\underset{\mathbf{PLR}\in {\mathcal{S}}_j}{min}\hfill & \hfill & \sum _{i=1}^n{P}_i\left(PL{R}_i\right)\hfill \end{array}$$

(8a)

$$\begin{array}{ccc}\mathrm{subject} \mathrm{to}\hfill & & \sum _{i=1}^{n}PL{R}_i·Q_{100\%,i}=Q_{load}\hfill \end{array}$$

(8b)

The $4^n$ problems $\mathbf{QP}\left(j\right)$ can be partitioned in two subsets, $\mathcal{C}$ and $\overline{\mathcal{C}}$:

-

$\mathcal{C}=\{j\mid s_{ji}\ne 3,\forall i\}$: all the partial load ratios are fixed so that ${\mathcal{S}}_j$ has cardinality one;

-

$\overline{\mathcal{C}}$, when there is at least one chiller operating at intermediate part load ($\exists i:s_{ji}=3$).

Consider, for example, ${\mathcal{S}}_7$, whose multi-chiller code is ${\mathbf{s}}_{\mathbf{7}}=[0,1,2]$: chiller #1 is switched off, chiller #2 is operating at minimum part load, and chiller #3 is operating at maximum part load. Within this subset, no optimization is actually needed because all the chillers’ $PLR$s are fixed and

$${\mathcal{S}}_7={\left[\begin{array}{ccc}0& PL{R}_{min}& 1\end{array}\right]}^T$$

has cardinality one. Therefore, only a feasibility check is required: if constraint (8b) is satisfied, then ${\mathcal{S}}_7$ is the optimal solution of $\mathbf{QP}\left(7\right)$. Otherwise, $\mathbf{QP}\left(7\right)$ does not admit a solution. It is easy to see that the number of elements of the subset $\mathcal{C}$ is $3^n$.

As a second example, consider ${\mathcal{S}}_8$, whose multichiller code is ${\mathbf{s}}_{\mathbf{8}}=[0,1,3]$: here, the chiller #3 is operating at intermediate part load, i.e.

$${\mathcal{S}}_8=\left\{\begin{array}{ccc}\mathbf{PLR}& |& \mathbf{PLR}={\left[\begin{array}{ccc}0& PL{R}_{min}& x_3\end{array}\right]}^T\end{array}\right\}$$

with $x_3\in {\mathcal{F}}_3$. In this case, $\mathbf{QP}\left(8\right)$ is a constrained quadratic programming problem in the unknown $x_3$.

As will be shown later, for $j\in \overline{\mathcal{C}}$, the $\mathbf{QP}\left(j\right)$ problems enjoy a remarkable property: their optimal solution, if it exists, is a critical point and no more than one critical point exists. In the following, ${\mathbf{PLR}}^{*}\left(j\right)$ will denote:

• the optimal solution of $\mathbf{QP}\left(j\right)$, if $j\in \mathcal{C}$;
• the unique feasible critical point of $\mathbf{QP}\left(j\right)$, if $j\in \overline{\mathcal{C}}$.

Let $\mathcal{A}$ denote the set of integers j s.t. ${\mathbf{PLR}}^{*}\left(j\right)$ exists. The associated value of the cost function will be denoted by

$$P_{tot}^{*}\left(j\right):=\sum _{i=1}^n{P}_i\left(PL{R}_i^{*}\left(j\right)\right)$$

(9)

Then, the key idea is to exploit the partition of the solution space by a two-step procedure:

• Solve $\mathbf{QP}\left(j\right)$, obtaining ${\mathbf{PLR}}^{*}\left(j\right)$ and $P_{tot}^{*}\left(j\right)$ for $j=1,\dots ,4^n$;
• Letting

  $$j^{*}=arg\underset{j\in \mathcal{A}}{min}{P}_{tot}^{*}\left(j\right)$$

  where obtain the globally optimal part load vector as ${\mathbf{PLR}}^{*}={\mathbf{PLR}}^{*}\left(j^{*}\right)$.

In the next subsection, it is shown how to reduce the inequality-constrained problems associated with $j\in \overline{\mathcal{C}}$ to equality-constrained quadratic problems (EQP), for which a closed form solution is available.

2.4. Reduction to Equality-Constrained Problems

For a given $j\in \overline{\mathcal{C}}$, we denote by ${\mathcal{V}}_j=\{i\in \{1,2,\dots ,n\}\mid s_{ji}=3\}$ the set of chillers operating at intermediate part loads, i.e., between $PL{R}_{min}$ and 1. We also let $\kappa \left(j\right)$ denote the cardinality of ${\mathcal{V}}_j$. It is then possible to rewrite $\mathbf{QP}\left(j\right)$ as a reduced-order quadratic problem in the $\kappa \left(j\right)\le n$ unknowns $PL{R}_i,i\in {\mathcal{V}}_j$.

$$\begin{array}{ccc}\underset{PL{R}_i,i\in {\mathcal{V}}_j}{min}\hfill & \hfill & \sum _{i\in {\mathcal{V}}_j}{P}_i\left(PL{R}_i\right)\hfill \end{array}$$

(10a)

$$\begin{array}{ccc}\mathrm{subject} \mathrm{to}\hfill & & \sum _{i\in {\mathcal{V}}_j}PL{R}_i·Q_{100\%,i}={\tilde{Q}}_{load}\hfill \end{array}$$

(10b)

$$\begin{array}{ccc}& & PL{R}_{min}<PL{R}_i<1,\forall i\in {\mathcal{V}}_j\hfill \end{array}$$

(10c)

above, ${\tilde{Q}}_{Load}$ is

$${\tilde{Q}}_{Load}=Q_{Load}-\sum _{i\in \overline{{\mathcal{V}}_j}}^{}PL{R}_i·Q_{100\%,i}$$

(11)

is the cooling load that must be supplied by the chillers operating at intermediate part loads.

Now, we associate to each $\mathbf{QP}\left(j\right)$ the corresponding equality-constrained quadratic problem $\mathbf{EQP}\left(j\right)$, that is obtained by removing the inequality constraints (10c).

Problem 2.

$\mathbf{EQP}\left(j\right)$

$$\begin{array}{ccc}\underset{PL{R}_i,i\in {\mathcal{V}}_j}{min}\hfill & \hfill & \sum _{i\in {\mathcal{V}}_j}{P}_i\left(PL{R}_i\right)\hfill \end{array}$$

(12a)

$$\begin{array}{ccc}\mathrm{subject} \mathrm{to}\hfill & & \sum _{i\in {\mathcal{V}}_j}PL{R}_i·Q_{100\%,i}={\tilde{Q}}_{load}\hfill \end{array}$$

(12b)

It is convenient to rewrite $\mathbf{EQP}\left(j\right)$ in matrix form. For this purpose, we introduce a selection matrix $\mathbf{M}\left({\mathcal{V}}_j\right)\in {\mathbb{R}}^{\kappa \left(j\right)\times n}$ that selects $\kappa \left(j\right)$ elements out of n.

Note that, being integers, the elements of ${\mathcal{V}}_j$ admit an obvious ordering. Then,

$$\mathbf{M}\left({\mathcal{V}}_j\right)={\left[M\right]}_{k,i}=\left\{\begin{array}{c}1\mathrm{if}i=k\text{-}\mathrm{th}\mathrm{element}\mathrm{of}{\mathcal{V}}_j\hfill \\ 0\mathrm{otherwise}\hfill \end{array}\right.$$

In short, $\mathbf{M}\left({\mathcal{V}}_j\right)$ will be denoted by ${\mathbf{M}}_j$. The reduced-order matrices are thus given by:

$$\begin{array}{cc}\hfill \tilde{\mathbf{Q}}& ={\mathbf{M}}_j\mathbf{Q}{\mathbf{M}}_j^T,\tilde{\mathbf{Q}}\in {\mathbb{R}}^{\kappa \times \kappa }\hfill \\ \hfill \tilde{\mathbf{E}}& =\mathbf{E}{\mathbf{M}}_j^T,\tilde{\mathbf{E}}\in {\mathbb{R}}^{1\times \kappa }\hfill \\ \hfill \tilde{\mathbf{c}}& ={\mathbf{M}}_j\mathbf{c},\tilde{\mathbf{c}}\in {\mathbb{R}}^{\kappa \times 1}\hfill \\ \hfill \tilde{d}& ={\tilde{Q}}_{Load}\hfill \end{array}$$

(13)

Then, $\mathbf{EQP}\left(j\right)$ can be restated as:

$$\begin{array}{cc}\hfill {\tilde{\mathbf{x}}}^{*}\left(j\right):=arg& \underset{\tilde{\mathbf{x}}}{min}\frac{1}{2}{\tilde{\mathbf{x}}}^T\tilde{\mathbf{Q}}\tilde{\mathbf{x}}+{\tilde{\mathbf{c}}}^T\tilde{\mathbf{x}},\tilde{\mathbf{x}}\in {\mathbb{R}}^{\kappa \times 1}\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \tilde{\mathbf{E}}\tilde{\mathbf{x}}=\tilde{d}\hfill \end{array}$$

(14b)

By applying the first-order Karush–Kuhn–Tucker (KKT) necessary condition to the EQP$\left(j\right)$ problem, the following linear system is obtained:

$$\left[\begin{array}{cc}\tilde{\mathbf{Q}}& {\tilde{\mathbf{E}}}^T\\ \tilde{\mathbf{E}}& 0\end{array}\right]\left[\begin{array}{c}{\tilde{\mathbf{x}}}^{*}\\ {\lambda }^{*}\end{array}\right]=\left[\begin{array}{c}-\tilde{\mathbf{c}}\\ \tilde{d}\end{array}\right]$$

(15)

where ${\tilde{\mathbf{x}}}^{*}$ identifies a critical point, either maximum, minimum or saddle, and ${\lambda }^{*}\in \mathbb{R}$ is the associated Lagrange multiplier. In order to guarantee the existence of the solution, a technical assumption is introduced.

Assumption 2.

$\tilde{\mathbf{E}}{\tilde{\mathbf{Q}}}^{-1}{\tilde{\mathbf{E}}}^T\ne 0$.

Note that Assumption 2 is immediately satisfied if $q_i>0,\forall i$, that is when the quadratic power consumption curves (3) are all convex, although this is not necessary.

Theorem 1.

Under Assumption 1, $\mathbf{EQP}\left(j\right)$ admits a unique critical point ${\mathbf{x}}^{*}$, given by

$$\begin{array}{ccc}\hfill {\lambda }^{*}& =& -\frac{\tilde{d}+\tilde{\mathit{E}}{\tilde{\mathit{Q}}}^{-1}\tilde{\mathit{c}}}{\tilde{\mathit{E}}{\tilde{\mathit{Q}}}^{-1}{\tilde{\mathit{E}}}^T}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\tilde{\mathit{x}}}^{*}& =& -{\tilde{\mathit{Q}}}^{-1}(\tilde{\mathit{c}}+{\tilde{\mathit{E}}}^T{\lambda }^{*})\hfill \end{array}$$

(17)

Proof of Theorem 1.

In view of Assumption 1, $det\left(\mathbf{Q}\right)\ne 0$, because $q_i\ne 0,\forall i$. Moreover, Assumption 2 guarantees that $\tilde{\mathbf{E}}{\tilde{\mathbf{Q}}}^{-1}{\tilde{\mathbf{E}}}^T\ne 0$. Then, it is immediate to see that the KKT condition (15) admits (16)–(17) as a unique solution. □

Given the critical point ${\tilde{\mathbf{x}}}^{*}$, it is easy to obtain a critical point for $\mathbf{QP}\left(j\right)$, as well. For this purpose, it is convenient to introduce an auxiliary vector $\overline{\mathbf{x}}\in {\mathbb{R}}^{n\times 1}$, such that:

$$\overline{x_i}=\left\{\begin{array}{c}\begin{array}{cc}\hfill {\mathcal{S}}_j\left[i\right],& \mathrm{if}i\in \overline{{\mathcal{V}}_j}\hfill \\ \hfill 0,& \mathrm{otherwise}\hfill \end{array}\hfill \end{array}\right.$$

The candidate critical point for $\mathbf{QP}\left(j\right)$ is thus given by:

$${\widehat{\mathbf{PLR}}}^{*}\left(j\right)=\overline{\mathbf{x}}+{\mathbf{M}}_j^T{\tilde{\mathbf{x}}}^{*}$$

(18)

The keystone of the solution procedure is the connection between the critical points of $\mathbf{QP}\left(j\right)$ and $\mathbf{EQP}\left(j\right)$, as stated in the following theorem.

Theorem 2.

The critical point ${\mathbf{PLR}}^{*}\left(j\right)$ exists if ${\widehat{\mathbf{PLR}}}^{*}\left(j\right)\in {\mathcal{S}}_j$. In such a case, ${\mathbf{PLR}}^{*}\left(j\right)={\widehat{\mathbf{PLR}}}^{*}\left(j\right)$.

Proof of Theorem 2.

Sufficiency. Assume that the critical point ${\widehat{\mathbf{PLR}}}^{*}$ for EQP(j) belongs to ${\mathcal{S}}_j$. Observe that EQP(j) has less contraints than QP(j). Therefore, if a critical point for EQP(j) is feasible for QP(j), it is ipso facto a critical point for QP(j), as well.

Necessity. Assume that QP(j) admits a critical point, say ${\mathbf{PLR}}^{*}\left(j\right)$. Given that EQP(j) and QP(j) differ only for strict inequality constraints, any critical point for QP(j) is critical also for EQP(j). Since EQP(j) admits at most one critical point, necessity is proven. □

2.5. Summary of the X-OCL Algorithm

We are now in a position to summarize the steps of the proposed algorithm, hereafter named X-OCL, for the exact solution of the OCL problem.

The partition of the solution set in the $4^n$ subsets ${\mathcal{S}}_j,j=1,\dots 4^n$ allows one to divide the MINLP problem into $4^n$ sub-problems $\mathbf{QP}\left(j\right)$ (8). For each subset ${\mathcal{S}}_j$, two situations can occur:

• all the chillers part load ratios are fixed;
• there is at least one chiller working at intermediate part load.

In the former case, only a feasibility check is required to decide whether the PLR configuration is to be kept as a candidate solution. In the latter case, the solution of the $\mathbf{QP}\left(j\right)$ problem is reduced to the solution of an $\mathbf{EQP}\left(j\right)$ problem that admits a unique critical point, easily computable in closed form. As stated in Theorem 2, if the critical point of $\mathbf{EQP}\left(j\right)$ belongs to ${\mathcal{S}}_j$, it coincides with the critical point of $\mathbf{QP}\left(j\right)$. Otherwise, $\mathbf{QP}\left(j\right)$ does not admit a critical point.

Once all the $\mathbf{QP}\left(j\right)$ have been processed, the corresponding set of critical points $\{{\mathbf{PLR}}^{*}\left(j\right),j=1,\dots ,4^n\}$ include the optimal solution of the overall OCL problem, which can be found just by comparing the associated system power consumptions $P_{tot}^{*}\left(j\right)$. A pseudo-code summary is reported in Algorithm 1.

Algorithm 1: X-OCL.

1: Input:$\mathit{a},\mathit{c},\mathit{q}\in {\mathbb{R}}^{n\times 1}$, $\mathit{s}\in {\mathbb{R}}^{4^n\times n}$, $Q_{load}\in \mathbb{R}$   2: Output:${\mathit{PLR}}^{*},P_{tot}^{*}$   3:      4: for$j=1,\dots ,4^n$do   5:   ${\mathcal{V}}_j=\{i\in \{1,2,\dots ,n\}:s_{ji}=3\}$, $\kappa =|{\mathcal{V}}_j|$    6:   if${\mathcal{V}}_j=\varnothing$ then   7:                                                                                                                       $\{▹$ feasibility check}   8:    all the chillers part load ratios are fixed   9:    $\mathit{x}\leftarrow {\mathcal{S}}_j$ 10:    if ${\sum }_{i=1}^n{x}_i·Q_{100\%,i}=Q_{load}$ then 11:     ${\mathit{PLR}}^{*}\left(j\right)=\mathit{x}$ 12:     $P_{tot}^{*}\left(j\right)={\sum }_{i=1}^n{P}_i\left(PL{R}_i^{*}\left(j\right)\right)$ 13:    else 14:     ${\mathit{PLR}}^{*}\left(j\right)=\varnothing$ 15:     $P_{tot}^{*}\left(j\right)=\varnothing$  16:    end if 17:   else 18:                                                                                   $\{▹$ solve the EQP$\left(j\right)$ associated to QP$\left(j\right)$} 19:    ${\mathcal{V}}_j\Rightarrow \tilde{\mathbf{Q}},\tilde{\mathbf{E}},\tilde{\mathbf{c}},\tilde{d}$   20:    ${\lambda }^{*}=-{\displaystyle \frac{\tilde{d}+\tilde{\mathit{E}}{\tilde{\mathit{Q}}}^{-1}\tilde{\mathit{c}}}{\tilde{\mathit{E}}{\tilde{\mathit{Q}}}^{-1}{\tilde{\mathit{E}}}^T}},{\lambda }^{*}\in \mathbb{R}$   21:    ${\tilde{\mathit{x}}}^{*}=-{\tilde{\mathit{Q}}}^{-1}(\tilde{\mathit{c}}+{\tilde{\mathit{E}}}^T{\lambda }^{*})$   22:    $\overline{\mathit{x}}=\left\{\begin{array}{cc}\hfill {\mathcal{S}}_j\left[i\right],& \mathrm{if}i\in \overline{{\mathcal{V}}_j}\hfill \\ \hfill 0,& \mathrm{otherwise}\hfill \end{array}\right.$   23:    ${\widehat{\mathit{PLR}}}^{*}\left(j\right)=\overline{\mathit{x}}+{\mathit{M}}_j^T{\tilde{\mathit{x}}}^{*}$  24:    if ${\widehat{\mathit{PLR}}}^{*}\left(j\right)\in {\mathcal{S}}_j$ then 25:     ${\mathit{PLR}}^{*}\left(j\right)=\widehat{\mathit{PLR}}\left(j\right)$ 26:     $P_{tot}^{*}\left(j\right)={\sum }_{i=1}^n{P}_i\left(PL{R}_i^{*}\left(j\right)\right)$, 27:    else 28:     ${\mathit{PLR}}^{*}\left(j\right)=\varnothing$ 29:     $P_{tot}^{*}\left(j\right)=\varnothing$  30:    end if 31:   end if 32: end for 33:    34: $j^{*}={min}_j{P}_{tot}\left(j\right)$  35: ${\mathit{PLR}}^{*}={\mathit{PLR}}^{*}\left(j^{*}\right)$ 36: $P_{tot}^{*}=P_{tot}\left(j^{*}\right)$

Summarizing the difference between OCL and OCS is that the former one is a static problem, whereas the second one is intrinsically a dynamic problem. An OCS problem stripped of its dynamic constraints could be solved just as a sequence of OCL problems.

3. Test on Hsinchu Benchmark Model

3.1. Hsinchu Cooling Plant Model

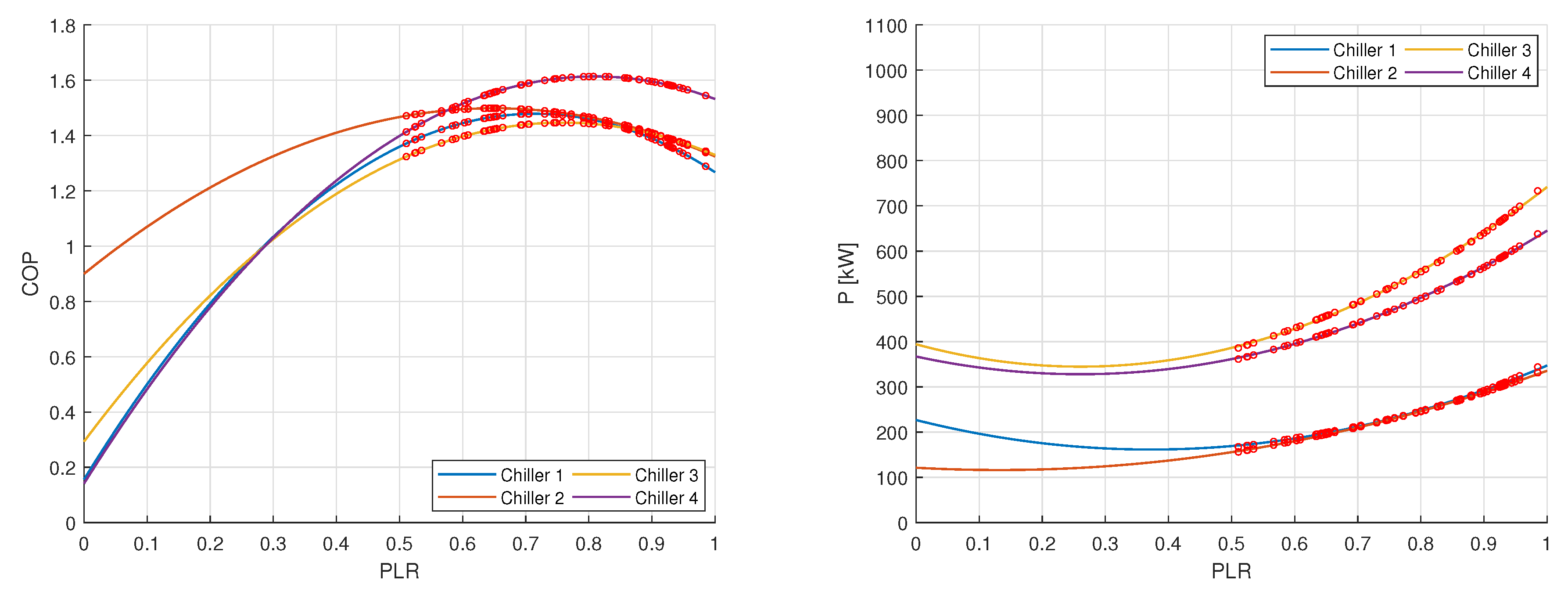
The Hsinchu chiller system, originally described in [7], has become a widely used benchmark for the testing and comparison of OCL algorithms [6,15,17,18,19]. The case study involves six chillers installed in a semiconductor factory located in Hsinchu Scientific Garden (Taiwan) with a 7620 kW total cooling capacity. Quadratic models of the chillers’ energy consumption were obtained and validated from data collected every 5 min over a 5-month period [7]. The benchmark problem assumes that the condenser inlet water temperature is 24.5 ${}^{°}$C. The coefficients of the six chillers’ energy consumption models (3) are reported in [7] (Table 3) and the corresponding P-PLR curves are displayed in Figure 1. It is asked to solve the OCL problem for five different cooling loads, ranging from 70% to 90% of the system total cooling capacity. It is also required that the partial load ratio of each chiller never goes below 0.3. According to our notation, the following parameter settings are used:

-

$a_i,c_i,$ and $q_i$ from [7];

-

$Q_{Load}=90\%,85\%,80\%,75\%$, and $70\%$ of the chillers’ maximum capacity (${\sum }_{i=1}^n{Q}_{nom}$);

-

$PL{R}_{min,i}=0.3,\forall i$.

3.2. OCL Benchmark: Results

The comparison between the X-OCL optimal solution and those obtained by the six literature methods in Table 1 sheds light on some errors in the published results.

For the three highest cooling load demands ($Q_{Load}=\{6858,6477,6096\}$ [kW]), the X-OCL optimal solution coincides with the common solution provided by the six algorithms, thus confirming that they had reached the optimum. In the remaining two cases ($Q_{Load}=5717$ and 5334 [kW]), the solution computed by X-OCL coincides with those of GAMS, EIWO and DCEDA, which, however, are apparently outperformed by IFA and DCSA. The worst performance is that of TLBO.

However, concerning the solution provided by IFA and DCSA, four wrong values of power consumption (identified by asterisks in Table 1) were published in [15,17]:

-

$P_{tot,IFA}$ at load 75% and 70%;

-

$P_{tot,DCSA}$ at load 75% and 70%.

In fact, Table 1 reports $P_{tot,IFA}=P_{tot,DCSA}\approx 3507.3$ [kW] at 70% cooling load, which is inconsistent with the $PL{R}_i$ reported in the same table. Such inconsistency is easily verified by plugging the $PL{R}_i$’s into the chillers’ power consumption Equation (3) in order to obtain the individual chiller power consumptions of the $P_i$ [kW] column (the papers [15,17] describing algorithms IFA and DCSA do not report these individual consumptions). Apparently, the source of the error is the mechanical use of the chiller’s quadratic power consumption model out of its operational range, that is, in correspondence with the null partial load ratio. Obviously, the associated power consumption is null as well, but if the quadratic model has a negative constant term, as is the case for chillers 3–5, the formula will return a negative power consumption as if a turned-off chiller could generate free power.

In

Table 2. Published chillers’ power consumptions and the corresponding corrected values.

${\mathit{Q}}_{\mathit{load}}$ [kW]	i	IFA			DCSA
		${\mathit{PLR}}_{\mathit{i}}[-]$	${\mathit{P}}_{\mathit{p},\mathit{i}}$ [kW]	${\mathit{P}}_{\mathit{c},\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}[-]$	${\mathit{P}}_{\mathit{p},\mathit{i}}$ [kW]	${\mathit{P}}_{\mathit{c},\mathit{i}}$ [kW]
$\mathbf{5717}(\mathbf{75}\%)$	1	0.842218	843.0026	843.0026	0.843697	844.7431	844.7431
	2	0.781365	777.3214	777.3214	0.783794	780.1789	780.1789
	3	0.000002	−120.5019	0.0000	0.000001	−120.5035	0.0000
	4	0.999995	781.4855	781.4855	1.000000	781.4890	781.4890
	5	1.000000	755.2010	755.2010	1.000000	755.2010	755.2010
	6	0.887053	803.5604	803.5604	0.883049	798.9460	798.9460
	∑		$3840.0690$	$3960.5709$		$3840.0545$	$3960.5580$
$\mathbf{5334}(\mathbf{70}\%)$	1	0.759350	750.8680	750.8680	0.749969	741.1047	741.1047
	2	0.691121	677.0164	677.0164	0.682477	668.0074	668.0074
	3	0.000021	−120.4730	0.0000	0.000012	−120.4867	0.0000
	4	1.000000	781.4890	781.4890	1.000000	781.4890	781.4890
	5	1.000000	755.2010	755.2010	1.000000	755.2010	755.2010
	6	0.757897	663.1834	663.1834	0.776363	682.1826	682.1826
	∑		$3507.2848$	$3627.7578$		$3507.4980$	$3627.9847$

, the published chillers’ power consumption $P_{p,i}$ and the corresponding corrected values $P_{c,i}$ are reported for both IFA and DCSA. The values highlighted in red are the unfeasible chillers’ power consumption, of which the correction is reported in column $P_{c,i}$.

Once the errors have been corrected, IFA and DCSA are no more optimal at $75\%$ and $70\%$ loads. At load $75\%$$P_{tot,IFA}$ rises from $3840.0690$ to $3960.5709$ [kW] ($+3.14\%$), while at $70\%$, it rises from $3507.2848$ to $3627.7578$ [kW] ($+3.43\%$). Analogously, for DCSA, $P_{tot,DCSA}$ goes from $3840.0545$ to $3960.5580$ [kW] ($+3.14\%$) at $75\%$ and from $3507.2848$ to $3627.7578$ [kW] ($+3.43\%$) at $70\%$. The corrected results for all the six literature methods are reported in

Table 3. Comparison of the results of IFA, DCSA, GAMS, TLBO, EIWO, DCEDA and X-OCL on Hsinchu benchmark.

${\mathit{Q}}_{\mathit{load}}$ [kW]	i	IFA (2013)		DCSA (2014)		GAMS (2015)		TLBO (2017)		EIWO (2018)		DCEDA (2020)		X-OCL
		${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]	${\mathit{PLR}}_{\mathit{i}}$	${\mathit{P}}_{\mathit{i}}$ [kW]
$\mathbf{6858}(\mathbf{90}\%)$	1	0.812774	809.0541	0.812726	808.9999	0.8127	808.9736	0.8186	815.6654	0.8127	808.9705	0.8126	808.8595	0.8127	809.0002
	2	0.749527	740.6313	0.749619	740.7353	0.7496	740.7275	0.7523	743.7705	0.7492	740.2618	0.7489	739.9230	0.7496	740.7352
	3	1.000000	903.3450	1.000000	903.3450	1.0000	903.3450	1.0000	903.3450	1.0000	903.3450	1.0000	903.3450	1.0000	903.3450
	4	1.000000	781.4890	1.000000	781.4890	1.0000	781.4890	1.0000	781.4890	1.0000	781.4890	1.0000	781.4890	1.0000	781.4890
	5	1.000000	755.2010	1.000000	755.2010	1.0000	755.2010	1.0000	755.2010	1.0000	755.2010	1.0000	755.2010	1.0000	755.2010
	6	0.838603	748.8520	0.838559	748.8035	0.8386	748.8392	0.8297	739.0666	0.8390	749.2903	0.8395	749.8425	0.8386	748.8030
	∑		4738.576		4738.575		4738.5753		4738.54		4738.575		4738.66		4738.5733
$\mathbf{6477}(\mathbf{85}\%)$	1	0.727803	718.5742	0.727731	718.5023	0.7277	718.5040	0.727731	718.5023	0.7275	718.2715	0.7280	718.7731	0.7277	718.5010
	2	0.656174	641.2379	0.656132	641.1959	0.6561	641.1960	0.656132	641.1959	0.6563	641.3638	0.6564	641.4637	0.6561	641.1960
	3	1.000000	903.3450	1.000000	903.3450	1.0000	903.3450	1.000000	903.3450	1.0000	903.3450	1.0000	903.3450	1.0000	903.3450
	4	1.000000	781.4890	1.000000	781.4890	1.0000	781.4890	1.000000	781.4890	1.0000	781.4890	1.0000	781.4890	1.0000	781.4890
	5	1.000000	755.2010	1.000000	755.2010	1.0000	755.2010	1.000000	755.2010	1.0000	755.2010	1.0000	755.2010	1.0000	755.2010
	6	0.716408	621.8000	0.716524	621.9132	0.7165	621.9135	0.716524	621.9132	0.7166	621.9874	0.7160	621.4020	0.7165	621.9136
	∑		4421.649		4421.649		4421.6486		4421.65		4421.649		4421.6739		4421.6466
$\mathbf{6096}(\mathbf{80}\%)$	1	0.642725	639.1269	0.642735	639.1356	0.6427	639.1411	0.6431	639.4526	0.6427	639.1052	0.6431	639.4546	0.6427	639.1359
	2	0.562642	553.8980	0.562645	553.9006	0.5626	553.8955	0.5621	553.4276	0.5628	554.0352	0.5622	553.5144	0.5626	553.9010
	3	1.000000	903.3450	1.000000	903.3450	1.0000	903.3450	1.000000	903.3450	1.0000	903.3450	1.0000	903.3450	1.0000	903.3450
	4	1.000000	781.4890	1.000000	781.4890	1.0000	781.4890	1.000000	781.4890	1.0000	781.4890	1.0000	781.4890	1.0000	781.4890
	5	1.000000	755.2010	1.000000	755.2010	1.0000	755.2010	1.000000	755.2010	1.0000	755.2010	1.0000	755.2010	1.0000	755.2010
	6	0.594504	510.6442	0.594490	510.6324	0.5945	510.6347	0.5946	510.7257	0.5944	510.5561	0.5946	510.7257	0.5945	510.6325
	∑		$\mathbf{4143.706}$		$\mathbf{4143.706}$		$\mathbf{4143.7064}$		$\mathbf{4143.64}$		$\mathbf{4143.706}$		$\mathbf{4143.7297}$		$\mathbf{4143.3704}$
$\mathbf{5717}(\mathbf{75}\%)$	1	0.842218	843.0026	0.843697	844.7431	0.0000	0.0000	0.55765	570.8354	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	2	0.781365	777.3214	0.783794	780.1780	0.7150	702.4809	0.46918	478.8657	0.7151	702.5557	0.5831	701.7987	0.7150	702.4808
	3	0.000002	0.0000	0.000001	0.0000	1.0000	903.3450	0.99995	903.3189	1.0000	903.3450	1.0000	903.3450	1.0000	903.3450
	4	0.999995	781.4855	1.000000	781.4890	1.0000	781.4890	1.00000	781.4890	1.0000	781.4890	1.0000	781.4890	1.0000	781.4890
	5	1.000000	755.2010	1.000000	755.2010	1.0000	755.2010	1.00000	755.2010	1.0000	755.2010	1.0000	755.2010	1.0000	755.2010
	6	0.887053	803.5604	0.883049	798.9460	0.7934	700.0373	0.47250	414.9916	0.7933	699.9229	0.7941	700.7682	0.7934	700.0374
	∑		$\mathbf{3960.579}$		$\mathbf{3960.558}$		$\mathbf{3842.5532}$		$\mathbf{3904.70}$		$\mathbf{3842.553}$		$\mathbf{3842.602}$		$\mathbf{3842.5532}$
$\mathbf{5334}(\mathbf{70}\%)$	1	0.759350	750.8680	0.749969	741.1047	0.0000	0.0000	0.64179	638.3158	0.0000	0.0000	0.000	0.0000	0.0000	0.0000
	2	0.691121	677.0164	0.682477	668.0074	0.5835	572.3074	0.66219	647.2751	0.5834	572.2236	0.5831	571.9545	0.5835	572.3068
	3	0.000021	0.0000	0.000012	0.0000	1.0000	903.3450	0.33009	328.4962	1.0000	903.3450	1.0000	903.3450	1.0000	903.3450
	4	1.000000	781.4890	1.000000	781.4890	1.0000	781.4890	0.99059	774.8702	1.0000	781.4890	1.0000	781.4890	1.0000	781.4890
	5	1.000000	781.2010	1.000000	755.2010	1.0000	755.2010	0.99900	754.7026	1.0000	755.2010	1.0000	755.2010	1.0000	755.2010
	6	0.757897	663.1834	0.776363	682.1826	0.6217	534.0950	0.58047	489.8474	0.6218	534.1803	0.6221	534.4433	0.6217	534.0957
	∑		$\mathbf{3627.758}$		$\mathbf{3627.98}$		$\mathbf{3546.4375}$		$\mathbf{3642.51}$		$\mathbf{3546.438}$		$\mathbf{3546.4327}$		$\mathbf{3546.6437}$

.

In conclusion, on the Hsinchu benchmark, GAMS, EIWO and DCEDA prove to be the best heuristic algorithms, as their solutions coincide with the optimal ones computed by X-OCL, for all considered loads.

4. The Optimal Chiller Sequencing Problem

The cooling load demand of a building can be subject to significant variations during the day. Consequently, solving the OCL problem in each time step t (for example, 20 min), just ignoring minimum up/down time constraints on the chillers, could lead to frequent switchings (chiller startups and shutdowns). In order to preserve chillers from excessive mechanical stress and increase their operating life, each machine should not be switched off before a minimal up-time is reached. Analogously, it should not be switched on too quickly. To comply with these requirements, minimum up/down-time constraints must be enforced in the formulation of the so-called optimal chiller sequencing (OCS) problem. In its full formulation, OCS is a dynamical problem, because, in order to minimize the cumulative power consumption, the current decision should also take into account future constraints. As a consequence, the solution approaches proposed in the literature range from dynamic programming to heuristic methods were designed to alleviate the complexity of the problem.

4.1. A Lower Bound to the OCS Problem

Any solution to the OCS problem must face some level of approximation. Even when dynamic programming is used, there is the necessity of forecasting future loads, which introduces a suboptimality margin with respect to the ideal solution based on perfect knowledge of the future load profile. The availability of an easy-to-compute limit of performance against which the results of heuristic methods can be benchmarked is therefore of interest. In order to derive such a limit, one can consider the relaxed OCS problem (R-OCS), that is, an OCS problem without up- and down-time constraints. The relaxed OCS problem boils down to a sequence of independent OCL problems to be solved at each step in correspondence with the associated load. The availability of an exact OCL solver, such as X-OCS, makes it possible to compute the exact solution of the relaxed OCS as well. Notably, in view of the independence of the OCL problems, what matters is not the load sequence but the load distribution, so that the R-OCS bound could be easily derived based on statistical distributions reflecting different production and weather scenarios.

Such a bound can be used to quantitatively assess the existing margin of improvement for a given heuristic OCS solver. In fact, if the achieved power consumption is close enough to the bound, there is no scope for the search of further improvements. Along this direction, in the following section, the X-OCL solver is used to derive a greedy OCS algorithm, whose performance is then assessed against the R-OCS bound.

4.2. X-OCS, a Greedy Approach to OCS

X-OCS is a greedy algorithm that reduces OCS to a sequence of OCL problems, solvable through X-OCL. The approach is greedy because at each time step, future constraints are ignored, and the optimal OCL solution, compatible with the current minimum up/down time constraint, is searched for. In the mathematical form, the greedy OCS problem can be written as a mixed-integer quadratic problem with linear constraints:

Problem 3.

$\mathbf{greedy}\mathbf{OCS}$

$$\begin{array}{cccc}\hfill {\mathbf{PLR}}^{*}\left(t\right):=& arg\underset{\mathbf{PLR}}{min}\hfill & \hfill & \sum _{i=1}^n{P}_i(PL{R}_i\left(t\right),T_i\left(t\right))\hfill \end{array}$$

(19a)

$$\begin{array}{cccc}& \mathrm{subject} \mathrm{to}\hfill & & \sum _{i=1}^{n}PL{R}_i\left(t\right)·Q_{100\%,i}=Q_{load}\left(t\right)\hfill \end{array}$$

(19b)

$$\begin{array}{cccc}& & & PL{R}_i\left(t\right)={\delta }_i\left(t\right)·x_i\left(t\right)\hfill \end{array}$$

(19c)

$$\begin{array}{cccc}& & & PL{R}_{min}\le x_i\left(t\right)\le 1\hfill \end{array}$$

(19d)

$$\begin{array}{cccc}\hfill & & & (T_i^{ON}(t-1)-MU{T}_i)({\delta }_i\left(t\right)-{\delta }_i(t-1))\le 0\hfill \end{array}$$

(19e)

$$\begin{array}{cccc}\hfill & & & (T_i^{OFF}(t-1)-MD{T}_i)({\delta }_i\left(t\right)-{\delta }_i(t-1))\ge 0\hfill \end{array}$$

(19f)

$$\begin{array}{cccc}& & & {\delta }_i\in \{0,1\}\hfill \end{array}$$

(19g)

where $MU{T}_i$ and $MD{T}_i$ are the i-th chiller’s minimum up-time and minimum down-time limits, expressed in number of time steps. The time counters $T_i^{ON}\left(t\right)$ and $T_i^{OFF}\left(t\right)$ are expressed as:

$$\begin{array}{ccc}\hfill T_i^{ON}\left(t\right)& =& (1+T_i^{ON}(t-1)){\delta }_i\left(t\right)\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill T_i^{OFF}\left(t\right)& =& (1+T_i^{OFF}(t-1))(1-{\delta }_i\left(t\right))\hfill \end{array}$$

(21)

It is easy to observe that the greedy OCS problem is an OCL problem with the two additional constraints (19e–f) which force some chillers to be online/offline depending on their previous states $\delta \left(\tau \right),\tau =t-1,t-2,\dots$.

At each time step t, two situations can occur:

-

all the chillers’ states ${\delta }_i\left(t\right)$ are free, i.e., all the chillers have been online/offline for more time steps than those prescribed by MUT/MDT;

-

there is at least one chiller, say the i-th one, whose state ${\delta }_i\left(t\right)$ is constrained to be online or offline (${\delta }_i\left(t\right)=1$ or ${\delta }_i\left(t\right)=0$) by the MUT or MDT.

Concerning the first case, the minimum up/down-time constraints are not active, therefore the step of the greedy OCS boils down to an OCL problem and its optimal solution can be found by the X-OCL algorithm. In the second case, instead, at each time t, the optimal solution is found by applying the X-OCL algorithm to a suitable subset of the OCL solution space $\mathcal{S}$. At each time step t, the solution space of the greedy OCS is therefore given by:

$$\mathcal{P}\left(t\right)=\{j\in \{1,\dots ,4^n\}\mid s_{j,i}\ne 0,\forall i\in {\mathcal{B}}^{ON}\left(t\right),s_{j,i}=0,\forall i\in {\mathcal{B}}^{OFF}\left(t\right)\}$$

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{B}}^{ON}\left(t\right)& =\{i\in \{1,\dots ,n\}\mid (T_i^{ON}(t-1)-MU{T}_i)<0\}\hfill \\ \hfill {\mathcal{B}}^{OFF}\left(t\right)& =\{i\in \{1,\dots ,n\}\mid (T_i^{OFF}(t-1)-MD{T}_i)<0\}\hfill \end{array}\end{array}$$

are the sets of chillers which must be on and off, respectively.

The idea is to exploit the partitions of the solution space ${\mathcal{P}}_j$ by the typical two-step procedure of X-OCL:

• Solve $\mathbf{QP}\left(j\right)$, obtaining ${\mathbf{PLR}}^{*}\left(j\right)$ and $P_{tot}^{*}\left(j\right)$ for $j\in \mathcal{A}\left(t\right)\cap \mathcal{P}\left(t\right)$;
• Letting

  $$j^{*}=arg\underset{j\in \mathcal{A}\left(t\right)\cap \mathcal{P}\left(t\right)}{min}{P}_{tot}^{*}\left(j\right)$$

  obtain the globally optimal part load vector as ${\mathbf{PLR}}^{*}={\mathbf{PLR}}^{*}\left(j^{*}\right)$.

Herein, $\mathcal{A}\left(t\right)$, which denotes that the set of integers j s.t. ${\mathbf{PLR}}^{*}\left(j\right)$ exists, is a function of t because the load changes with time.

4.3. OCS Simulated Example

In this section, the performance of the X-OCS method is assessed on two case studies taken from the literature [23]. Case study 1 involves a hotel in Taipei with two 450 refrigeration tons (RT) chillers and two 1000 RT chillers, while case study 2, again from the Hsinchu Science Industrial District, features nine 1250 RT chillers. In both cases, chillers are described by their COP-PLR curves, expressed by a second-order polynomial model:

$$CO{P}_i={\alpha }_i+{\beta }_{i}PL{R}_i+{\gamma }_{i}PL{R}_i^2$$

(22)

where ${\alpha }_i$, ${\beta }_i$ and ${\gamma }_i$ are the chiller’s coefficients, reported in

Table A1. Coefficients of chillers’ COP-PLR curves.

Systems	Chiller	${\mathit{\alpha }}_{\mathit{i}}$	${\mathit{\beta }}_{\mathit{i}}$	${\mathit{\gamma }}_{\mathit{i}}$	${\mathit{Q}}_{\mathit{nom}}$
Case 1	1	0.1561	3.9023	−2.5909	450
	2	0.9000	1.8432	−1.4188	450
	3	0.2932	3.0419	−2.0054	1000
	4	0.1415	3.6376	−2.2469	1000
Case 2	1	1.5652	1.8094	−0.9803	1250
	2	1.0519	4.1471	−2.4173	1250
	3	0.5703	3.1602	−2.0912	1250
	4	0.3257	2.3513	−1.4265	1250
	5	0.5438	1.8668	−1.2361	1250
	6	1.5271	1.0634	−0.7238	1250
	7	0.7865	1.8473	−1.1633	1250
	8	0.8499	3.7768	−2.2859	1250
	9	1.1191	1.0228	−0.7542	1250

.

The first step was the identification of quadratic power consumption models (3) using data sampled from the COP-PLR curves. Further details regarding the identification procedure are reported in Appendix A. The coefficients of the quadratic P-PLR curves in Figure 2 are reported in

Table A2. Estimated parameters of chillers’ P-PLR curves.

Systems	Chiller	${\mathit{a}}_{\mathit{i}}$	${\mathit{c}}_{\mathit{i}}$	${\mathit{q}}_{\mathit{i}}$	${\mathit{Q}}_{\mathit{nom}}$
Case 1	1	243.58	−398.01	504.00	450
	2	130.81	−103.53	309.65	450
	3	417.51	−444.57	771.99	1000
	4	383.79	−347.84	611.64	1000
Case 2	1	95.54	321.92	103.60	1250
	2	170.68	41.43	235.46	1250
	3	371.09	−307.99	693.76	1250
	4	477.85	−217.09	733.35	1250
	5	433.17	−186–20	810.89	1250
	6	104.21	358.47	205.50	1250
	7	272.33	116.22	457.96	1250
	8	218.68	−20–94	333.72	1250
	9	191.69	276.56	429.51	1250

.

The aim of both benchmarks is to compute the sequence of chillers’ partializations over one day, assuming 20-min stages, so as to minimize the cumulative power consumption, while satisfying the cooling demand constraint at each stage. The load demand profiles are displayed in Figure 3.

The parameters’ settings were as follows:

-

$PL{R}_{min}=0.5$;

-

$MU{T}_i=3\forall i$;

-

$MD{T}_i=1\forall i$.

Recall that $MU{T}_i=3$ means that the i-th chiller must be on at least 3 consecutive steps before being turned off. Likewise, $MD{T}_i=1$ indicates that the i-th chiller, once turned off, must remain off at least 1 step.

The results obtained via X-OCS were compared with those obtained by dynamic programming, as reported in [23]. Where optimization was carried out under the ideal condition that all future loads are known in advance.

For sake of comparability with DP, the chillers power consumption associated with X-OCS was evaluated by plugging the PLRs computed by X-OCS into the original benchmark’s COP model [23] and not via the approximate quadratic power consumption curves used by X-OCS.

4.4. OCS Benchmark: Results

The results are shown in

Table 4. Case study 1.

$\mathit{Stage}$	$\mathit{Load}$	R-OCS		DP		X-OCS
		$\mathit{kW}$	$\mathit{Chiller}$	$\mathit{kW}$	$\mathit{Chiller}$	$\mathit{kW}$	$\mathit{Chiller}$	$[{\mathit{PLR}}_{\mathbf{1}},{\mathit{PLR}}_{\mathbf{2}},{\mathit{PLR}}_{\mathbf{3}},{\mathit{PLR}}_{\mathbf{4}}]$
1	700	441.13	4	441.15	4	441.13	4	[0.00, 0.00, 0.00, 0.70]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
20	890	556.53	4	556.55	4	556.53	4	[0.00, 0.00, 0.00, 0.89]
21	1100	695.32	4 2	695.56	4 2	695.32	4 2	[0.00, 0.63, 0.00, 0.82]
22	1250	801.66	4 2	801.78	4 2	801.66	4 2	[0.00, 0.73, 0.00, 0.92]
23	1100	695.32	4 2	695.56	4 2	695.32	4 2	[0.00, 0.63, 0,00, 0.82]
24	1000	634.42	4 2	636.73	4 2	634.42	4 2	[0.00, 0.50, 0,00, 0.77]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
28	920	579.96	4	579.98	4	579.96	4	[0.00, 0.00, 0.00, 0.92]
29	1610	1048.59	4 2 1	1048.43	4 2 1	1048.59	4 2 1	[0.75, 0.75, 0.00, 0.94]
30	1650	1081.63	4 3	1082.07	4 2 1	1082.07	4 2 1	[0.76, 0.77, 0.00, 0.96]
31	1670	1096.43	4 3	1099.69	4 2 1	1099.43	4 2 1	[0.77, 0.78, 0.00, 0.97]
32	1700	1118.96	4 3	1122.12	4 2 3	1118.96	4 3	[0.00, 0.00, 0.78, 0.91]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
36	1900	1246.74	4 3 2	1247.61	4 2 3	1246.74	4 3 2	[0.00, 0.67, 0.74, 0.86]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
43	1750	1150.68	4 3 2	1151.60	4 2 3	1150.68	4 2 3	[0.00, 0.61, 0.69, 0.79]
44	1575	1020.82	4 2 1	1030.56	4 3	1020.82	4 2 1	[0.74, 0.73, 0.00, 0.92]
45	1900	1246.81	4 3 2	1250.32	4 3 1	1249.42	4 3 1	[0.70, 0.00, 0.73, 0.85]
46	1790	1175.08	4 3 2	1180.75	4 3 1	1179.56	4 3 1	[0.67, 0.00, 0.69, 0.79]
47	1725	1135.32	4 3 2	1142.76	4 3 1	1135.32	4 3 2	[0.00, 0.50, 0.70, 0.80]
48	1775	1165.89	4 3 2	1166.78	4 3 2	1165.89	4 3 2	[0.00, 0.62, 0.69, 0.80]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
57	1900	1246.75	4 3 2	1247.61	4 3 2	1246.75	4 3 2	[0.00, 0.67, 0.74, 0.86]
58	2100	1385.03	4 3 2 1	1386.08	4 3 2 1	1385.03	4 3 2 1	[0.68, 0.63, 0.70, 0.81]
59	2000	1319.66	4 3 1	1326.20	4 3 2 1	1319.66	4 3 1	[0.73, 0.00, 0.77, 0.90]
60	2100	1385.03	4 3 2 1	1386.08	4 3 2 1	1385.03	4 3 2 1	[0.68, 0.63, 0.70, 0.81]
61	1900	1246.75	4 3 2	1247.61	4 3 2	1246.75	4 3 2	[0.00, 0.67, 0.74, 0.86]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
67	1750	1150.68	4 3 2	1151.60	4 3 2	1150.68	4 3 2	[0.00, 0.61, 0.69, 0.79]
68	1475	948.04	4 2 1	948.08	4 2 1	948.04	4 2 1	[0.71, 0.67, 0.00, 0.85]
69	1200	763.59	4 2	765.20	4 1	765.45	4 1	[0.72, 0.00, 0.00, 0.88]
70	1050	664.47	4 2	671.50	4 1	670.46	4 1	[0.65, 0.00, 0.00, 0.76]
71	1100	695.32	4 2	700.10	4 1	695.32	4 2	[0.00, 0.63, 0.00, 0.82]
72	800	495.80	4	495.82	4	539.23	4 2	[0.00, 0.50, 0.00, 0.57]
$P_{day}$		64,432.56 kW		64,883.84 * kW		64,495.91 kW

and

Table 5. Case study 3.

$\mathit{Stage}$	$\mathit{Load}$	X-OCL		DP		X-OCS
		$\mathit{kW}$	$\mathit{chiller}$	$\mathit{kW}$	$\mathit{Chiller}$	$\mathit{kW}$	$\mathit{Chiller}$	$[{\mathit{PLR}}_{\mathbf{1}},{\mathit{PLR}}_{\mathbf{2}},{\mathit{PLR}}_{\mathbf{3}},{\mathit{PLR}}_{\mathbf{4}},{\mathit{PLR}}_{\mathbf{5}},{\mathit{PLR}}_{\mathbf{6}},{\mathit{PLR}}_{\mathbf{7}},{\mathit{PLR}}_{\mathbf{8}},{\mathit{PLR}}_{\mathbf{9}}]$
1	6210	2899.68	8 6 3 2 1	2899.69	8 6 3 2 1	2899.68	8 6 3 2 1	[1.00 1.00 0.97 0.00 0.00 1.00 0.00 1.00 0.00]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
21	6150	2848.50	8 6 3 2 1	2852.34	8 6 3 2 1	2848.50	8 6 3 2 1	[1.00 1.00 0.92 0.00 0.00 1.00 0.00 1.00 0.00]
22	6280	2974.84	8 6 3 2 1 9	3039.86	8 6 3 2 1 7	2974.84	8 6 3 2 1 9	[1.00 1.00 0.72 0.00 0.00 0.80 0.00 1.00 0.50]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
27	7355	3658.93	8 6 3 2 1 7	3672.69	8 6 3 2 1 7	3658.93	8 6 3 2 1 7	[1.00 1.00 0.93 0.00 0.00 1.00 0.95 1.00 0.00]
28	7520	3768.28	8 6 3 2 1 7 9	3847.81	8 6 3 2 1 7 9	3768.28	8 6 3 2 1 7 9	[1.00 1.00 0.79 0.00 0.00 1.00 0.73 1.00 0.50]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
34	8720	4659.67	8 6 3 2 1 7 9	4659.65	8 6 3 2 1 7 9	4659.67	8 6 3 2 1 7 9	[1.00 1.00 0.98 0.00 0.00 1.00 1.00 1.00 1.00]
35	8910	4791.00	8 6 3 2 1 7 9 4	4891.13	8 6 3 2 1 7 9 4	4791.00	8 6 3 2 1 7 9 4	[1.00 1.00 0.85 0.74 0.00 1.00 0.83 1.00 0.70]
36	9090	4917.89	8 6 3 2 1 7 9 4	5015.07	8 6 3 2 1 7 9 4	4917.89	8 6 3 2 1 7 9 4	[1.00 1.00 0.88 0.77 0.00 1.00 0.87 1.00 0.74]
37	9245	5032.60	8 6 3 2 1 7 9 4	5125.26	8 6 3 2 1 7 9 4	5032.60	8 6 3 2 1 7 9 4	[1.00 1.00 0.91 0.80 0.00 1.00 0.91 1.00 0.78]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
47	9820	5511.19	8 6 3 2 1 7 9 4	5552.25	8 6 3 2 1 7 9 4	5511.19	8 6 3 2 1 7 9 4	[1.00 1.00 1.00 0.90 0.00 1.00 1.00 1.00 0.96]
48	9870	5552.25	8 6 3 2 1 7 9 4 5	5582.17	8 6 3 2 1 7 9 4	5552.25	8 6 3 2 1 7 9 4 5	[1.00 1.00 0.87 0.76 0.67 1.00 0.86 1.00 0.73]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
63	8780	4703.10	8 6 3 2 1 7 9 4	4804.11	8 6 3 2 1 7 9 4	4703.10	8 6 3 2 1 7 9 4	[1.00 1.00 0.83 0.73 0.00 1.00 0.80 1.00 0.66]
64	8555	4511.80	8 6 3 2 1 7 9	4543.81	8 6 3 2 1 7 9	4511.80	8 6 3 2 1 7 9	[1.00 1.00 0.96 0.00 0.00 1.00 1.00 1.00 0.88]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
67	7740	3907.96	8 6 3 2 1 7 9	3985.58	8 6 3 2 1 7 9	3907.96	8 6 3 2 1 7 9	[1.00 1.00 0.81 0.00 0.00 1.00 0.76 1.00 0.62]
68	7455	3728.52	8 6 3 2 1 7 9	3745.20	8 6 3 2 1 7	3728.52	8 6 3 2 1 7 9	[1.00 1.00 0.77 0.00 0.00 0.98 0.71 1.00 0.50]
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
72	6425	3055.91	8 6 3 2 1 9	3115.53	8 6 3 2 1 7	3055.91	8 6 3 2 1 9	[1.00 1.00 0.74 0.00 0.00 0.89 0.00 1.00 0.50]
$P_{day}$		296,440.08 kW		289,525.25 * kW		295,605.88 kW

. In case study 1, the power consumption obtained by the X-OCS method was, at each stage, lower than or equal to that obtained by the DP method. From stage 1 to stage 29, the DP and X-OCS methods selected the same chillers. Since the MUT and MDT constraints were not active, the solutions coincided with the R-OCS ones. At stage 30, the R-OCS solution had chillers 4 and 3 switched on. However, the MUT constraint forced the DP and X-OCS to leave chillers 1 and 2 switched on. The same goes for stage 31. At stage 32, 44 and 59 the X-OCS method performed better than the DP one. Although the chillers were not constrained by minimum up/down time limits, apparently the DP method, as implemented in [23], could not find the global minimum. Notably, the greedy X-OCS method achieves a total electric power consumption (46,495.91 [kW]) which is less than 0.1 % greater than the minimum achievable bound R-OCS (64,432.56 [kW]), meaning that there is no practical margin of improvement left).

In the second case study, the cooling load demand varied slowly over time, so that the MUT and MDT constraints were never active. Therefore, the X-OCS, notwithstanding its greedy nature, attains the best achievable performance bound R-OCS. For the majority of the cooling loads, DP and X-OCS gave the same results, the only exceptions being at stages 22, 48–62, 68–72, where X-OCS performed slightly better. For both the case studies, the cumulative daily power consumptions obtained by DP (marked by asterisks) had been reported incorrectly in [23]:

-

Case study 1: $P_{day}=$ 645,220.08 [kW] instead of 64,883.84 [kW]

-

Case study 2: $P_{day}=$ 298,425.69 [kW] instead of 289,525.25 [kW]

As a matter of fact, the daily power consumption values reported in the paper did not match with the sums of the power consumptions at each step, which we used for the correction.

So far, the performances of alternative methods have been compared on OCL and OCS benchmark problems whose quadratic consumption models were taken from the literature. Moreover, a limited number of loads were considered.

In this section, the feasibility of HVAC efficient management based on the exact solution of the OCL problem is validated against a real-world scenario that includes the estimation of the chillers’ consumption models from the field data.

4.5. Field Data

The study was based on experimental data from a large HVAC system installed in a semiconductor fab located in Austria. The chiller unit is composed by five water-cooled centrifugal chillers, see

Table 6. Estimated parameters of the quadratic power consumption model (2) and corresponding $CV\%$.

Chiller	${\mathit{\beta }}_{0,\mathit{i}}$	${\mathit{\beta }}_{1,\mathit{i}}$	${\mathit{\beta }}_{2,\mathit{i}}$	${\mathit{\beta }}_{3,\mathit{i}}$	${\mathit{Q}}_{\mathit{nom}}$
	($\mathit{CV}\%$)	($\mathit{CV}\%$)	($\mathit{CV}\%$)	($\mathit{CV}\%$)	[kW]
1	49.6367	124.7681	269.5769	3.1950	2700
	(5.24)	(2.50)	(0.82)	(3.21)
2	56.2047	154.9900	278.0211	2.2997	2700
	(11.97)	(7.98)	(2.95)	(8.32)
3	−10.9883	520.3125	−45.1983	−0.3309	2700
	(22.49)	(0.85)	(6.98)	(24.57)
4	−159.0637	112.2988	15.7524	14.1461	2700
	(6.15)	(19.80)	(8.21)	(0.74)
5	46.7748	461.7221	−8.3474	−1.1835	2700
	(27.74)	(1.84)	(79.87)	(47.23)

, connected in parallel, in a constant primary flow chilled water system. Quarter-hourly data were recorded at different working conditions over a period of almost two years, from February 2017 to January 2019. Collected data include: temperatures, PLR, power consumption.

The time series of the cooling load demand is shown in Figure 4.

The chillers were subject to the following operating constraints:

-

$PL{R}_{min}=0.2$;

-

$MU{T}_i=4$ (one hour), $\forall i$;

-

$MD{T}_i=2$ (half an hour), $\forall i$.

4.6. Chiller Energy Consumption Models

The chillers’ power consumption models were estimated using the evaporator cooling capacity $Q_{evap}$ [kW] and the condenser inlet water temperature T [${}^{°}$C], as covariates, and the compressor power consumption data P [kW], as target.

For each chiller, the dataset was randomly partitioned in two subsets: 70% for training and 30% for testing, respectively. The parameters ${\beta }_{p,i}$ of the model (2) were estimated via least squares fitting of the training data, discarding data with $PLR<PL{R}_{min}=0.2$. The values of the estimated parameters ${\beta }_{p,i}$ are reported in Table 6, together with the percentage coefficient of variation, defined as $\mathrm{CV}\%=100\times \mathrm{SE}\left({\beta }_{p,i}\right)/\left|{\beta }_{p,i}\right|$. The cooling capacity $Q_{nom}$ are the nominal values provided by the manufacturer.

In Figure 5, the fitted surfaces $P(PLR,T)$ are displayed against the validation data for each of the five chillers. It is seen that the the quadratic model, in spite of a few outliers that are not uncommon when data are collected in industrial frameworks, predicts the consumptions at different operating conditions well, as also confirmed by the goodness-of-fit (GOF) plots in Figure 6.

The 3-D histogram of the covariates $(Q_{evap},T)$ sketched in Figure 7 shows that T, i.e., the condenser inlet water temperature depicted in Figure 8, is mainly concentrated in a narrow range centered around the setpoint, namely 21.5 ${}^{°}$C. Following what is usually done in the literature benchmarks, one could neglect temperature variations around the set point and solve the OCL and OCS problems using the chillers consumption curves at 21.5 ${}^{°}$C, displayed in Figure 9. However, the inspection of Figure 5 shows that for chiller 4, the power consumption is significantly affected by the temperature, especially in summer. Therefore, differently from other literature studies, OCL and OCS solutions, we computed this based on the complete model $P(PLR,T)$.

4.7. Real HVAC System: Assessment of Potential Savings

The field data were used to perform a retrospective analysis of the efficiency of the HVAC system management. More precisely, starting from the historical decisions and the associated cumulative power consumption, two comparisons were performed for the 2-year OCS problem. First of all, the lower bound R-OCS on the best achievable consumption was computed in order to quantitatively assess the potential improvement margin. Being a lower bound, R-OCS may be overly optimistic, so that it is important to evaluate the performance that can be obtained in practice. This was done by running the X-OCS solver, whose energy consumption could then be compared with the (ideal) R-OCS bound and the historically recorded power consumption.

The cumulative energy consumption recorded during the 2-year monitoring was $1.758\times {10}^6$ [kWh]. This figure can be compared with the R-OCS lower bound, equal to $1.600\times {10}^6$ [kWh]. This means that the potential margin of improvement is not larger than $8.97\%$.

When the X-OCS algorithm was applied, the cumulative energy power consumption was $1.601\times {10}^6$ [kWh]. As a matter of fact, for this HVAC system, the loss of performance due to the suboptimality of the greedy algorithm is definitely negligible (it is less than $0.1\%$). On average, the power saving is $0.157\times {10}^6/(2\times 365\times 24)=8.96$ [kW]. In Figure 10, the difference between the consumption achieved by X-OCS and the lower bound is plotted on a weekly basis. The black and blue lines overlap almost perfectly, so that they cannot be distinguishable.

5. Execution Time

The X-OCL and X-OCS algorithms, coded in Matlab^®, were executed on a standard laptop (Intel(R) i7-7500U dual-core with hyperthreading, RAM 16GB, 2.7 GHz). While no explicit parallelization of the algorithm was implemented, the solution of the $4^n$ QP problems was formulated as a unique algebraic computation using sparse matrices. This means that the algorithm may have benefited from some optimization automatically enforced by the Matlab^® compiler. In order to compare the numerical efficiency, the Hsinchu benchmark was also solved using the CPLEX solver for costrained mixed integer problems as implemented in the GAMS environment, used by [6]. The results concerning the computational times are summarized in

Table 7. Execution times for OCL and OSC benchmarks.

	N${}^{°}$ Chillers	N${}^{°}$ Loads	X-OCL [s]	R-OCS [s]	X-OCS [s]	GAMS [s]
OCL Hsinchu benchmark	6	5	0.110	-	-	1.991
OCS benchmark 1	4	72	-	0.302	0.368	-
OCS benchmark 2	9	72	-	226.77	228.29	-
OCS Field data	5	68,110	-	354.03	573.96	-

.

Concerning the Hsinchu OCL benchmark, the computational cost of X-OCL was negligible ($0.11$ s) and, more importantly, definitely lower than the time ($1.991$ s) spent by GAMS.

Concerning the three OCS benchmarks, in all cases, the X-OCS computation time was larger than that for R-OCS, because the greedy algorithm performs the additional task of looking for solutions that satisfy the up-/down-time constraints.

In the OCS examples, the larger number of loads makes it possible to assess the average computation time per load. For a small number of chillers, the average computation time per load of X-OCS is remarkably small: $0.368/72=5\times {10}^{-3}$ s for OCS benchmark 1 (4 chillers) and $573.96/\mathrm{68,110}=8.4\times {10}^{-3}$ s for the OCS on field data (5 chillers). In the latter case, X-OCS took less than 6 min to solve the OCS problem over 2-year data with quarter-hour sampling.

As expected, in view of the exponential growth of the number of QP problems, the maximal average computation time per load is found in correspondence with the OCS benchmark 2, where 9 chillers are present. Nevertheless, the average time per load amounts to $228.29/72=3.17$ s, which is totally affordable.

Finally, a simulated benchmark was set up in order to better assess the average computation time per load as a function of the number of chillers. In particular, nine OCL simulated experiments, characterized by a variable number of chillers, ranging from two to ten, were considered. The ten-chiller system was composed by the six Hsinchu chillers, whose models are reported in [7] (Table 3), with the first four replicated. For each experiment, the OCL problem was solved for five different cooling loads ranging from 70% to 90% of the chiller’s total cooling capacity. In Figure 11, the average computation time per load is displayed as a function of the number of chillers. The plot highlights the exponential growth but, at the same time, it shows that, even for a large HVAC system made of 10 chillers, the computation time per load (10 s) is all but prohibitive.

6. Discussion

The main purpose of the paper was the derivation of an exact algorithm for the solution to the OCL problem. This goal was successfully completed by a decomposition approach that exploits a suitable partition of the solution space. The availability of an exact method has been immediately exploited along two directions. First, it has become possible to give a definitive assessment on the performances of different literature methods that had been applied to some consolidated benchmark problems. By the way, the comparison with the exact solution revealed that some unrealistic performances had been declared in the literature, due to erroneous extrapolations of the power consumption curve. The exact method has been exploited also in relation with the optimal chiller sequencing problem. For a given cooling demand profile, if the dynamic up/down-time constraints are neglected, a sequence of OCL problems can be exactly solved to yield a lower bound limit, called R-OCS, to the performance of any feasible solution.

Concerning the practical applicability of the exact solution in place of heuristic approaches discuss in the literature, two main objections may be raised: (i) the explosion of the computational cost with the number of chillers, (ii) the need to make overly restrictive assumptions on the shape of the power consumption curves.

On the first side, it is indeed true that the OCL problem as formulated in (4) is NP-hard, as confirmed by Figure 11, where the exponential growth of the computations time is apparent. At the same time, the figure shows that, even for a medium/large-sized chiller system, e.g., 6–10 chillers, the computation time per load is less than 2 s. This suggests that, even for chiller systems used in large semiconductor factories, the cost of the exact solution is all but prohibitive. The numerical efficiency is a direct consequence of the tiny number of computations required to solve the elementary EQP problems, see (12). Moreover, the partition strategy underlying X-OCL implies that it is totally parallelizable into $4^n$ threads, a feature that has not been explicitly exploited and that could further speed up the solution.

The second objection to the general applicability of the exact solution has to do with the quadratic assumption made on the power consumption curve. Even if the majority of benchmarks satisfy this assumption, there is no stringent reason to rule out other functional descriptions. Nevertheless, when confronted with real data (see the field data benchmark), we found that a quadratic power consumption fitted well the recorded data, see Figure 6. Moreover, even when a single quadratic function is not adequate, it is still possible to switch to a piece-wise quadratic description. In that case, it would be immediate to generalize the exact algorithm by just increasing the number of partitions ${\mathcal{S}}_j$, in such a way that the problem still boils down to a set of easy-to-solve EQP problems.

In view of its numerical efficiency, the application of X-OCS to the solution of the OCS problem also appears very promising. Indeed, in the OCS benchmarks taken from the literature and in the field data OCS benchmark, the performance of X-OCS is very close to the lower bound, implying that there is no scope for the use of more sophisticated algorithms.