Validation of the Stolwijk and Tanabe Human Thermoregulation Models for Predicting Local Skin Temperatures of Older People under Thermal Transient Conditions
Abstract
1. Introduction
2. Materials and Methods
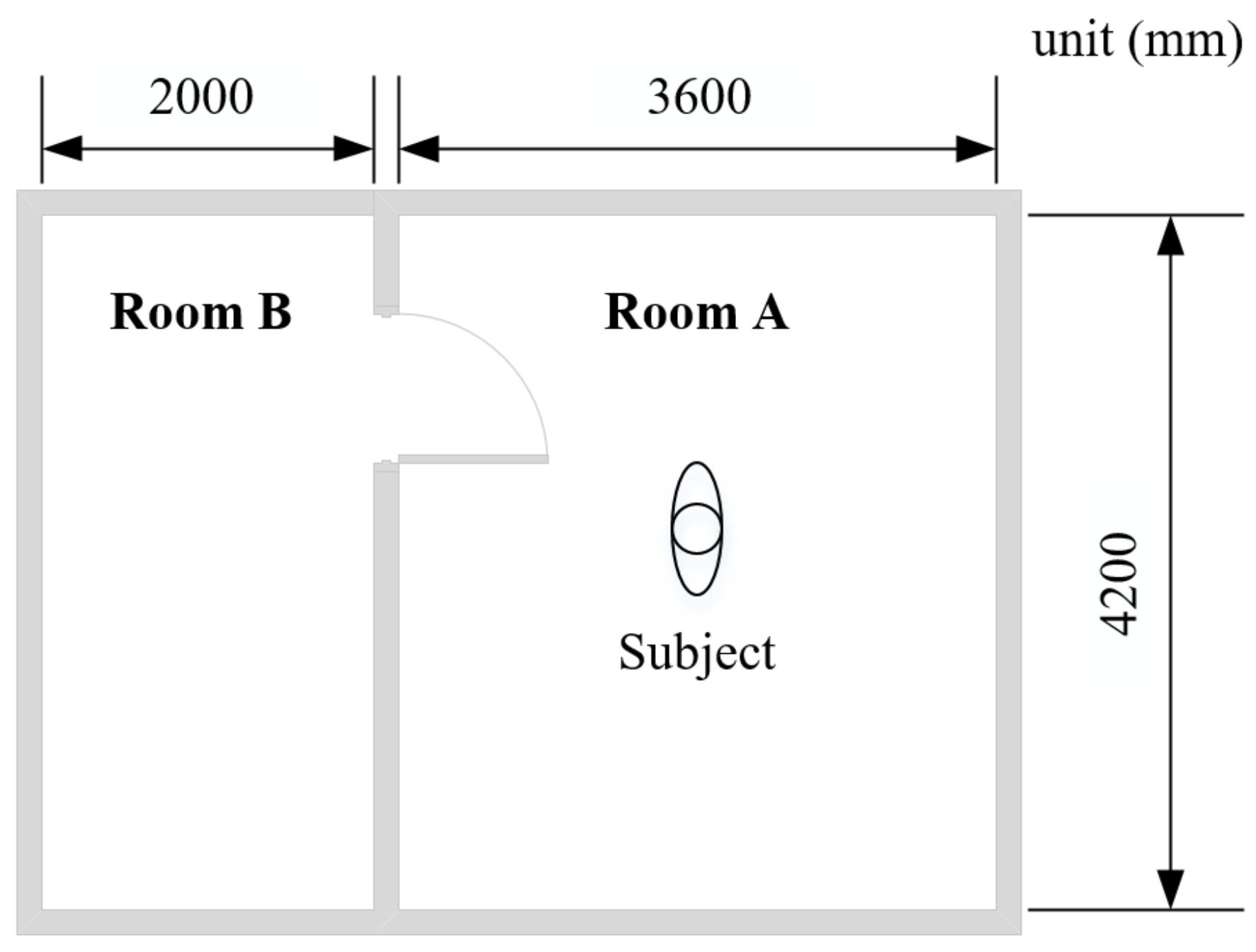
2.1. Lab Experiments
2.2. Calculation Settings of the Stolwijk Model and the Tanabe Model
2.3. Calculation Setting of the UCB Thermal Sensation Model
- (1)
- The skin temperature distribution of the left and right extremities was symmetrical.
- (2)
- The UCB sensation thermal model was adapted to the measurement and the two thermoregulation models according to the body segment correspondence shown in Table 5. The temperature of the face, breath, and neck was assumed to be the same as the head temperature. The temperature of the back and pelvis was assumed to be the same as the chest temperature. The upper arm temperature was assumed to be the same as the lower arm temperature.
- (3)
- The influence of the core temperature was neglected.
- (4)
- The skin temperature set point of each body segment for older people, which represents the neutral local skin temperature, was set according to the average values of the measurements in Stage 1 (26 °C) of both Schedule 1 and Schedule 2 (see Table 6 in Section 3.1), where the subjects’ responses were thermally neutral.
3. Results
3.1. Experimental Results
3.2. Validation of Predictions by the Stolwijk Model and the Tanabe Model
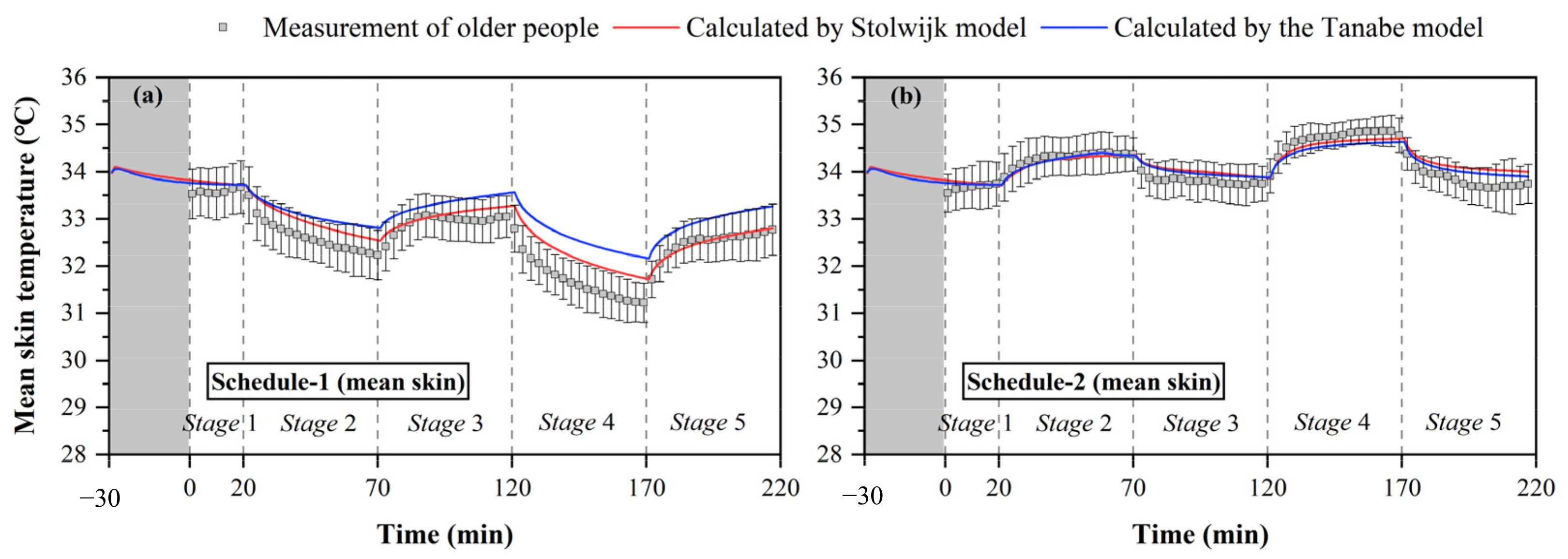
3.2.1. Validation of Prediction for Mean Skin Temperature
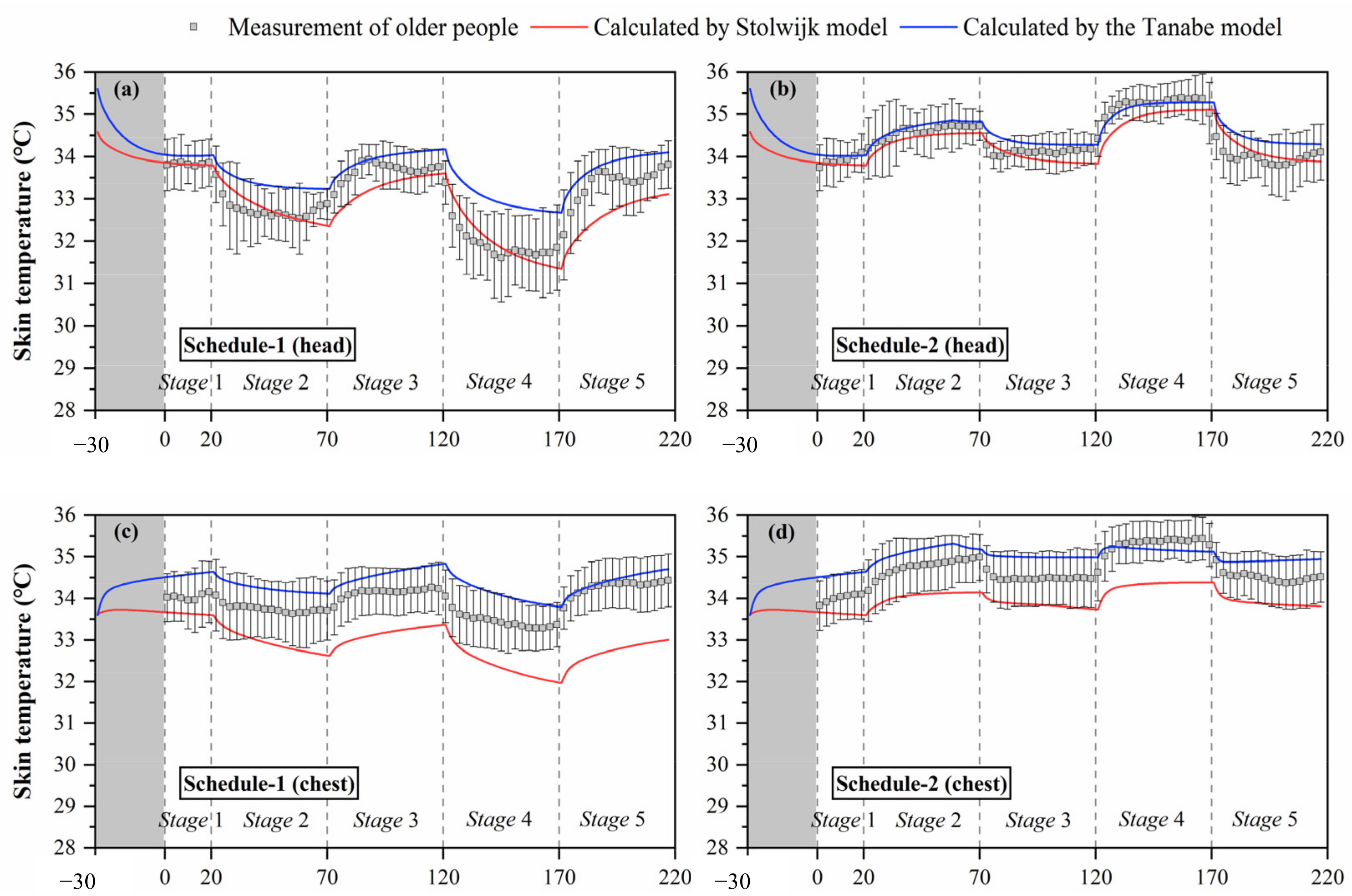
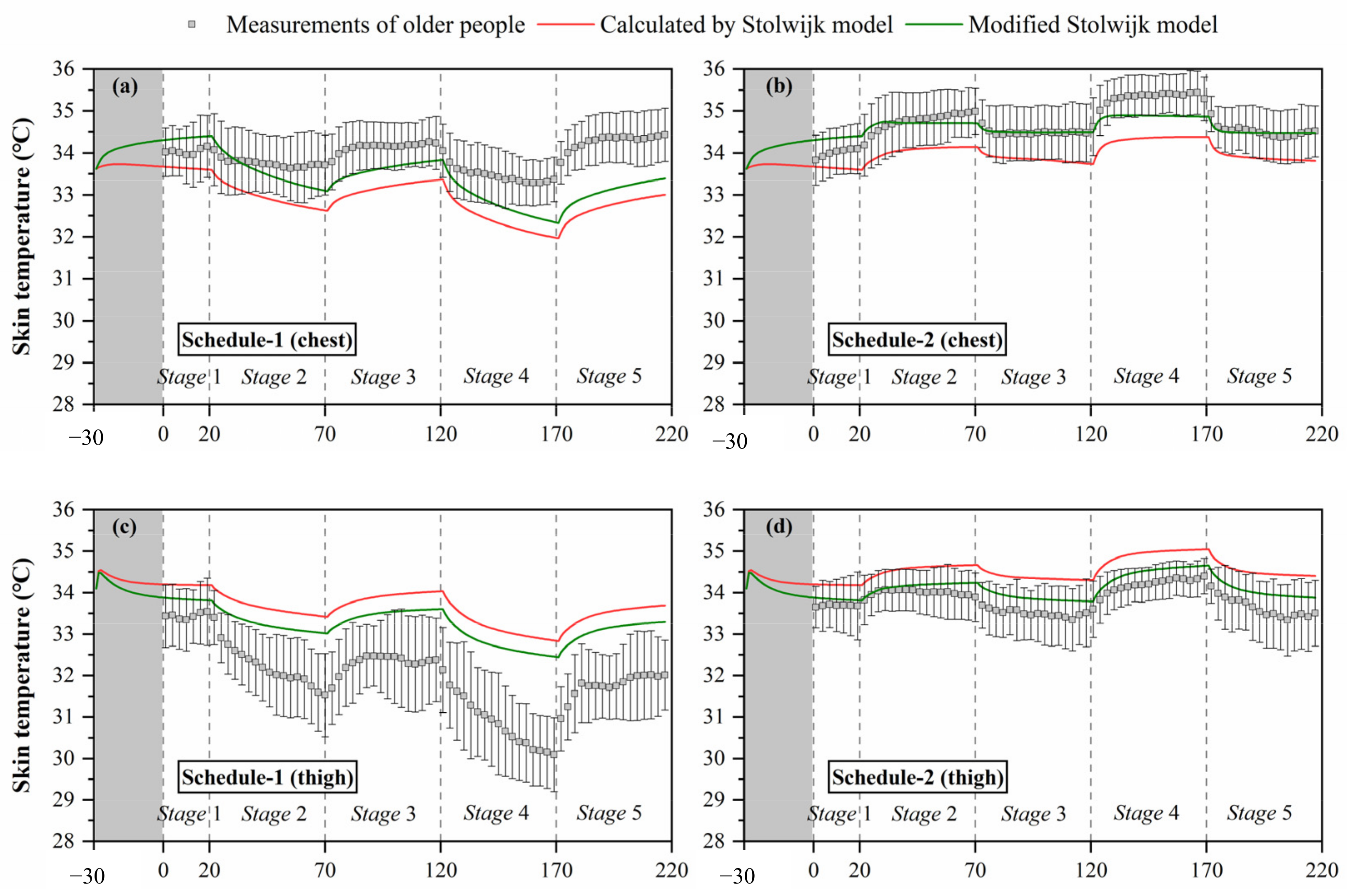
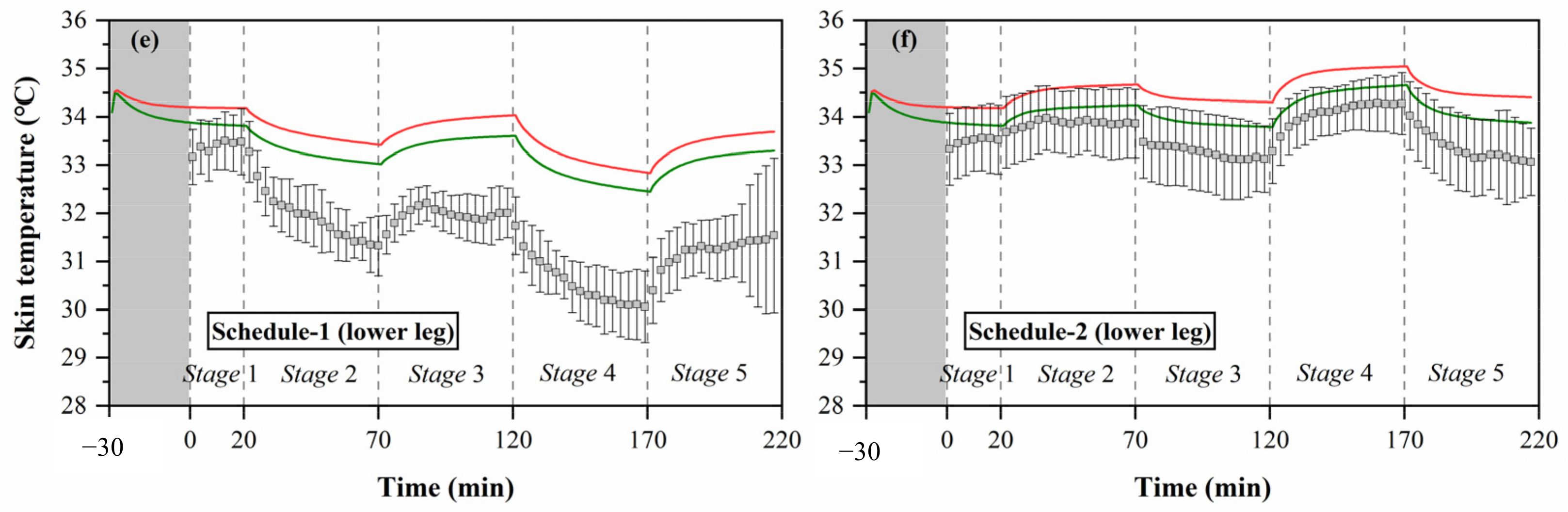
3.2.2. Validation of Prediction for Local Skin Temperature
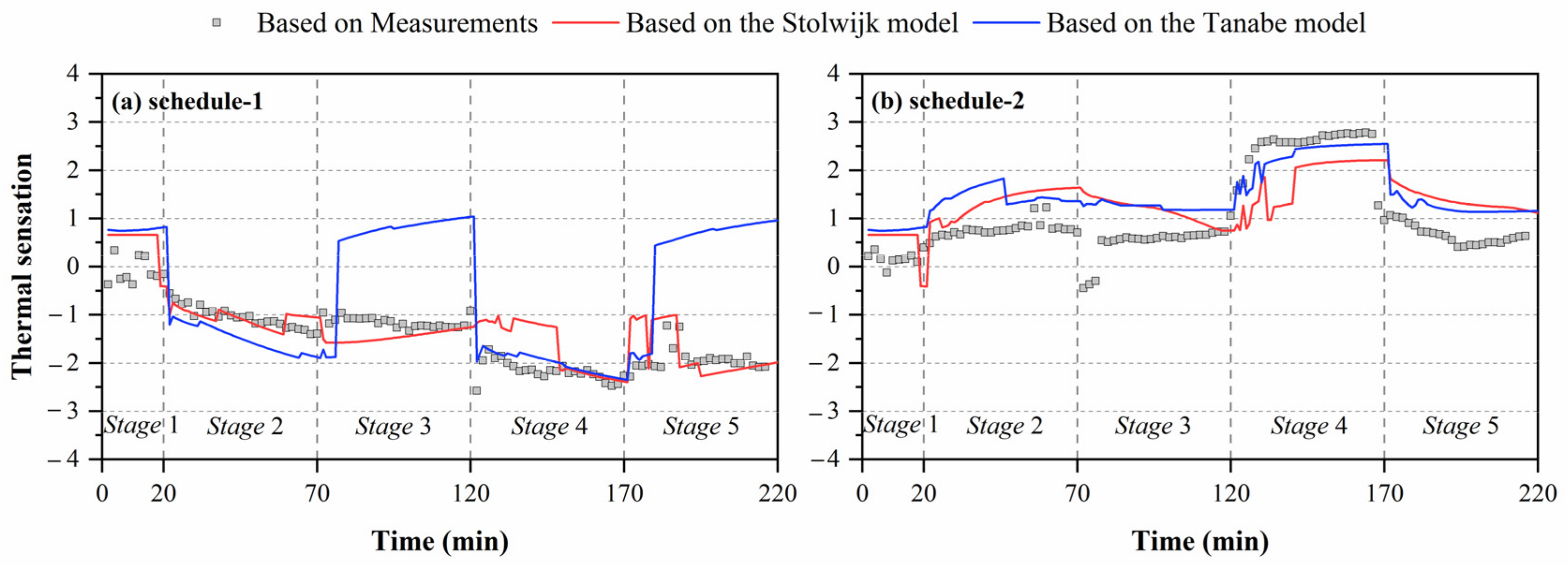
3.3. Influence of Local Skin Temperature’s Deviation on Thermal Sensation Prediction
4. Discussion
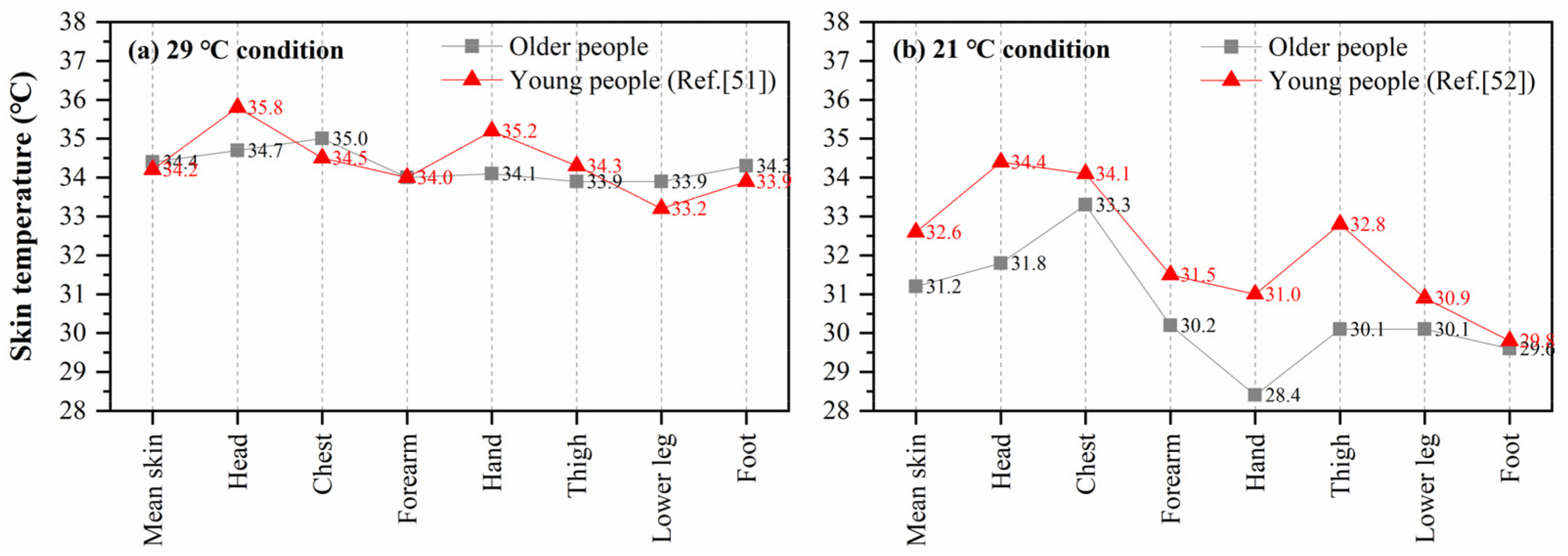
4.1. Comparisons of Local Skin Temperature Distribution Between Young and Older People
4.2. Improvement of the Human Thermoregulation Model for Older People
4.3. Limitations and Future Studies
- (1)
- The environmental parameters were measured only at one height. The environmental uniformity at different heights around the subjects needs further verification, and the difference in the environmental inputs to various body segments of the thermoregulation models needs to be further considered.
- (2)
- The input of the metabolic rate value was not measured in this study. The metabolic rate value is a key factor in the calculation of human thermoregulation models, and the determination of metabolic rate in the elderly deserves further study.
- (3)
- There was a lack of comparative experiments for young people, which makes it difficult to analyze the causes of deviation between predicted and measured skin temperatures. Thus, the reference sample of young people deserves further study.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- U.N. Department of Economic and Social Affairs. World Population Prospects; United Nations: New York, NY, USA, 2020. [Google Scholar]
- Waller, J.M.; Maibach, H.I. Age and skin structure and function, a quantitative approach (I): Blood flow, pH, thickness, and ultrasound echogenicity. Skin Res. Technol. 2005, 11, 221–235. [Google Scholar] [CrossRef] [PubMed]
- Anderson, G.S.; Meneilly, G.S.; Mekjavic, I.B. Passive temperature lability in the elderly. Eur. J. Appl. Physiol. 1996, 73, 278–286. [Google Scholar] [CrossRef] [PubMed]
- Yochihara, Y.; Ohnaka, T.; Nagai, Y.; Tokuda, T.; Kawashima, Y. Physiological responses and thermal sensations of the elderly in cold and hot environments. J. Therm. Biol. 1993, 18, 355–361. [Google Scholar] [CrossRef]
- Collins, K.J.; Exton-Smith, A.N.; Dore, C. Urban hypothermia: Preferred temperature and thermal perception in old age. Br. Med. J. (Clin. Res. Ed.) 1981, 282, 175–177. [Google Scholar] [CrossRef] [PubMed]
- Vandentorren, S.; Bretin, P.; Zeghnoun, A.; Mandereau-Bruno, L.; Croisier, A.; Cochet, C.; Ribéron, J.; Siberan, I.; Declercq, B.; Ledrans, M. August 2003 heat wave in France: Risk factors for death of elderly people living at home. Eur. J. Public Health 2006, 16, 583–591. [Google Scholar] [CrossRef] [PubMed]
- Hajat, S.; Bird, W.; Haines, A. Cold weather and GP consultations for respiratory conditions by elderly people in 16 locations in the UK. Eur. J. Epidemiol. 2004, 19, 959–968. [Google Scholar] [CrossRef]
- Van Hoof, J.; Schellen, L.; Soebarto, V.; Wong, J.K.W.; Kazak, J.K. Ten questions concerning thermal comfort and ageing. Build. Environ. 2017, 120, 123–133. [Google Scholar] [CrossRef]
- Giamalaki, M.; Kolokotsa, D. Understanding the thermal experience of elderly people in their residences: Study on thermal comfort and adaptive behaviors of senior citizens in Crete, Greece. Energy Build. 2019, 185, 76–87. [Google Scholar] [CrossRef]
- Jiao, Y.; Yu, H.; Yu, Y.; Wang, Z.; Wei, Q. Adaptive thermal comfort models for homes for older people in Shanghai, China. Energy Build. 2020, 215, 109918. [Google Scholar] [CrossRef]
- Cheng, Y.; Niu, J.; Gao, N. Thermal comfort models: A review and numerical investigation. Build. Environ. 2012, 47, 13–22. [Google Scholar] [CrossRef]
- Enescu, D. Models and Indicators to Assess Thermal Sensation Under Steady-State and Transient Conditions. Energies 2019, 12, 841. [Google Scholar] [CrossRef]
- Charny, C.K. Mathematical models of bioheat transfer. In Advances in Heat Transfer; Cho, Y.I., Ed.; Elsevier: Amsterdam, The Netherlands, 1992; Volume 22, pp. 19–155. [Google Scholar]
- Fu, M.; Weng, W.; Chen, W.; Luo, N. Review on modeling heat transfer and thermoregulatory responses in human body. J. Therm. Biol. 2016, 62, 189–200. [Google Scholar] [CrossRef] [PubMed]
- Katić, K.; Li, R.; Zeiler, W. Thermophysiological models and their applications: A review. Build. Environ. 2016, 106, 286–300. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal sensation and comfort models for non-uniform and transient environments: Part I: Local sensation of individual body parts. Build. Environ. 2010, 45, 380–388. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal sensation and comfort models for non-uniform and transient environments, part II: Local comfort of individual body parts. Build. Environ. 2010, 45, 389–398. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal sensation and comfort models for non-uniform and transient environments, part III: Whole-body sensation and comfort. Build. Environ. 2010, 45, 399–410. [Google Scholar] [CrossRef]
- Lan, L.; Xia, L.; Tang, J.; Wyon, D.P.; Liu, H. Mean skin temperature estimated from 3 measuring points can predict sleeping thermal sensation. Build. Environ. 2019, 162, 106292. [Google Scholar] [CrossRef]
- Liu, K.; Nie, T.; Liu, W.; Liu, Y.; Lai, D. A machine learning approach to predict outdoor thermal comfort using local skin temperatures. Sustain. Cities Soc. 2020, 59, 102216. [Google Scholar] [CrossRef]
- Liu, S.; Schiavon, S.; Das, H.P.; Jin, M.; Spanos, C.J. Personal thermal comfort models with wearable sensors. Build. Environ. 2019, 162, 106281. [Google Scholar] [CrossRef]
- Tejedor, B.; Casals, M.; Gangolells, M.; Macarulla, M.; Forcada, N. Human comfort modelling for elderly people by infrared thermography: Evaluating the thermoregulation system responses in an indoor environment during winter. Build. Environ. 2020, 186, 107354. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, H.; Luo, M.; Wang, Z.; Zhang, H.; Jiao, Y. Predicting older people’s thermal sensation in building environment through a machine learning approach: Modelling, interpretation, and application. Build. Environ. 2019, 161, 106231. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, H.; Li, B.; Kosonen, R.; Kong, D.; Zhou, S.; Yao, R. Thermal adaptation of the elderly during summer in a hot humid area: Psychological, behavioral, and physiological responses. Energy Build. 2019, 203, 109450. [Google Scholar] [CrossRef]
- Schellen, L.; Loomans, M.G.L.C.; Kingma, B.R.M.; de Wit, M.H.; Frijns, A.J.H.; van Marken Lichtenbelt, W.D. The use of a thermophysiological model in the built environment to predict thermal sensation: Coupling with the indoor environment and thermal sensation. Build. Environ. 2013, 59, 10–22. [Google Scholar] [CrossRef]
- Pokorny, J.; Jicha, M. Coupling of the models of human physiology and thermal comfort. EPJ Web Conf. 2013, 45, 01077. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, H.; Zhou, X. Coupling a 65-node thermoregulation model and a data-driven thermal sensation model to forecast Chinese elderly’s thermal sensation in Buildings. In Proceedings of the 16th Conference of the International Society of Indoor Air Quality & Climate (Indoor Air 2020), Seoul, Korea, 1 November 2002. [Google Scholar]
- Veselá, S.; Kingma, B.R.M.; Frijns, A.J.H. Local thermal sensation modeling—A review on the necessity and availability of local clothing properties and local metabolic heat production. Indoor Air 2017, 27, 261–272. [Google Scholar]
- Stolwijk, J.A.J. A Mathematical Model of Physiological Temperature Regulation in Man; NASA: Washington, DC, USA, 1971.
- Tanabe, S.-I.; Nakano, J.; Kobayashi, K. Development of 65-node thermoregulation-model for evaluation of thermal environment. J. Archit. Plan. Environ. Eng. 2001, 541, 9–16. [Google Scholar]
- Tanabe, S.; Kobayashi, K.; Nakano, J.; Ozeki, Y.; Konishi, M. Evaluation of thermal comfort using combined multi-node thermoregulation (65MN) and radiation models and computational fluid dynamics (CFD). Energy Build. 2002, 34, 637–646. [Google Scholar] [CrossRef]
- Fiala, D. Dynamic Simulation of Human Heat Transfer and Thermal Comfort. Ph.D. Thesis, De Montfort University, Leicester, UK, 1998. [Google Scholar]
- Fiala, D.; Lomas, K.J.; Stohrer, M. A computer model of human thermoregulation for a wide range of environmental conditions: The passive system. J. Appl. Physiol. (1985) 1999, 87, 1957–1972. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. Computer prediction of human thermoregulatory and temperature responses to a wide range of environmental conditions. Int. J. Biometeorol. 2001, 45, 143–159. [Google Scholar] [CrossRef]
- Huizenga, C.; Zhang, H.; Arens, E. A model of human physiology and comfort for assessing complex thermal environments. Build. Environ. 2001, 36, 691–699. [Google Scholar] [CrossRef]
- Zhang, H.; Huizenga, C.; Arens, E.; Yu, T. Considering individual physiological differences in a human thermal model. J. Therm. Biol. 2001, 26, 401–408. [Google Scholar] [CrossRef]
- Novieto, D.T. Adapting a human thermoregulation model for predicting the thermal response of older persons. Prog. Brain Res. 2013, 204, 169–190. [Google Scholar]
- Rida, M.; Ghaddar, N.; Ghali, K.; Hoballah, J. Elderly bioheat modeling: Changes in physiology, thermoregulation, and blood flow circulation. Int. J. Biometeorol. 2014, 58, 1825–1843. [Google Scholar] [CrossRef]
- Hirata, A.; Nomura, T.; Laakso, I. Computational estimation of body temperature and sweating in the aged during passive heat exposure. Int. J. Therm. Sci. 2015, 89, 154–163. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, H.; Jiao, Y.; Chu, X.; Luo, M. Chinese older people’s subjective and physiological responses to moderate cold and warm temperature steps. Build. Environ. 2019, 149, 526–536. [Google Scholar] [CrossRef]
- Hardy, J.D.; Du Bois, E.F. The technic of measuring radiation and convection. J. Nutr. 1938, 15, 461–475. [Google Scholar] [CrossRef]
- Tang, Y.; Yu, H.; Wang, Z.; Luo, M.; Zhang, K.; Jiao, Y.; Li, C. Typical winter clothing characteristics and thermal insulation of ensembles for older people in China. Build. Environ. 2020, 182, 107127. [Google Scholar] [CrossRef]
- ISO9920. Ergonomics of the Thermal Environment—Estimation of the Thermal Insulation and Evaporative Resistance of a Clothing Ensemble; International Standards Organization: Geneva, Switzerland, 2007.
- ISO7726. Thermal Environments—Instruments and Methods for Measuring Physical Quantities; International Organization for Standardization: Geneva, Switzerland, 1998.
- Hussan, J.R.; Hunter, P.J. Comfort simulator: A software tool to model thermoregulation and perception of comfort. J. Open Res. Softw. 2020, 8, 16. [Google Scholar] [CrossRef]
- Fu, M.; Yu, T.; Zhang, H.; Arens, E.; Weng, W.; Yuan, H. A model of heat and moisture transfer through clothing integrated with the UC Berkeley comfort model. Build. Environ. 2014, 80, 96–104. [Google Scholar] [CrossRef]
- Salloum, M.; Ghaddar, N.; Ghali, K. A new transient bioheat model of the human body and its integration to clothing models. Int. J. Therm. Sci. 2007, 46, 371–384. [Google Scholar] [CrossRef]
- Piers, L.S.; Soares, M.J.; McCormack, L.M.; O’Dea, K. Is there evidence for an age-related reduction in metabolic rate? J. Appl. Physiol. 1998, 85, 2196–2204. [Google Scholar] [CrossRef] [PubMed]
- Tsuzuki, K.; Ohfuku, T. Thermal Sensation and Thermoregulation in Elderly Compared to Young People in Japanese Winter Season. In Proceedings of the 9th International Conference on Indoor Air Quality and Climate (Indoor Air 2002), Monterey, CA, USA, 30 June–5 July 2002; pp. 659–664. [Google Scholar]
- Inoue, Y.; Nakao, M.; Araki, T.; Ueda, H. Thermoregulatory responses of young and older men to cold exposure. Eur. J. Appl. Physiol. 1992, 65, 492–498. [Google Scholar] [CrossRef] [PubMed]
- Munir, A.; Takada, S.; Matsushita, T. Re-evaluation of Stolwijk‘s 25-node human thermal model under thermal-transient conditions: Prediction of skin temperature in low-activity conditions. Build. Environ. 2009, 44, 1777–1787. [Google Scholar] [CrossRef]
- Zhou, X. A multi-node thermal comfort model based on Chinese thermo-biological features. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, 2015. [Google Scholar]



| Gender | Number | Age (year) | Height (cm) | Weight (kg) |
|---|---|---|---|---|
| Male | 9 | 68.3 ± 6.2 | 168.4 ± 4.1 | 63.5 ± 10.3 |
| Female | 9 | 66.7 ± 2.7 | 156.6 ± 5.3 | 58.7 ± 8.2 |
| Segment | Icl,i (clo) | Re,cl,i (m2·kPa/W) | fcl,i |
|---|---|---|---|
| Head | 0.02 | 0.001 | 1.01 |
| Trunk | 0.71 | 0.020 | 1.20 |
| Arm | 0.23 | 0.006 | 1.06 |
| Hand | 0.00 | 0.000 | 1.00 |
| Leg | 0.64 | 0.018 | 1.18 |
| Feet | 0.67 | 0.019 | 1.19 |
| ta (°C) | RH (%) | va (m/s) | tg (°C) | ||
|---|---|---|---|---|---|
| Room A | Schedule 1 | ||||
| Stage 1 | 23.2 ± 0.4 | 63.8 ± 4.6 | 0.03 ± 0.02 | 23.0 ± 0.4 | |
| Stage 3 | 21.6 ± 0.5 | 65.9 ± 1.2 | 0.05 ± 0.02 | 21.3 ± 0.5 | |
| Schedule 2 | |||||
| Stage 1 | 29.3 ± 0.6 | 53.7 ± 7.4 | 0.03 ± 0.01 | 28.9 ± 0.3 | |
| Stage 3 | 31.9 ± 0.4 | 54.0 ± 5.6 | 0.04 ± 0.03 | 31.7 ± 0.5 | |
| Room B | 26.1 ± 0.5 | 63.7 ± 3.6 | 0.03 ± 0.02 | 26.2 ± 0.5 |
| Parameter | Instrument | Range | Accuracy | Accuracy Requirements in ISO7726 (Class C) |
|---|---|---|---|---|
| Air temperature | WSZY-1, Tianjianhuayi, China | 0–+50 °C | ±0.5 °C | Required: ±0.5 °C Desirable: ±0.2 °C |
| Relative humidity | 10–90% | ±2% | Partial pressure of water vapor: ±0.15 kPa | |
| Globe temperature | Globe thermometer, KIMO, France | −50–+250 °C | ±0.2 °C | Required: ±2 °C Desirable: ±0.2 °C |
| Air velocity | Air velocity meter, TSI, USA | 0–20 m/s | ±0.025 m/s | Required: ±0.05 m/s Desirable: ±0.02 m/s |
| Skin temperature | Pyrobutton-L, OPULUS, USA | −40–+85 °C | ±0.2 °C | Required: ±1 °C Desirable: ±0.5 °C |
| Measurement | The Stolwijk Model | The Tanabe Model | UCB Thermal Sensation Model |
|---|---|---|---|
| Head | Head | Head | Head |
| Face | |||
| Breath | |||
| Neck | |||
| Chest | Trunk | Chest | Chest |
| Back | |||
| Pelvis | |||
| Lower arm | Lower arm | Lower arm | Upper arm |
| Lower arm | |||
| Hand | Hand | Hand | Hand |
| Thigh | Leg | Thigh | Thigh |
| Lower leg | Lower leg | Lower leg | |
| Foot | Foot | Foot | Foot |
| Skin Temperature | Mean (°C) | Standard Deviation (°C) | Maximum (°C) | Minimum (°C) |
|---|---|---|---|---|
| Mean skin temperature | 33.6 | 0.5 | 34.6 | 32.3 |
| Local skin temperature | ||||
| Head | 33.9 | 0.5 | 34.9 | 32.8 |
| Chest | 34.0 | 0.6 | 35.0 | 32.8 |
| Forearm | 32.8 | 0.8 | 34.0 | 30.8 |
| Hand | 33.4 | 1.0 | 35.5 | 30.7 |
| Thigh | 33.6 | 0.7 | 35.5 | 31.7 |
| Lower leg | 33.5 | 0.6 | 34.3 | 31.6 |
| Foot | 33.8 | 0.8 | 35.8 | 32.2 |
| Skin Temperature | Schedule 1 | Schedule 2 | ||
|---|---|---|---|---|
| Stolwijk Model | Tanabe Model | Stolwijk Model | Tanabe Model | |
| Mean skin temperature | 0.3 | 0.6 | 0.2 | 0.2 |
| Local skin temperature | ||||
| Head | 0.5 | 0.7 | 0.3 | 0.3 |
| Chest | 1.1 | 0.5 | 0.7 | 0.4 |
| Forearm | 0.4 | 1.1 | 0.7 | 0.4 |
| Hand | 0.6 | 1.1 | 1.1 | 0.8 |
| Thigh | 1.7 | 0.9 | 0.8 | 0.1 |
| Lower leg | 2.1 | 0.3 | 0.9 | 1.0 |
| Foot | 0.5 | 0.5 | 1.4 | 0.6 |
| Mean | 1.0 ± 0.7 | 0.7 ± 0.3 | 0.8 ± 0.4 | 0.5 ± 0.3 |
| Segment | Basal Skin Blood Flow (L/h) | |
|---|---|---|
| The Stolwijk Model | The Tanabe Model | |
| Head | 1.44 | 2.24 |
| Trunk | 2.10 | 5.23 1 |
| Arms | 0.50 | 2.62 2 |
| Hands | 2.00 | 1.82 |
| Legs | 2.85 | 0.98 3 |
| Feet | 3.00 | 0.90 |
| Total | 11.89 | 13.79 |
| Skin Temperature | Schedule 1 | Schedule 2 |
|---|---|---|
| Mean skin temperature | 0.4 | 0.2 |
| Local skin temperature | ||
| Head | 0.3 | 0.3 |
| Chest | 0.7 | 0.3 |
| Arm | 0.4 | 0.7 |
| Hand | 0.9 | 1.2 |
| Thigh | 1.3 | 0.3 |
| Lower leg | 1.7 | 0.5 |
| Foot | 0.7 | 1.5 |
| Mean | 0.9 ± 0.5 | 0.7 ± 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Yu, H.; Wang, Z.; Luo, M.; Li, C. Validation of the Stolwijk and Tanabe Human Thermoregulation Models for Predicting Local Skin Temperatures of Older People under Thermal Transient Conditions. Energies 2020, 13, 6524. https://doi.org/10.3390/en13246524
Tang Y, Yu H, Wang Z, Luo M, Li C. Validation of the Stolwijk and Tanabe Human Thermoregulation Models for Predicting Local Skin Temperatures of Older People under Thermal Transient Conditions. Energies. 2020; 13(24):6524. https://doi.org/10.3390/en13246524
Chicago/Turabian StyleTang, Yin, Hang Yu, Zi Wang, Maohui Luo, and Chaoen Li. 2020. "Validation of the Stolwijk and Tanabe Human Thermoregulation Models for Predicting Local Skin Temperatures of Older People under Thermal Transient Conditions" Energies 13, no. 24: 6524. https://doi.org/10.3390/en13246524
APA StyleTang, Y., Yu, H., Wang, Z., Luo, M., & Li, C. (2020). Validation of the Stolwijk and Tanabe Human Thermoregulation Models for Predicting Local Skin Temperatures of Older People under Thermal Transient Conditions. Energies, 13(24), 6524. https://doi.org/10.3390/en13246524







