Dutch Offshore Wind Atlas Validation against Cabauw Meteomast Wind Measurements
Abstract
1. Introduction
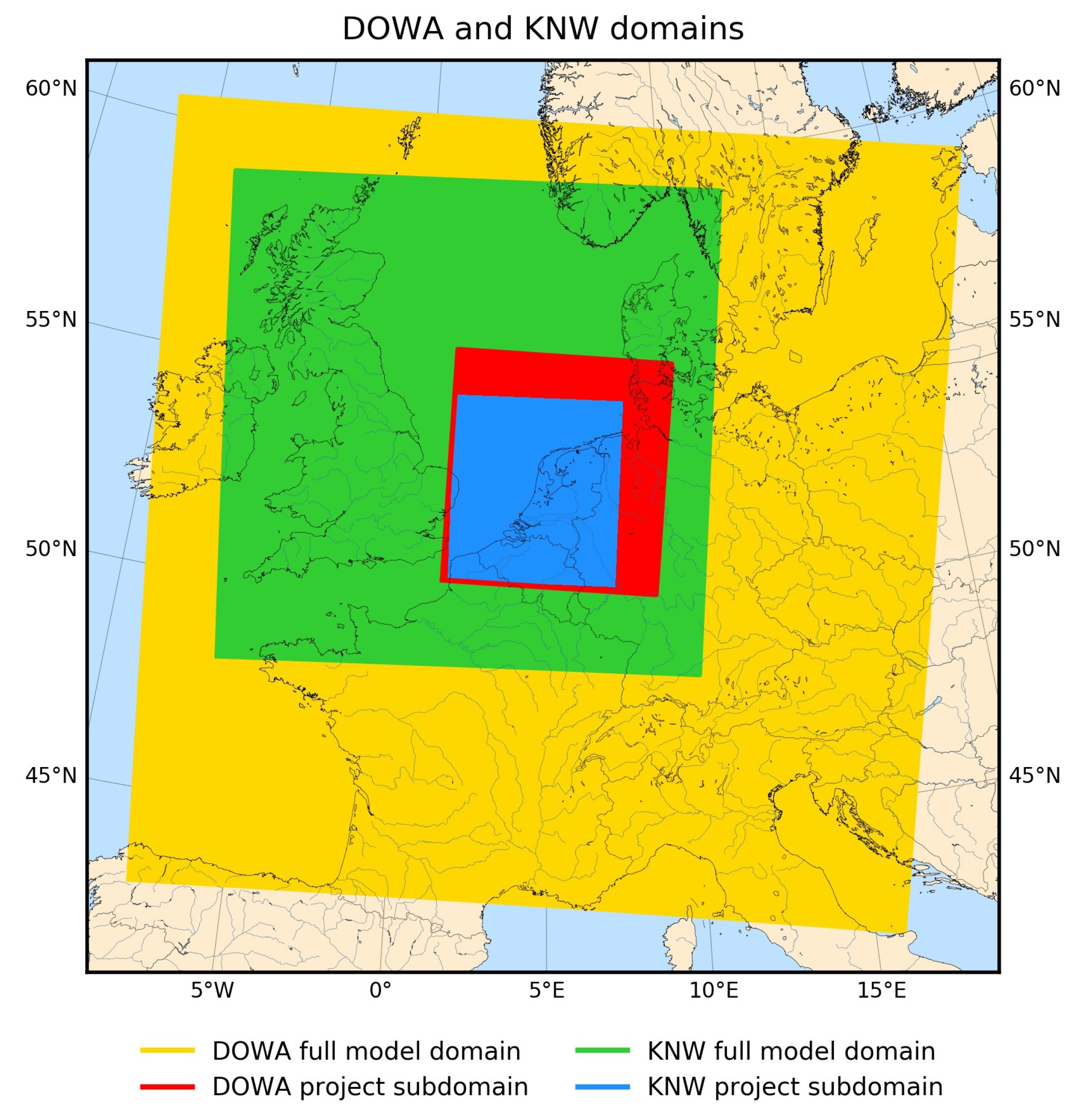
2. DOWA and KNW Atlas
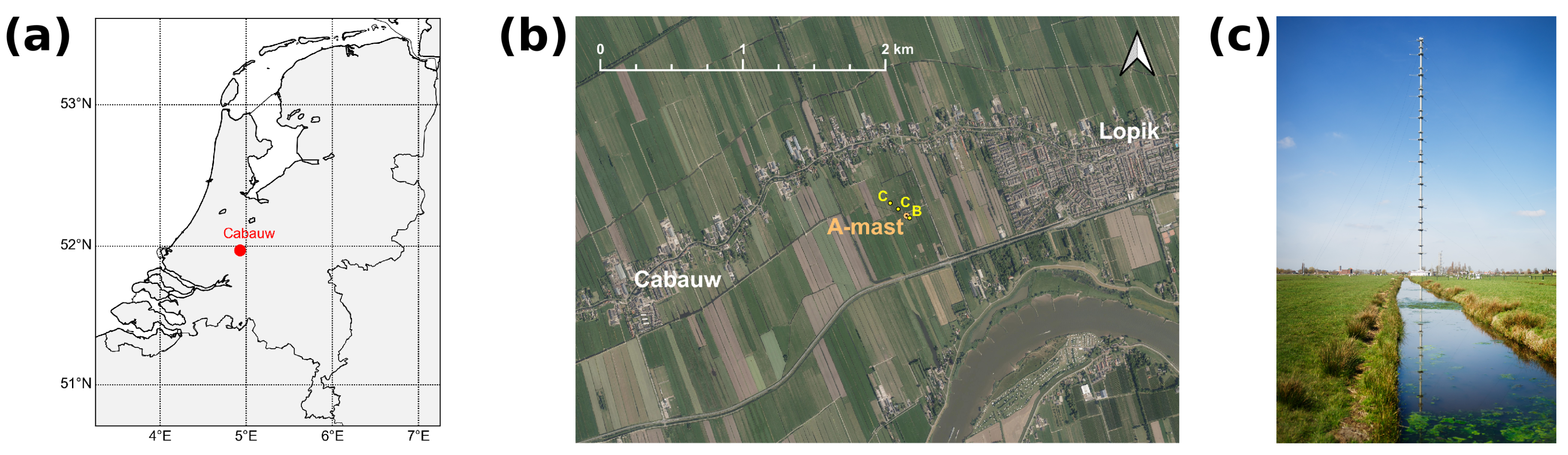
3. Cabauw Meteorological Mast Wind Measurements
- At levels 40 m, 80 m, 140 m, and 200 m of the A-mast, the wind direction is measured at three booms and wind speed is measured at two booms; the selection between the booms depends on the wind direction.
- At levels 10 m and 20 m the wind direction and wind speed are measured at smaller masts: “B-mast” (30 m SE of A-mast) and two “C-masts” (70 m and 140 m NE of A-mast for wind measurements at 20 m and 10 m height, respectively) of the main building; the selection between these masts depends on the wind direction.
4. Materials and Methods
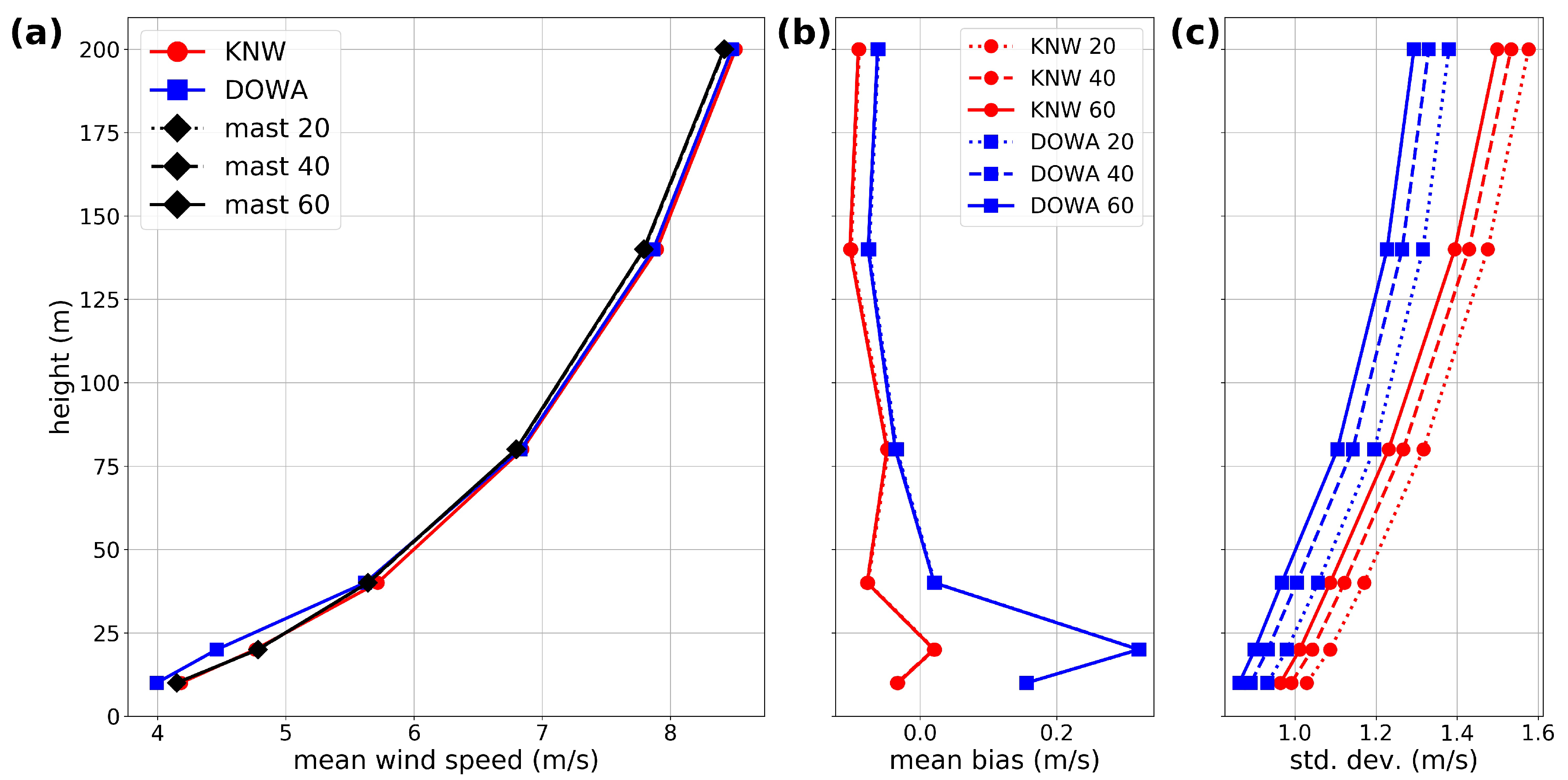
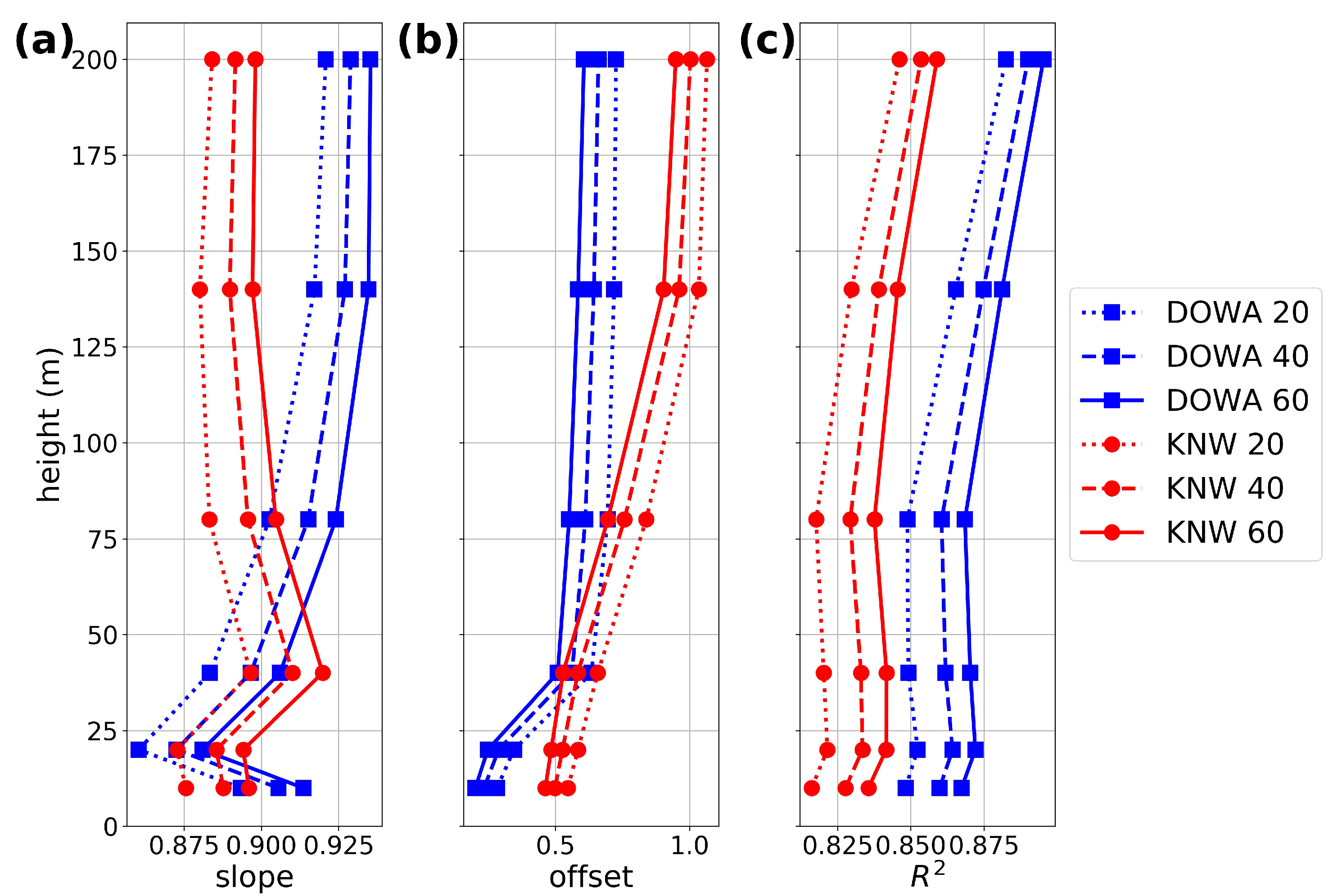
- The wind atlases have an hourly output (except ERA-Interim, which is 6-h) that represents the state of the atmosphere at the full hour. The Cabauw meteomast measurements used are 10-min averages. To validate DOWA with Cabauw measurements, one hour of Cabauw measurements is averaged, i.e., six 10-min averaged data values are taken, namely those belonging to the half hour before and the half hour after the full hour. This 60 min average was compared to the hourly DOWA output (that represents a 2.5 by 2.5 km grid box average). The method to compare the wind atlases with the Cabauw measurements is conform the one used to validate the KNW atlas [12]. In Appendix A, results based on shorter averaging times are shown.
- The validation is conducted for all measuring heights of the Cabauw meteomast: 10 m, 20 m, 40 m, 80 m, 140 m, and 200 m. These levels are all present within the DOWA; for the KNW atlas, a cubic-spline interpolation scheme was used to interpolate the model data to 140 m.The sigma levels from ERA-Interim and ERA5 are converted into heights. A constant height for each level is taken, based on the averages over the 10-year period. For both ERA-Interim and ERA5 the lowest 15 levels are taken into account. For ERA-Interim those correspond to 9.9, 35, 71, 123, 193, 285, 400 m, ... , 2.3 km; for ERA5 to 10, 31, 54, 79, 107, 137, 170, 205, 245, 288 m, ... , 566 m. A cubic-spline interpolation scheme was used to interpolate the model data to the measuring heights.
- For both temporal averaging and height interpolation, “scalar averaging” of wind speed and wind direction is applied. This means that the wind speed and wind direction are averaged independently (in contrast to “vector averaging” in which the wind vector is averaged; therefore, the wind direction is weighted with the corresponding wind speed).
- For the Cabauw meteomast measurements, we filter out wind speed and wind direction data for which the wind speed is less than 0.5 m/s.
- We only consider hourly wind atlas information for which there is a valid Cabauw meteomast measurement. Thus, timestamps for which Cabauw meteomast measurements are missing, or the measured wind speed is too low for a reliable measurement, are filtered out. No more than 0.4% of the data is filtered out.
- We derived KNW-wowsc by applying the inverse of Equation (1) to the KNW output data:where U is the wind speed, and h is the height.
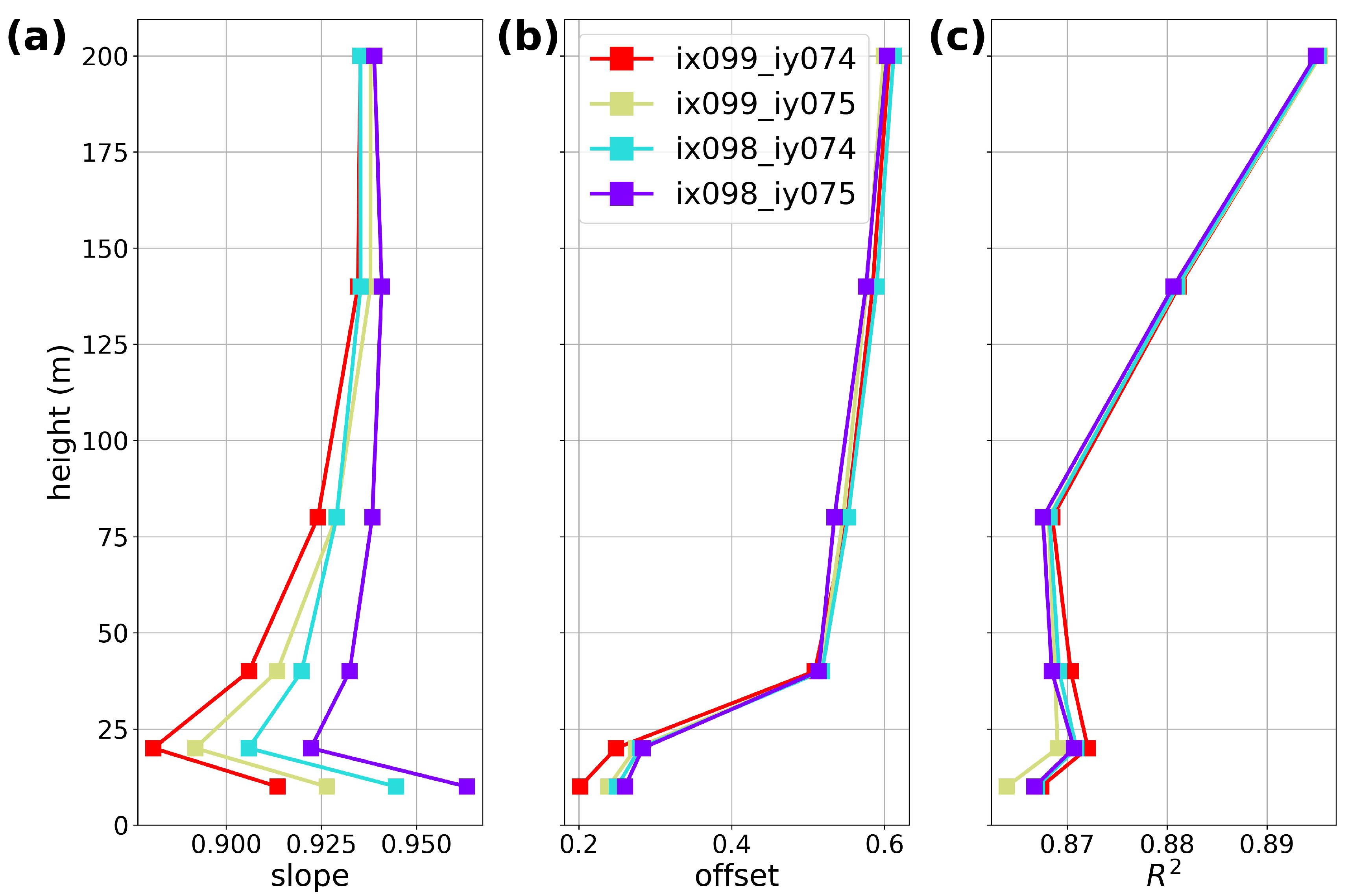
- For DOWA and KNW, no spatial interpolation of the wind atlas data has been performed. We simply took the nearest grid point to the Cabauw meteomast. Details on the coordinates and chosen grid points, and a sensitivity study on the neighboring grid points, are given in Appendix B. For ERA-Interim and ERA5, four grid points close to Cabauw were obtained from ECMWF (with a spacing of 0.125°; also see Appendix B) and further interpolated to the location of the Cabauw meteomast.
- The model variance is used to assess the significance of the differences between the atlases and the measurements (i.e., the bias). The model variance is estimated by calculating the standard deviation of the mean, taking into account an equivalent sample size (ESS) based on an autoregression of order 1 model (see Appendix C). We apply (and show) the uncertainty estimates solely on the bias (measurements-model) to avoid seasonal effects, and only on the model part, not taking into account the measurement uncertainty (which is described in Section 3).
5. Results
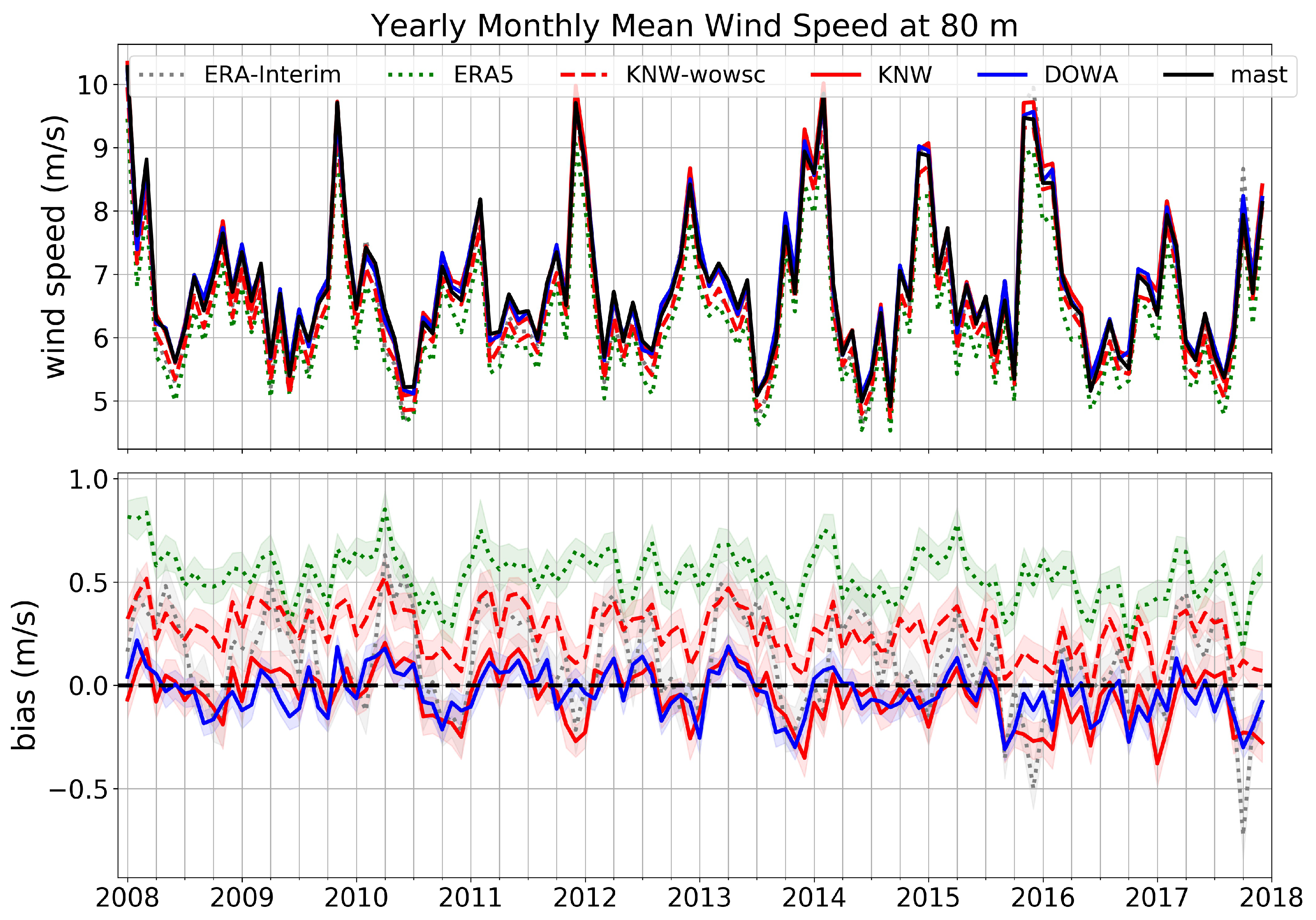
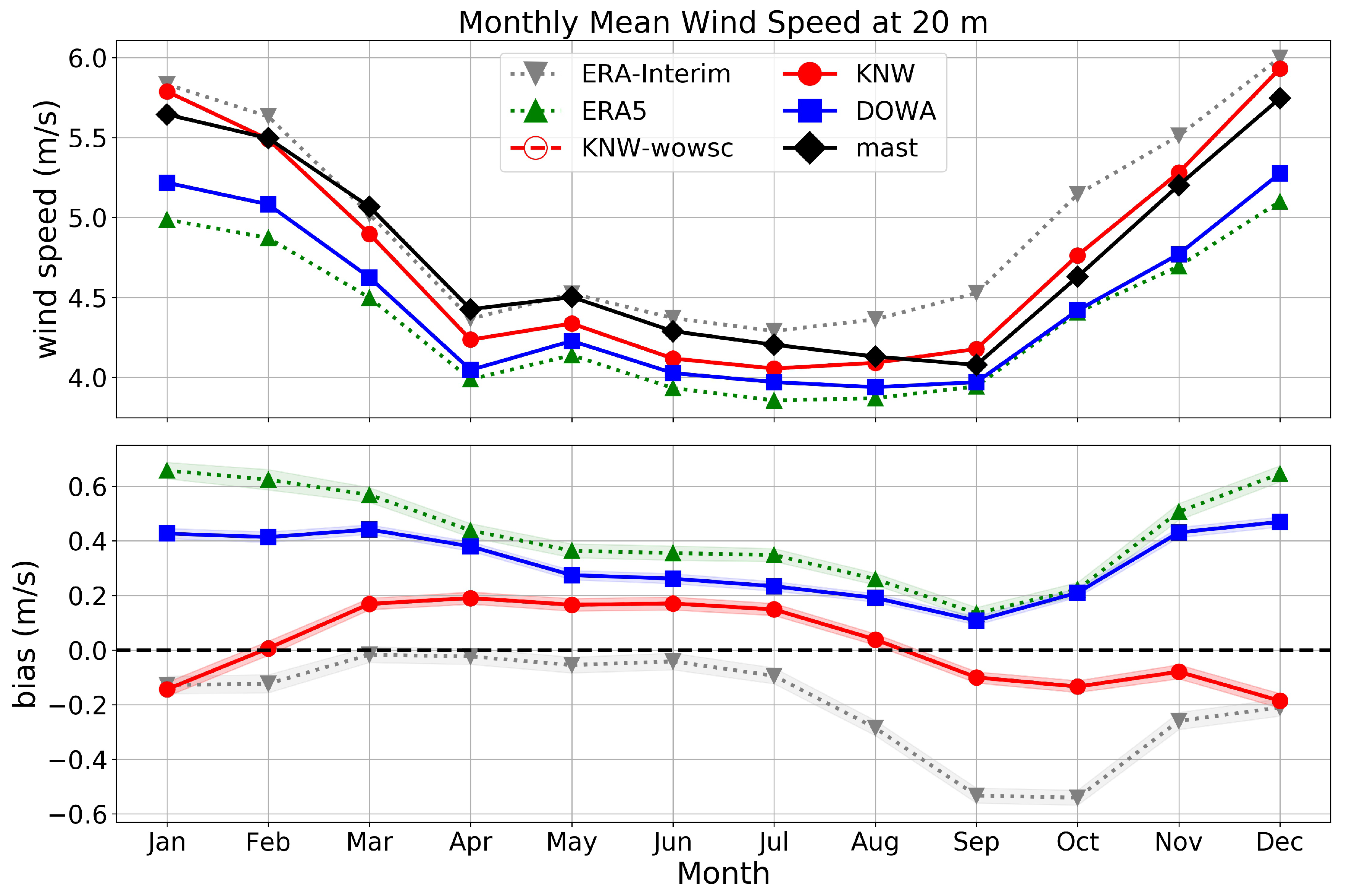
5.1. Mean Wind Speed
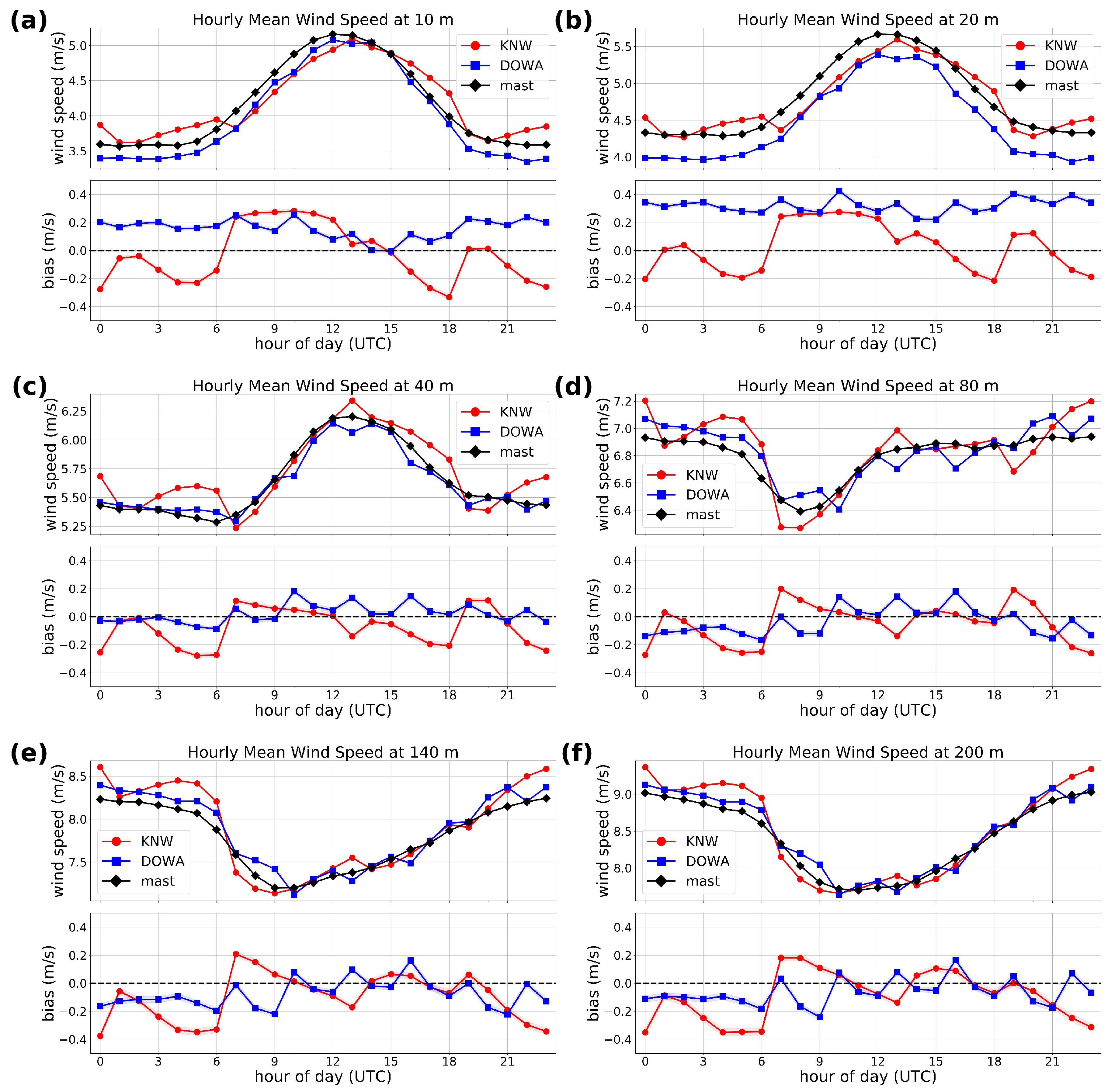
5.2. Diurnal Cycle
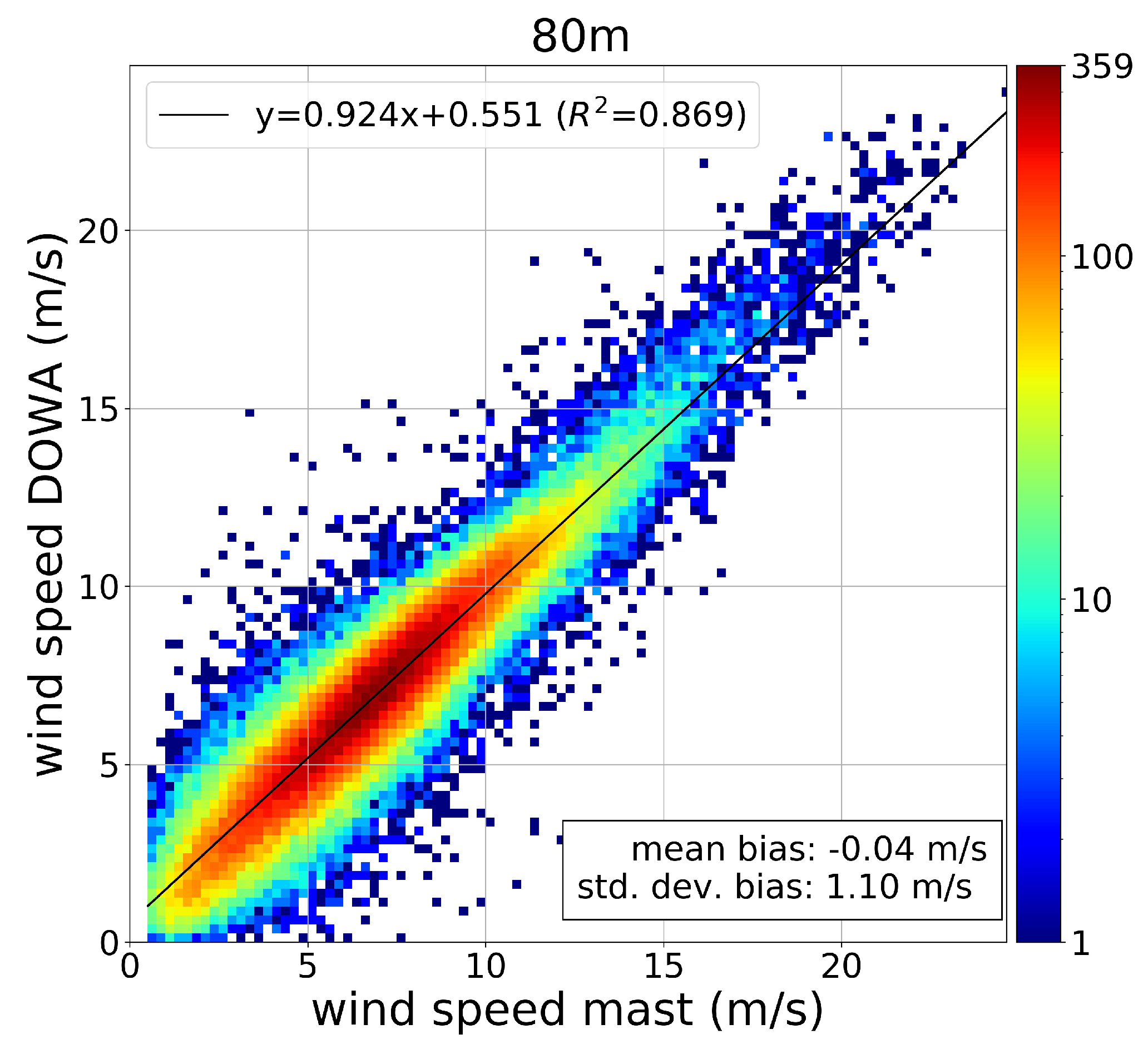
5.3. Hourly Wind Speed Correlation
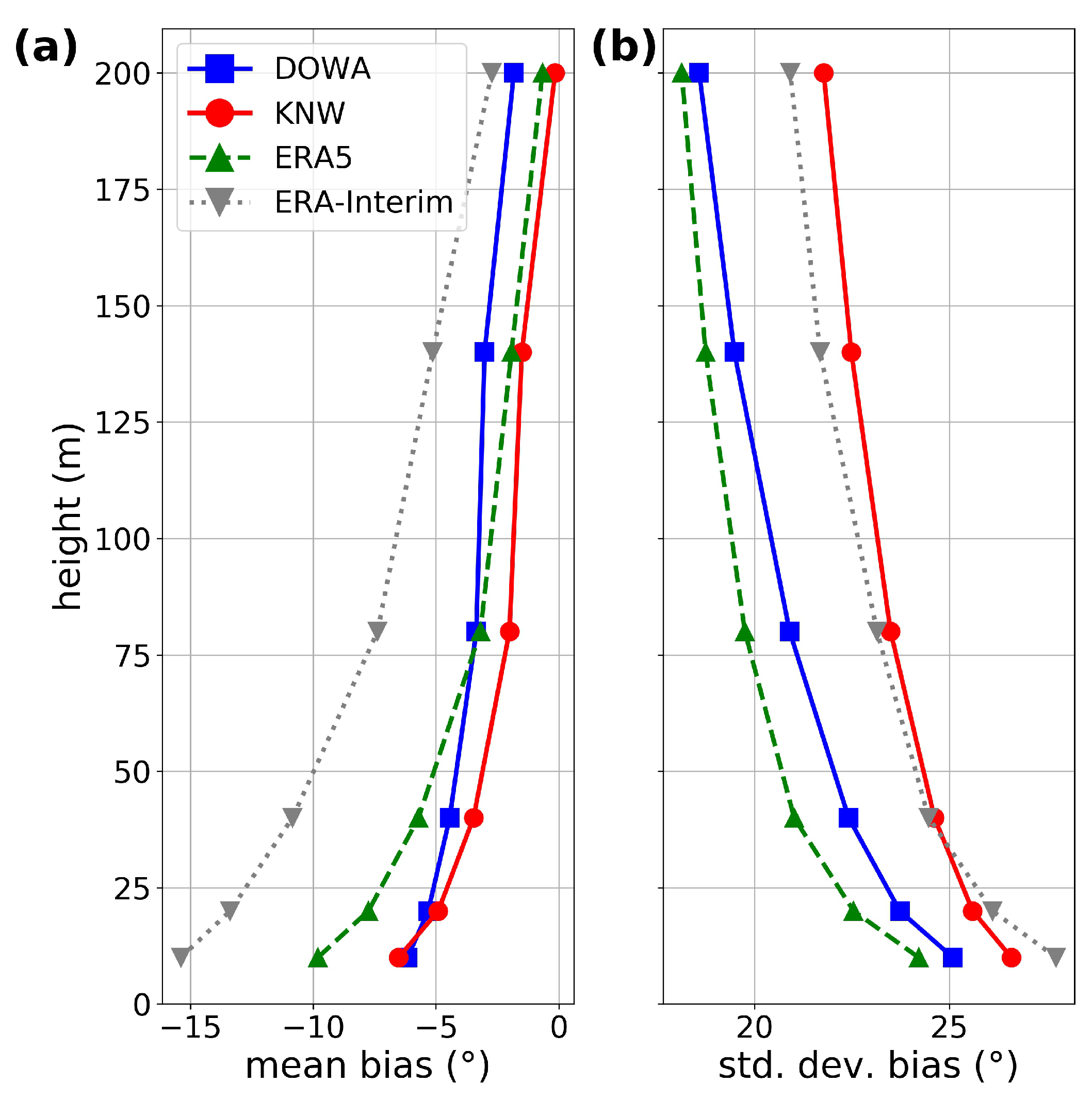
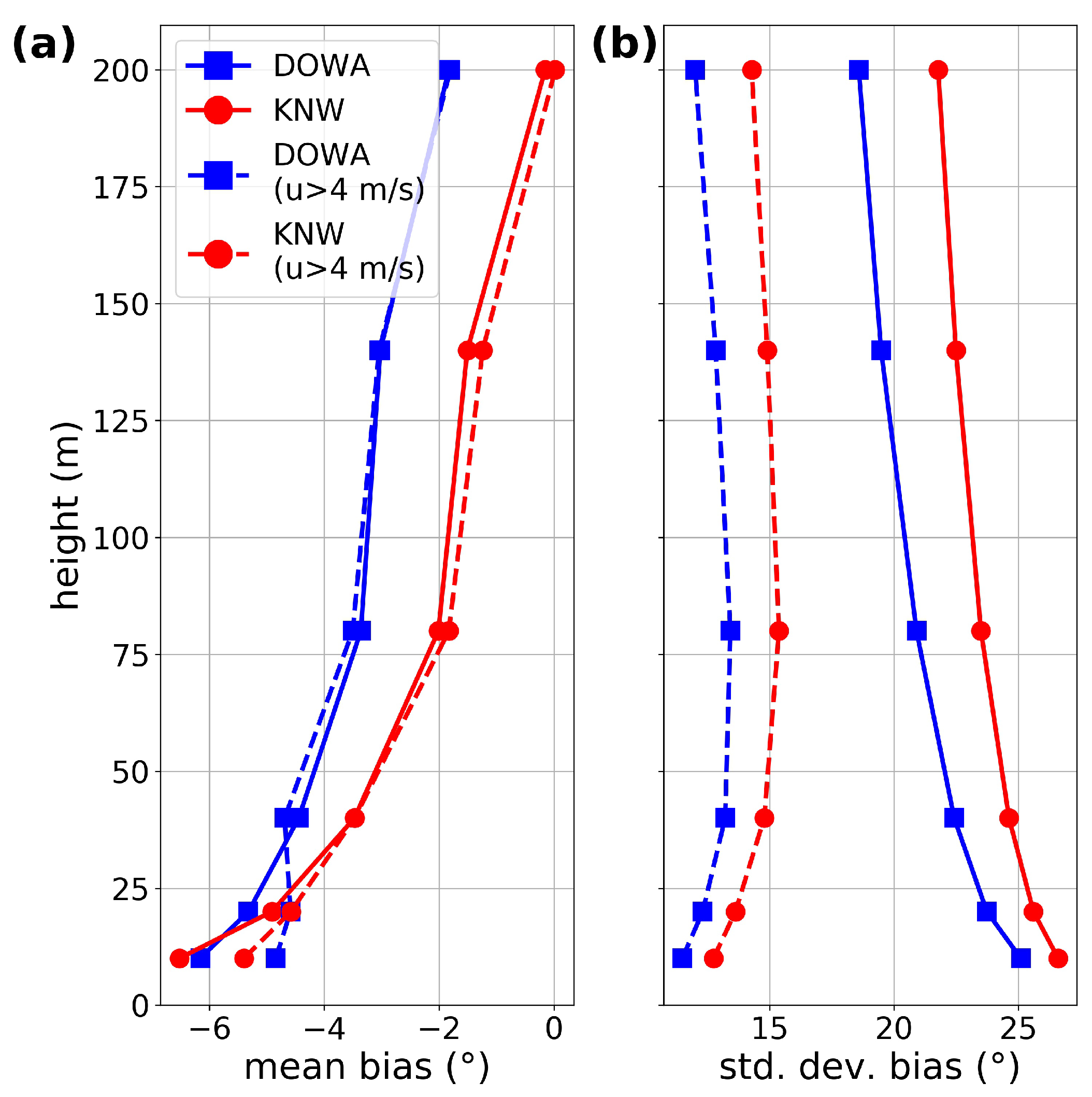
5.4. Wind Direction
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ASCAT | Advanced Scatterometer |
| CESAR | Cabauw Experimental Site for Atmospheric Research |
| DOWA | Dutch Offshore Wind Atlas |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| EHS | Enhanced Surveillance |
| ERA | ECMWF Reanalysis |
| ESS | equivalent sample size |
| HARATU | HARMONIE with RACMO Turbulence |
| HARMONIE | HIRLAM ALADIN Research on Mesoscale Operational NWP In Euromed |
| HIRLAM | High Resolution Limited Area Model |
| KNMI | Royal Netherlands Meteorological Institute |
| KNW | KNMI North sea Wind |
| KNW-wowsc | KNW without wind shear correction |
| LES | Large Eddy Simulations |
| NEWA | New European Wind Atlas |
| NWP | Numerical Weather Prediction |
| RACMO | Regional Atmospheric Climate Model |
| RANS | Reynolds-Averaged Navier–Stokes |
| WMO | World Meteorological Organization |
| WRF | Weather Research and Forecasting model |
Appendix A. Mast Measurement Time Averaging

Appendix B. Grid Point Selection
- DOWA:
- -
- grid point indices x = 99, y = 74;
- -
- 51.96548° N, 4.936425° E;
- KNW:
- -
- grid point indices x = 95, y = 71;
- -
- 51.962802° N, 4.918203° E;

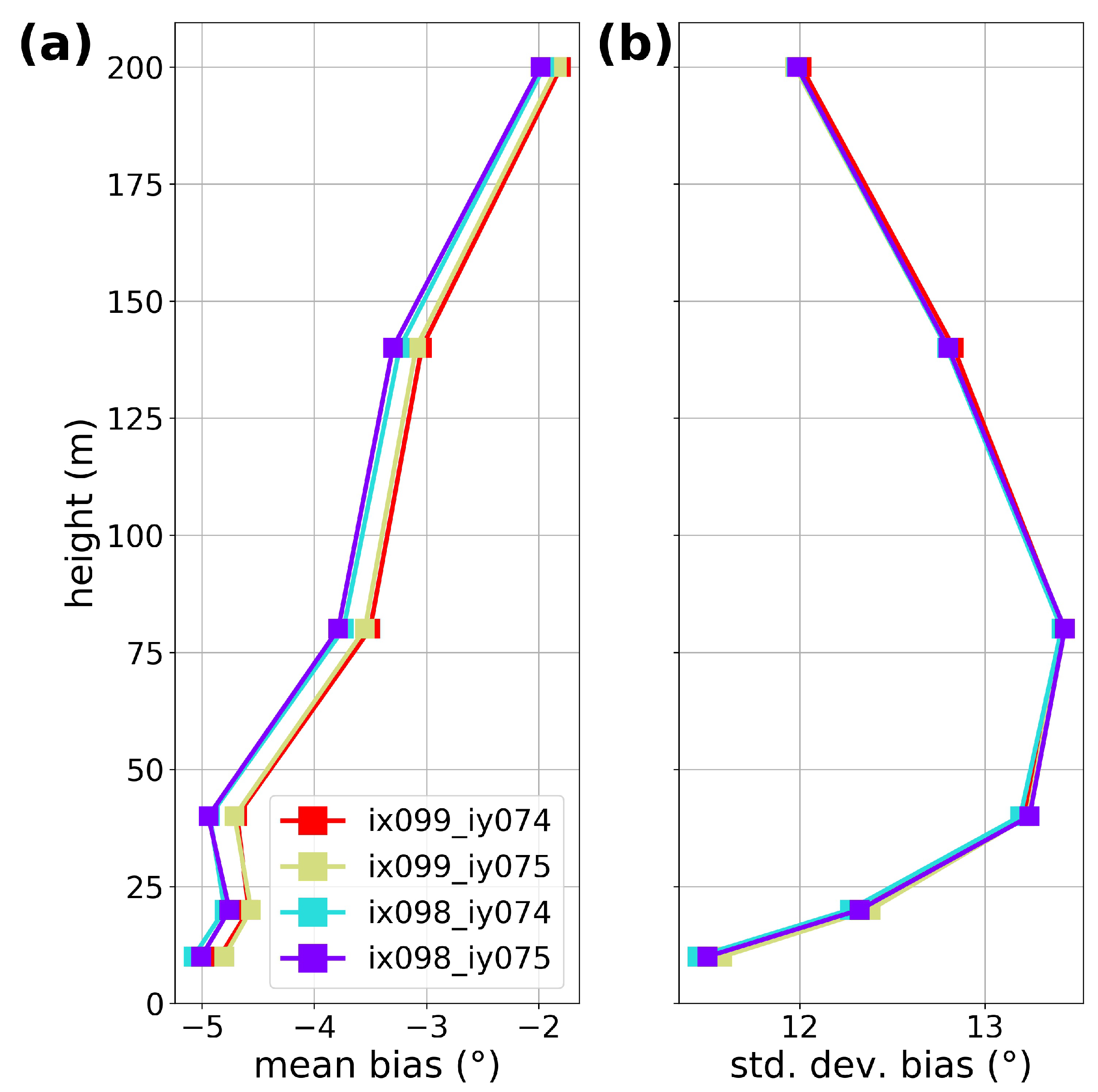
Appendix C. Model Uncertainty Estimates
| Height (m) | DOWA | KNW | ERA5 | ERA-Interim |
|---|---|---|---|---|
| 200 | 3.2 | 4.3 | 4.7 | 1.0 |
| 140 | 3.0 | 4.0 | 4.5 | 1.0 |
| 80 | 2.7 | 3.7 | 4.1 | 1.0 |
| 40 | 2.5 | 3.6 | 4.2 | 1.0 |
| 20 | 2.8 | 4.0 | 5.7 | 1.0 |
| 10 | 3.0 | 4.3 | 7.2 | 1.0 |
References
- Bleeg, J.; Purcell, M.; Ruisi, R.; Traiger, E. Wind Farm Blockage and the Consequences of Neglecting Its Impact on Energy Production. Energies 2018, 11, 1609. [Google Scholar] [CrossRef]
- Strickland, J.M.I.; Stevens, R.J. Effect of thrust coefficient on the flow blockage effects in closely-spaced spanwise-infinite turbine arrays. J. Phys. 2020, 1618, 062069. [Google Scholar] [CrossRef]
- Nygaard, N.G.; Steen, S.T.; Poulsen, L.; Pedersen, J.G. Modelling cluster wakes and wind farm blockage. J. Phys. 2020, 1618, 062072. [Google Scholar] [CrossRef]
- Asmuth, H.; Olivares-Espinosa, H.; Ivanell, S. Actuator line simulations of wind turbine wakes using the lattice Boltzmann method. Wind Energy Sci. 2020, 5, 623. [Google Scholar] [CrossRef]
- Segalini, A.; Dahlberg, J. Blockage effects in wind farms. Wind Energy 2020, 23, 120. [Google Scholar] [CrossRef]
- Wijnant, I.L.; van den Brink, H.W.; Stepek, A. North Sea Wind Climatology Part 1: A Review of Existing Wind Atlases; KNMI Tech. Rep. TR-342; KNMI: De Bilt, The Netherlands, 2014. [Google Scholar]
- Troen, I.; Petersen, E.L. European Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 1989. [Google Scholar]
- Donkers, J.; Brand, A.; Eecen, P. Offshore Wind Atlas of the Dutch part of the North Sea. In Proceedings of the EWEA 2011, Brussels, Belgium, 14–17 March 2011. [Google Scholar]
- Hasager, C.B.; Badger, M.; Mouche, A.; Stoffelen, A.; Driesenaar, T.; Karagali, I.; Bingöl, F.; Pena Diaz, A.; Astrup, P.; Nielsen, M.; et al. NORSEWInD Satellite Wind Climatology; DTU-Wind-Energy-E-0007(EN); DTU Wind Energy; 2012. Available online: https://orbit.dtu.dk/en/publications/norsewind-satellite-wind-climatology (accessed on 10 December 2020).
- SenterNovem. Windkaart van Nederland op 100 m Hoogte. Available online: https://docplayer.nl/7262374-Windkaart-van-nederland-op-100-m-hoogte.html (accessed on 25 November 2020).
- KNMI North Sea Wind Atlas. Available online: http://projects.knmi.nl/knw/index.html (accessed on 25 November 2020).
- Stepek, A.; Savenije, M.; van den Brink, H.W.; Wijnant, I.L. Validation of KNW Atlas with Publicly Available Mast Observations; KNMI Tech. Rep. TR-352; KNMI: De Bilt, The Netherlands, 2015. [Google Scholar]
- Wijnant, I.L.; Marseille, G.J.; Stoffelen, A.; van den Brink, H.W.; Stepek, A. Validation of KNW Atlas with Scatterometer Winds; KNMI Tech. Rep. TR-353; KNMI: De Bilt, The Netherlands, 2015. [Google Scholar]
- Dutch Offshore Wind Atlas. Available online: http://www.dutchoffshorewindatlas.nl (accessed on 25 November 2020).
- Wijnant, I.; van Ulft, B.; van Stratum, B.; Barkmeijer, J.; Onvlee, J.; de Valk, C.; Knoop, S.; Kok, S.; Klein Baltink, H.; Stepek, A. The Dutch Offshore Wind Atlas (DOWA): Description of the dataset. KNMI Tech. Rep. 2019, TR-380. Available online: https://www.dutchoffshorewindatlas.nl/publications/reports/2019/12/05/knmi-report-dowa-dataset (accessed on 25 November 2020).
- Duncan, J.B.; Marseille, G.J.; Wijnant, I.L. DOWA Validation against ASCAT Satellite Winds. TNO Report 2018 R11649. 2018. Available online: https://www.dutchoffshorewindatlas.nl/publications/reports/2019/01/18/tno-report-dowa-validation-against-ascat-satellite-winds (accessed on 25 November 2020).
- Duncan, J.B.; Wijnant, I.L.; Knoop, S. DOWA Validation against Offshore Meteorological Mast and Lidar Measurements. TNO Report 2019 R10062. 2019. Available online: https://www.dutchoffshorewindatlas.nl/publications/reports/2019/05/21/tno-report-dowa-validation-against-offshore-mast-and-lidar-measurements (accessed on 25 November 2020).
- Van Stratum, B.J.H.; Basu, S.; Wijnant, I.L.; Barkmeijer, J.; Onvlee, J.; Siebesma, A.P. Wind Turbine Parametrisation in HARMONIE-AROME. KNMI Tech. Rep. 2019, TR-377. Available online: https://www.dutchoffshorewindatlas.nl/publications/reports/2019/12/06/knmi-report-wind-turbine-parameterisation (accessed on 25 November 2020).
- Petersen, E.L.; Troen, I.; Ejsing Jørgensen, H.; Mann, J. The new European wind atlas. Energy Bull. 2014, 17, 34. [Google Scholar]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting model: Overview, system efforts, and future directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717. [Google Scholar] [CrossRef]
- Hallgren, C.; Arnqvist, J.; Ivanell, S.; Körnich, H.; Vakkari, V.; Sahlée, E. Looking for an Offshore Low-Level Jet Champion among Recent Reanalyses: A Tight Race over the Baltic Sea. Energies 2020, 13, 3670. [Google Scholar] [CrossRef]
- Kalverla, P.C.; Holtslag, A.A.M.; Ronda, R.J.; Steeneveld, G.J. Quality of wind characteristics in recent wind atlases over the North Sea. Q. J. R. Meteorol. Soc. 2020, 146, 1. [Google Scholar] [CrossRef]
- Seity, Y.; Brousseau, P.; Malardel, S.; Hello, G.; Bénard, P.; Bouttier, F.; Lac, C.; Masson, V. The AROME-France Convective-Scale Operational Model. Mon. Weather Rev. 2010, 139, 976. [Google Scholar] [CrossRef]
- Bengtsson, L.; Andraea, U.; Aspelien, T.; Batrak, Y.; Calvo, J.; de Rooy, W.; Gleeson, E.; Hansen-Sass, B.; Homleid, M.; Hortal, M.; et al. The Harmonie–Arome Model Configuration in the Aladin–Hirlam NWP System. Mon. Weather Rev. 2017, 145, 1919. [Google Scholar] [CrossRef]
- De Rooy, W.C.; de Vries, H. HARMONIE verification and evaluation. HIRLAM Tech. Rep. 2017, 70. Available online: http://www.hirlam.org/index.php/hirlam-documentation/doc_download/1805-hirlam-technicalreport-70 (accessed on 10 December 2020).
- Masson, V.; Champeaux, J.L.; Chauvin, F.; Meriguet, C.; Lacaze, R. A global dataset of land surface parameters at 1-km resolution in meteorological and climate models. J. Clim. 2003, 16, 1261. [Google Scholar] [CrossRef]
- Faroux, S.; Kaptué Tchuenté, A.T.; Roujean, J.L.; Masson, V.; Martin, E.; Moigne, P.L. ECOCLIMAP-II/Europe: A twofold database of ecosystems and surface parameters at 1km resolution based on satellite information for use in land surface, meteorological and climate models. Geosci. Model Dev. 2013, 6, 563. [Google Scholar] [CrossRef]
- Geertsema, G.; van den Brink, H. Windkaart van Nederland op 100 m Hoogte; KNMI Tech. Rep. TR-351; KNMI: De Bilt, The Netherlands, 2014. [Google Scholar]
- Van Ulden, A.P.; Wieringa, J. Atmospheric boundary layer research at Cabauw. Bound. Layer Meteorol. 1996, 78, 39. [Google Scholar] [CrossRef]
- Verkaik, J.W.; Holtslag, A.A.M. Wind profiles, momentum fluxes and roughness lengths at Cabauw revisited. Bound. Layer Meteorol. 2007, 122, 701. [Google Scholar] [CrossRef]
- Bosveld, F.C. The Cabauw In-Situ Observational Program 2000—Present: Instruments, Calibrations and Set-Up; KNMI Tech. Rep. TR-384; KNMI: De Bilt, The Netherlands, 2020. [Google Scholar]
- Van den Brink, H.W.; Bosveld, F.C. Bringing modelled and observed surface winds together. Int. J. Climatol. 2017, 37, 4783. [Google Scholar] [CrossRef]
- Baas, P.; de Rooy, W.C.; Onvlee, J. (Royal Netherlands Meteorological Institute, De Bilt, Netherlands). Personal communication. 2019. [Google Scholar]
- Albergel, C.; Boone, A.; Belamari, S.; Decharme, B.; Dumont, M.; Moigne, P.L.; Masson, V. SURFEX Scientific Documentation. SURFEX V8.1 2018, 3. Available online: http://www.umr-cnrm.fr/surfex/IMG/pdf/surfex_scidoc_v8.1.pdf (accessed on 10 December 2020).
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]


| Height (m) | Slope | Offset (m/s) | ||||
|---|---|---|---|---|---|---|
| DOWA | KNW | DOWA | KNW | DOWA | KNW | |
| 10 | 0.91 | 0.90 | 0.20 | 0.46 | 0.87 | 0.84 |
| 20 | 0.88 | 0.89 | 0.25 | 0.48 | 0.87 | 0.84 |
| 40 | 0.91 | 0.92 | 0.51 | 0.53 | 0.87 | 0.84 |
| 80 | 0.92 | 0.90 | 0.55 | 0.70 | 0.87 | 0.84 |
| 140 | 0.93 | 0.90 | 0.58 | 0.90 | 0.88 | 0.85 |
| 200 | 0.94 | 0.90 | 0.61 | 0.95 | 0.90 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knoop, S.; Ramakrishnan, P.; Wijnant, I. Dutch Offshore Wind Atlas Validation against Cabauw Meteomast Wind Measurements. Energies 2020, 13, 6558. https://doi.org/10.3390/en13246558
Knoop S, Ramakrishnan P, Wijnant I. Dutch Offshore Wind Atlas Validation against Cabauw Meteomast Wind Measurements. Energies. 2020; 13(24):6558. https://doi.org/10.3390/en13246558
Chicago/Turabian StyleKnoop, Steven, Pooja Ramakrishnan, and Ine Wijnant. 2020. "Dutch Offshore Wind Atlas Validation against Cabauw Meteomast Wind Measurements" Energies 13, no. 24: 6558. https://doi.org/10.3390/en13246558
APA StyleKnoop, S., Ramakrishnan, P., & Wijnant, I. (2020). Dutch Offshore Wind Atlas Validation against Cabauw Meteomast Wind Measurements. Energies, 13(24), 6558. https://doi.org/10.3390/en13246558







