Design and Implementation of Model Predictive Control Based PID Controller for Industrial Applications
Abstract
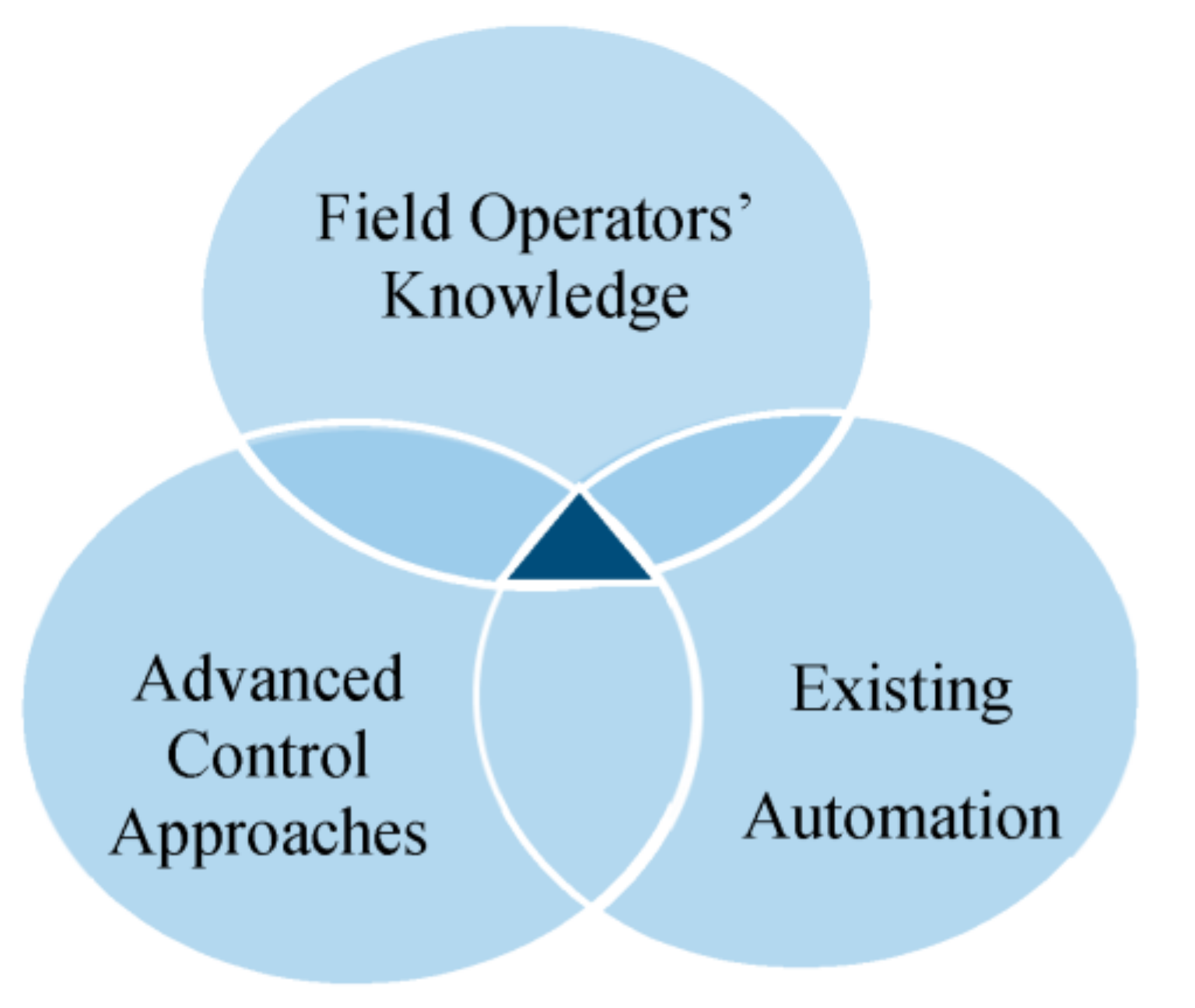
:1. Introduction
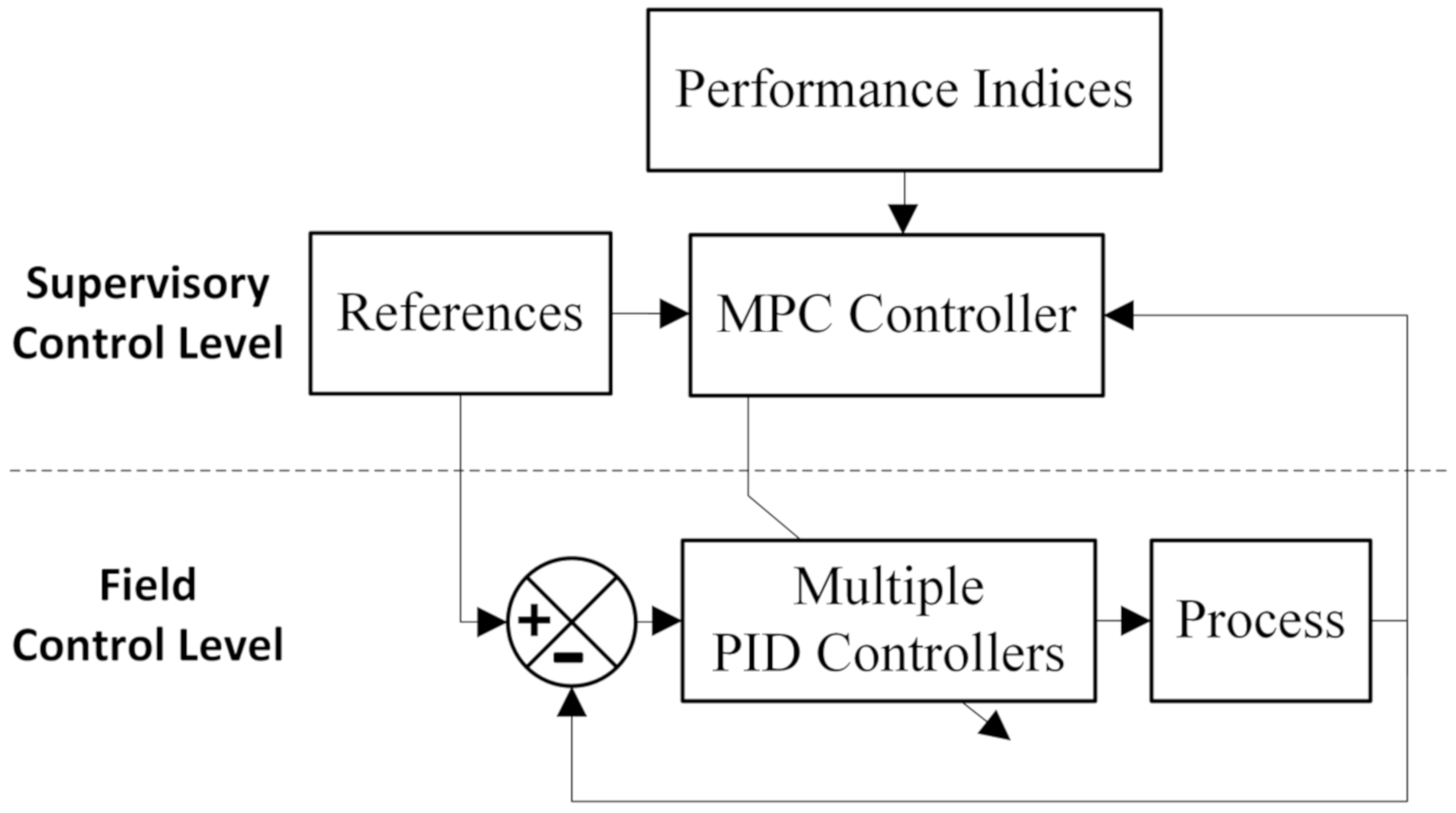
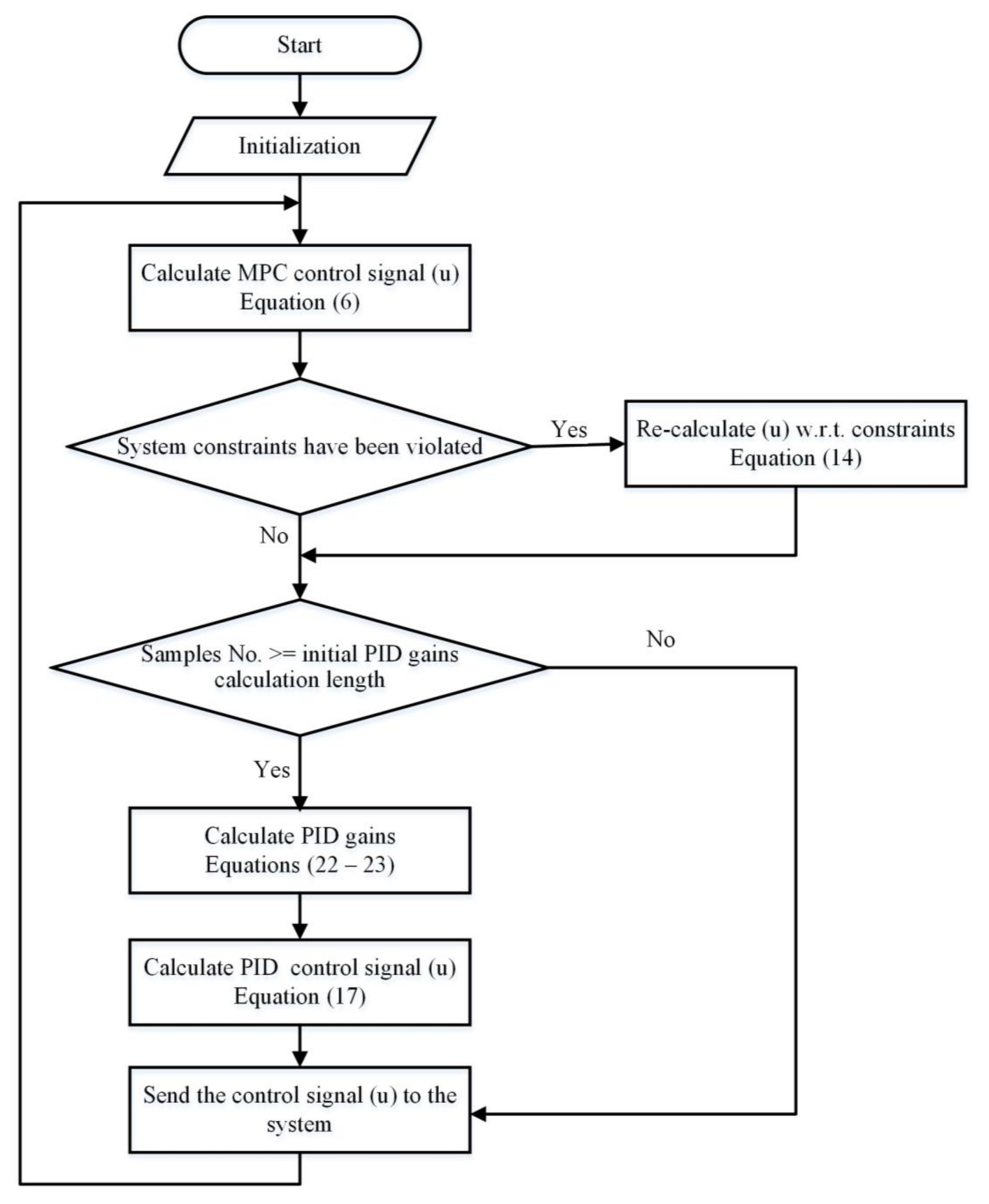
2. The Proposed Algorithm
2.1. MPC Design
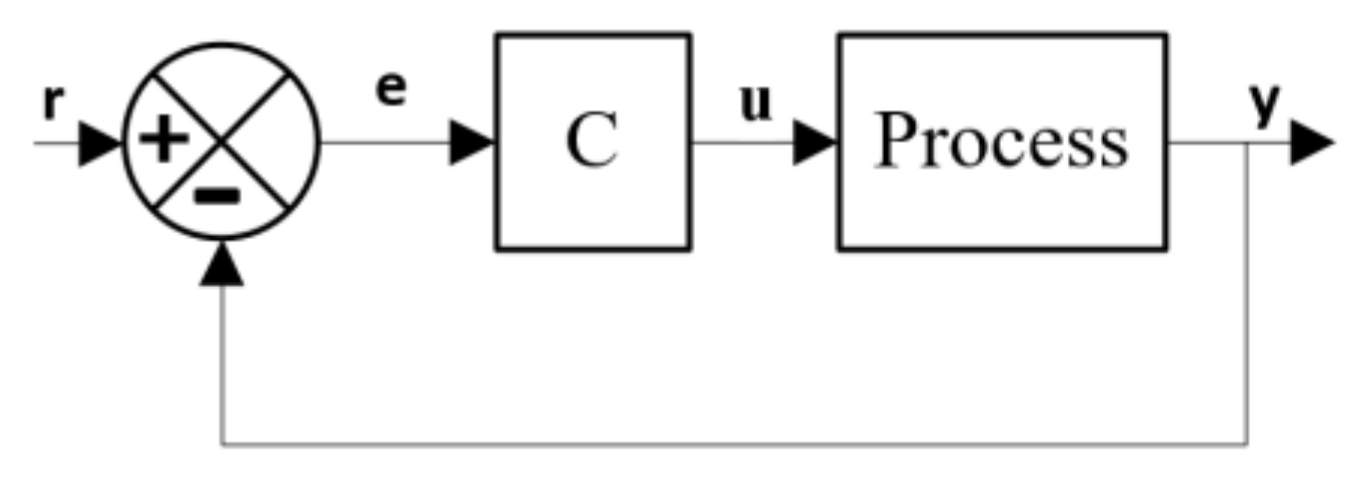
2.2. PID Controller Tuning
3. Simulation
4. Experimental Work
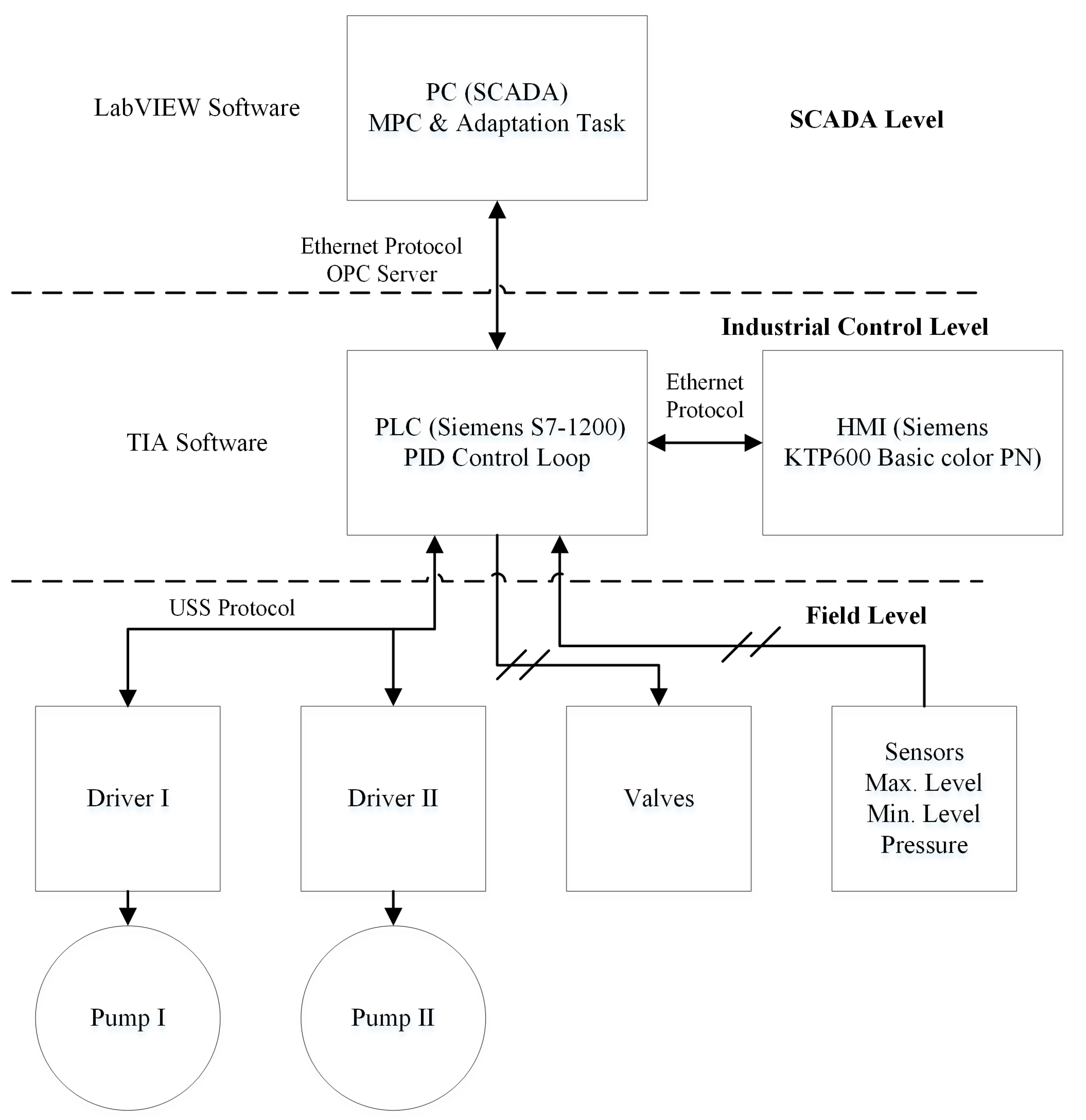
4.1. System Description
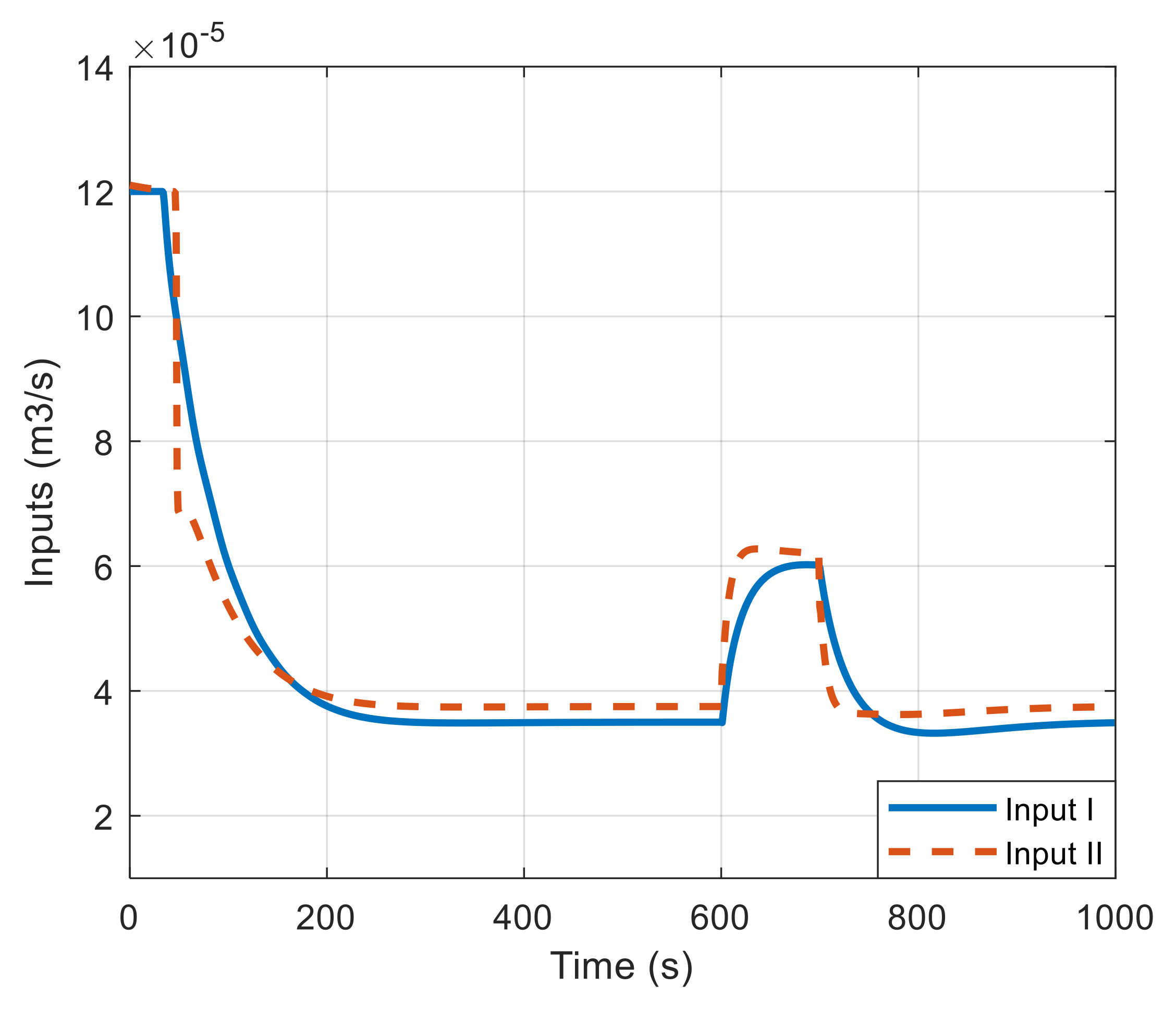
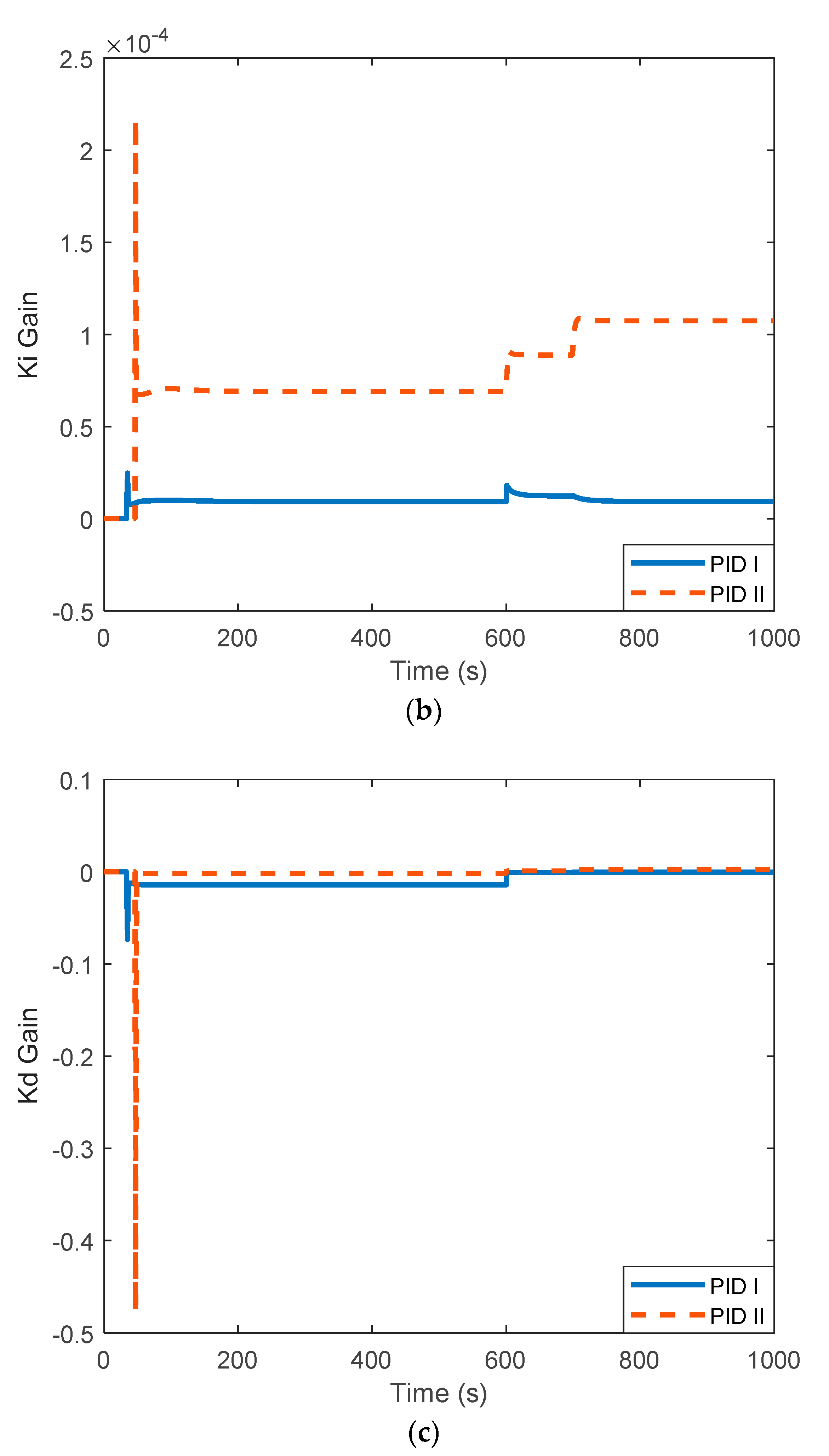
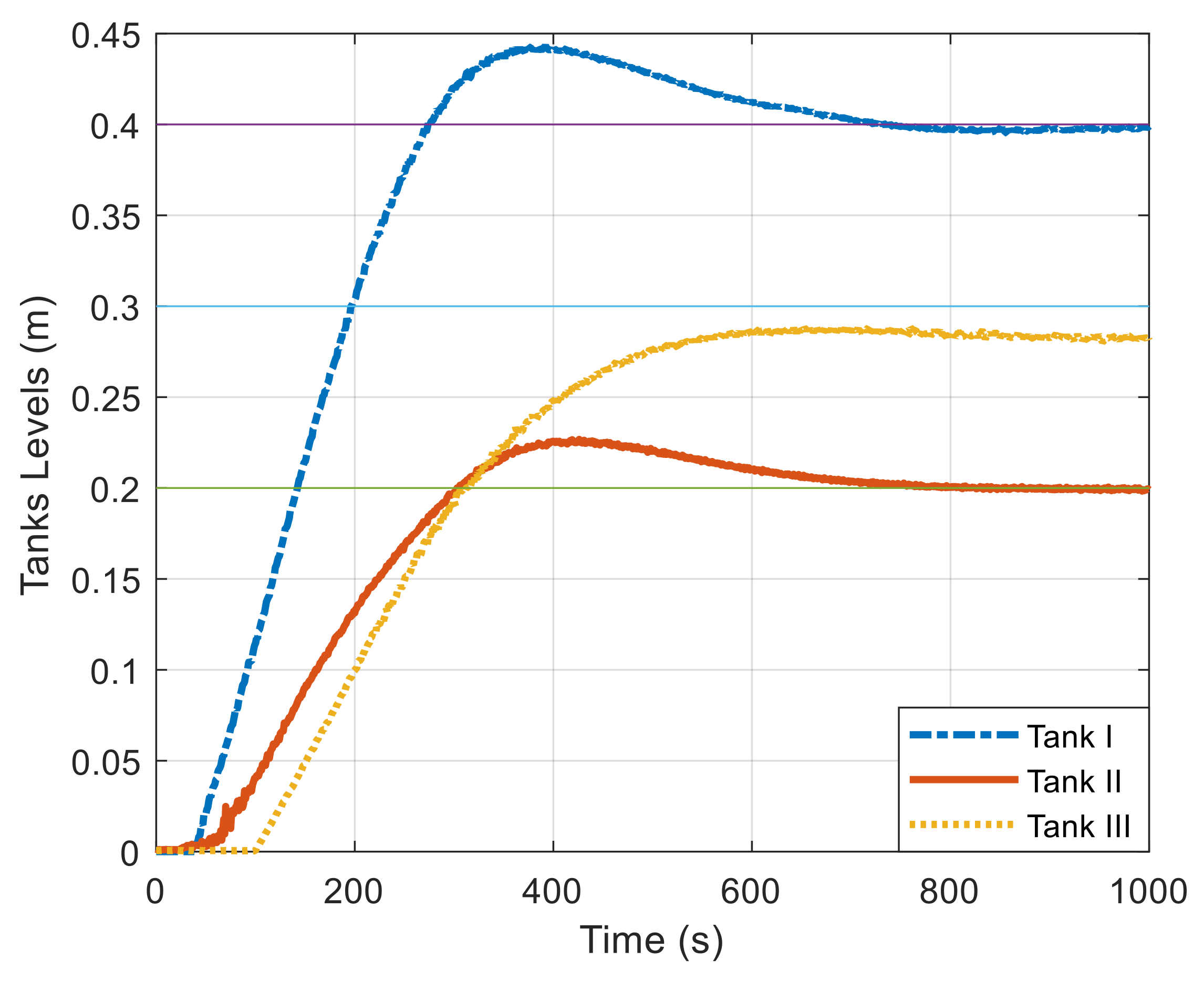
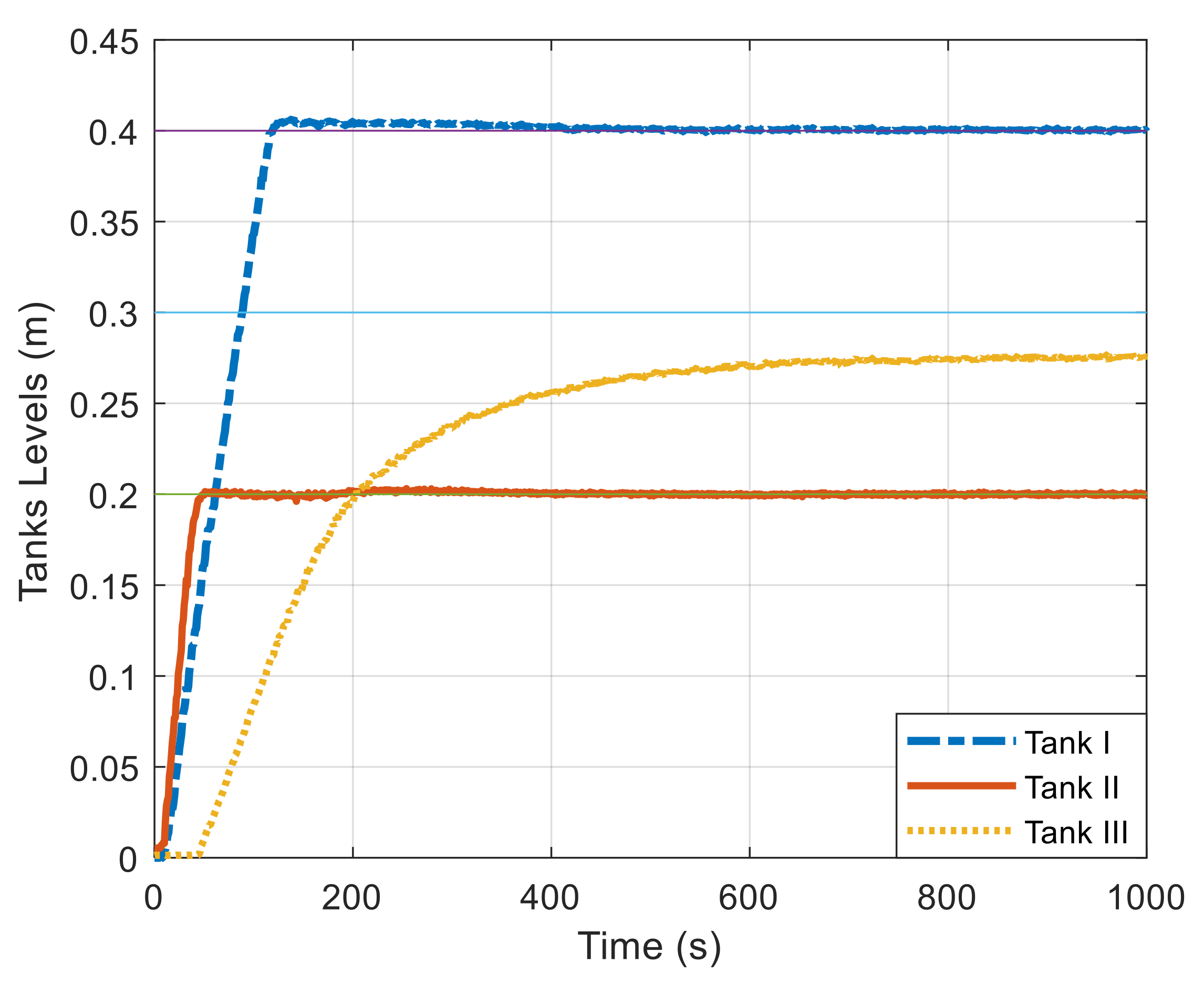
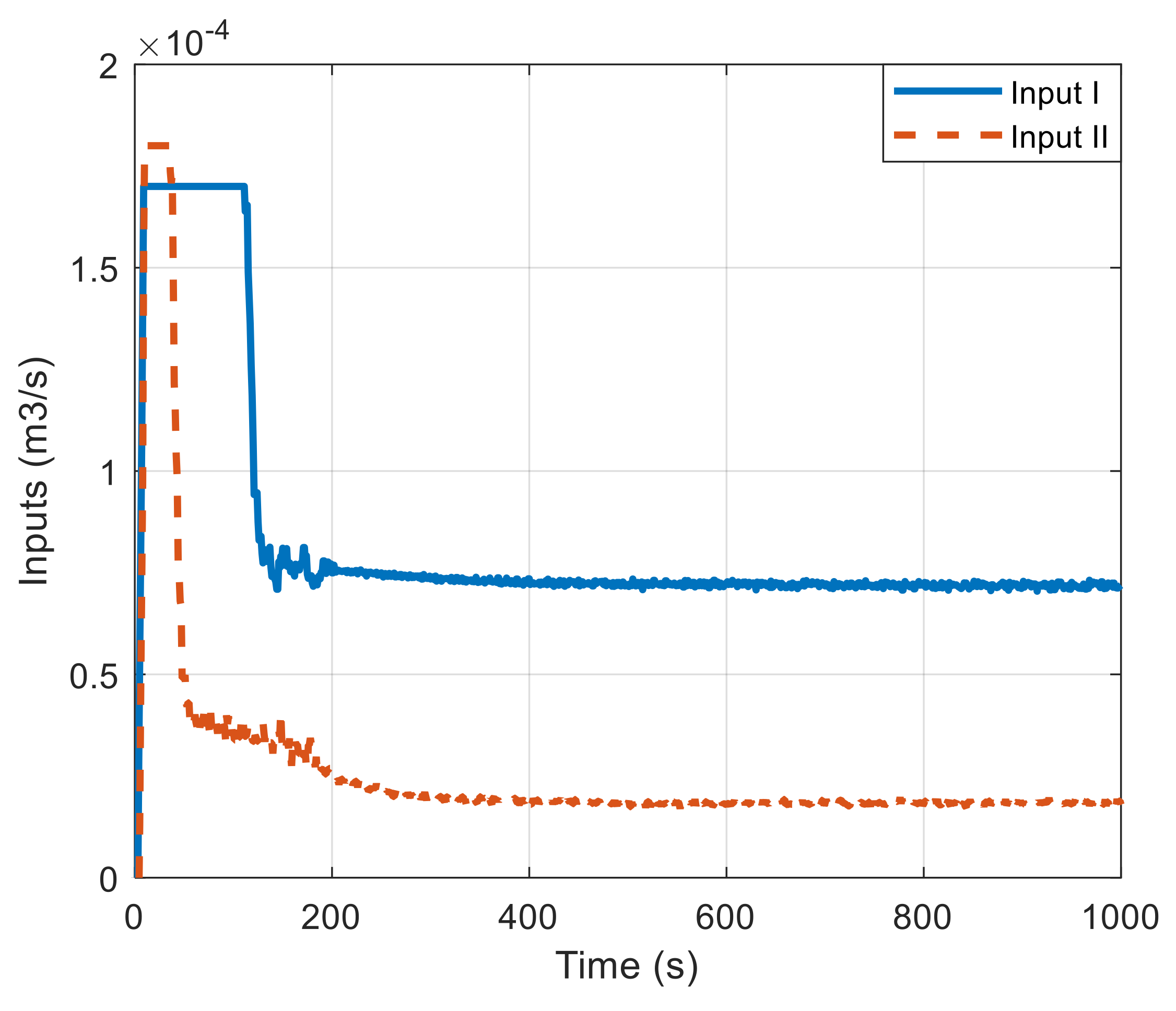
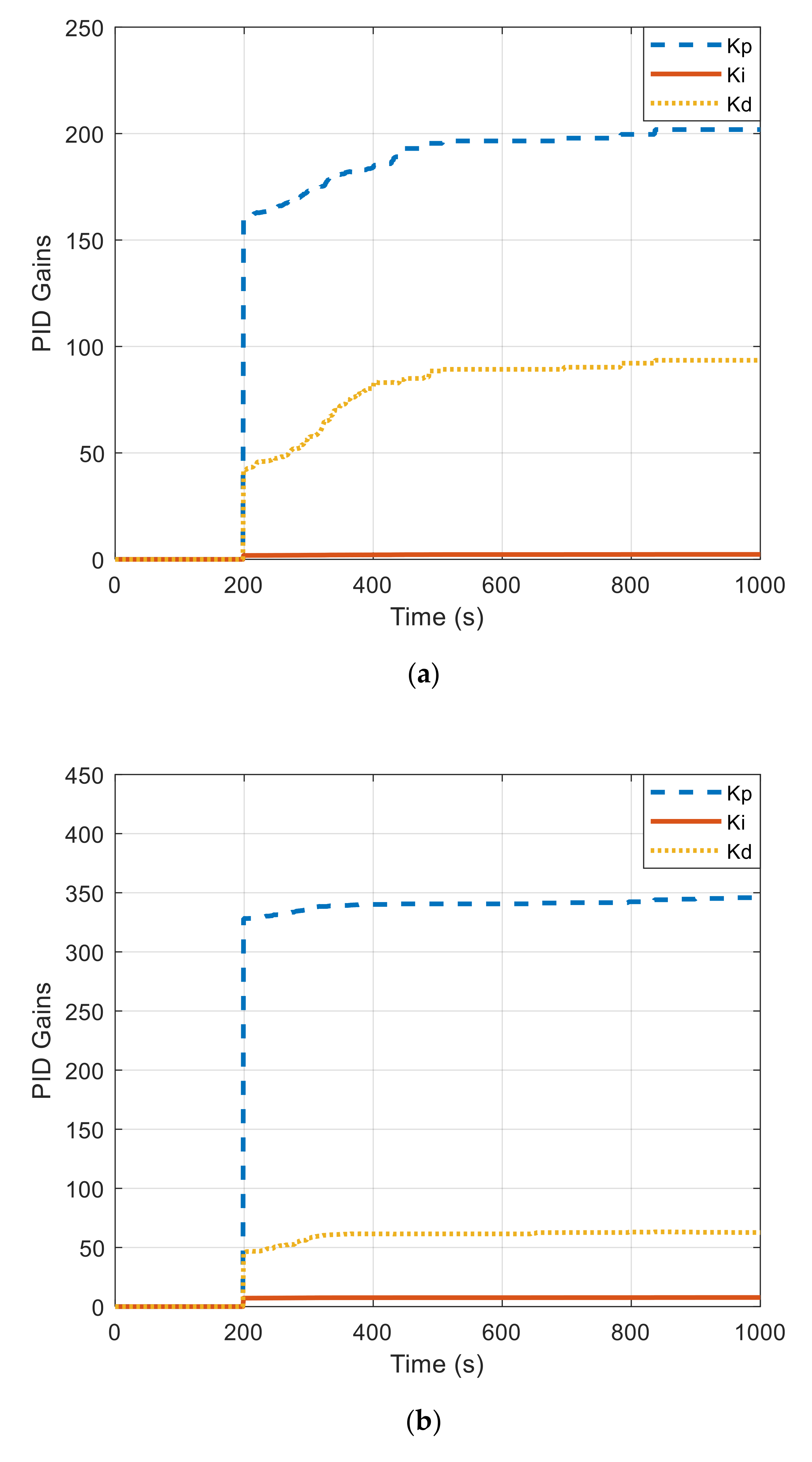
4.2. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vandoren, V. Advances in Control Loop Optimization. Control Engineering 1 May 2008. Available online: https://www.controleng.com/articles/advances-in-control-loop-optimization (accessed on 15 July 2016).
- Taghizadeh, M.; Yarmohammadi, M.J. Development of a Self-tuning PID Controller on Hydraulically Actuated Stewart Platform Stabilizer with Base Excitation. Int. J. Control. Autom. Syst. 2018, 16, 2990–2999. [Google Scholar] [CrossRef]
- Wade, H.L. Basic and Advanced Regulatory Control: System Design and Application; ISA: Durham, NC, USA, 2017. [Google Scholar]
- Visioli, A. Practical PID Control; Springer Science and Business Media LLC: Berlin, Germany, 2006. [Google Scholar]
- Malouche, I.; Bouani, F. A New Adaptive Partially Decentralized PID Controller for Non-square Discrete-time Linear Parameter Varying Systems. Int. J. Control. Autom. Syst. 2018, 16, 1670–1680. [Google Scholar] [CrossRef]
- Nishikawa, Y.; Sannomiya, N.; Ohta, T.; Tanaka, H. A method for auto-tuning of PID control parameters. Automatica 1984, 20, 321–332. [Google Scholar] [CrossRef]
- Gyöngy, I.; Clarke, D. On the automatic tuning and adaptation of PID controllers. Control. Eng. Pract. 2006, 14, 149–163. [Google Scholar] [CrossRef]
- Li, M.; Zhou, P.; Zhao, Z.; Zhang, J. Two-degree-of-freedom fractional order-PID controllers design for fractional order processes with dead-time. ISA Trans. 2016, 61, 147–154. [Google Scholar] [CrossRef] [Green Version]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process. Control. 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Begum, K.G.; Rao, A.S.; Radhakrishnan, T. Enhanced IMC based PID controller design for non-minimum phase (NMP) integrating processes with time delays. ISA Trans. 2017, 68, 223–234. [Google Scholar] [CrossRef]
- Wang, Q.; Lu, C.; Pan, W. IMC PID controller tuning for stable and unstable processes with time delay. Chem. Eng. Res. Des. 2016, 105, 120–129. [Google Scholar] [CrossRef]
- Savran, A.; Kahraman, G. A fuzzy model based adaptive PID controller design for nonlinear and uncertain processes. ISA Trans. 2014, 53, 280–288. [Google Scholar] [CrossRef]
- Fadaei, A.; Salahshoor, K. A novel real-time fuzzy adaptive auto-tuning scheme for cascade PID controllers. Int. J. Control. Autom. Syst. 2011, 9, 823–833. [Google Scholar] [CrossRef]
- Freire, H.; Oliveira, P.B.M.; Pires, E.J.S. From single to many-objective PID controller design using particle swarm optimization. Int. J. Control. Autom. Syst. 2017, 15, 918–932. [Google Scholar] [CrossRef]
- Chiou, J.-S.; Tsai, S.-H.; Liu, M.-T. A PSO-based adaptive fuzzy PID-controllers. Simul. Model. Pract. Theory 2012, 26, 49–59. [Google Scholar] [CrossRef]
- Sharma, R.; Kumar, V.; Gaur, P.; Mittal, A.P. An adaptive PID like controller using mix locally recurrent neural network for robotic manipulator with variable payload. ISA Trans. 2016, 62, 258–267. [Google Scholar] [CrossRef] [PubMed]
- Reynoso-Meza, G.; Carrillo-Ahumada, J.; Boada, Y.; Picó, J. PID controller tuning for unstable processes using a multi-objective optimisation design procedure. Ifac-Pap. 2016, 49, 284–289. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Du, W. Design of PID controller based on a self-adaptive state-space predictive functional control using extremal optimization method. J. Frankl. Inst. 2018, 355, 2197–2220. [Google Scholar] [CrossRef]
- Çetin, M.; Iplikci, S. A novel auto-tuning PID control mechanism for nonlinear systems. ISA Trans. 2015, 58, 292–308. [Google Scholar] [CrossRef]
- Agarwal, R. How Advanced Process Control Lowers Cost and Enhances Industrial Production Efficiency; Schneider Electric: Rueil-Malmaison, France, 2014. [Google Scholar]
- Mehta, B.R.; Reddy, Y.J. Chapter 1—Industrial automation. In Industrial Process Automation Systems; Mehta, B.R., Reddy, Y.J., Eds.; Butterworth-Heinemann: Oxford, UK, 2015; pp. 1–36. [Google Scholar]
- Omer, A.I.; Taleb, M.M. Architecture of Industrial Automation Systems. Eur. Sci. J. 2014, 10, 273–283. [Google Scholar]
- Agundis-Tinajero, G.; Segundo-Ramírez, J.; Visairo-Cruz, N.; Savaghebi, M.; Guerrero, J.M.; Barocio, E. Power flow modeling of islanded AC microgrids with hierarchical control. Int. J. Electr. Power Energy Syst. 2019, 105, 28–36. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Qin, J.-C.; Dong, Z.-Y.; Liu, S.-A.; Zheng, H.-L. Multilayer hierarchical control for robotic coax-helicopter based on the H∞ robustness and mixing control scheme. Adv. Mech. Eng. 2017, 9, 1687814017720088. [Google Scholar] [CrossRef]
- Abd-Elgeliel, M.; Badreddin, E.; Gambier, A. Application of model predictive control for fault tolerant system using dynamic safety margin. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar]
- Zhang, J.; Yang, H.; Li, M.; Wang, Q. Robust Model Predictive Control for Uncertain Positive Time-delay Systems. Int. J. Control. Autom. Syst. 2019, 17, 307–318. [Google Scholar] [CrossRef]
- Lee, J.H. Model predictive control: Review of the three decades of development. Int. J. Control. Autom. Syst. 2011, 9, 415–424. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, T.; Giangrande, P.; Galea, M.; Garcia, C.; Rivera, M.; Wheeler, P.; Rodriguez, J. Voltage Utilization Enhancement of Dual Inverters by Model Predictive Control for Motor Drive Applications. In Proceedings of the IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Quanzhou, China, 31 May–2 June 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Supervisory model predictive controller (MPC) for residential HVAC systems: Implementation and experimentation on archetype sustainable house in Toronto. Energy Build. 2017, 154, 268–282. [Google Scholar] [CrossRef]
- Riverso, S.; Mancini, S.; Sarzo, F.; Ferrari-Trecate, G. Model Predictive Controllers for Reduction of Mechanical Fatigue in Wind Farms. IEEE Trans. Control. Syst. Technol. 2016, 25, 535–549. [Google Scholar] [CrossRef] [Green Version]
- Ouammi, A.; Achour, Y.; Zejli, D.; Dagdougui, H. Supervisory Model Predictive Control for Optimal Energy Management of Networked Smart Greenhouses Integrated Microgrid. IEEE Trans. Autom. Sci. Eng. 2020, 17, 117–127. [Google Scholar] [CrossRef]
- Sato, T. Design of a GPC-based PID controller for controlling a weigh feeder. Control. Eng. Pract. 2010, 18, 105–113. [Google Scholar] [CrossRef]
- Xu, M.; Li, S.; Qi, C.; Cai, W. Auto-tuning of PID controller parameters with supervised receding horizon optimization. ISA Trans. 2005, 44, 491–500. [Google Scholar] [CrossRef]
- Kubalčik, M.; Bobál, V. Adaptive control of three tank system: Comparison of two methods. In Proceedings of the 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 1041–1046. [Google Scholar]
- Abdelrauf, A.A.; Abdel-Geliel, M.; Zakzouk, E. Adaptive PID controller based on model predictive control. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 746–751. [Google Scholar]
- Abdelrauf, A.A.; Saad, W.W.; Hebala, A.; Galea, M. Model Predictive Control Based PID Controller for PMSM for Propulsion Systems. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–7. [Google Scholar]
- Maciejowski, J.M. Predictive Control: With Constraints; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Zhao, K.; Lü, X.; Zheng, W.; Huang, C. Direct relaxation of hard-constraint in Model Predictive Control. In Proceedings of the 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery, Sichuan, China, 29–31 May 2012; pp. 2366–2370. [Google Scholar]
- Li, Y.; Liu, J.; Wang, Y. Design approach of weighting matrices for LQR based on multi-objective evolution algorithm. In Proceedings of the 2008 International Conference on Information and Automation, Changsha, China, 20–23 June 2008; pp. 1188–1192. [Google Scholar]
- Ikonen, E.; Najim, K. Advanced Process Identification and Control; Informa UK Limited: London, UK, 2001. [Google Scholar]
- Noura, H.; Theilliol, D.; Ponsart, J.C.; Chamseddine, A. Fault-Tolerant Control Systems: Design and Practical Applications; Springer: London, UK, 2009. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA-The Instrumentation, Systems, and Automation Society: Pittsburg, PA, USA, 2006. [Google Scholar]
- Möller-Nehring, W.; Bohrer, W. Universal Serial Interface Protocol USS Protocol; Siemens Company: Munich, Germany, 1994. [Google Scholar]
- Galea, M.; Giangrande, P.; Madonna, V.; Buticchi, G. Reliability-Oriented Design of Electrical Machines: The Design Process for Machines’ Insulation Systems MUST Evolve. IEEE Ind. Electron. Mag. 2020, 14, 20–28. [Google Scholar] [CrossRef]

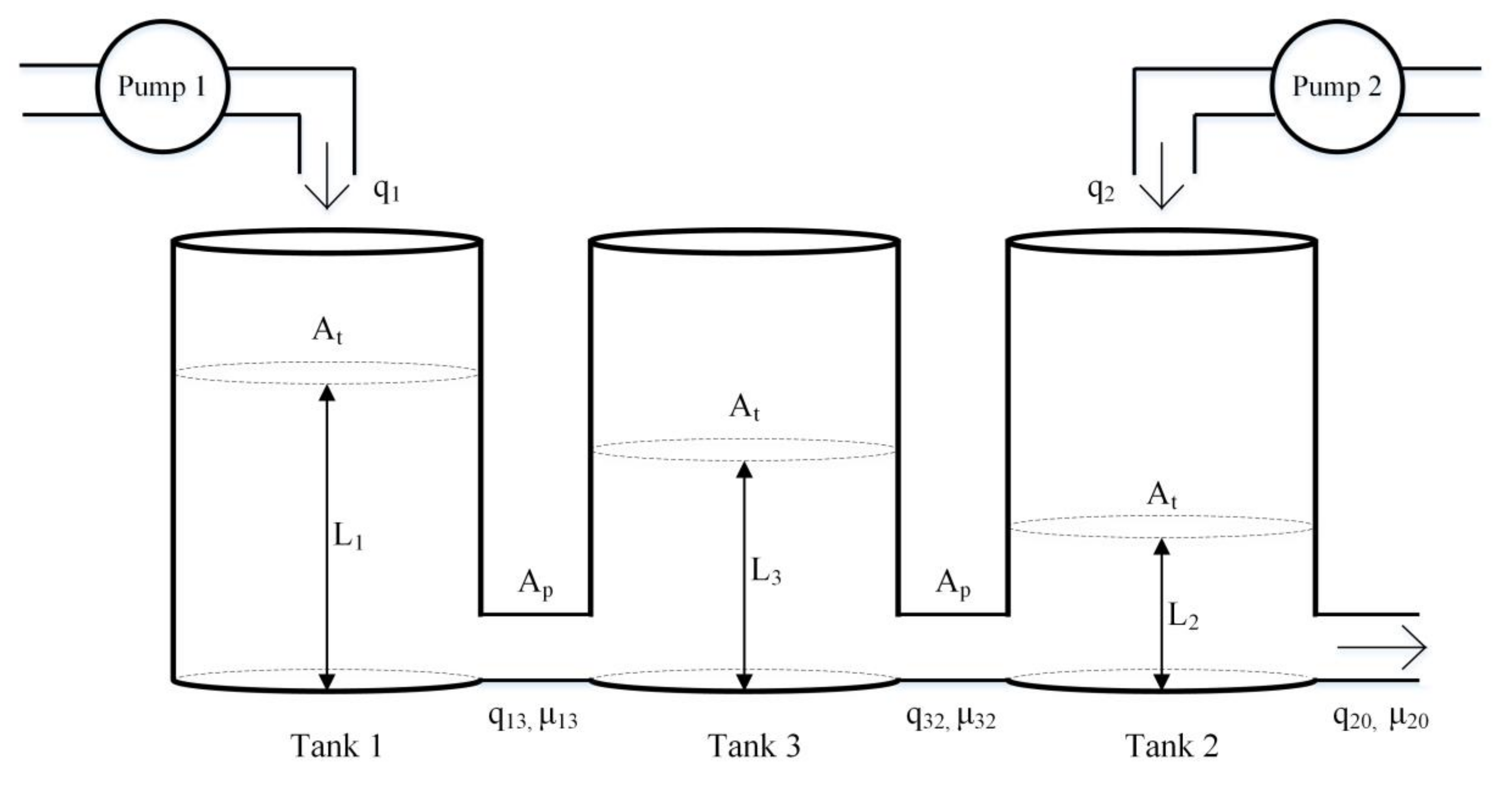





| Tank cross section area (At) | 0.0154 m2 |
| Pipe cross-section area (Ap) | 5 × 10−5 m2 |
| Outflow coefficient (µmn) | µ13 = 0.5, µ32 = 0.5, µ20 = 0.675 |
| Maximum flow rate constraint (Qmax) | 1.2 × 10−4 m3/s |
| Maximum level (Lmax) | 0.62 m |
| Operating point | Q1 = 0.35 × 10−4 m3/s, Q2 = 0.375 × 10−4 m3/s L10 = 0.4 m, L20 = 0.2 m, L30 = 0.3 m |
| PID I | PID II | ||
|---|---|---|---|
| KP | 4.29×10−4 | KP | 10.83 × 10−4 |
| KI | 5.32 × 10−6 | KI | 3.94 × 10−5 |
| KD | −1.42 × 10−4 | KD | −13.51 × 10−4 |
| Prediction horizon (ny) | 10 |
| Control horizon (nu) | 10 |
| Sampling time (Ts) | 1 s |
| Tank cross-section area (At) | 0.021 m2 |
| Pipe cross-section area (Ap) | 1.26677 × 10−4 m2 |
| Outflow coefficients (µmn) | |
| Maximum flow rates (Qmax) | Q1 = 1.7 × 10−4 m3/s (1350 RPM) Q2 = 1.8 × 10−4 m3/s (1350 RPM) |
| Maximum level (Lmax) | 0.65 m |
| Operating points | = 7.5 × 10−5 m3/s (875 RPM) = 1.7 × 10−5 m3/s (535 RPM) L10= 0.4 m L20= 0.2 m L30= 0.3 m |
| PID I | PID II | ||
|---|---|---|---|
| KP | 100 | KP | 100 |
| KI | 1 | KI | 1 |
| KD | 10 | KD | 10 |
| Controller | PID | MPC | MPC Based PID | |
|---|---|---|---|---|
| Criteria | ||||
| Performance | Settling Time (s) | 700 | 150 | 150 |
| Overshoot % | 10.9 | 0 | 0 | |
| Realization | Simple & centralized in PLC | Difficult & centralized in SCADA | Simple & distributed in PLC and SCADA | |
| Constraints | Not applicable | Easy to handle | Easy to handle | |
| Sampling time | Low | High | Low | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aboelhassan, A.; Abdelgeliel, M.; Zakzouk, E.E.; Galea, M. Design and Implementation of Model Predictive Control Based PID Controller for Industrial Applications. Energies 2020, 13, 6594. https://doi.org/10.3390/en13246594
Aboelhassan A, Abdelgeliel M, Zakzouk EE, Galea M. Design and Implementation of Model Predictive Control Based PID Controller for Industrial Applications. Energies. 2020; 13(24):6594. https://doi.org/10.3390/en13246594
Chicago/Turabian StyleAboelhassan, Ahmed, M. Abdelgeliel, Ezz Eldin Zakzouk, and Michael Galea. 2020. "Design and Implementation of Model Predictive Control Based PID Controller for Industrial Applications" Energies 13, no. 24: 6594. https://doi.org/10.3390/en13246594
APA StyleAboelhassan, A., Abdelgeliel, M., Zakzouk, E. E., & Galea, M. (2020). Design and Implementation of Model Predictive Control Based PID Controller for Industrial Applications. Energies, 13(24), 6594. https://doi.org/10.3390/en13246594






