Process Configuration Studies of Methanol Production via Carbon Dioxide Hydrogenation: Process Simulation-Based Optimization Using Artificial Neural Networks
Abstract
:1. Introduction
2. Process Simulation and Economic Evaluation
2.1. Process Simulation
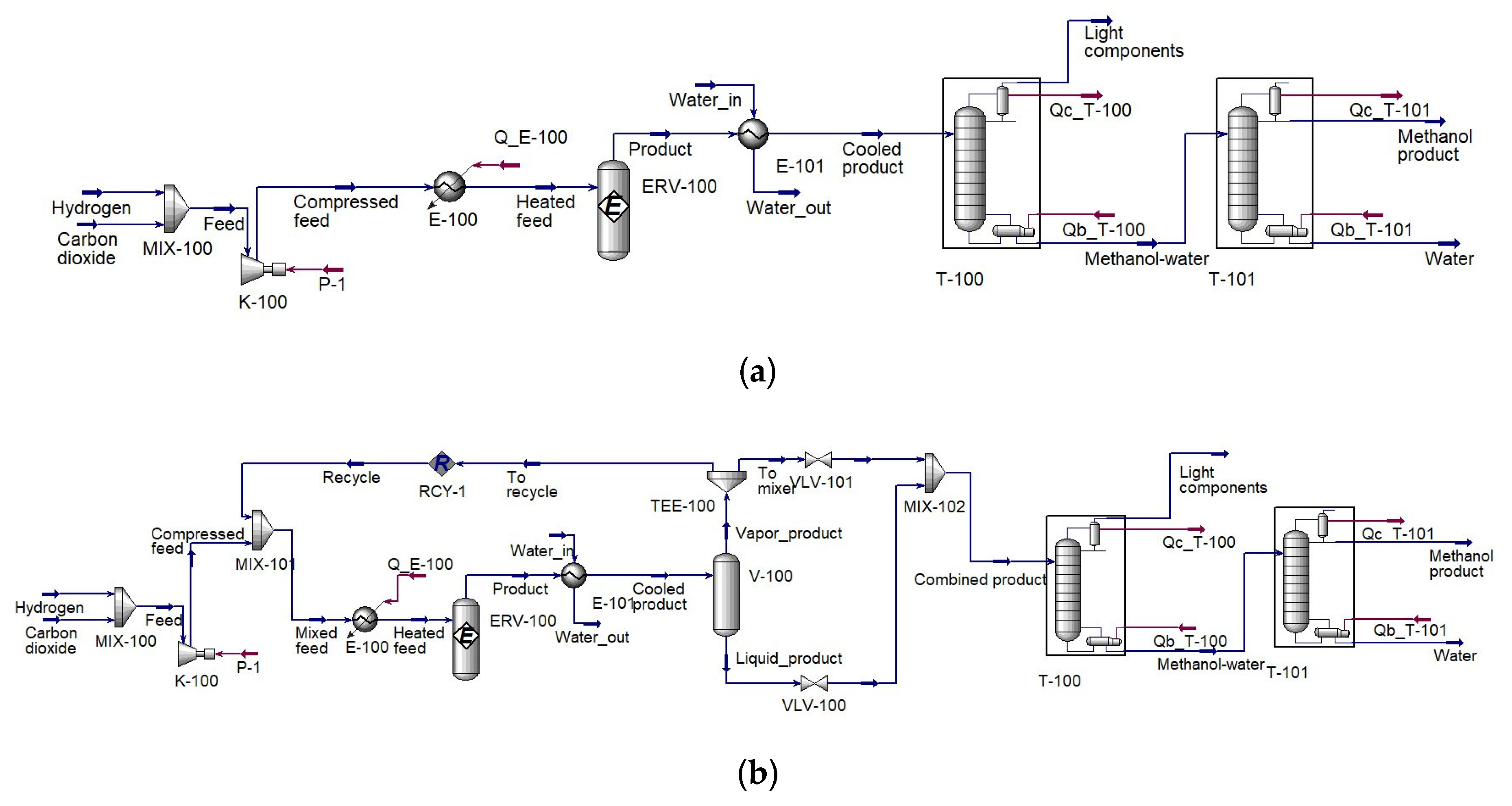
2.1.1. Configuration I: Once-Through Reactor Methanol Production
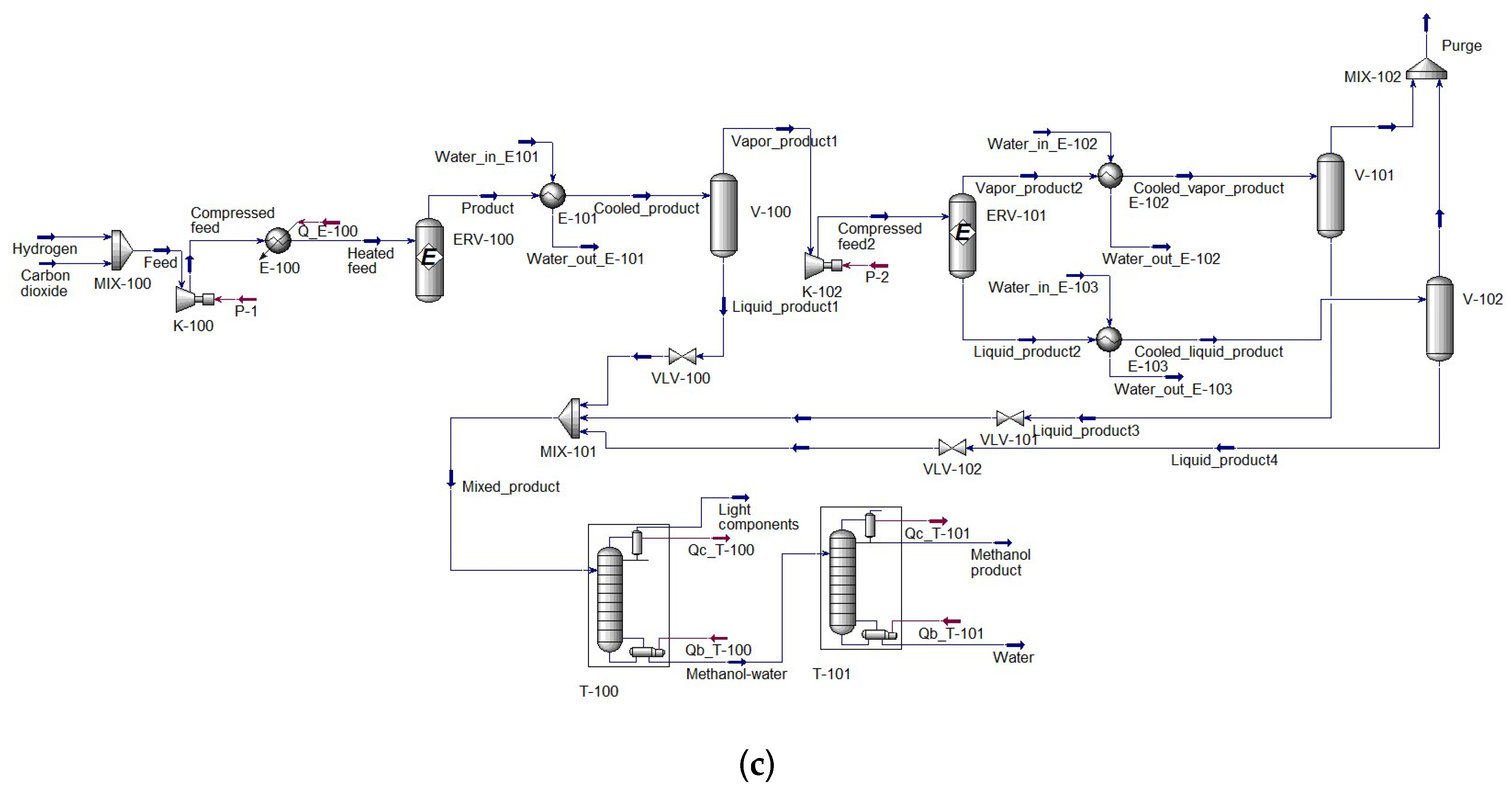
2.1.2. Configuration II: Methanol Production with a Recycle
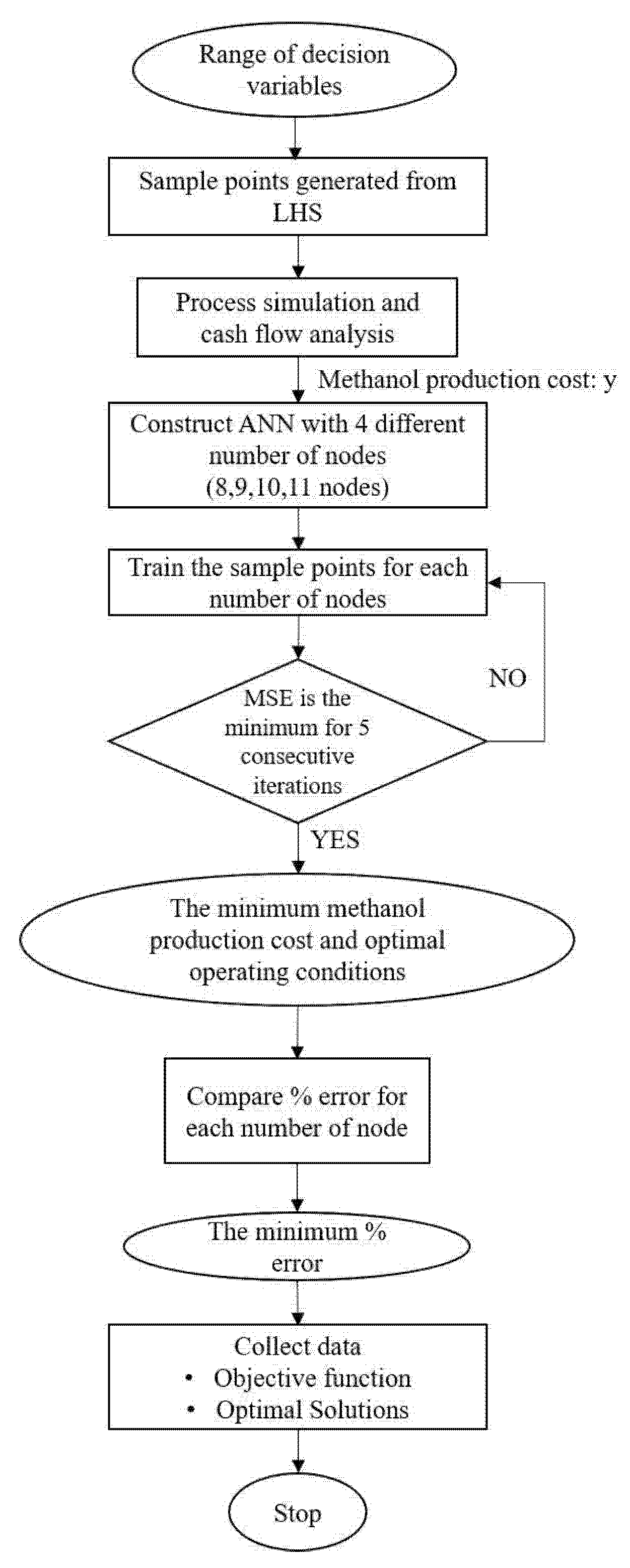
2.1.3. Configuration III: Methanol Production with Two Reactors in Series
2.2. Economic Evaluation
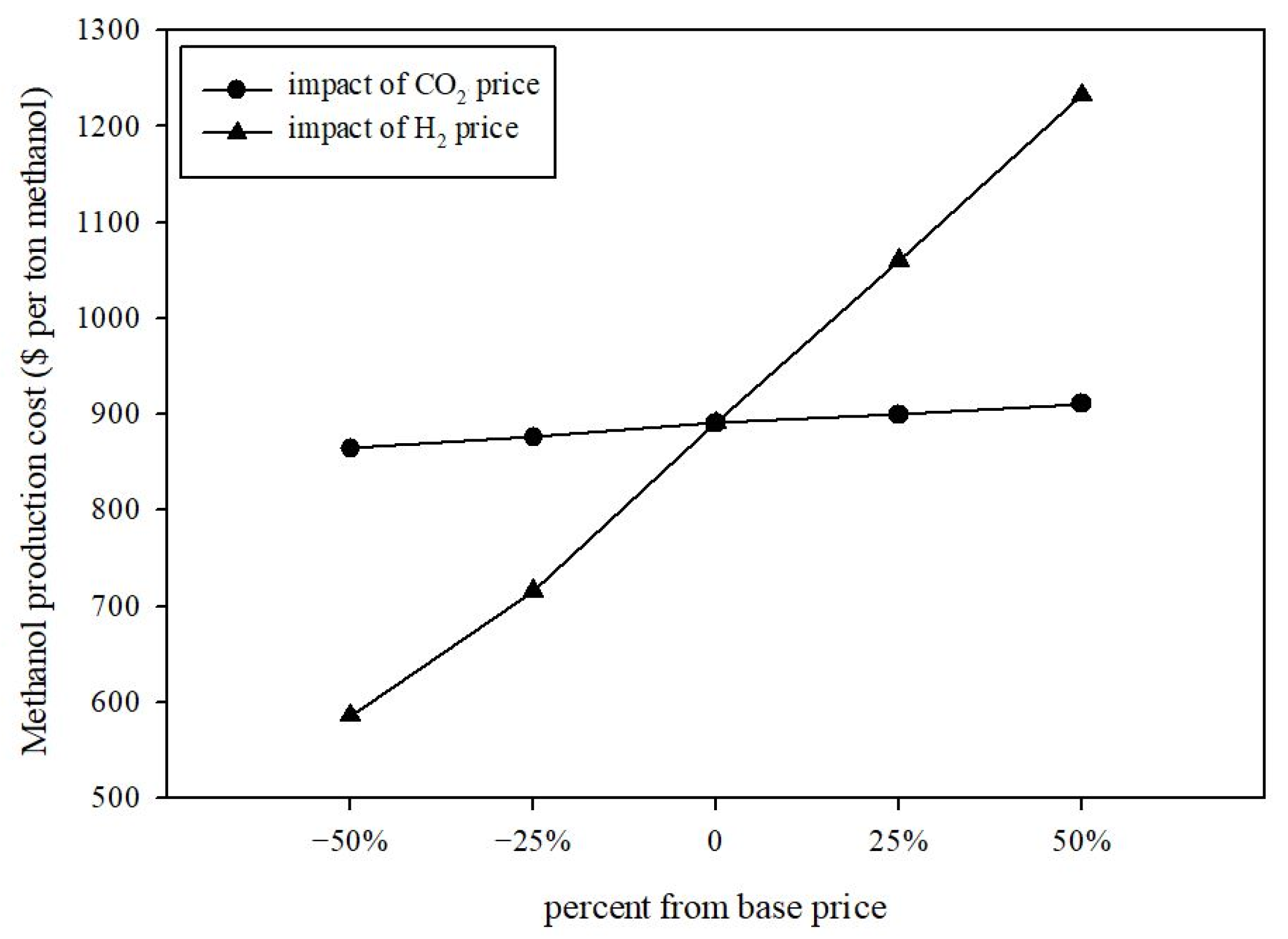
Price Sensitivity
3. Simulation-Optimization Methodology
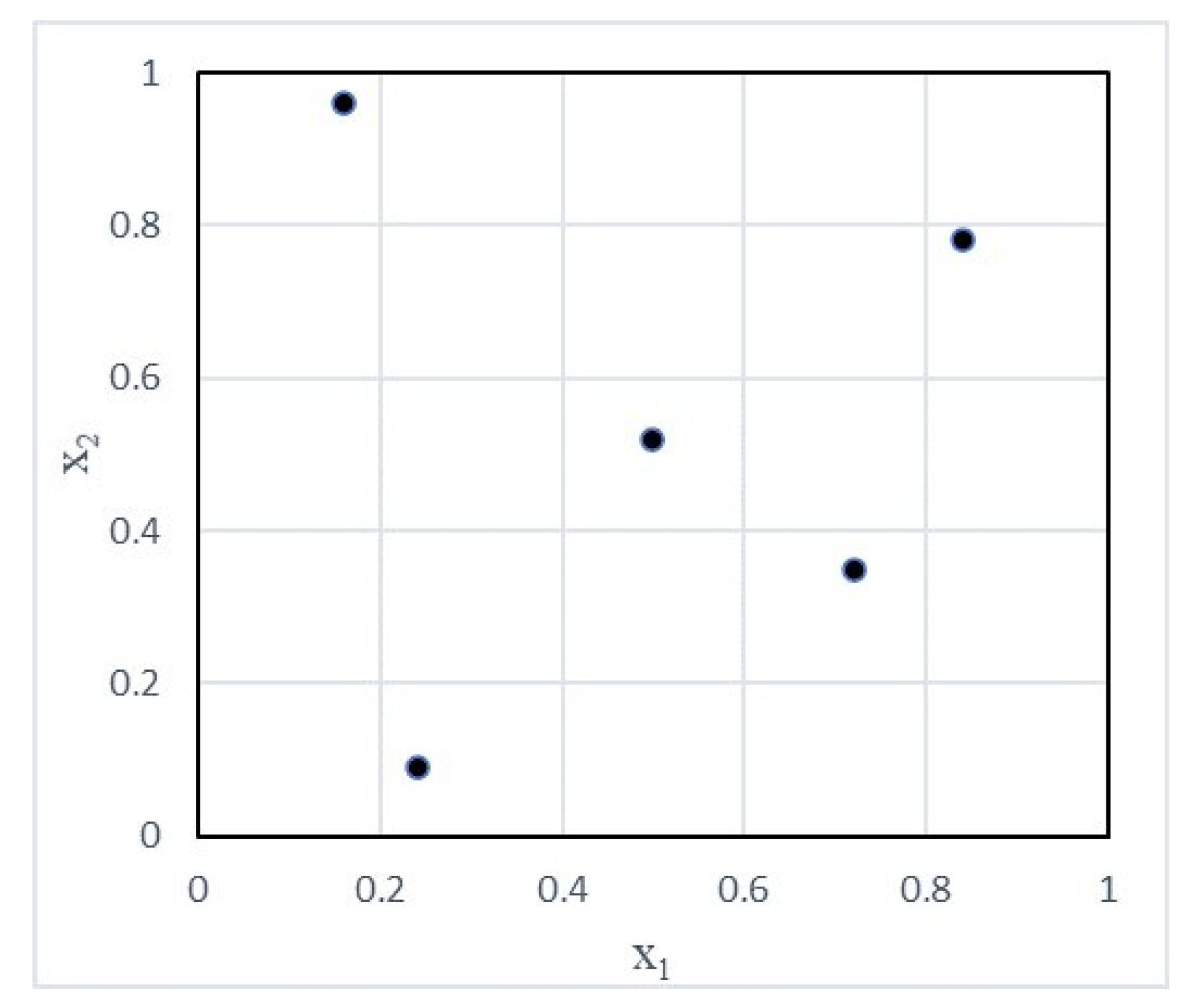
3.1. Latin Hypercube Sampling (LHS)
3.2. Artificial Neural Networks
3.3. Optimization Formulation
4. Results and Discussion
4.1. Price Sensitivity
4.2. Comparison of Different Process Configurations
4.3. The Optimal Solutions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Mukherjee, A.; Okolie, J.A.; Abdelrasoul, A.; Niu, C.H.; Dalai, A.K. Review of post-combustion carbon dioxide capture technologies using activated carbon. J. Environ. Sci. 2019, 83, 46–63. [Google Scholar] [CrossRef] [PubMed]
- Arena, F.; Mezzatesta, G.; Spadaro, L.; Trunfio, G. Latest Advances in the Catalytic Hydrogenation of Carbon Dioxide to Methanol/Dimethylether; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2014; pp. 103–130. [Google Scholar]
- Naims, H. Economics of carbon dioxide capture and utilization—A supply and demand perspective. Environ. Sci. Pollut. Res. 2016, 23, 22226–22241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowker, M. Methanol Synthesis from CO2 Hydrogenation. Chem. Cat Chem. 2019, 11, 4238–4246. [Google Scholar] [PubMed] [Green Version]
- Zander, S.; Kunkes, E.L.; Schuster, M.E.; Schumann, J.; Weinberg, G.; Teschner, D.; Jacobsen, N.; Schlögl, R.; Behrens, M. The Role of the Oxide Component in the Development of Copper Composite Catalysts for Methanol Synthesis. Angew. Chem. Int. Ed. 2013, 52, 6536–6540. [Google Scholar] [CrossRef] [PubMed]
- Bill, A. Carbon Dioxide Hydrogenation to Methanol at Low Pressure and Temperature. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 1998. Available online: https://www.semanticscholar.org/paper/Carbon-dioxide-hydrogenation-to-methanol-at-low-and-Bill/c1a6edf6b9b6f79aadd29b095b9a3ab0d44f45ab#citing-papers (accessed on 20 October 2020).
- Nexant. Market Analytics: Methanol and Derivatives—2018. 2018. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwjluLX_la_tAhVC73MBHaAACc8QFjAAegQIARAC&url=https%3A%2F%2Fwww.nexantsubscriptions.com%2Ffile%2F125740%2Fdownload%3Ftoken%3DZov46cz-&usg=AOvVaw0dmSgIX1sVUAq5zSR7rFAh (accessed on 20 October 2020).
- Liang, X.-L.; Dong, X.; Lin, G.-D.; Zhang, H.-B. Carbon nanotube-supported—ZnO catalyst for hydrogenation of CO2 to methanol. Appl. Catal. B Environ. 2009, 88, 315–322. [Google Scholar] [CrossRef]
- Liu, C.; Guo, X.; Guo, Q.; Mao, D.; Yu, J.; Lu, G. Methanol synthesis from CO2 hydrogenation over copper catalysts supported on MgO-modified TiO2. J. Mol. Catal. A Chem. 2016, 425, 86–93. [Google Scholar] [CrossRef]
- Jadhav, S.G.; Vaidya, P.D.; Bhanage, B.M.; Joshi, J.B. Catalytic carbon dioxide hydrogenation to methanol: A review of recent studies. Chem. Eng. Res. Des. 2014, 92, 2557–2567. [Google Scholar] [CrossRef]
- Tidona, B.; Koppold, C.; Bansode, A.; Urakawa, A.; Von Rohr, P.R. CO2 hydrogenation to methanol at pressures up to 950bar. J. Supercrit. Fluids 2013, 78, 70–77. [Google Scholar] [CrossRef]
- Machado, F.R.C.; Medeiros, J.L.D.; Araújo, O.F.Q. Comparative analysis of methanol production routes: Synthesis gas versus CO2 hydrogenation. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Bali, Indonesia, 7–9 January 2014; Available online: http://iieom.org/ieom2014/pdfs/294.pdf (accessed on 20 October 2020).
- Atsonios, K.; Panopoulos, K.D.; Kakaras, E. Thermocatalytic CO 2 hydrogenation for methanol and ethanol production: Process improvements. Int. J. Hydrogen Energy 2016, 41, 792–806. [Google Scholar] [CrossRef]
- Pellegrini, L.A.; Soave, G.; Gamba, S.; Langè, S. Economic analysis of a combined—Methanol production plant. Appl. Energy 2011, 88, 4891–4897. [Google Scholar] [CrossRef]
- Roh, K.; Nguyen, T.B.; Suriyapraphadilok, U.; Lee, J.H.; Gani, R. Development of sustainable CO2 conversion processes for the methanol production. In Computer Aided Chemical Engineering; Gernaey, K.V., Huusom, J.K., Gani, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1145–1150. [Google Scholar]
- Leonzio, G. Optimization through Response Surface Methodology of a Reactor Producing Methanol by the Hydrogenation of Carbon Dioxide. Processes 2017, 5, 62. [Google Scholar] [CrossRef] [Green Version]
- Matr, D.L. Process Modelling and Simulation of a Methanol Synthesis Plant Using Syngas Streams Obtained from Biomass; Politecnico di Milano: Milan, Italy, 2018. [Google Scholar]
- Ullmann’s Encyclopedia of Industrial Chemistry, VCH. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/14356007 (accessed on 20 October 2020).
- Leonzio, G.; Zondervan, E.; Foscolo, P.U. Methanol production by CO2 hydrogenation: Analysis and simulation of reactor performance. Int. J. Hydrogen Energy 2019, 44, 7915–7933. [Google Scholar] [CrossRef]
- Pérez-Fortes, M.; Schöneberger, J.C.; Boulamanti, A.; Tzimas, E. Methanol synthesis using captured CO2 as raw material: Techno-economic and environmental assessment. Appl. Energy 2016, 161, 718–732. [Google Scholar] [CrossRef]
- Borisut, P.; Nuchitprasittichai, A. Methanol Production via CO2 Hydrogenation: Sensitivity Analysis and Simulation—Based Optimization. Front. Energy Res. 2019, 7. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Li, J.; Du, W.; Qian, F. Adaptive Sampling for Surrogate Modelling with Artificial Neural Network and its Application in an Industrial Cracking Furnace. Can. J. Chem. Eng. 2016, 94, 262–272. [Google Scholar] [CrossRef]
- Eason, J.; Cremaschi, S. Adaptive sequential sampling for surrogate model generation with artificial neural networks. Comput. Chem. Eng. 2014, 68, 220–232. [Google Scholar] [CrossRef]
- Sudakov, O.; Koroteev, D.; Belozerov, B.; Burnaev, E. Artificial Neural Network Surrogate Modeling of Oil Reservoir: A Case Study. In Public-Key Cryptography—PKC 2018; Springer: Berlin/Heidelberg, Germany, 2019; pp. 232–241. [Google Scholar]
- Ye, J. Artificial neural network modeling of methanol production from syngas. Pet. Sci. Technol. 2019, 37, 629–632. [Google Scholar] [CrossRef]
- Vaferi, B.; Bahmani, M.; Babakhani, S.M.; Khademi, M.A. Modification and optimization of the industrial methanol production process. Indian J. Chem. Technol. 2014, 10, 51–59. [Google Scholar]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A. Analysis, Synthesis and Design of Chemical Processes, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Jenkins, S. CEPCI Updates: January 2018 (Prelim.) and December 2017 (Final), in January 2017. 2018. Available online: https://www.chemengonline.com/cepci-updates-january-2018-prelim-and-december-2017-final/?printmode=1 (accessed on 20 October 2020).
- Timperley, J. Renewable Hydrogen ‘Already Cost Competitive’, Say Researchers. November 2019. Available online: https://www.carbonbrief.org/renewable-hydrogen-already-cost-competative-say-researchers (accessed on 20 October 2020).
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]

| (a) | ||
| Decision Variables | Range | |
| Upper | Lower | |
| Pressure of the equilibrium reactor | 69 | 73 |
| Temperature of the equilibrium reactor | 189 | 193 |
| Temperature of the stream entering a separator | 65 | 75 |
| (b) | ||
| Decision Variables | Range | |
| Upper | Lower | |
| Pressure of the equilibrium reactor | 50 | 70 |
| Temperature of the equilibrium reactor | 190 | 210 |
| Temperature of the stream entering a separator | 60 | 80 |
| Recycle ratio | 0 | 1 |
| (c) | ||
| Decision Variables | Range | |
| Upper | Lower | |
| Pressure of the first equilibrium reactor | 50 | 70 |
| Temperature of the first equilibrium reactor | 190 | 210 |
| Temperature of the stream entering a separator | 60 | 80 |
| Pressure of the second equilibrium reactor | 100 | 140 |
| Outlet temperature of the liquid stream cooler after the second equilibrium reactor | 60 | 80 |
| (a) | ||||
| Number of nodes (N) | 8 | 9 | 10 | 11 |
| R-squared | 0.9987 | 0.9891 | 0.9717 | 0.9925 |
| Mean square error (MSE) | 1.01 × 10−3 | 3.63 × 10−3 | 5.46 × 10−3 | 5.74 × 10−3 |
| Predicted cost ($/ton) | 2340.31 | 2284.50 | 2291.88 | 2280.82 |
| Actual cost ($/ton) | 2353.56 | 2330.03 | 2334.02 | 2337.94 |
| Error (%) | 0.563 | 1.954 | 1.805 | 2.443 |
| (b) | ||||
| Number of nodes (N) | 8 | 9 | 10 | 11 |
| R-squared | 0.9981 | 0.9972 | 0.9966 | 0.9983 |
| MSE | 1.42 × 10−3 | 3.02 × 10−3 | 1.38 × 10−3 | 1.15 × 10−3 |
| Predicted cost ($/ton) | 928.76 | 973.41 | 770.24 | 724.95 |
| Actual cost ($/ton) | 928.04 | 964.83 | 949.68 | 942.38 |
| Error (%) | 0.077 | 0.889 | 18.895 | 23.072 |
| (c) | ||||
| Number of nodes (N) | 8 | 9 | 10 | 11 |
| R-squared | 0.9669 | 0.9910 | 0.9922 | 0.9884 |
| MSE | 7.21 × 10−3 | 3.02 × 10−3 | 2.01 × 10−3 | 2.91 × 10−3 |
| Predicted cost ($/ton) | 887.93 | 886.95 | 889.81 | 889.14 |
| Actual cost ($/ton) | 888.85 | 888.70 | 968.31 | 968.31 |
| Error (%) | 0.104 | 0.197 | 8.106 | 8.177 |
| Decision Variables | Optimal Conditions | ||
|---|---|---|---|
| Configuration I | Configuration II | Configuration III | |
| Pressure of the first equilibrium reactor | 71.95 | 70 | 70 |
| Temperature of the first equilibrium reactor | 191.99 | 192.10 | 199.04 |
| Temperature of the stream entering a separator | - | 61.24 | 80 |
| Temperature of cooler | 71.14 | - | - |
| Recycle ratio | - | 1 | - |
| Pressure of the second equilibrium reactor | - | - | 100 |
| Outlet temperature of the liquid stream cooler after the second equilibrium reactor | - | - | 80 |
| Predicted cost ($/ton) | 2340.31 | 928.76 | 887.93 |
| Actual cost ($/ton) | 2353.56 | 928.04 | 888.85 |
| Error (%) | 0.563 | 0.077 | 0.104 |
| Configuration | Energy Consumption/ Energy Cost | ||
|---|---|---|---|
| Equipment | Energy (kW) | Cost ($/year) | |
| I | K-100 | 5645.8 | 6,022,885.6 |
| E-100 | 201.8 | 215,234.6 | |
| II | K-100 | 5502.0 | 5,869,491.4 |
| E-100 | 6739.8 | 7,189,968.1 | |
| III | K-100 | 5502.0 | 5,869,491.4 |
| E-100 | 607.6 | 648,201.5 | |
| K-102 | 926.6 | 988,473.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borisut, P.; Nuchitprasittichai, A. Process Configuration Studies of Methanol Production via Carbon Dioxide Hydrogenation: Process Simulation-Based Optimization Using Artificial Neural Networks. Energies 2020, 13, 6608. https://doi.org/10.3390/en13246608
Borisut P, Nuchitprasittichai A. Process Configuration Studies of Methanol Production via Carbon Dioxide Hydrogenation: Process Simulation-Based Optimization Using Artificial Neural Networks. Energies. 2020; 13(24):6608. https://doi.org/10.3390/en13246608
Chicago/Turabian StyleBorisut, Prapatsorn, and Aroonsri Nuchitprasittichai. 2020. "Process Configuration Studies of Methanol Production via Carbon Dioxide Hydrogenation: Process Simulation-Based Optimization Using Artificial Neural Networks" Energies 13, no. 24: 6608. https://doi.org/10.3390/en13246608
APA StyleBorisut, P., & Nuchitprasittichai, A. (2020). Process Configuration Studies of Methanol Production via Carbon Dioxide Hydrogenation: Process Simulation-Based Optimization Using Artificial Neural Networks. Energies, 13(24), 6608. https://doi.org/10.3390/en13246608





