Thermodynamic Analysis of a High-Temperature Latent Heat Thermal Energy Storage System
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Governing Equations
2.2. Thermodynamic Analysis
2.2.1. Energy Analysis
2.2.2. Entropy Analysis
2.3. Boundary Conditions
2.4. Mesh Generation, Independence Tests, and Solver Settings
3. Results and Discussion
3.1. Validation
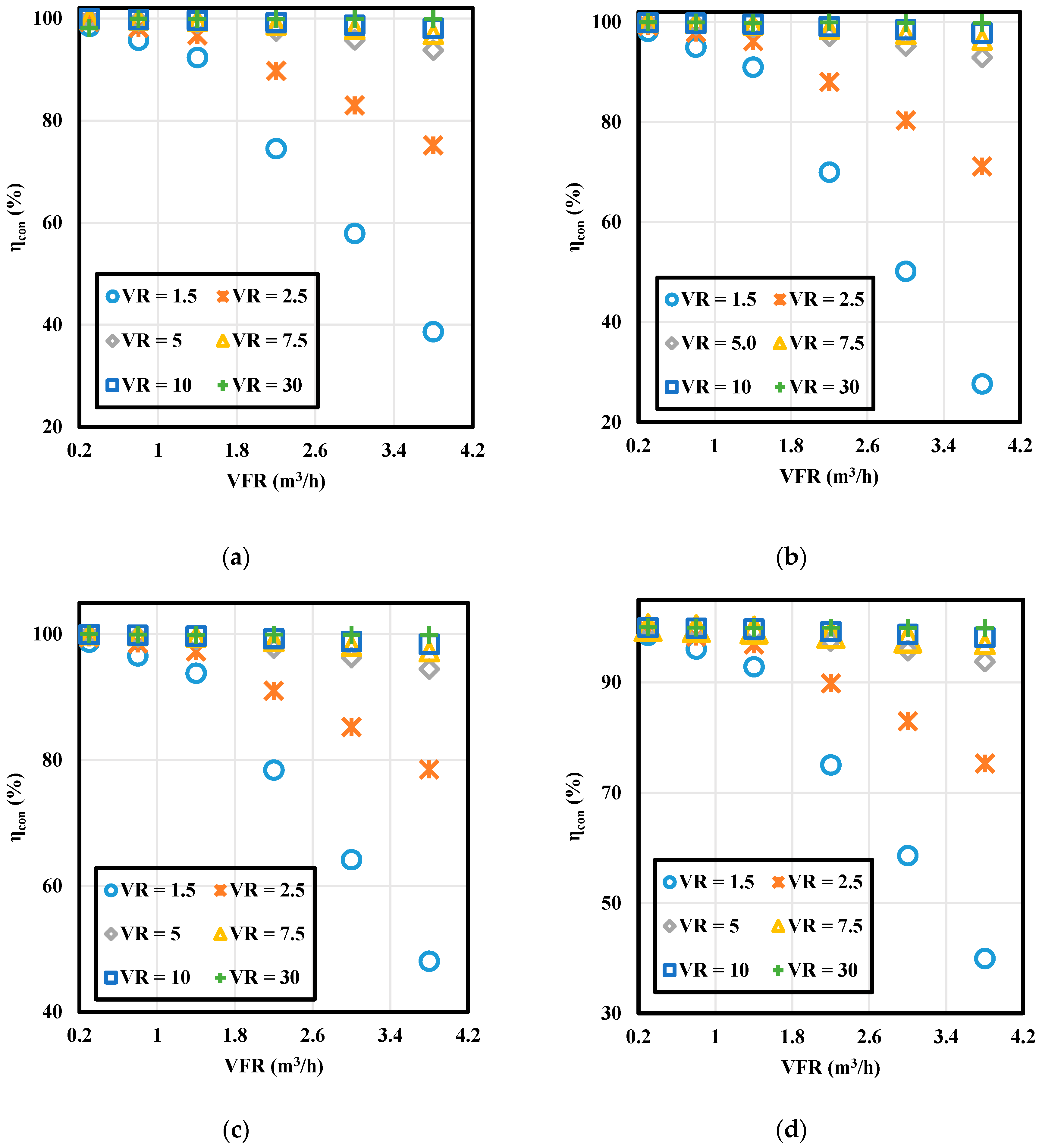
3.2. Thermodynamic Efficiencies
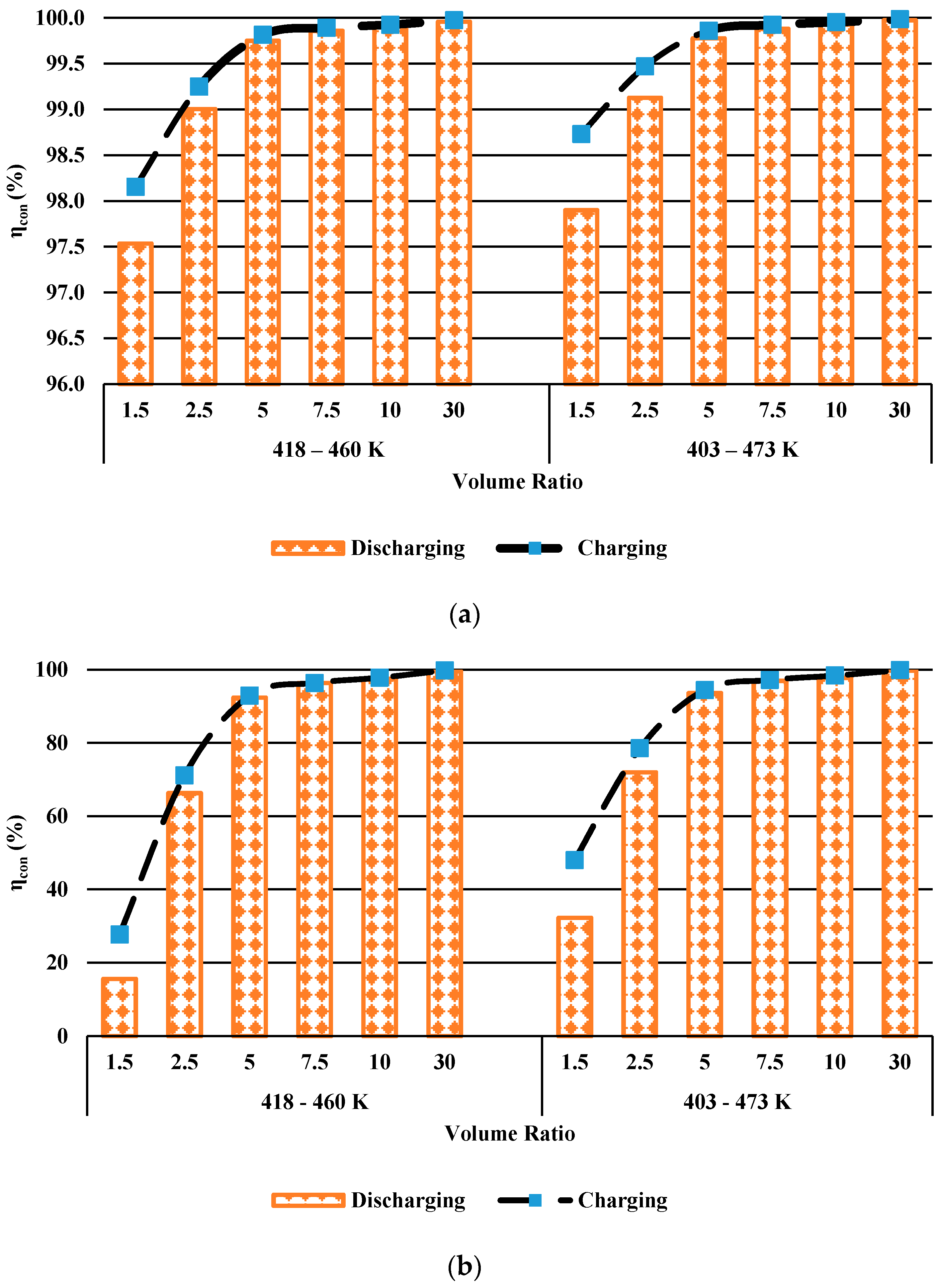
3.2.1. First Law Efficiency
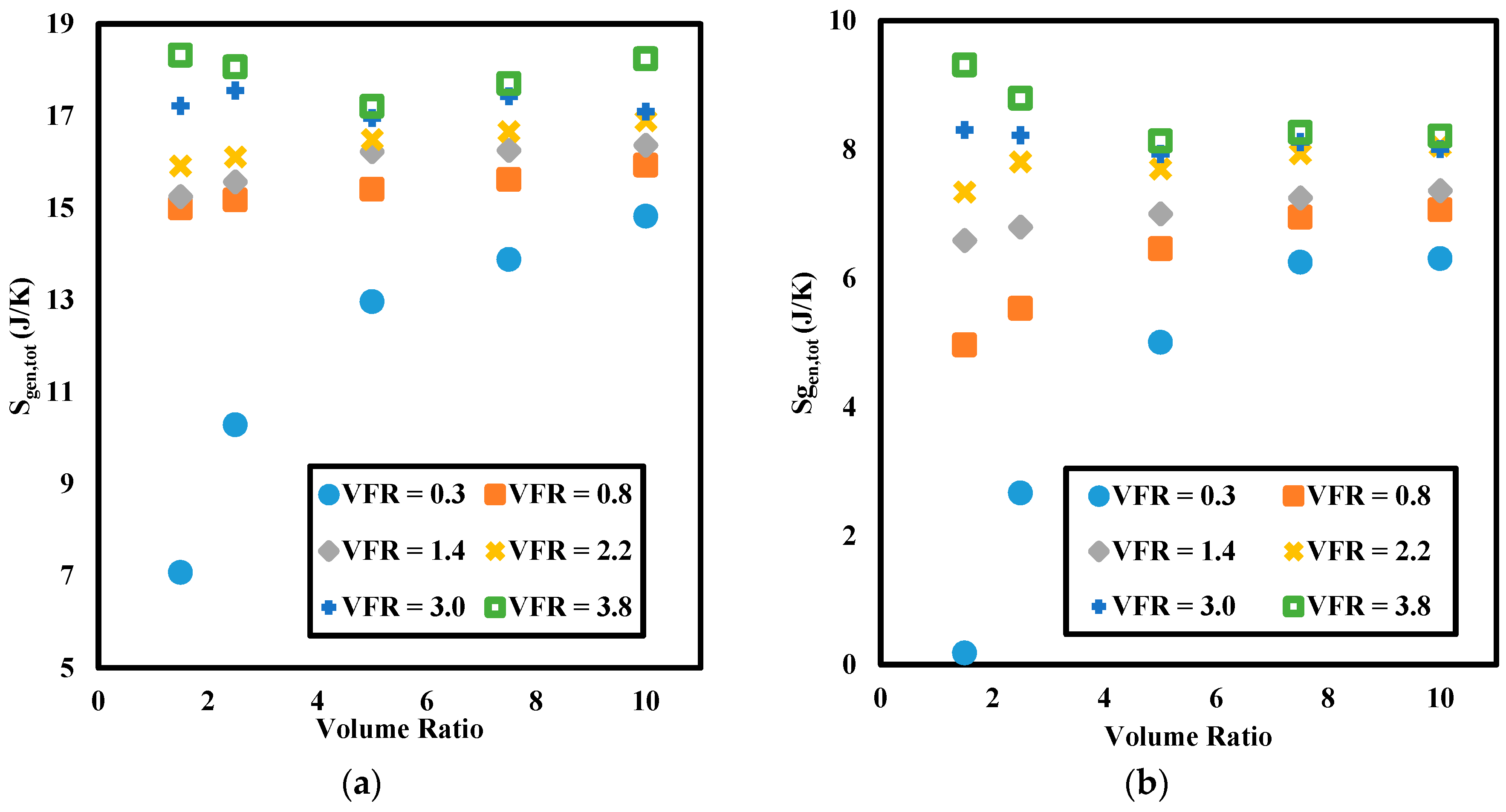
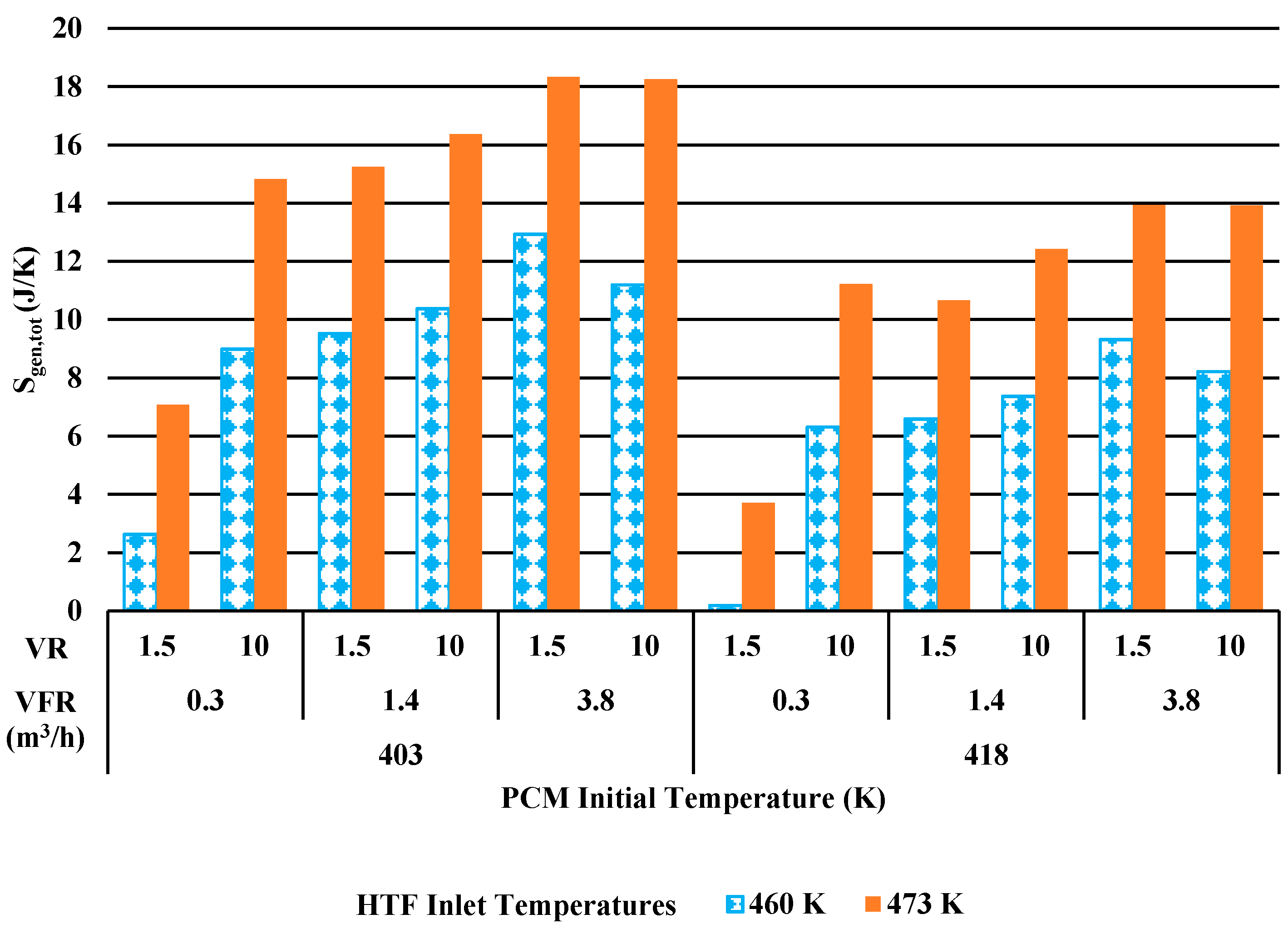
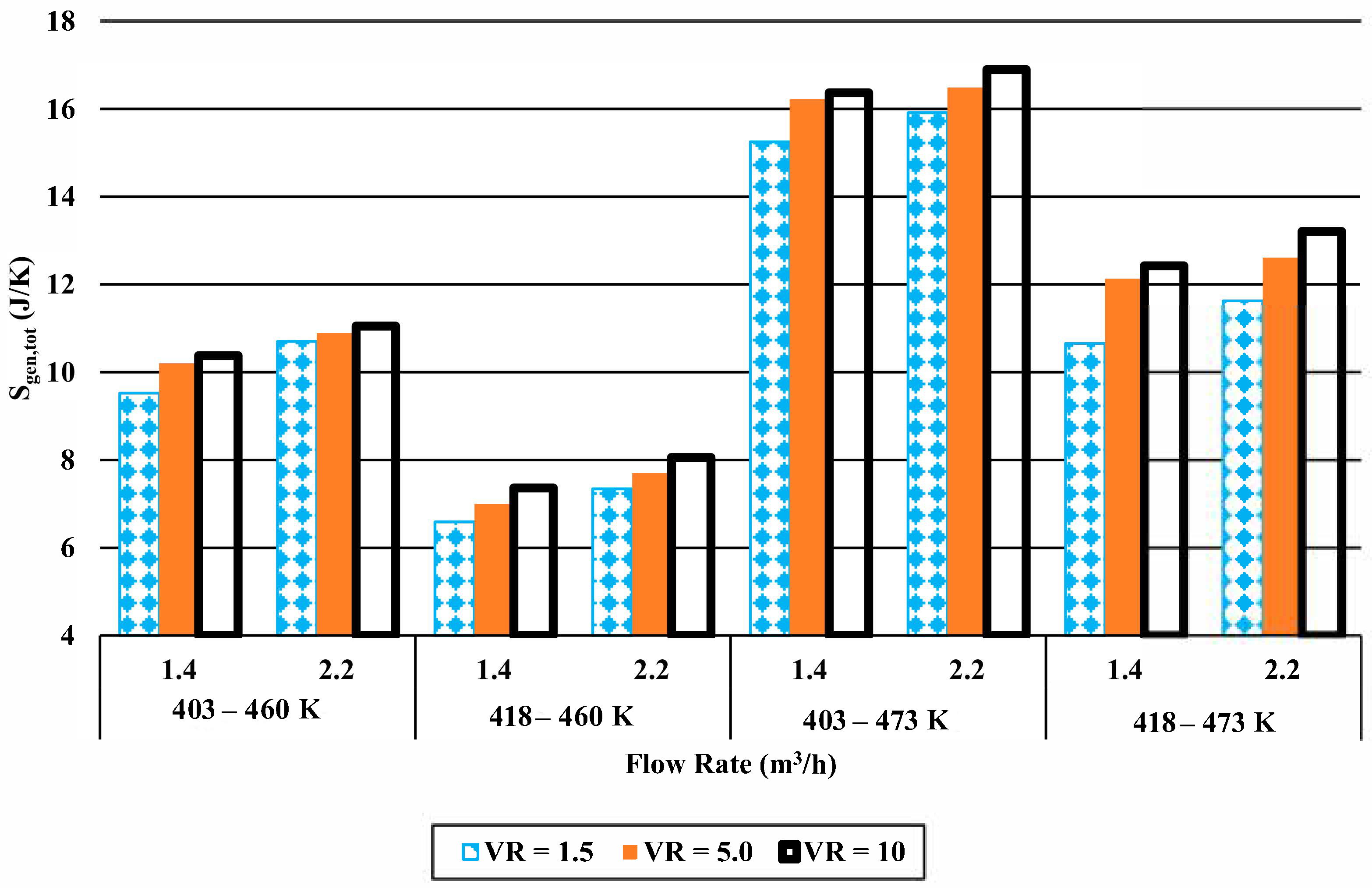
3.2.2. Entropy Generation
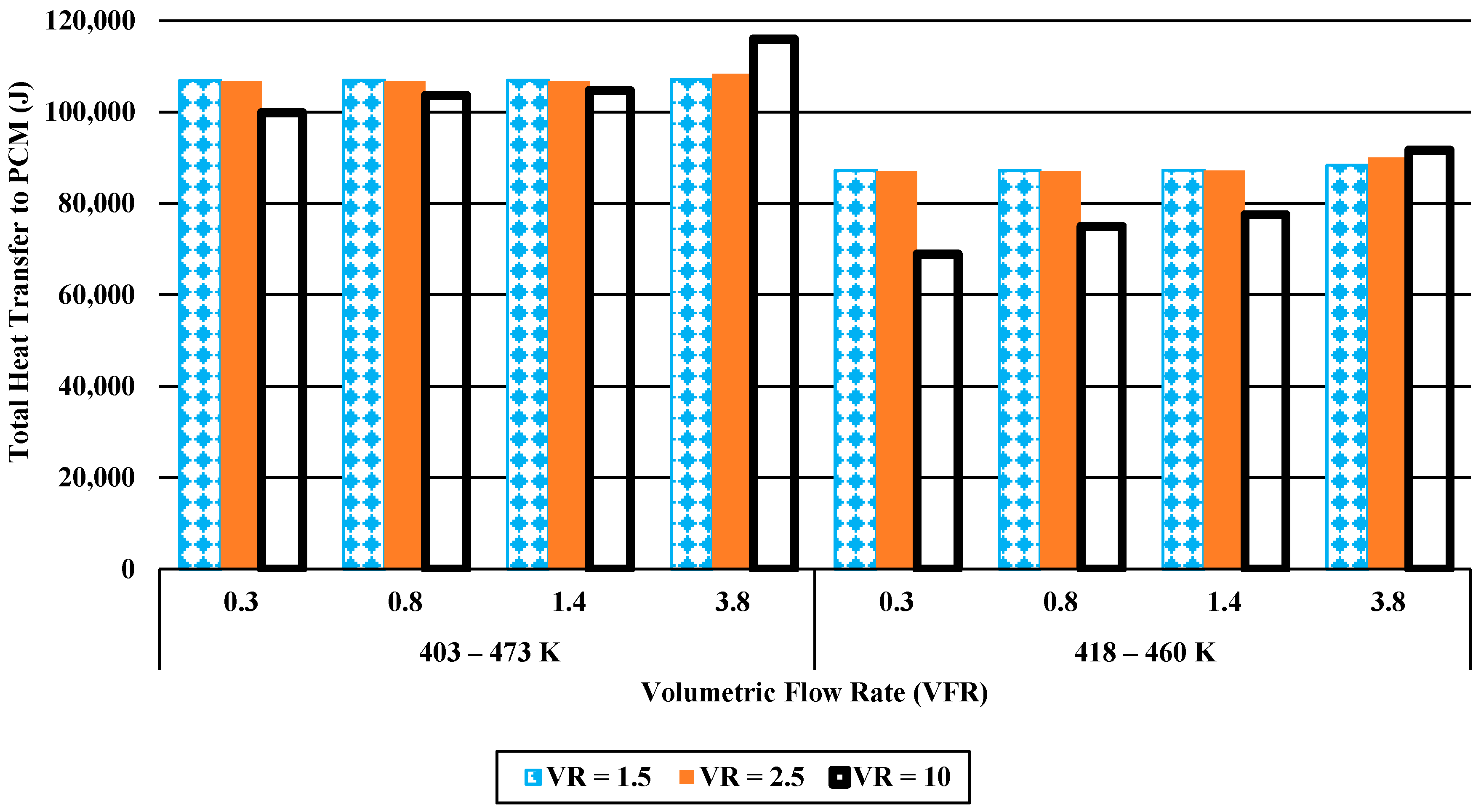
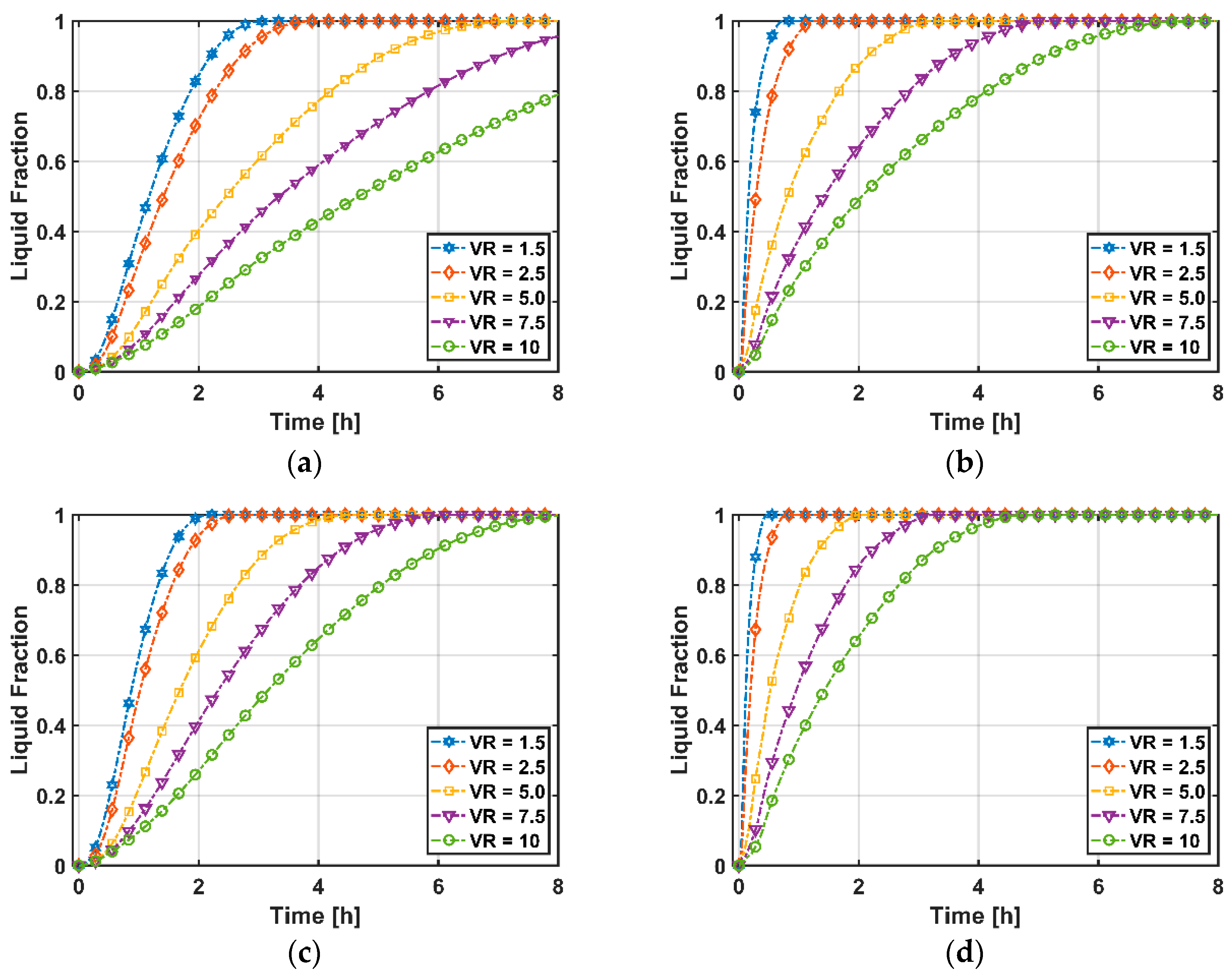
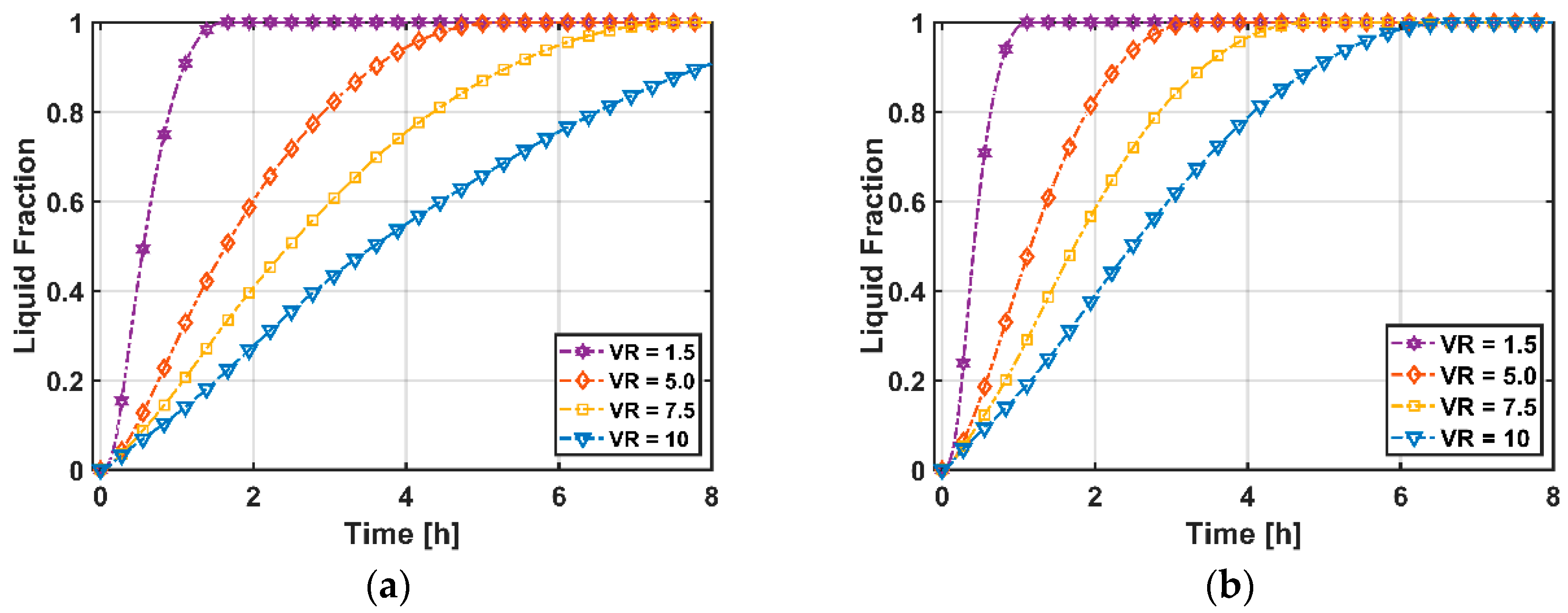
3.2.3. Total Heat Transfer and Melting Time
3.2.4. Case Study
4. Conclusions
- Due to the minor effect of viscous dissipation, energy efficiencies are over 99% in all cases.
- While energy efficiencies decrease with increasing volumetric flow rate, entropy generations increase due to higher viscous heating with velocity. Volumetric flow rate shows a positive and negative relationship between heat transfer ratio and PCM melting time, respectively.
- Whereas there is an increasing trend in the energy efficiencies with increasing volume ratio, the trend differs for lower and higher velocities for entropy generation.
- While entropy generation increases with increasing volume ratio for lower flow rates, it decreases with higher flow rate.
- Both energy efficiency and entropy generation increase with increasing HTF inlet temperature.
- The effect of volume ratio on the energy efficiency is higher than that of HTF inlet temperatures.
- PCM melting time decreases with decreasing volume ratio due to higher heat transfer surfaces.
- Entropy generation is lowered with reduced volume ratio and decreased heat transfer rate. Since the purpose of the LHTES system is to store heat energy, entropy generation may then not be the most appropriate design tool as system costs for lower volume ratios will become prohibitive.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | ||
| C | specific heat (J/kg K) | |
| D | pipe diameter (m) | |
| E | energy (J) | |
| h | enthalpy (J/kg) | |
| H | total specific enthalpy (J) | |
| k | thermal conductivity (W/m K) | |
| L | latent heat (J/kg) | |
| m | mass (kg) | |
| P | static pressure (Pa) | |
| S | entropy (J/K) | |
| Q | total heat transfer rate (W) | |
| T | temperature (K) | |
| t | time (s) | |
| to | total | |
| U | internal energy (J) | |
| V | volume (m3) | |
| Greek Letters and Special Symbols | ||
| Δ | “change in” | |
| ∞ | dead state | |
| η | energy efficiency | |
| ṁ | mass flow rate (kg/s) | |
| ρ | density (kg/m3) | |
| φ | liquid fraction | |
| Subscript | ||
| con | contracted | |
| b | bulk | |
| ch | charging | |
| d | destroyed | |
| des | desired | |
| dis | discharging | |
| gen | generated | |
| in | inlet | |
| ini | initial | |
| l | liquid | |
| out | outlet | |
| o | reference | |
| sys | system | |
| vd | viscous dissipation | |
| HTF | heat transfer fluid | |
| VR | volume ratio | |
| VFR | volumetric flow rate (m3/h) | |
| LHTES | latent heat thermal energy storage | |
| TES | thermal energy storage | |
| PCM | phase change material | |
References
- Dincer, I.; Ezan, M.A. Heat Storage: A Unique Solution For Energy Systems; Green Energy and Technology; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-91892-1. [Google Scholar]
- Sarbu, I.; Sebarchievici, C. A comprehensive review of thermal energy storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef] [Green Version]
- Mahmud, R.; Erguvan, M.; MacPhee, D.W. Underground CSP Thermal Energy Storage. In Proceedings of the ASME 2019 Power Conference, Salt Lake City, UT, USA, 15–18 July 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar]
- Nomura, T.; Okinaka, N.; Akiyama, T. Technology of latent heat storage for high temperature application: A review. ISIJ Int. 2010, 50, 1229–1239. [Google Scholar] [CrossRef] [Green Version]
- Oró, E.; Gil, A.; Miró, L.; Peiró, G.; Álvarez, S.; Cabeza, L.F. Thermal Energy Storage Implementation Using Phase Change Materials for Solar Cooling and Refrigeration Applications. Energy Proc. 2012, 30, 947–956. [Google Scholar] [CrossRef] [Green Version]
- Gil, A.; Oró, E.; Peiró, G.; Álvarez, S.; Cabeza, L.F. Material selection and testing for thermal energy storage in solar cooling. Renew. Energy 2013, 57, 366–371. [Google Scholar] [CrossRef]
- Gil, A.; Oró, E.; Castell, A.; Cabeza, L.F. Experimental analysis of the effectiveness of a high temperature thermal storage tank for solar cooling applications. Appl. Therm. Eng. 2013, 54, 521–527. [Google Scholar] [CrossRef]
- Gil, A.; Peiró, G.; Oró, E.; Cabeza, L.F. Experimental analysis of the effective thermal conductivity enhancement of PCM using finned tubes in high temperature bulk tanks. Appl. Therm. Eng. 2018, 142, 736–744. [Google Scholar] [CrossRef]
- Gil, A.; Oró, E.; Miró, L.; Peiró, G.; Ruiz, Á.; Salmerón, J.M.; Cabeza, L.F. Experimental analysis of hydroquinone used as phase change material (PCM) to be applied in solar cooling refrigeration. Int. J. Refrig. 2014, 39, 95–103. [Google Scholar] [CrossRef]
- Peiró, G.; Gasia, J.; Miró, L.; Prieto, C.; Cabeza, L.F. Experimental analysis of charging and discharging processes, with parallel and counter flow arrangements, in a molten salts high temperature pilot plant scale setup. Appl. Energy 2016, 178, 394–403. [Google Scholar] [CrossRef] [Green Version]
- Sodhi, G.S.; Vigneshwaran, K.; Jaiswal, A.K.; Muthukumar, P. Assessment of Heat Transfer Characteristics of a Latent Heat Thermal Energy Storage System: Multi Tube Design. Energy Proc. 2019, 158, 4677–4683. [Google Scholar] [CrossRef]
- Niyas, H.; Muthukumar, P. A novel heat transfer enhancement technique for performance improvements in encapsulated latent heat storage system. Sol. Energy 2018, 164, 276–286. [Google Scholar] [CrossRef]
- Comsol Inc. Available online: https://www.comsol.com/ (accessed on 20 June 2020).
- Meng, Z.N.; Zhang, P. Experimental and numerical investigation of a tube-in-tank latent thermal energy storage unit using composite PCM. Appl. Energy 2017, 190, 524–539. [Google Scholar] [CrossRef]
- Niyas, H.; Prasad, S.; Muthukumar, P. Performance investigation of a lab–scale latent heat storage prototype—Numerical results. Energy Convers. Manag. 2017, 135, 188–199. [Google Scholar] [CrossRef]
- Jegadheeswaran, S.; Pohekar, S.D.; Kousksou, T. Exergy based performance evaluation of latent heat thermal storage system: A review. Renew. Sustain. Energy Rev. 2010, 14, 2580–2595. [Google Scholar] [CrossRef]
- Guelpa, E.; Sciacovelli, A.; Verda, V. Entropy generation analysis for the design improvement of a latent heat storage system. Energy 2013, 53, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Riahi, S.; Jovet, Y.; Saman, W.Y.; Belusko, M.; Bruno, F. Sensible and latent heat energy storage systems for concentrated solar power plants, exergy efficiency comparison. Sol. Energy 2019, 180, 104–115. [Google Scholar] [CrossRef]
- Rahimi, M.; Ardahaie, S.S.; Hosseini, M.J.; Gorzin, M. Energy and exergy analysis of an experimentally examined latent heat thermal energy storage system. Renew. Energy 2020, 147, 1845–1860. [Google Scholar] [CrossRef]
- MacPhee, D.; Dincer, I. Thermal modeling of a packed bed thermal energy storage system during charging. Appl. Therm. Eng. 2009, 29, 695–705. [Google Scholar] [CrossRef]
- MacPhee, D.; Dincer, I. Thermodynamic Analysis of Freezing and Melting Processes in a Bed of Spherical PCM Capsules. J. Sol. Energy Eng. 2009, 131, 31011–31017. [Google Scholar] [CrossRef]
- MacPhee, D.; Dincer, I.; Beyene, A. Numerical simulation and exergetic performance assessment of charging process in encapsulated ice thermal energy storage system. Energy 2012, 41, 491–498. [Google Scholar] [CrossRef]
- Voller, V.R.; Swaminathan, C.R. Eral Source-Based Method for Solidification Phase Change. Numer. Heat Transf. Part B Fundam. 1991, 19, 175–189. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Erguvan, M.; MacPhee, D.W. A Numerical Case Study: Effect of Heat Leakage on Thermodynamic Efficiency of Cylinders in Cross-Flow. J. Heat Transf. 2019, 141. [Google Scholar] [CrossRef]
- Erguvan, M. Numerical and Thermodynamic Analysis of External Flow Over Tube Banks for Waste Heat Recovery. Ph.D. Thesis, University of Alabama Libraries, Tuscaloosa, AL, USA, 2018. [Google Scholar]
- Erguvan, M.; MacPhee, D. Energy and Exergy Analyses of Tube Banks in Waste Heat Recovery Applications. Energies 2018, 11, 2094. [Google Scholar] [CrossRef] [Green Version]
- Erguvan, M.; MacPhee, D.W. Second law optimization of heat exchangers in waste heat recovery. Int. J. Energy Res. 2019, 43, 5714–5734. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M. Thermal Energy Storage Systems and Applications; Wiley: West Sussex, UK, 2011; ISBN 9780470747063. [Google Scholar]
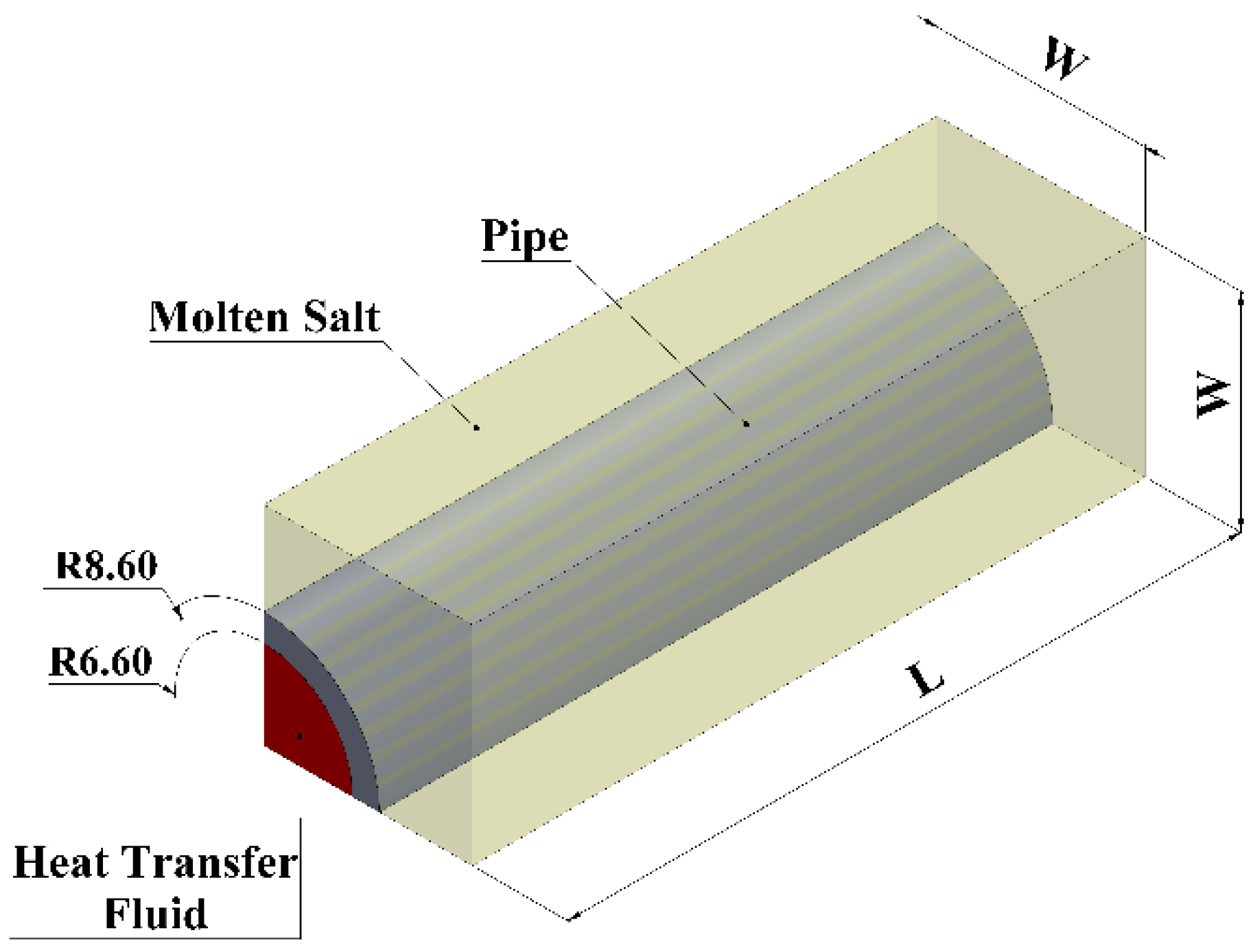

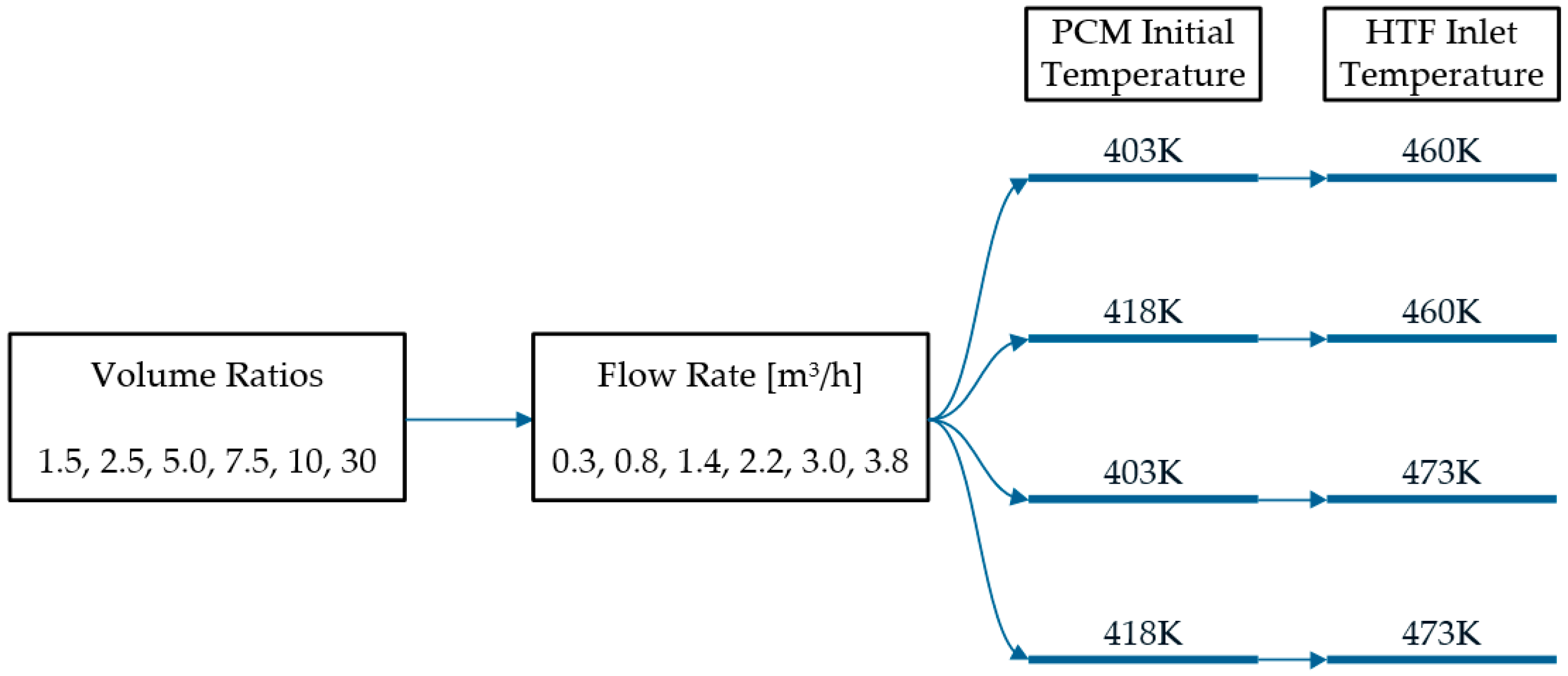


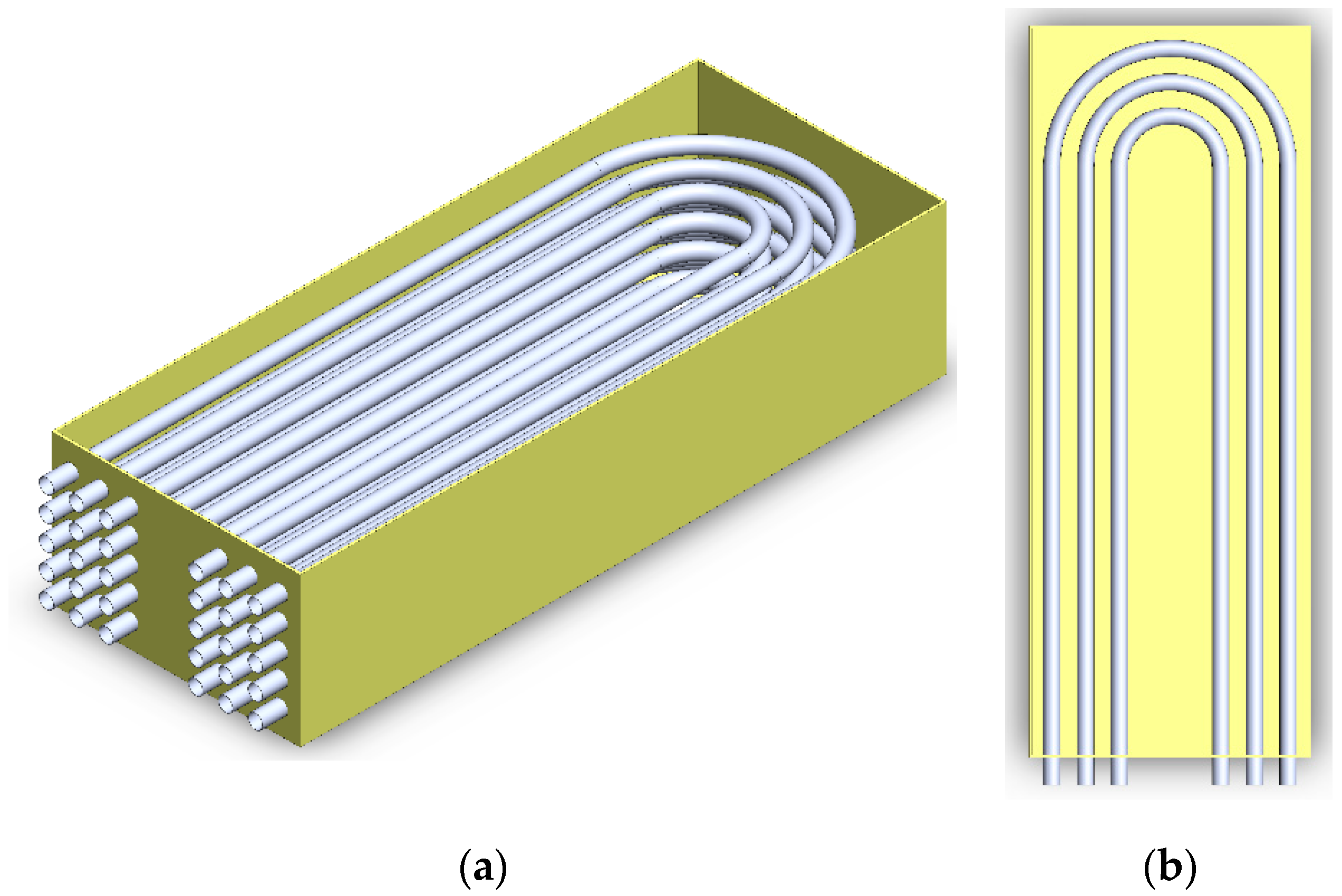
| Properties | Hydroquinone [PCM] [8] | Therminol VP-1 @ 473 K [HTF] [10] | Stainless Steel |
|---|---|---|---|
| Density (kg/m3) | 1180 | 913 | 8030 |
| Specific Heat (J/kgK) | 2500 | 2048 | 502 |
| Thermal Conductivity (W/mK) | 0.1 | 0.1138 | 16.27 |
| Melting Temperature (°C) | 168–173 | N/A | N/A |
| Melting Enthalpy (kJ/kg) | 205.8 | N/A | N/A |
| Viscosity (mPas) | 0.97 | 0.395 | N/A |
| Volume Ratio | W [mm] | L [mm] | PCM Volume [mm3] | PCM Mass [kg] |
|---|---|---|---|---|
| 1.5 | 10.46 | 4614 | 236,800 | 0.279 |
| 2.5 | 11.99 | 2764 | ||
| 5.0 | 15.50 | 1300 | ||
| 7.5 | 17.74 | 923 | ||
| 10 | 20.01 | 692 | ||
| 30 | 32.94 | 231 |
| PCM Initial Temperature | VFR (m3/h) | VR | HTF Initial Temperature | S_gen_ht (J/K) | S_gen vd (J/K) | S_gen_to (J/K) | S_gen_vd/S_gen_to |
|---|---|---|---|---|---|---|---|
| 403 K | 0.3 | 1.5 | 460 K | 2.57 | 0.05 | 2.62 | 1.84% |
| 10 | 8.99 | 0.00 | 8.99 | 0.01% | |||
| 0.8 | 1.5 | 11.04 | 1.89 | 12.93 | 14.62% | ||
| 10 | 11.14 | 0.05 | 11.19 | 0.40% | |||
| 418 K | 0.3 | 1.5 | 460 K | 0.14 | 0.05 | 0.18 | 26.09% |
| 10 | 6.31 | 0.00 | 6.31 | 0.02% | |||
| 0.8 | 1.5 | 7.42 | 1.89 | 9.31 | 20.29% | ||
| 10 | 8.17 | 0.05 | 8.21 | 0.55% | |||
| 403 K | 0.3 | 1.5 | 473 K | 7.03 | 0.04 | 7.08 | 0.61% |
| 10 | 14.82 | 0.00 | 14.82 | 0.01% | |||
| 0.8 | 1.5 | 16.57 | 1.75 | 18.32 | 9.57% | ||
| 10 | 18.20 | 0.04 | 18.25 | 0.23% | |||
| 418 K | 0.3 | 1.5 | 473 K | 3.67 | 0.04 | 3.71 | 1.15% |
| 10 | 11.23 | 0.00 | 11.23 | 0.01% | |||
| 0.8 | 1.5 | 12.18 | 1.75 | 13.93 | 12.58% | ||
| 10 | 13.88 | 0.04 | 13.92 | 0.30% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MacPhee, D.W.; Erguvan, M. Thermodynamic Analysis of a High-Temperature Latent Heat Thermal Energy Storage System. Energies 2020, 13, 6634. https://doi.org/10.3390/en13246634
MacPhee DW, Erguvan M. Thermodynamic Analysis of a High-Temperature Latent Heat Thermal Energy Storage System. Energies. 2020; 13(24):6634. https://doi.org/10.3390/en13246634
Chicago/Turabian StyleMacPhee, David W., and Mustafa Erguvan. 2020. "Thermodynamic Analysis of a High-Temperature Latent Heat Thermal Energy Storage System" Energies 13, no. 24: 6634. https://doi.org/10.3390/en13246634
APA StyleMacPhee, D. W., & Erguvan, M. (2020). Thermodynamic Analysis of a High-Temperature Latent Heat Thermal Energy Storage System. Energies, 13(24), 6634. https://doi.org/10.3390/en13246634





