Experimental Characterization and Evaluation of the Vibroacoustic Field of Hydraulic Pumps: The Case of an External Gear Pump
Abstract
:1. Introduction
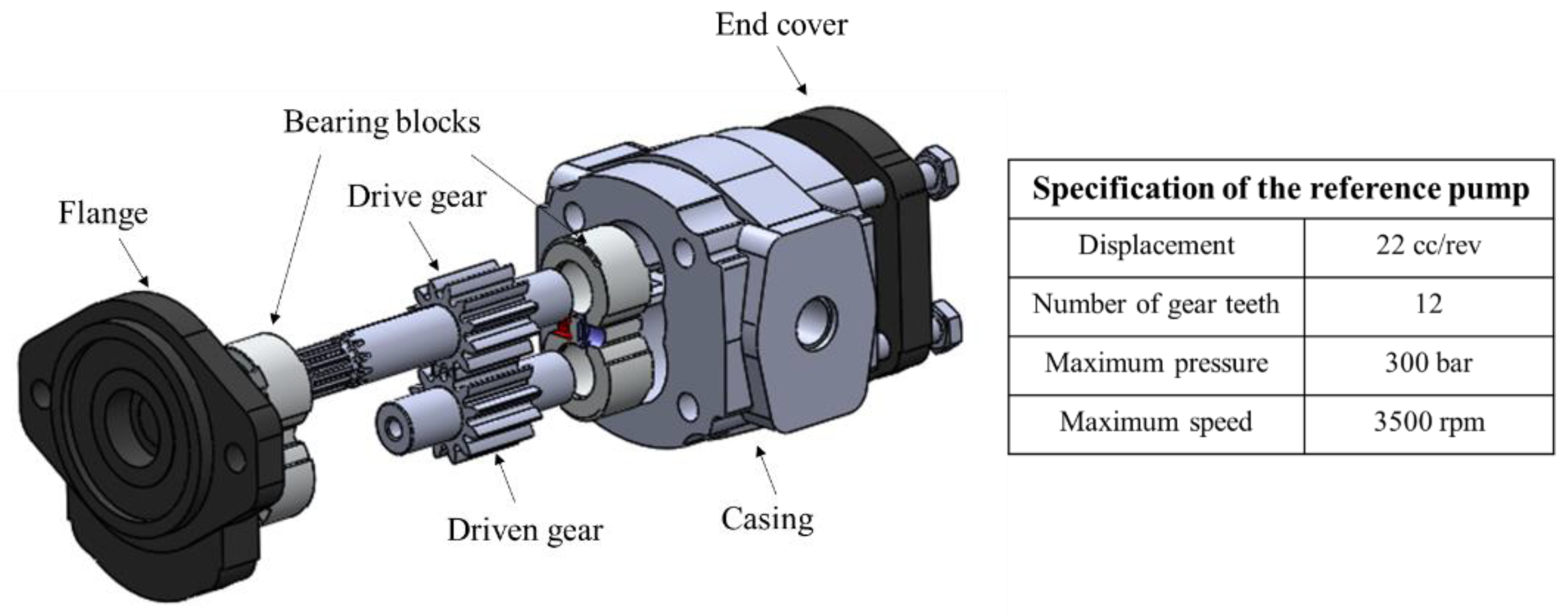
2. Hydraulic Test Setup
3. Characterization of Vibroacoustic Field during Operation
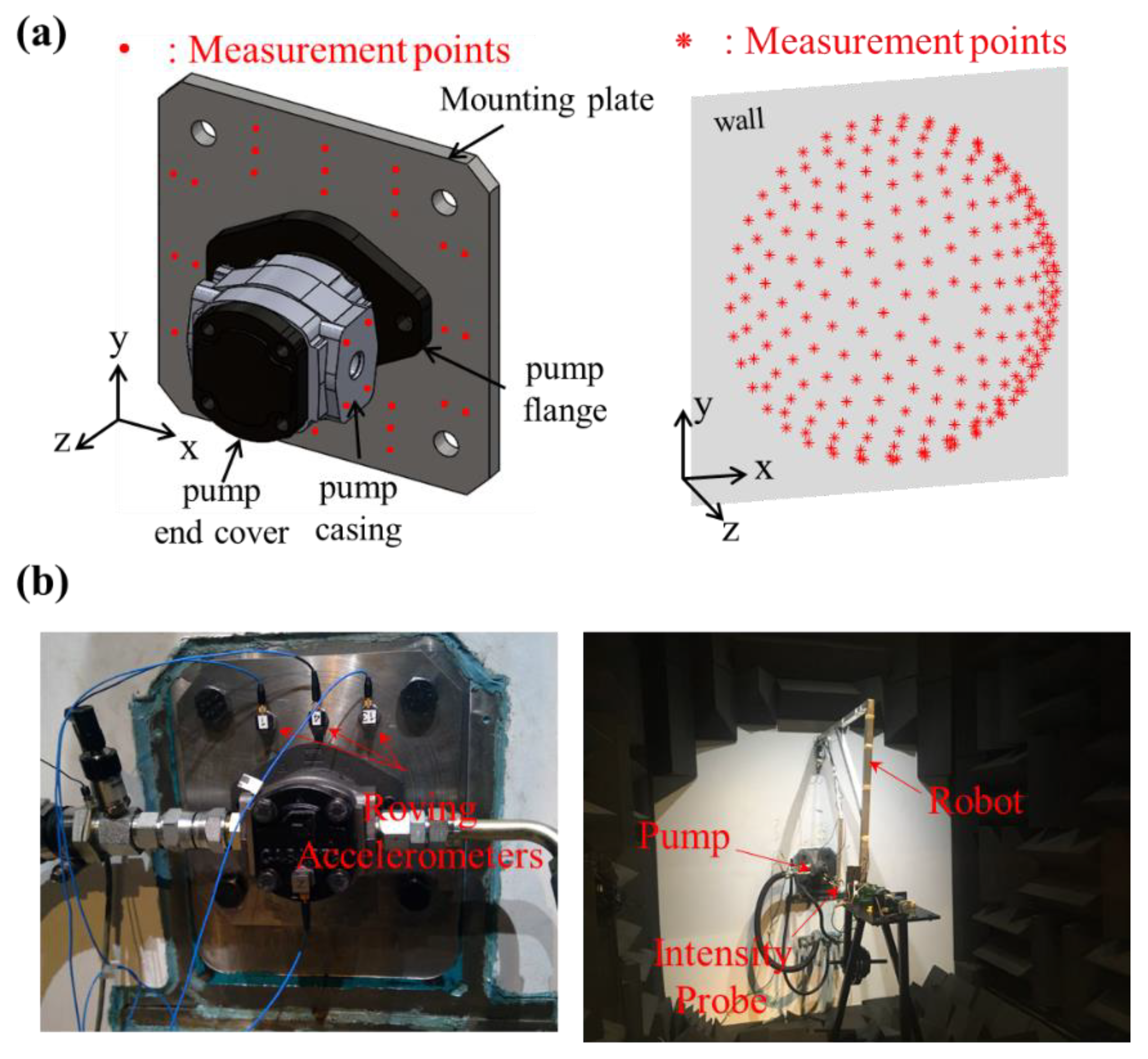
3.1. Procedures to Obtain ODS and Radiated Sound Field
3.1.1. Steady-State Operation of the Pump
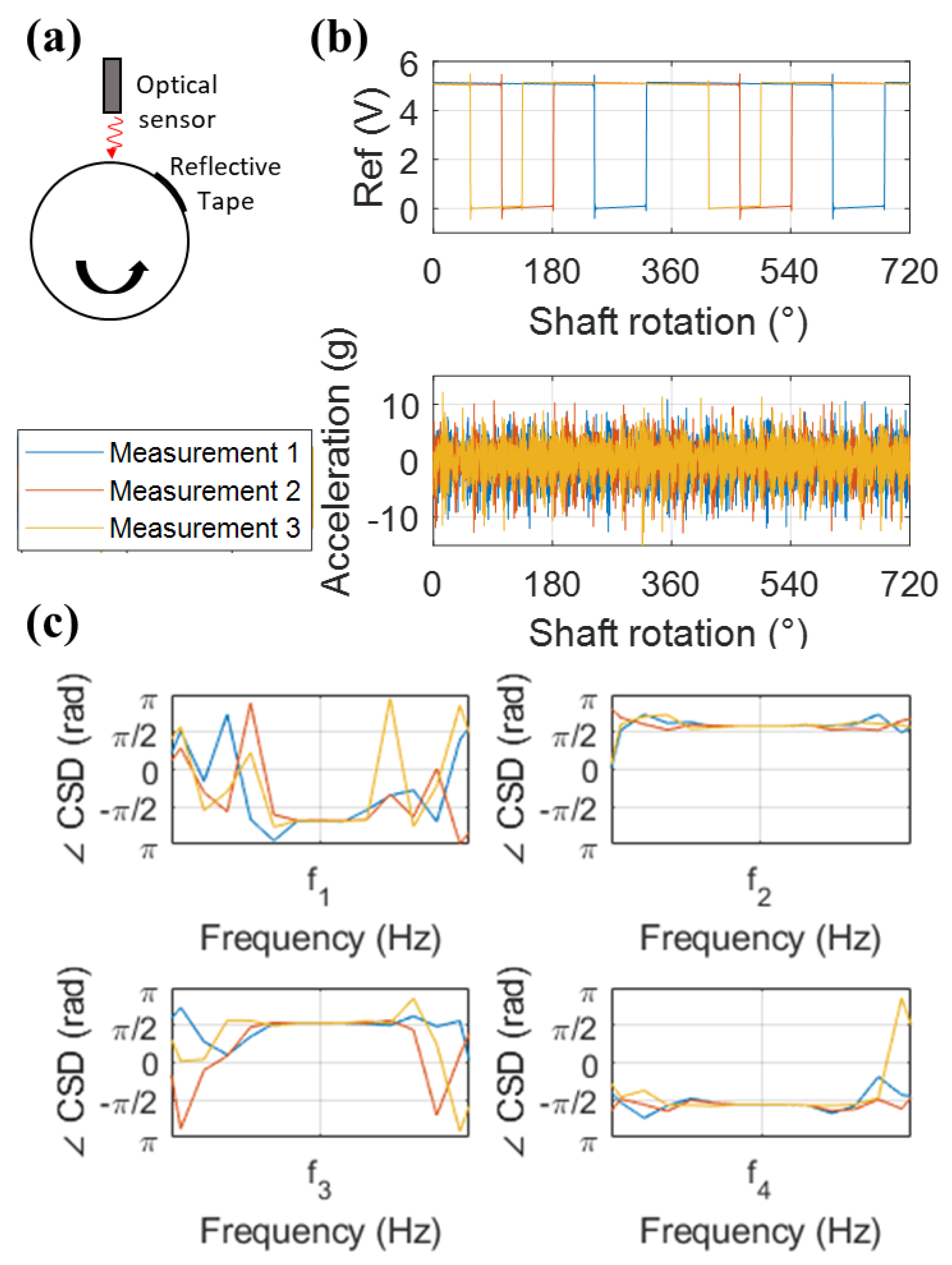
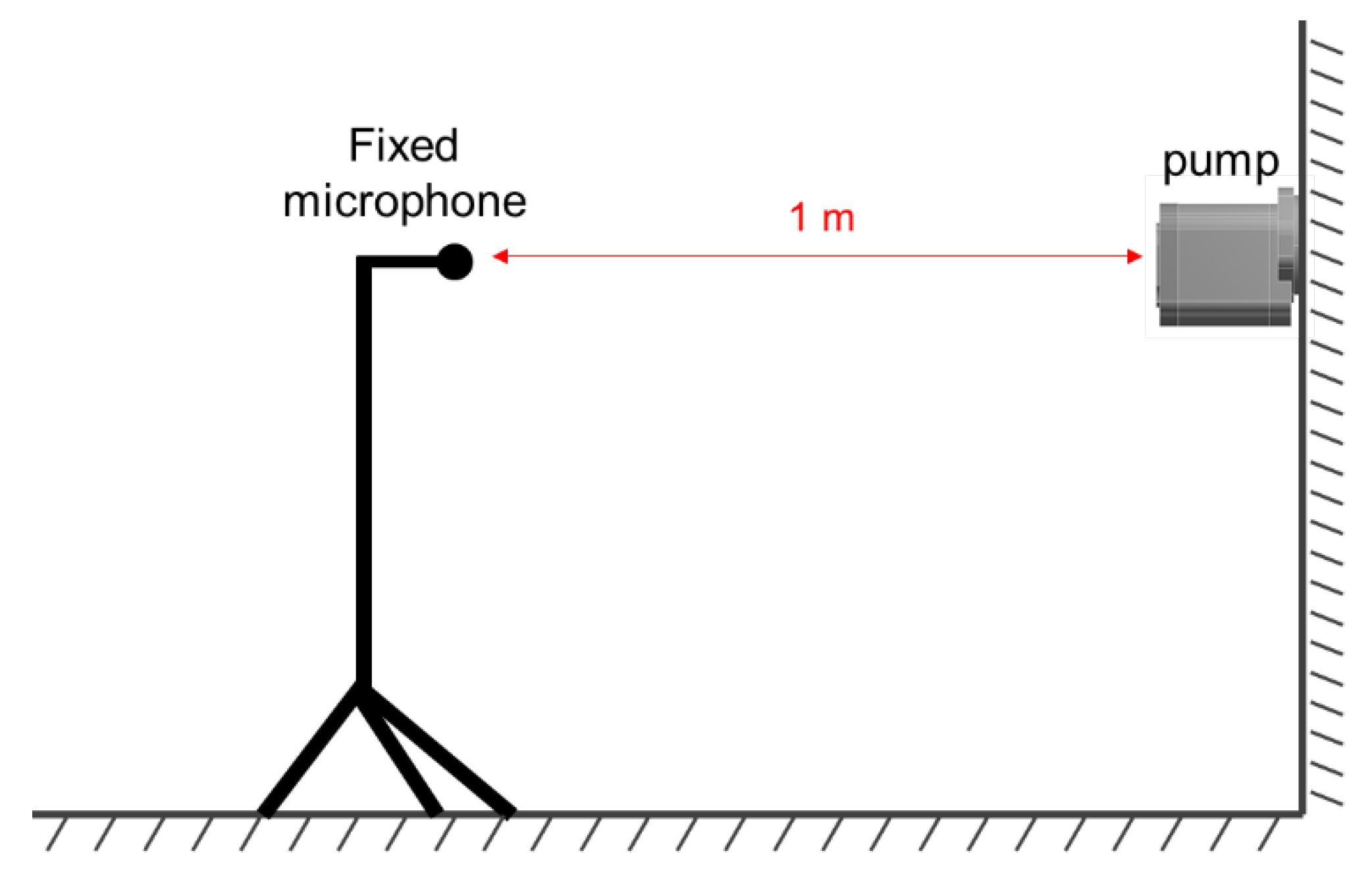
3.1.2. Noise and Vibration Measurements
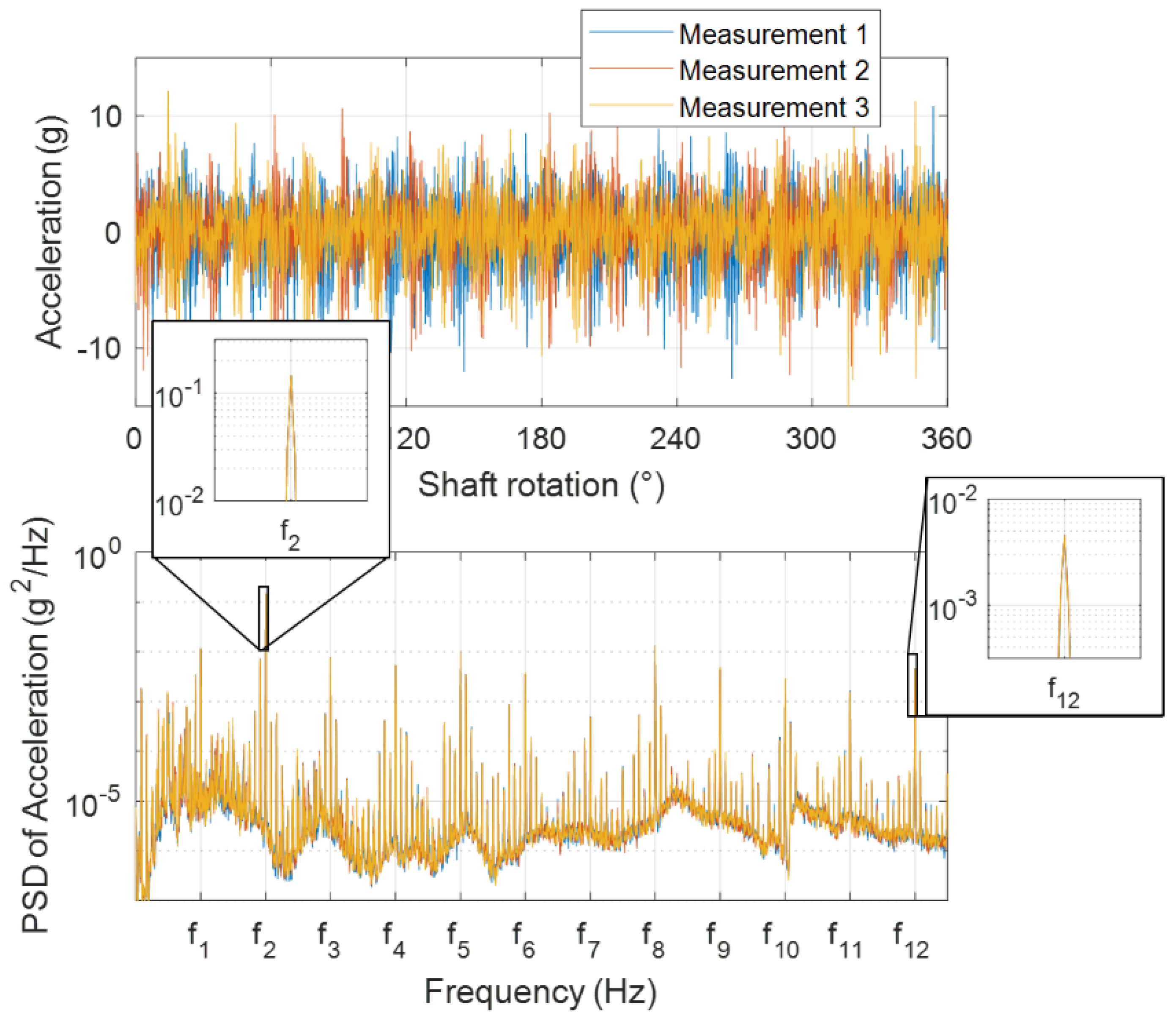
3.1.3. Signal Processing of Measured Signals
- (a)
- Magnitude Evaluation
- (b)
- Relative Phase Evaluation
3.1.4. Visualization of ODS & Radiated Sound Fields
3.2. Results and Discussions
3.2.1. Results and Observations
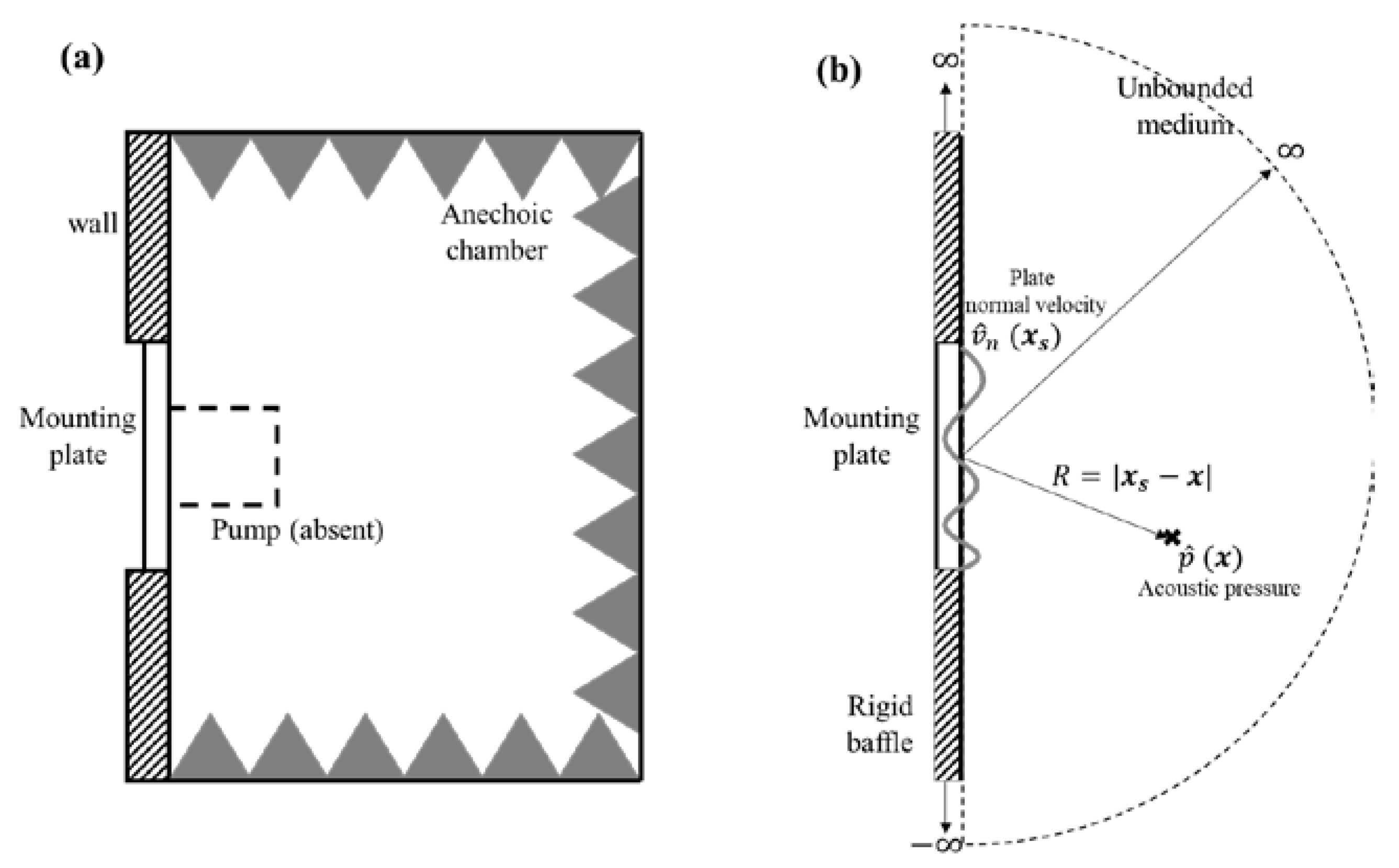
3.2.2. Sound Radiation by the Mounting Plate
3.2.3. Discussion
4. Evaluation of Noise Performance
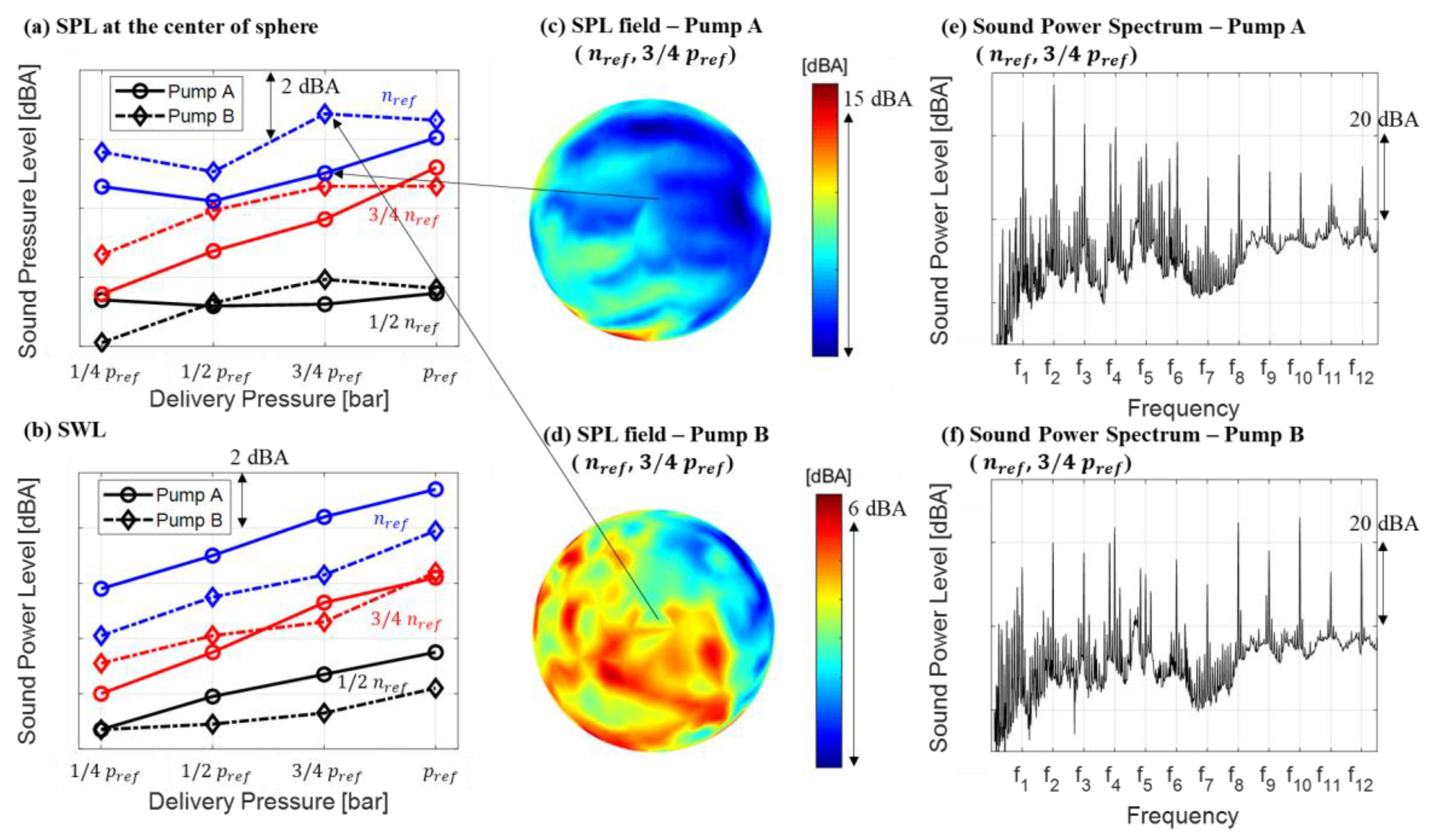
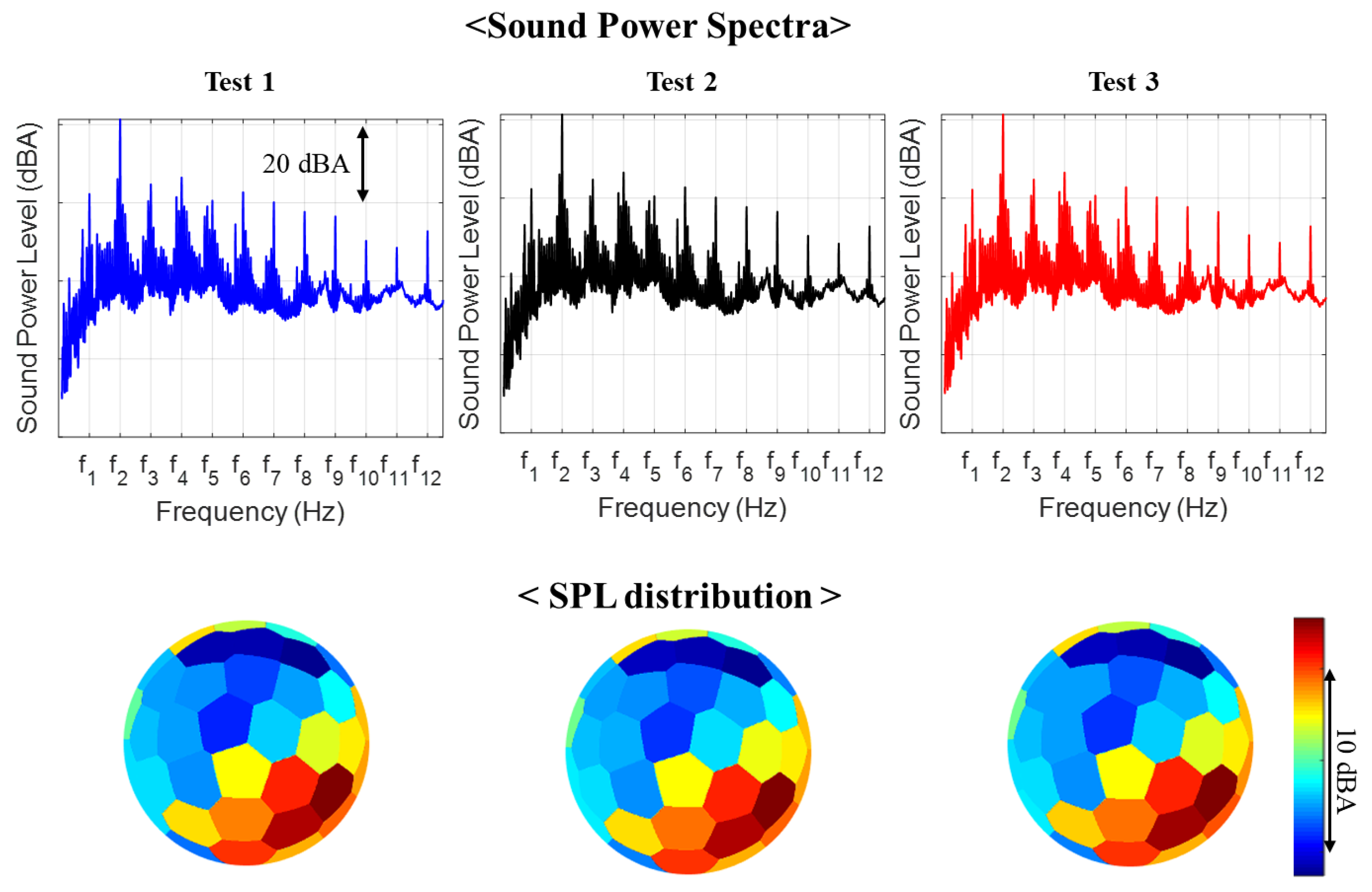
4.1. Sound Power Levels & Sound Pressure Levels
4.2. Reliable Sound Power Measurement
4.2.1. Grid Study
4.2.2. Repeatability Test
5. Conclusions
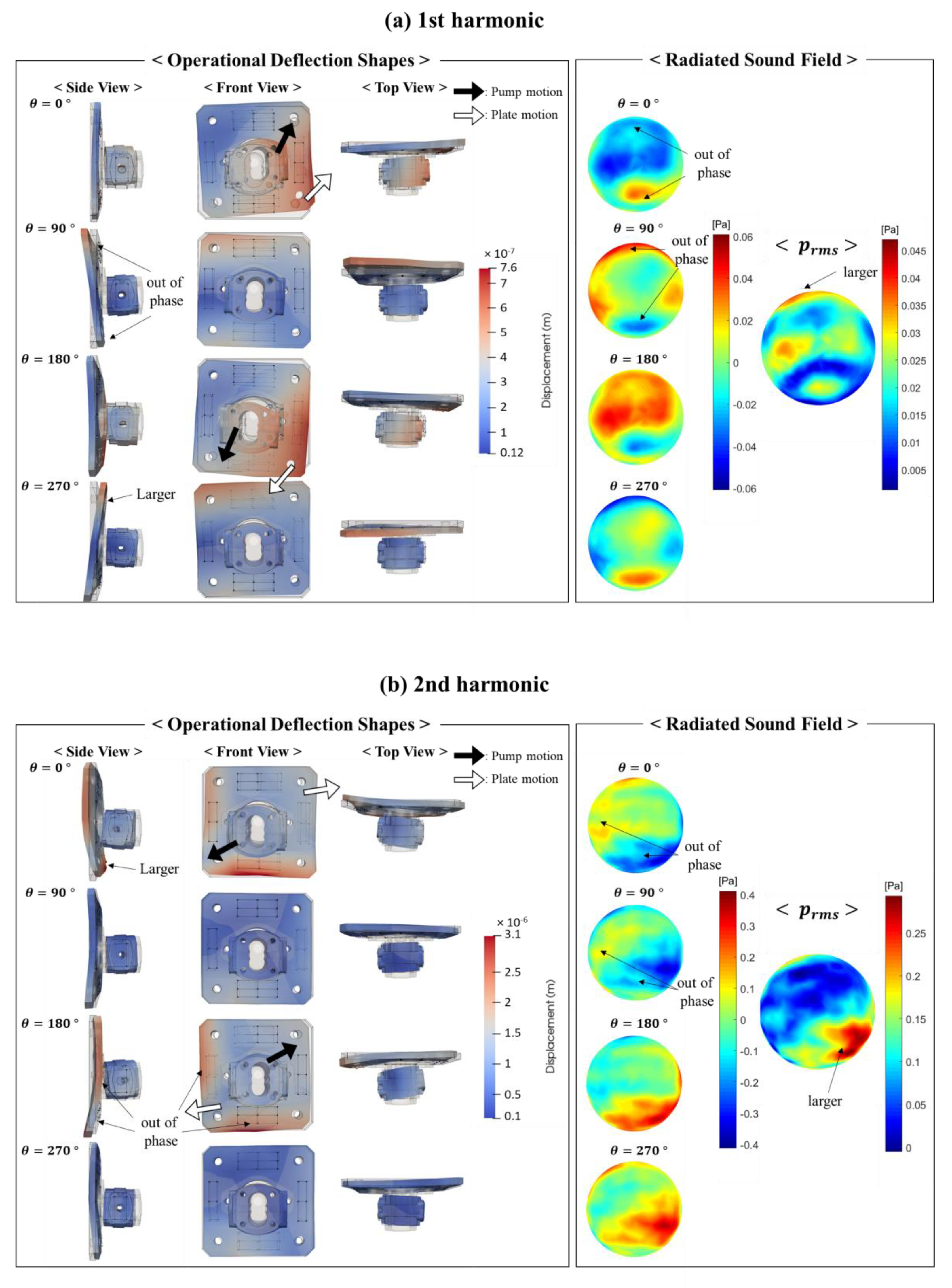
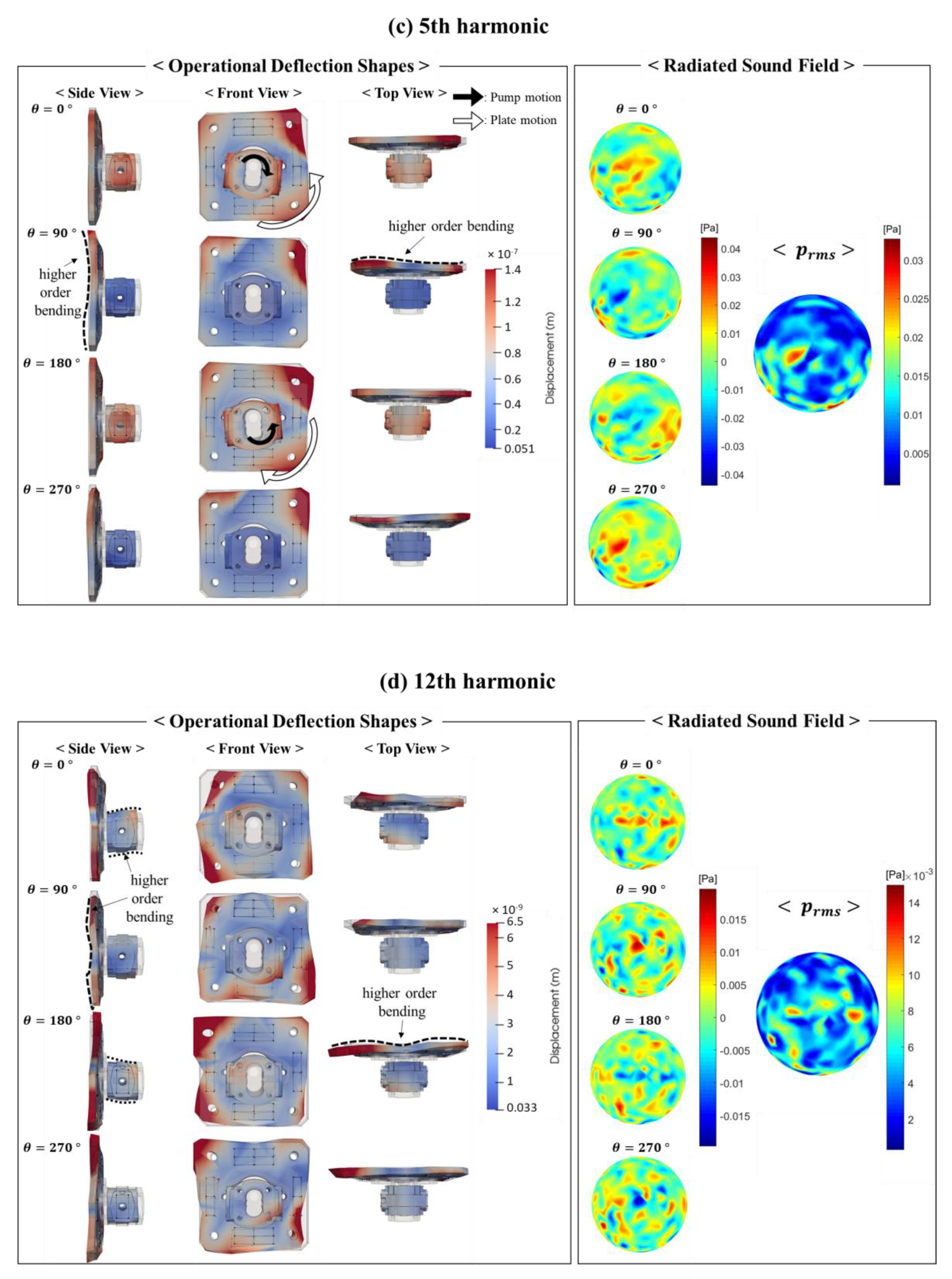
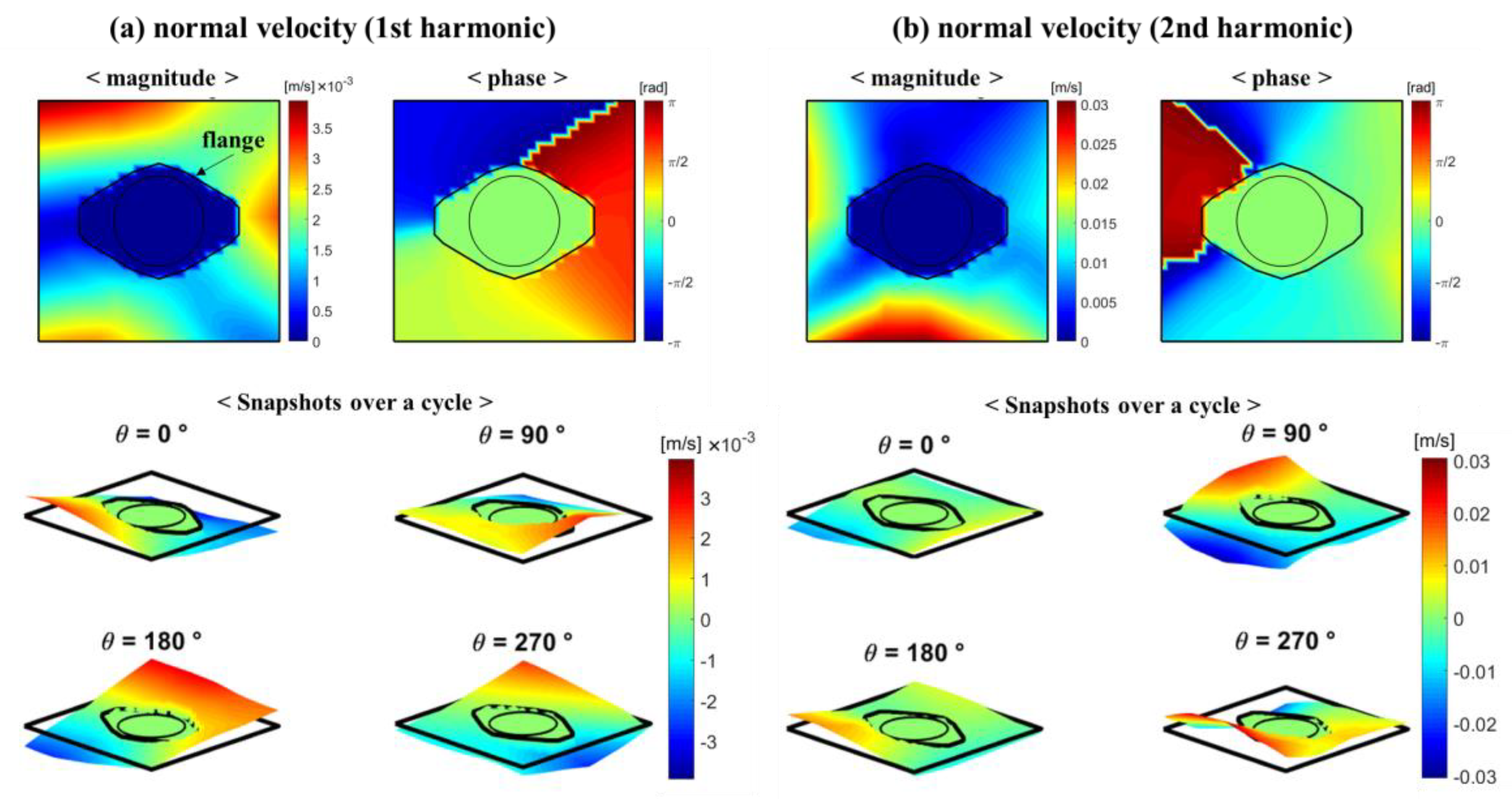
- As the frequency increases, the dominant pump body motion becomes the superposition of more complicated motions in the following order: simple horizontal and vertical bending, torsion, and the higher order bending. Similarly, the motion of the mounting plate and acoustic field have larger spatial variations at the higher frequency.
- At low frequencies, noisy area exists independent of the direction where the pump bending motion takes place. Furthermore, while the pump bending motions appear quite symmetric, noise radiation pattern is asymmetric at the low frequency range. It concludes that the motion of the pump does not predominantly dictate the sound field.
- The acoustic field and the motions of the mounting plate have several things in common at the low frequencies. First, both of their distributions are in an asymmetric manner. Second, the rms magnitudes of acoustic pressures are larger in the similar region in which the larger deflections of the mounting plate occur. Third, the similar out-of-phase behaviors of the plate motion and the acoustic pressure are observed in the similar regions of the plate and hemispherical acoustic measurement surface.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ge, L.; Quan, L.; Zhang, X.; Zhao, B.; Yang, J. Efficiency improvement and evaluation of electric hydraulic excavator with speed and displacement variable pump. Energy Convers. Manag. 2017, 150, 62–71. [Google Scholar] [CrossRef]
- Naayagi, R.T. A review of more electric aircraft technology. In Proceedings of the 2013 International Conference on Energy Efficient Technologies for Sustainability (ICEETS 2013), Nagercoil, India, 10–12 April 2013; pp. 750–753. [Google Scholar]
- Korane, K. Electrification Exposes Hydraulic-Pump Shortcomings. Available online: https://www.fluidpowerworld.com/electrification-exposes-hydraulic-pump-shortcomings/ (accessed on 15 December 2020).
- Edge, K. Designing quieter hydraulic systems—Some recent developments and contributions. Proc. JFPS Int. Symp. Fluid Power 1999, 1999, 3–27. [Google Scholar] [CrossRef]
- Pettersson, M.E.; Weddfelt, K.G.; Palmberg, J.O.S. Methods of reducing flow ripple from fluid power piston pumps—An experimental approach. SAE Tech. Pap. 1991, 100, 158–167. [Google Scholar] [CrossRef]
- Kojima, E.; Yu, J.; Ichiyanagi, T. Experimental determining and theoretical predicting of source flow ripple generated by fluid power piston pumps. SAE Trans. 2000, 109, 348–357. [Google Scholar]
- Drew, J.E.; Longmore, D.K.; Johnston, D.N. Theoretical analysis of pressure and flow ripple in flexible hoses containing tuners. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 1998, 212, 405–422. [Google Scholar] [CrossRef]
- Johnston, D.N.; Drew, J.E. Measurement of positive displacement pump flow ripple and impedance. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 1996, 210, 65–74. [Google Scholar] [CrossRef]
- Kalbfleisch, P.K.; Ding, D.; Baruah, A.; Ivantysynova, M.; Franzoni, G.; Zhang, H. Swashplate plate type axial piston pump noise diagnostics for design. In Proceedings of the Sixteenth Scandinavian International Conference on Fluid Power, Tampere, Finland, 22–24 May 2019. [Google Scholar]
- Ivantysynova, M.; Huang, C.; Christiansen, S.K. Computer aided valve plate design—An effective way to reduce noise. SAE Tech. Pap. 2004, 113, 162–173. [Google Scholar]
- Seeniraj, G.K.; Ivantysynova, M. Impact of valve plate design on noise, volumetric efficiency and control effort in an axial piston pump. In Proceedings of the American Society of Mechanical Engineers, The Fluid Power and Systems Technology Division (FPST), Chicago, IL, USA, 5–10 November 2006; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2006; pp. 77–84. [Google Scholar]
- Ye, S.G.; Zhang, J.H.; Xu, B. Noise reduction of an axial piston pump by valve plate optimization. Chin. J. Mech. Eng. 2018, 31, 57. [Google Scholar] [CrossRef] [Green Version]
- Devendran, R.S.; Vacca, A. Optimal design of gear pumps for exhaust gas aftertreatment applications. Simul. Model. Pr. Theory 2013, 38, 1–19. [Google Scholar] [CrossRef]
- Manring, N.D.; Kasaragadda, S.B. The theoretical flow ripple of an external gear pump. J. Dyn. Syst. Meas. Control 2003, 125, 396. [Google Scholar] [CrossRef]
- Ransegnola, T.; Zhao, X.; Vacca, A. A comparison of helical and spur external gear machines for fluid power applications: Design and optimization. Mech. Mach. Theory 2019, 142, 103604. [Google Scholar] [CrossRef]
- Devendran, R.S.; Vacca, A. Design potentials of external gear machines with asymmetric tooth profile. In Proceedings of the ASME/BATH 2013 Symposium on Fluid Power and Motion Control (FPMC 2013), Sarasota, FL, USA, 6–9 October 2013; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2013. [Google Scholar]
- Zhao, X.; Vacca, A. Analysis of continuous-contact helical gear pumps through numerical modeling and experimental validation. Mech. Syst. Signal. Process. 2018, 109, 352–378. [Google Scholar] [CrossRef]
- Nagamura, K.; Ikejo, K.; Tutulan, F.G. Design and performance of gear pumps with a non-involute tooth profile. Proc. Institution Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 699–711. [Google Scholar] [CrossRef]
- Mucchi, E.; Dalpiaz, G.; Fernandez del Rincon, A. Elastodynamic analysis of a gear pump. Part I: Pressure distribution and gear eccentricity. Mech. Syst. Signal. Process. 2010, 24, 2160–2179. [Google Scholar] [CrossRef]
- Borghi, M.; Paltrinieri, F.; Milani, M.; Zardin, B. The influence of cavitation and areation on gear pumps and motors meshing volumes pressures. In Proceedings of the American Society of Mechanical Engineers, The Fluid Power and Systems Technology Division (FPST), Chicago, IL, USA, 5–10 November 2006; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2006; pp. 47–56. [Google Scholar]
- Edge, K.A.; Lipscombe, B.R. The reduction of gear pump pressure ripple. Proc. Inst. Mech. Eng. Part B Manag. Eng. Manuf. 1987, 201, 99–106. [Google Scholar] [CrossRef]
- Woo, S.; Opperwall, T.; Vacca, A.; Rigosi, M. Modeling noise sources and propagation in external gear pumps. Energies 2017, 10, 1068. [Google Scholar] [CrossRef] [Green Version]
- Mucchi, E.; Rivola, A.; Dalpiaz, G. Modelling dynamic behaviour and noise generation in gear pumps: Procedure and validation. Appl. Acoust. 2014, 77, 99–111. [Google Scholar] [CrossRef]
- Opperwall, T.; Vacca, A. A combined FEM/BEM model and experimental investigation into the effects of fluid-borne noise sources on the air-borne noise generated by hydraulic pumps and motors. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 457–471. [Google Scholar] [CrossRef]
- Carletti, E.; Miccoli, G.; Pedrielli, F.; Parise, G. Vibroacoustic measurements and simulations applied to external gear pumps. An integrated simplified approach. Arch. Acoust. 2016, 41, 285–296. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.; Wang, Y.S.; Gao, J.H.; Guo, H. Fluid-sound coupling simulation and experimental validation for noise characteristics of a variable displacement external gear pump. Noise Control. Eng. J. 2014, 62, 123–131. [Google Scholar] [CrossRef]
- Pan, Y.; Li, Y.; Huang, M.; Liao, Y.; Liang, D. Noise source identification and transmission path optimisation for noise reduction of an axial piston pump. Appl. Acoust. 2018, 130, 283–292. [Google Scholar] [CrossRef]
- Rodionov, L.; Makaryants, G. Simulation of gear pump noise generation. In Proceedings of the 9th FPNI Ph.D. Symposium on Fluid Power, Florianópolis, Brazil, 26–28 October 2016; pp. 1–9. [Google Scholar]
- Schleihs, C.; Murrenhoff, H. Acoustical simulation of a hydraulic swash plate motor. In Proceedings of the ASME/BATH 2015 Symposium on Fluid Power and Motion Control (FPMC 2015), Chicago, IL, USA, 12–14 October 2015. [Google Scholar]
- Bonanno, A.; Pedrielli, F. A study on the structureborne noise of hydraulic gear pumps. Proc. JFPS Int. Symp. Fluid Power 2008, 2008, 641–646. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, S.; Ye, S.; Xu, B.; Song, W.; Zhu, S.; Tang, H.; Xiang, J. Experimental investigation on the noise reduction of an axial piston pump using free-layer damping material treatment. Appl. Acoust. 2018. [Google Scholar] [CrossRef]
- Wang, H.; Cao, S.; Luo, X.; He, X.; Zhang, Z.; Zhu, Y. Study on the influence of rubber isolator’s dynamic stiffness on the dynamic behavior of seawater hydraulic piston pump. Ocean Eng. 2019, 182, 14–20. [Google Scholar] [CrossRef]
- Xu, B.; Ye, S.; Zhang, J. Numerical and experimental studies on housing optimization for noise reduction of an axial piston pump. Appl. Acoust. 2016, 110, 43–52. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, S.; Ye, S.; Xu, B.; Zhu, S.; Xiang, J.; Tang, H. Experimental investigation on the sharpness reduction of an axial piston pump with reinforced shell. Appl. Acoust. 2018, 142, 36–43. [Google Scholar] [CrossRef]
- Rodionov, L.; Rekadze, P. Exploration of acoustic characteristics of gear pumps with polymeric pinion shafts. Procedia Eng. 2015, 106, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.; Ivantysynova, M. Active vibration control of swash plate-type axial piston machines with two-weight notch least mean square/filtered-x least mean square (LMS/FxLMS) filters. Energies 2017, 10, 645. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.; Ivantysynova, M. Active vibration/noise control of axial piston machine using swash plate control. In Proceedings of the ASME/BATH 2017 Symposium on Fluid Power and Motion Control (FPMC 2017), Sarasota, FL, USA, 16–19 October 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control and Testing; Tech Books International Pvt. Ltd.: Maharashtra, India, 2003. [Google Scholar]
- Hydraulic Fluid Power: Positive-Displacement Pumps, Motors and Integral Transmissions: Methods of Testing and Presenting Basic Steady-State Performance; ISO 4409; International Organization for Standardization: Geneva, Switzerland, 2007.
- Kalbfleisch, P.; Kim, T.; Ivantysynova, M. Robotic arm for automatic sound intensity measurements. In Proceedings of the BATH/ASME 2016 Symposium on Fluid Power and Motion Control (FPMC 2016), Bath, UK, 7–9 September 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar]
- Pierce, A.D. Acoustics: An Introduction to its Physical Principles and Applications; The Acoustical Society of America: Melville, NY, USA, 1989. [Google Scholar]
- Woo, S.; Vacca, A.; Rigosi, M. A model based approach for the evaluation of noise emissions in external gear pumps. In Proceedings of the 11th International Fluid Power Conference (IFK), Aachen, Germany, 19–21 March 2018. [Google Scholar]
- Hydraulic Fluid Power—Test Code for the Determination of Sound Power Levels of Pumps Using Sound Intensity Techniques: Engineering Method—Part 1: Pumps; ISO 16902-1; International Organization for Standardization: Geneva, Switzerland, 2003.
- Hydraulic Fluid Power—Test Code for Determination of Airborne Noise Levels—Part 1: Pumps; ISO 4412-1; International Organization for Standardization: Geneva, Switzerland, 1991.
- Acoustics—Determination of Sound Power Levels of Noise Sources Using Sound Intensity—Part 1: Measurement at Discrete Points; ISO 9614-1; International Organization for Standardization: Geneva, Switzerland, 1993.
- Acoustics—Determination of Sound Power Levels of Noise Sources—Engineering Methods for Free-Field Conditions over a Reflecting Plane; ISO 3744; International Organization for Standardization: Geneva, Switzerland, 1981.
- Carfagni, M.; Pierini, M. A critical revision of ISO standard 9614-1: Determination of sound power levels of noise sources using sound intensity. In Proceedings of the 15th International Congress on Sound & Vibration, Adelaide, Australia, 15–18 December 1997. [Google Scholar]
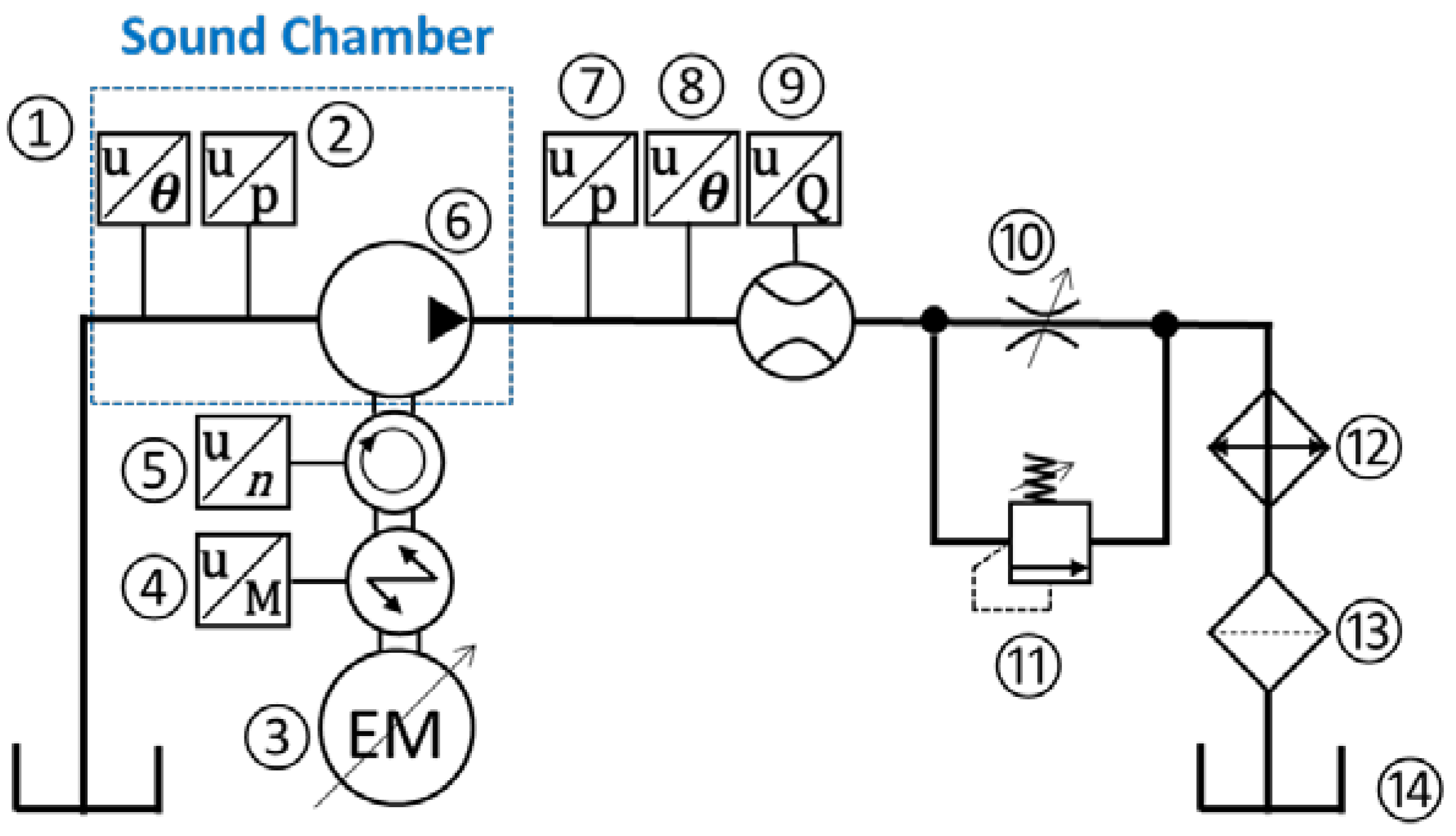

| No. | Description | Details |
|---|---|---|
| 1 | Inlet temperature sensor | Omega Thermocouple Type K (Ni-Cr), Temperature range: −200–850 °C, Accuracy: +1 °C |
| 2 | Inlet pressure sensor | Hydac HDA 4185-B-0050-000-F1—Piezoresistive type —Range: 0–3.4 bar, Accuracy: ±0.5% |
| 3 | Variable electric motor | SSB, Maximum operating torque: 500 Nm, Speed range: ±3000 rpm |
| 4 | Torque meter | HBM T30FNA Torque range: ±500 Nm, Speed range: ±3000 rpm, |
| 5 | Shaft speed sensor | Accuracy: ±0.1% |
| 6 | Test pump | External gear pumps |
| 7 | Outlet pressure sensor | Hydac 4745—Strain gauge type—Range: 0–400bar, Accuracy: ±0.25% |
| 8 | Outlet temperature sensor | Omega Thermocouple Type K (Ni-Cr), Temperature range: −200–850 °C, Accuracy: +1 °C |
| 9 | Outlet flow meter | VSE VS4 GPO 12V—Fixed displacement volume (gear type)—Range: 1–250 L/min, Accuracy: ±0.3% |
| 10 | Needle valve | Sun Hydraulics NFECKEN, Capacity: 30 gpm (113.6 L/min), Maximum operating pressure: 5000 psi (344.7 bar) |
| 11 | Pressure relief valve | Sun Hydraulics RPICKCN, Capacity: 100 gpm (378.5 L/min), Maximum operating pressure: 5000 psi (344.7 bar) |
| 12 | Heat exchanger | Parker OAW 46-60, Cooling Capacity: 23–142 hp (17.2–105.9 kW) |
| 13 | Filter | Parker 50AT, Nominal Filter Rating: 10 micron, Nominal Flow Rating: 40 gpm (151.4 L/min) |
| 14 | Reservoir | Buyers UR 70S, Capacity: 70 gallon (265.0 L), ISO 46 oil |
| Number of Grid Points (N) | ∆SWL (dB/dBA) | Measurement Time (mins) | (ISO 9614-1) | ||
|---|---|---|---|---|---|
| Grade 1 (Precision) | Grade 2 (Engineering) | Grade 3 (Survey) | |||
| 1 | −8.53/−7.97 | 0.1 | No | No | No |
| 3 | −0.56/−0.56 | 1 | No | No | No |
| 6 | +0.33/0.30 | 2 | No | No | No |
| 10 | −0.47/−0.48 | 2.5 | No | No | Yes |
| 20 | +0.03/0.00 | 4 | No | No | Yes |
| 36 | −0.25/−0.24 | 7 | No | Yes | Yes |
| 50 | −0.05/−0.07 | 10 | No | Yes | Yes |
| 100 | −0.04/−0.05 | 19.5 | Yes | Yes | Yes |
| 150 | −0.06/−0.07 | 28 | Yes | Yes | Yes |
| 225 | 0.00/0.00 | 41.5 | Yes | Yes | Yes |
| Test 1 | Test 2 | Test 3 | |
|---|---|---|---|
| ∆SWL (dBA) | 0 | 0.004 | 0.012 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, S.; Vacca, A. Experimental Characterization and Evaluation of the Vibroacoustic Field of Hydraulic Pumps: The Case of an External Gear Pump. Energies 2020, 13, 6639. https://doi.org/10.3390/en13246639
Woo S, Vacca A. Experimental Characterization and Evaluation of the Vibroacoustic Field of Hydraulic Pumps: The Case of an External Gear Pump. Energies. 2020; 13(24):6639. https://doi.org/10.3390/en13246639
Chicago/Turabian StyleWoo, Sangbeom, and Andrea Vacca. 2020. "Experimental Characterization and Evaluation of the Vibroacoustic Field of Hydraulic Pumps: The Case of an External Gear Pump" Energies 13, no. 24: 6639. https://doi.org/10.3390/en13246639
APA StyleWoo, S., & Vacca, A. (2020). Experimental Characterization and Evaluation of the Vibroacoustic Field of Hydraulic Pumps: The Case of an External Gear Pump. Energies, 13(24), 6639. https://doi.org/10.3390/en13246639






