An Active FTC Strategy Using Generalized Proportional Integral Observers Applied to Five-Phase PMSG based Tidal Current Energy Conversion Systems

Abstract

In recent years, multi-phase permanent magnet synchronous generators (PMSGs) have become attractive in the field of tidal current energy conversion systems (TCECS) due to their high-power density, reliability, and availability. However, external disturbances and malfunctions in power conversion chains will bring challenges to achieving stable and continuous tidal current energy harnessing. Using generalized proportional integral observers, an active fault-tolerant control (AFTC) strategy is therefore proposed for a five-phase PMSG based TCECS that is subjected to an open switch fault (OSF) in the generator side converter. This proposed AFTC strategy is applied into q-axis current control loops, which contain fault detection and compensation. The fault compensator will be smoothly activated using a sigmoid function once the OSF is detected. Finally, a small-scale power experimental platform emulating the TCECS is established in order to verify the feasibility and efficiency of the proposed FTC strategy. Experiment results show that this AFTC strategy can detect faults rapidly and effectively attenuate torque ripples in the post-fault operation mode.

1. Introduction

Tidal current energy has predominant advantages relative to other types of renewable energies, such as predictability, high power density, and energy continuity at almost all times, which significantly facilitates controller designs and grid connection [1]. Nevertheless, the power generation equipment, the so called tidal current turbine, is always vulnerable to harsh marine conditions that pose daunting challenges for maintenance [2]. As a result, the exploration of advanced solutions with high fault tolerance has become a main objective to practitioners and theoreticians.

For this concern, breakthroughs can be made utilizing multi-phase machines, which meet the requirements of fault tolerance since they provide redundant structures than the classical three-phase machinery [3]. Thus, the multi-phase machine nowadays is widely applied into the fields of offshore marine energies, warships, aerospace and so on [4]. A great number of works have been undertaken in the past few decades concerning the FTC approaches related to multiphase machines. All of these contributions can be generally categorized [5] into passive FTC (PFTC) and active FTC (AFTC) methods. PFTC is usually realized based on robust controlling theories [6] that will force the controller with low sensitivities to fault components. For instance, Mekri et al. [7] provide a comparative study between three and five-phase permanent magnet synchronous generator (PMSG) in a tidal current energy conversion system (TCECS) by imposing an optimal torque reference and second-order sliding mode torque/current controllers. Pham et al. [8] proposed a fault tolerant strategy incorporating finite control set and model predictive control methods for a five-phase PMSG based TCECS. Single-phase and double-phase open circuits are focused on in this work with the concern of constant and variable marine tidal current velocities. A fault-tolerant controller design is proposed by Baudart et al. [9] through Lagrangian formulation based optimal torque references as well as reconfiguration of current controllers. A limitation torque control strategy according to the response of torque commands was designed by Guo et al. [10] considering both short circuit and open circuit faults in a dual stator based ten-phase machine. These PFTC methodologies are able to achieve great robustness and implementability in normal and abnormal operation modes while they have obvious shortcomings, such as complicated design process of controllers, lack of supports of fault information. Consequently, research of AFTC has become a promising direction in recent years. Conventionally, an AFTC mechanism lies in utilization of results from fault detection and diagnosis, offering evidences for further actions in post-fault operation modes. Fault status, size, and locations can be recognized by using fault estimation techniques, which plays an essential role in building AFTC theories [11,12]. Many efforts [11,13,14,15,16] have been made on the basis of this consensus. Among all of these research achievements, fault estimation and compensation based on disturbance observer (DOB) has attracted a lot of attentions benefit from more degrees of control freedom, high implementability in real-time, etc. A generalized DOB family defined by Chen et al. [17] contains linear and nonlinear DOB, equivalent input disturbance, extended state observer (ESO), generalized proportional integral observer (GPIO) [18,19], extended high-gain state observer and so forth. Almost all of these DOB methods can provide information of multi-state estimation, which plays an important role in disturbance attenuation. Selecting an appropriate DOB method is a main concern in practice, which depends on the complexity of parameter setting and realizability of online deployment.

In order to increase the reliability and availability of the tidal application in real time, an AFTC strategy is proposed by GPIO and applied to a five-phase PMSG based TCECS. Under the framework of GPIO, this proposed method contains an adaptive threshold-based fault detection method using form factors (FFs) [20] and fault compensation-based FTC are developed. Specially, a smooth activation-based fault compensation mechanism is incorporated to improve the transient behaviors due to the sudden action of compensation. Finally, a small-scale power full-physical experimental platform is carefully established to validate the effectiveness and efficiency of the proposed AFTC strategy.

The remainder of this paper is organized as follows. Section 2 introduces system modelling and basic descriptions of the whole TCECS, which concentrates on the generator side. Section 3 gives detailed design procedures of the proposed AFTC strategy. In Section 4, the effectiveness and performance of the proposed strategy will be experimentally verified under an OSF case. In the end, Section 5 concludes this paper.

2. System Description and Modelling

The studied system shown in Figure 1 presents the generator side of a tidal current energy conversion system. It is composed by a five-phase PMSG which is connected to a DC load through a five-leg converter. Figure 1 also indicates a most fundamental type of fault in the TCECS investigated in this paper, namely the OSF of the power switch. The OSF condition is achieved by blocking the switching part excluding the anti-parallel diode.

2.1. Resource of Tidal Current

The acquired hydrodynamic energy [21] from the tidal current can be calculated by

$$P=0.5\rho \mathsf{\pi }{R}^2{\nu }_{tides}^{3}Cp$$

(1)

where ρ represents the density of sea water, ν_tides means the tidal current velocity, and R indicates the radius of turbine blade. Cp is the power coefficient, depending on tip speed ratio (TSR, λ = ΩR/ν_tides) and pitch angle β, whose expression is given by Equation (2).

$$\left\{\begin{array}{l}Cp(\lambda ,\beta )=C_1\left(\frac{C_2}{{\lambda }_i}-C_3\beta -C_4\right){\mathrm{e}}^{-\frac{C_5}{{\lambda }_i}}+C_6{\lambda }_i\\ {\lambda }_i=1/\left(\frac{1}{\lambda +0.008\beta }-\frac{0.003}{{\beta }^3+1}\right)\end{array}\right.$$

(2)

where C₁–C₆ are the coefficients of Cp(λ, β).

2.2. Tidal Current Turbine

A Cp curve is given as shown in Figure 2a. The mechanical speed is denoted as Ω. P-Ω characteristics of the turbine are depicted in Figure 2b under various tidal current velocities. Working process of a tidal current turbine can be divided into 3 parts: starting, maximum power point tracking (MPPT), and constant power operational stages. This paper focuses on the second one where the pitch angle control is not carried out yet (β = 0). In this paper, cut-in speed and rated speed are 1 m/s and 3.2 m/s, respectively.

2.3. Dynamic Model of Five-Phase PMSG

To facilitate the dynamic modelling, here magnetic saturation, core losses and temperature variations are neglected. Figure 3 describes an equivalent structure of star connected windings. M₁ and M₂ represent mutual inductances among the adjacent (2π/5 phase shift) and non-adjacent (4π/5 phase shift) phase windings, respectively.

The electrical voltage equation of five-phase PMSG can be written as below in original abcde frames.

$$U=E-R_{s}I-L\frac{dI}{dt}$$

(3)

subject to

$$\begin{array}{c}\begin{array}{l}U={\left[u_a,u_b,u_c,u_d,u_e\right]}^T\\ E={\left[e_a,e_b,e_c,e_d,e_e\right]}^T\\ I={\left[i_a,i_b,i_c,i_d,i_e\right]}^T\end{array}\end{array}\begin{array}{c}L=\left[\begin{array}{cccc}{L}_s& M_1& M_2& \begin{array}{cc}{M}_2& M_1\end{array}\\ M_1& L_s& M_1& \begin{array}{cc}{M}_2& M_2\end{array}\\ M_2& M_1& L_s& \begin{array}{cc}{M}_1& M_2\end{array}\\ \begin{array}{c}{M}_2\\ M_1\end{array}& \begin{array}{c}{M}_2\\ M_2\end{array}& \begin{array}{c}{M}_1\\ M_2\end{array}& \begin{array}{cc}\begin{array}{c}{L}_s\\ M_1\end{array}& \begin{array}{c}{M}_1\\ L_s\end{array}\end{array}\end{array}\right]\end{array}$$

where U, E, R, I, and L represent the output, back-electromagnetic forces (back-EMFs), phase resistances, phase current and generator inductances, respectively. The self-inductance of phase windings is defined as L_s. The expression of back-EMFs in original abcde frames are given by

$$\left[\begin{array}{l}{e}_a\\ e_b\\ e_c\\ e_d\\ e_e\end{array}\right]={\displaystyle \sum _{\begin{array}{l}h \mathrm{is} \mathrm{positive} \\ \mathrm{odd} \mathrm{numbers}\end{array}}hp\mathrm{\Omega }{\Phi }_h\left[\begin{array}{l}\sin \left(h\theta \right)\\ \sin \left(h\left(\theta -2\mathsf{\pi }/5\right)\right)\\ \sin \left(h\left(\theta -4\mathsf{\pi }/5\right)\right)\\ \sin \left(h\left(\theta -6\mathsf{\pi }/5\right)\right)\\ \sin \left(h\left(\theta -8\mathsf{\pi }/5\right)\right)\end{array}\right]}$$

(4)

where the positive odd number h represents the harmonic orders. θ and p represent the electrical angle and the number of pole pairs of the generator, respectively. Φ_h represents the magnet flux corresponding to the hth order harmonic component of the back-EMFs.

As a result, the experimental waveforms of the trapezoidal back-EMFs for the small-scale power five-phase PMSG can be seen in Figure 4a. In Figure 4b, the harmonic orders become clear to see that the back-EMFs mainly contain 1st, 3rd, 5th, 7th, and 9th harmonic components.

A five-phase PMSG can be decomposed into three 3-phase sub-machines [22,23] (primary, secondary and homopolar sub-machines).

Table 1. Distribution rule of back-EMF harmonic components in a five-phase PMSG.

Principal Sub-Machine	Secondary Sub-Machine	Homopolar Sub-Machine
1, 9, 11, …, 5 h ± 4	3, 7, 13, …, 5 h ± 2	5, 15, …, 5 h

presents a harmonic distribution rule with respect to the three sub-machines.

Without connecting the neutral point, the homopolar sub-machine is negligible in this paper. By using a transformation matrix T_Park given in Equation (6), Equation (3) will be thereby projected into stationary coordinate frames (Park frames) as

$$U^{\prime }=E^{\prime }-R^{\prime }{I}^{\prime }-L^{\prime }\frac{d{I}^{\prime }}{dt}$$

(5)

where

$$\begin{gathered} \begin{array}{c}\begin{array}{l}{U}^{\prime }={\left[u_{pd},u_{pq},u_{sd},u_{sq}\right]}^T\\ E^{\prime }={\left[e_{pd},e_{pq},e_{sd},e_{sq}\right]}^T\\ R^{\prime }=diag[R_{pd},R_{pq},R_{sd},R_{sq}]\\ I^{\prime }={\left[i_{pd},i_{pq},i_{sd},i_{sq}\right]}^T\end{array}\end{array}\begin{array}{c}\begin{array}{c}{L}^{\prime }=diag{\left[L_{pd},L_{pq},L_{sd},L_{sq}\right]}^T\\ \mathrm{here}\left\{\begin{array}{c}{L}_{pd}=L_{pq}=L_{pr}=L_s+\frac{\left(\sqrt{5}-1\right)M_1-\left(\sqrt{5}+1\right)M_2}{2}\\ L_{sd}=L_{sq}=L_{se}=L_s+\frac{\left(\sqrt{5}-1\right)M_2-\left(\sqrt{5}+1\right)M_1}{2}\end{array}\right.\end{array}\end{array} \\ {T}_{\mathrm{Park}}=\sqrt{\frac{2}{5}}\left[\begin{array}{ccccc}\cos (\theta )& \cos \left(\theta -\frac{2\mathsf{\pi }}{5}\right)& \cos \left(\theta -\frac{4\mathsf{\pi }}{5}\right)& \cos \left(\theta -\frac{6\mathsf{\pi }}{5}\right)& \cos \left(\theta -\frac{8\mathsf{\pi }}{5}\right)\\ -\sin (\theta )& -\sin \left(\theta -\frac{2\mathsf{\pi }}{5}\right)& -\sin \left(\theta -\frac{4\mathsf{\pi }}{5}\right)& -\sin \left(\theta -\frac{6\mathsf{\pi }}{5}\right)& -\sin \left(\theta -\frac{8\mathsf{\pi }}{5}\right)\\ \cos (3\theta )& \cos \left(3\theta -\frac{6\mathsf{\pi }}{5}\right)& \cos \left(3\theta -\frac{2\mathsf{\pi }}{5}\right)& \cos \left(3\theta -\frac{8\mathsf{\pi }}{5}\right)& \cos \left(3\theta -\frac{4\mathsf{\pi }}{5}\right)\\ -\sin (3\theta )& -\sin \left(3\theta -\frac{6\mathsf{\pi }}{5}\right)& -\sin \left(3\theta -\frac{2\mathsf{\pi }}{5}\right)& -\sin \left(3\theta -\frac{8\mathsf{\pi }}{5}\right)& -\sin \left(3\theta -\frac{4\mathsf{\pi }}{5}\right)\end{array}\right] \end{gathered}$$

(6)

With respect to Equation (4), the expressions of back-EMFs in Park frames are thereby deduced as

$$\left\{\begin{array}{l}{e}_{pd}=-9\sqrt{\frac{5}{2}}p\Omega {\mathsf{\Phi }}_9\sin (10\theta )\\ e_{pq}=\sqrt{\frac{5}{2}}p\Omega {\mathsf{\Phi }}_1-9\sqrt{\frac{5}{2}}p\Omega {\mathsf{\Phi }}_9\cos (10\theta )\end{array}\right.\left\{\begin{array}{l}{e}_{sd}=-7\sqrt{\frac{5}{2}}p\Omega {\mathsf{\Phi }}_7\sin (10\theta )\\ e_{sq}=3\sqrt{\frac{5}{2}}p\Omega {\mathsf{\Phi }}_3-7\sqrt{\frac{5}{2}}p\Omega {\mathsf{\Phi }}_7\cos (10\theta )\end{array}\right.$$

(7)

It should be noted that only 1st and 3rd harmonic components in the back-EMFs will be taken into account for controller designs by neglecting 7th and 9th ones. That is to say, the 10 times terms in Equation (7) will be unconsidered in this paper.

Electrical torque can be thus written as below by using vectors in Park frames.

$${\mathrm{\Gamma }}_{em}=-\left(i_{pd}{e}_{pd}+i_{pq}{e}_{pq}+i_{sd}{e}_{sd}+i_{sq}{e}_{sq}\right)/\mathrm{\Omega }$$

(8)

Additionally, the five-phase PMSG is essentially an inertial motion system that can be indicated by a first order mechanical equation as below.

$$J\frac{d\mathrm{\Omega }}{dt}=\mathrm{\Gamma }-{\mathrm{\Gamma }}_{em}-f\mathrm{\Omega }$$

(9)

where Γ and Γ_em represent the mechanical and electromagnetic torques. Moment of inertia and friction coefficient are denoted as J and f, respectively.

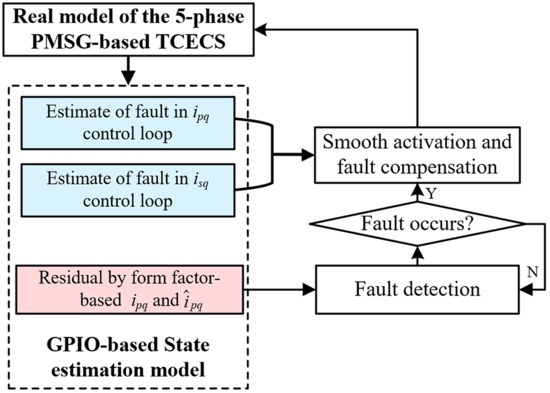
3. Proposed AFTC Strategy

3.1. Principle of GPIO-Based AFTC Strategy in a Classical Close-Loop System

A scalar second order SISO system with a concern of systematic lumped disturbance can be expressed as

$$\left\{\begin{array}{l}{\dot{x}}_1=a_1{x}_1+\left(u+d_l\right)/b_1\\ {\dot{x}}_2={\dot{d}}_l\\ y=c_1{x}_1\end{array}\right.$$

(10)

where x₁ represents the system state. x₂ is a augmented state used to estimate the lumped disturbance d_l. The system input gain, output gain and measurement gain are denoted as a₁, b₁ and c₁, respectively. Here, c₁ is equal to 1 and b₁ ≠ 0.

In fact, the lumped disturbance d_l represents a bounded perturbated term, which may contain linear or nonlinear perturbations from model uncertainties and external noises. In detail, the model uncertainties originated from modeling mismatches, which are mainly caused by parameter variations and fault occurrences. The lump disturbance term can be expressed as below by a combination of model uncertainties or external interferences.

$$d_l={\Delta }_{para}+{\Delta }_f+{\Delta }_{noise}$$

(11)

where Δ_para represents a time varying output term due to the parameter variation. Δ_f represents the fault component, which highly relies on the type of fault, which will determine its size, harmonic content, and degree of nonlinearity. It should be noted that the measurement noises Δ_noise can be neglected by using some engineering techniques, such as filters. The parameters a₁ and b₁ will vary from the nominal value during operations, which can be expressed as

$$\left\{\begin{array}{l}{a}_1=a_{1\_\mathrm{nominal}}+\Delta a_1\\ b_1=b_{1\_\mathrm{nominal}}+\Delta b_1\end{array}\right.$$

(12)

According to Equations (10) and (12), the term Δ_para can be deduced as

$${\Delta }_{para}=\left(\Delta a_1\Delta b\right)x_1-\Delta b_1{\dot{x}}_1$$

(13)

Compared with the most used ESO, GPIO is chosen in this paper to design the compensator since it is easy to implement and will provide more state information to increase the estimation accuracy. According to Equations (10)–(13), a full order expression of GPIO can be given by

$$\left\{\begin{array}{l}{\dot{\widehat{x}}}_1=a_1{\widehat{x}}_1+b_{1}u+{\widehat{x}}_2+{\alpha }_1\left(y-\widehat{y}\right)\\ {\dot{\widehat{x}}}_2={\widehat{x}}_3+{\alpha }_2\left(y-\widehat{y}\right)\\ \cdots \\ {\dot{\widehat{x}}}_n={\alpha }_n\left(y-\widehat{y}\right)\\ \widehat{y}=c_1{\widehat{x}}_1\end{array}\right.$$

(14)

where n is a positive integer that represents the order of states. α₁ to α_n are the observer gains. Importantly, ESO can be obtained without using any auxiliary states.

In terms of a feedback close loop, the PI controller can be formulated as Kp + Ki/s, where s represents the operator in s-plane. Hence, the compensated output can be written as below. Hereafter the superscript “*” represents the corresponding reference value.

$$u_{comp}=u-fc{n}_{act}{K}_{comp}{\widehat{x}}_2=\left(Kp+\frac{Ki}{s}\right)\left(x_1^{*}-x_1\right)-fc{n}_{act}{K}_{comp}{\widehat{x}}_2$$

(15)

where K_comp means an adjustable gain of compensation, which related to the working conditions, such as healthy and faulty operation modes. In nominal condition, K_comp = 1. The activation function fcn_act should maintain the system operating smoothly concerning avoidance of high transient overshoots with the sudden injection. The diagram of this AFTC strategy for the system Equation (10) can be organized in Figure 5. The fault detection will be realized by comparing the residual and the threshold. Fault compensation will be activated immediately once fault is detected via the activation function.

3.2. GPIO-Based AFTC Strategy Design Example for a Five-Phase PMSG Power Convertion System

Relying on the description in the previous subsection, a five-phase PMSG based TECES example is taking into account here. Figure 6 indicates the whole control strategy of the five-phase PMSG based TECES using the field-oriented control (FOC) theory and the GPIO-based AFTC sstrategy. Since current in q-axis is directly related to the electromagnetic torque, this AFTC strategy is carried out in the q-axis of the inner current loops. Firstly, the fault detection part is realized only based on the estimated residual of q-axis current corresponding the primary sub-machine. Once fault is detected, the compensation will be activated promptly into the q-axis control loops relative to the two sub-machines.

3.2.1. Basic Control Strategy in Dual Loops

First of all, PI-based controllers in dual loops plus an optimal TSR-MPPT algorithm will be presented as follows in order to provide a foundation for the proposed GPIO-based AFTC strategy in speed loop.

• Optimal control references

In this paper, an optimal TSR-based MPPT algorithm [24] is introduced to offer an expected speed reference. This algorithm can guarantee the whole system to capture needed maximum powers under each ν_tides by exploiting the optimal TSR λ_opt and the max power coefficient Cp_max. Thus, expected speed reference and optimal mechanical torque are expressed as

$${\mathrm{\Omega }}^{*}=\frac{{\nu }_{tides}}{R}{\lambda }_{opt}, {\mathrm{\Gamma }}_{opt}=\frac{\rho \mathsf{\pi }{R}^{5}C{p}_{max}}{2{\lambda }_{opt}^3}{\mathrm{\Omega }}^2$$

(16)

To minimize copper losses [25,26], the current vectors and the back-EMF vectors will satisfy Fleming’s right-hand rule, which can be expressed as below (e_pd = e_sd = 0).

$$X_r=\frac{i_{sq}}{i_{pq}}=\frac{e_{sq}}{e_{pq}}=\frac{{3\mathsf{\Phi }}_3}{{\mathsf{\Phi }}_1}$$

(17)

where X_r represents a magnetic ratio between the two sub-machines.

According to the FOC theory, the expected torque can be calculated by

$${\mathrm{\Gamma }}_{em}^{*}=-\frac{i_{pd}^{*}{e}_{pd}+i_{pq}^{*}{e}_{pq}+i_{sd}^{*}{e}_{sd}+i_{sq}^{*}{e}_{sq}}{\mathrm{\Omega }}$$

(18)

Substituting Equations (17) and (18), the current references are given by

$$\left\{\begin{array}{l}{i}_{pd}^{*}=0, i_{pq}^{*}=\frac{e_{pq}}{e_{pd}^2+e_{pq}^2}{\mathrm{\Gamma }}_{em}^{*}\mathrm{\Omega }=\frac{{\mathrm{\Gamma }}_{em}^{*}}{K_t}\\ i_{sd}^{*}=0, i_{sq}^{*}=X_r{i}_{pq}^{*}\end{array}\right.,\mathrm{here} K_t=\sqrt{\frac{5}{2}}p{\Phi }_1\left(1+X_r^2\right)$$

(19)

where K_t represents a conversion gain between reference electromagnetic torque and reference of q axis current in the primary sub-machine.

• PI-based controller design in dual loops

Here, the generator side converter can be modeled by a nonlinear delay as K_pwm/(1 + 1.5T_pwms) due to sampling and switching time, where T_pwm (is equal to 1/f_pwm) is the time constant of switching frequency. K_pwm, the equivalent gain of the PWM modulator, can be expressed as K_pwm = V_dc/V_carrier in the linear range, V_carrier is the amplitude of carrier signals, which is usually set as 1. Thus, PI parameters in current loop controllers can be calculated by

$$K{p}_{pd}=\frac{L_{pr}}{3K_{pwm}{T}_{pwm}},K{p}_{sd}=\frac{L_{se}}{3K_{pwm}{T}_{pwm}},K{i}_{sd}=K{i}_{pd}=\frac{R_s}{3K_{pwm}{T}_{pwm}}$$

(20)

Moreover, for the outer speed loop controller, the PI parameters are given by

$$K{p}_{\mathrm{\Omega }}=\frac{3J}{5K_t{T}_{\mathrm{\Omega }}},K{i}_{\mathrm{\Omega }}=\frac{3}{25K_t{T}_{\mathrm{\Omega }}^2}$$

(21)

where T_Ω = (τ_Ω + 3T_pwm). τ_Ω is denoted as the sampling delay of the speed. In this paper, τ_Ω = 5T_pwm.

3.2.2. Observer Design

State form currents in q-axis for primary and secondary sub-machines can be rewritten as below according to Equations (5) and (6), and Equations (10) and (11). It should be noted that here the coupling terms are also incorporated in the lumped disturbances for sake of compensation.

$$\left\{\begin{array}{l}{\dot{i}}_{pq}=\frac{1}{L_{pr}}\left(-R_s{i}_{pq}\underset{d_{l\_pq}}{\underbrace{-p\mathrm{\Omega }{L}_{pr}{i}_{pd}+\sqrt{\frac{5}{2}}p\mathrm{\Omega }{\mathsf{\Phi }}_1+{\Delta }_{pq}+{\Delta }_{f\_pq}}}-u_{pq}\right)\\ {\dot{i}}_{sq}=\frac{1}{L_{se}}\left(-R_s{i}_{sq}\underset{d_{l\_sq}}{\underbrace{-3p\mathrm{\Omega }{L}_{se}{i}_{sq}+3\sqrt{\frac{5}{2}}p\mathrm{\Omega }{\mathsf{\Phi }}_3+{\Delta }_{sq}+{\Delta }_{f\_sq}}}-u_{sq}\right)\end{array}\right.$$

(22)

where d_{l_pq} and d_{l_sq} are the lumped disturbance in the q-axis for primary and secondary sub-machines, respectively.

• Analysis of lumped disturbance terms

Similar to Equations (11)–(13), these two lumped disturbance terms can be generally extracted as

$$\left\{\begin{array}{l}{d}_{l\_pq}={\Delta }_{para\_pq}+{\Delta }_{f\_pq}+{\Delta }_{noise}{}_{\_pq}\\ d_{l\_sq}={\Delta }_{para\_sq}+{\Delta }_{f\_sq}+{\Delta }_{noise}{}_{\_sq}\end{array}\right.$$

(23)

The noise terms will not be discussed by the analysis in Equation (11). There exist variations of machine parameters relative to their nominal values in different working conditions, which can be expressed as

$$\left\{\begin{array}{l}{R}_s=R_s{}_{\_\mathrm{nominal}}+\Delta R_s\\ L_{pr}=L_{pr}{}_{\_\mathrm{nominal}}+\Delta L_{pr};{\Phi }_1={\Phi }_1{}_{\_\mathrm{nominal}}+\Delta {\Phi }_1\\ L_{se}=L_{se}{}_{\_\mathrm{nominal}}+\Delta L_{se};{\Phi }_3={\Phi }_3{}_{\_\mathrm{nominal}}+\Delta {\Phi }_3\end{array}\right.$$

(24)

Accordingly, the time varying output terms (Δ_{para_pq}, Δ_{para_sq}) in q-axis for the five-phase PMSG can be expressed as

$$\begin{array}{l}{\Delta }_{para\_pq}=\Delta R_s{i}_{pq}+\Delta L_{pr}\frac{d{i}_{pq}}{dt}-\sqrt{\frac{5}{2}}p\mathrm{\Omega }\Delta {\mathsf{\Phi }}_1+p\mathrm{\Omega }\Delta L_{pr}{i}_{pd}\\ {\Delta }_{para\_sq}=\Delta R_s{i}_{sq}+\Delta L_{se}\frac{d{i}_{sq}}{dt}-3\sqrt{\frac{5}{2}}p\mathrm{\Omega }\Delta {\mathsf{\Phi }}_3+p\mathrm{\Omega }\Delta L_{se}{i}_{sd}\end{array}$$

(25)

In a leg of the generator side converter, the phase current in one period under an OSF situation (e.g., the OSF occurs at a lower switch) can be expressed as

$$i_k=\left\{\begin{array}{l}{\Delta }_{distortion}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em},\theta \in \left[\left(k-1\right)\frac{2\mathsf{\pi }}{5},\left(k-1\right)\frac{2\mathsf{\pi }}{5}+\mathsf{\pi }\right]\\ {\displaystyle \sum _{h=1,3}{I}_h\sin \left[h\left(\theta -\left(k-1\right)\frac{2\pi }{5}\right)+{\phi }_{k,h}\right]},\theta \in \left[\left(k-1\right)\frac{2\mathsf{\pi }}{5}+\mathsf{\pi },\left(k-1\right)\frac{2\mathsf{\pi }}{5}+2\mathsf{\pi }\right]\end{array}\right.$$

(26)

where k = 1, 2, 3, 4, 5 represents the kth phase from phase ‘a’ to phase ‘e’. h is the number of harmonic orders in back-EMF of the five-phase PMSG. I_h represents the magnitude of hth harmonic component of the phase current.

For a generator side converter, the half cycle under the single OSF condition exists some distortions instead of complete null blocking values due to the conduction of unremoved diodes. For instance, the unexpected current will form a close loop passing D₁, load and D₆ as shown in Figure 1. The distorted signal will not be blocked during the cycle where the faulty switch S₆ should have been triggered. This term of conducted distortions is denoted as Δ_distortion, which is determined by the system power scale, control, and load parameters, etc. After fast Fourier transform (FFT) of the faulty signal in Equation (26), the additional harmonics are mainly constituted by DC component and other even-order frequencies relative to the spectrum in healthy condition. In stationary coordinate frames, the fault signal f_pd and f_pq will mainly contain the harmonics except for the DC component. This issue will be discussed latter.

• Construction of GPIO

Constituting Equations (22) and (23), we have

$$\left\{\begin{array}{l}{\dot{i}}_{pq}=\frac{1}{L_{pr}}\left(-R_s{i}_{pq}+d_{l\_pq}-u_{pq}\right)\\ {\dot{i}}_{sq}=\frac{1}{L_{se}}\left(-R_s{i}_{sq}+d_{l\_sq}-u_{sq}\right)\end{array}\right.$$

(27)

Define the states i_pq and i_sq as x_pq1 and x_sq1, d_{l_pq} and d_{l_sq} as x_pq2 and x_sq2, respectively. Augmented state space form can be expressed as

$$\left\{\begin{array}{l}{\dot{x}}_{pq1}=-\frac{R_s}{L_{pr}}{x}_{pq1}+x_{pq2}-\frac{u_{pq}}{L_{pr}}\\ {\dot{x}}_{pq2}={\dot{d}}_{l\_pq}\end{array}\right.,\left\{\begin{array}{l}{\dot{x}}_{sq1}=-\frac{R_s}{L_{se}}{x}_{sq1}+x_{sq2}-\frac{u_{sq}}{L_{se}}\\ {\dot{x}}_{sq2}={\dot{d}}_{l\_sq}\end{array}\right.$$

(28)

In order to estimate the current states x_pq1, x_sq1 as well as the lumped disturbance states x_pq2, x_sq2, generalized proportional integral observers in the speed loop will be designed as

$$\left\{\begin{array}{l}{\dot{\widehat{x}}}_{pq1}={\alpha }_{pq1}\left({\widehat{x}}_{pq1}-x_{pq1}\right)-\frac{R_s}{L_{pr}}{\widehat{x}}_{pq1}+{\widehat{x}}_{pq2}-\frac{u_{pq}}{L_{pr}}\\ {\dot{\widehat{x}}}_{pq2}={\widehat{x}}_{pq3}+{\alpha }_{pq2}\left({\widehat{x}}_{pq1}-x_{pq1}\right)\\ \cdots \\ {\dot{\widehat{x}}}_{pqn}={\alpha }_{pqn}\left({\widehat{x}}_{pq1}-x_{pq1}\right)\end{array}\right.\left\{\begin{array}{l}{\dot{\widehat{x}}}_{sq1}={\alpha }_{sq1}\left({\widehat{x}}_{sq1}-x_{sq1}\right)-\frac{R_s}{L_{pr}}{\widehat{x}}_{sq1}+{\widehat{x}}_{sq2}-\frac{u_{sq}}{L_{se}}\\ {\dot{\widehat{x}}}_{sq2}={\widehat{x}}_{sq3}+{\alpha }_{sq2}\left({\widehat{x}}_{sq1}-x_{sq1}\right)\\ \cdots \\ {\dot{\widehat{x}}}_{sqn}={\alpha }_{sqn}\left({\widehat{x}}_{sq1}-x_{sq1}\right)\end{array}\right.$$

(29)

where α_pq1–α_pqn, α_sq1–α_sqn represent observer gains, and they are positive real numbers.

3.2.3. Procedures of the Proposed AFTC Strategy

On the basis of the designed GPIO in Section 3.2.1, steps of this proposed AFTC strategy can be summarized as:

• Fault detection

The form factors (FFs) [20] of i_pq and its measurement are given by

$$i_{pq\_ff}(t)=\frac{{\left|i_{pq}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq}(t)\right|}_{\mathrm{ave}}}=\frac{{\left|x_{pq1}(t)\right|}_{\mathrm{RMS}}}{{\left|x_{pq1}(t)\right|}_{\mathrm{ave}}},{\widehat{i}}_{pq\_ff}=\frac{{\left|{\widehat{i}}_{pq}(t)\right|}_{\mathrm{RMS}}}{{\left|{\widehat{i}}_{pq}(t)\right|}_{\mathrm{ave}}}=\frac{{\left|{\widehat{x}}_{pq1}(t)\right|}_{\mathrm{RMS}}}{{\left|{\widehat{x}}_{pq1}(t)\right|}_{\mathrm{ave}}}$$

(30)

The RMS value reflects the variation of distance for phase currents from their corresponding average values, and is sensitive by deviations from the unrectified average values, such as the OSF. Thus, here FFs are utilized for fault detections. The notation “_ave” represents average operations within one fundamental period.

A residual between the two form factors is yielded by

$$r_{pq}(t)={\widehat{i}}_{pq\_ff}(t)-i_{pq\_ff}(t)=\frac{{\left|i_{pq\_ff}(t)+e_{pq}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)+e_{pq}(t)\right|}_{\mathrm{ave}}}-\frac{{\left|i_{pq\_ff}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)\right|}_{\mathrm{ave}}}$$

(31)

where e_pq is the observer error given by

$$e_{pq}(t)={\widehat{i}}_{pq}(t)-i_{pq}(t)={\widehat{x}}_{pq1}(t)-x_{pq1}(t)$$

(32)

Thus, the residual in (31) is subject to the following relationship:

$$r_{pq}(t)\le \frac{{\left|i_{pq\_ff}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)+e_{pq}(t)\right|}_{\mathrm{ave}}}+\frac{{\left|e_{pq}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)+e_{pq}(t)\right|}_{\mathrm{ave}}}-\frac{{\left|i_{pq\_ff}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)\right|}_{\mathrm{ave}}}\le \frac{{\left|e_{pq}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)+e_{pq}(t)\right|}_{\mathrm{ave}}}\le \frac{{\left|e_{pq}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)\right|}_{\mathrm{ave}}}$$

(33)

Finally, the adaptive threshold for fault detection can be expressed by

$$t{h}_f(t)=\frac{{\left|e_{pq}(t)\right|}_{\mathrm{RMS}}}{{\left|i_{pq\_ff}(t)\right|}_{\mathrm{ave}}}$$

(34)

where th_f determines the value of fault status FD that it will be 0 or 1 only in healthy and faulty conditions, respectively.

• Fault compensation

The dynamic performance of the compensation is closely related to the way of activation in a close-loop control system. This paper utilizes a smooth activation mechanism based on a sigmoid function. This sigmoid function is actually a nonlinear activation function, whose advantages have been validated and already used widely in the field of neural networks [27].

The sigmoid function is indicated by the red curve in Figure 7 where γ, t₀, t₁ represent the coefficient of bandwidth, starting time of compensation and ending time of compensation, respectively. As mentioned earlier, the compensation in q-axis current control loops will be activated once a fault is detected. In fact, the dynamic behaviors of compensation can be tuned by modifying γ, t₁. Instantaneous compensation will be triggered at t₀ once fault status FD = 1. The output of the activation function will be equal to zeros if FD = 0. Compared with a classical step activation function (blue dotted curve), a sigmoid function will bring satisfied transient behaviors for the whole system which smooths the sudden action of compensation.

By (15) and (27)–(29), the composite controllers with compensation can be reconfigured as

$$\left\{\begin{array}{l}{u}_{pq\_comp}=u_{pq}+fc{n}_{sigmoid}{K}_{pr}{\widehat{x}}_{pq2}=u_{pq}=\left(K{p}_{pq}+\frac{K{i}_{pq}}{s}\right)\left(x_{pq1}^{*}-x_{pq1}\right)+fc{n}_{sigmoid}{K}_{pr}{\widehat{x}}_{pq2}\\ u_{sq\_comp}=u_{sq}+fc{n}_{sigmoid}{K}_{pr}{\widehat{x}}_{sq2}=\left(K{p}_{sq}+\frac{K{i}_{sq}}{s}\right)\left(x_{sq1}^{*}-x_{sq1}\right)+fc{n}_{sigmoid}{K}_{se}{\widehat{x}}_{sq2}\end{array}\right.$$

(35)

where K_pr and K_se are respectively the adjustable compensation gains for u_pq and u_sq. Their theoretical values are equal to 1 in a nominal condition.

The above step by step design procedures of the proposed AFTC strategy are synthesized in Figure 8. The error between i_pq and ${\widehat{i}}_{pq}$ is firstly converted into form factors. If the fault status FD equal to 1, the fault information will be injected in the u_pq and u_sq, respectively.

4. Experimental Verification

A small-scale power experimental platform by full-physical devices is built so as to validate the proposed AFTC strategy.

4.1. Description of Small-Scale Power Experimental Platform

As shown in Figure 9, this full-physic experimental platform is able to convert power from a five-phase PMSG to the DC-link. Here, a 3.3 kW five-phase PMSG is adopted that is driven by a DC motor. Original position information of the generator is acquired by a 12-bit absolute encoder. The five-leg converter incorporates two three-leg converters. DC supplies ranging from 10–30 V are adopted to offer constant voltage to conditioning circuit, dSPACE (Paderborn, Germany) plant (MicroAutobox II), I/O connector, the drive boards of the converter and the pulse width modulation (PWM) activation card. A personal computer (PC) installed MATLAB/SIMULINK and ControlDesk softwares will be used for program execution, real-time parameters turning and system monitoring. A multi-channel oscilloscope (Yokogawa DL-750) is utilized to acquire experimental results. With the assistance of dSPACE, the conditioning circuit can well adapt the input and output analog signals. Speed and electrical angle calculation unit provides precise θ and Ω in real-time operations relying on the high-efficient encoder. The main parameters of this platform are summarized in

Table A1. Parameters of the full-physical experiment platform.

Symbol	Description	Value/Type
Pn-gen	Nominal power of five-phase PMSG working at 110 Hz	3.3 kW
f	Friction of five-phase PMSG	0.123
J	Inertia of generator	0.00137 kg·m2
Vdc	Voltage in DC link	100 V
Ωn	Nominal speed of generator working at 110 Hz	2200 rpm
p	Number of pole pairs	3
Φ1, Φ3	Magnet flux relative to 1st and 3rd harmonics	0.150 Wb, 0.0149 Wb
Rs	Generator stator resistance	0.540 Ω
IGBT module	Power switch module integrated two Infineon IGBTs	Semikron SKM50 GB12T4
Cdc	4 × (2200 µF/400 V) SKC 2M2 40A-150	2.20 mF
Load	A resistive load	242 Ω
Lpr	Equivalent inductance of primary sub-machine	5.1 mH
Lse	Equivalent inductance of second sub-machine	3.2 mH
Tpwm	Switching period	0.1 ms
FD	Fault status	0 (healthy) or 1 (faulty)

of Appendix A.

Particularly, two voltage regulators are quite essential, which control the speed of DC motor in order to emulate the tidal current velocity. During the experimental process, variable speed reference can be obtained by manual or programmable adjustment of voltage regulator for the rotor. The speed controller is thus accessible when the voltage for the stator and the load are constant. Under careful investigations, mechanical speed Ω and voltage of the DC motor’s rotor V_rotor roughly subjects to a linear curve as Ω = 12 × (V_rotor − 4.7) when load = 242 Ohm, V_stator = 100 V.

Furthermore, hereafter validations of the proposed AFTC strategy will be carried out under a constant velocity profile considering a short period over time, such as one hour. Consequently, the gear ratio can be set as 1:40 to emulate the actual tidal profiles described in Figure 2.

4.2. Performance in Healthy and Faulty Conditions

Different with majority of research works about the disturbance attenuation under healthy conditions, post-fault tolerant control performance will be the main interest in this paper.

Number of states n in the GPIO formulated in Equation (29) is fixed as 3 taking into account of the complexity of parameter setting as well as performance of the AFTC strategy. To tradeoff the estimation errors and robustness of those estimates through the GPIO, parameters of the designed fault-tolerant composite controllers will be a key factor, which are organized in

Table A2. Parameters of fault-tolerant composite controllers in the experimental platform.

Composite Controllers	Symbol	Value
Speed loop controller	KpΩ	2.12
	KiΩ	848.85
Current loop controllers	Kppd, Kppq	17
	Kipd, Kipq	1800
	Kpsd, Kpsq	10.67
	Kisd, Kisq	1800
	αpq1 = αpq2 = αpq3	0.9 × 104
	αpq1 = αpq2 = αpq3	1.5 × 104
	Kpr, Kse	0.95

.

Torque’s ripple will be concerned since it can directly reflect the operational situation of the machine. Thus, torque’s ripple is the main regards to evaluate post-fault operation performances in this paper. There are no torque sensors involved in the platform, this electromagnetic torque can be thus derived from the calculation by current vectors in Park frames as Equation (8). A calculation method of the torque ripples is given by.

$${\mathrm{\Gamma }}_{em}{}_{\_ripple}=\left(\max \left({\mathrm{\Gamma }}_{em}\right)-\min \left({\mathrm{\Gamma }}_{em}\right)\right)/{\left({\mathrm{\Gamma }}_{em}\right)}_{\mathrm{ave}}$$

(36)

4.2.1. Disturbance Suppression in Healthy Conditions

As shown in Figure 10, the compensation part is put into use in healthy conditions. Obvious to see, the compensation using the proposed strategy will significantly suppress the torque ripples and disturbances in phase current. The compensators in the proposed method will contribute about 10% reduction of the torque ripples from 4.82% to 3.04%. In order to specify the oscillations of torque, its waveform is recorded by means of “AC”. The actual information of the signals by the oscilloscope can be found in the footnotes of the Figure 10a. As the depicted harmonic orders in Figure 10b, the additional first harmonic in the torque signal is effectively suppressed and the rest of harmonic order from 2nd to 9th can be almost also reduced using the compensators in healthy conditions. Therefore, the compensation mechanism described in Equation (35) is also feasible in healthy conditions.

According to Equations (11) and (23), the lumped disturbance mainly contains the issue by model uncertainties and noises. In this practical machinery system, the model uncertainties mainly attribute to the unmodeled terms, such as parameter variation effects, cogging torque, and non-linearity of magnetizing curve, etc. The test results thereby demonstrate that the compensation strategy can also be adapted to the issue of disturbance suppression in healthy conditions.

4.2.2. Performance of Active Fault-Tolerant Control in Faulty Conditions

• Performance under an OSF case without using AFTC

In accordance with the expressions from (26, there exist current distortions during the blocking cycles of switch S₆ as shown in the right most subfigure in Figure 11. Based on Equation (36), this five-phase PMSG has 4.81% and 28.48% torque ripples in the healthy and faulty conditions. Once the OSF occurs, speed also has periodical perturbations in a small range around 600 rpm. Whereas torque has more significant oscillation with around 1.45 N·m. Similarly, the mechanical speed and its references are recorded by using the channel “AC” to observe the oscillating effect due to the OSF occurrence.

• Performance under an OSF case using AFTC

In the condition that switch S₆ is open, using form factors will maintain the robustness and efficiency of fault detection, which will be completed within 5.6 ms (around 1/6 of fundamental period) as shown in the leftmost illustration of Figure 12. In the rightmost illustration of Figure 12, there will be only 0.64 N·m oscillated range of the torque in the post-fault operation process utilizing the proposed AFTC strategy. Thanks to the compensation mechanism, almost 60% of torque ripples can be suppressed. The speed fluctuations can be neglected relative to the improvements of torque ripples.

In terms of the results from Figure 11, it can be demonstrated that this proposed AFTC strategy owns high efficiency and feasibility in real-time operations with OSF occurrence, which is able to actively reduce the torque ripples. Thanks to the sigmoid activation function, the settling time and overshoots of either the electromagnetic torque or phase current are maintained satisfied dynamic transient behaviors. It can also be observed from the middle subfigure that the completion of compensating duration costs around 0.4 s. To obtain satisfied transient behaviors and robustness in faulty conditions, the parameters of the designed fault-tolerant composite controllers will be a key factor, as organized in Table A2.

• Spectrum analysis of torque

In order to explore the effects of the compensation in different conditions, the spectrum of the signal Γ_em is analyzed in the healthy condition, OSF condition of switch S₆ and fault-tolerant condition, which are shown as Figure 13. It is clear to see that torque in the healthy condition mainly contains a constant DC component. Once switch S₆ is open, the DC component is decreased by 0.05 N·m. The 1st harmonic becomes a most dominant additional component, which will impose a fluctuation operating at a fundamental frequency to the torque as shown in the rightmost illustration of Figure 11. In fact, the OSF occurrence will make the fault component become a main factor in the lumped disturbance. Compared to the spectrum in the healthy condition, 2nd–6th harmonics are also greater in the same time with fault occurrence, whose analysis keeps in line with the description in Section 3.1. The proposed AFTC strategy can effectively suppress by about 67% of the most important harmonic component (1st). As well, this proposed strategy can have attenuated functions for 2nd and 3rd harmonics. However, this compensation mechanism will bring a rise of 5th and 6th harmonic orders, which are negligible concerning the attenuation of the dominant harmonics from 1st to 4th.

By comparing the strategies that rely on the fault status or fault categories in advance, the proposed AFTC strategy has superior advantages that lie in there being no need of the prior knowledge of the faults and automatically proceeding with real-time fault detection and fault compensation once the strategy is established.

The two most relevant studies introduced here are given in terms of performance. The iterative learning control (ILC)-based FTC method developed by Mohammadpour et al. [28] is able to suppress around 48.6% of the torque ripples due to the occurrence of an open circuit. Furthermore, a detailed survey of FTC strategies was performed by Xiong et al. [29] who designed an FTC strategy that can reduce the torque ripples by about 54% at maximum. The proposed method can reduce around 60% of torque ripples with an automatic AFTC mechanism. Relative to the ILC compensators [28], the proposed method considers the dynamic performance of the compensation process using a smooth activation mechanism. Compared with the fault-tolerant control strategies in [29], the parameter setting of the proposed method is less complicated to design and simpler to implement in real-time.

As a result, the compensation in current loops can be used for active FTC issues. The experimental tests verify that the proposed strategy is effective to suppress torque ripples in OSF conditions.

5. Conclusions

This paper mainly proposes an AFTC strategy for five-phase trapezoidal PMSG-based tidal current energy applications that are subjected to single switch open circuit fault. This proposed strategy can provide a fault detection and compensation mechanism using generalized proportional integral observers in q-axis current control loops. A full-physical, small-scale power experimental platform is well established to verify the effectiveness and efficiency of this proposed strategy.

The experimental test results show that fault detection is completed with around 1/6 fundamental period. Using a sigmoid function, the close loop system obtains satisfied transient behaviors during the compensation. The experimental tests and spectrum analysis demonstrate that the proposed strategy is easy to implement and can effectively suppress the torque ripples, especially the dominant fluctuation operating at a fundamental frequency. This reinforces the reliability and availability of the whole system. This work will be investigated further in terms of fault-tolerant characteristics of the system at the nonlinear region of the generator’s magnetic curve.