A Support Vector Machine Learning-Based Protection Technique for MT-HVDC Systems
Abstract
1. Introduction
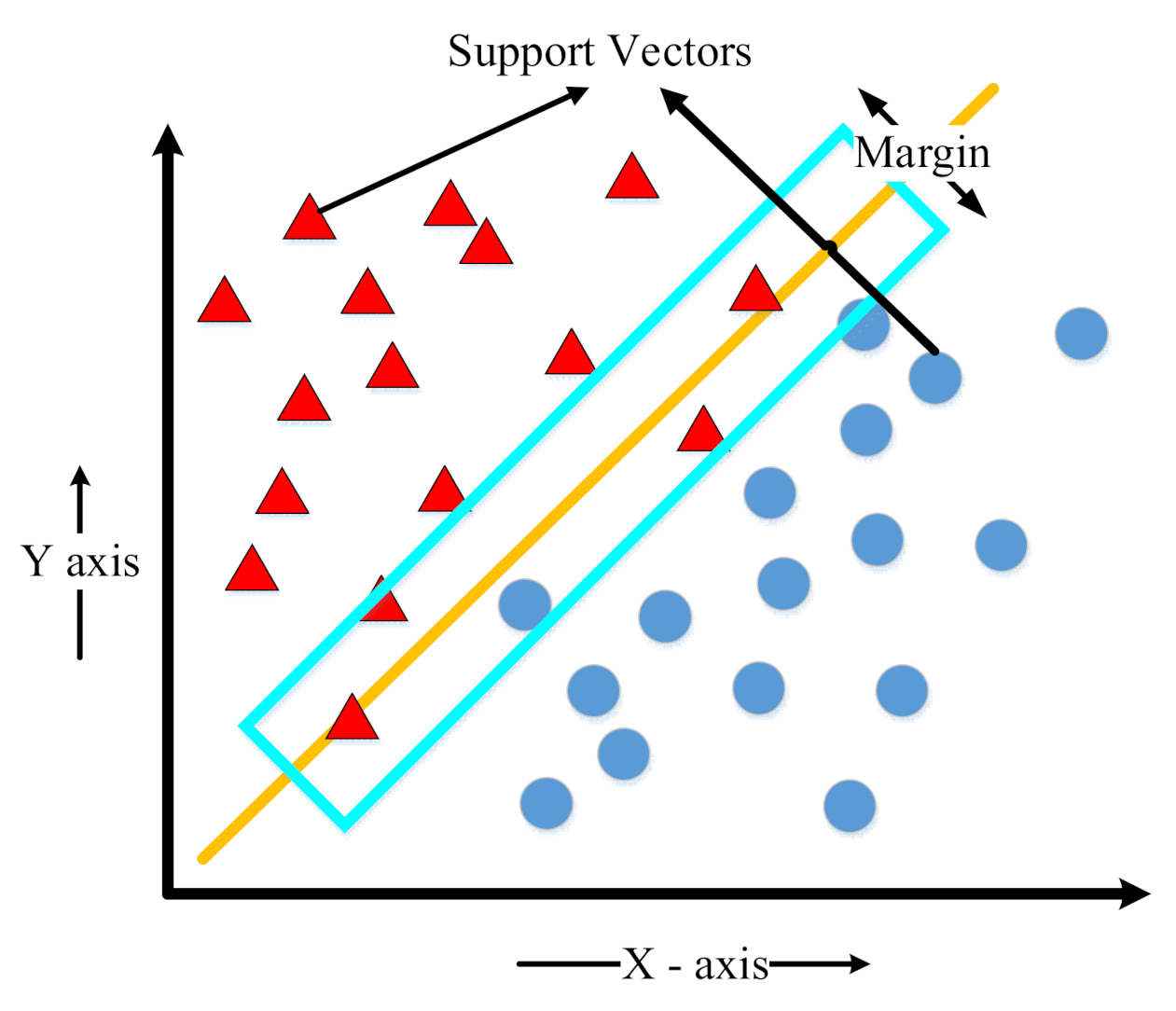
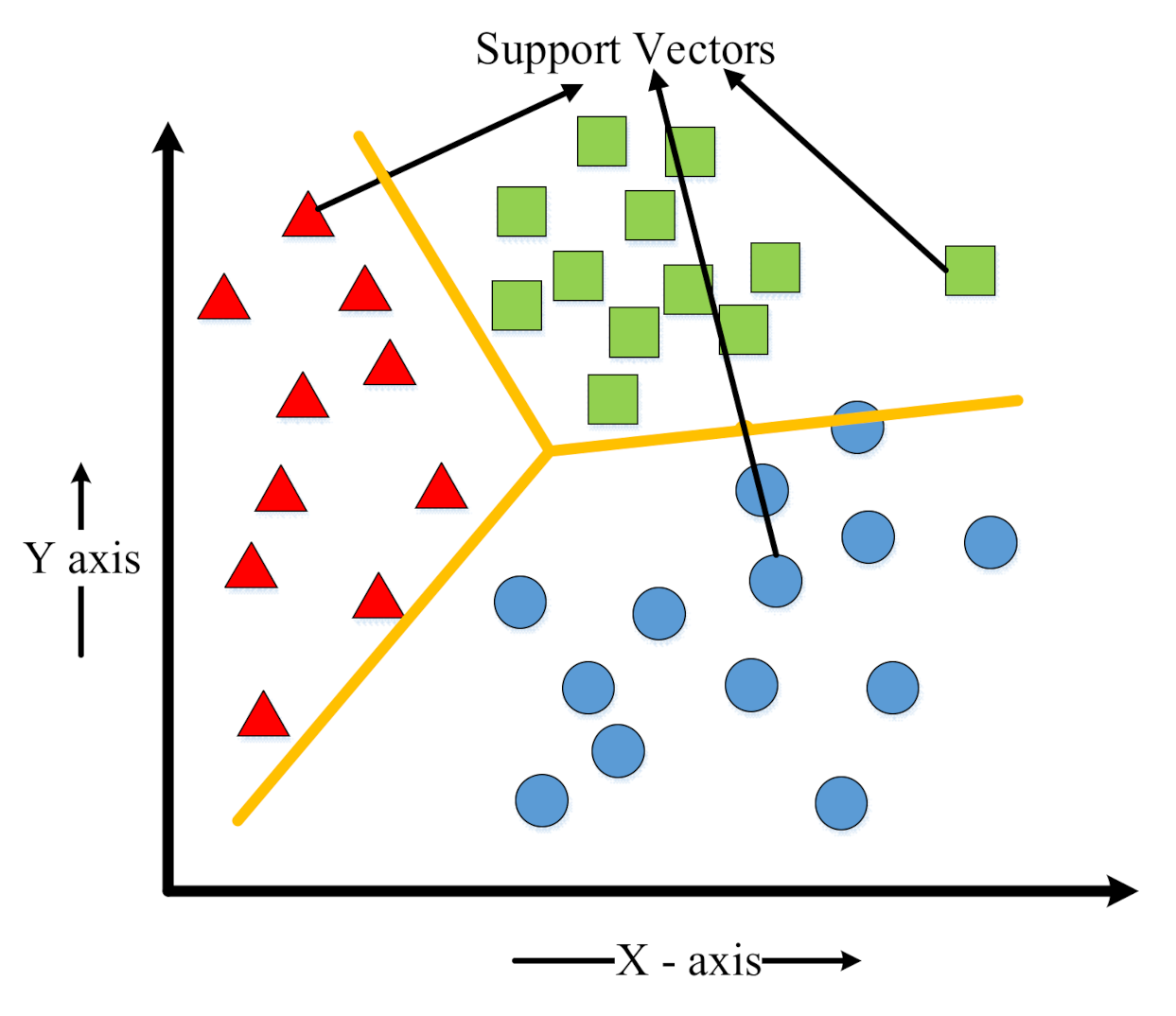
2. Support Vector Machines (SVM)
2.1. Mathematical Formulation
2.2. Principal Component Analysis (PCA)
2.3. PCA-Based SVM
- Sensed data obtained from different sensing terminals are employed as input.
- Data is normalized with zero mean and unit variance.
- Eigenvalue decomposition is carried out for normalized data. Optimal principal components are determined by the employment of the Scree test [55] given as:where is used to minimize the number of principal components and determine the optimal components. Each q process variable is associated with communalities . , when and , otherwise . In general, high eigenvalues based components are retained, and low eigenvalues based components are eliminated.
- An indication S is created based on the optimal principal components.
- The indication is classified based on the model of SVM based . PCA model is trained to extract each . Indicators has the indexes . In the process of training, samples of sensed data are used to prepare each indicator.
- The proposed algorithm is terminated with the results of fault identification and classification.
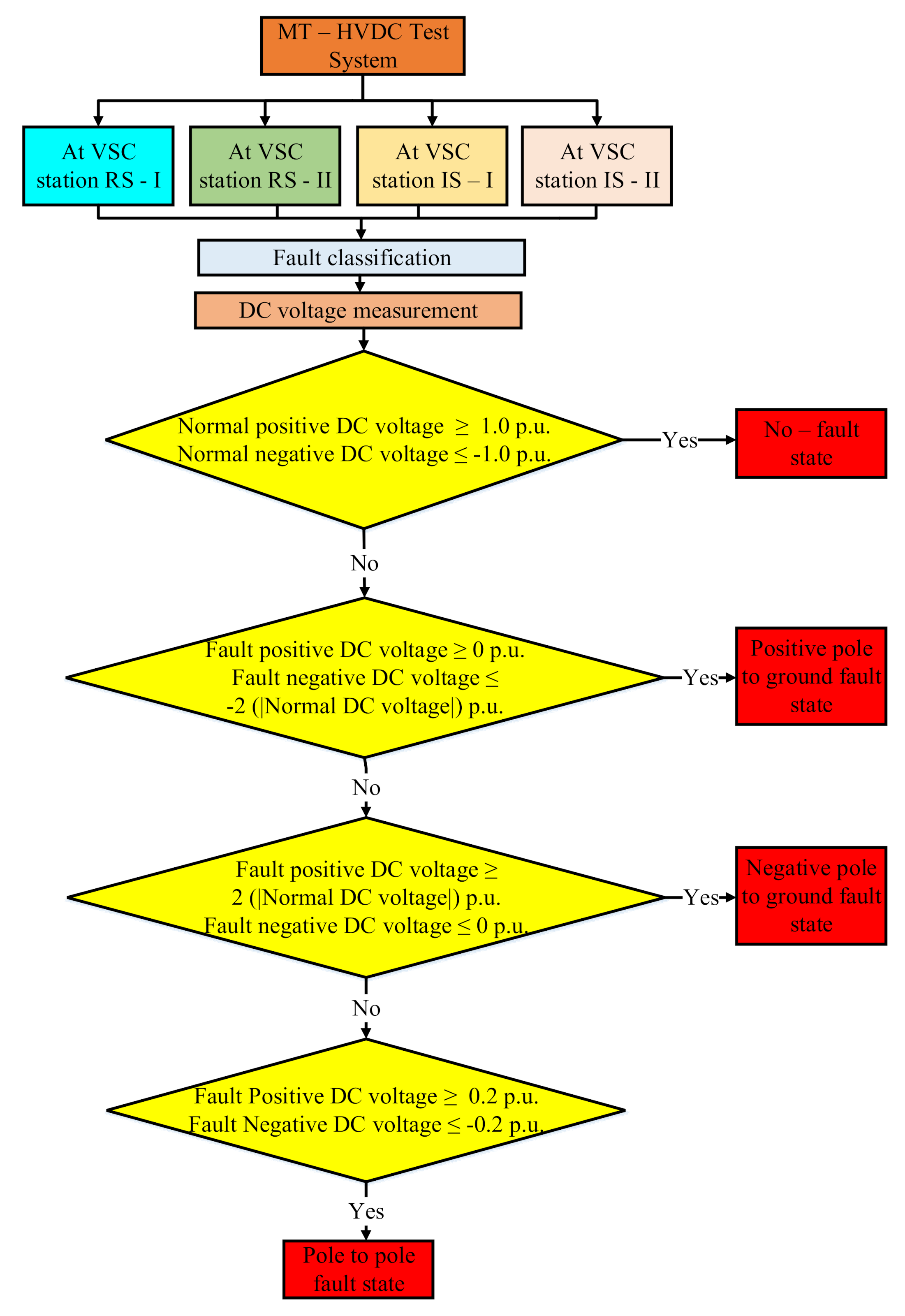
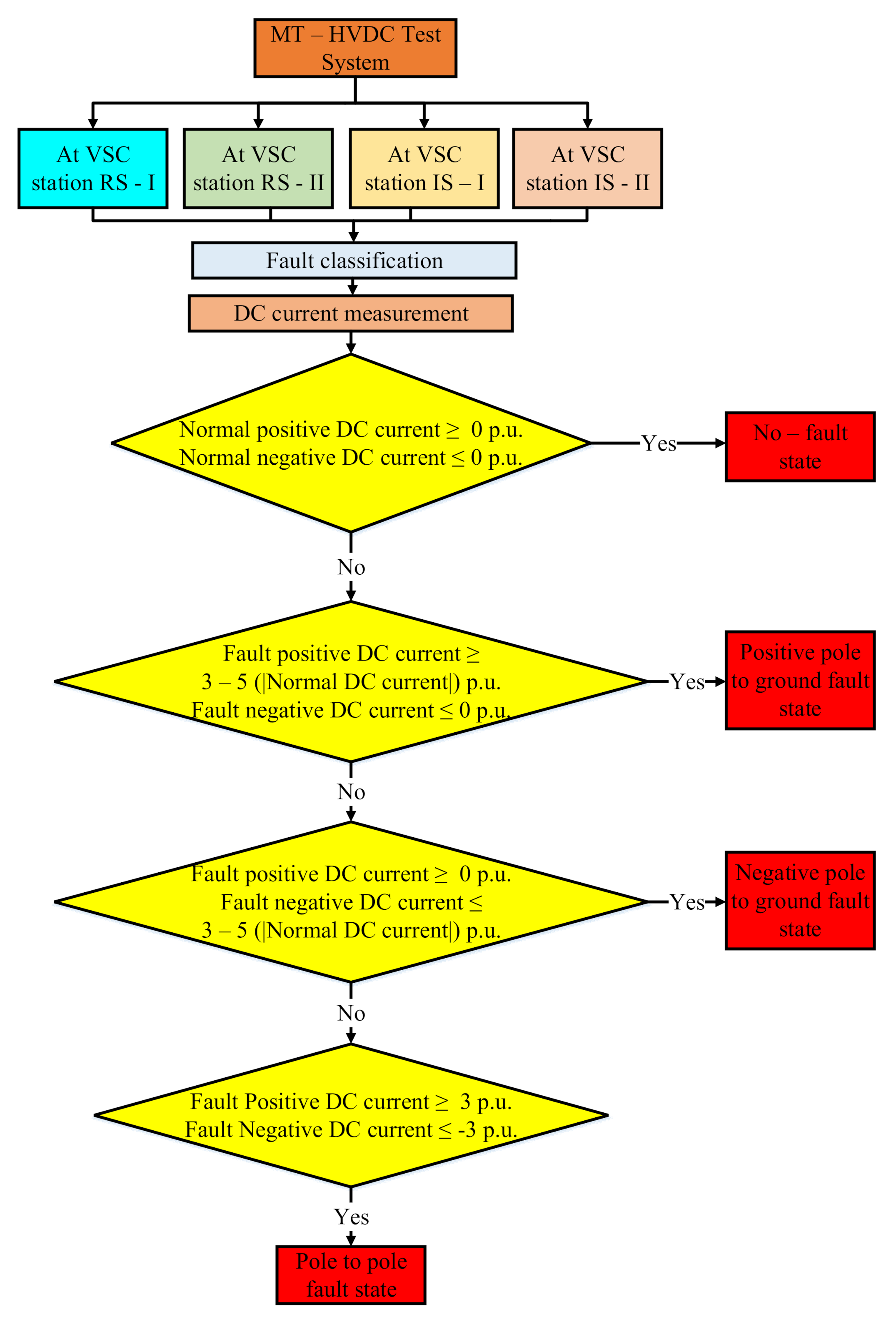
2.4. Proposed SVM-Based Protection Algorithm
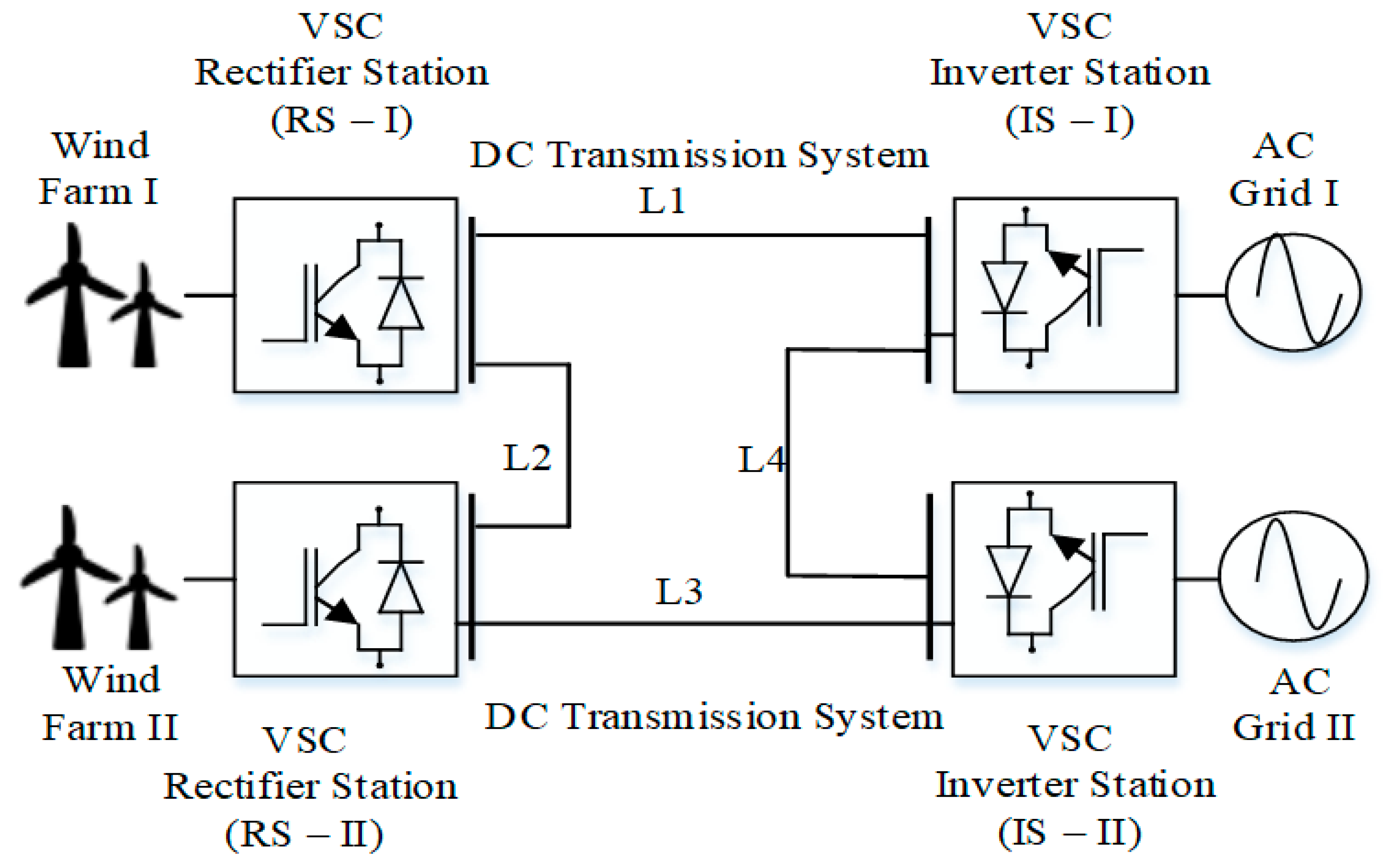
3. MT-HVDC Test System Understudy
4. Simulations and Discussion
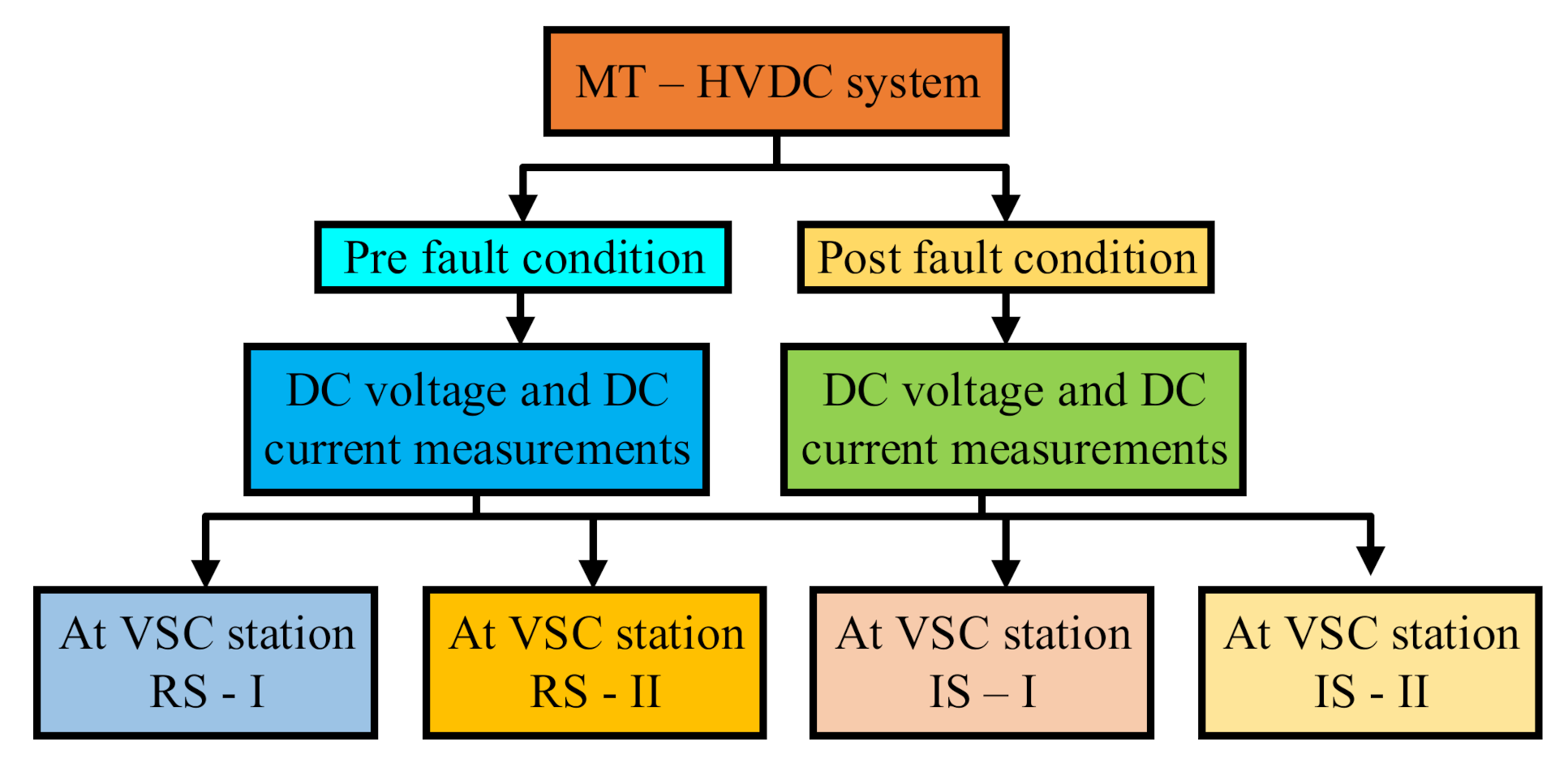
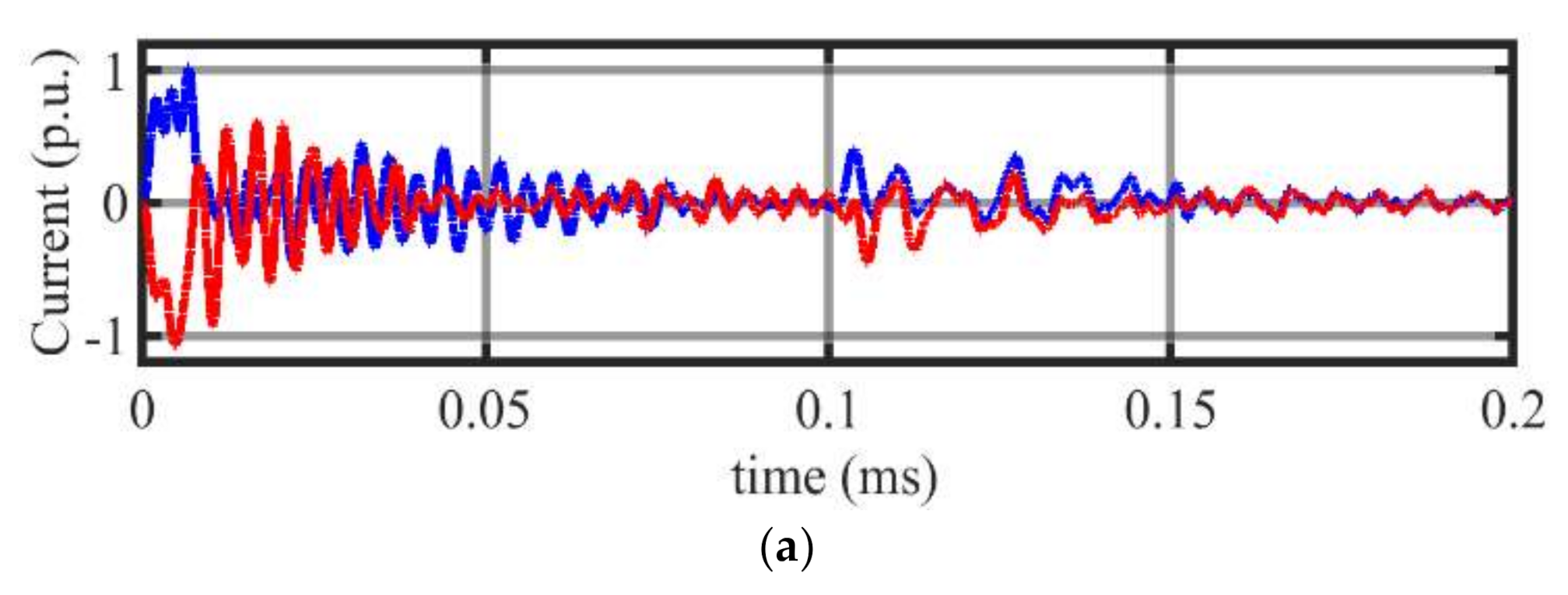
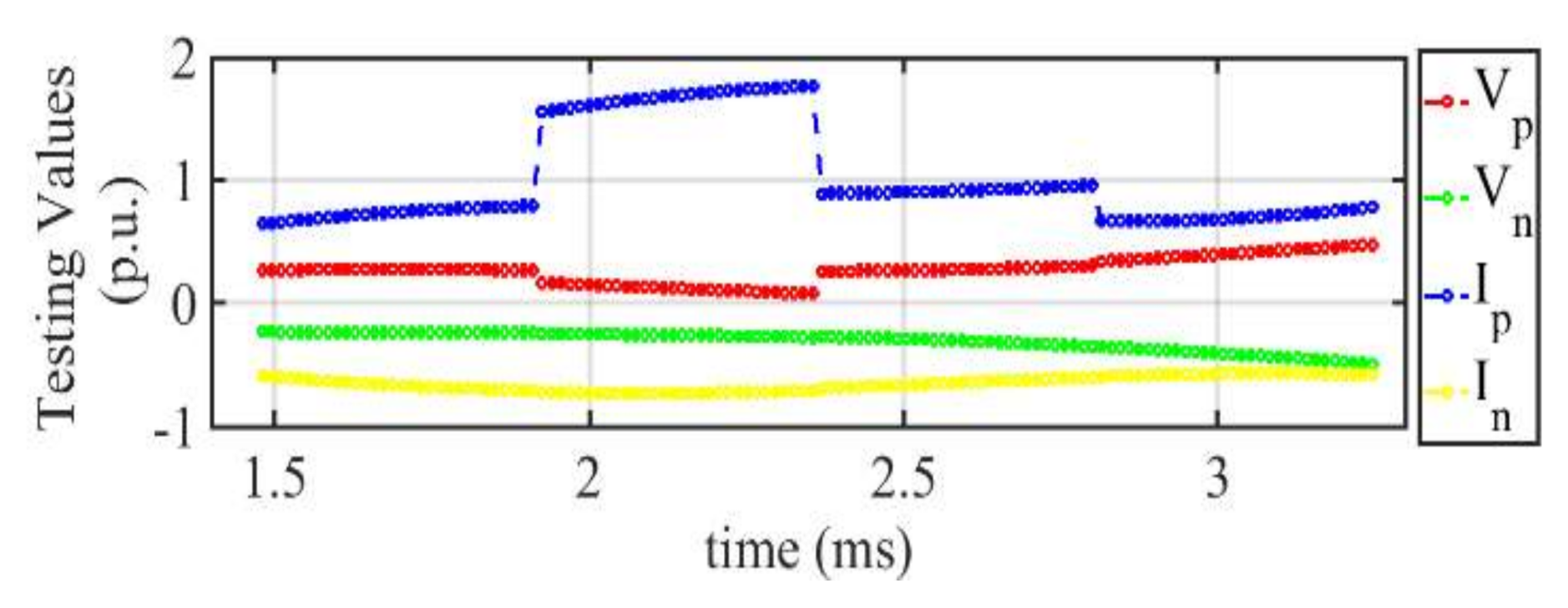
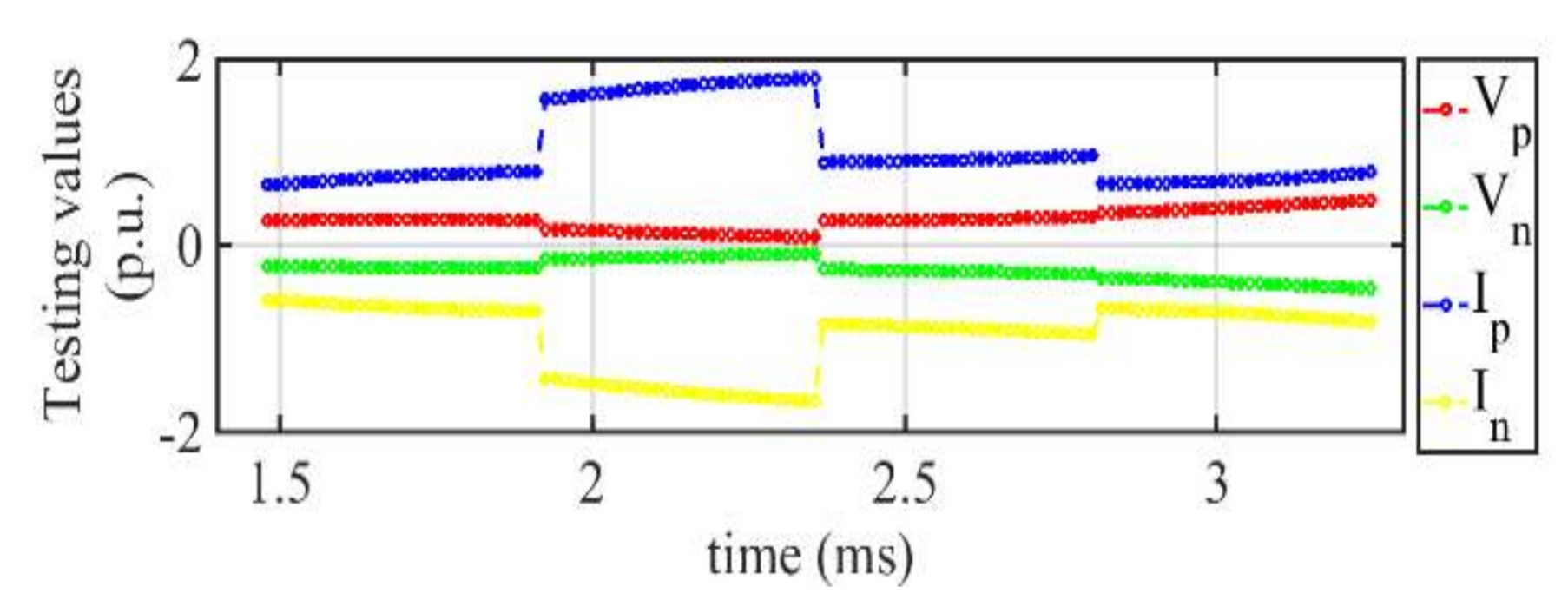
4.1. DC Voltage and DC Current Analysis
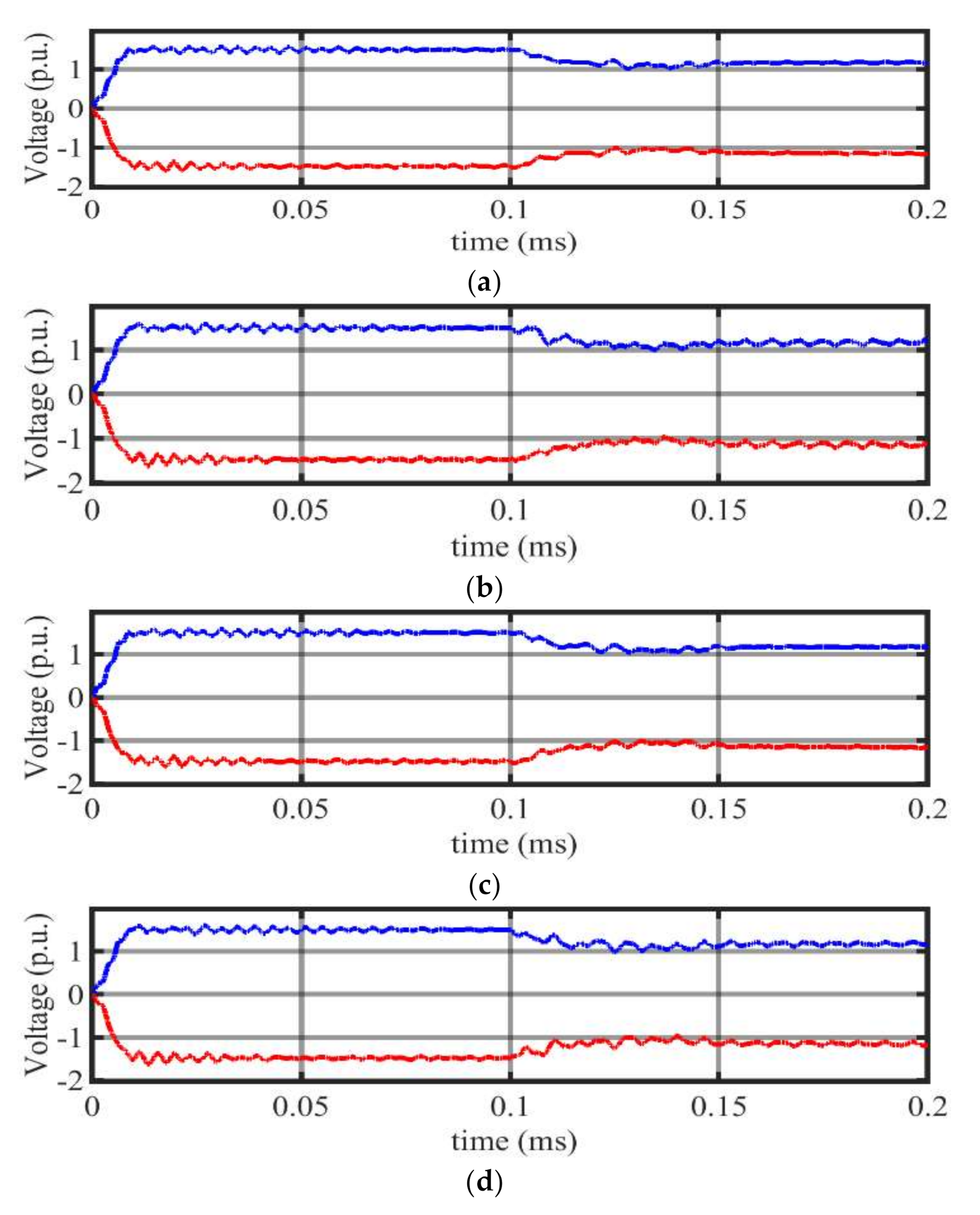
4.1.1. Scenario 1: No-Fault
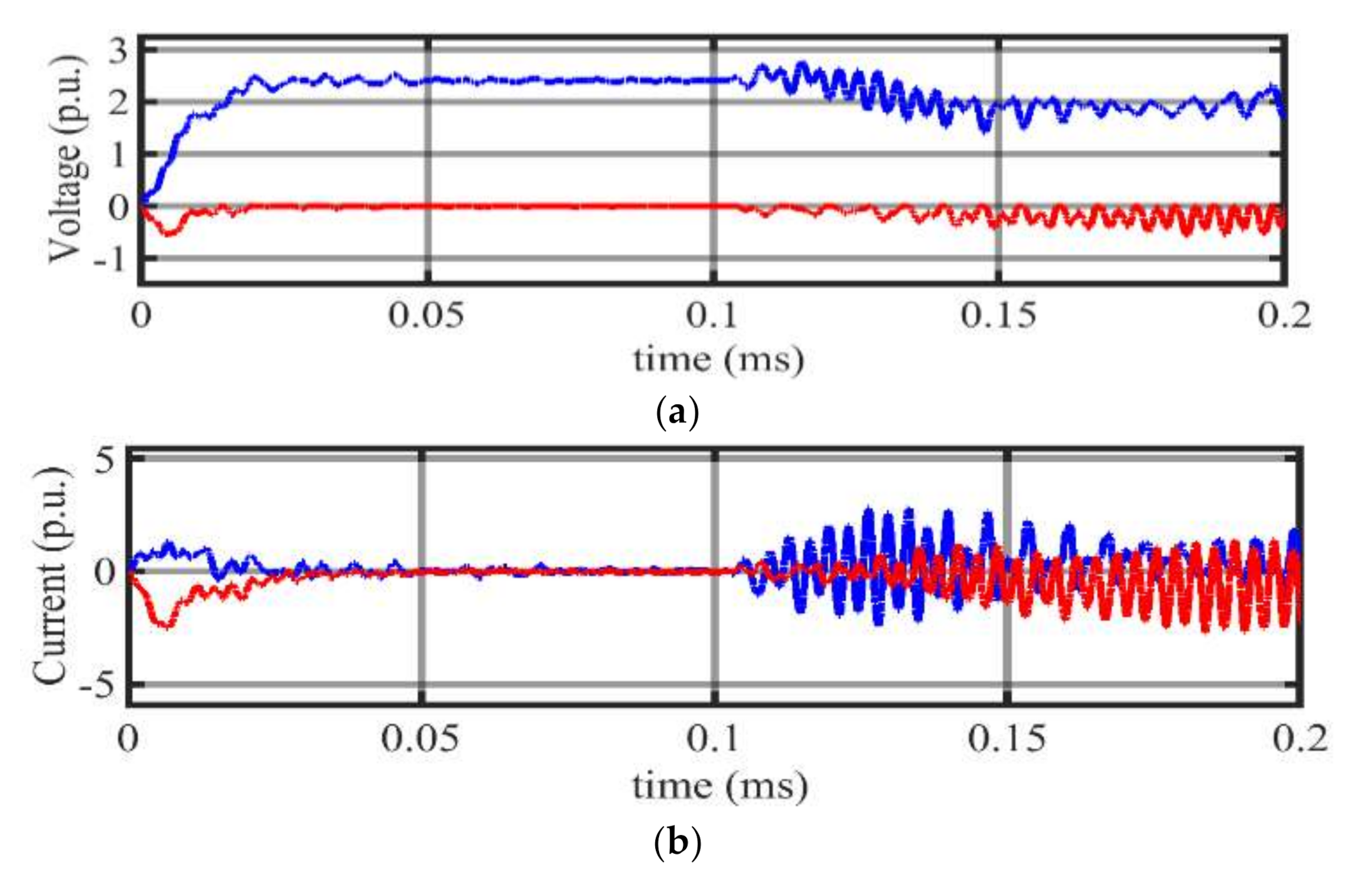
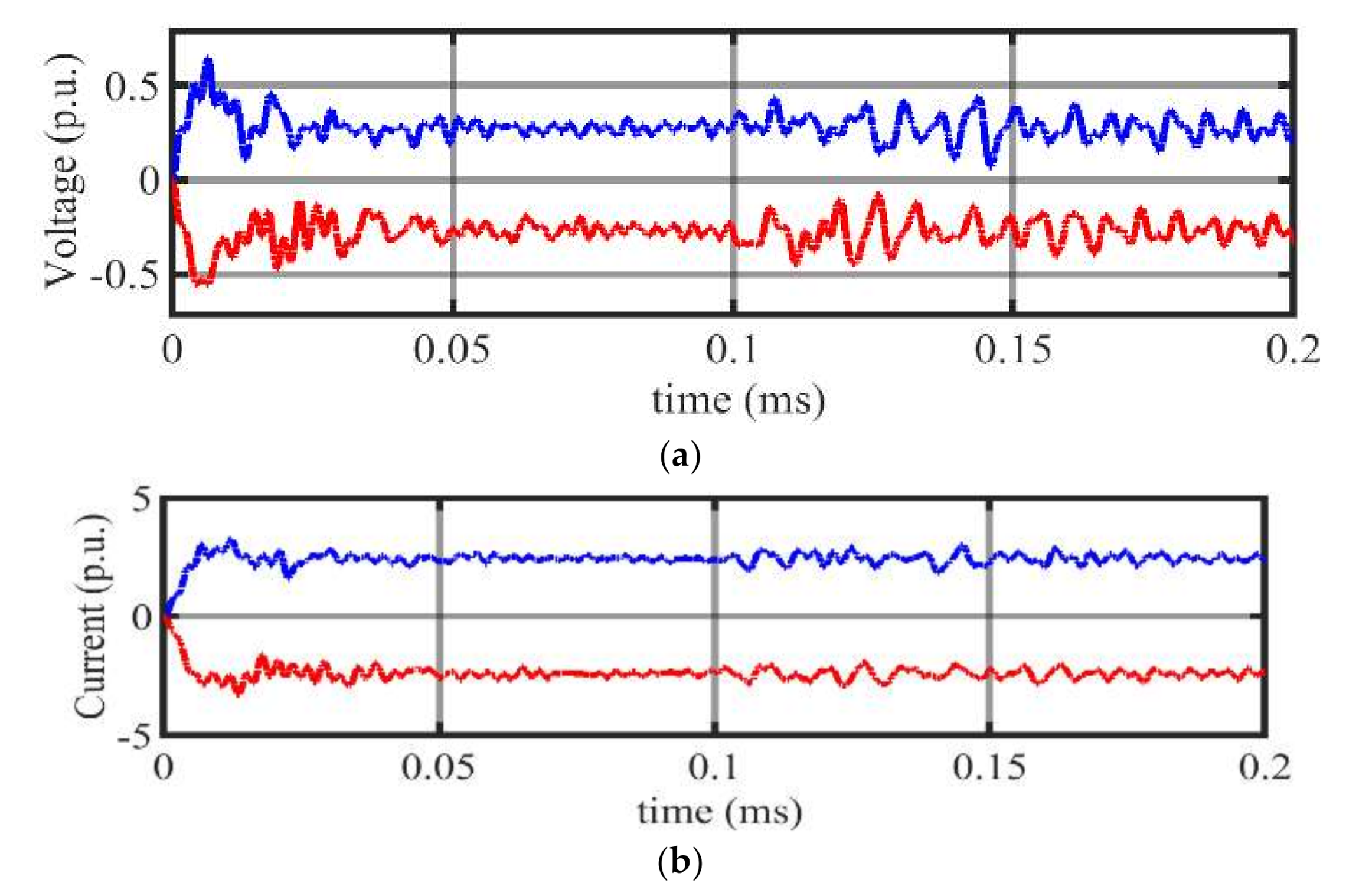
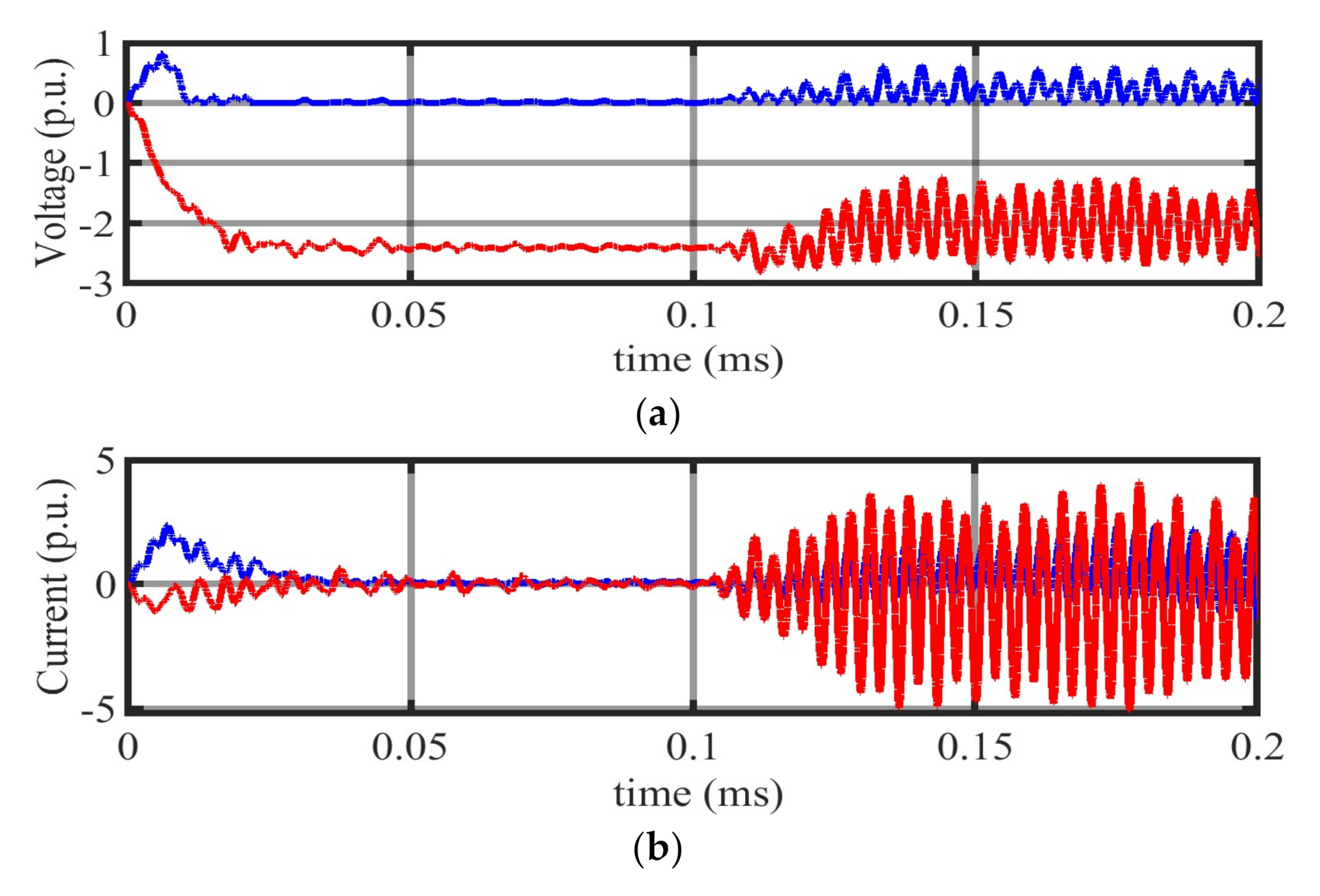
4.1.2. Scenario 2: DC Fault at RS-I
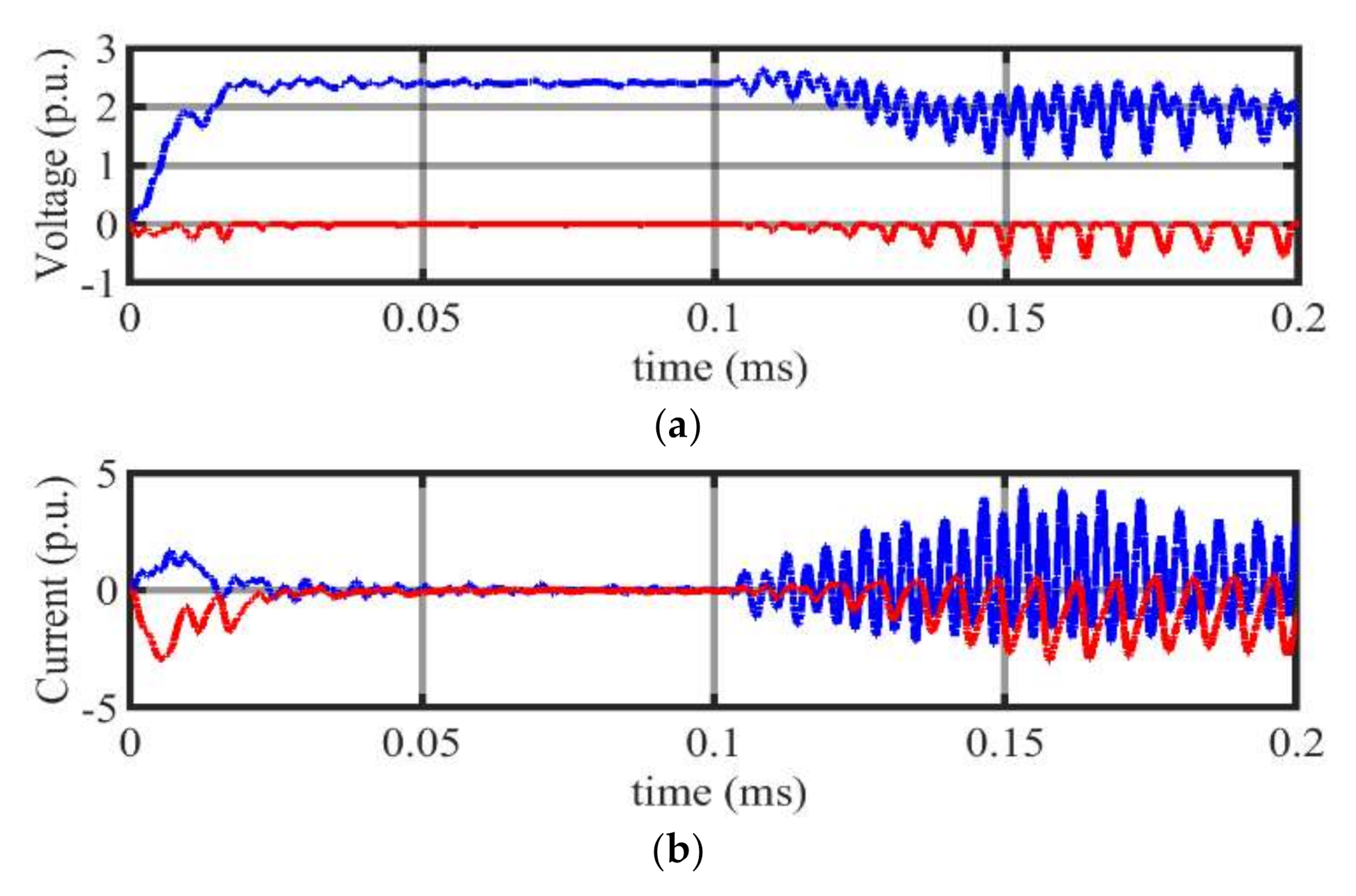
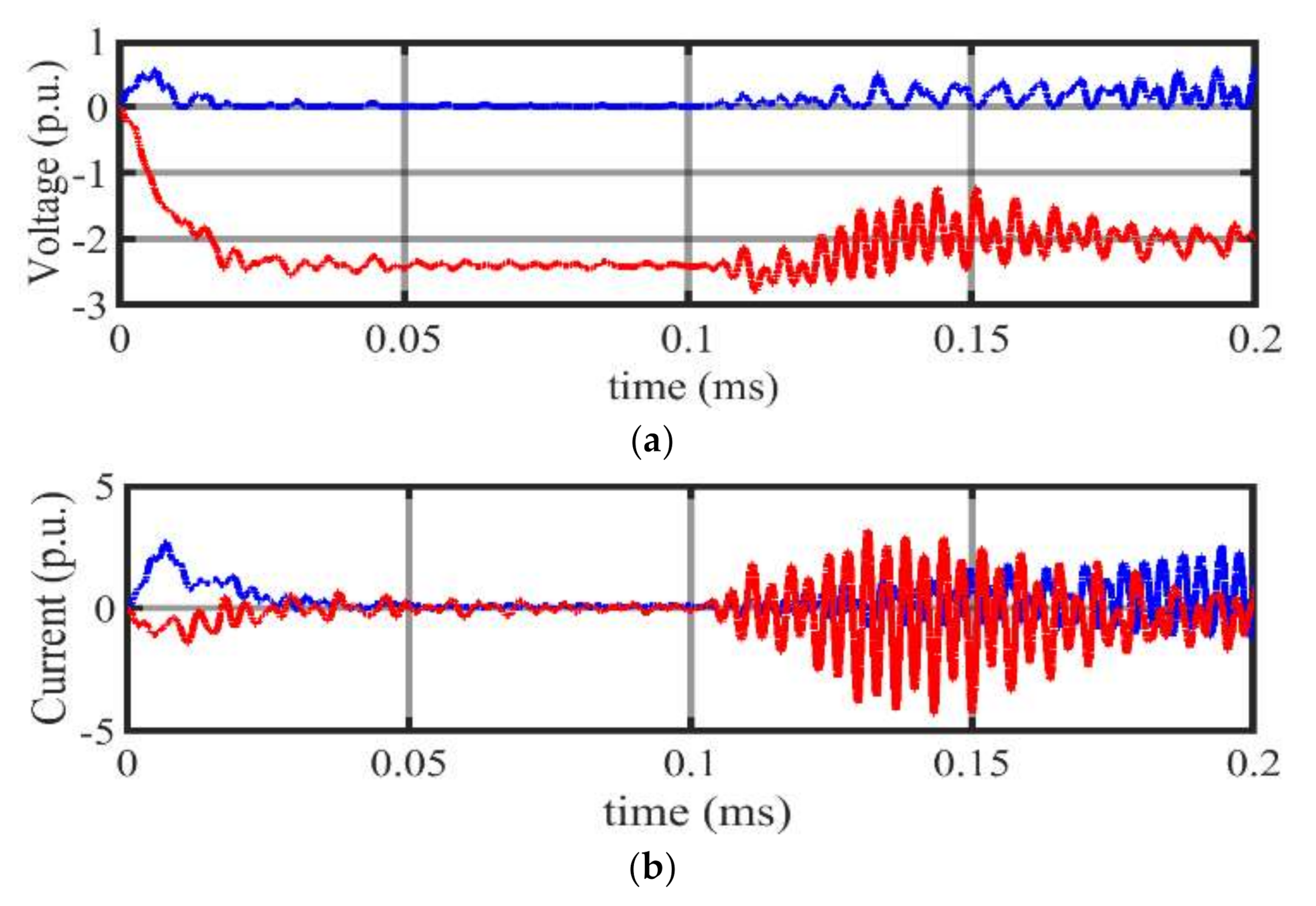
4.1.3. Scenario 3: Fault at 100 km from RS-I at Line L1
4.1.4. Scenario 4: Fault at 200 km from RS-I at Line L1
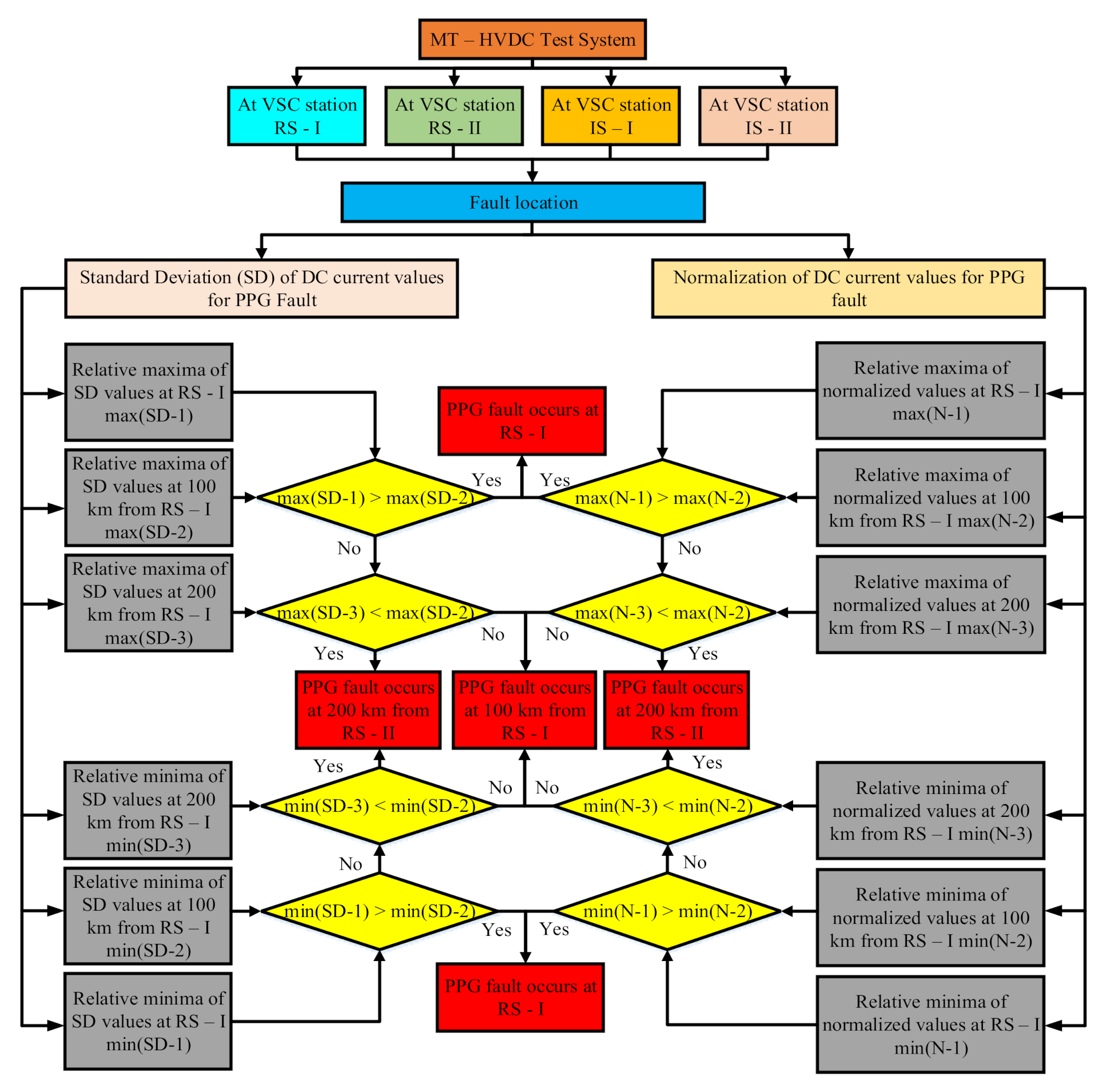
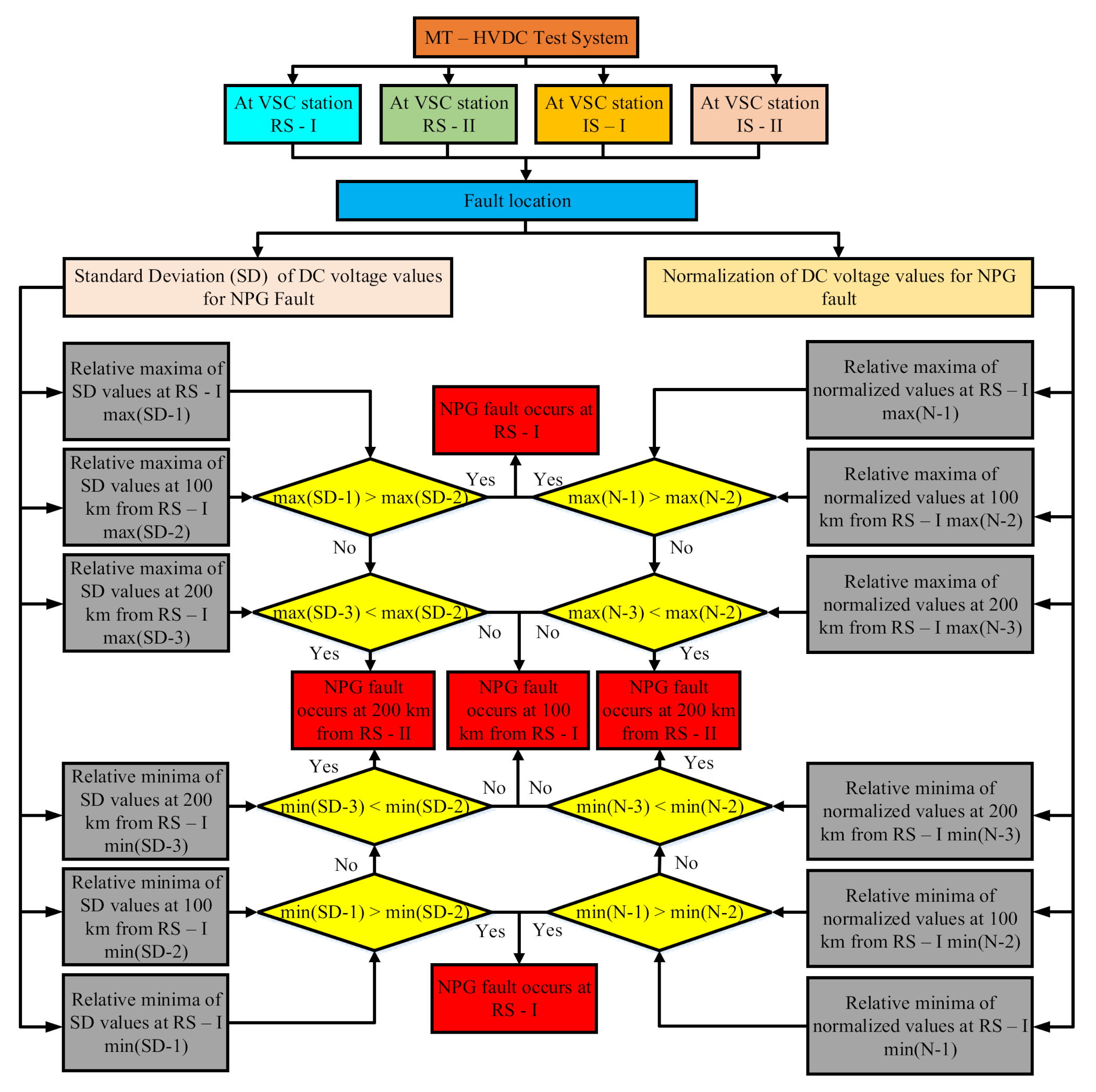
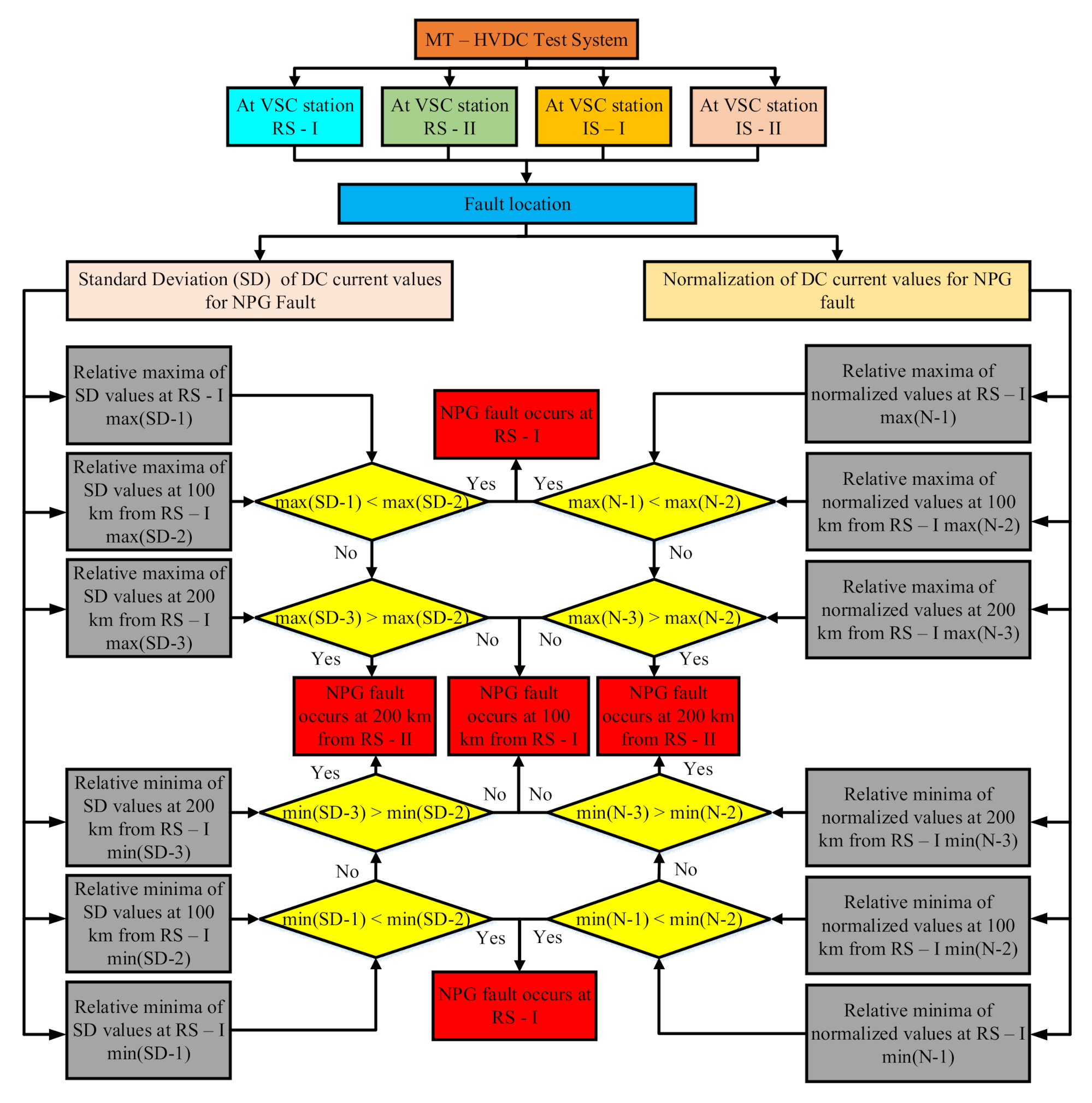
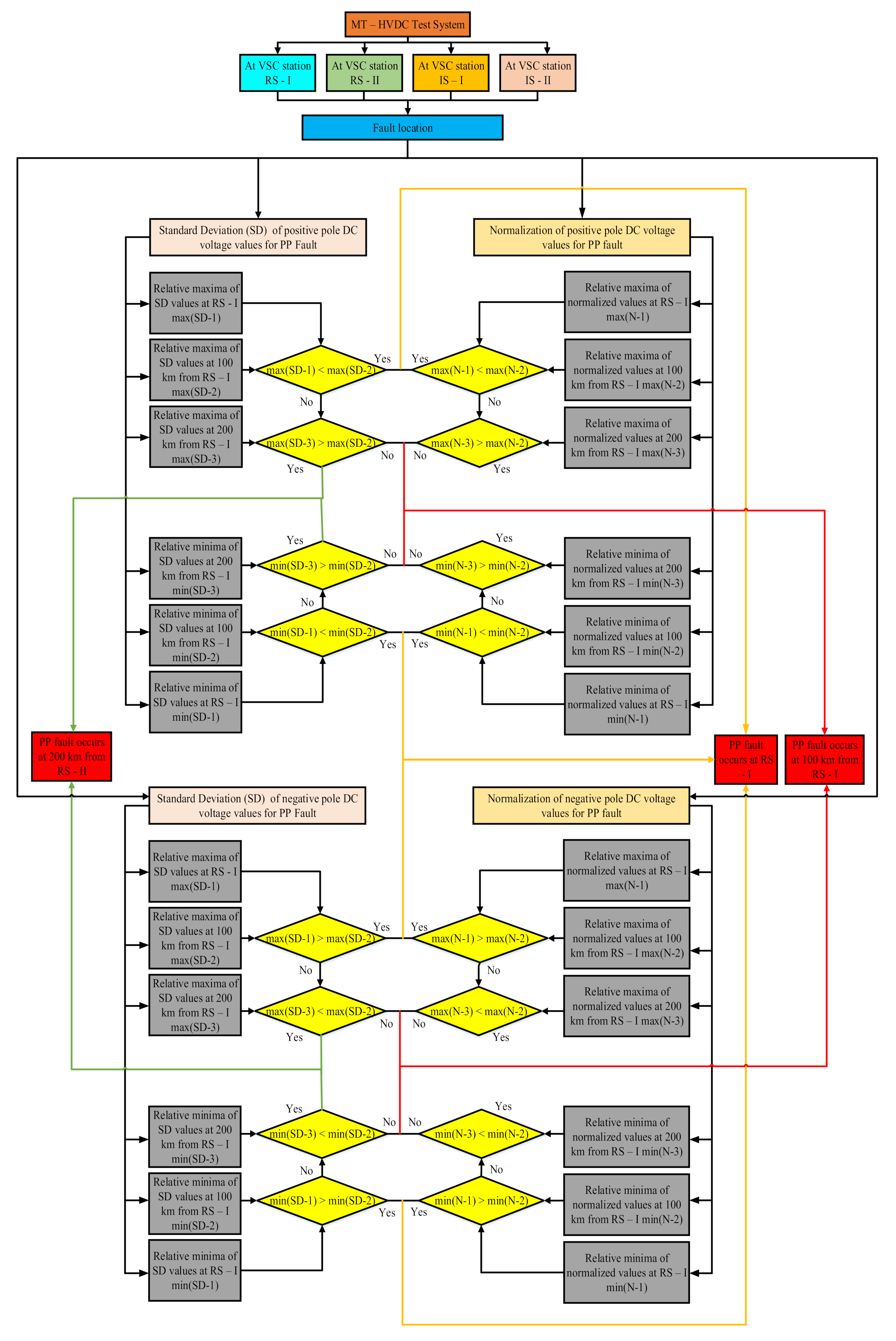
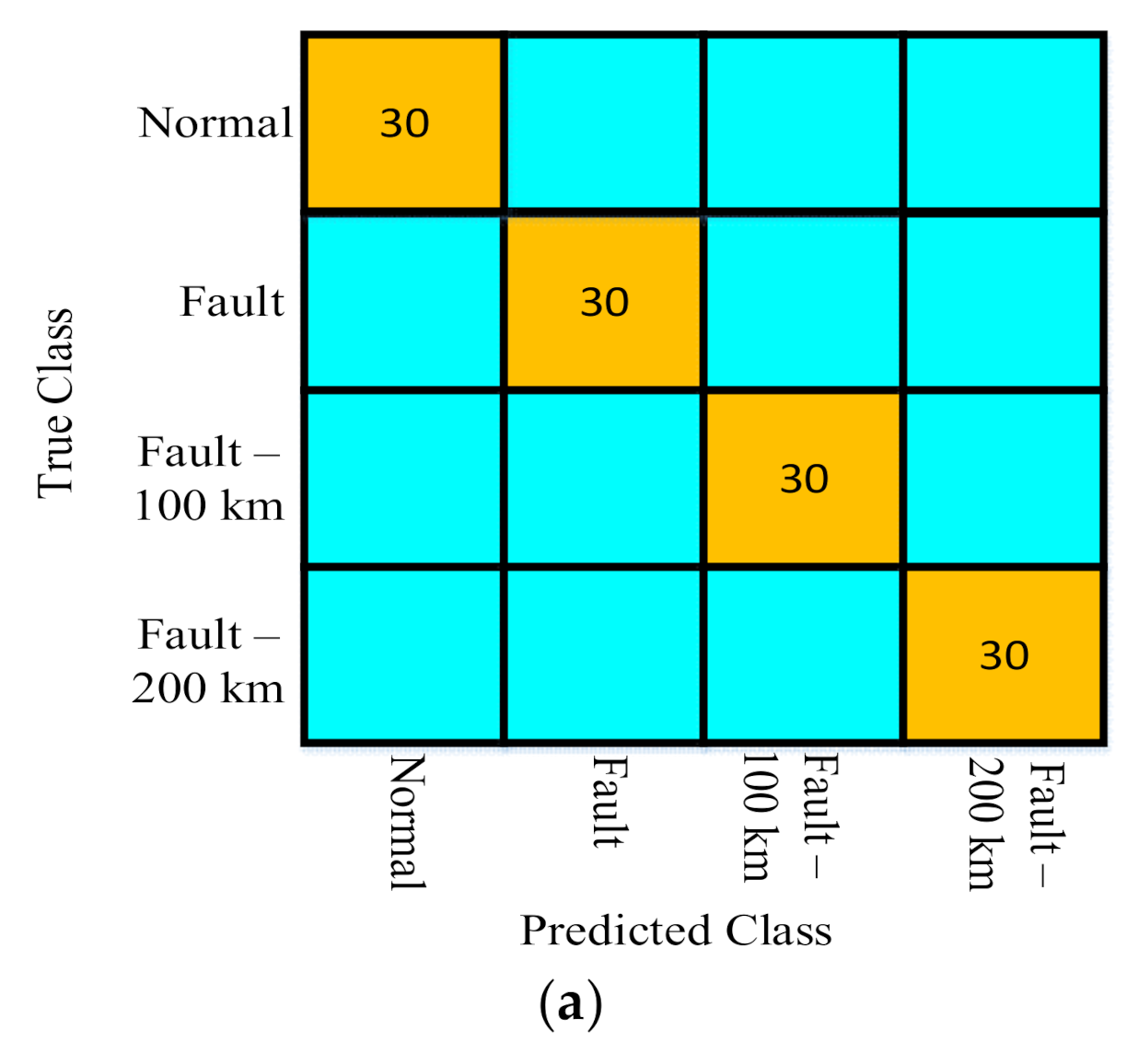
4.2. SVM Algorithm for Fault Location
4.2.1. Scenario I
4.2.2. Scenario II
4.2.3. Scenario III
4.3. Proposed Structure of SVM-Based Protection Algorithem
4.4. Performance Comparison of Protection Techniques
5. Additional Discussion and Achievements
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Input vector | |
| Class corresponding to the ith input vector. | |
| Slack variable | |
| User specified parameter | |
| Training data set | |
| Weight vector | |
| Dimensions of input space | |
| Dimensions of feature space | |
| Point of transformed feature space | |
| Coefficients of the Lagrange multiplier | |
| Traditional Euclidean inner product of the input vector with the support vector . | |
| Raw samples | |
| Process variables | |
| Covariance matrix | |
| and | Projection vectors of |
| Indicators | |
| , , and | Line lengths |
| Direct-quadrature | |
| AC Voltage | |
| DC Voltage | |
| AC | Alternating Current |
| ANN | Artificial Neural Networks |
| DC | Direct Current |
| HVDC | High Voltage Direct Current |
| IGBTs | Insulated Gate Bipolar Transistors |
| IRIF | Immediate Rising–Immediate Falling |
| IS—I and IS—II | Inverter Station I and Inverter Station II |
| ML | Machine Learning |
| MT-HVDC | Multi-terminal High Voltage Direct Current |
| N | Normalization |
| NPG | Negative Pole to Ground |
| PCA | Principal Component Analysis |
| PP | Pole to Pole |
| PPG | Positive Pole to Ground |
| Pu | Per Unit |
| R1 and B1 | Relay 1 and DC Breaker 1 |
| RS-I and RS-II | Rectifier Station I and Rectifier Station II |
| SD | Standard Deviation |
| SVM | Support Vector Machine |
| TW | Traveling Wave |
| VSCs | Voltage Source Converters |
Appendix A
| Parameters | VSC-I | VSC-II | VSC-III | VSC-IV |
|---|---|---|---|---|
| Function | Rectifier (RS-I) | Inverter (IS-I) | Rectifier (RS-II) | Inverter (IS-II) |
| AC Voltage (kV) | 230 | 230 | 230 | 230 |
| DC Voltage (kV) | 100 | 100 | 100 | 100 |
| Transformer (MVA) | 200 | 200 | 200 | 200 |
| AC Filters (MVAR) | 40 | 40 | 40 | 40 |
| Phase Reactor’s Resistance (Ohms) | 0.0075 | 0.0075 | 0.0075 | 0.0075 |
| Phase Reactor’s Inductance (mH) | 23.8 | 23.8 | 23.8 | 23.8 |
| DC Capacitance (F) | 70 | 70 | 70 | 70 |
| 3rd Harmonic Filter Capacitance (F) | 12 | 12 | 12 | 12 |
| 3rd Harmonic Filter Resistance (Ohms) | 0.15 | 0.15 | 0.15 | 0.15 |
| 3rd Harmonic Filter Inductance (mH) | 47 | 47 | 47 | 47 |
| Smoothing Reactor’s Resistance (Ohms) | 0.025 | 0.025 | 0.025 | 0.025 |
| Smoothing Reactor’s Inductance (mH) | 8.0 | 8.0 | 8.0 | 8.0 |
| Power Electronic Component | IGBTs | IGBTs | IGBTs | IGBTs |
References
- Van Hertem, D.; Ghandhari, M. Multi-terminal VSC HVDC for the European supergrid: Obstacles. Renew. Sustain. Energy Rev. 2010, 14, 3156–3163. [Google Scholar] [CrossRef]
- Azizi, S.; Sanaye-Pasand, M.; Abedini, M.; Hassani, A. A traveling-wave-based methodology for wide-area fault location in multi-terminal DC systems. IEEE Trans. Power Deliv. 2014, 29, 2552–2560. [Google Scholar] [CrossRef]
- Muzzammel, R. Restricted Boltzmann machines based fault estimation in multi terminal HVDC transmission system. In Intelligent Technologies and Applications. INTAP 2019, Communications in Computer and Information Science; Bajwa, I.S., Sibalija, T., Jawawi, D., Eds.; Springer: Singapore, 2020; Volume 1198, pp. 772–790. [Google Scholar]
- Gomis-Bellmunt, O.; Liang, J.; Ekanayake, J.; King, R.; Jenkins, N. Topologies of multi-terminal HVDC-VSC transmission for large offshore wind farms. Electr. Power Syst. Res. 2011, 81, 271–281. [Google Scholar] [CrossRef]
- Yang, Q.; Le Blond, S.; Aggarwal, R.; Wang, Y.; Li, J. New ANN method for multi-terminal HVDC protection relaying. Electr. Power Syst. Res. 2017, 148, 192–201. [Google Scholar] [CrossRef]
- Flourentzou, N.; Agelidis, V.G.; Demetriades, G.D. VSC-based HVDC power transmission systems: An overview. IEEE Trans. Power Electr. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Sano, K.; Takasaki, M. A surgeless solid-state DC circuit breaker for voltage-source-converter-based HVDC systems. IEEE Trans. Ind. Appl. 2014, 50, 2690–2699. [Google Scholar] [CrossRef]
- Das, S.; Santoso, S.; Gaikwad, A.; Patel, M. Impedance-based fault location in transmission networks: Theory and application. IEEE Access 2014, 2, 537–557. [Google Scholar] [CrossRef]
- Agarwal, S.; Swetapadma, A.; Panigrahi, C.; Dasgupta, A. Fault analysis method of integrated high voltage direct current transmission lines for onshore wind farm. J. Mod. Power Syst. Clean Energy 2019, 7, 621–632. [Google Scholar] [CrossRef]
- Daisy, M.; Dashti, R.; Shaker, H.R. A new fault-location method for HVDC transmission-line based on DC components of voltage and current under line parameter uncertainty. Electr. Eng. 2017, 99, 573–582. [Google Scholar] [CrossRef]
- Luo, G.; Yao, C.; Liu, Y.; Tan, Y.; He, J.; Wang, K. Stacked auto-encoder based fault location in VSC-HVDC. IEEE Access 2018, 6, 33216–33224. [Google Scholar] [CrossRef]
- Muzzammel, R.; Fateh, H.M.; Ali, Z. Analytical behaviour of thyrister based HVDC transmission lines under normal and faulty conditions. In Proceedings of the International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 22–23 February 2018; IEEE: Lahore, Pakistan; pp. 1–5. [Google Scholar]
- Naidoo, D.; Ijumba, N.M. HVDC Line protection for the proposed HVDC systems. In Proceedings of the International Conference on Power System Technology, Singapore, 21–24 November 2004; pp. 21–24. [Google Scholar]
- Muzzammel, R.; Raza, A.; Hussain, M.R.; Abbas, G.; Ahmed, I.; Qayyum, M.; Rasool, M.A.; Khaleel, M.A. MT–HVdc systems fault classification and location methods based on traveling and non-traveling waves—A comprehensive review. Appl. Sci. 2019, 9, 4760. [Google Scholar] [CrossRef]
- Muzzammel, R. Traveling waves-based method for fault estimation in HVDC transmission system. Energies 2019, 12, 3614. [Google Scholar] [CrossRef]
- Wang, D.; Hou, M. Travelling wave fault location principle for hybrid multi-terminal LCC-VSC-HVDC transmission line based on R-ECT. Electr. Power Energy Syst. 2020, 117, 1–9. [Google Scholar] [CrossRef]
- Pathirana, V.; McLaren, P. A hybrid algorithm for high speed transmission line protection. IEEE Trans. Power Deliv. 2005, 20, 2422–2428. [Google Scholar] [CrossRef]
- Liu, X.; Osman, A.H.; Malik, O.P. Real-time implementation of a hybrid protection scheme for bipolar HVDC line using FPGA. IEEE Trans. Power Deliv. 2011, 26, 101–108. [Google Scholar] [CrossRef]
- Nanayakkara, O.; Rajapakse, A.D.; Wachal, R. Traveling-wave-based line fault location in star-connected multi-terminal HVDC systems. IEEE Trans. Power Deliv. 2012, 27, 2286–2294. [Google Scholar] [CrossRef]
- Nanayakkara, O.; Rajapakse, A.D.; Wachal, R. Location of DC line faults in conventional HVDC systems with segments of cables and overhead lines using terminal measurements. IEEE Trans. Power Deliv. 2012, 27, 279–288. [Google Scholar] [CrossRef]
- Saha, M.M.; Izykowski, J.J.; Rosolowski, E. Fault Location on Power Networks; Springer Science & Business Media: London, UK, 2009; pp. 1–432. [Google Scholar]
- Leterme, W.; Beerten, J.; van Hertem, D. Nonunit protection of HVDC grids with inductive DC cable termination. IEEE Trans. Power Deliv. 2016, 31, 820–828. [Google Scholar] [CrossRef]
- Zheng, X.; Tai, N.; Yang, G.; Ding, H. A transient protection scheme for HVDC transmission line. IEEE Trans. Power Deliv. 2012, 27, 718–724. [Google Scholar] [CrossRef]
- Liu, X.; Osman, A.; Malik, O. Hybrid traveling wave/boundary protection for monopolar HVDC line. IEEE Trans. Power Deliv. 2009, 24, 569–578. [Google Scholar] [CrossRef]
- De Kerf, K.; Srivastava, K.; Reza, M.; Bekaert, D.; Cole, S.; van Hertem, D.; Belmans, R. Wavelet-based protection strategy for DC faults in multi-terminal VSC HVDC systems. IET Gener. Transm. Distrib. 2011, 5, 496–503. [Google Scholar] [CrossRef]
- Zheng, X.; Tai, N.; Thorp, J.S.; Yang, G. A transient harmonic current protection scheme for HVDC transmission line. IEEE Trans. Power Deliv. 2012, 27, 2278–2285. [Google Scholar]
- Hajian, M.; Zhang, L.; Jovcic, D. DC transmission grid with low-speed protection using mechanical DC circuit breakers. IEEE Trans. Power Deliv. 2015, 30, 1383–1391. [Google Scholar] [CrossRef]
- Azad, S.P.; Leterme, W.; van Hertem, D. A DC grid primary protection algorithm based on current measurements. In Proceedings of the 17th IEEE European Conference on Power Electronics and Applications (EPE15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; IEEE: Geneva, Switzerland, 2015; pp. 1–10. [Google Scholar]
- Abu-Elanien, A.E.; Elserougi, A.A.; Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. A differential protection technique for multi-terminal HVDC. Electr. Power Syst. Res. 2016, 130, 78–88. [Google Scholar] [CrossRef]
- Valipour, M. Optimization of neural networks for precipitation analysis in a humid region to detect drought and wet year alarms. Meteorol. Appl. 2016, 23, 91–100. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Mirzaei, M.; Ab Kadir, M.; Moazami, E.; Hizam, H. Review of fault location methods for distribution power system. Aust. J. Basic Appl. Sci. 2009, 3, 2670–2676. [Google Scholar]
- Silva, K.; Souza, B.; Brito, N. Fault detection and classification in transmission lines based on wavelet transform and ANN. IEEE Trans. Power Deliv. 2006, 21, 2058–2063. [Google Scholar] [CrossRef]
- Martín, F.; Aguado, J.A. Wavelet-based ANN approach for transmission line protection. IEEE Trans. Power Deliv. 2003, 18, 1572–1574. [Google Scholar] [CrossRef]
- Le Blond, S.; Bertho, R.; Coury, D.; Vieira, J. Design of protection schemes for multi-terminal HVDC systems. Renew. Sustain. Energy Rev. 2016, 56, 965–974. [Google Scholar] [CrossRef]
- Le Blond, S.P.; Deng, Q.; Burgin, M. High frequency protection scheme for multi-terminal HVDC overhead lines. In Proceedings of the 12th IET International Conference on Developments in Power System Protection (DPSP 2014), Copenhagen, Denmark, 31 March–3 April 2014; IET: Copenhagen, Denmark; pp. 1–5. [Google Scholar]
- Zou, J.; Han, Y.; So, S.S. Overview of artificial neural networks. In Artificial Neural Networks; Humana Press: New York, NY, USA, 2008; Volume 458, pp. 14–22. [Google Scholar]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Johnson, J.M.; Yadav, A. Complete protection scheme for fault detection, classification and location estimation in HVDC transmission lines using support vector machines. IET Sci. Meas. Technol. 2017, 11, 279–287. [Google Scholar] [CrossRef]
- Keshri, J.P.; Tiwari, H. Fault classification in VSC-HVDC transmission system using machine learning approach. In Proceedings of the 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; IEEE: Jaipur, India; pp. 1–6. [Google Scholar]
- Muzzammel, R. Machine learning based fault diagnosis in HVDC transmission lines. In Intelligent Technologies and Applications. INTAP 2018, Communications in Computer and Information Science; Bajwa, I.S., Kamareddine, F., Costa, A., Eds.; Springer: Singapore, 2018; Volume 932, pp. 496–510. [Google Scholar]
- Van Hertem, D.; Gomis-Bellmunt, O.; Liang, J. HVDC Grids: For Offshore and Supergrid of the Future; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 1–528. [Google Scholar]
- Callavik, M.; Blomberg, A.; Häfner, J.; Jacobson, B. Break-through!: ABB’s hybrid HVDC breaker, an innovation breakthrough enabling reliable HVDC grids. Abb. Rev. 2013. Available online: https://www.researchgate.net/publication/297049686_Break-through_ABB’s_hybrid_HVDC_breaker_an_innovation_breakthrough_enabling_reliable_HVDC_grids (accessed on 13 December 2020).
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; p. 736. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998; p. 842. [Google Scholar]
- Ren, J. ANN vs. SVM: Which one performs better in classification of MCCs in mammogram imaging. Knowl. Based Syst. 2012, 26, 144–153. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Cao, W.; Ding, M. A genetic-algorithm support vector machine and D-S evidence theory based fault diagnostic model for transmission line. IEEE Trans. Power Syst. 2019, 34, 4186–4194. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, H. Fault location for MMC–MTDC transmission lines based on least squares-support vector regression. J. Eng. 2019, 2125–2130. [Google Scholar] [CrossRef]
- Lala, H.; Karmakar, S.; Singh, A.K. MATLAB-based GUI development for the detection and localization of faults in transmission line. In Proceedings of the IEEE Region 10 Symposium (TENSYMP), Kolkata, India, 20–22 December 2019; IEEE: Kolkata, India; pp. 654–659. [Google Scholar]
- Wang, Q.; Yu, Y.; Ahmed, H.O.A.; Darwish, M.; Nandi, A.K. Fault Detection and Classification in MMC-HVDC Systems Using Learning Methods. Sensors 2020, 20, 4438. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mlakić, D.; Nikolovski, S.; Dragicević, T. Support vector machine-based islanding and grid fault detection in active distribution networks. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2385–2403. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mlakić, D.; Nikolovski, S.; Dragičević, T. Anti-islanding protection of PV-based microgrids consisting of PHEVs using SVMs. IEEE Trans. Smart Grid 2020, 11, 483–500. [Google Scholar] [CrossRef]
- Hsu, C.W.; Lin, C.J. A comparison of methods for multi-class support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar]
- Jackson, J.E. A Users Guide to Principal Components; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Peralta, J.; Saad, H.; Dennetière, S.; Mahseredjian, J. Dynamic performance of average-value models for multi-terminal VSC-HVDC systems. In Proceedings of the Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; IEEE: San Diego, CA, USA; pp. 1–8. [Google Scholar]
- Liang, J.; Jing, T.; Gomis-Bellmunt, O.; Ekanayake, J.; Jenkins, N. Operation and control of multi-terminal HVDC transmission for offshore wind farms. IEEE Trans. Power Deliv. 2011, 26, 2596–2604. [Google Scholar] [CrossRef]
- Wang, M.; Beerten, J.; van Hertem, D. Frequency domain based DC fault analysis for bipolar HVDC grids. J. Mod. Power Syst. Clean Energy 2017, 5, 548–559. [Google Scholar] [CrossRef]
- Raza, A.; Dianguo, X.; Yuchao, L.; Xunwen, S.; Williams, B.; Cecati, C. Coordinated operation and control of VSC based multi-terminal high voltage DC transmission systems. IEEE Trans. Sustain. Energy 2016, 7, 364–373. [Google Scholar] [CrossRef]
- Raza, A.; Liu, Y.; Rouzbehi, K.; Jamil, M.; Gilani, S.O.; Dianguo, X.; Williams, B.W. Power dispatch and voltage control in multi-terminal HVDC systems: A flexible approach. IEEE Access 2017, 5, 24608–24616. [Google Scholar] [CrossRef]
















| Scenarios | Location of Fault | Fault Type |
|---|---|---|
| 1 | RS-I | No-fault |
| RS-II | ||
| IS-I | ||
| IS-II | ||
| 2 | RS-I | PPG fault |
| RS-II | NPG fault | |
| IS-I | PP fault | |
| IS-II | ||
| 3 | 100 km at from RS-I | PPG fault |
| NPG fault | ||
| PP fault | ||
| 4 | 200 km at from RS-I | PPG fault |
| NPG fault | ||
| PP fault | ||
| 5 | 100 km at from RS-I | PPG fault |
| NPG fault | ||
| PP fault | ||
| 6 | 200 km at from RS-I | PPG fault |
| NPG fault | ||
| PP fault | ||
| 7 | 100 km at from RS-II | PPG fault |
| NPG fault | ||
| PP fault | ||
| 8 | 200 km at from RS-II | PPG fault |
| NPG fault | ||
| PP fault | ||
| 9 | 100 km at from RS-II | PPG fault |
| NPG fault | ||
| PP fault | ||
| 10 | 200 km at from RS-II | PPG fault |
| NPG fault | ||
| PP fault |
| Scenarios | Training Data | Testing Data |
|---|---|---|
| I | Positive Pole Voltage Negative Pole Voltage Positive Pole Current Negative Pole Current | No-Fault Case |
| PPG Fault at RS-I | ||
| PPG Fault at 100 km from RS-I | ||
| PPG Fault at 200 km from RS-I | ||
| II | No-Fault Case | |
| NPG Fault at RS-I | ||
| NPG Fault at 100 km from RS-I | ||
| PPG Fault at 200 km from RS-I | ||
| III | No-Fault Case | |
| PP Fault at RS-I | ||
| PP Fault at 100 km from RS-I | ||
| PP Fault at 200 km from RS-I |
| Fault State | Parameters | Standard Deviation (STD) Values | Normalized Values | ||
|---|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | ||
| No-Fault | Positive Voltage Negative Voltage Positive Current | +2.75 | −0.80 | 0.50 | +0.26 |
| +0.90 | −2.50 | −0.24 | −0.49 | ||
| +1.20 | −1.65 | 0.79 | +0.52 | ||
| +2.00 | −1.80 | −0.57 | −0.72 | ||
| PPG Fault | Positive Voltage Positive Current | −0.90 | −1.80 | +0.16 | +0.08 |
| +1.80 | +1.35 | +1.76 | +1.54 | ||
| PPG Fault—100 km | +0.35 | −0.15 | +0.30 | +0.25 | |
| −0.15 | −0.25 | +0.95 | +0.89 | ||
| PPG Fault—200 km | +2.00 | +0.70 | +0.47 | +0.33 | |
| −0.60 | −0.75 | +0.78 | +0.67 | ||
| NPG Fault | Negative Voltage Negative Current | +1.60 | +1.10 | −0.03 | −0.09 |
| −1.25 | −1.90 | −1.41 | −1.65 | ||
| NPG Fault—100 km | 0.00 | −0.50 | −0.27 | −0.32 | |
| 0.00 | +0.35 | −0.84 | −0.96 | ||
| NPG Fault—200 km | −0.75 | −1.90 | −0.37 | −0.47 | |
| +0.40 | +0.75 | −0.70 | −0.83 | ||
| PP Fault | Positive Voltage Negative Voltage Positive Current | −0.90 | −1.80 | +0.16 | +0.08 |
| +1.80 | +1.35 | +1.76 | +1.54 | ||
| +1.60 | +1.10 | −0.03 | −0.09 | ||
| −1.25 | −1.90 | −1.41 | −1.65 | ||
| PP Fault—100 km | +0.35 | −0.15 | +0.30 | +0.25 | |
| −0.15 | −0.25 | +0.95 | +0.89 | ||
| 0.00 | −0.50 | −0.27 | −0.32 | ||
| 0.00 | +0.35 | −0.84 | −0.96 | ||
| PP Fault—100 km | +2.00 | +0.70 | +0.47 | +0.33 | |
| −0.60 | −0.75 | +0.78 | +0.67 | ||
| −0.75 | −1.90 | −0.37 | −0.47 | ||
| +0.40 | +0.75 | −0.70 | −0.83 | ||
| Parameters | Proposed SVM Technique | Traditional SVM Technique | Traveling Waves Technique |
|---|---|---|---|
| Arrival time measurement | Not required | Not required | Required. It is affected by parameters of the transmission line |
| Faults Near or at Converter Stations | Readily identified and classified | Not yet proven. Additional features will be required to train so that fault near or at the converter station could be identified and classified. | Not Applicable. Additional transformations like Fourier and Wavelet Transform will be required. |
| Computational time | Rapidly identified and classified within 0.15 ms | 0.3 s will be required to identify and classify. | Complex computations increase computational time. Moreover, synchronization is required in two-terminal methods. |
| Response Time | ~0.05 ms | Closed to 1 ms | Few ms are required to respond to abnormal conditions |
| Length of the time window | Length of 0.2 ms time window is enough for fault identification and classification | A length of 0.3 s time window is required. | It varies and depends upon the detection of the first traveling wave-head. |
| Accuracy | Accuracy is higher and closed to 100 percent in all types of DC faults. | Accuracy is higher in the case of two-terminal data, and accuracy is compromised in the case of single terminal data. | Accuracy is greatly affected by wave-speed, non-synchronization, and sampling frequency. |
| Complexity | Implementation is easy. | Implementation is easy | Complex digital processing techniques and synchronization (for two-terminal) is required. |
| Realization and Practicality | A simple analysis of relative maxima and minima of standard deviation and normalization is done to prove its realization. | Error analysis is done to prove its realization | Traveling wave-based relays are practically developed for Brasada–Harney transmission system and Bonneville Power Administration’s field. Attenuation and dispersion are the factors that change the accuracy of finding fault location. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzzammel, R.; Raza, A. A Support Vector Machine Learning-Based Protection Technique for MT-HVDC Systems. Energies 2020, 13, 6668. https://doi.org/10.3390/en13246668
Muzzammel R, Raza A. A Support Vector Machine Learning-Based Protection Technique for MT-HVDC Systems. Energies. 2020; 13(24):6668. https://doi.org/10.3390/en13246668
Chicago/Turabian StyleMuzzammel, Raheel, and Ali Raza. 2020. "A Support Vector Machine Learning-Based Protection Technique for MT-HVDC Systems" Energies 13, no. 24: 6668. https://doi.org/10.3390/en13246668
APA StyleMuzzammel, R., & Raza, A. (2020). A Support Vector Machine Learning-Based Protection Technique for MT-HVDC Systems. Energies, 13(24), 6668. https://doi.org/10.3390/en13246668






