Branch and Bound Algorithm Based on Prediction Error of Metamodel for Computational Electromagnetics
Abstract
1. Introduction
- The number of samples exponentially increases as the optimization problem’s dimensionality does (the curse of dimension). Thus, the size of the correlation matrix increases and consequently the time needed to fit the metamodel. This time can even exceed the evaluation time of the FE model.
- The infill criteria optimization problem is highly multimodal, and their modality is highly correlated to the sample size of the expensive model evaluations; when the number of samples increases, the number of local optima increases too. Therefore, it becomes highly difficult to solve these optimization problems [8].
- When dealing with constrained optimization, the infill criteria tend to sample inside the feasible region but not on the feasibility boundaries, which affects the solution accuracy [9].
2. Metamodel Approach
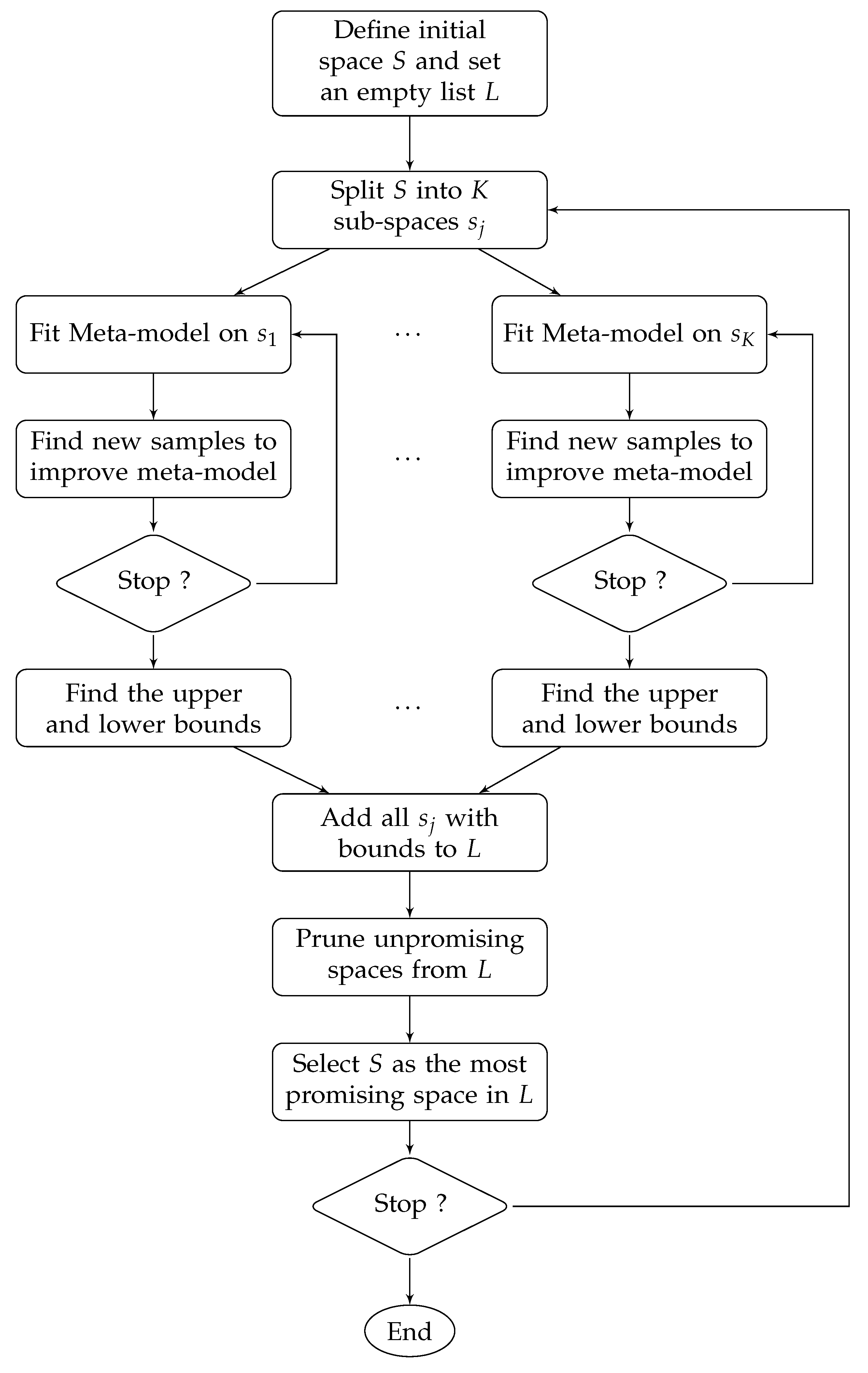
2.1. B2M2 Algorithm
2.1.1. Initialization
2.1.2. Branching
2.1.3. MetaModeling
2.1.4. Bounding
2.1.5. Elimination
2.1.6. Selection Priority
2.1.7. Termination
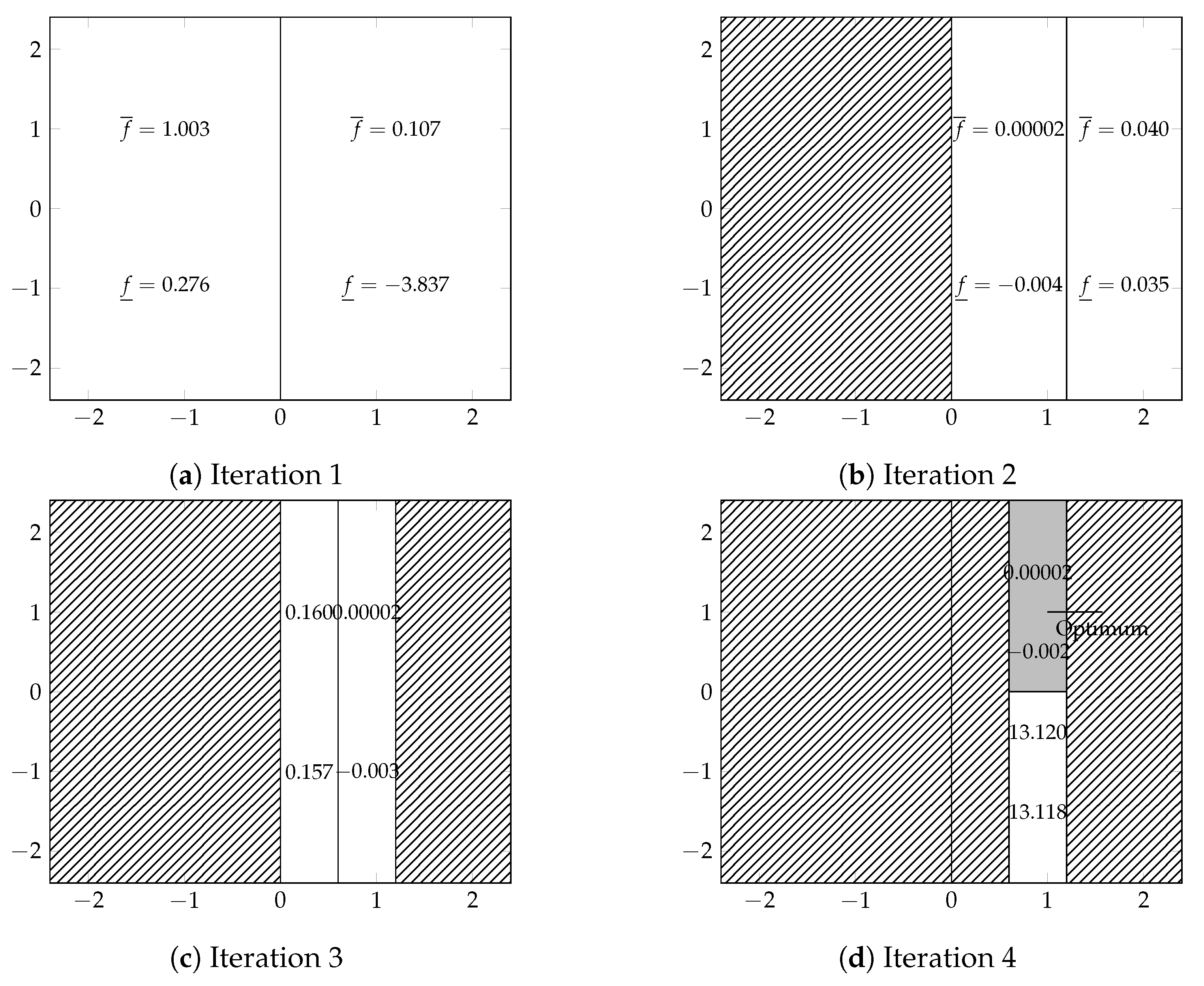
2.2. Test Function
- The maximum depth level is .
- On each subspace, the initial sample is chosen using Hammersley sequence with 4 sample points, the same number of sample points is added using the prediction error as an ISC and two points are added using EI.
3. Expensive Model Approaches
3.1. Derivative-Free
3.2. Derivative-Based
3.2.1. Finite-Difference
3.2.2. Adjoint Variable Method
3.2.3. Globalization Strategy
4. Comparison Protocol
5. Algorithms Settings
5.1. B2M2 Algorithm
5.2. SQP Algorithm Assisted by Adjoint Variable Method
5.3. DIRECT
5.4. Genetic Algorithm
- Size equal to 100 individuals for the unconstrained case and 200 for the constrained one.
- Selection function is uniform
- Crossover function is “scattered“
- Crossover fraction is 80% of the population
- Mutation function is Gaussian
- Elite fraction is 5% of the population
6. Test Cases
6.1. TEAM Workshop Problem 25
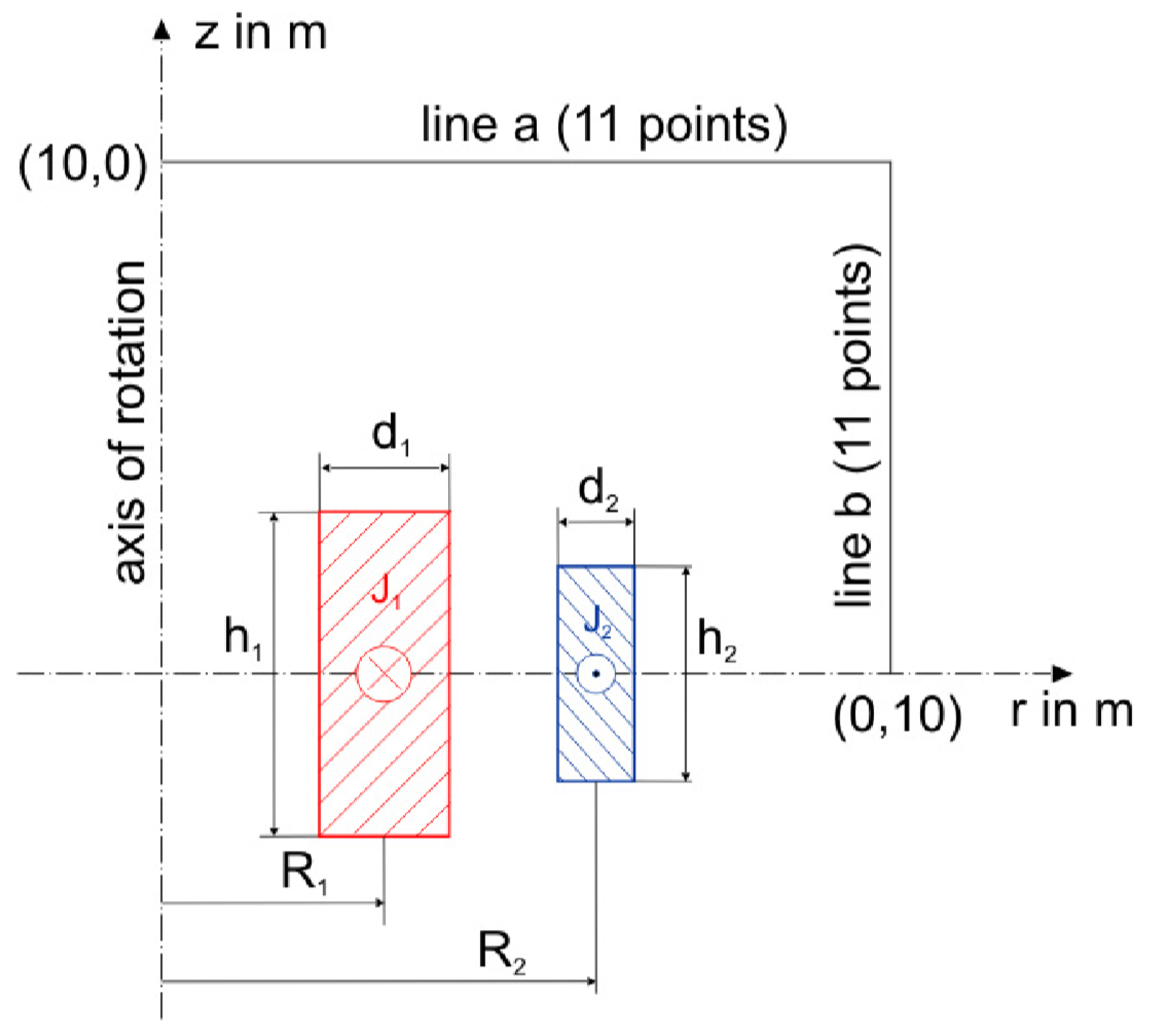
6.2. TEAM Workshop Problem 22
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Alotto, P.; Eranda, C.; Brandstatter, B.; Furntratt, G.; Magele, C.; Molinari, G.; Nervi, M.; Preis, K.; Repetto, M.; Richter, K.R. Stochastic algorithms in electromagnetic optimization. IEEE Trans. Magn. 1998, 34, 3674–3684. [Google Scholar] [CrossRef]
- Berkani, M.S.; Giurgea, S.; Espanet, C.; Coulomb, J.L.; Kieffer, C. Study on optimal design based on direct coupling between a FEM simulation model and L-BFGS-B algorithm. IEEE Trans. Magn. 2013, 49, 2149–2152. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, S.; Rotaru, M.; Sykulski, J.K. A Kriging-Based Optimization Approach for Large Data Sets Exploiting Points Aggregation Techniques. IEEE Trans. Magn. 2017, 53, 7001704. [Google Scholar] [CrossRef]
- Li, M.; Gabriel, F.; Alkadri, M.; Lowther, D.A. Kriging-Assisted Multi-Objective Design of Permanent Magnet Motor for Position Sensorless Control. IEEE Trans. Magn. 2016, 52, 7001904. [Google Scholar] [CrossRef]
- Mohammadi, H.; Riche, R.L.; Durrande, N.; Touboul, E.; Bay, X. An analytic comparison of regularization methods for Gaussian Processes. arXiv 2016, arXiv:1602.00853. [Google Scholar]
- Ababou, R.; Bagtzoglou, A.C.; Wood, E.F. On the condition number of covariance matrices in kriging, estimation, and simulation of random fields. Math. Geol. 1994, 26, 99–133. [Google Scholar] [CrossRef]
- Picheny, V.; Wagner, T.; Ginsbourger, D. A benchmark of kriging-based infill criteria for noisy optimization. Struct. Multidiscip. Optim. 2013, 48, 607–626. [Google Scholar] [CrossRef]
- Sasena, M.J.; Papalambros, P.; Goovaerts, P. Exploration of Metamodeling Sampling Criteria for Constrained Global Optimization. Eng. Optim. 2002, 34, 263–278. [Google Scholar] [CrossRef]
- The MathWorks Inc. Matlab, Global Optimization Toolbox; The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Finkel, D.E. DIRECT Optimization Algorithm User Guide; Center for Research in Scientific Computation, North Carolina State University: Raleigh, NC, USA, 2003; Volume 2, pp. 1–14. [Google Scholar]
- Lee, H.B.; Ida, N. Interpretation of adjoint sensitivity analysis for shape optimal design of electromagnetic systems. IET Sci. Meas. Technol. 2015, 9, 1039–1042. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Takahashi, N. Optimization of Die Press Model: TEAM Workshop Problem 25. COMPUMAG TEAM Worksho. 1996, pp. 1–9. Available online: http://www.compumag.org/jsite/images/stories/TEAM/problem25.pdf (accessed on 10 November 2020).
- Alotto, P.; Baumgartner, U.; Freschi, F. SMES Optimization Benchmark: TEAM Workshop Problem 22. COMPUMAG TEAM Workshop. 2008, pp. 1–4. Available online: http://www.compumag.org/jsite/images/stories/TEAM/problem22.pdf (accessed on 10 November 2020).
- Brandstätter, B.; Ring, W. Optimization of a SMES Device Under Nonlinear Constraints. Citeseer 1997. Available online: https://imsc.uni-graz.at/ring/papers/smes.pdf (accessed on 10 November 2020).
- El Bechari, R.; Guyomarch, F.; Brisset, S.; Clenet, S.; Mipo, J.-C. Efficient Computation of Adjoint Sensitivity Analysis for Electromagnetic Devices Modeled by FEM. Electr. Magn. Fields 2018. [Google Scholar] [CrossRef]

| p | ||||
|---|---|---|---|---|
| min | 5.0 | 12.6 | 14 | 4 |
| max | 9.4 | 18 | 45 | 19 |
| Approach | SQP | GA | DIRECT | B2M2 |
|---|---|---|---|---|
| R1 | 7.31 | 7.51 | 7.31 | 7.28 |
| L2 | 14.21 | 14.64 | 14.20 | 14.17 |
| L3 | 14.11 | 14.39 | 14.08 | 14.06 |
| L4 | 14.37 | 14.44 | 14.39 | 14.34 |
| W | 7.62 × 10−5 | 12.44 × 10−5 | 7.61 × 10−5 | 9.73 × 10−5 |
| # FEM evals | 280 | 10100 | 24255 | 2575 |
| CR | 34% | 2% | 100% | 100% |
| Expected # FEM evals | 3585 | 2,146,501 | 24,255 | 2575 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| min | 1.0 | 1.8 | 0.1 | 0.1 | 0.1 | 0.1 | 10 | −30 |
| max | 4.0 | 5.0 | 1.8 | 1.8 | 0.8 | 0.8 | 30 | −10 |
| Approach | SQP | GA | DIRECT | B2M2 |
|---|---|---|---|---|
| 1.336 | 1.457 | 1.543 | 1.369 | |
| 0.027 | 0.481 | 0.229 | 0.054 | |
| 1.011 | 1.209 | 0.951 | 0.888 | |
| 1.452 | 1.800 | 1.526 | 1.394 | |
| 0.677 | 0.347 | 0.374 | 0.791 | |
| 0.269 | 0.121 | 0.217 | 0.203 | |
| 15.579 | 19.834 | 22.346 | 14.099 | |
| −15.069 | −17.305 | −13.441 | −18.273 | |
| 0.00197 | 0.03502 | 0.04881 | 0.00510 | |
| # FEM evals | 1902 | 160,201 | 421,995 | 106,308 |
| CR | 1 % | 2 % | 100 % | 100 % |
| Expected # FEM evals | 529,640 | 94,276,389 | 421,995 | 106,308 |
| Ref. [15] | Ref. [16] | Ref. [2] | Ref. [4] | |
|---|---|---|---|---|
| 1.296 | 1.3012 | 1.432 | 1.103 | |
| 1.800 | 1.8000 | 2.023 | 2.318 | |
| 1.089 | 1.1325 | 0.784 | 1.596 | |
| 1.513 | 1.5422 | 1.411 | 0.144 | |
| 0.583 | 0.5802 | 0.787 | 0.259 | |
| 0.195 | 0.1961 | 0.178 | 0.734 | |
| 16.695 | 16.422 | 14.290 | 22.5 | |
| −18.910 | −18.925 | −18.010 | −22.5 | |
| Reported | 0.0018 | 0.0020 | 0.0030 | 0.0014 |
| Calculated | 0.0092 | 0.0025 | 0.0131 | 25.2714 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Bechari, R.; Brisset, S.; Clénet, S.; Guyomarch, F.; Mipo, J.C. Branch and Bound Algorithm Based on Prediction Error of Metamodel for Computational Electromagnetics. Energies 2020, 13, 6749. https://doi.org/10.3390/en13246749
El Bechari R, Brisset S, Clénet S, Guyomarch F, Mipo JC. Branch and Bound Algorithm Based on Prediction Error of Metamodel for Computational Electromagnetics. Energies. 2020; 13(24):6749. https://doi.org/10.3390/en13246749
Chicago/Turabian StyleEl Bechari, Reda, Stéphane Brisset, Stéphane Clénet, Frédéric Guyomarch, and Jean Claude Mipo. 2020. "Branch and Bound Algorithm Based on Prediction Error of Metamodel for Computational Electromagnetics" Energies 13, no. 24: 6749. https://doi.org/10.3390/en13246749
APA StyleEl Bechari, R., Brisset, S., Clénet, S., Guyomarch, F., & Mipo, J. C. (2020). Branch and Bound Algorithm Based on Prediction Error of Metamodel for Computational Electromagnetics. Energies, 13(24), 6749. https://doi.org/10.3390/en13246749





