Investigation of the Noise Induced by Unstable Flow in a Centrifugal Pump
Abstract
:1. Introduction
2. Experimental Facility and Numerical Method
2.1. Experimental Facility
2.2. Numerical Method
3. Results and Discussion
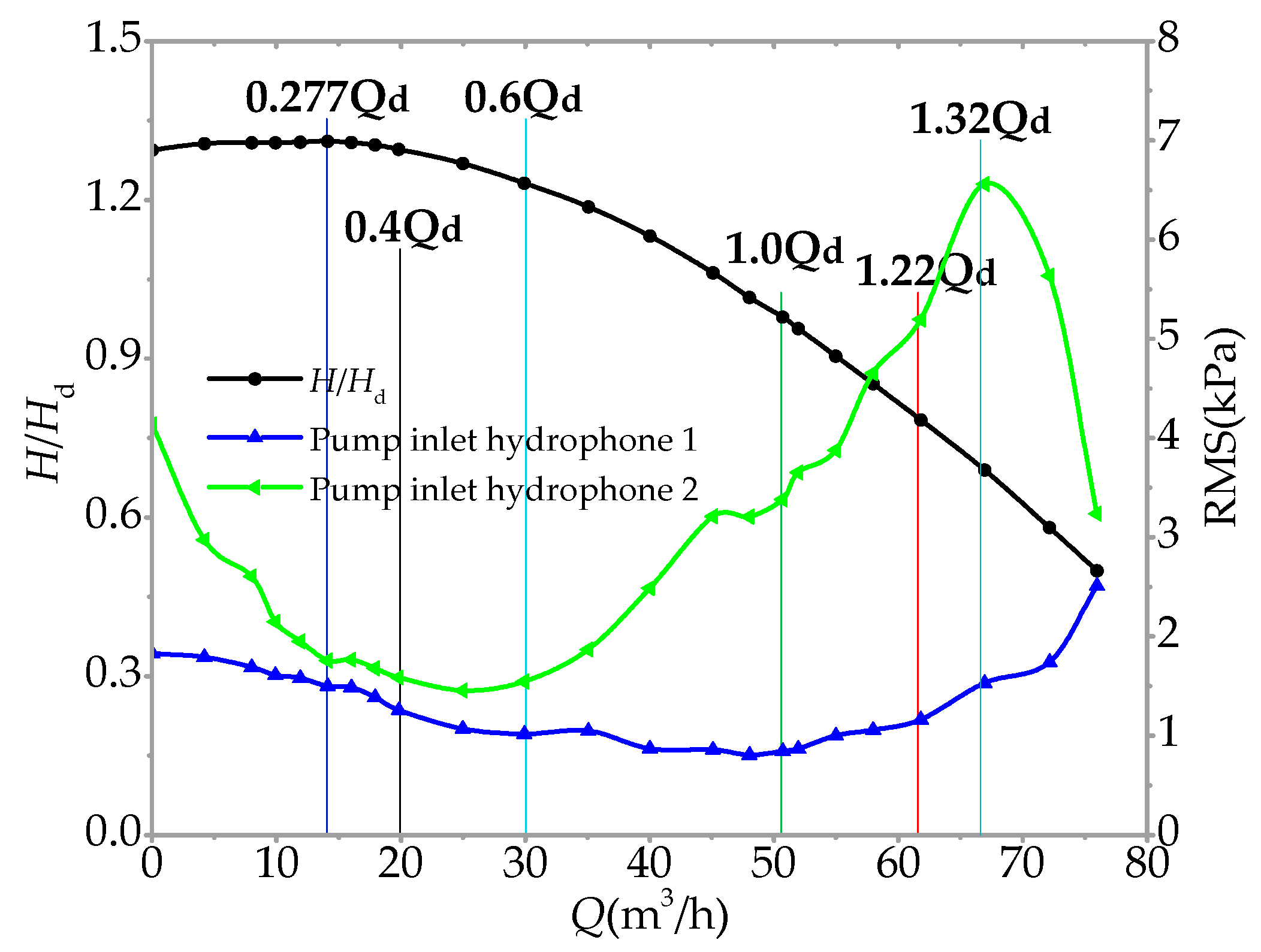
3.1. The Performance of the Pump
3.2. Numerical Results
3.3. Time Domain of the Noise
3.4. Root Mean Square (RMS) of the Noise
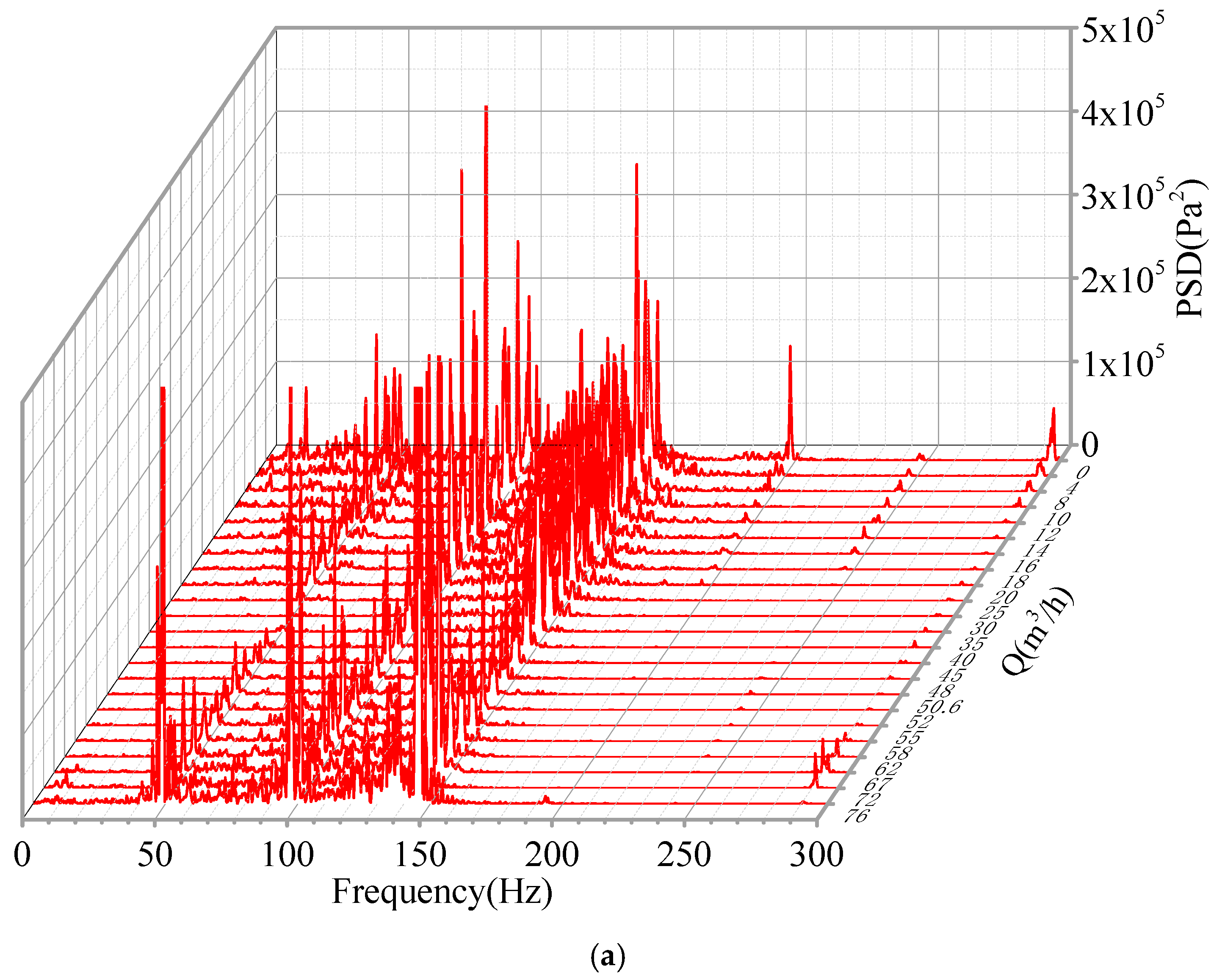
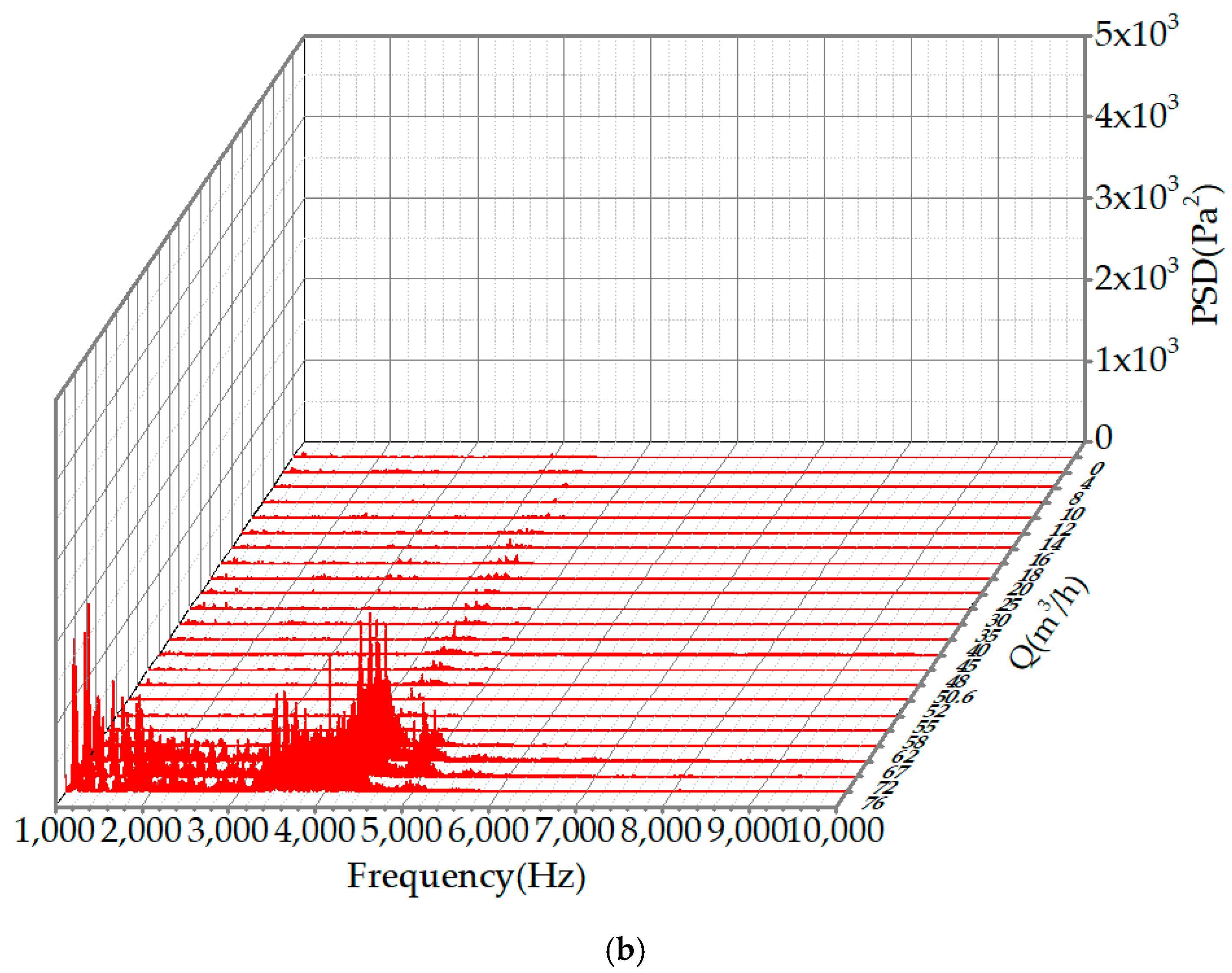
3.5. Power Spectral Density (PSD) of the Noise Measured at the Pump Inlet
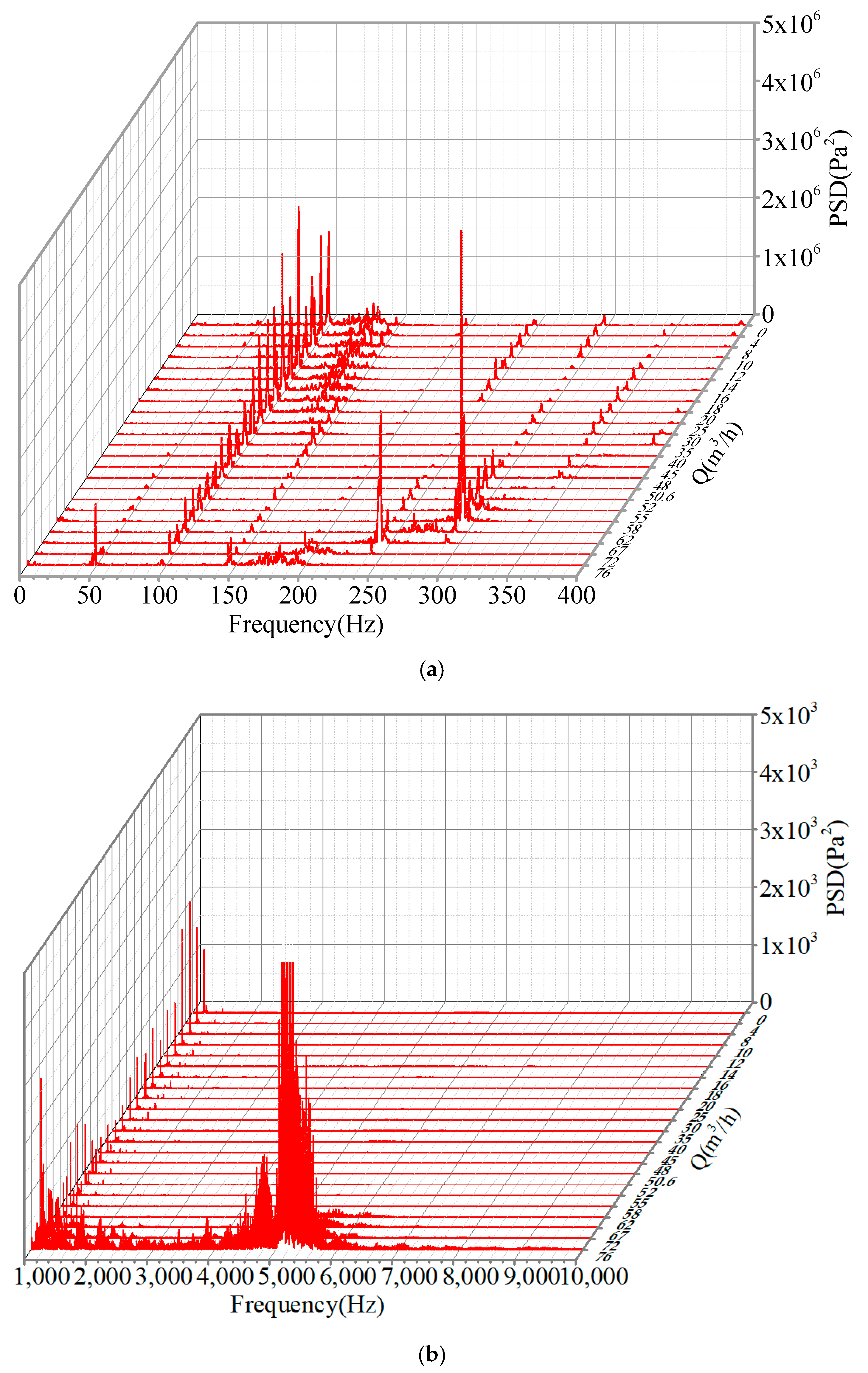
3.6. PSD of the Noise Measured at the Pump Outlet
4. Conclusions
- (a)
- The inlet and outlet noise-measuring points should be as close as possible to the pump to accurately detect the unstable flow inside the pump.
- (b)
- The recirculation and prewhirl regions in the pump upstream pipe, which were caused by the backflow and the rotation of the impeller, presented the circumferential movement with a spiral shape, causing apparent broadband fluctuations at low frequency band of the acoustic pressure. The backflow and rotating stall could also result in the broadband fluctuations of the pump outlet noise, which was distributed from 100 Hz to 150 Hz.
- (c)
- The broadband fluctuations of the pump outlet acoustic pressure distributed from 100 Hz to 300 Hz, which was produced by the occurrence of cavitation, moved to the lower frequency band as the flow rate increased.
- (d)
- The enhanced broadband fluctuations of the pump inlet and outlet noise distributed from 1 kHz to 6 kHz were caused by the coupling between the cavitation-induced noise and the system-produced noise. Meanwhile, the broadband fluctuations of the pump inlet noise distributed between 6 kHz and 9 kHz were regarded as the typical frequency band of cavitation in the centrifugal pump.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Latin Symbols | ||
| fd | Blade-passing frequency | Hz |
| f0 | Shaft frequency | Hz |
| H | Head | m |
| Hd | Rated head of the pump | m |
| k | Constant | - |
| n | Rotational speed | rpm |
| N | Constant | - |
| Q | Flow rate | m3/s |
| Qd | Rated flow rate | m3/s |
| Xk | Acoustic pressure | Pa |
| Abbreviations | ||
| PSD | Power spectral density | |
| RMS | Root mean square | |
References
- He, X.; Zhang, Y.; Wang, C.; Zhang, C.; Cheng, L.; Chen, K.; Hu, B. Influence of critical wall roughness on the performance of double-channel sewage pump. Energies 2020, 13, 464. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Zhu, R.; Wang, X.; Wang, Y.; Fu, Q.; Ye, D. Study on the complete rotational characteristic of coolant pump in the gas-liquid two-phase operating condition. Ann. Nucl. Energy 2019, 123, 180–189. [Google Scholar]
- Wang, C.; He, X.; Cheng, L.; Luo, C.; Xu, J.; Chen, K.; Jiao, W. Numerical simulation on hydraulic characteristics of nozzle in waterjet propulsion system. Processes 2019, 7, 915. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.X.; Yuan, S.Q.; Luo, Y.; Yuan, J.P.; Zhou, B.L.; Sun, H. Numerical and experimental investigation on the development of cavitation in a centrifugal pump. Proc. Inst. Mech. Eng. Part E 2016, 230, 171–182. [Google Scholar] [CrossRef]
- Lu, J.X.; Yuan, S.Q.; Parameswaran, S.; Yuan, J.P.; Ren, X.D.; Zhou, B.L. The characteristics investigation under the unsteady cavitation condition in a centrifugal pump. J. Mech. Sci. Technol. 2017, 31, 1213–1222. [Google Scholar] [CrossRef]
- Choi, J.S.; McLaughlin, D.K.; Thompson, D.E. Experiments on the unsteady flow field and noise generation in a centrifugal pump impeller. J. Sound Vib. 2003, 263, 493–514. [Google Scholar] [CrossRef]
- Lu, J.X.; Yuan, S.Q.; Yuan, J.P.; Si, Q.R.; Luo, Y. Experiments on effects of AC motor water-cooling device on performance of centrifugal pump. J. Drain. Irrig. Mach. Eng. 2014, 32, 737–741. [Google Scholar]
- Cumpsty, N.A. A critical review of turbomachinery noise. J. Fluids Eng. 1977, 99, 278–293. [Google Scholar] [CrossRef]
- Brennen, C.E. Hydrodynamics of Pumps; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Langthjem, M.A.; Olhoff, N. A numerical study of flow-induced noise in a two-dimensional centrifugal pump. Part I. Hydrodynamics. J. Fluids Struct. 2004, 19, 349–368. [Google Scholar] [CrossRef]
- Langthjem, M.A.; Olhoff, N. A numerical study of flow-induced noise in a two-dimensional centrifugal pump. Part II. Hydroacoustics. J. Fluids Struct. 2004, 19, 369–386. [Google Scholar] [CrossRef]
- Gao, M.; Dong, P.X.; Lei, S.H.; Turan, A. Computational study of the noise radiation in a centrifugal pump when flow rate changes. Energies 2017, 10, 221. [Google Scholar] [CrossRef] [Green Version]
- Simpson, H.C. A theoretical investigation of hydraulic noise in pumps. J. Sound Vib. 1967, 5, 456–488. [Google Scholar] [CrossRef]
- Mongeau, L. Experimental study of the mechanism of sound generation by a rotating stall in centrifugal turbomachines. J. Acoust. Soc. Am. 1992, 91, 2288. [Google Scholar] [CrossRef]
- Chu, S.; Dong, R.; Katz, J. Relationship between unsteady flow, pressure fluctuations, and noise in a centrifugal pump—Part A: Use of PDV data to compute the pressure field. J. Fluids Eng. 1995, 117, 24–29. [Google Scholar] [CrossRef]
- Chu, S.; Dong, R.; Katz, J. Relationship between unsteady flow, pressure fluctuations, and noise in a centrifugal pump—Part B: Effects of blade-tongue interactions. J. Fluids Eng. 1995, 117, 30–35. [Google Scholar] [CrossRef]
- Dong, R.; Chu, S.; Katz, J. Effect of modification to tongue and impeller geometry on unsteady flow, pressure fluctuations, and noise in a centrifugal pump. J. Turbomach. 1997, 119, 506–515. [Google Scholar] [CrossRef] [Green Version]
- Si, Q.R.; Yuan, S.Q.; Yuan, J.P.; Wang, C.; Yang, J. Study on the influence of volute to flow–induced noise in centrifugal pump. Adv. Mater. Res. 2012, 516, 1009–1017. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.X.; Qiu, N.; Zhu, Y.; Shi, W.D. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 481. [Google Scholar] [CrossRef]
- Rzentkowski, G.; Zbroja, S. Experimental characterization of centrifugal pumps as an acoustic source at the blade-passing frequency. J. Fluids Struct. 2000, 14, 529–558. [Google Scholar] [CrossRef]
- Guo, C.; Gao, M.; Lu, D.Y.; Wang, K. An Experimental study on the radiation noise characteristics of a centrifugal pump with various working conditions. Energies 2017, 10, 2139. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.P.; Ge, A.X.; Sun, W.; Fu, Y.X.; Xue, F. A study of flow–induced noise in the volute of centrifugal pump based on sysnoise. Adv. Mater. Res. 2012, 468–471, 643–649. [Google Scholar] [CrossRef]
- Ye, X.M.; Pei, J.J.; Li, C.X.; Liu, Z. Experimental study on nosie characteristics of centrifugal pump based on near–field acoustic pressure method. Chin. J. Power Eng. 2013, 33, 375–380. [Google Scholar]
- Parrondo, J.; Pérez, J.; Barrio, R.; González, J. A simple acoustic model to characterize the internal low frequency sound field in centrifugal pumps. Appl. Acoust. 2011, 72, 59–64. [Google Scholar] [CrossRef]
- Si, Q.R.; Yuan, S.Q.; Yuan, J.P. Experimental study on the influence of impeller–tongue gap on the performance and flow-induced noise characteristics of centrifugal pumps. J. Vib. Shock 2016, 35, 164–168. [Google Scholar]
- Lu, D.Y. Experimental Study on Flow-Noise of Centrifugal Pump in Variable Working Condition. Master’s Thesis, Shandong University, Jinan, China, 2017. [Google Scholar]
- Sun, Y.D.; Zhong, R.; Wang, S.Q.; Hao, X.Y.; Wang, J. Experimental research on hydrodynamic noise of centrifugal pumps based on two-port source characteristic test method. J. Ship Mech. 2016, 20, 198–205. [Google Scholar]
- Yuan, S.Q.; Yang, J.; Yuan, J.P.; Luo, Y.; Pei, J. Experimental investigation on the flow–induced noise under variable conditions for centrifugal pumps. Chin. J. Mech. Eng. 2012, 25, 456–462. [Google Scholar]
- Lu, J.X.; Yuan, S.Q.; Yuan, J.P.; Ren, X.D.; Pei, J.; Si, Q.R. Research on the noise induced by cavitation under the asymmetric cavitation condition in a centrifugal pump. J. Phys. Conf. Ser. 2015, 656, 012102. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.P. Inner Flow PIV Measurement and its Unsteady Turbulent Flow Numerical Simulation for a Centrifugal Pump with Multi-Programs. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 2008. [Google Scholar]
- Hou, J.S. Research on the Dynamic Characteristics of Inlet Backflow Vortex Cavitation in Centrifugal Pumps. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2018. [Google Scholar]
- Lu, J.X.; Liu, X.B.; Zeng, Y.Z.; Zhu, B.S.; Hu, B.; Yuan, S.Q.; Hua, H. Detection of the flow state for a centrifugal pump based on vibration. Energies 2019, 12, 3066. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.Y.; Yuan, S.Q. Fundamentals of Cavitation in Pumps; Jiangsu University Press: Zhenjiang, China, 2013. [Google Scholar]
- Li, X.J.; Chen, B.; Luo, X.W.; Zhu, Z.C. Effects of flow pattern on hydraulic performance and energy conversion characterisation in a centrifugal pump. Renew. Energy 2019. [Google Scholar] [CrossRef]
- Mao, X.L.; Pavesi, G.; Chen, D.Y.; Xu, H.S.; Mao, G.J. Flow induced noise characterization of pump turbine in continuous and intermittent load rejection processes. Renew. Energy 2019, 139, 1029–1039. [Google Scholar] [CrossRef]
- Xu, Z.H.; Xu, D.H.; Wu, Y.L.; Chen, N.X.; Chen, R. Monitor and diagnose of cavitation in pump and hydro turbine. Trans. Chin. Soc. Agric. Mach. 2003, 34, 139–142. [Google Scholar]
- Tan, L.; Zhu, B.S.; Cao, S.L.; Wang, Y.C.; Wang, B.B. Influence of prewhirl regulation by inlet guide vanes on cavitation performance of a centrifugal pump. Energies 2014, 7, 1050–1065. [Google Scholar] [CrossRef]
- Si, Q.R. Investigation on Hydraulic Design of Centrifugal Pumps with Low Noise and Mechanism of Rotor-Stator Interaction. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 2014. [Google Scholar]



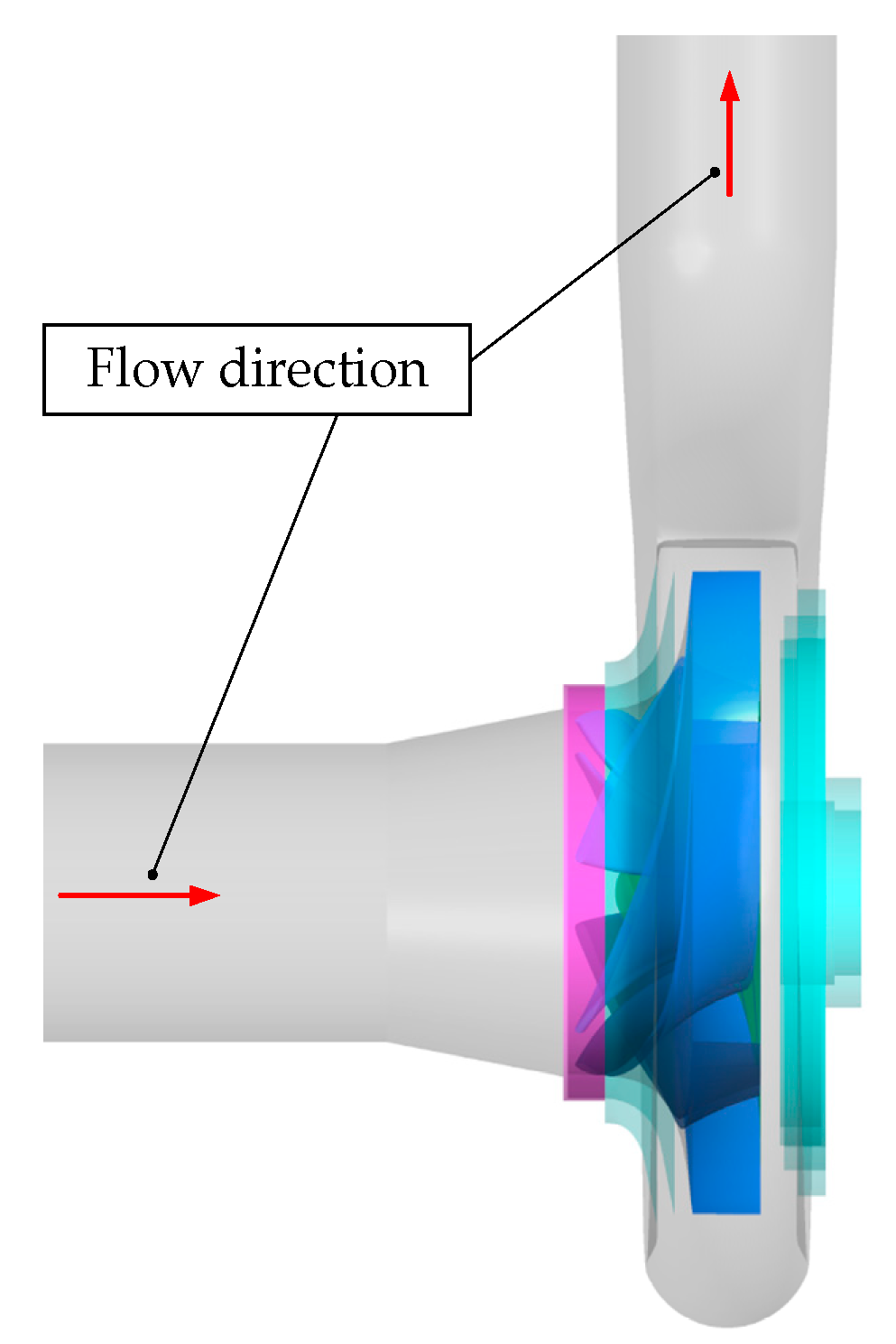


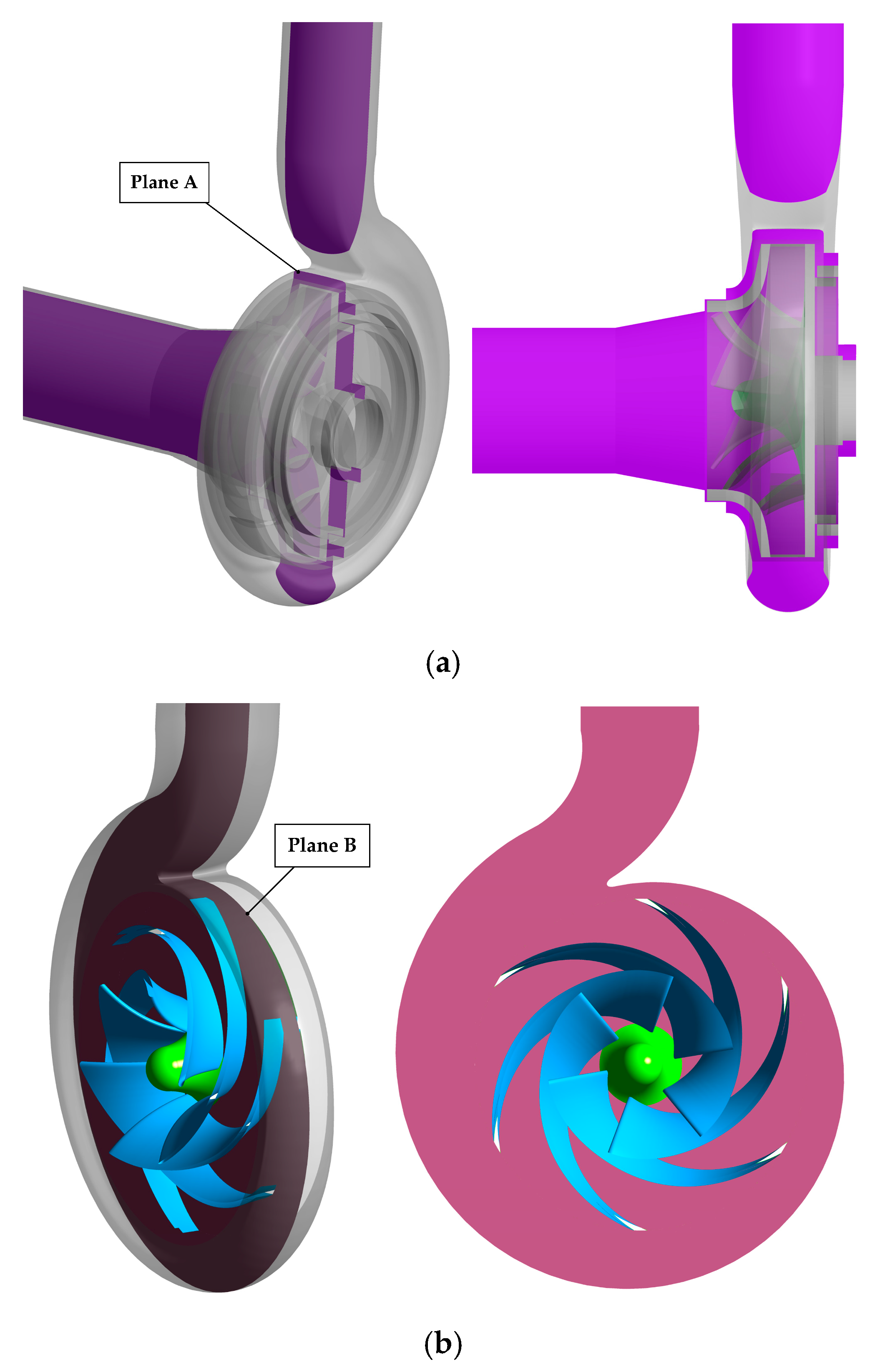

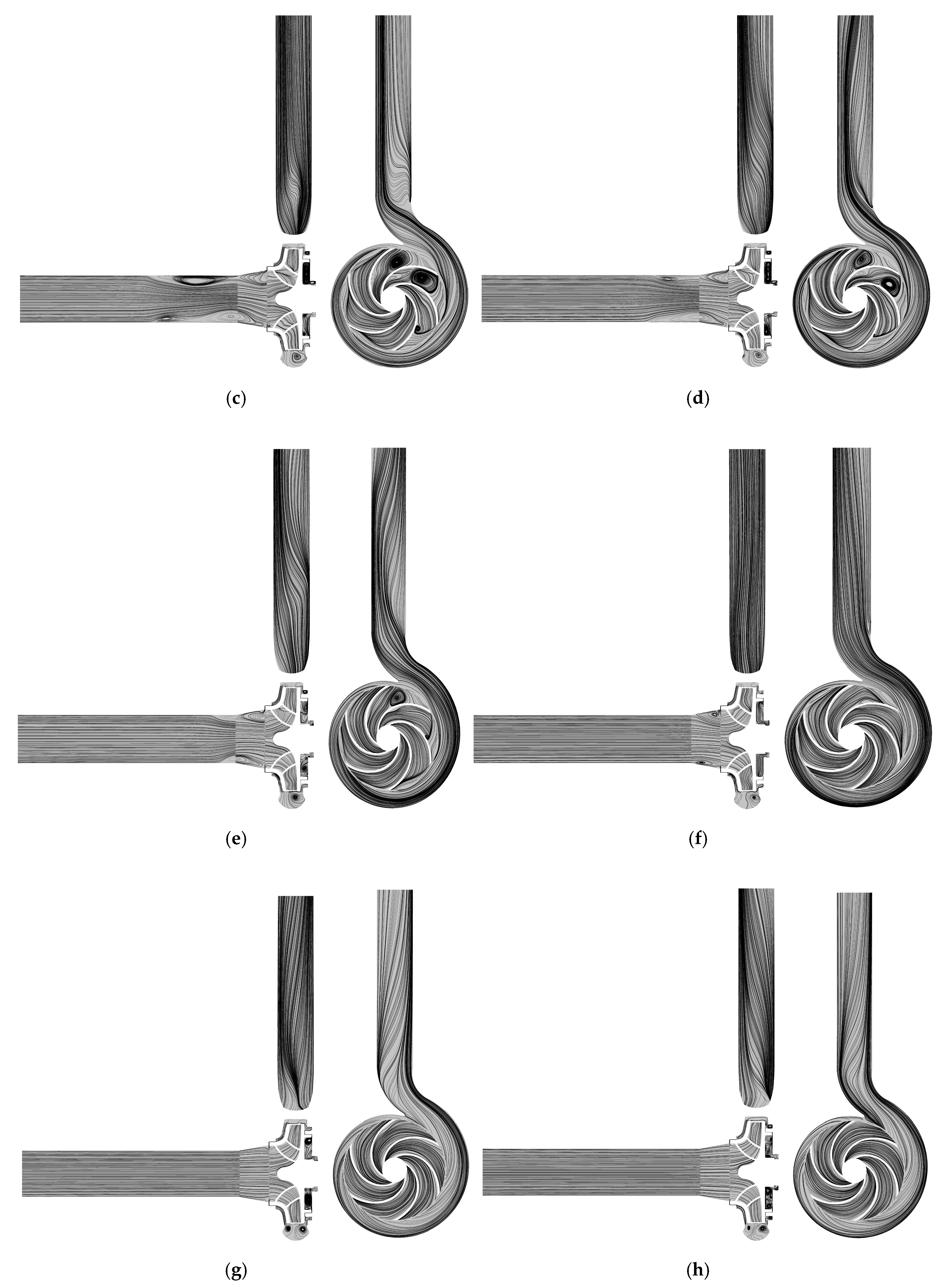








| Primary Parameters | Value | Unit |
|---|---|---|
| Rated head Hd | 20.2 | m |
| Rated rotating speed n | 2910 | rpm |
| Rated flow rate Qd | 50.6 | m3/h |
| Blade passing frequency fd | 291 | Hz |
| Shaft frequency f0 | 48.5 | Hz |
| Outlet angle of the blade | 23 | degree |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Liu, X.; Zeng, Y.; Zhu, B.; Hu, B.; Hua, H. Investigation of the Noise Induced by Unstable Flow in a Centrifugal Pump. Energies 2020, 13, 589. https://doi.org/10.3390/en13030589
Lu J, Liu X, Zeng Y, Zhu B, Hu B, Hua H. Investigation of the Noise Induced by Unstable Flow in a Centrifugal Pump. Energies. 2020; 13(3):589. https://doi.org/10.3390/en13030589
Chicago/Turabian StyleLu, Jiaxing, Xiaobing Liu, Yongzhong Zeng, Baoshan Zhu, Bo Hu, and Hong Hua. 2020. "Investigation of the Noise Induced by Unstable Flow in a Centrifugal Pump" Energies 13, no. 3: 589. https://doi.org/10.3390/en13030589





