Design of a Finite-Time Terminal Sliding Mode Controller for a Nonlinear Hydro-Turbine Governing System
Abstract
:1. Introduction
2. A Nonlinear Model of HGS
3. Controller Design
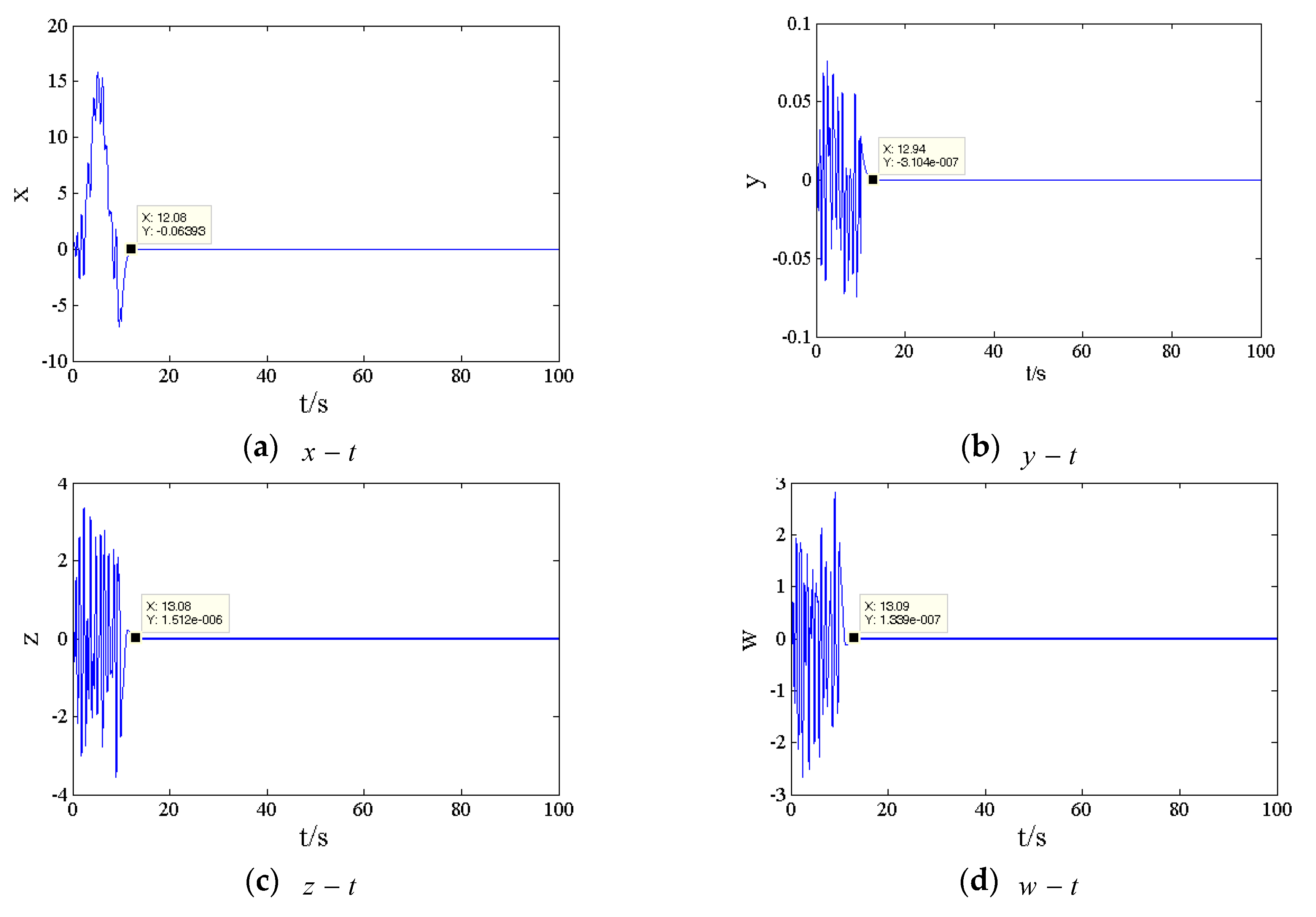
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Generator rotor angle. | Rotational speed relative of the generator. | ||
| Hydro-turbine output incremental torque. | Incremental of the guide vane opening. | ||
| Inertia time constant of the rotating part. | Damping coefficient of the generator. | ||
| Transient electromotive force of axis. | Infinite system bus voltage of the power system. | ||
| Transient reactance of axis. | Synchronous reactance of axis. | ||
| Transfer coefficient of turbine flow on the head. | Water inertia time constant. | ||
| Transfer coefficient of turbine torque on the main servomotor stroke. | Transfer coefficient. | ||
| Transfer time of turbine servomotor stroke. | Proportional adjustment coefficient. | ||
| Integral adjustment coefficient. | Differential adjustment coefficient. |
References
- Petrie, J.; Diplas, P.; Gutierrez, M.; Nam, S. Characterizing the mean flow field in rivers for resource and environmental impact assessments of hydrokinetic energy generation sites. Renew. Energy 2014, 69, 393–401. [Google Scholar] [CrossRef]
- Proskuryakova, L.N.; Ermolenko, G.V. The future of Russia’s renewable energy sector: Trends, scenarios and policies. Renew. Energy 2019, 143, 1670–1686. [Google Scholar] [CrossRef]
- Ling, D.J.; Tao, Y. An analysis of the Hopf bifurcation in a hydroturbine governing system with saturation. IEEE Trans. Energy Convers. 2006, 21, 512–515. [Google Scholar] [CrossRef]
- Ostergaard, P.A.; Duic, N.; Noorollahi, Y.; Mikulcic, H.; Kalogirou, S. Sustainable development using renewable energy technology. Renew. Energy 2020, 146, 2430–2437. [Google Scholar] [CrossRef]
- Li, C.L.; Zhou, J.Z.; Ouyang, S.; Ding, X.L.; Chen, L. Improved decomposition-coordination and discrete differential dynamic programming for optimization of large-scale hydropower system. Energy Convers. Manag. 2014, 84, 363–373. [Google Scholar] [CrossRef]
- Sun, S.K.; Wang, Y.B.; Liu, J.; Cai, H.J.; Wu, P.T.; Geng, Q.L.; Xu, L.J. Sustainability assessment of regional water resources under the DPSIR framework. J. Hydrol. 2016, 532, 140–148. [Google Scholar] [CrossRef]
- Pico, H.V.; McCalley, J.D.; Angel, A.; Leon, R.; Castrillon, N.J. Analysis of very low frequency oscillations in hydro-dominant power systems using multi-unit modeling. IEEE Trans. Power Syst. 2012, 27, 1906–1915. [Google Scholar] [CrossRef]
- Yan, D.L.; Wang, W.Y.; Chen, Q.J. Nonlinear Modeling and Dynamic Analyses of the Hydro-Turbine Governing System in the Load Shedding Transient Regime. Energies 2018, 11, 1244. [Google Scholar] [CrossRef] [Green Version]
- Goel, P.K.; Singh, B.; Murthy, S.S.; Kishore, N. Isolated wind-hydro hybrid system using cage generators and battery storage. IEEE Trans. Ind. Electron. 2011, 58, 1141–1153. [Google Scholar] [CrossRef]
- Tan, W. Unified tuning of PID load frequency controller for power systems via IMC. IEEE Trans. Power Syst. 2010, 25, 341–350. [Google Scholar] [CrossRef]
- Chen, D.Y.; Ding, C.; Ma, X.Y.; Yuan, P.; Ba, D.D. Nonlinear dynamical analysis of hydro-turbine governing system with a surge tank. Appl. Math. Model. 2013, 37, 7611–7623. [Google Scholar] [CrossRef]
- Guo, W.C. A Review of the Hydraulic Transient and Dynamic Behavior of Hydropower Plants with Sloping Ceiling Tailrace Tunnels. Energies 2019, 12, 3220. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Zhang, L.X.; Guo, Y.K.; Qian, J.; Zhang, C. The generalized Hamiltonian model for the shafting transient analysis of the hydro turbine generating sets. Nonlinear Dyn. 2014, 76, 1921–1933. [Google Scholar] [CrossRef] [Green Version]
- Yi, Y.P.; Chen, D.Y. Disturbance observer-based backstepping sliding mode fault-tolerant control for the hydro-turbine governing system with dead-zone input. ISA Trans. 2019, 88, 127–141. [Google Scholar] [CrossRef]
- Lai, X.J.; Li, C.S.; Guo, W.C.; Xu, Y.H.; Li, Y.G. Stability and dynamic characteristics of the nonlinear coupling system of hydropower station and power grid. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104919. [Google Scholar] [CrossRef]
- Faraji-Niri, M.; Asadzadeh, V.; Fard, J.R. Stabilization of Arbitrary Switched Nonlinear Fractional Order Dynamical Systems: Application to Francis Hydro-Turbine Governing System. Inf. Technol. Control. 2019, 48, 401–414. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.F.; Chen, D.Y.; Xu, B.B.; Zhang, H. Nonlinear dynamics of a novel fractional-order Francis hydro-turbine governing system with time delay. Chaos Solitons Fractals 2016, 91, 329–338. [Google Scholar] [CrossRef] [Green Version]
- Ansel, A.; Robyns, B. Modelling and simulation of an autonomous variable speed micro hydropower station. Math. Comput. Simul. 2006, 71, 320–332. [Google Scholar] [CrossRef]
- Li, C.S.; Zhou, J.Z. Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm. Energy Convers. Manag. 2011, 52, 374–381. [Google Scholar] [CrossRef]
- Kishor, N.; Saini, R.P.; Singh, S.P. A review on hydropower plant models and control. Renew. Sustain. Energy Rev. 2007, 11, 776–796. [Google Scholar] [CrossRef]
- Mobayen, S. A novel global sliding mode control based on exponential reaching law for a class of underactuated systems with external disturbances. J. Comput. Nonlinear Dyn. 2016, 11, 021011. [Google Scholar] [CrossRef]
- Pan, H.H.; Sun, W.C.; Gao, H.J.; Kaynak, O.; Alsaadi, F.; Hayat, T. Robust adaptive control of non-linear time-delay systems with saturation constraints. IET Control Theory Appl. 2015, 9, 103–113. [Google Scholar] [CrossRef]
- Wang, B.; Xue, J.Y.; Wu, F.J.; Zhu, D.L. New conditions for fuzzy control of uncertain fractional order nonlinear systems with random disturbances. IET Control Theory Appl. 2016, 10, 637–647. [Google Scholar] [CrossRef]
- Zhao, X.D.; Wu, T.T.; Zheng, X.L.; Li, R. Discussions on observer design of nonlinear positive systems via T-S fuzzy modeling. Neurocomputing 2015, 157, 70–75. [Google Scholar] [CrossRef]
- Jiang, C.M.; Ma, Y.C.; Wang, C.M. PID controller parameters optimization of hydro-turbine governing systems using deterministic-chaotic-mutation evolutionary programming (DCMEP). Energy Convers. Manag. 2006, 47, 1222–1230. [Google Scholar] [CrossRef]
- Bartolini, G.; Orani, N.; Pisano, A.; Punta, E.; Usai, E. A combined first-/second-order sliding-mode technique in the control of a jet-propelled vehicle. Int. J. Robust Nonlinear 2008, 18, 570–585. [Google Scholar] [CrossRef]
- Chen, Z.H.; Yuan, X.H.; Ji, B.; Wang, P.T.; Tian, H. Design of a fractional order PID controller for hydraulic turbine regulating system using chaotic non-dominated sorting genetic algorithm II. Energy Convers. Manag. 2014, 84, 390–404. [Google Scholar] [CrossRef]
- Yu, S.H.; Yu, X.H.; Shirinzadeh, B.; Man, Z.H. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Han, Y.Z.; Ma, R.L.; Cui, J.H. Adaptive Higher-Order Sliding Mode Control for Islanding and Grid-Connected Operation of a Microgrid. Energies 2018, 11, 1459. [Google Scholar] [CrossRef] [Green Version]
- Ou, M.Y.; Du, H.B.; Li, S.H. Finite-time formation control of multiple nonholonomic mobile robots. Int. J. Robust Nonlinear 2014, 24, 140–165. [Google Scholar] [CrossRef]
- He, X.Y.; Wang, Q.Y.; Yu, W.W. Finite-time distributed cooperative attitude tracking control for multiple rigid spacecraft. Appl. Math. Comput. 2015, 256, 724–734. [Google Scholar] [CrossRef]
- Kishor, N.; Singh, S.P.; Raghuvanshi, A.S. Dynamic simulations of hydro turbine and its state estimation based LQ control. Energy Convers. Manag. 2006, 47, 3119–3137. [Google Scholar] [CrossRef]
- Shen, Z.Y. Hydraulic Turbine Regulation; China Water Power Press: Beijing, China, 1998. [Google Scholar]
- Xu, B.B.; Chen, D.Y.; Zhang, H.; Wang, F.F. Modeling and stability analysis of a fractional-order Francis hydro-turbine governing system. Chaos Solitons Fractals 2015, 75, 50–61. [Google Scholar] [CrossRef]
- Ling, D.J. Bifurcation and Chaos of Hydraulic Turbine Governor; Nanjing Hohai University: Jiangsu, China, 2007. [Google Scholar]
- Yin, J.L.; Khoo, S.; Man, Z.H.; Yu, X.H. Finite-time stability and instability of stochastic nonlinear systems. Automatica 2011, 47, 2671–2677. [Google Scholar] [CrossRef]
- Chen, D.Y.; Zhao, W.L.; Ma, X.Y.; Zhang, R.F. No-chattering sliding mode control chaos in Hindmarsh-Rose neurons with uncertain parameters. Comput. Math. Appl. 2011, 61, 3161–3171. [Google Scholar] [CrossRef] [Green Version]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Wang, B.; Chen, P. Design of a Finite-Time Terminal Sliding Mode Controller for a Nonlinear Hydro-Turbine Governing System. Energies 2020, 13, 634. https://doi.org/10.3390/en13030634
Yang T, Wang B, Chen P. Design of a Finite-Time Terminal Sliding Mode Controller for a Nonlinear Hydro-Turbine Governing System. Energies. 2020; 13(3):634. https://doi.org/10.3390/en13030634
Chicago/Turabian StyleYang, Tianyu, Bin Wang, and Peng Chen. 2020. "Design of a Finite-Time Terminal Sliding Mode Controller for a Nonlinear Hydro-Turbine Governing System" Energies 13, no. 3: 634. https://doi.org/10.3390/en13030634




