Earth-Cooling Air Tunnels for Thermal Power Plants: Initial Design by CFD Modelling
Abstract
:1. Introduction
2. Methodology
2.1. Scale of the Design
2.2. CFD Modelling
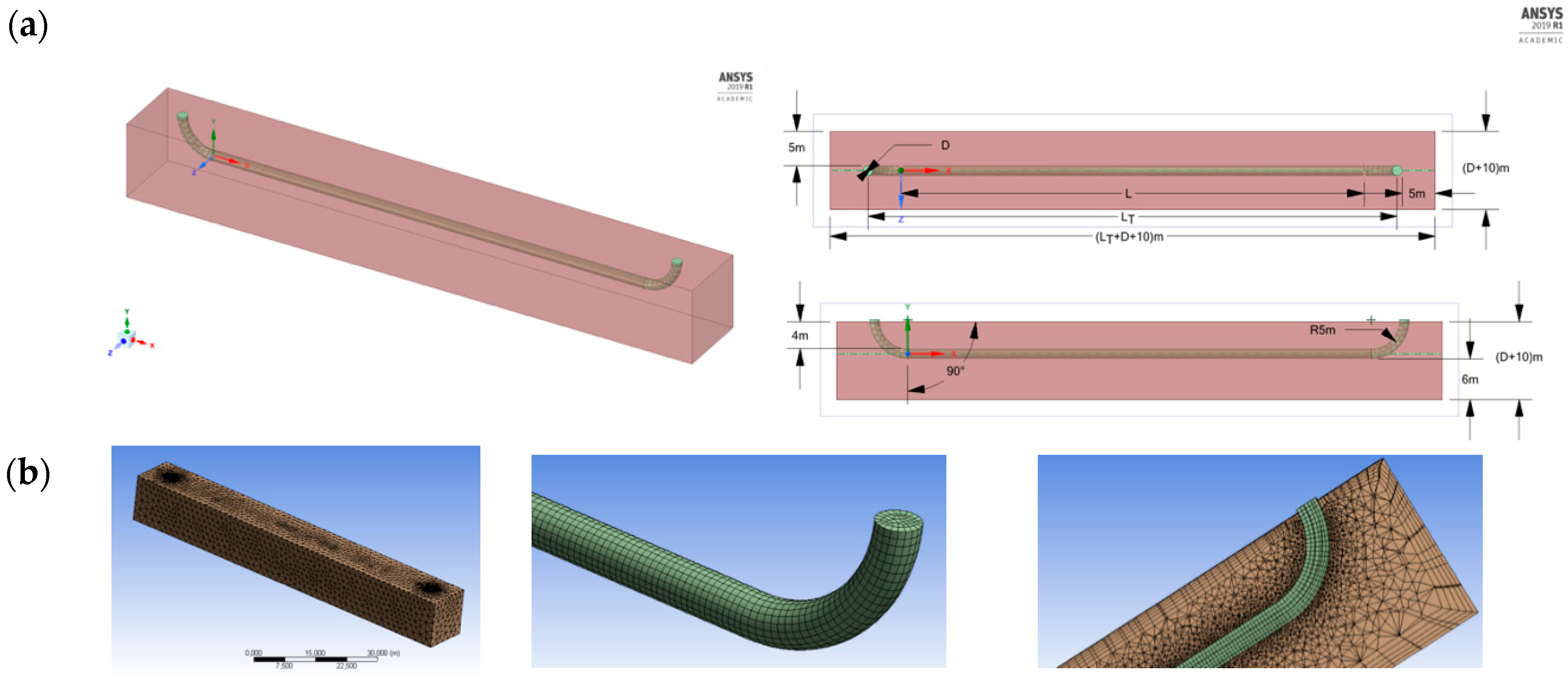
2.2.1. Geometry
2.2.2. Mesh
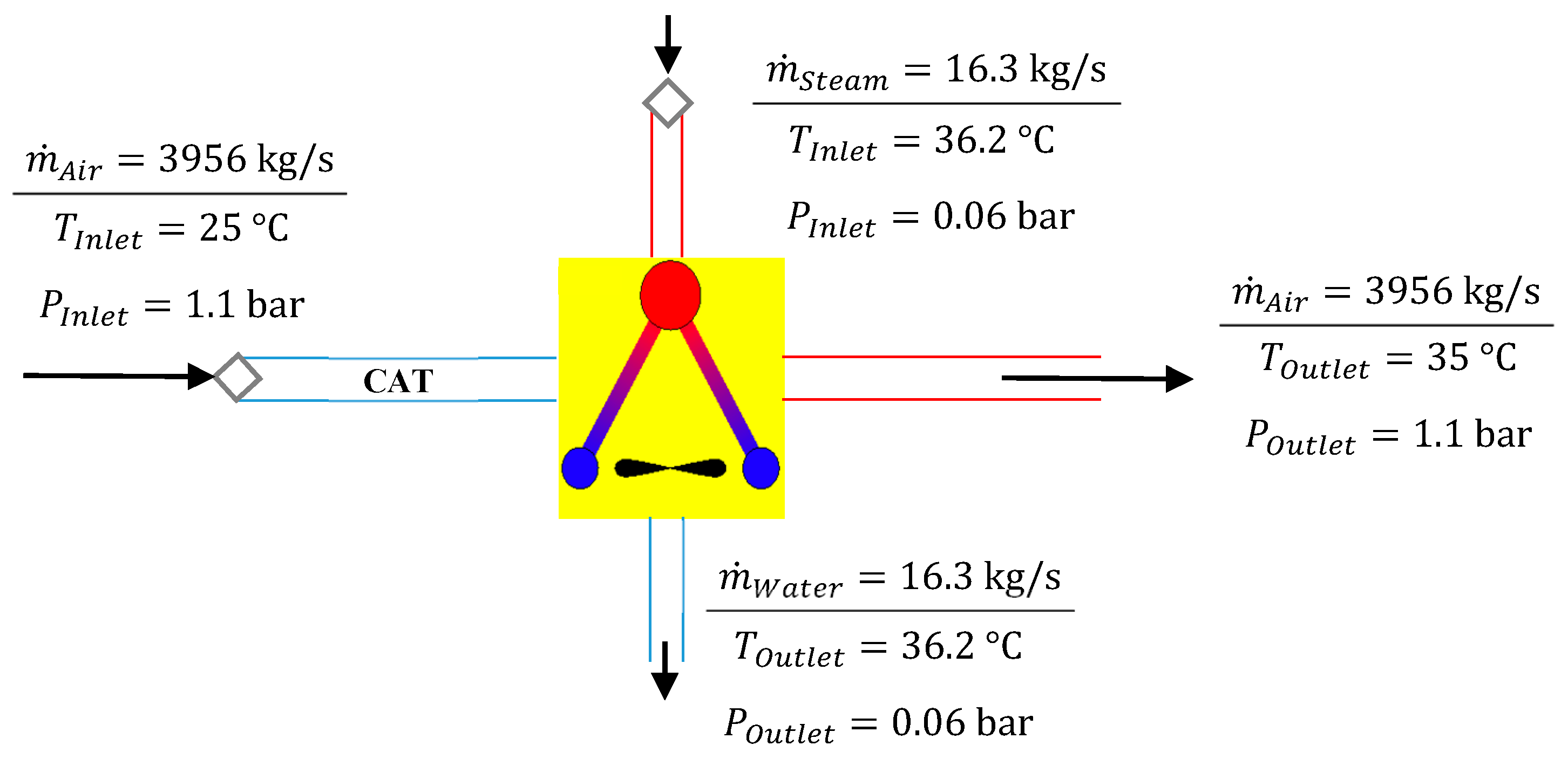
2.2.3. Materials and Boundary Conditions
2.2.4. Solver
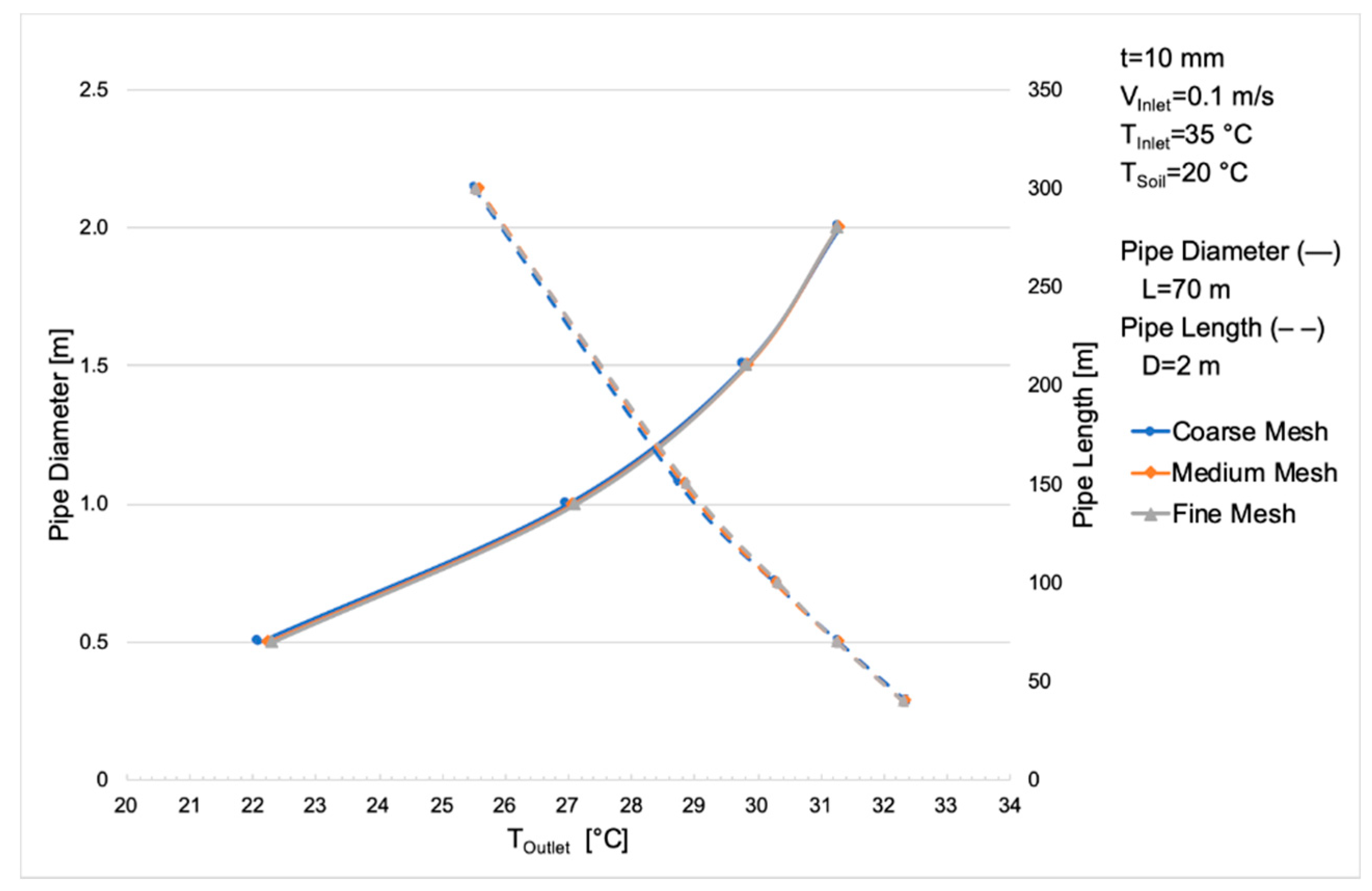
2.2.5. Grid Study
2.2.6. Model Validation
2.2.7. Sensitivity Study
3. Results and Discussion
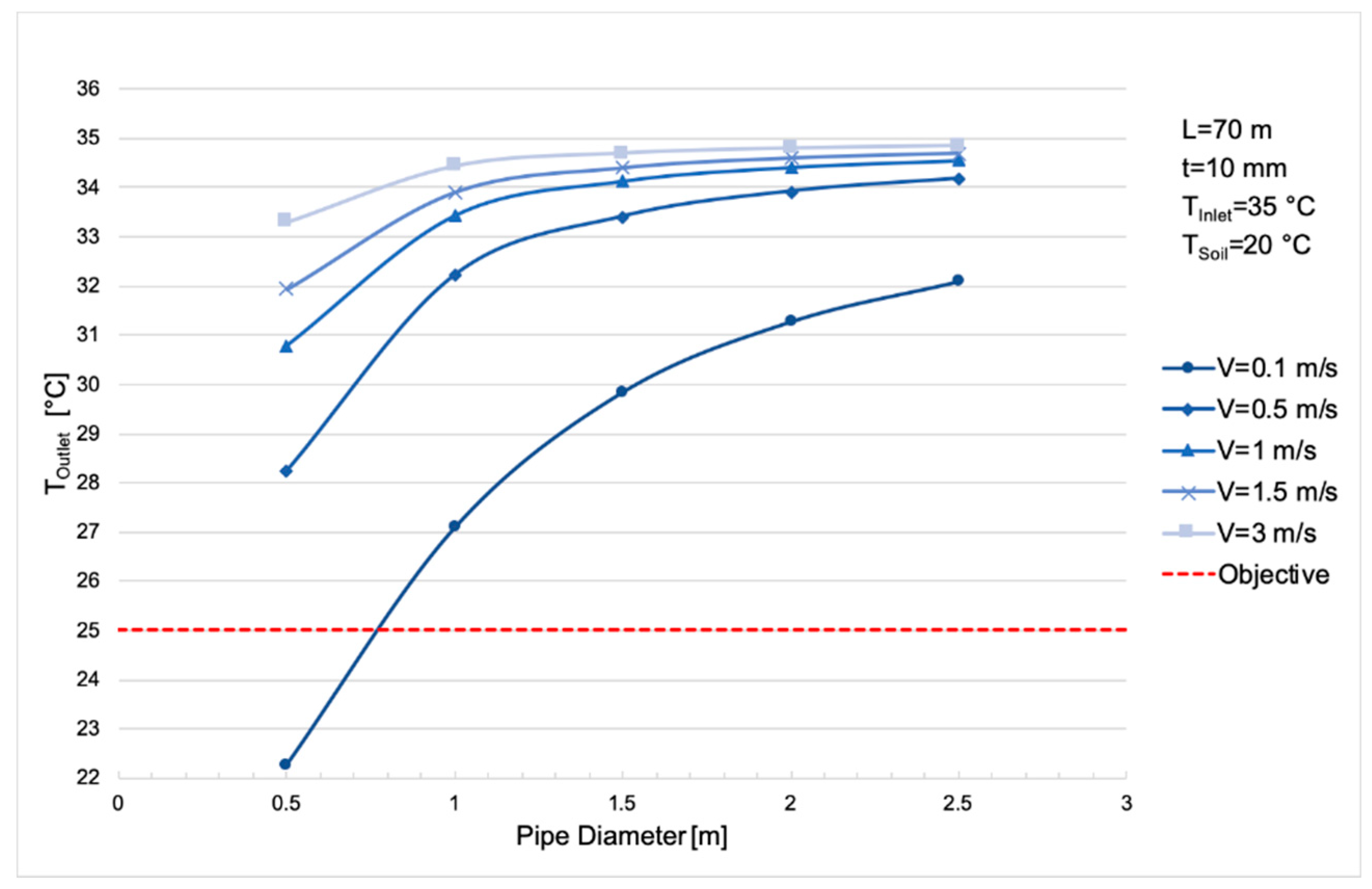
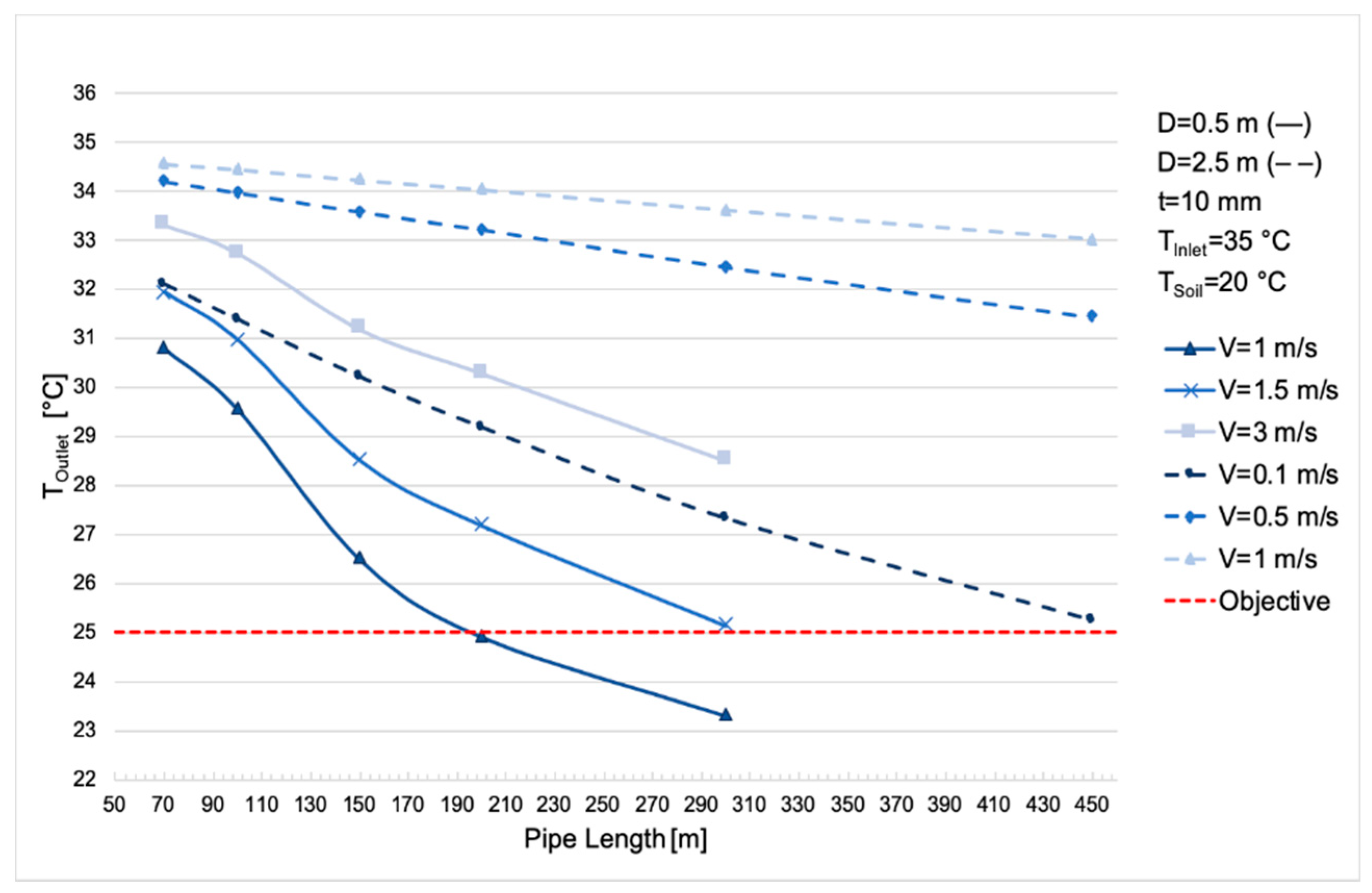
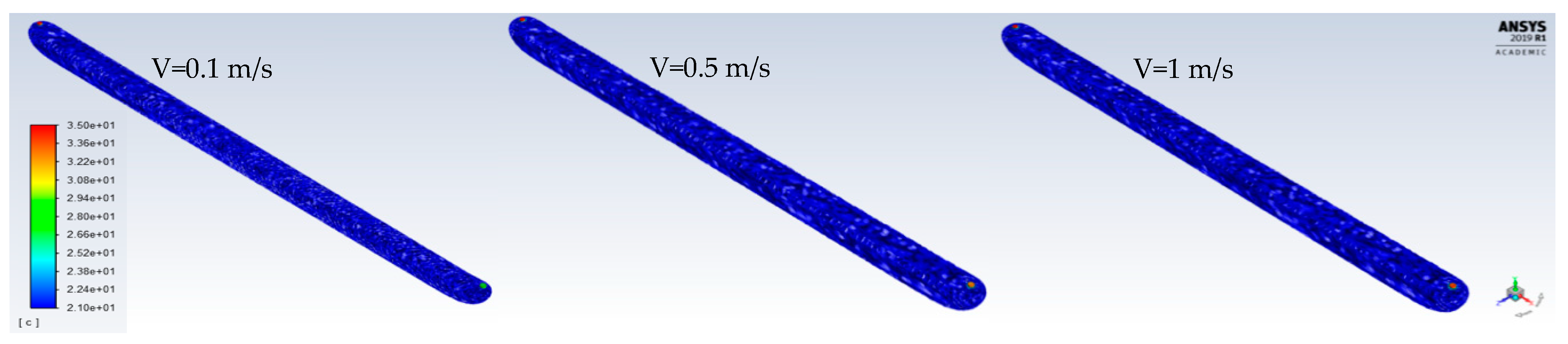
3.1. Pipe Diameter
3.2. Pipe Number and Length
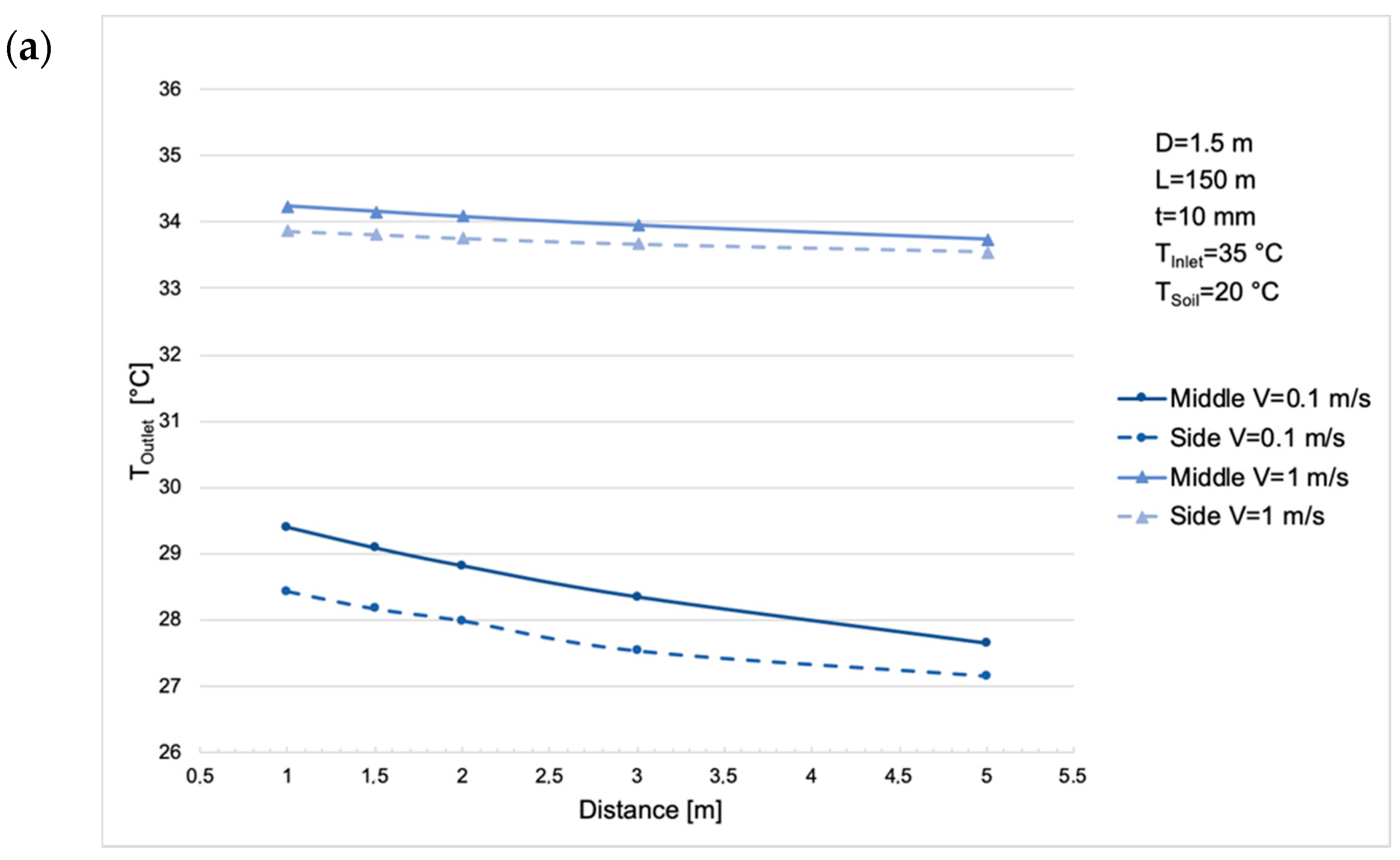
3.3. Pipe Thickness, Pipe Material, and Distance between Pipes
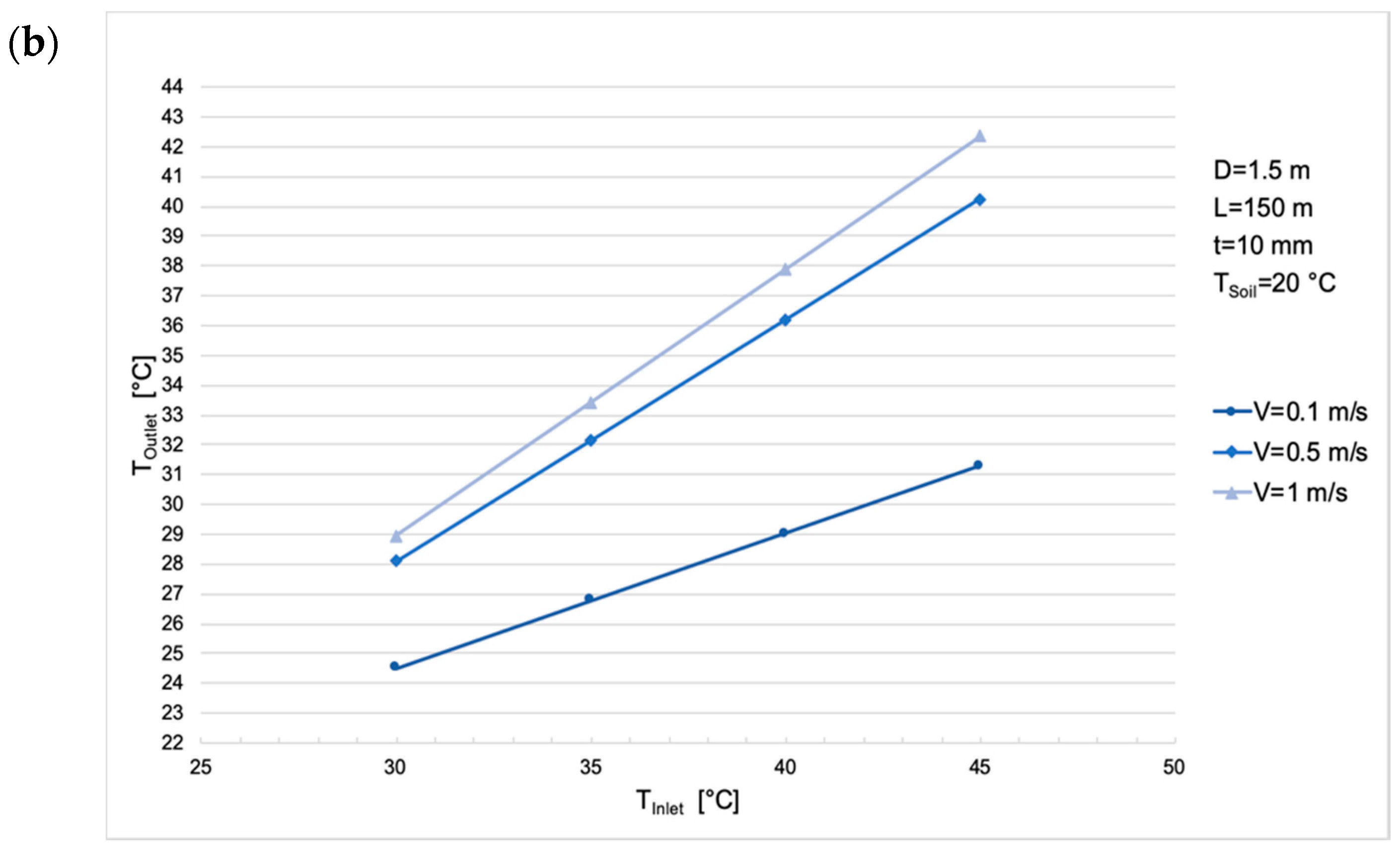
3.4. Inlet and Pipe Wall Temperature
3.5. Soil Temperature
3.6. Viability of the Design
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Three-Dimensional Numerical Modelling
References
- Global Issues: Climate Change. United Nations. Available online: https://www.un.org/en/sections/issues-depth/climate-change/index.html (accessed on 3 April 2019).
- Cronin, J.; Anandarajah, G.; Dessens, O. Climate change impacts on the energy system: A review of trends and gaps. Clim. Change 2018, 151, 79–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petrakopoulou, F. Elimination of water use in power plants with Earth cooling air tunnels. Memoria científico-técnica de proyectos explora convocatoria. 2017. Unpublished Work. [Google Scholar]
- Olsson, G. Water and Energy: Threats and Opportunities - Second Edition, 1st ed.; IWA Publishing: London, UK, 2015; Volume 14, ISBN 9781780406947. [Google Scholar]
- Endo, A.; Burnett, K.; Orencio, P.M.; Kumazawa, T.; Wada, C.A.; Ishii, A.; Tsurita, I.; Taniguchi, M. Methods of the water-energy-food nexus. Water (Switzerland) 2015, 7, 5806–5830. [Google Scholar] [CrossRef] [Green Version]
- The United Nations World Water Development Report 2018: Nature-Based Solutions for Water. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000261424 (accessed on 9 March 2019).
- Water for Life Cycle-Water Scarcity. United Nations, 2014. Available online: http://www.un.org/waterforlifedecade/scarcity.shtml (accessed on 9 March 2019).
- Zhou, Q.; Hanasaki, N.; Fujimori, S. Economic Consequences of Cooling Water Insufficiency in the Thermal Power Sector under Climate Change Scenarios. Energies 2018, 11, 2686. [Google Scholar] [CrossRef] [Green Version]
- Macknick, J.; Newmark, R.; Heath, G.; Hallett, K.C. A Review of Operational Water Consumption and Withdrawal Factors for Electricity Generating Technologies. Natl. Renew. Energy Lab. 2011. [Google Scholar]
- Packman, A.I.; Pan, S.-Y.; Chiang, P.-C.; Snyder, S.W.; Lin, Y.J. Cooling water use in thermoelectric power generation and its associated challenges for addressing water-energy nexus. Water-Energy Nexus 2018, 1, 26–41. [Google Scholar]
- Delgado, A. Water for thermal power plants: Understanding a piece of the water energy nexus. Glob. Water Forum 2015. Available online: http://www.globalwaterforum.org/2015/06/22/water-for-thermal-power-plants-understanding-a-piece-of-the-water-energy-nexus/ (accessed on 13 March 2013).
- Kablouti, G. Cost of Water Use: A Driver of Future Investments into Water-efficient Thermal Power Plants? Aquat. Procedia 2015, 5, 31–43. [Google Scholar] [CrossRef]
- Lubega, W.N.; Stillwell, A.S. Analyzing the economic value of thermal power plant cooling water consumption. Water Resour. Econ. 2019, 27, 100137. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Voisin, N.; Fazio, J.; Hua, D.; Jourabchi, M. Compound climate events transform electrical power shortfall risk in the Pacific Northwest. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef]
- Van Vliet, M.T.H.; Yearsley, J.R.; Ludwig, F.; Vögele, S.; Lettenmaier, D.P.; Kabat, P. Vulnerability of US and European electricity supply to climate change. Nat. Clim. Chang. 2012, 2, 676–681. [Google Scholar] [CrossRef]
- Lin, L.; Chen, Y. Evaluation of Future Water Use for Electricity Generation under Different Energy Development Scenarios in China. Sustainability 2017, 10, 30. [Google Scholar] [CrossRef] [Green Version]
- Stark, A.K.; Klausner, J.F. An R&D Strategy to Decouple Energy from Water. Joule 2017, 1, 416–420. [Google Scholar]
- Elberry, M.F.; Elsayed, A.A.; Teamah, M.A.; Abdel-Rahman, A.A.; Elsafty, A.F. Performance improvement of power plants using absorption cooling system. Alexandria Eng. J. 2018, 57, 2679–2686. [Google Scholar] [CrossRef]
- Yang, L.; Du, X.; Wu, T.; Ge, Z.; Wei, H. Cooling water mass flow optimization for indirect dry cooling system of thermal power unit under variable output load. Int. J. Heat Mass Transf. 2018, 133, 1–10. [Google Scholar]
- Ma, J.; Wang, Y.; Feng, X.; Xu, D. Synthesis cooling water system with air coolers. Chem. Eng. Res. Des. 2018, 131, 643–655. [Google Scholar] [CrossRef]
- Liu, H.; Weibel, J.; Groll, E. Performance analysis of an updraft tower system for dry cooling in large-scale power plants. Energies 2017, 10, 1812. [Google Scholar] [CrossRef] [Green Version]
- United Nations Environment Programme. Available online: https://www.unenvironment.org/explore-topics/energy/about-energy#ourwork (accessed on 24 March 2019).
- CORDIS-EUROPEAN COMISSION. Available online: https://cordis.europa.eu/en (accessed on 24 March 2019).
- Materials Technologies for performance improvement of Cooling Systems in Power Plants. CORDIS HORIZON 2020-EUROPEAN COMISSION, 2017. Available online: https://cordis.europa.eu/project/rcn/200817/factsheet/es (accessed on 23 March 2019).
- Aresti, L.; Christodoulides, P.; Florides, G. A review of the design aspects of ground heat exchangers. Renew. Sustain. Energy Rev. 2018, 92, 757–773. [Google Scholar] [CrossRef]
- Vidhi, R.; Goswami, D.Y.; Stefanakos, E. Supercritical rankine cycle coupled with ground cooling for low temperature power generation. Energy Procedia 2014, 57, 524–532. [Google Scholar] [CrossRef] [Green Version]
- Jakhar, S.; Soni, M.S.; Gakkhar, N. Performance Analysis of Earth Water Heat Exchanger for Concentrating Photovoltaic Cooling. Energy Procedia 2015, 90, 145–153. [Google Scholar] [CrossRef]
- Vidhi, R. A Review of Underground Soil and Night Sky as Passive Heat Sink: Design Configurations and Models. Energies 2018, 11, 2941. [Google Scholar] [CrossRef] [Green Version]
- Bisoniya, T.S.; Kumar, A.; Baredar, P. Study on Calculation Models of Earth-Air Heat Exchanger Systems. J. Energy 2014, 2014, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Amaludin, A.; Darius, D.; Misaran, M.S.; Rahman, M.M.; Ismail, M.A. Working parameters affecting earth-air heat exchanger (EAHE) system performance for passive cooling: A review. IOP Conf. Ser. Mater. Sci. Eng. 2017, 217, 012021. [Google Scholar]
- Agrawal, K.K.; Bhardwaj, M.; Misra, R.; Das Agrawal, G.; Bansal, V. Optimization of operating parameters of earth air tunnel heat exchanger for space cooling: Taguchi method approach. Geotherm. Energy 2018, 6, 1–17. [Google Scholar] [CrossRef]
- Singh, R.; Sawhney, R.L.; Lazarus, I.J.; Kishore, V.V.N. Recent advancements in earth air tunnel heat exchanger (EATHE) system for indoor thermal comfort application: A review. Renew. Sustain. Energy Rev. 2018, 82, 2162–2185. [Google Scholar] [CrossRef]
- Bisoniya, T.S. Design of earth–air heat exchanger system. Geotherm. Energy 2015, 3. [Google Scholar] [CrossRef] [Green Version]
- Bordoloi, N.; Sharma, A.; Nautiyal, H.; Goel, V. An intense review on the latest advancements of Earth Air Heat Exchangers. Renew. Sustain. Energy Rev. 2018, 89, 261–280. [Google Scholar] [CrossRef]
- Bansal, V.; Mishra, R.; Das Agarwal, G.; Mathur, J. Performance analysis of integrated earth-air-tunnel-evaporative cooling system in hot and dry climate. Energy Build. 2012, 47, 525–532. [Google Scholar] [CrossRef]
- Chen, J.; Qiao, W.; Xue, Q.; Zheng, H.; An, E. Research on ground-coupled heat exchangers. Int. J. Low-Carbon Technol. 2010, 5, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Mathur, A. Comparative study of straight and spiral earth air tunnel heat exchanger system operated in cooling and heating modes. Renew. Energy 2017, 108, 474–487. [Google Scholar]
- Soni, S.K.; Pandey, M.; Bartaria, V.N. Ground coupled heat exchangers: A review and applications. Renew. Sustain. Energy Rev. 2015, 47, 83–92. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Robinson, A.; Loizidou, M. Simulation and evaluation of a hybrid concentrating-solar and wind power plant for energy autonomy on islands. Renew. Energy 2016, 96, 863–871. [Google Scholar] [CrossRef]
- Phoenix Analysis and Design Technologies ANSYS Meshing Advanced Techniques PADT Lunch & Learn Series. 2016. Available online: https://docplayer.net/48950759-Ansys-meshing-advanced-techniques.html (accessed on 1 July 2019).
- Barakat, S.; Ramzy, A.; Hamed, A.M.; El Emam, S.H. Enhancement of gas turbine power output using earth to air heat exchanger (EAHE) cooling system. Energy Convers. Manag. 2016, 111, 137–146. [Google Scholar] [CrossRef]
- Márquez, J.M.A.; Bohórquez, M.Á.M.; Melgar, S.G. Ground thermal diffusivity calculation by direct soil temperature measurement. application to very low enthalpy geothermal energy systems. Sensors (Switzerland) 2016, 16. [Google Scholar]
- ANSYS Sustainable Design - Excellence in Engineering Simulation. 2011, Volume V. Available online: http://grupossc.com/pdf/publicacion_5611517286.pdf#page=43 (accessed on 14 September 2019).
- Bansal, V.; Misra, R.; Agrawal, G.D.; Mathur, J. Performance analysis of earth-pipe-air heat exchanger for summer cooling. Energy Build. 2010, 42, 645–648. [Google Scholar] [CrossRef]
- Belatrache, D.; Bentouba, S.; Bourouis, M. Numerical analysis of earth air heat exchangers at operating conditions in arid climates. Int. J. Hydrogen Energy 2017, 42, 8898–8904. [Google Scholar] [CrossRef]
- Benhammou, M.; Draoui, B. Parametric study on thermal performance of earth-to-air heat exchanger used for cooling of buildings. Renew. Sustain. Energy Rev. 2015, 44, 348–355. [Google Scholar] [CrossRef]
- Hasan, M.I.; Noori, S.W. Numerical Investigation of Earth to Air Heat Exchanger for Cooling and Heating Applications. In Proceedings of the 3rd Int. Sci. Conf. Renew. energy (ISCRE2018), Southreernne Tech. Univ., Basrah, Iraq, 24–25 March 2018; pp. 1–11. [Google Scholar]
- Agrawal, K.K.; Agrawal, G.D.; Misra, R.; Bhardwaj, M.; Jamuwa, D.K. A review on effect of geometrical, flow and soil properties on the performance of Earth air tunnel heat exchanger. Energy Build. 2018, 176, 120–138. [Google Scholar] [CrossRef]
- TorresolEnergy-Gemasolar. Available online: https://torresolenergy.com/gemasolar/ (accessed on 30 September 2019).
- Tarifa de Precios Tuberías plásticas Edición 01-CEMAT Grupo Industrial. Available online: https://cemat.es/wp-content/uploads/2014/01/tarifa-tuberias-plasticas-012014.pdf (accessed on 7 October 2019).
- Fazlikhani, F.; Goudarzi, H.; Solgi, E. Numerical analysis of the efficiency of earth to air heat exchange systems in cold and hot-arid climates. Energy Convers. Manag. 2017, 148, 78–89. [Google Scholar] [CrossRef]
- Bordoloi, N.; Sharma, A. Performance analysis of EAHE for different pipe geometries and pipe materials using CFD. Indian J. Sci. Res. 2017, 17, 181–189. [Google Scholar]
- Kaushal, M.; Dhiman, P.; Singh, S.; Patel, H. Finite volume and response surface methodology based performance prediction and optimization of a hybrid earth to air tunnel heat exchanger. Energy Build. 2015, 104, 25–35. [Google Scholar] [CrossRef]
- Shear-Stress Transport (SST) k-w Model - ANSYS FLUENT 12.0/12.1 Documentation. Available online: http://www.afs.enea.it/project/neptunius/docs/fluent/html/th/node67.htm (accessed on 10 September 2019).

| Material | Density [kg m−1] | Specific Heat [J kg−1 K−1] | Thermal Conductivity [W m−1 K−1] |
|---|---|---|---|
| Air | 1.225 | 1006 | 0.02 |
| PVC | 1380 | 900 | 0.16 |
| Soil | 2050 | 1840 | 0.52 |
| Boundary Condition | Type | Parameter | Value | Material |
|---|---|---|---|---|
| Inlet | Velocity-Inlet | Velocity Temperature | 0.1–3 m s−1 Ambient | Air |
| Air | Interior | - | - | Air |
| Exterior Pipe Wall | Wall | Thickness Temperature | 10 mm Ambient | PVC |
| Pipe Wall | Wall-Coupled | Thickness | 10 mm | PVC |
| Outlet | Pressure-Outlet | Gauge pressure | 8675 Pa | Air |
| Soil | Interior | - | - | Soil |
| Soil Wall | Wall | Temperature | 20 °C | Soil |
| Present Model | Bansal et al. (2012) | Belatrache et al. (2017) | Barakat et al. (2016) | Benhammou et al. (2015) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Relative Error [%] | [°C] | Relative Error [%] | Relative Error [%] | Relative Error [%] | Relative Error [%] | ||||||||
| 2 | 43.4 | 31.42 | 18.04 | 16.60 | 8.67 | 33.10 | 5.08 | 33.40 | 5.93 | 31.23 | 0.61 | 30.05 | 4.56 |
| 3 | 42.5 | 33.07 | 36.77 | 33.77 | 8.88 | 33.10 | 0.09 | 35.30 | 6.32 | 32.36 | 2.19 | 31.66 | 4.45 |
| 4 | 42.3 | 34.36 | 61.15 | 56.06 | 9.08 | 33.50 | 2.57 | 36.60 | 6.12 | 33.35 | 3.03 | 33.04 | 4.00 |
| 5 | 42.2 | 35.34 | 90.90 | 83.19 | 9.27 | 34.20 | 3.33 | 37.40 | 5.51 | 34.16 | 3.75 | 34.10 | 3.64 |
| Material | Density [kg m−1] | Specific Heat [J kg−1 K−1] | Thermal Conductivity [W m−1 K−1] |
|---|---|---|---|
| Air (30 °C and 60% RH) | 1.153 | 1021 | 0.0265 |
| PVC | 1380 | 900 | 0.16 |
| Soil | 1868 | 1995.4 | 1.74 |
| Parameter | Value |
|---|---|
| Pipe depth [m] | 5 |
| Pipe inner diameter [m] | 0.35 |
| Pipe length [m] | 85 |
| Air inlet velocity [m s−1] | 4.5 |
| Soil temperature [°C] | 25 |
| Air inlet temperature [°C] | 40 |
| Present Model | Barakat et al. (2016) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Relative Error [%] | Relative Error [%] | |||||||||
| 25 | 0.35 | 4.4 | 25 | 40 | 36.23 | 27.42 | 24.53 | 11.78 | 35.50 | 2.06 |
| 75 | 32.89 | 59.45 | 54.67 | 8.74 | 30.00 | 9.63 | ||||
| 125 | 29.06 | 94.92 | 84.81 | 11.92 | 27.00 | 7.63 | ||||
| 85 | 0.2 | 4.5 | 25 | 40 | 25.32 | 142.32 | 124.84 | 14.00 | 25.50 | 0.71 |
| 0.4 | 33.51 | 58.77 | 53.77 | 9.30 | 30.00 | 11.70 | ||||
| 0.6 | 36.13 | 35.34 | 33.02 | 7.03 | 33.00 | 9.48 | ||||
| 85 | 0.35 | 2 | 25 | 40 | 27.32 | 15.76 | 14.92 | 5.63 | 26.50 | 3.09 |
| 4 | 30.97 | 54.57 | 51.19 | 6.60 | 28.80 | 7.53 | ||||
| 6 | 33.38 | 113.50 | 105.84 | 7.24 | 30.30 | 10.17 | ||||
| 0.5 | 0.1 | 0.0241 | 164,480 | 22.28 | 0.05 |
| 0.5 | 0.1203 | 32,896 | 28.25 | 0.81 | |
| 1 | 0.2405 | 16,448 | 30.79 | 2.71 | |
| 1.5 | 0.3608 | 10,965 | 31.93 | 5.56 | |
| 3 | 0.7216 | 5483 | 33.31 | 19.19 | |
| 1 | 0.1 | 0.0962 | 41,120 | 27.09 | 0.02 |
| 0.5 | 0.4811 | 8224 | 32.22 | 0.34 | |
| 1 | 0.9621 | 4112 | 33.43 | 1.18 | |
| 1.5 | 1.4432 | 2741 | 33.90 | 2.45 | |
| 3 | 2.8863 | 1371 | 34.43 | 8.63 | |
| 1.5 | 0.1 | 0.2165 | 18,276 | 29.84 | 0.01 |
| 0.5 | 1.0824 | 3655 | 33.41 | 0.23 | |
| 1 | 2.1648 | 1828 | 34.13 | 0.80 | |
| 1.5 | 3.2471 | 1218 | 34.40 | 1.67 | |
| 3 | 6.4943 | 609 | 34.69 | 5.95 | |
| 2 | 0.1 | 0.3848 | 10,280 | 31.27 | 0.01 |
| 0.5 | 1.9242 | 2056 | 33.92 | 0.17 | |
| 1 | 3.8485 | 1028 | 34.41 | 0.59 | |
| 1.5 | 5.7727 | 685 | 34.60 | 1.24 | |
| 3 | 11.5454 | 343 | 34.79 | 4.45 | |
| 2.5 | 0.1 | 0.6013 | 6579 | 32.09 | 0 |
| 0.5 | 3.0066 | 1316 | 34.18 | 0.14 | |
| 1 | 6.0132 | 658 | 34.55 | 0.50 | |
| 1.5 | 9.0198 | 439 | 34.70 | 1.07 | |
| 3 | 18.0396 | 219 | 34.84 | 3.90 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de la Rocha Camba, E.; Petrakopoulou, F. Earth-Cooling Air Tunnels for Thermal Power Plants: Initial Design by CFD Modelling. Energies 2020, 13, 797. https://doi.org/10.3390/en13040797
de la Rocha Camba E, Petrakopoulou F. Earth-Cooling Air Tunnels for Thermal Power Plants: Initial Design by CFD Modelling. Energies. 2020; 13(4):797. https://doi.org/10.3390/en13040797
Chicago/Turabian Stylede la Rocha Camba, Eduardo, and Fontina Petrakopoulou. 2020. "Earth-Cooling Air Tunnels for Thermal Power Plants: Initial Design by CFD Modelling" Energies 13, no. 4: 797. https://doi.org/10.3390/en13040797
APA Stylede la Rocha Camba, E., & Petrakopoulou, F. (2020). Earth-Cooling Air Tunnels for Thermal Power Plants: Initial Design by CFD Modelling. Energies, 13(4), 797. https://doi.org/10.3390/en13040797




