Effects of Temperature on the Flow and Heat Transfer in Gel Fuels: A Numerical Study
Abstract
:1. Introduction
2. Methods
2.1. Mathematical Approach
2.1.1. Governing Equations
Conservation of Mass:
Conservation of Momentum:
Conservation of Energy:
2.1.2. Constitutive Equation for the Stress Tensor and Heat Flux Vector
Stress Tensor:
Internal Energy:
Heat Flux Vector:
2.1.3. Expanded Form of the Governing Equations
2.2. Parameters in the Constitutive Equation for the Stress Tensor
3. Problem Descriptions
4. Results and Discussion
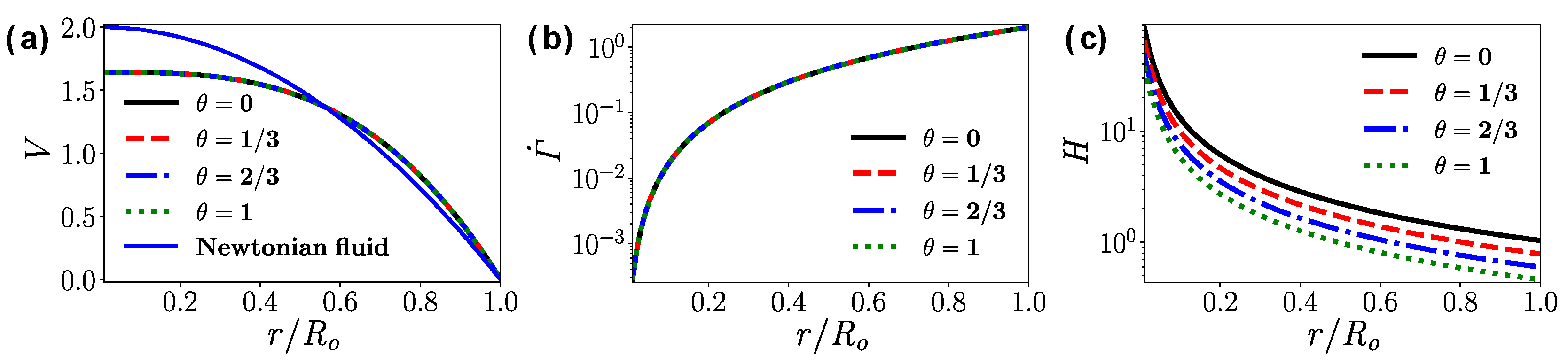
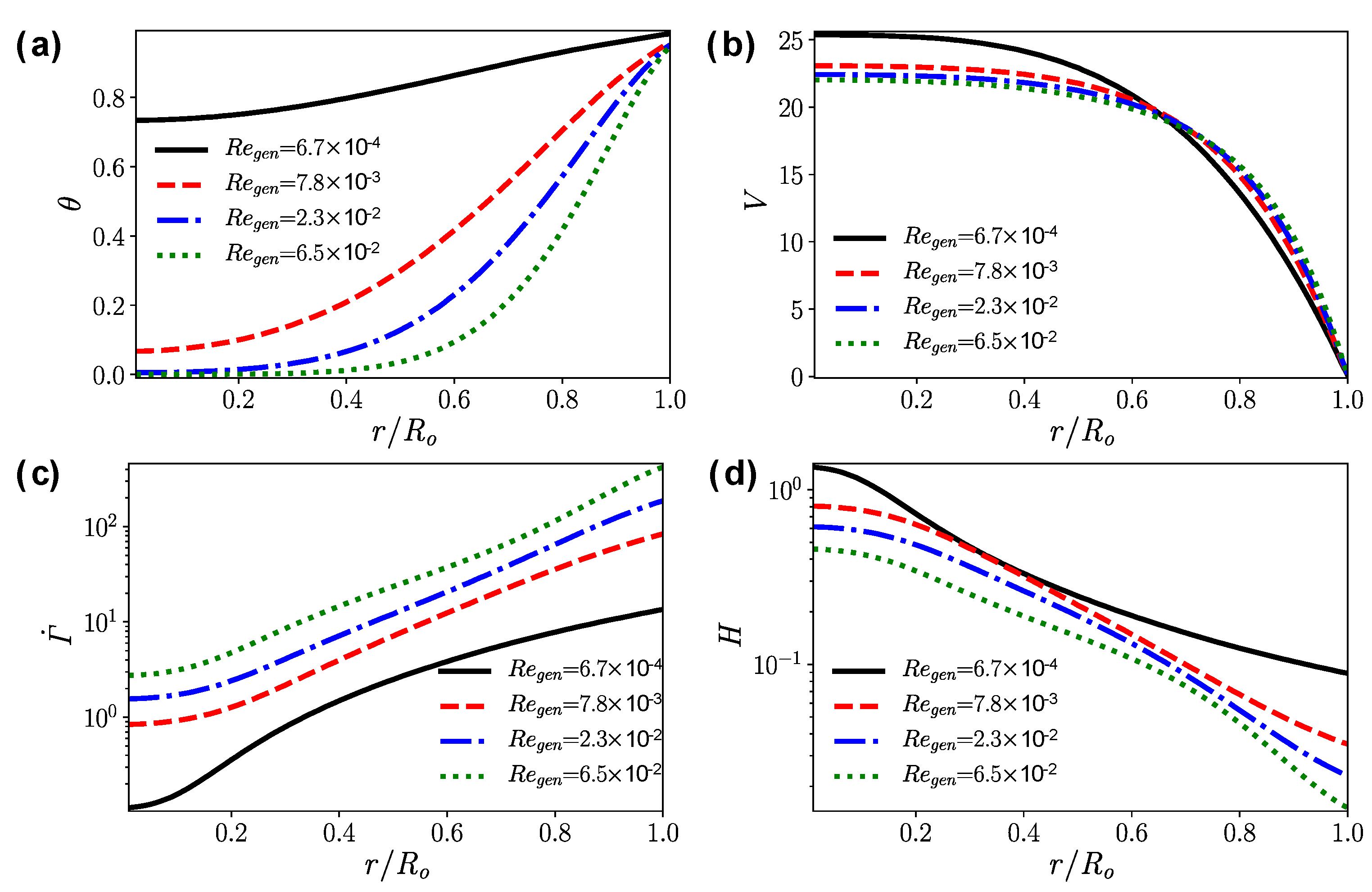
4.1. Straight Pipe
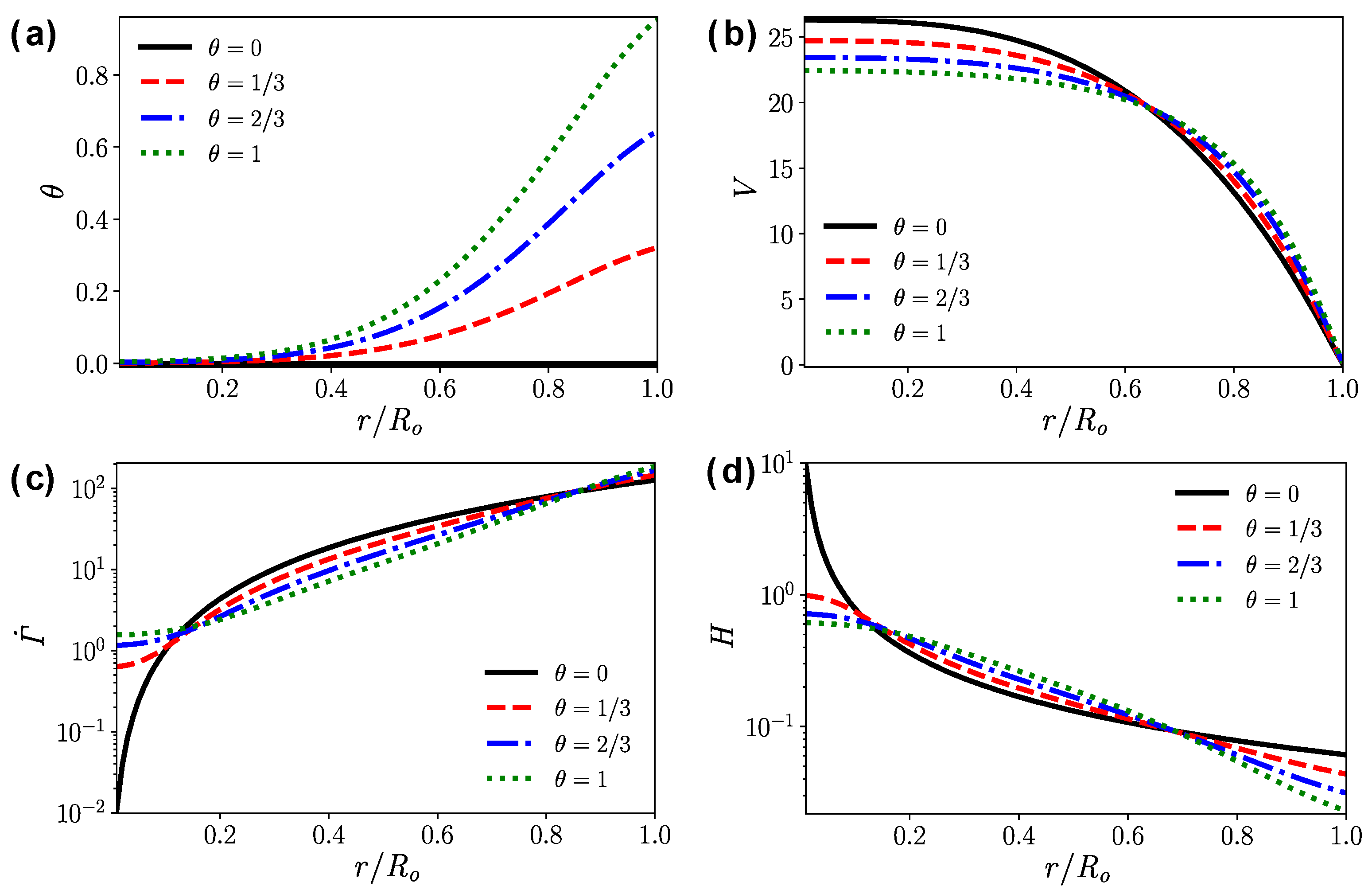
4.2. Tapered Injector
5. Conclusions
- (a)
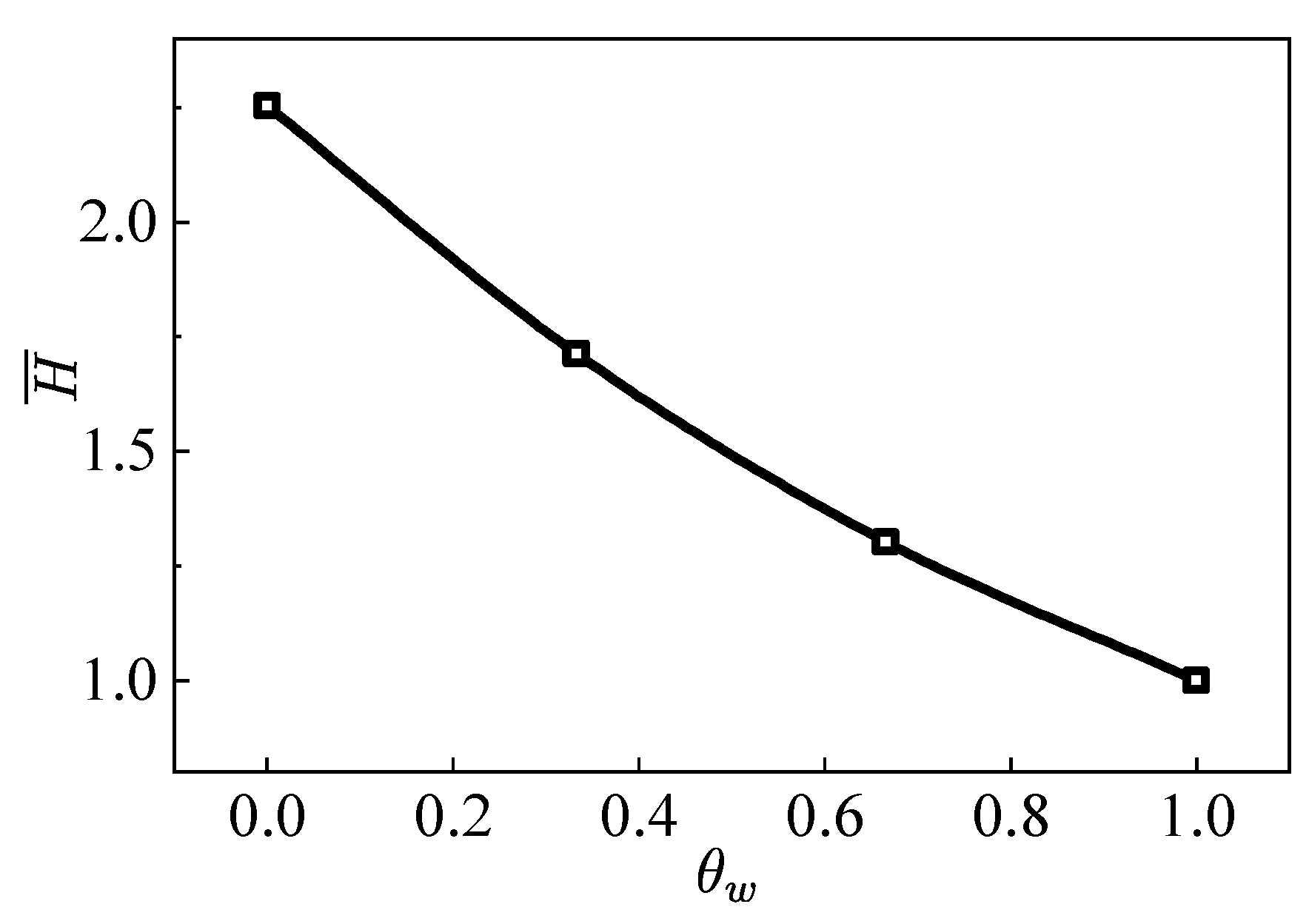
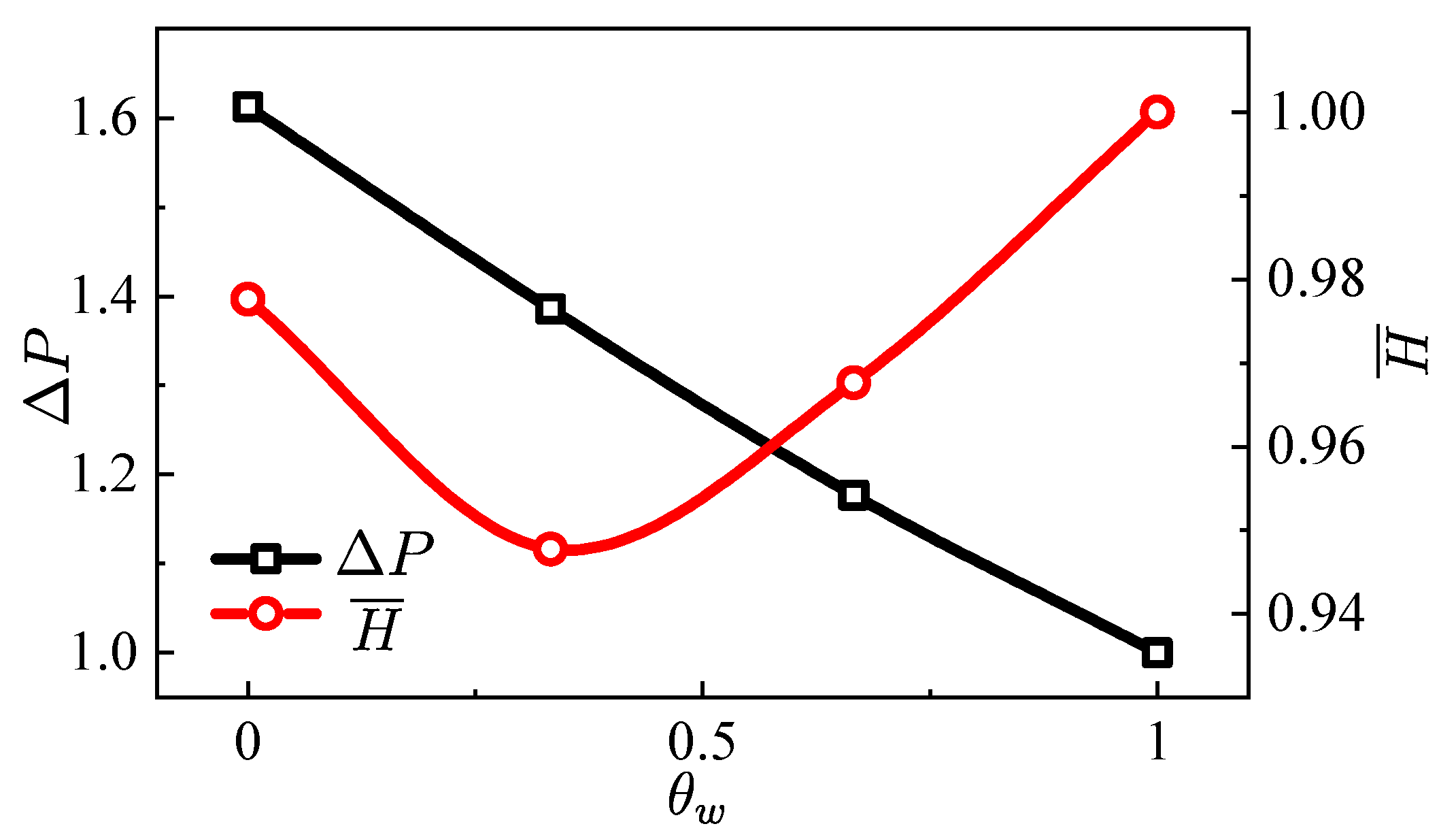
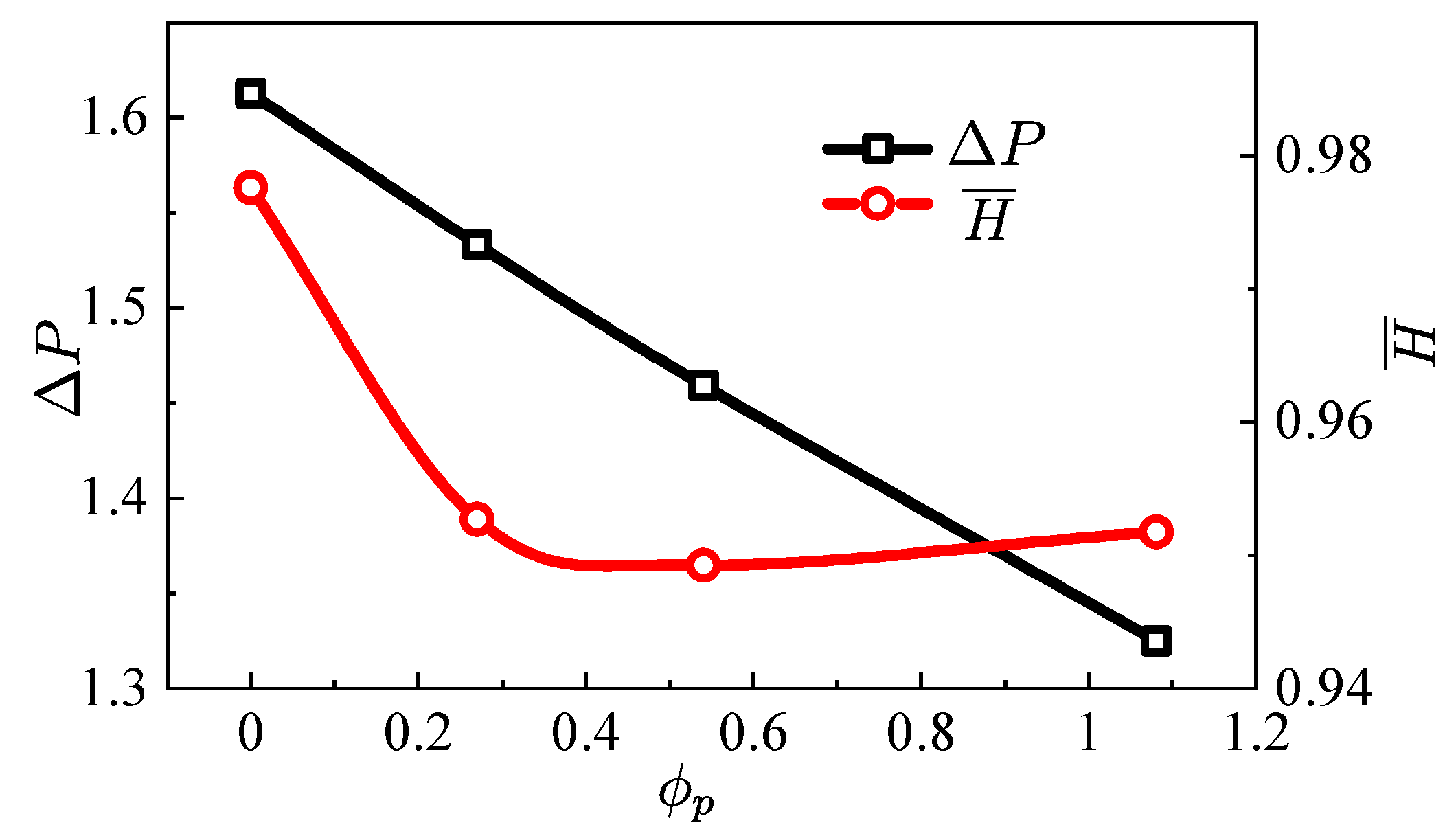
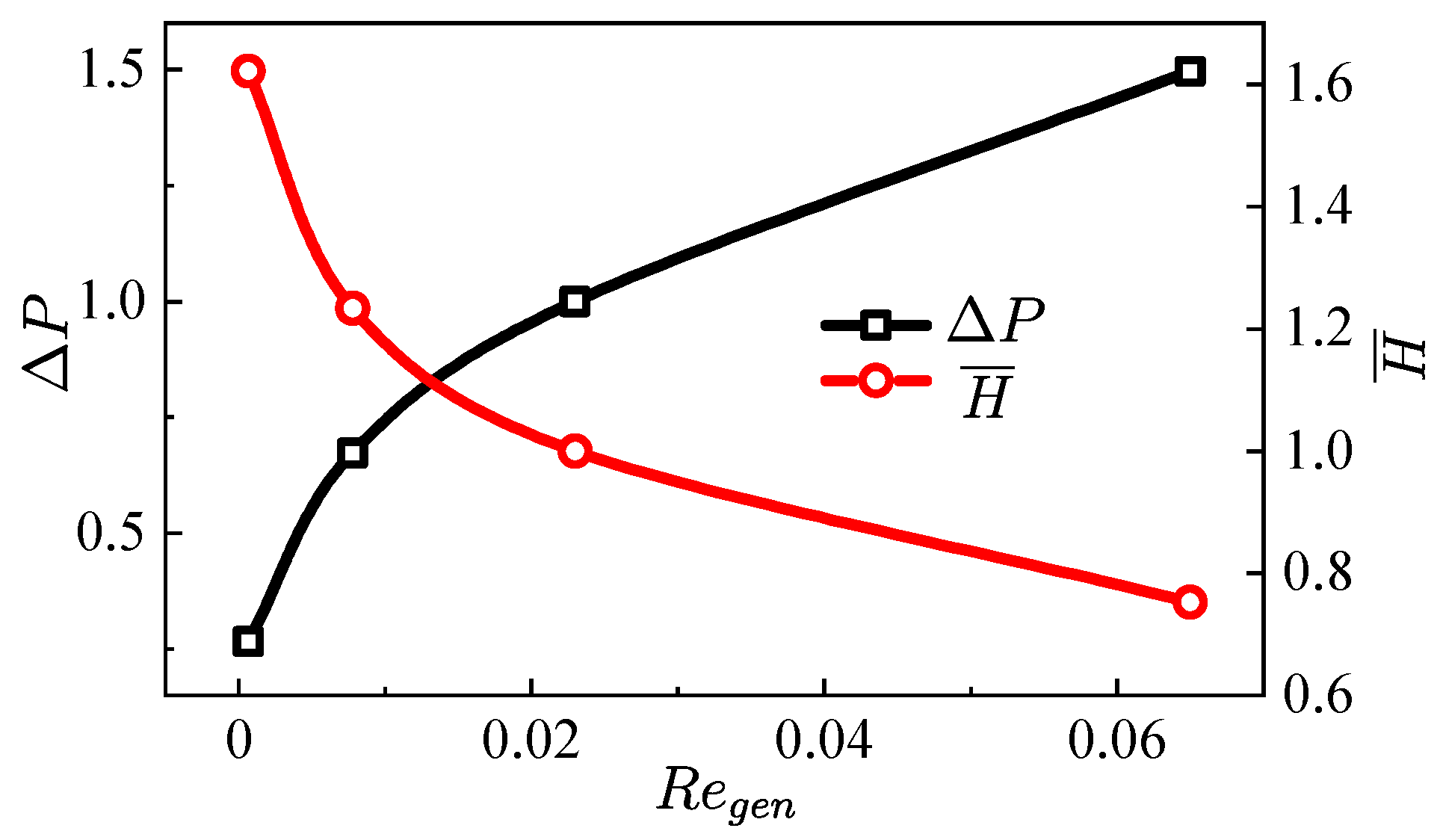
- For the fully developed flow in the straight pipe, the apparent viscosity decreases significantly with the increase of the wall temperature. For the simulation reported here, the mean apparent viscosity when is only 44% of the case when .
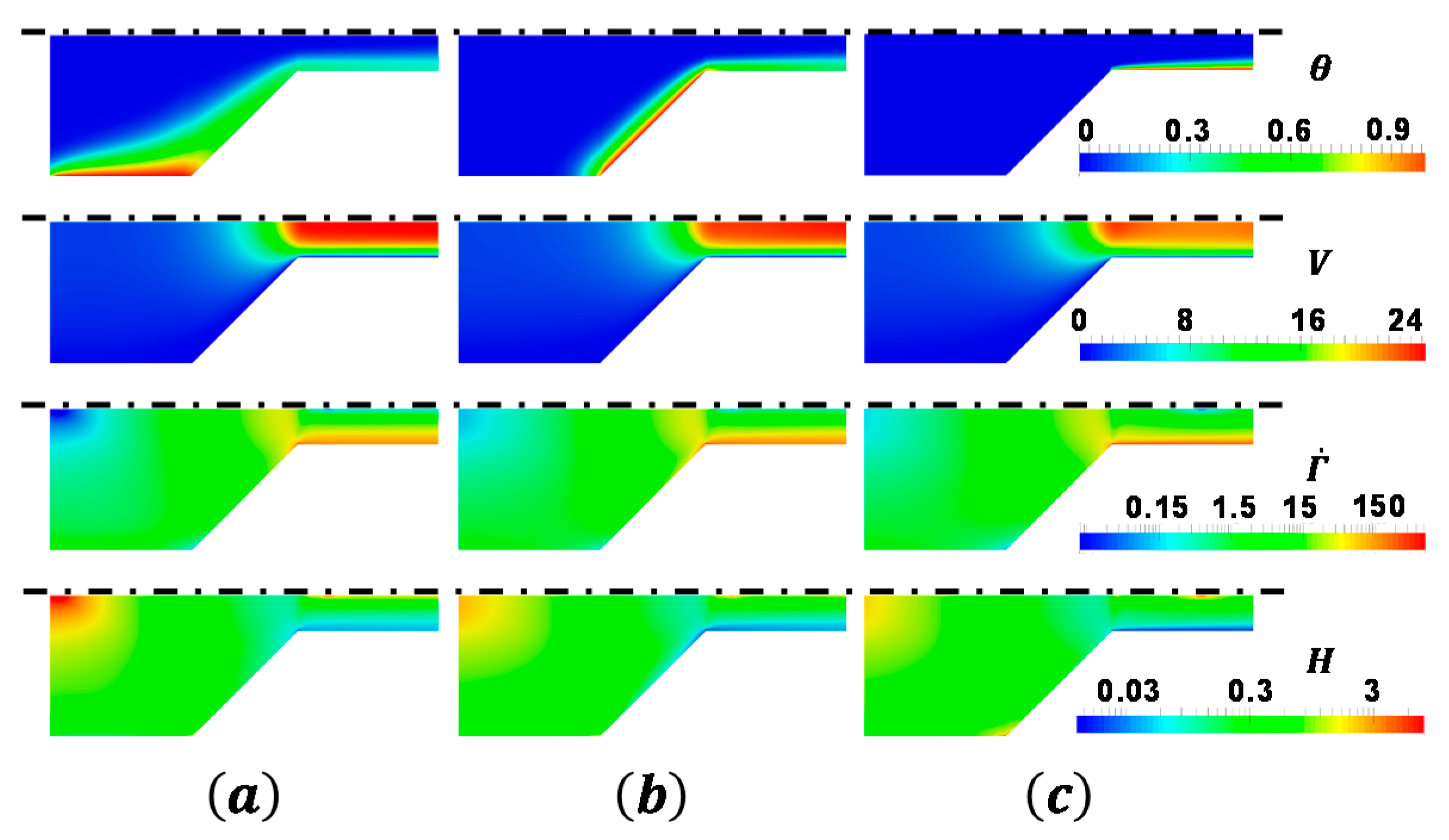
- (b)
- In the tapered injector, the gel is not fully heated before flowing out of the injector. The temperature gradient has a significant effect on the flow field. The larger the temperature gradient is, the blunter the velocity profile is.
- (c)
- Higher wall temperature significantly reduces the near-wall apparent viscosity, but it has the opposite effect on the apparent viscosity far away from the hot wall. In terms of the mean outlet apparent viscosity, the influence of temperature on the viscosity reduction is less than 5%.
- (d)
- Wall heating can greatly reduce the pressure drop in the transport system. In the range of the wall temperatures studied here, the pressure drop of the heated injector was reduced up to 38% when compared with the unheated condition.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| consistency index () | |
| power-law exponent | |
| velocity vector () | |
| reference velocity () | |
| dimensionless velocity | |
| stress tensor () | |
| time () | |
| body force vector () | |
| gradient of velocity () | |
| heat flux vector () | |
| internal energy density () | |
| identity tensor | |
| pressure () | |
| dimensionless pressure | |
| symmetric part of the velocity gradient () | |
| temperature () | |
| , | reference temperatures () |
| dimensionless length of straight pipe | |
| temperature index () | |
| heat capacity () | |
| thermal conductivity () | |
| reference length scale () | |
| dimensionless radius of straight pipe | |
| dimensionless radius of the inlet of injector | |
| dimensionless radius of the outlet of injector | |
| Reynolds number | |
| generalized Reynolds number | |
| dimensionless number related to the viscous dissipation | |
| Lewis number | |
| dimensionless position vector | |
| position vector () | |
| Greek symbols | |
| density () | |
| shear rate () | |
| dynamic viscosity () | |
| reference viscosity () | |
| mean apparent viscosity () | |
| dimensionless temperature | |
| dimensionless inlet temperature | |
| dimensionless wall temperature | |
| convergence angle of injector () | |
| dimensionless time | |
| dimensionless apparent viscosity | |
| dimensionless mean apparent viscosity | |
| dimensionless heat flux | |
| dimensionless shear rate |
References
- Ciezki, H.K.; Negri, M.; Weiser, V.; Naumann, K.W.; Program, P.T.; Program, T.; Grund, L.; Heterogenious, H.; Group, S.; Grund, L.; et al. Overview of the German Gel Propulsion Technology. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; pp. 1–16. [Google Scholar]
- Cao, Q.; Liao, W.; Wu, W.-T.; Feng, F. Combustion characteristics of inorganic kerosene gel droplet with fumed silica as gellant. Exp. Therm. Fluid Sci. 2019, 103, 377–384. [Google Scholar] [CrossRef]
- Natan, B.; Rahimi, S. The status of gel propellants in year 2000. Int. J. Energetic Mater. Chem. Propuls. 2009, 5, 172–194. [Google Scholar] [CrossRef]
- Arnold, R.; Anderson, W. Droplet burning of JP-8/Silica gels. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; pp. 1–12. [Google Scholar]
- Yang, L.J.; Fu, Q.F.; Qu, Y.Y.; Zhang, W.; Du, M.L.; Xu, B.R. Spray characteristics of gelled propellants in swirl injectors. Fuel 2012, 97, 253–261. [Google Scholar] [CrossRef]
- Nahamoni, G.; Natan, B.; Nahamoni, G.; Natan, B. Investigation of the combustion process of gel propellants. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997; p. 2973. [Google Scholar]
- Ciezki, H.K.; Naumann, K.W.; Weiser, V. Status of Gel Propulsion in the Year 2010 with a Special View on the German Activities. In Proceedings of the Dtsch. Luft-Und Raumfahrtkongress 2010, Hamburg, Germany, 31 August–2 September 2010. [Google Scholar]
- Gafni, G.; Kuznetsov, A.; Har-Lev, D.; Natan, B. Experimental Investigation of a Ramjet Combustor Using an Aluminized Gel Fuel. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; p. 3748. [Google Scholar]
- Matsibeker, E.; Natan, B. Numerical Solution of the Flowfield in an Aluminized Gel Fuel Ramjet. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint PropulsionConference, San Jose, CA, USA, 14–17 July 2013; p. 3976. [Google Scholar]
- Natan, B.; Haddad, A.; Arieli, R. Performance assessments of a boron containing gel fuel ramjet. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 1421. [Google Scholar]
- Doi, M. Explanation for the 3.4-power law for viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Phys. Ed. 1983, 21, 667–684. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3.4 power law of viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Lett. Ed. 1981, 19, 265–273. [Google Scholar] [CrossRef]
- Krieger, I.M. Rheology of monodisperse latices. Adv. Colloid Interface Sci. 1972, 3, 111–136. [Google Scholar] [CrossRef]
- Rahimi, S.; Natan, B. Numerical solution of the flow of power-law gel propellants in converging injectors. Propellants Explos. Pyrotech. 2000, 25, 203–212. [Google Scholar] [CrossRef]
- Rahimi, S.; Natant, B. The Injection Process of Gel fuels. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997. [Google Scholar]
- Rahimi, S.; Natan, B. Flow of gel fuels in tapered injectors. J. Propuls. Power 2000, 16, 458–464. [Google Scholar] [CrossRef]
- Bo, Z.; Mengzheng, Z. Numerical simulation of tube flow characteristics for gel simulation. J. Rocket Propuls. 2008, 34, 27–34. [Google Scholar]
- Yoon, C.; Heister, S.D.; Xia, G.; Merkle, C.L. Numerical modeling of injection of shear-thinning gel propellants through plain-orifice atomizer. J. Propuls. Power 2011, 27, 944–954. [Google Scholar] [CrossRef]
- Cao, Q.-L.; Massoudi, M.; Liao, W.-H.; Feng, F.; Wu, W.-T. Flow Characteristics of Water-HPC Gel in Converging Tubes and Tapered Injectors. Energies 2019, 12, 1643. [Google Scholar] [CrossRef] [Green Version]
- Shin, S.; Cho, Y.I. Laminar heat transfer in a rectangular duct with a non-Newtonian fluid with temperature-dependent viscosity. Int. J. Heat Mass Transf. 1994, 37, 19–30. [Google Scholar] [CrossRef]
- Varghese, T.L.; Gaindhar, S.C.; David, J.; Jose, J.; Muthiah, R.; Rao, S.S.; Ninan, K.N.; Krishnamurthy, V.N. Developmental studies on metallised UDMH and kerosene gels. Def. Sci. J. 1995, 45, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Rahimi, S.; Peretz, A.; Natan, B. Rheological matching of gel propellants. J. Propuls. Power 2010, 26, 376–379. [Google Scholar] [CrossRef]
- Rahimi, S.; Natan, B. Atomization characteristics of gel fuels. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998; p. 3830. [Google Scholar]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Fu, Q.; Duan, R.; Cui, K.; Yang, L. Spray of gelled propellants from an impinging-jet injector under different temperatures. Aerosp. Sci. Technol. 2014, 39, 552–558. [Google Scholar] [CrossRef]
- Jyoti, B.V.S.; Baek, S.W. Rheological characterization of ethanolamine gel propellants. J. Energetic Mater. 2016, 34, 260–278. [Google Scholar] [CrossRef]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transfer 2006, 128, 240. [Google Scholar] [CrossRef]
- Wu, W.T.; Aubry, N.; Massoudi, M. Flow of granular materials modeled as a non-linear fluid. Mech. Res. Commun. 2013, 52, 62–68. [Google Scholar] [CrossRef]
- Roscoe, R. Suspensions, Flow Properties of Disperse Systems; Flow Properties of Disperse Systems; North. Holl. Publisher Company: Amsterdam, The Netherlands, 1953. [Google Scholar]
- Schowalter, W.R. Mechanics of Non-Newtonian Fluid; Pergamon Press: New York, NY, USA, 1978. [Google Scholar]
- Macosko, C.W.; Larson, R.G. Rheology: Principles, Measurements, and Applications, 1st ed.; Wiley-VCH: Weinheim, Germany, 1994. [Google Scholar]
- Carreau, P.J.; De Kee, D.C.R.; Chhabra, R.P. Rheology of Polymeric Systems: Principles and Applications Hanser; Hanser Publications: Cincinnati, OH, USA, 1997. [Google Scholar]
- Arnold, R.; Anderson, W.; Santos, P.H.S.; deRidder, M.; Campanella, O.H. Comparison of Monomethylhydrazine/hydroxypropylcellulose and Hydrocarbon/silica Gels. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 422. [Google Scholar]
- Macosko, C.W.; Krieger, I.M. Rheology: Principles, Measurements, and Applications. J. Colloid Interface Sci. 1996, 178, 382. [Google Scholar]
- Massoudi, M.; Christie, I. Effects of variable viscosity and viscous dissipation on the flow of a third grade fluid in a pipe. Int. J. Non-Linear Mech. 1995, 30, 687–699. [Google Scholar] [CrossRef]
- Winterton, R.H.S. Early study of heat transfer: Newton and Fourier. Heat Transf. Eng. 2001, 22, 3–11. [Google Scholar] [CrossRef]
- Massoudi, M. On the heat flux vector for flowing granular materials—Part I: Effective thermal conductivity and background. Math. Methods Appl. Sci. 2006, 29, 1585–1598. [Google Scholar] [CrossRef]
- Massoudi, M. On the heat flux vector for flowing granular materials—Part II: Derivation and special cases. Math. Methods Appl. Sci. 2006, 29, 1599–1613. [Google Scholar] [CrossRef]
- Zhang, M.; Che, Z.; Chen, J.; Zhao, H.; Yang, L.; Zhong, Z.; Lu, J. Experimental Determination of Thermal Conductivity of Water−Agar Gel at Different Concentrations and Temperatures. J. Chem. Eng. Data 2010, 56, 859–864. [Google Scholar] [CrossRef]
- OpenCFD. OpenFOAM Programmer’s Guide Version 2.1.0; OpenCFD, Ed.; Free Software Foundation, Inc.: Boston, MA, USA, 2011. [Google Scholar]
- Metzner, A.B.; Reed, J.C. Flow of non-newtonian fluids—Correlation of the laminar, transition, and turbulent-flow regions. Aiche J. 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Dodge, D.W.; Metzner, A.B. Turbulent flow of non-Newtonian systems. Aiche J. 1959, 5, 189–204. [Google Scholar] [CrossRef]
- Rahimi, S.; Peretz, A.; Natan, B. On Shear Rheology of Gel Propellants. Propellants Explos. Pyrotech. Int. J. Deal. Sci. Technol. Asp. Energetic Mater. 2010, 32, 165–174. [Google Scholar] [CrossRef]
- Greenshields, C.J. OpenFOAM User Guide Version 7.0; OpenFOAM Found. Ltd.: London, UK, 2019. [Google Scholar]
- Li, X.F.; Tang, G.H.; Gao, T.Y.; Tao, W.Q. Simulation of Newtonian and non-Newtonian axisymmetric flow with an axisymmetric lattice Boltzmann model. Int. J. Mod. Phys. 2010, 21, 1237–1254. [Google Scholar] [CrossRef]


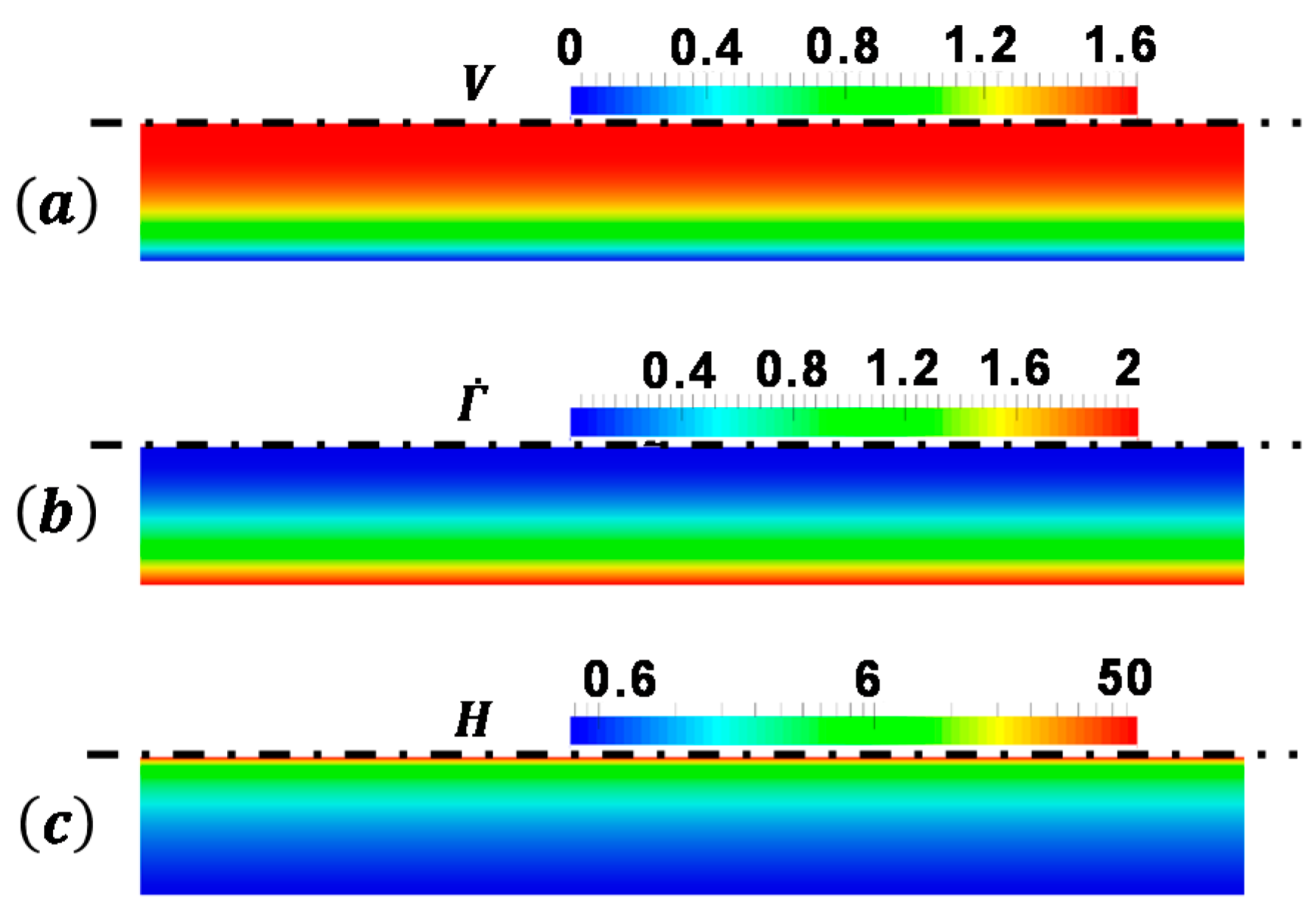



| Boundary Type | Straight Pipe | ||
| Pressure | Velocity | Temperature | |
| Wall | Zero gradient | Fixed value (0) | Fixed value |
| Inlet | Cyclic | Cyclic | Cyclic |
| Outlet | Cyclic | Cyclic | Cyclic |
| Boundary type | Tapered injector | ||
| Pressure | Velocity | Temperature | |
| Wall | Zero gradient | Fixed value (0) | Fixed value/gradient |
| Inlet | Zero gradient | Fixed value | Fixed value |
| Outlet | Fixed value (0) | Zero gradient | Zero gradient |
| Grid Number | Mean Apparent Viscosity (Pa·s) | |
|---|---|---|
| Grid A | 1750 | 1.026 |
| Grid B | 7000 | 1.049 |
| Grid C | 28,000 | 1.059 |
| Non-heated | Case a | Case b | Case c | All-heated | |
|---|---|---|---|---|---|
| 1.613 | 1.296 | 1.226 | 1.219 | 1.000 | |
| 0.978 | 0.950 | 0.973 | 1.035 | 1.000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.-L.; Wu, W.-T.; Liao, W.-H.; Feng, F.; Massoudi, M. Effects of Temperature on the Flow and Heat Transfer in Gel Fuels: A Numerical Study. Energies 2020, 13, 821. https://doi.org/10.3390/en13040821
Cao Q-L, Wu W-T, Liao W-H, Feng F, Massoudi M. Effects of Temperature on the Flow and Heat Transfer in Gel Fuels: A Numerical Study. Energies. 2020; 13(4):821. https://doi.org/10.3390/en13040821
Chicago/Turabian StyleCao, Qin-Liu, Wei-Tao Wu, Wen-He Liao, Feng Feng, and Mehrdad Massoudi. 2020. "Effects of Temperature on the Flow and Heat Transfer in Gel Fuels: A Numerical Study" Energies 13, no. 4: 821. https://doi.org/10.3390/en13040821
APA StyleCao, Q.-L., Wu, W.-T., Liao, W.-H., Feng, F., & Massoudi, M. (2020). Effects of Temperature on the Flow and Heat Transfer in Gel Fuels: A Numerical Study. Energies, 13(4), 821. https://doi.org/10.3390/en13040821








