Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra
Abstract
:1. Introduction
- (1)
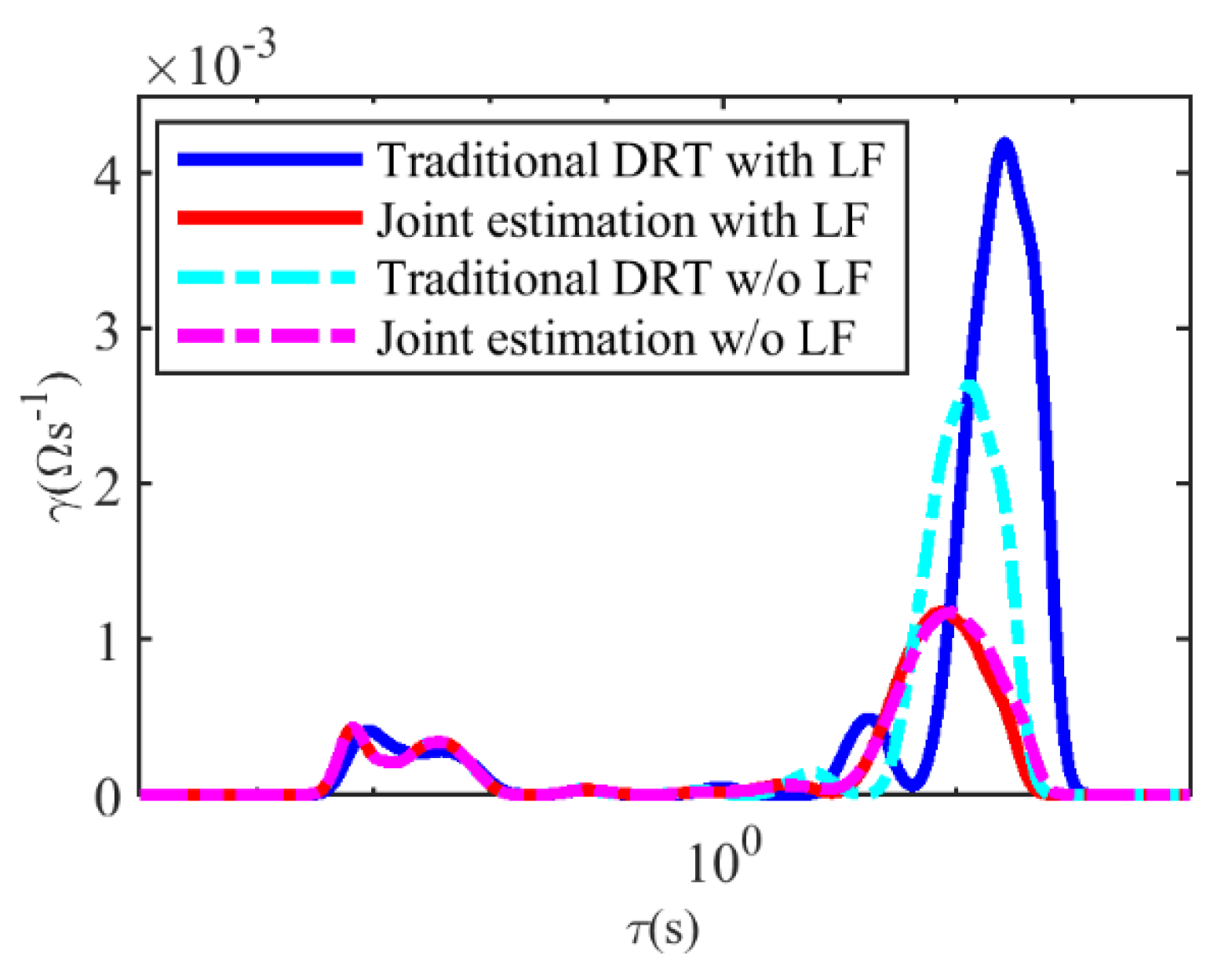
- A joint estimation method with Tikhonov regularization is proposed to simultaneously estimate the differential capacity and the DRT with the aim of minimizing the estimation errors and to obtain more information about the diffusion processes by EIS.
- (2)
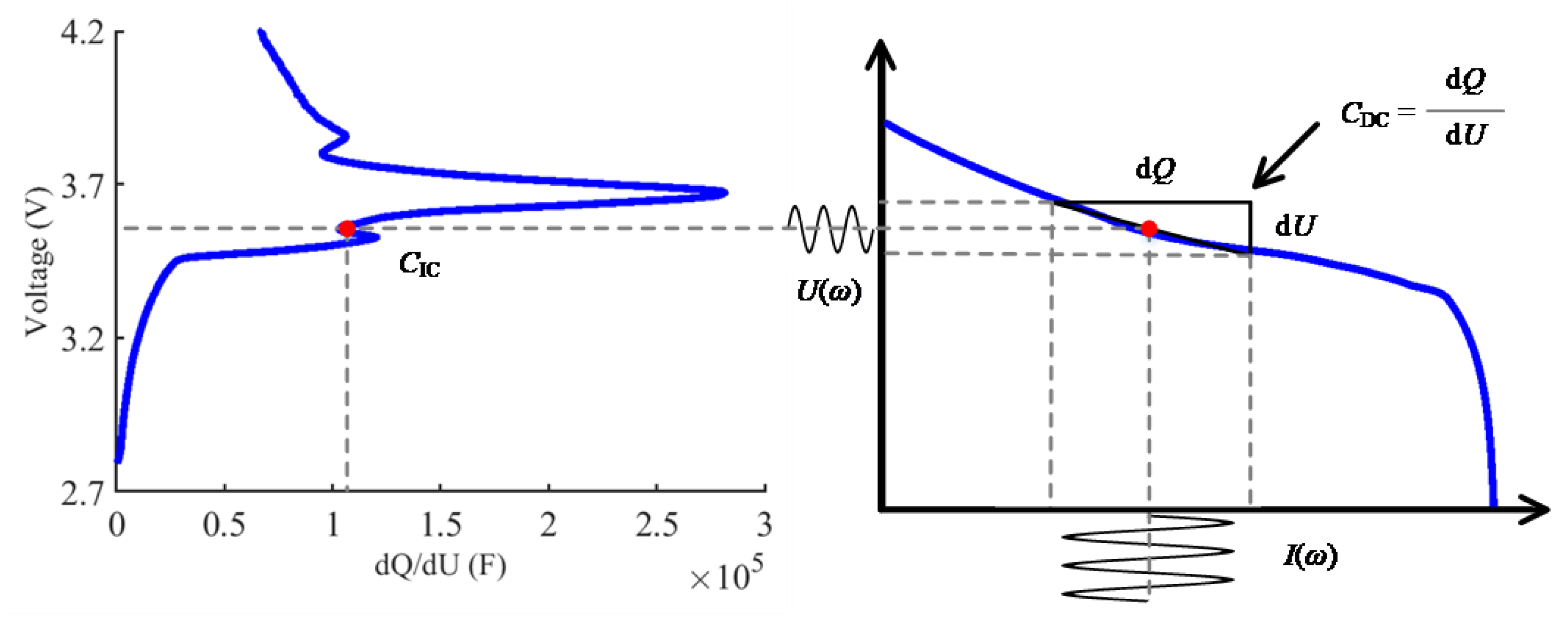
- Moreover, the equivalence of the differential capacity CDC and the incremental capacity CIC is proven in Section 2.
- (3)
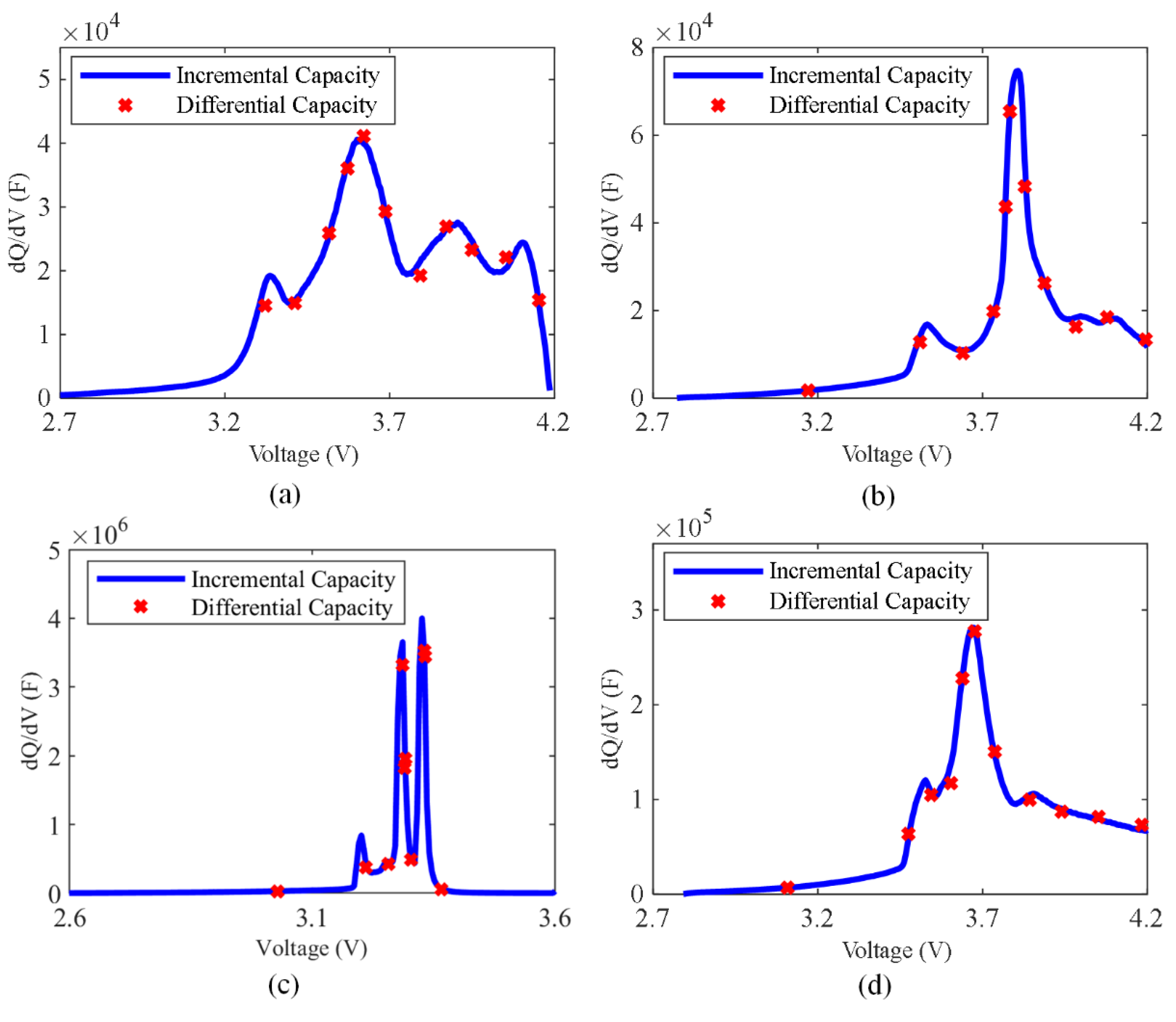
- Four types of commercial lithium-ion batteries are tested in Section 3 to validate the joint estimation method and to verify the equivalence of the CDC and CIC.
- (4)
- Subsequently, the estimation results of the DRT and the CDC are discussed in Section 4.
- (5)
- In addition, an efficient state-of-health (SOH) evaluation method is demonstrated based on the relationship between the CDC and the cell capacity in Section 4.
- (6)
- The conclusions of the work are summarized in Section 5.
2. Theoretical
2.1. The Relationship between EIS and ICA
2.2. The Joint Estimation Method with Tikhonov Regularization
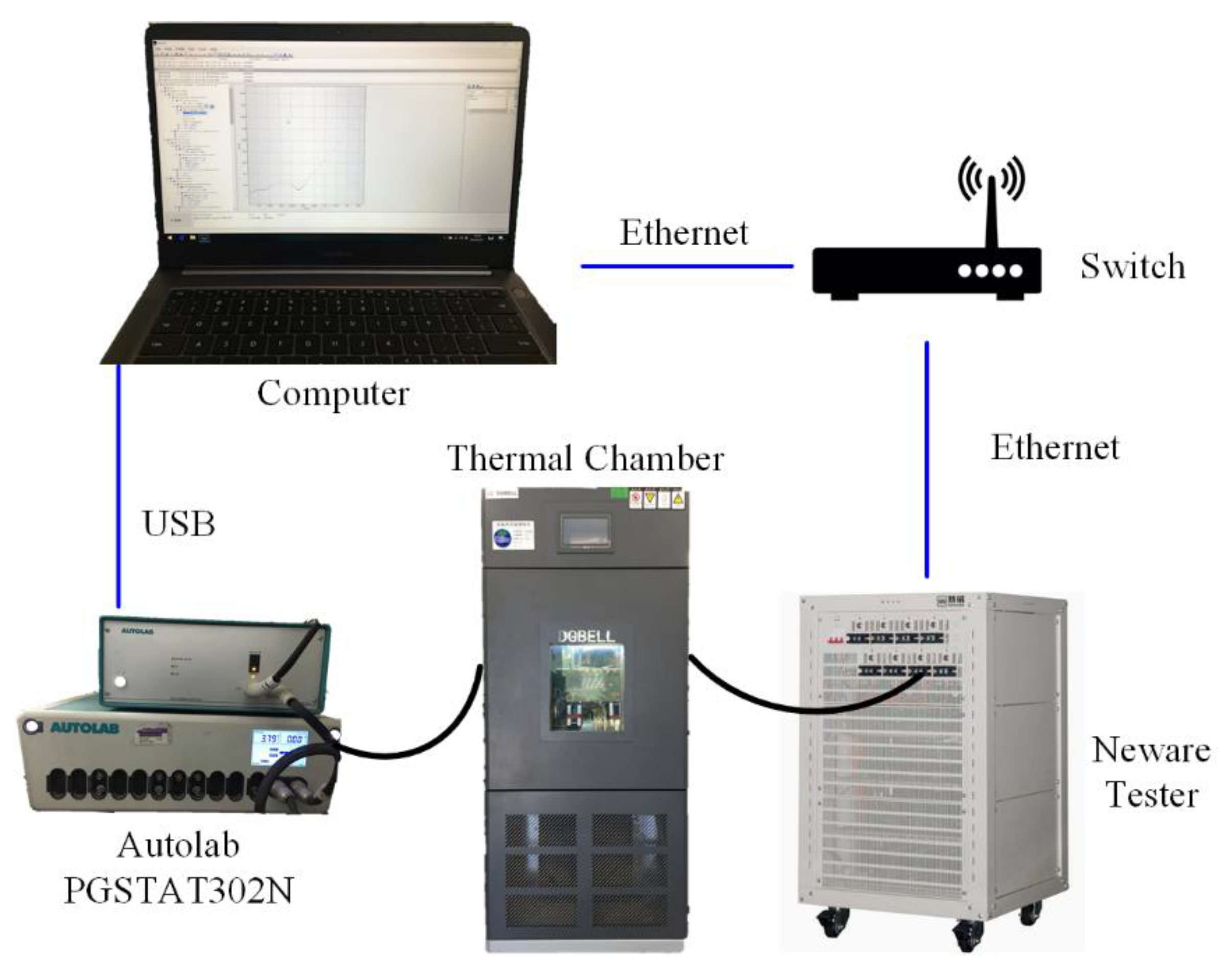
3. Experimental
3.1. The Test Conditions
3.2. The Test Profiles
3.3. Aging Characterization of the Cells
4. Results and Discussion
4.1. The Estimation Results of the DRT and the CDC
4.2. SOH Evaluation Based on the Relationship between the CDC and the Cell Capacity
5. Conclusions
- (1)
- A joint estimation method with Tikhonov regularization is proposed to simultaneously estimate the differential capacity CDC and the DRT with the aim of minimizing the estimation errors and to obtain more information about the diffusion processes by EIS.
- (2)
- The equivalence of the differential capacity CDC and the incremental capacity CIC was shown.
- (3)
- An efficient state-of-health (SOH) evaluation method is demonstrated based on the relationship between the CDC and the cell capacity.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A′ | approximation matrix of the DRT for the real part of the EIS |
| A″ | approximation matrix of the DRT for the imaginary part of the EIS |
| a, b | fitting coefficient of CDC and Q |
| CDC | differential capacity |
| CIC | incremental capacity |
| g | distribution of the polarization resistance |
| j | imaginary unit |
| J | modified Tikhonov regularization function |
| current response | |
| M | regularization matrix |
| Q | capacity of the cell |
| actual capacity of the present condition | |
| nominal capacity of the cell | |
| ohmic resistance | |
| polarization resistance | |
| voltage excitation | |
| x | vector of the parameter for DRT approximation |
| impedance model of the DRT | |
| DRT model considering differential capacity | |
| experimental data of the EIS | |
| real part of the experimental data | |
| imaginary part of the experimental data | |
| 1 | column vector with n entries all equal to 1 |
| λ | regularization coefficient |
| characteristic time constants | |
| angular frequency | |
| frequency matrix of the DRT |
Abbreviations
| DDC | distribution function of the differential capacity |
| DDT | distribution of the diffusion times |
| DIA | differential impedance analysis |
| DRT | distribution of the relaxation times |
| ECM | equivalent-circuit model |
| EIS | electrochemical impedance spectroscopy |
| FS | full-scale |
| ICA | incremental capacity analysis |
| LFP | LiFePO4 |
| LMO | LiMn2O4 |
| NCM | LiNixCoyMnzO2 |
| OCV | open-circuit voltage |
| probability density function | |
| PHM | prognostics and health management |
| RC | resistor-capacitor |
| SOC | state of charge |
| SOFC | solid oxide fuel cell |
| SOH | state-of-health |
Appendix A
References
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Walz, H.; Soczka-Guth, T.; Sauer, D. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. II: Modelling. J. Power Sources 2011, 196, 5349–5356. [Google Scholar] [CrossRef]
- Nara, H.; Mukoyama, D.; Shimizu, R.; Momma, T.; Osaka, T. Systematic analysis of interfacial resistance between the cathode layer and the current collector in lithium-ion batteries by electrochemical impedance spectroscopy. J. Power Sources 2019, 409, 139–147. [Google Scholar] [CrossRef]
- Gruet, D.; Delobel, B.; Sicsic, D.; Lucas, I.T.; Vivier, V. On the electrochemical impedance response of composite insertion electrodes–Toward a better understanding of porous electrodes. Electrochim. Acta 2019, 295, 787–800. [Google Scholar] [CrossRef]
- Li, W.; Huang, Q.-A.; Yang, C.; Chen, J.; Tang, Z.; Zhang, F.; Li, A.; Zhang, L.; Zhang, J. A fast measurement of Warburg-like impedance spectra with Morlet wavelet transform for electrochemical energy devices. Electrochim. Acta 2019, 322, 134760. [Google Scholar] [CrossRef]
- Rodríguez, A.; Plett, G.L.; Trimboli, M.S. Comparing four model-order reduction techniques, applied to lithium-ion battery-cell internal electrochemical transfer functions. eTransportation 2019, 1, 100009. [Google Scholar] [CrossRef]
- Schichlein, H.; Müller, A.C.; Voigts, M.; Krügel, A.; Ivers-Tiffée, E. Deconvolution of electrochemical impedance spectra for the identification of electrode reaction mechanisms in solid oxide fuel cells. J. Appl. Electrochem. 2002, 32, 875–882. [Google Scholar] [CrossRef]
- Klotz, D.; Schmidt, J.P.; Kromp, A.; Weber, A.; Ivers-Tiffée, E. The distribution of relaxation times as beneficial tool for equivalent circuit modeling of fuel cells and batteries. ECS Trans. 2012, 41, 25–33. [Google Scholar]
- Oz, A.; Hershkovitz, S.; Belman, N.; Tal-Gutelmacher, E.; Tsur, Y. Analysis of impedance spectroscopy of aqueous supercapacitors by evolutionary programming: Finding DFRT from complex capacitance. Solid State Ionics 2016, 288, 311–314. [Google Scholar] [CrossRef]
- Helseth, L. Modelling supercapacitors using a dynamic equivalent circuit with a distribution of relaxation times. J. Energy Storage 2019, 25, 100912. [Google Scholar] [CrossRef]
- Illig, J.; Ender, M.; Chrobak, T.; Schmidt, J.P.; Klotz, D.; Ivers-Tiffée, E. Separation of charge transfer and contact resistance in LiFePO4-cathodes by impedance modeling. J. Electrochem. Soc. 2012, 159, A952–A960. [Google Scholar] [CrossRef]
- Illig, J.; Schmidt, J.P.; Weiss, M.; Weber, A.; Ivers-Tiffée, E. Understanding the impedance spectrum of 18650 LiFePO4-cells. J. Power Sources 2013, 239, 670–679. [Google Scholar] [CrossRef]
- Sabet, P.S.; Sauer, D.U. Separation of predominant processes in electrochemical impedance spectra of lithium-ion batteries with nickelmanganesecobalt cathodes. J. Power Sources 2019, 425, 121–129. [Google Scholar] [CrossRef]
- Rahbari, O.; Omar, N.; Van Mierlo, J.; A Rosen, M.; Coosemans, T.; Berecibar, M. Electric Vehicle Battery Lifetime Extension through an Intelligent Double-Layer Control Scheme. Energies 2019, 12, 1525. [Google Scholar] [CrossRef] [Green Version]
- Waag, W.; Käbitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Spinner, N.S.; Love, C.T.; Rose-Pehrsson, S.L.; Tuttle, S.G. Expanding the operational limits of the single-point impedance diagnostic for internal temperature monitoring of lithium-ion batteries. Electrochim. Acta 2015, 174, 488–493. [Google Scholar] [CrossRef]
- Gordon, I.A.J.; Grugeon, S.; Takenouti, H.; Tribollet, B.; Armand, M.; Davoisne, C.; Débart, A.; Laruelle, S. Electrochemical Impedance Spectroscopy response study of a commercial graphite-based negative electrode for Li-ion batteries as function of the cell state of charge and ageing. Electrochim. Acta 2017, 223, 63–73. [Google Scholar] [CrossRef]
- Van Nguyen, D.; Limmer, S.; Yang, K.; Olhofer, M.; Bäck, T. Modeling and Prediction of Remaining Useful Lifetime for Maintenance Scheduling Optimization of a Car Fleet. Int. J. Perform. Eng. 2019, 15, 2318–2328. [Google Scholar]
- Limmer, S. Evaluation of Optimization-Based EV Charging Scheduling with Load Limit in a Realistic Scenario. Energies 2019, 12, 4730. [Google Scholar] [CrossRef] [Green Version]
- Schoenleber, M.; Ivers-Tiffée, E. Approximability of impedance spectra by RC elements and implications for impedance analysis. Electrochem. Commun. 2015, 58, 15–19. [Google Scholar] [CrossRef]
- Gantenbein, S.; Weiss, M.; Ivers-Tiffée, E. Impedance based time-domain modeling of lithium-ion batteries: Part I. J. Power Sources 2018, 379, 317–327. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Dai, H. Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge. J. Energy Storage 2019, 21, 618–631. [Google Scholar] [CrossRef]
- Collin, R.; Miao, Y.; Yokochi, A.; Enjeti, P.; von Jouanne, A. Advanced Electric Vehicle Fast-Charging Technologies. Energies 2019, 12, 1839. [Google Scholar] [CrossRef] [Green Version]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Sun, B.; Bian, J.; Ruan, H.; Zhang, W.; Ren, P.; Cong, X. Modeling Study for Li-ion Batteries Considering High-frequency Inductance Characteristics Based on Electrochemical Impedance Spectroscopy. DEStech Trans. Environ. Energy Earth Sci. 2018. [Google Scholar] [CrossRef]
- Cheng, C.-S.; Chung, H.S.-H.; Lau, R.W.-H.; Hong, K.Y.-W. Experimental Assessment and Stability Analysis of a Discrete-Time Battery Model with Multiple Constant Phase Elements. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1090–1097. [Google Scholar]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L. Lithium-ion battery fast charging: A review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Chrobak, T.; Ender, M.; Illig, J.; Klotz, D.; Ivers-Tiffée, E. Studies on LiFePO4 as cathode material using impedance spectroscopy. J. Power Sources 2011, 196, 5342–5348. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the discretization methods on the distribution of relaxation times deconvolution: Implementing radial basis functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Sabet, P.S.; Stahl, G.; Sauer, D.U. Non-invasive investigation of predominant processes in the impedance spectra of high energy lithium-ion batteries with Nickel-Cobalt-Aluminum cathodes. J. Power Sources 2018, 406, 185–193. [Google Scholar] [CrossRef]
- Zhou, X.; Pan, Z.; Han, X.; Lu, L.; Ouyang, M. An easy-to-implement multi-point impedance technique for monitoring aging of lithium ion batteries. J. Power Sources 2018, 417, 188–192. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, J.; Pan, Z.; Ouyang, M. Impedance characterization of lithium-ion batteries aging under high-temperature cycling: Importance of electrolyte-phase diffusion. J. Power Sources 2019, 426, 216–222. [Google Scholar] [CrossRef]
- Boukamp, B.A. Derivation of a Distribution Function of Relaxation Times for the (fractal) Finite Length Warburg. Electrochim. Acta 2017, 252, 154–163. [Google Scholar] [CrossRef]
- Malkow, K.T. A theory of distribution functions of relaxation times for the deconvolution of immittance data. J. Electroanal. Chem. 2019, 838, 221–231. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Berg, P.; Schönleber, M.; Weber, A.; Ivers-Tiffée, E. The distribution of relaxation times as basis for generalized time-domain models for Li-ion batteries. J. Power Sources 2013, 221, 70–77. [Google Scholar] [CrossRef]
- Schichlein, H.; Feuerstein, M.; Müller, A.; Weber, A.; Krügel, A.; Ivers-Tiffée, E. System identification: A new modelling approach for SOFC single cells. ECS Proc. Vol. 1999, 1999, 1069–1077. [Google Scholar] [CrossRef]
- Oldenburger, M.; Bedürftig, B.; Gruhle, A.; Grimsmann, F.; Richter, E.; Findeisen, R.; Hintennach, A. Investigation of the low frequency Warburg impedance of Li-ion cells by frequency domain measurements. J. Energy Storage 2019, 21, 272–280. [Google Scholar] [CrossRef]
- Ciucci, F. Modeling Electrochemical Impedance Spectroscopy. Curr. Opin. Electrochem. 2018, 13, 132–139. [Google Scholar] [CrossRef]
- Schönleber, M.; Ivers-Tiffée, E. The Distribution Function of Differential Capacity as a new tool for analyzing the capacitive properties of Lithium-Ion batteries. Electrochem. Commun. 2015, 61, 45–48. [Google Scholar] [CrossRef]
- Song, J.; Bazant, M.Z. Electrochemical impedance imaging via the distribution of diffusion times. Phys. Rev. Lett. 2018, 120, 116001. [Google Scholar] [CrossRef] [Green Version]
- Vladikova, D.; Stoynov, Z. Secondary differential impedance analysis–a tool for recognition of CPE behavior. J. Electroanal. Chem. 2004, 572, 377–387. [Google Scholar] [CrossRef]
- Vladikova, D.; Kilner, J.; Skinner, S.; Raikova, G.; Stoynov, Z. Differential impedance analysis of single crystal and polycrystalline yttria stabilized zirconia. Electrochim. Acta 2006, 51, 1611–1621. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Incremental capacity analysis and close-to-equilibrium OCV measurements to quantify capacity fade in commercial rechargeable lithium batteries. Electrochem. solid. State. Lett. 2006, 9, A454–A457. [Google Scholar] [CrossRef]
- Feng, X.; Li, J.; Ouyang, M.; Lu, L.; Li, J.; He, X. Using probability density function to evaluate the state of health of lithium-ion batteries. J. Power Sources 2013, 232, 209–218. [Google Scholar] [CrossRef]
- Saccoccio, M.; Wan, T.H.; Chen, C.; Ciucci, F. Optimal regularization in distribution of relaxation times applied to electrochemical impedance spectroscopy: Ridge and Lasso regression methods-A theoretical and experimental Study. Electrochim. Acta 2014, 147, 470–482. [Google Scholar] [CrossRef]
- Ciucci, F.; Chen, C. Analysis of electrochemical impedance spectroscopy data using the distribution of relaxation times: A Bayesian and hierarchical Bayesian approach. Electrochim. Acta 2015, 167, 439–454. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W. A review on state of health estimation for lithium ion batteries in photovoltaic systems. eTransportation 2019, 2, 100028. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Qu, X.; Pecht, M. Aging characteristics-based health diagnosis and remaining useful life prognostics for lithium-ion batteries. eTransportation 2019, 1, 100004. [Google Scholar] [CrossRef]
- Ren, D.; Hsu, H.; Li, R.; Feng, X.; Guo, D.; Han, X.; Lu, L.; He, X.; Gao, S.; Hou, J.; et al. A comparative investigation of aging effects on thermal runaway behavior of lithium-ion batteries. eTransportation 2019, 2, 100034. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Park, G.-S.; Kim, H.-J. Online Remaining Useful Life Prediction for Lithium-Ion Batteries Using Partial Discharge Data Features. Energies 2019, 12, 4366. [Google Scholar] [CrossRef] [Green Version]


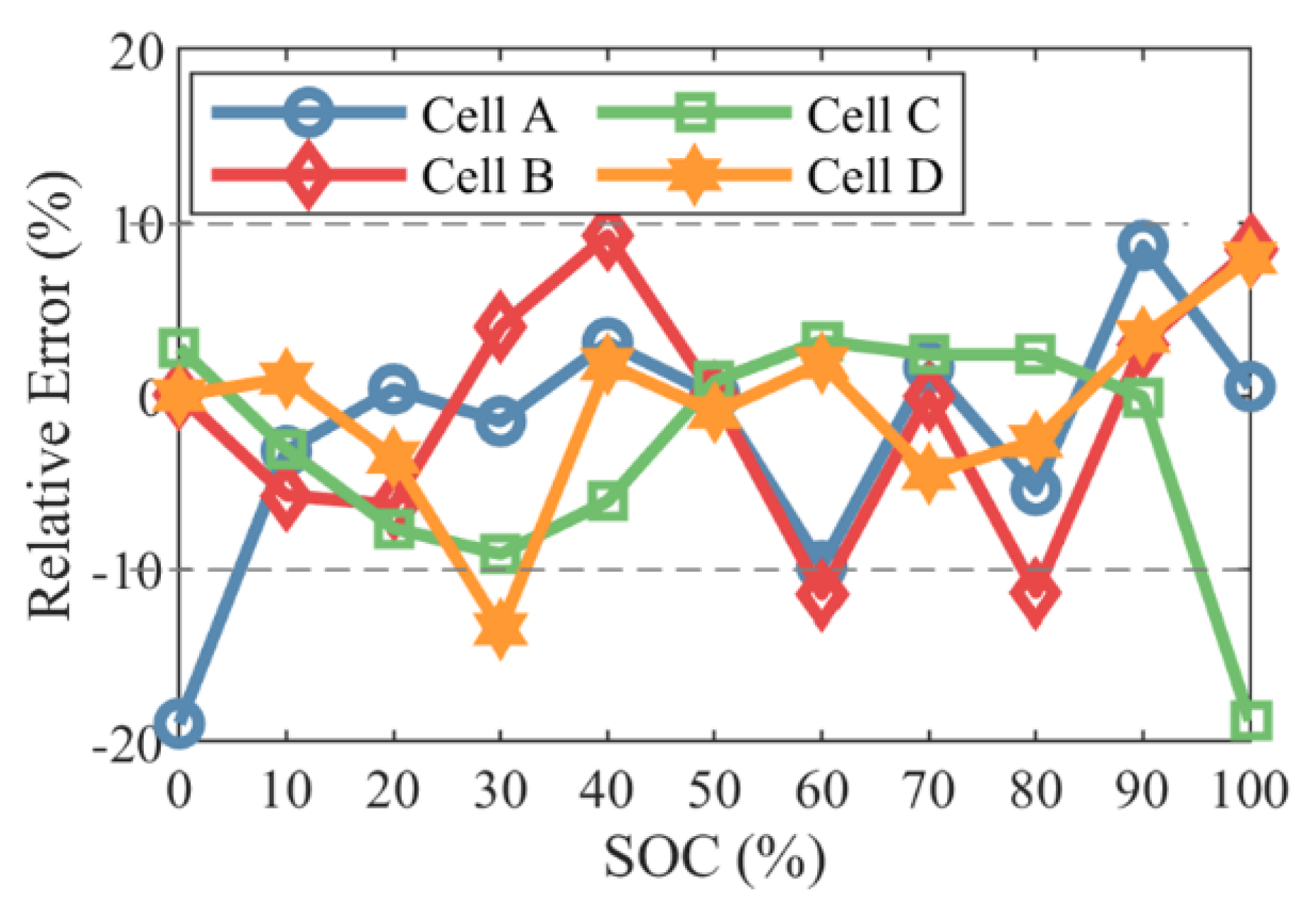

| Battery | Cathode | Anode | Capacity (Ah) | Voltage Range (V) |
|---|---|---|---|---|
| A | NCM | G | 3.2 | 2.5–4.2 |
| B | NCM | G | 4.8 | 2.5–4.2 |
| C | LFP | G | 20 | 2.0–3.65 |
| D | NCM + LMO | G | 24 | 2.5–4.2 |
| Step No. | Step Name | Duration | Current | Cycle No. |
|---|---|---|---|---|
| 1 | Rest | 180 min | ||
| 2 | EIS test | |||
| 3 | Discharge | 18 min | 1/3 C | |
| 4 | Cycle, step 1–3 | 10 | ||
| 5 | Rest | 180 min | ||
| 6 | EIS test | |||
| 7 | End | |||
| Step No. | Step Name | Duration | Current | Condition |
|---|---|---|---|---|
| 1 | Rest | 180 min | ||
| 2 | Discharge | I = 1/20 C | V = upper limit | |
| 3 | Rest | 180 min | ||
| 4 | Charge | I = 1/20 C | V = lower limit | |
| 5 | End |
| Cell Number | D1 | D2 | D3 | D4 | D5 | D6 | D7 |
|---|---|---|---|---|---|---|---|
| Capacity (Ah) | 24.2 | 22.6 | 22.0 | 21.1 | 20.1 | 19.3 | 15.5 |
| SOH (%) | 100 | 93.4 | 90.6 | 87.2 | 82.8 | 79.5 | 63.9 |
| Step No. | Step Name | Duration | Current |
|---|---|---|---|
| 1 | Rest | 180 min | |
| 2 | Discharge | I = 1/3 C | |
| 3 | Rest | 180 min | |
| 4 | Charge to 3.68 V | I = 1/20 C | |
| 5 | Rest | 180 min | |
| 6 | EIS test | ||
| 7 | End |
| Cell Number | D1 | D2 | D3 | D4 | D5 | D6 | D7 |
|---|---|---|---|---|---|---|---|
| CDC (105 F) | 1.80 | 1.33 | 1.12 | 0.928 | 0.857 | 0.785 | 0.673 |
| Fitting Coefficient | a1 | a2 | b1 | b2 |
|---|---|---|---|---|
| Value | 18.86 | −2550 | 1.386 × 10−6 | −9.197 × 10−5 |
| Cell Number | D1 | D2 | D3 | D4 | D5 | D6 | D7 |
|---|---|---|---|---|---|---|---|
| Real SOH (%) | 100 | 93.4 | 90.6 | 87.2 | 82.8 | 79.5 | 63.9 |
| Estimated SOH (%) | 100 | 93.6 | 90.7 | 86.5 | 83.8 | 79.1 | 64.0 |
| Relative error (%) | 0 | 0.23 | 0.02 | 0.80 | −1.13 | −0.51 | 0.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Yang, G.; Zhao, G.; Yi, M.; Feng, X.; Han, X.; Lu, L.; Ouyang, M. Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra. Energies 2020, 13, 915. https://doi.org/10.3390/en13040915
Guo D, Yang G, Zhao G, Yi M, Feng X, Han X, Lu L, Ouyang M. Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra. Energies. 2020; 13(4):915. https://doi.org/10.3390/en13040915
Chicago/Turabian StyleGuo, Dongxu, Geng Yang, Guangjin Zhao, Mengchao Yi, Xuning Feng, Xuebing Han, Languang Lu, and Minggao Ouyang. 2020. "Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra" Energies 13, no. 4: 915. https://doi.org/10.3390/en13040915
APA StyleGuo, D., Yang, G., Zhao, G., Yi, M., Feng, X., Han, X., Lu, L., & Ouyang, M. (2020). Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra. Energies, 13(4), 915. https://doi.org/10.3390/en13040915






